The Impact of SAR Parameter Errors on the Ionospheric Correction Based on the Range-Doppler Model and the Split-Spectrum Method
Abstract
:1. Introduction
2. Methods
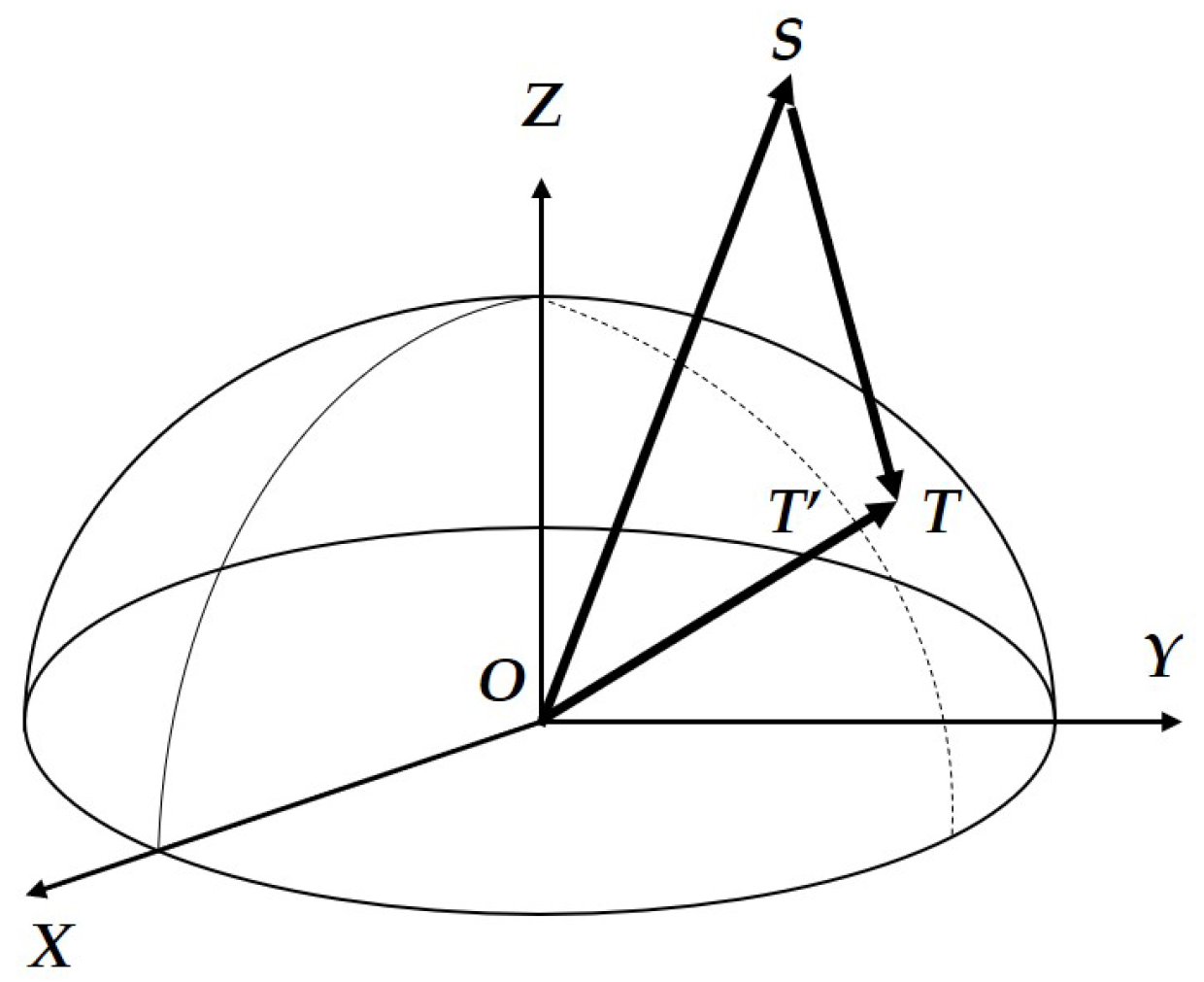
2.1. Impact of SAR Parameter Errors on the Geolocation Model
2.1.1. Orbit Vectors
2.1.2. Slant Range
2.1.3. Target Height
2.2. Impact of Geolocation Accuracy on the Ionospheric Phase
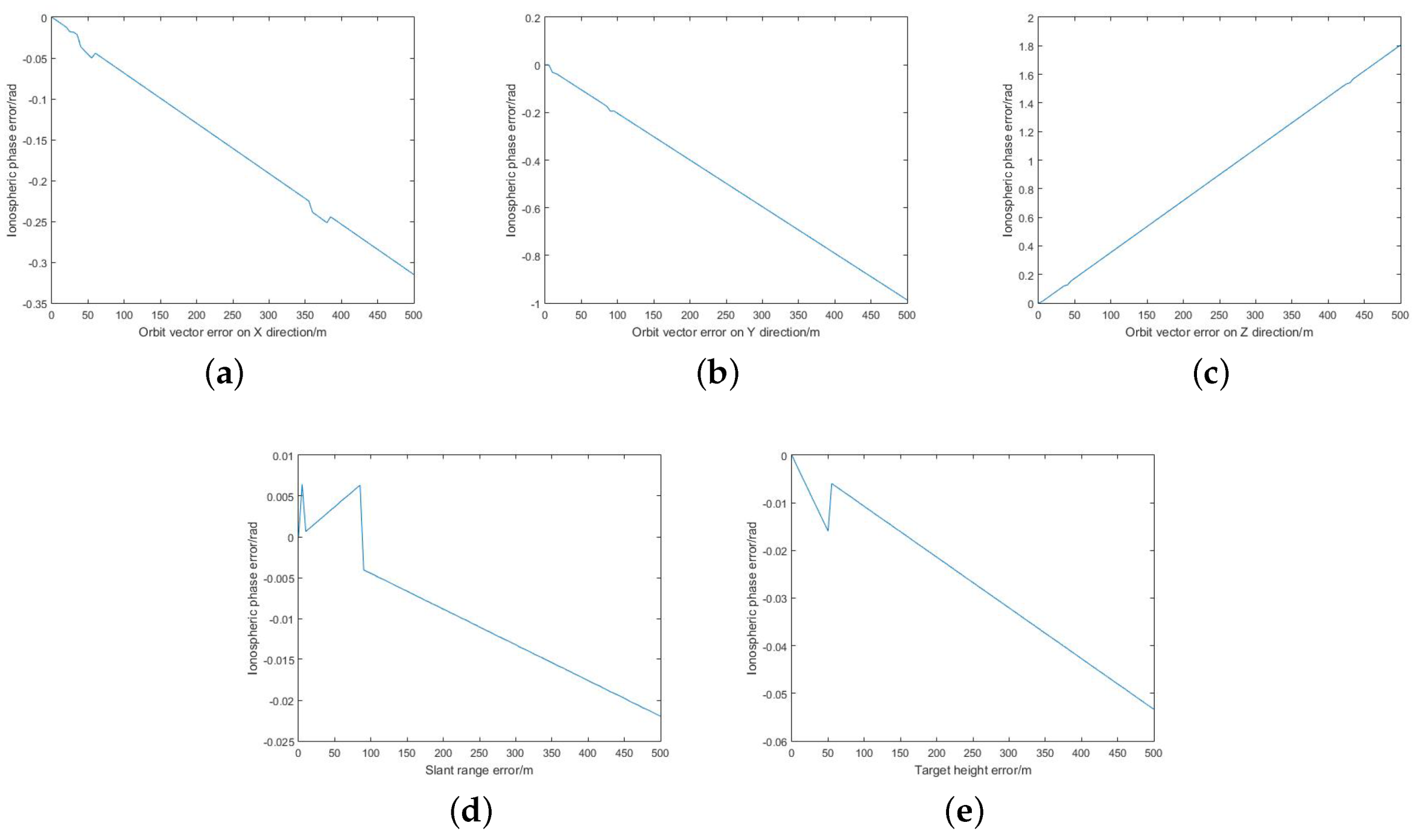
2.3. Impact of SAR Parameter Errors on the Ionospheric Phase
2.3.1. Orbit Vectors from Master SLC Parameter File
2.3.2. Master Slant Range
2.3.3. Target Height
3. Numerical Simulation
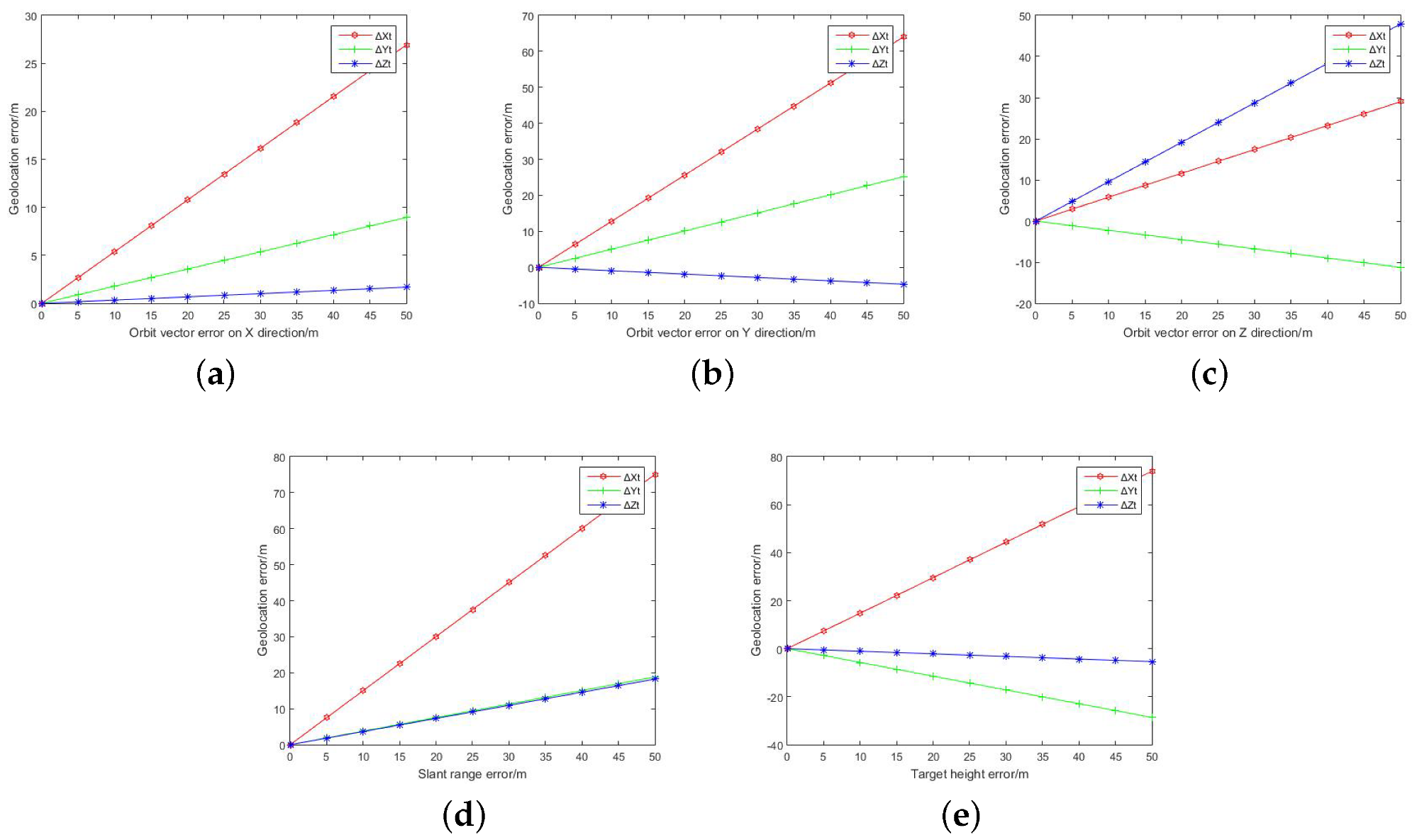
3.1. Impact of SAR Parameter Errors on the Geolocation Model
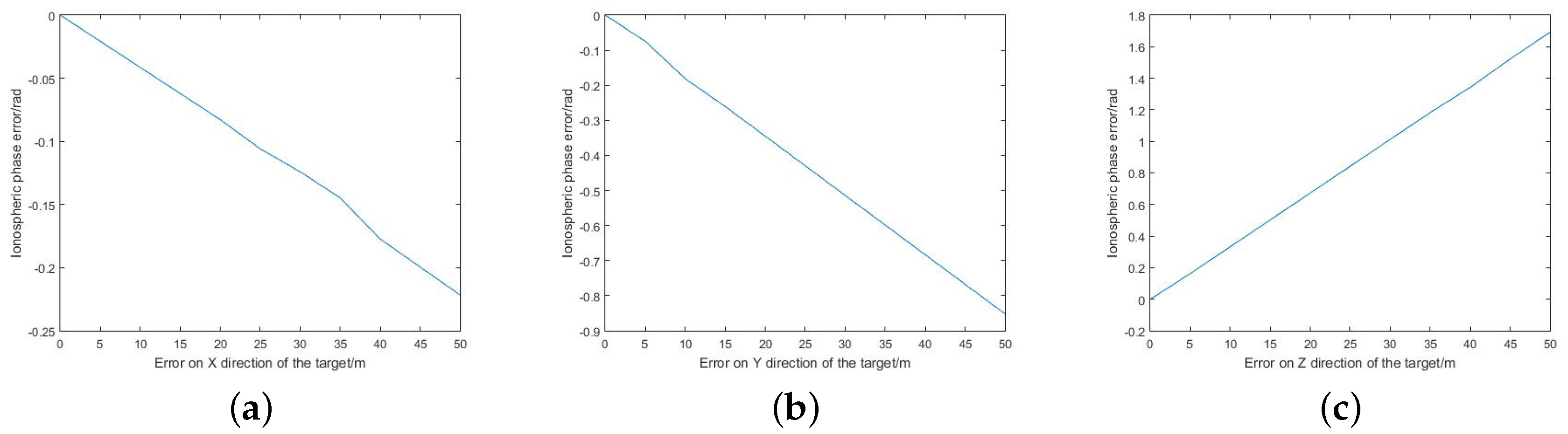
3.2. Impact of Geolocation Accuracy on the Ionospheric Phase
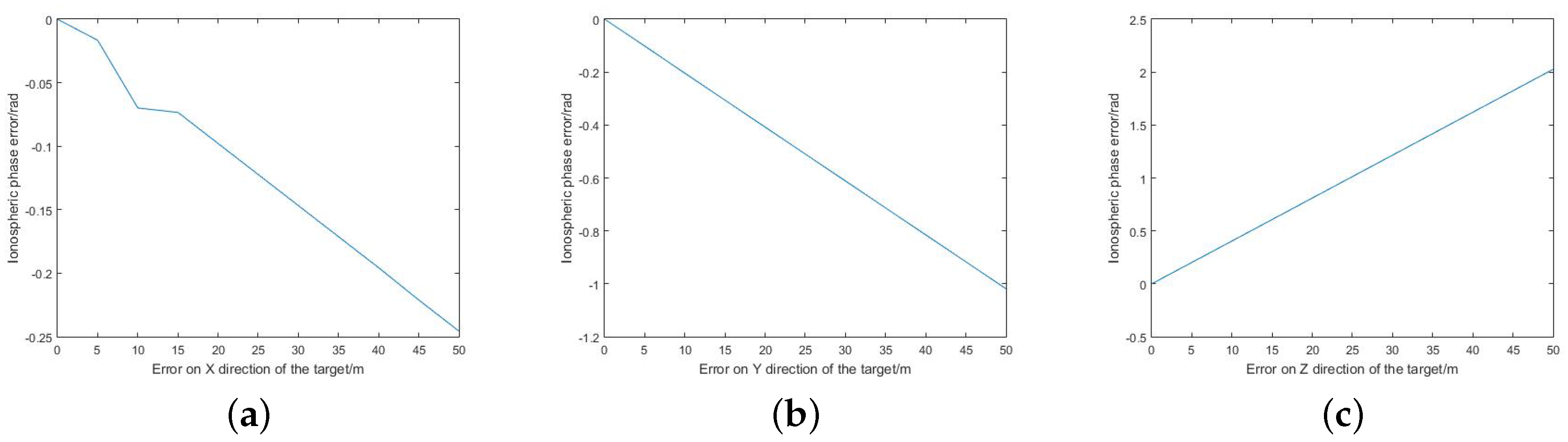
3.3. Impact of SAR Parameter Errors on the Ionospheric Phase
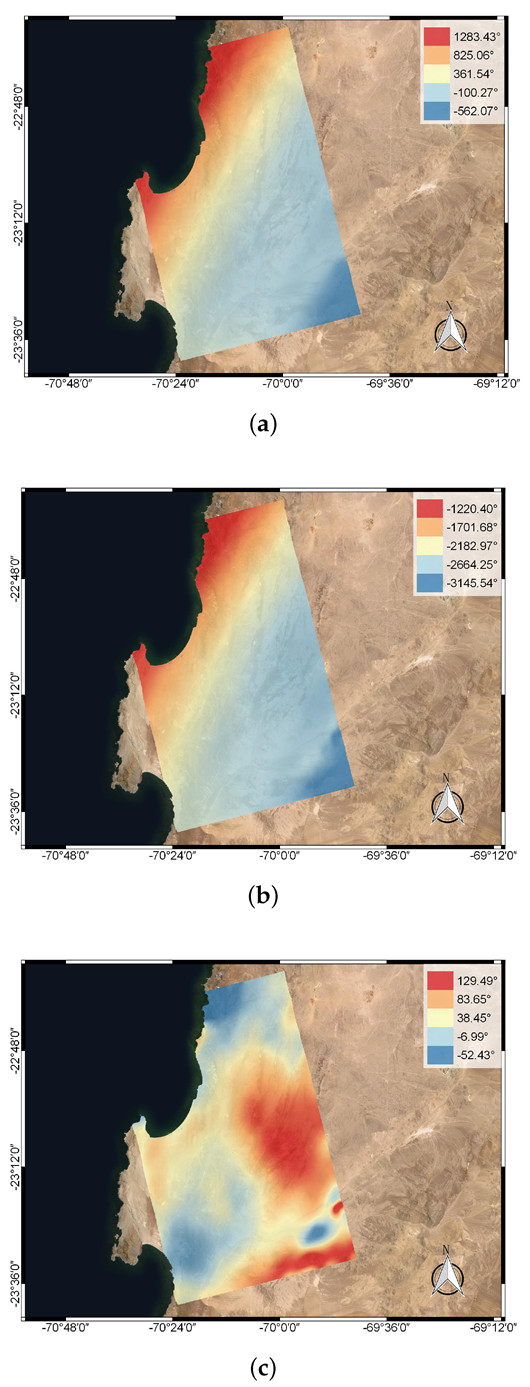
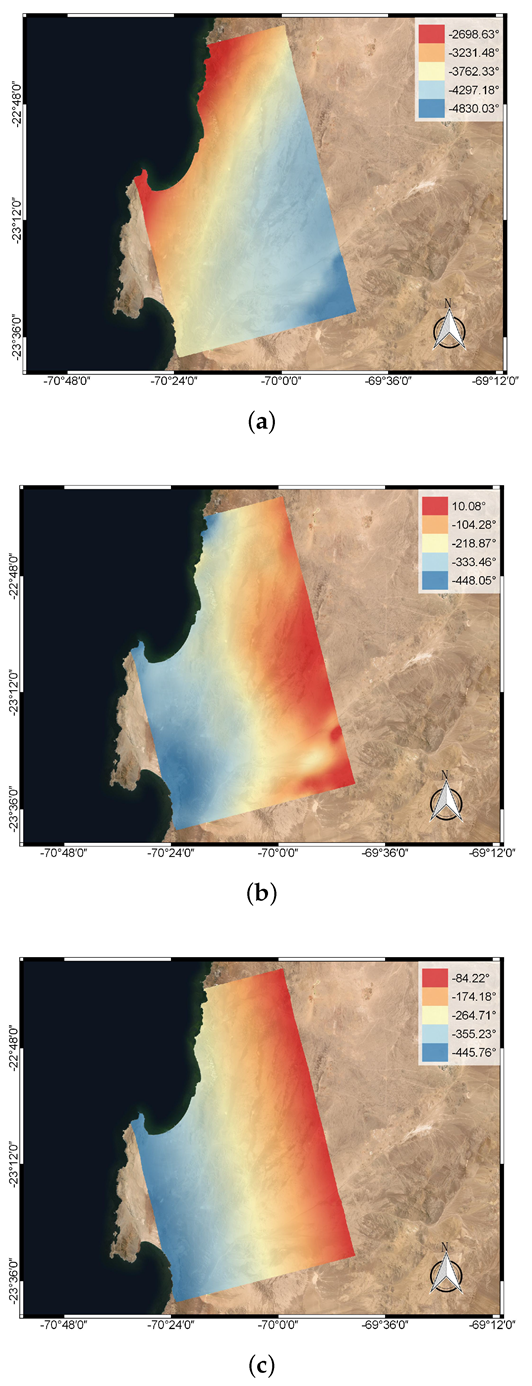
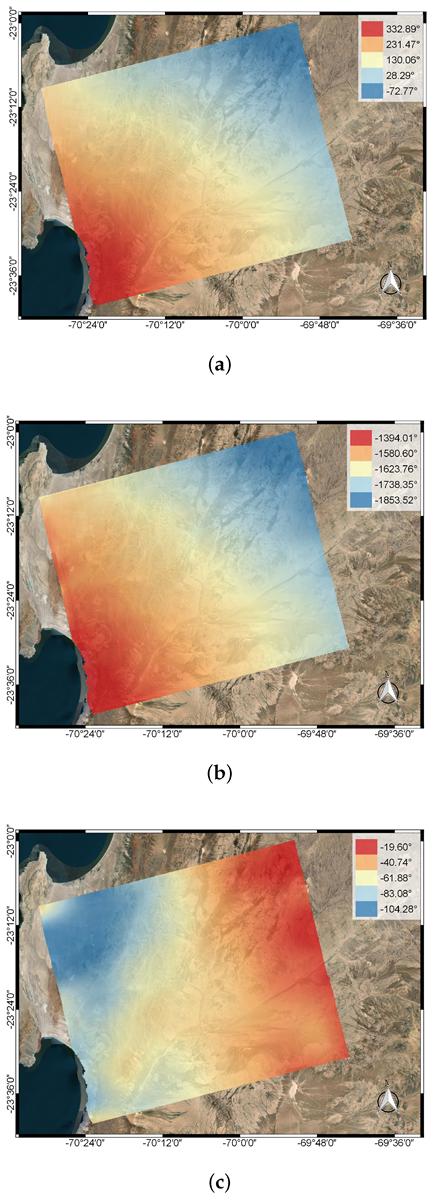
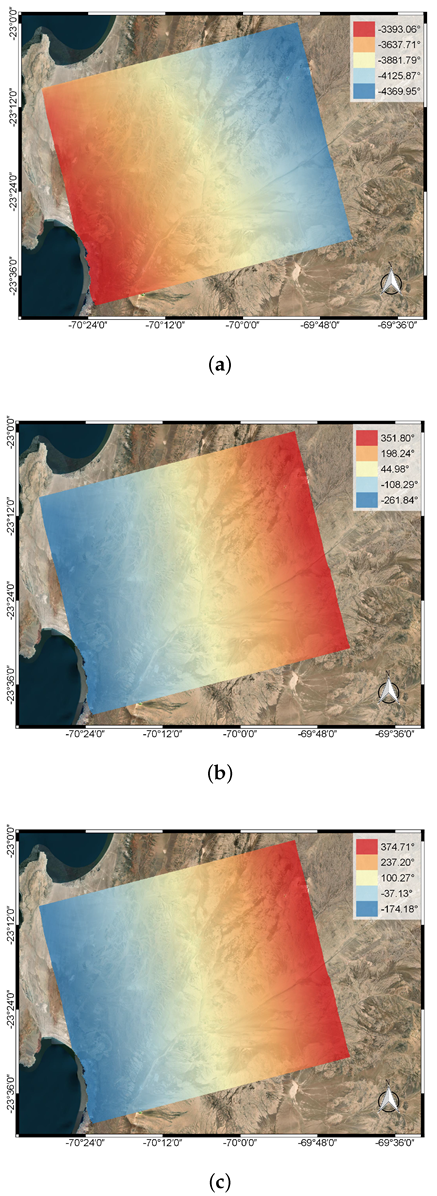
4. Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bamler, R.; Hartl, P. Synthetic aperture radar interferometry. Inverse Probl. 1998, 14, R1–R54. [Google Scholar] [CrossRef]
- Amelung, F.; Yun, S.H.; Walter, T.R.; Segall, P.; Kim, S.W. Stress control of deep rift intrusion at Mauna Loa volcano, Hawaii. Science 2007, 316, 1026–1030. [Google Scholar] [CrossRef] [PubMed]
- Hooper, A.; Bekaert, D.; Spaans, K.; Arikan, M. Recent advances in SAR interferometry time series analysis for measuring crustal deformation. Tectonophysics 2012, 514, 1–13. [Google Scholar] [CrossRef]
- Lu, Z.; Kwoun, O.; Rykhus, R. Interferometric synthetic aperture radar (InSAR): Its past, present and future. Photogramm. Eng. Remote Sens. 2007, 73, 217–221. [Google Scholar]
- Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef] [Green Version]
- Baer, G.; Magen, Y.; Nof, R.N.; Raz, E.; Lyakhovsky, V.; Shalev, E. InSAR Measurements and Viscoelastic Modeling of Sinkhole Precursory Subsidence: Implications for Sinkhole Formation, Early Warning, and Sediment Properties. J. Geophys. Res.-Earth Surf. 2018, 123, 678–693. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef] [Green Version]
- Lv, X.; Yazici, B.; Zeghal, M.; Bennett, V.; Abdoun, T. Joint-Scatterer Processing for Time-Series InSAR. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7205–7221. [Google Scholar] [CrossRef]
- Yun, Y.; Lv, X.; Fu, X.; Xue, F. Application of Spaceborne Interferometric Synthetic Aperture Radar to Geohazard Monitoring. J. Radars 2020, 9, 73–85. [Google Scholar]
- Bekaert, D.P.S.; Hooper, A.; Wright, T.J. A spatially variable power law tropospheric correction technique for InSAR data. J. Geophys. Res.-Solid Earth 2015, 120, 1345–1356. [Google Scholar] [CrossRef]
- Bekaert, D.P.S.; Walters, R.J.; Wright, T.J.; Hooper, A.J.; Parker, D.J. Statistical comparison of InSAR tropospheric correction techniques. Remote Sens. Environ. 2015, 170, 40–47. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.W.; Ding, X.L.; Liu, G. Modeling atmospheric effects on InSAR with meteorological and continuous GPS observations: Algorithms and some test results. J. Atmos. Solar-Terr. Phys. 2004, 66, 907–917. [Google Scholar] [CrossRef]
- Webley, P.W.; Bingley, R.M.; Dodson, A.H.; Wadge, G.; Waugh, S.J.; James, I.N. Atmospheric water vapour correction to InSAR surface motion measurements on mountains: Results from a dense GPS network on Mount Etna. Phys. Chem. Earth 2002, 27, 363–370. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T. Interferometric synthetic aperture radar atmospheric correction using a GPS-based iterative tropospheric decomposition model. Remote Sens. Environ. 2018, 204, 109–121. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T.; Crippa, P. Generic Atmospheric Correction Model for Interferometric Synthetic Aperture Radar Observations. J. Geophys. Res.-Solid Earth 2018, 123, 9202–9222. [Google Scholar] [CrossRef]
- Foster, J.; Brooks, B.; Cherubini, T.; Shacat, C.; Businger, S.; Werner, C.L. Mitigating atmospheric noise for InSAR using a high resolution weather model. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Jolivet, R.; Agram, P.S.; Lin, N.Y.; Simons, M.; Doin, M.P.; Peltzer, G.; Li, Z. Improving InSAR geodesy using Global Atmospheric Models. J. Geophys. Res.-Solid Earth 2014, 119, 2324–2341. [Google Scholar] [CrossRef]
- Jolivet, R.; Grandin, R.; Lasserre, C.; Doin, M.P.; Peltzer, G. Systematic InSAR tropospheric phase delay corrections from global meteorological reanalysis data. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef] [Green Version]
- Shimada, M. Correction of the satellite’s state vector and the atmospheric excess path delay in SAR interferometry—Application to surface deformation detection. In Proceedings of the IEEE 2000 International Geoscience and Remote Sensing Symposium, Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment, Honolulu, HI, USA, 24–28 July 2000; pp. 2236–2238. [Google Scholar]
- Shimada, M.; Minamisawa, M.; Isoguchi, O.; Ieee, I. Correction of atmospheric excess path delay appeared in repeat-pass SAR interferometry using objective analysis data. In Proceedings of the IGARSS 2001, Scanning the Present and Resolving the Future, IEEE 2001 International Geoscience and Remote Sensing Symposium (Cat. No.01CH37217), Sydney, NSW, Australia, 9–13 July 2001; pp. 2052–2054. [Google Scholar]
- Gray, A.L.; Mattar, K.E.; Sofko, G. Influence of ionospheric electron density fluctuations on satellite radar interferometry. Geophys. Res. Lett. 2000, 27, 1451–1454. [Google Scholar] [CrossRef]
- Mattar, K.E.; Gray, A.L. Reducing ionospheric electron density errors in satellite radar interferometry applications. Can. J. Remote Sens. 2002, 28, 593–600. [Google Scholar] [CrossRef]
- Rignot, E.J.M. Effect of Faraday rotation on L-band interferometric and polarimetric synthetic-aperture radar data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 383–390. [Google Scholar] [CrossRef] [Green Version]
- Rosen, P.A.; Hensley, S.; Chen, C. Measurement and Mitigation of the Ionosphere in L-band Interferometric SAR Data. In Proceedings of the 2010 Ieee Radar Conference, Washington, DC, USA, 10–14 May 2010; pp. 1459–1463. [Google Scholar] [CrossRef]
- Brcic, R.; Parizzi, A.; Eineder, M.; Bamler, R.; Meyer, F. Estimation and compensation of ionospheric delay for sar interferometry. In Proceedings of the 2010 Ieee International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 2908–2911. [Google Scholar] [CrossRef]
- Gomba, G.; Gonzalez, F.R.; De Zan, F. Ionospheric Phase Screen Compensation for the Sentinel-1 TOPS and ALOS-2 ScanSAR Modes. IEEE Trans. Geosci. Remote Sens. 2017, 55, 223–235. [Google Scholar] [CrossRef]
- Gomba, G.; Parizzi, A.; De Zan, F.; Eineder, M.; Bamler, R. Toward Operational Compensation of Ionospheric Effects in SAR Interferograms: The Split-Spectrum Method. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1446–1461. [Google Scholar] [CrossRef] [Green Version]
- Schubert, A.; Small, D.; Miranda, N.; Geudtner, D.; Meier, E. Sentinel-1A Product Geolocation Accuracy: Commissioning Phase Results. Remote Sens. 2015, 7, 9431–9449. [Google Scholar] [CrossRef] [Green Version]
- Dong, X.T.; Zhao, Y.H.; Yue, X.J.; Han, C.M. An Accurate Co-registration Method for Airborne Repeatpass InSAR. In Proceedings of the 2017 International Conference on Sustainable Development on Energy and Environment Protection, Yichang, China, 28–30 July 2017; Volume 86. [Google Scholar] [CrossRef] [Green Version]
- Johnsen, H.; Lauknes, L.; Guneriussen, T. Geocoding of fast-delivery ers-1 sar image mode product using dem data. Int. J. Remote Sens. 1995, 16, 1957–1968. [Google Scholar] [CrossRef]
- Liu, X.; Ma, H.; Sun, W. Study on the geolocation algorithm of space-borne SAR image. In Advances in Machine Vision, Image Processing, and Pattern Analysis; Zheng, N., Jiang, X., lan, X., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4153, pp. 270–280. [Google Scholar]
- Fattahi, H.; Amelung, F. InSAR uncertainty due to orbital errors. Geophys. J. Int. 2014, 199, 549–560. [Google Scholar] [CrossRef] [Green Version]
- Baehr, H.; Hanssen, R.F. Reliable estimation of orbit errors in spaceborne SAR interferometry The network approach. J. Geod. 2012, 86, 1147–1164. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Wan, L.; Lyu, X.; Hong, J. Baseline analysis and control of spaceborne repeat-pass InSAR based on relative orbital elements. J. Remote Sens. 2019, 23, 1123–1131. [Google Scholar]
- Ding, C.; Liu, J.; Lei, B.; Qiu, X. Preliminary Exploration of Systematic Geolocation Accuracy of GF-3 SAR Satellite System. J. Radars 2017, 6, 11–16. [Google Scholar]
- Cheng, C.; Zhang, J.; Huang, G.; Zhang, L. Range-Cocone equation with Doppler parameter for SAR imagery positioning. J. Remote Sens. 2013, 17, 1444–1458. [Google Scholar]
- Fattahi, H.; Simons, M.; Agram, P. InSAR Time-Series Estimation of the Ionospheric Phase Delay: An Extension of the Split Range-Spectrum Technique. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5984–5996. [Google Scholar] [CrossRef]
- Chen, E.; Li, Z. The algorithm for direct geo location of space-borne SAR imagery based on slant angle coordinate transformation. High Technol. Lett. 2006, 16, 1082–1086. [Google Scholar]
- Kang, Y. Study on the Influence of Spaceborne SAR Orbital Data on Image Geolocation. Master’s Thesis, Liaoning Technical University, Fuxin, China, 2015. [Google Scholar]
- Meyer, F.; Bamler, R.; Jakowski, N.; Fritz, T. The potential of low-frequency SAR systems for mapping ionospheric TEC distributions. IEEE Geosci. Remote Sens. Lett. 2006, 3, 560–564. [Google Scholar] [CrossRef]
- Milczarek, W.; Kopec, A.; Glabicki, D. Estimation of Tropospheric and Ionospheric Delay in DInSAR Calculations: Case Study of Areas Showing (Natural and Induced) Seismic Activity. Remote Sens. 2019, 11, 621. [Google Scholar] [CrossRef] [Green Version]







| SAR Parameters | Derivate of | Derivate of | Derivate of |
|---|---|---|---|
| 0.5384 | 0.1789 | 0.0338 | |
| 1.2801 | 0.5040 | −0.0936 | |
| 0.5803 | −0.2248 | 0.9576 | |
| R | 1.5015 | 0.3768 | 0.3633 |
| h | 1.4793 | −0.5732 | −0.1082 |
| SAR Parameters | Derivate of | Derivate of | Derivate of |
|---|---|---|---|
| 0.5376 | 0.1785 | 0.0349 | |
| 1.2777 | 0.5066 | −0.0965 | |
| 0.5860 | −0.2263 | 0.9558 | |
| R | 1.5016 | 0.3765 | 0.3638 |
| h | 1.4798 | −0.5714 | −0.1117 |
| Parameter Error | Doppler Frequency (90 Hz) | Baseline (0.20 m) | Height (925.60 m) |
|---|---|---|---|
| RMSE/cm | 17.40 | 5.22 | 9.29 |
| Parameter Error | Doppler Frequency (110 Hz) | Baseline (0.01 m) | Height (942.01 m) |
|---|---|---|---|
| RMSE/cm | 12.69 | 2.00 | 1.33 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dou, F.; Lv, X.; Chen, Q.; Sun, G.; Yun, Y.; Zhou, X. The Impact of SAR Parameter Errors on the Ionospheric Correction Based on the Range-Doppler Model and the Split-Spectrum Method. Remote Sens. 2020, 12, 1607. https://0-doi-org.brum.beds.ac.uk/10.3390/rs12101607
Dou F, Lv X, Chen Q, Sun G, Yun Y, Zhou X. The Impact of SAR Parameter Errors on the Ionospheric Correction Based on the Range-Doppler Model and the Split-Spectrum Method. Remote Sensing. 2020; 12(10):1607. https://0-doi-org.brum.beds.ac.uk/10.3390/rs12101607
Chicago/Turabian StyleDou, Fangjia, Xiaolei Lv, Qi Chen, Guangcai Sun, Ye Yun, and Xiao Zhou. 2020. "The Impact of SAR Parameter Errors on the Ionospheric Correction Based on the Range-Doppler Model and the Split-Spectrum Method" Remote Sensing 12, no. 10: 1607. https://0-doi-org.brum.beds.ac.uk/10.3390/rs12101607






