1. Introduction
The interferometric synthetic aperture radar (InSAR) is an effective remote sensing technique to obtain the multi-baseline interferograms and monitor the surface deformation via repeated observation [
1]. Multi-pass InSAR with the characteristics of high resolution and wide detection range has gained a great achievement in monitoring land subsidence, landslides, and small surface deformation [
2,
3]. The damage to urban buildings and bridges caused by slow geologic change seriously threaten people’s lives and production safety [
4]. Besides, with economic development and population increase, the groundwater funnels appear in urban areas because of the massive and irrational exploitation of groundwater, which impacts the sustainable development [
5]. Therefore, it is significant to apply the multi-pass InSAR to monitor the ground deformation in urban areas [
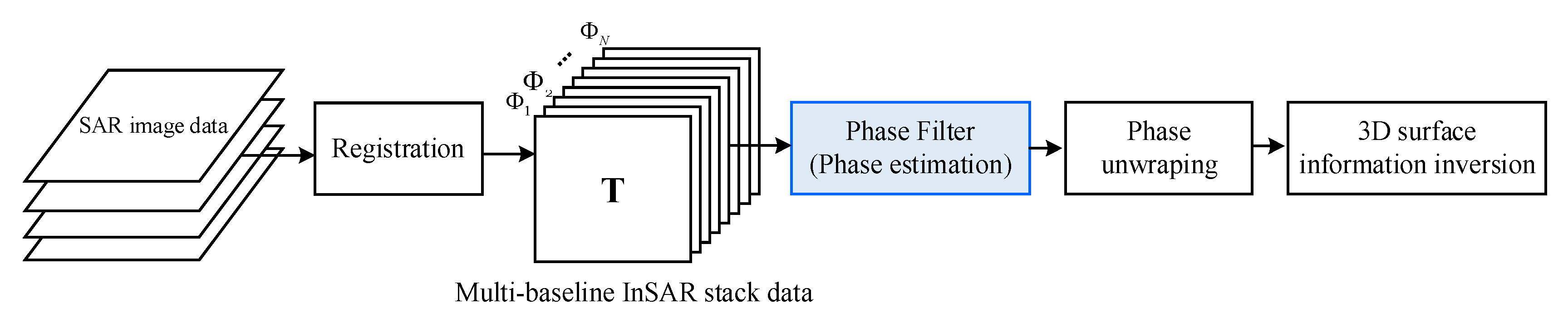
6]. The processing of multi-baseline InSAR stack data involves three important steps, including interferometric phase filtering, phase unwrapping, and 3D surface information inversion, which is shown in
Figure 1. The phase filtering is applied to eliminate the phase discontinuity and additive noise in interferograms, and thus realizes high-precision phase estimation. The purpose of the phase unwrapping is to recover the true phase from the wrapped phase. With the unwrapping phase as input, the process of 3D surface information inversion converts the phase components to elevation model, deformation model, tomographic model, and so on. There are many effective methods to achieve 3D surface information inversion. For example, some methods utilize the reliable reference points selected by amplitude or coherent threshold to monitor surface deformation, e.g., persistent scatterer InSAR (PSI) [
7] and small baseline subset (SBAS) [
8]. The localization of these reference points depends on the latitude and longitude information provided by standard SAR image products. If InSAR stack data has a layover effect caused by some tall buildings, tomographic interferometry is introduced to extract the scatter points and invert them to the ortho-coordinate [
9]. It can be seen that the accuracy of interferomeric phases affects the inversion of 3D surface information. Therefore, the high-precision phase estimation is a necessary step in the workflow of InSAR stack data processing. Especially in urban areas, the interferometric phase has complicated patterns and many noise factors, and it is important to filter the noisy InSAR stack data for urban interferometric big data.
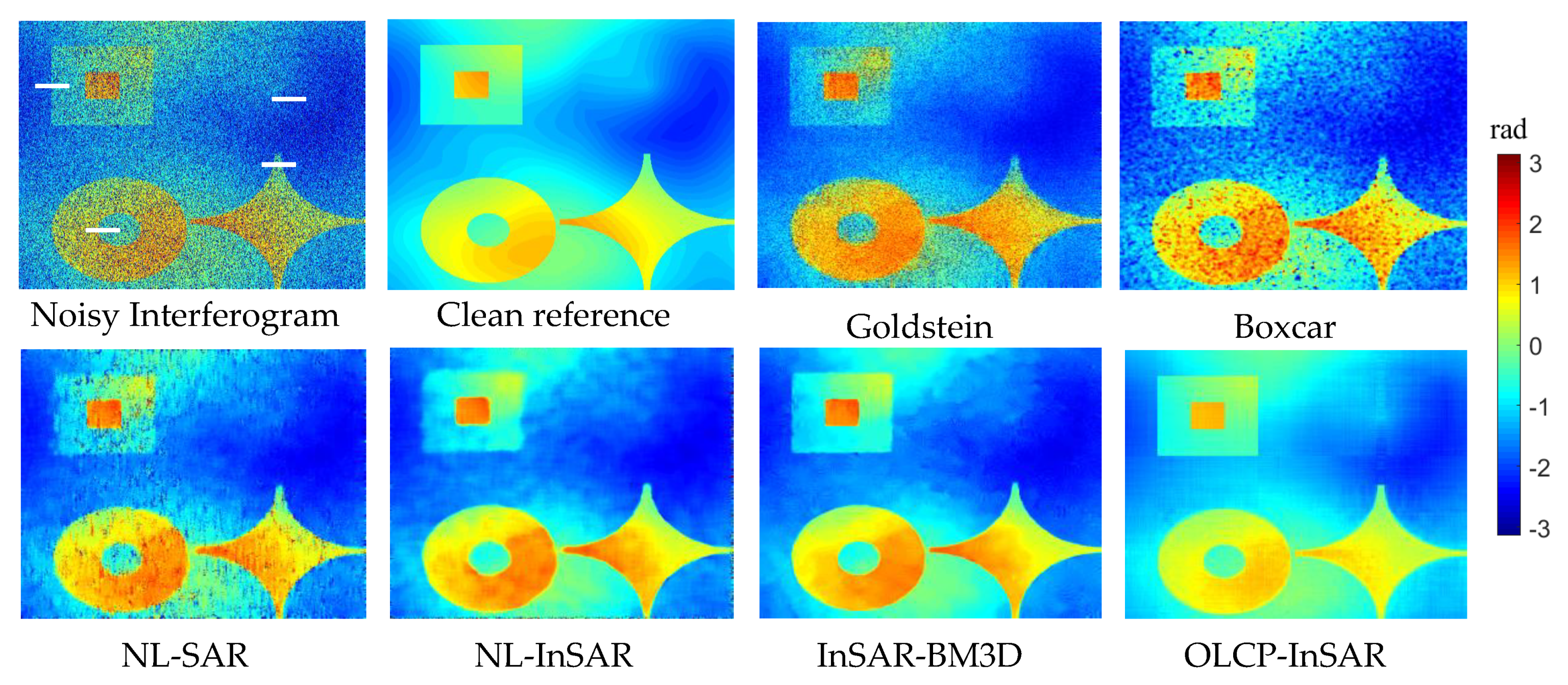
Many attempts are devoted to resolving the problem of noise suppression in a single interferometric pair. The boxcar filter [
10], as a common spatial domain denoising method, removes noise meanwhile sacrificing interferogram details. The Goldstein filter [
11] is established in the frequency domain, and the filter parameters can be adjusted by the coherence within an interferometric pair to improve the performance of reducing noise [
12]. Based on the self-similarity property of images, the nonlocal means (NL-means) [
13,
14] denoises by weighted averaging center pixels in several similar patches of an image. Recently, NL-means has been extended to filter an interferometric pair [
15,
16]. Nonlocal InSAR (NL-InSAR) [
15] combines non-local thought with the appropriate phase-oriented method. Nonlocal SAR (NL-SAR) [
16] further improves the robustness by adaptively selecting filter parameters in case of filtering the interferogram. Furthermore, combining with Wiener filtering [
17], a nonlocal block-matching 3-D (BM3D) algorithm [
18,
19] is proposed and performs well in SAR interferometric phase recovery with an appropriate phase-oriented method called InSAR-BM3D [
20]. These filters may obtain satisfactory denoising results in most situations, but in the region of rapid phase change, their performance seriously deteriorates [
20].
In addition to the above-mentioned filtering methods for a single interferometric pair, tensor decomposition has obtained great improvements as an effective filter to fuse and make full use of the information on multiple interferometric pairs. In fact, the multi-pass InSAR stack data conforms to the three-dimensional tensor mathematical representation [
21], where the first and second dimensions represent the spatial distribution of an interferogram, and the third dimension denotes the temporal variation of the interferograms, i.e., the number of interferometric pairs. The information on the interferograms in the InSAR stack data with the inner connection has a low sparsity meanwhile the noise has a high sparsity. Therefore, the authors of [
21,
22] fuse InSAR stack data and decompose them into low rank tensor and outlier tensor. The tensor decomposition model is transferred to the optimization problem by using Tucker rank [
23] to measure the sparsity of the InSAR tensor. Recently, in [
24] the authors proposed KBR-InSAR which further decomposes the InSAR tensor into the low-rank, Gaussian noise, and sparse noise tensors. Besides, Kronecker based representation (KBR) [
25,
26] is imported to definite InSAR tensor rank. KBR is a combination of the zero norm of the core tensor acquired by higher order singular value decomposition (HoSVD) [
27] and the relaxation of the Tucker rank [
28]. These filters have achieved a good performance in filtering InSAR tensor because of multi-pass data fusion, especially at the region of phase jump.
However, the accuracy can be further improved by a suitable measure of tensor sparsity. Tucker rank and KBR, utilized in HoRPCA and KBR-InSAR, both use kernel norm of mode-i tensor unfolding to measure the sparsity of tensor [
23,
25]. Tensor unfolding expands tensor into the matrix form and destroys the structure of tensor, which makes it difficult to extract tensor structural information. Different from them, CANDECAMP/PARAFAC (CP) rank [
29] is defined as the number of vector outer products, which keeps the tensor structure. Moreover, these tensor-based filters are based on the batch manner and required memorizing the whole tensor. And their filtering result is affected by the tensor depth (the number of interferograms in tensor). In order to ensure the accuracy of filtering, these methods need to fuse the interferograms as much as possible. Therefore, these filters cannot process the dynamic InSAR tensor, where the dynamic InSAR tensor indicates the InSAR tensor depth increases continuously due to the acquisition of new interferograms. Once a new single interferometric pair is obtained, these tensor-based filters cannot process it directly and need to re-run on the updated whole tensor containing the new pair, which is inefficient and inconvenient.
In fact, the low rank information of the accumulated InSAR tensor provides an effective reference for filtering the new acquired interferograms. Fortunately, tensor decomposition has many online forms [
30,
31,
32] and one of them based on CP rank can maintain structural features. Therefore, in order to filter dynamic InSAR tensor, we propose an unsupervised filtering framework to realize the InSAR data fusion by using online CP decomposition. The filter fuses the multi-pass interferograms and learns the low rank information of InSAR tensoronline, which can provide assistance to process new acquired interferograms. To this end, the contributions of this paper are threefold:
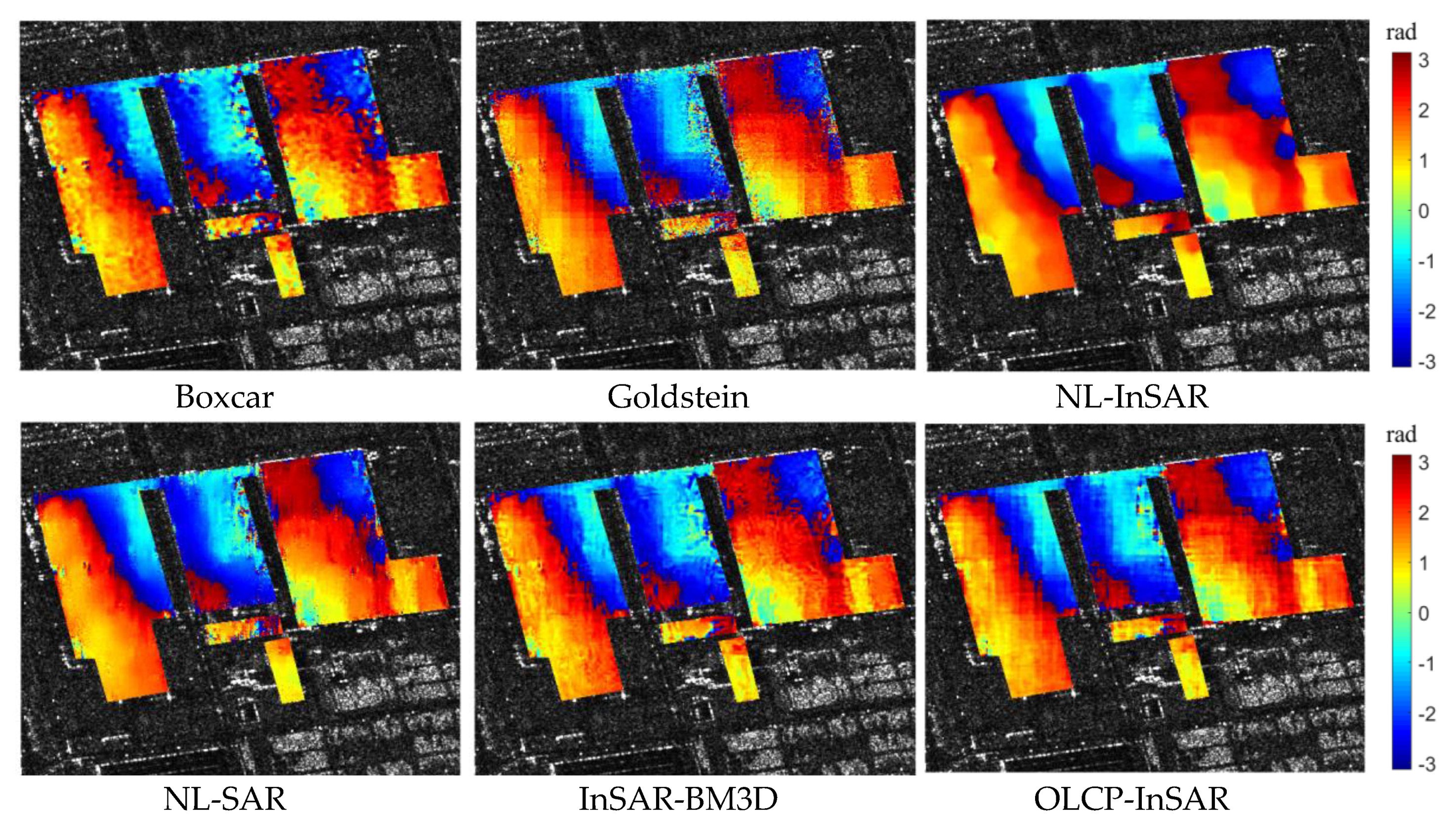
(1) Based on the properties of the InSAR tensor and the online CP decomposition, an effective filter is proposed, named as OLCP-InSAR, to handle the dynamic InSAR stack data. Compared with other filters, OLCP-InSAR can not only eliminate noise but also keep the fringe details well, especially for the fringe mutation at the edges of buildings in urban areas.
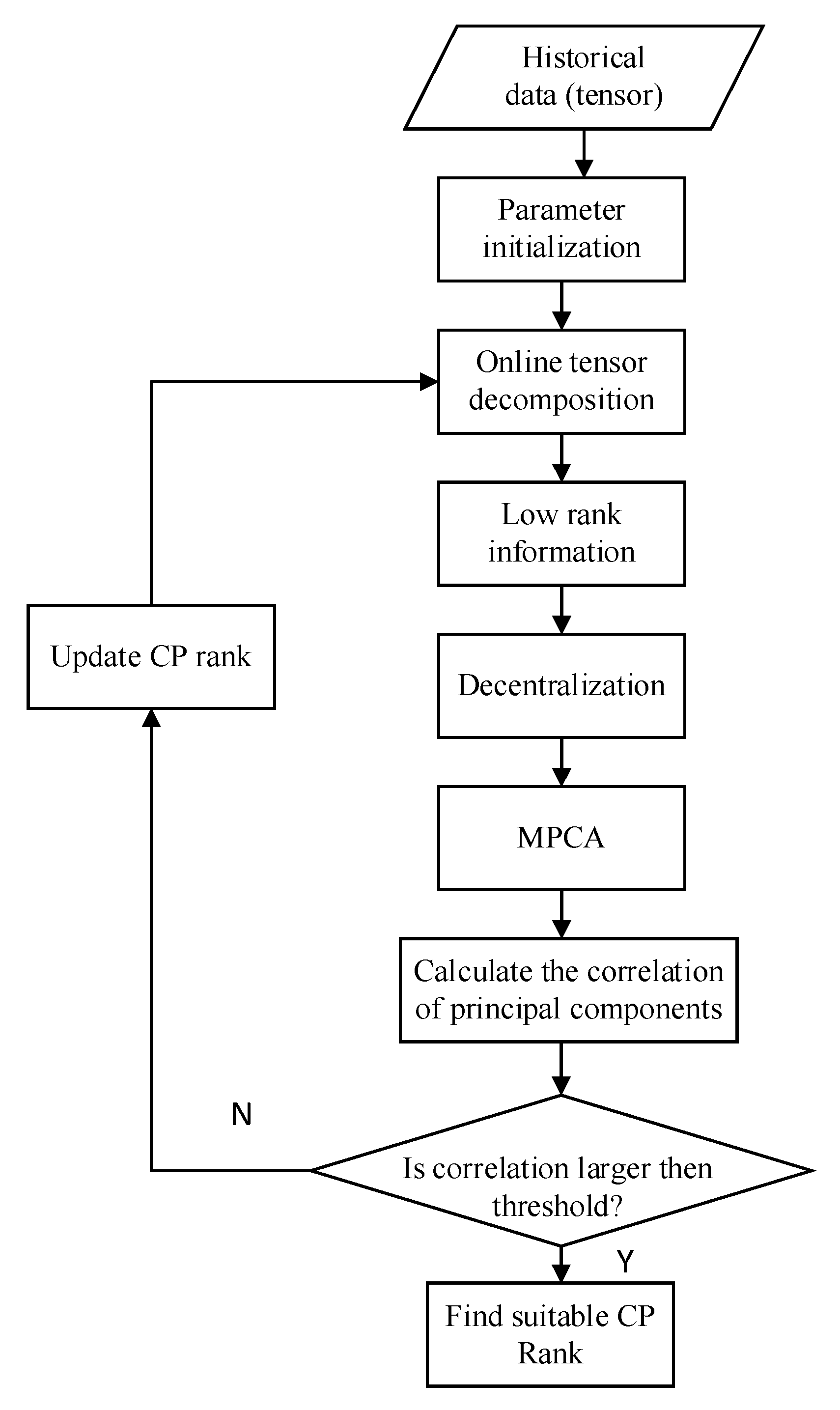
(2) The properties of the CP rank of InSAR tensor are analyzed and an effective method based on MPCA [
33] to estimate CP rank is proposed. Compared with other CP rank estimation algorithms [
34,
35], this method can estimate rank online and has good robustness with high noise intensity. The estimated CP rank, as an important parameter in OLCP-InSAR, helps to improve the robustness of our filtering method.
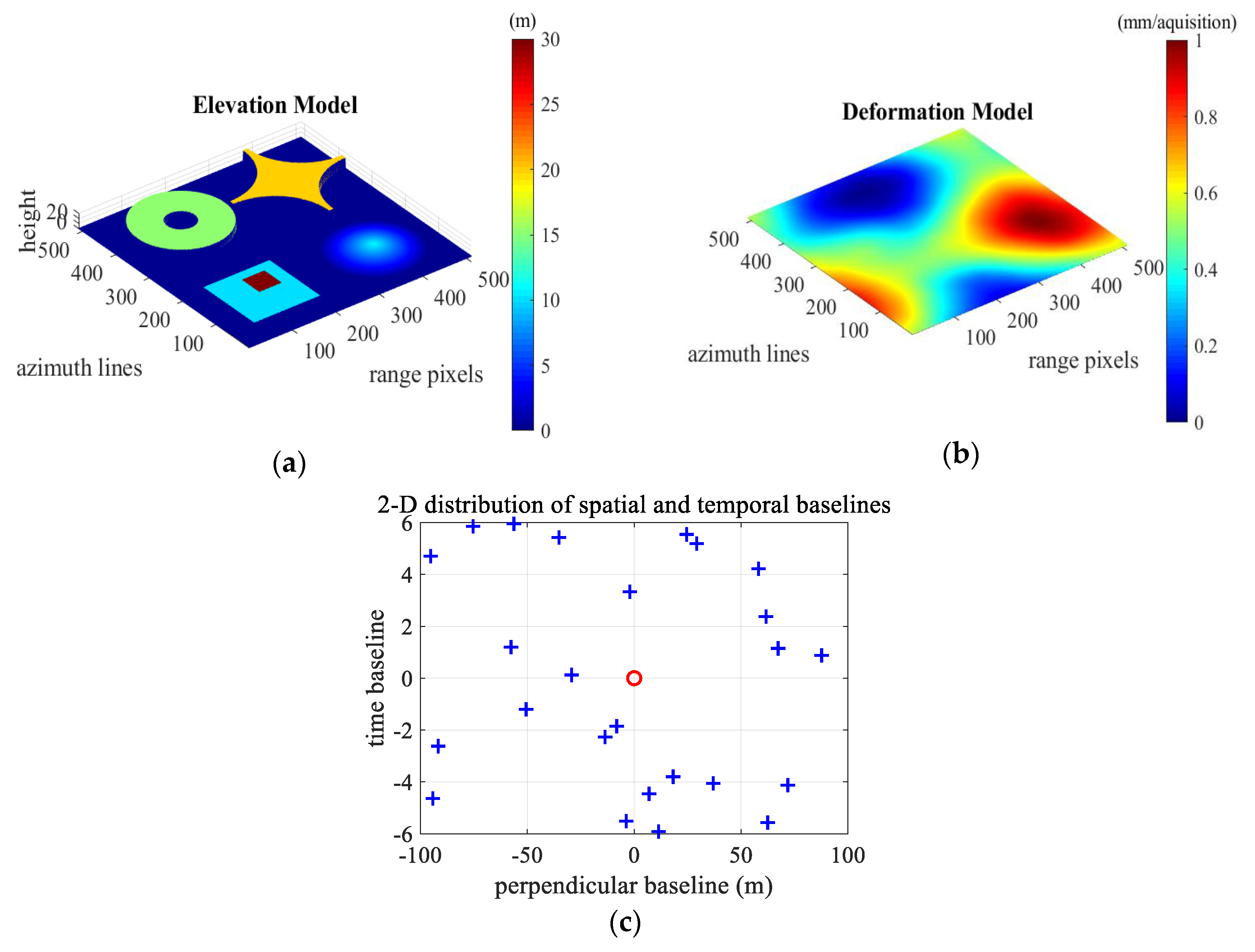
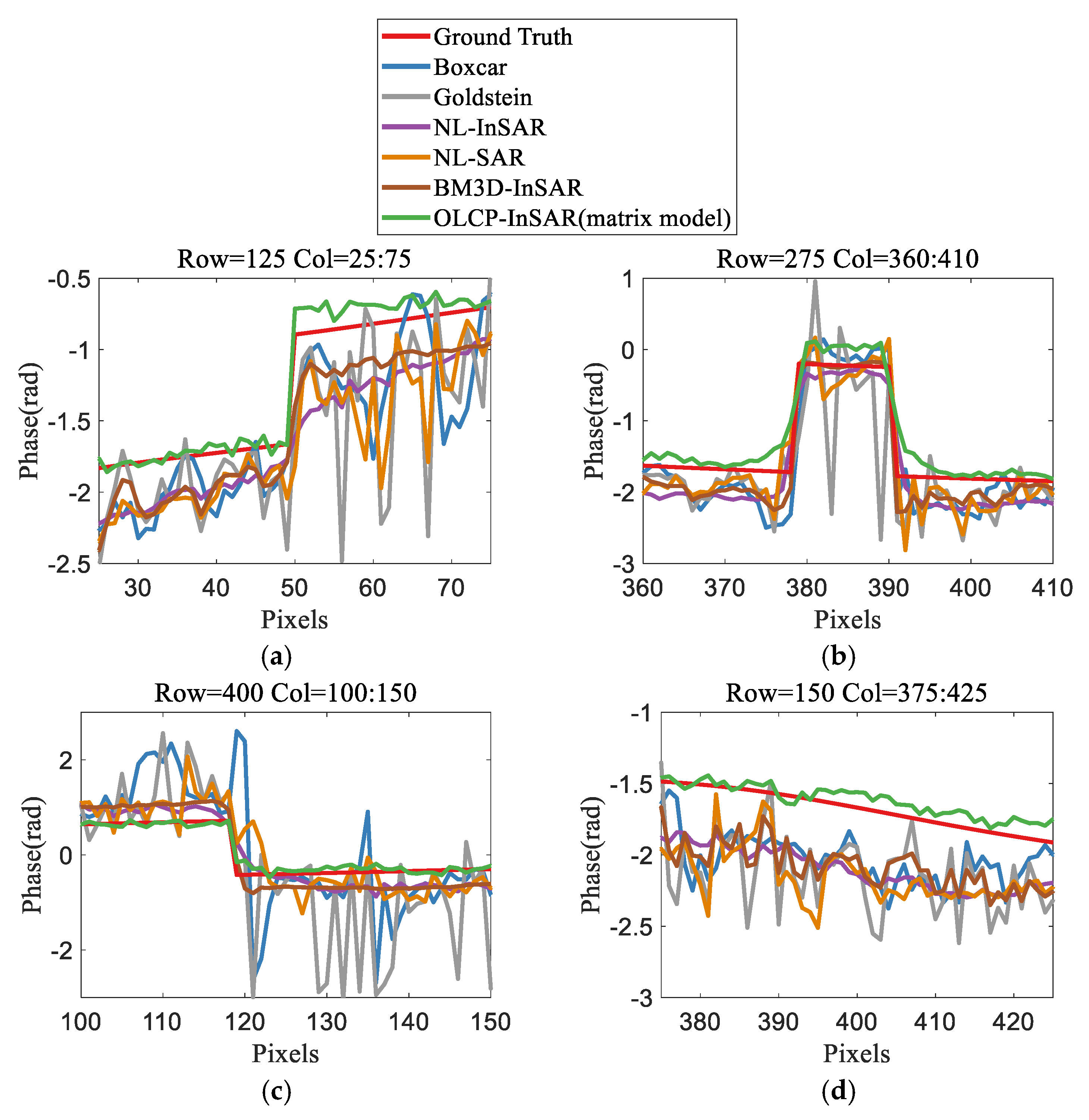
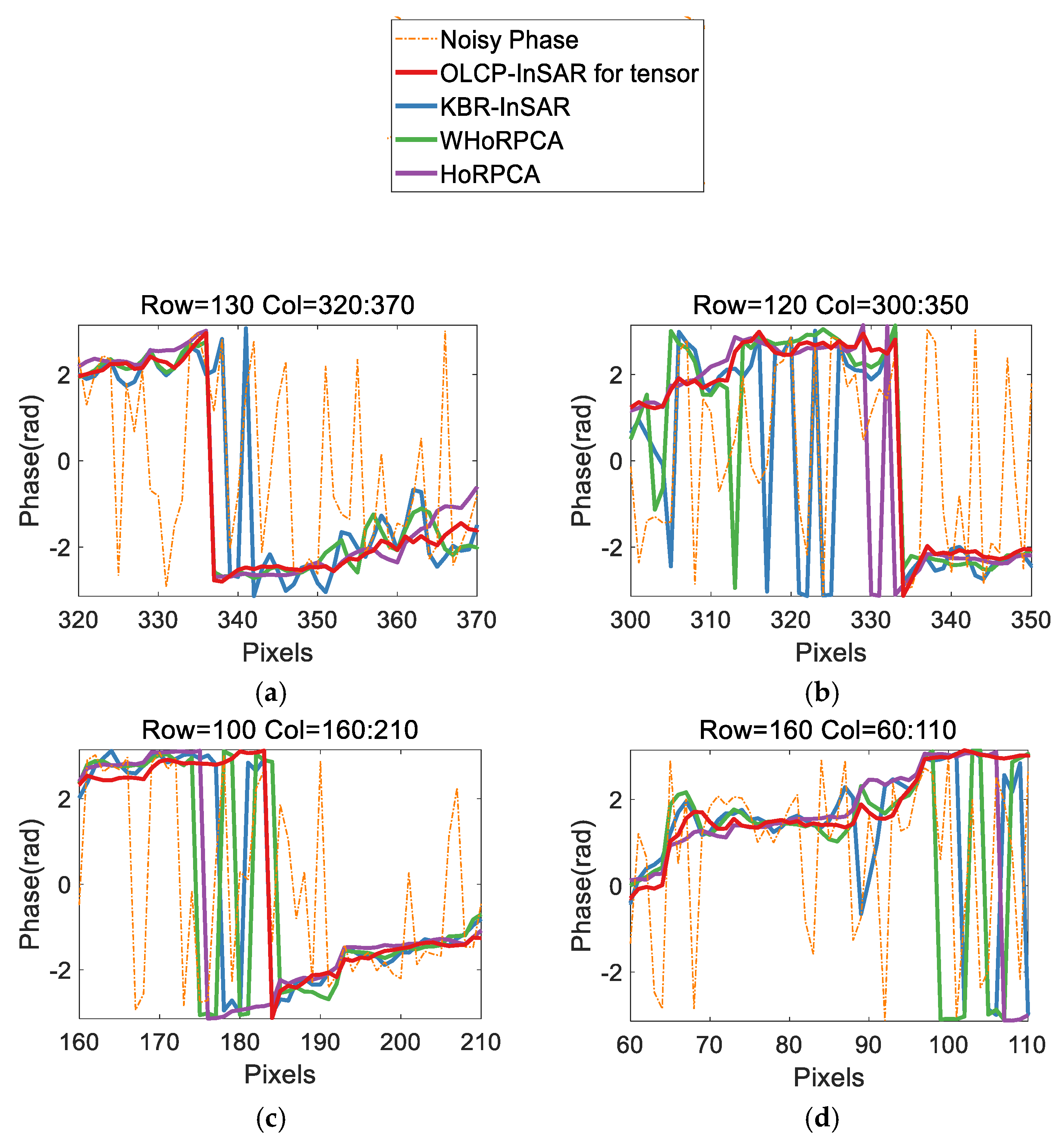
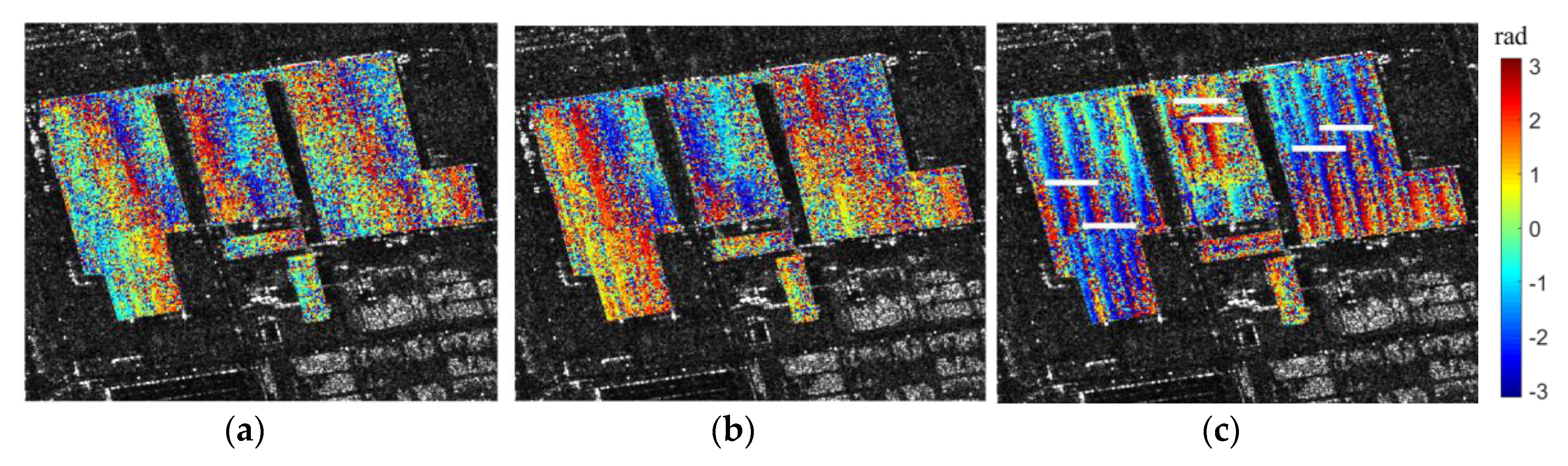
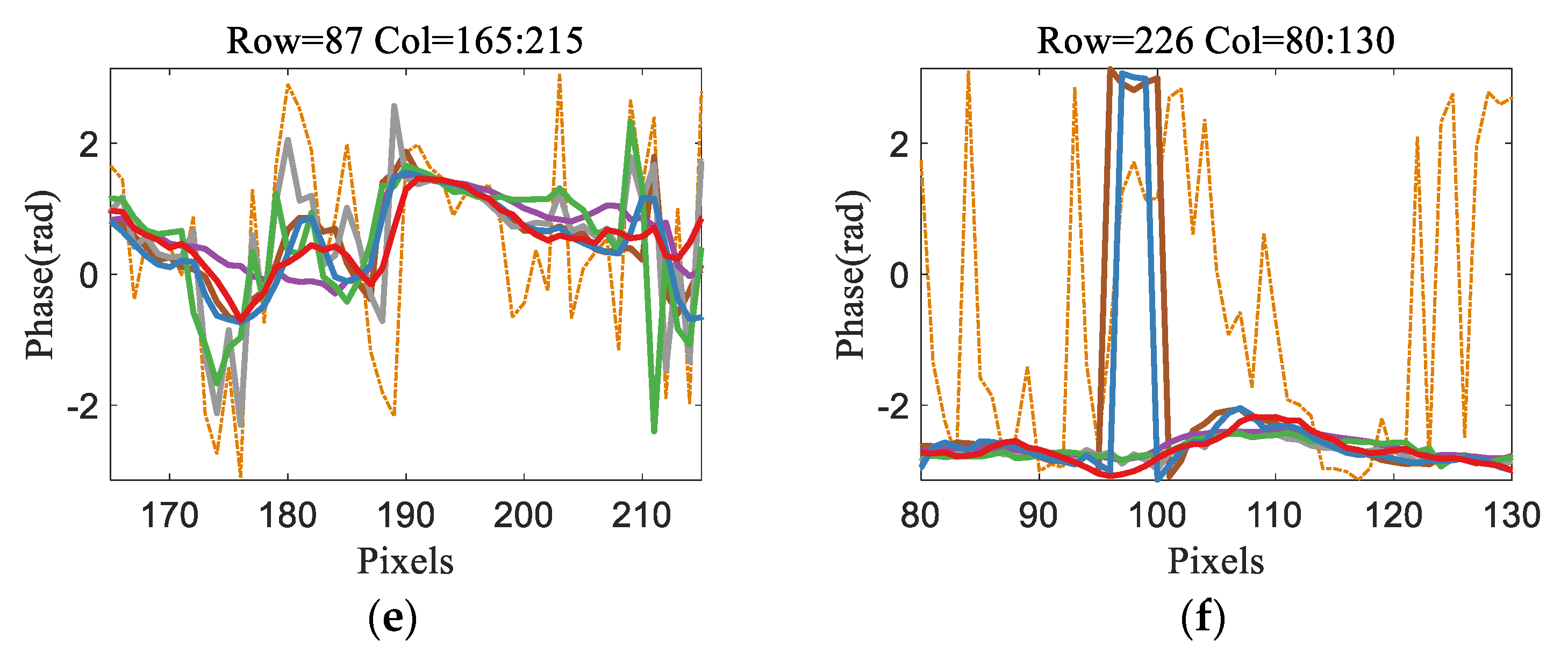
(3) The robustness and reliability of the framework are demonstrated by simulated data. Furthermore, 10 interferograms acquired by TerraSAR-X are used as experimental data to prove the effectiveness of the proposed framework. The framework can effectively filter the dynamic InSAR tensor and improve the accuracy of object-based interferometric phase estimation, especially at the regular building top with the high noise intensity and high outlier ratio.
The rest of this paper is organized as follows.
Section 2 briefly introduces the method applied in the paper and the overall workflow of online dynamic InSAR tensor filtering.
Section 3 presents some mathematical tensor notations and preliminaries.
Section 4 introduces OLCP-InSAR applied to the InSAR tensor.
Section 5 describes the CP rank and the way to estimate the InSAR tensor CP rank.
Section 6 elaborates the proposed online filtering framework in detail.
Section 7 provides experimental results by using simulated and real data to evaluate the filter performance. The conclusion is given in the final part.
3. Notions and Preliminaries
Tensor is the multi-dimensional extension of the vector and matrix, which equals to a multi-dimensional array. In the following sections, vectors are denoted as boldface lowercase letters, e.g., . Matrices are denoted as boldface capital letters, e.g., , where represents the ith row vector of and represents the ith column vector of . Tensors are denoted as boldface Euler script letters, e.g., , where represents the order of tensor, and () is the size of nth order. The mode-n unfolding of tensor is an unfolding matrix along the nth mode, i.e., . For example, assuming that , and then the mode-1 unfolding of tensor is .
Some symbols appear in the following sections, and their definitions are shown as follows.
represents the outer product of two matrices, e.g.,
, and the element of
is calculated as
where
.
denotes element-wise product of two matrices, e.g.,
, and the definition of the element of
is
denotes the vector outer product, e.g.,
, the element of
is calculated as
denotes n-mode product, which represents the product of tensor and matrix, e.g.,
, the element of
is calculated as
where
,
,
.
The definitions of some norms applied in this paper are introduced as follows. The Frobenius norm refers to the square root of the sum of all tensor elements squares, and is defined as
where
is the element in
-order tensor
.
The L2 norm of a vector refers to the square root of the sum of all vector elements squares, i.e., , which is Frobenius norm reduce to vectors.
The notation transfers a vector to a diagonal matrix.
7. Conclusions
The 3D information inversion in urban areas is an important research direction, but the processing of multi-pass InSAR data is difficult because of the requirement of high accurate phase estimation. The multi-pass interferometric stack data can be represented as InSAR tensor, and it can be filtered by solving an optimization problem and decomposed into low-rank, Gaussian noise, and outlier tensors. These tensor-based filters outperform the conventional filtering methods due to the data fusion framework. However, with the fast-growing InSAR data, it is difficult to handle the dynamic InSAR tensor for the existed tensor-based filters. Fortunately, online tensor decomposition proposed recently motivates us to fuse the InSAR stack data and estimate the steady structural feature, i.e., the low rank information, under the online decomposition framework. Therefore, a filter based on online CP decomposition, named as OLCP-InSAR, was proposed in this paper. This novel method requires CP rank and the position of outliers as auxiliary information, where CP rank is confirmed according to the correlation of the low rank information obtained by MPCA. OLCP-InSAR has two effective forms including tensor model and matrix model. One is to deal with the accumulated InSAR tensor and the accuracy can be further improved by cycling input of the interferograms in the tensor. The other is to process the new acquired interferograms by fusing the selected low rank information. The experiments were conducted with simulated data and real InSAR tensor generated from TerraSAR-X images, which proves the effectiveness and robustness of OLCP-InSAR when dealing with the InSAR data of urban areas. Comparing with tensor-based filters, OLCP-InSAR is not sensitive to the noise conditions because of the auxiliary information about outlier positions. Compared with other filters operating on a single interferogram (matrix), OLCP-InSAR can maintain the fringe details, especially at the regular building top with the high noise intensity and high outlier ratio. In conclusion, OLCP-InSAR can effectively filter the dynamic InSAR tensor and improve the accuracy of object-based interferometric phase estimation, which is an indispensable step in 3D surface information inversion. In the future work, we will continuously analyze the structural characteristics of InSAR tensor to improve the filtering accuracy and efficiency of online tensor decomposition.