1. Introduction
Remote sensing technology is an important source of Earth observation from different platforms and sensors, and it offers work on a large scale with cheap, accurate (depending on the research design), and faster results compared to the conventional methods. Thermal remote sensing is one of the branches of remote sensing that deals with the acquisition, processing, and interpretation of data acquired primarily in the Thermal Infrared (TIR) region of the Electromagnetic (EM) spectrum [
1,
2,
3]. Thermal remote sensing captures the radiation emitted from the ground primarily to estimate the surface temperature. In addition to surface temperature, surface emissivity, soil moisture, and evapotranspiration are the other crucial biophysical parameters estimated from TIR observations. Since these parameters govern the land-atmosphere interactions and the energy fluxes, their accurate evaluation is required to understand the behavior of the Earth.
Land Surface Temperature (LST) represents the temperature of the Earth’s surface, and it is one of the key parameters that affect surface energy balance, regional climates, heat fluxes, and energy exchanges [
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15]. Many researchers have investigated the importance and effects of LST on various topics, including urban climate and Surface Heat Island (SHI) studies [
16,
17,
18,
19,
20], evapotranspiration [
21], forest fire monitoring [
22], geological, and geothermal studies [
23,
24,
25,
26,
27]. Besides, LST has been approved as one of the high-priority parameters for the International Geosphere and Biosphere Program (IGBP) [
7,
28]. LST can be estimated from radiance measurements by meteorological stations. However, this method does not generally allow a large scale monitoring since it is a point-based measurement [
29,
30]. Remotely sensed TIR data allow temporal and spatial LST analysis on a large scale, even globally [
31].
Accurate LST retrieval from TIR data depends on atmospheric effects, sensor parameters, i.e., spectral range and viewing angle, and surface parameters such as emissivity and geometry [
32,
33,
34,
35,
36,
37,
38]. Since emissivity and atmospheric effects are two fundamental factors to derive LST from thermal data, many researchers have proposed different approaches for LST retrieval considering these factors [
39,
40,
41,
42,
43,
44,
45,
46]. These algorithms are named considering the number of TIR bands used. For instance, single-channel or mono-window algorithms use one TIR band. However, split window or multi-channel methods include more than one TIR band.
Accuracy assessment of space-based LST retrievals is one of the most important challenging procedure for the remote sensing community. In general, there are three methods utilized to validate LST values obtained from space, namely, the Temperature-based method (T-based), the Radiance-based method (R-based), and cross-validation [
7]. The R-based method considers the satellite-derived LST and in-situ atmospheric profiles and LSEs as initial input parameters to simulate the TOA radiance using radiative transfer simulations at the moment of the satellite overpass [
47]. The difference between the adjusted LST and the initial satellite-derived LST represents the accuracy of the retrieved LST [
7]. The cross-validation method considers a well-validated LST product as a reference and compares the satellite-derived LST with the referenced (well-validated) LST derived from other satellites [
7]. The T-based method, used by many researchers and also considered in this study, directly compares the satellite-based LST with ground-based LST measurements at the satellite overpass [
46,
48,
49,
50,
51,
52,
53,
54,
55]. The main advantage of the T-based method is that it enables evaluating the radiometric quality of the satellite sensor and the performance of LST retrieval methods depending on atmospheric and emissivity parameters. However, the effectiveness of the T-based assessments relies largely on the accuracy of the ground-based LSTs and how well they represent the LST at the satellite pixel scale [
7]. In addition, another issue that affects the correctness of the T-based validation method is the accuracy of calibration in TIR bands [
56].
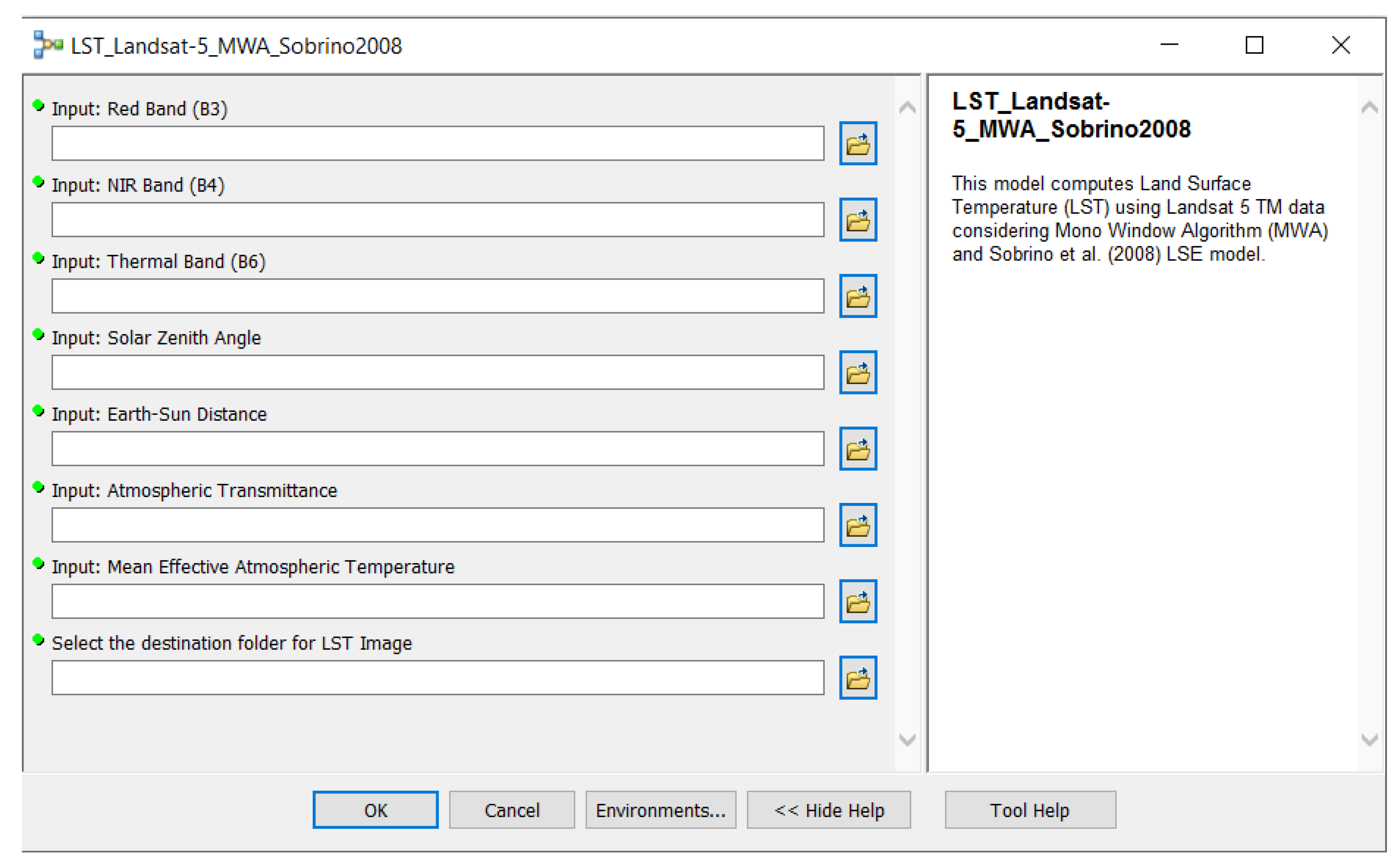
In this study, LST retrieval algorithms, namely, Radiative Transfer Equation (RTE) method [
39,
42], Single Channel Algorithm (SCA) [
44] and Mono Window Algorithm (MWA) [
43] were evaluated using Landsat 5 Thematic Mapper (TM), 7 Enhanced Thematic Mapper Plus (ETM+) and 8 Operational Land Imager (OLI) and Thermal Infrared Sensor (TIRS) data. Additionally, Split Window Algorithm (SWA) [
45,
46] was assessed for Landsat 8 OLI/TIRS data. Since LSE is one of the most important factors influencing the LST estimation reliability, the effects of different Normalized Difference Vegetation Index (NDVI)-based LSE models on LST accuracy were investigated in this study. In previous studies, many researchers have already examined the validation of different LST retrieval methods using Landsat data and in-situ LST measurements; however, they just considered one LSE model in the validation. Meng et al. [
52] used the National Oceanic and Atmospheric Administration (NOAA) Joint Polar Satellite System (JPSS) Enterprise algorithm and a hybrid LSE model to retrieve LST from Landsat-8 data. Yu et al. [
46] compared RTE, SWA, and SCA methods using Landsat 8 data and their NDVI-based LSE model reported in
Section 4.3. Zhang et al. [
57] utilized Sobrino et al.’s LSE model [
58] and the SCA method for LST retrieval from Landsat 8 data. Zhang et al. [
53] also investigated the accuracy of SCA using Landsat 8 imagery and Surface Radiation Budget Network (SURFRAD) measurements. Wang et al. [
54] proposed a Practical Single-Channel Algorithm (PSCA) using Sobrino et al.’s LSE model. Sekertekin [
59] used Skoković et al.’s LSE model [
60] and compared RTE-based LST from Landsat 8 with SURFRAD measurements. As pointed out above, researchers generally focused on the validation of Landsat 8 derived LST images with in-situ measurements. However, the LST validation results of Landsat 5 TM and 7 ETM+ still remain insufficiently explored. Therefore, this study provides the LST validation results of Landsat 5 TM, 7 ETM+, and 8 OLI/TIRS data examining different LST retrieval methods and LSE models.
This study aims to evaluate the performance of LST retrieval methods using different NDVI-based LSE models and data of old and current Landsat missions. The U.S. Geological Survey (USGS) has been producing and publishing LST products of Landsat missions considering LSE from Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) Global Emissivity Database (GED) data covering the US, Africa, Arabian Peninsula, Australia, Europe, and China; however, these LST products are geographically limited within the boundary of the North American Regional Reanalysis (NARR) grid, which is the climate data set used in the atmospheric correction algorithm [
61,
62]. Thus, it is still important to analyze Landsat data with different LST retrieval methods and over other climatological regions than North America. The ground-based measurement of LST requires accurate upwelling and downwelling thermal radiation measurements, and there are few stations in the world that measure these parameters to obtain in-situ LST. SURFRAD stations, established by the NOAA Office of United States (US) and located at different climatological regions of the US, are unique sources of information about in-situ LST over rural areas [
63]. In this work, a total of forty-five Landsat scenes, fifteen images for each Landsat mission, acquired in the Spring-Summer-Autumn period over rural areas in the mid-latitude region in the Northern Hemisphere were obtained over five SURFRAD stations in the period of 2000–2019. Simultaneous in-situ LST data with satellite acquisitions, obtained from the correspondent SURFRAD station, were utilized for accuracy analyses. For the aim of the work, we developed an enhanced toolbox for automated LST retrieval from Landsat data by RTE, SCA, MWA, and SWA algorithms using different LSE models (
Supplementary Materials). This toolbox is a first step to fill the gaps in the availability of different LST retrieval methods/LSE models in packaged Remote Sensing (RS) or Geographic Information System (GIS) software.
4. Land Surface Emissivity (LSE) Models
Surface emissivity stands for the surface ability that transforms heat energy into radiant energy [
36]. LSE (ε) is one of the key parameters to retrieve accurate LST from remotely sensed imagery. Semi-Empirical Methods (SEMs), Physically-Based Methods (PBMs), and multi-channel Temperature/Emissivity Separation (TES) methods are three distinctive categories for LSE retrieval from space [
7]. PBMs and multi-channel TES methods are not operational for Landsat data to obtain LSE due to the limitations presented in many studies, such as the requirement of more than two TIR bands or nighttime images [
7,
46,
76,
77,
78,
79]. SEMs contain the Classification Based Emissivity Method (CBEM) [
74,
80] and the NDVI Based Emissivity Method (NBEM) [
81,
82], which are suitable for LSE estimation from Landsat data. The CBEM generates an LSE image from a classified image by applying an emissivity value for each class. However, CBEM is not practical since it requires a good knowledge of the study area and emissivity measurements on the surfaces representative of the different classes [
70]. NDVI-based methods are operative and the most commonly utilized LSE retrieval methods since they are easy to apply and presenting satisfying results [
36,
58,
83]. Li et al. [
7] presented a detailed study showing the advantages, disadvantages, and limitations of different LSE models for LST retrieval from satellite data. Considering the study of Li et al. [
7] and other researches, a state-of-the-art table showing different LSE categories and models, as well as the correspondent satellite data used is reported (
Table 3).
As presented in
Table 3, there are six NDVI-based models introduced for Landsat data, specifically three for Landsat TM and three for Landsat 8 OLI/TIRS. Therefore, we investigated the effect of these six LSE models on the accuracy of LST retrieval methods. Details about LSE models are presented in the following sub-sections. The sensitivity of the LSE on LST retrieval methods is reported in
Appendix D.
4.1. LSE Model of Van de Griend and Owe
This model was applied to LST retrieval methods of all Landsat series (Landsat 5 TM, 7 ETM+, and 8 OLI/TIRS). Van de Griend and Owe [
83] proposed a logarithmic approach for an LSE retrieval model based on NDVI ranging from 0.157 to 0.727. NDVI is obtained using the Near-Infrared (NIR) and Red (R) bands—the calculation steps of NDVI for Landsat 5, 7, and 8, are presented in
Appendix C. The proposed model is given by:
4.2. LSE Model of Valor and Caselles
This model was applied to LST retrieval methods of all Landsat series (Landsat 5 TM, 7 ETM+, and 8 OLI/TIRS). Valor and Caselles [
82] proposed a theoretical model that relates the emissivity to the NDVI of a given surface by:
and
represent the emissivity of vegetation and soil, respectively.
is a term accounting for the cavity effect, which depends on the surface geometry. Pv (also referred to as fractional vegetation cover, FVC) is the proportion of vegetation calculated as [
103]:
where NDVI
max = 0.5 and NDVI
min = 0.2 in a global situation [
70]. As Valor and Caselles [
82] suggested,
and
as 0.985 and 0.960, respectively, for unknown emissivity and vegetation structures, we also regarded these emissivity values in the calculation. Besides, they calculated the mean value for
term as 0.015, and we utilized this value in LSE retrieval with this model. The final version of the LSE model can be given by:
4.3. NDVI Threshold (NDVITHM)-Based LSE Models
Sobrino et al. [
58], Skoković et al. [
60], Yu et al. [
46], and Li and Jiang [
76] estimated LSE from NDVI threshold (NDVI
THM) values considering three different cases as presented in Equation (21). In the first case (NDVI < 0.2), the pixel is considered as bare soil, and the emissivity is obtained from the reflectance values in the red region. In the second case (0.2 ≤ NDVI ≤ 0.5), the pixel is composed of a mixture of bare soil and vegetation, and in the third case (NDVI > 0.5), the pixels with NDVI values higher than 0.5 are considered as fully vegetated areas.
In Equation (21),
is the reflectance value of the red band,
and
are estimated from an empirical relationship between the red band reflectance and Moderate Resolution Imaging Spectroradiometer (MODIS) emissivity library.
and
are the soil and vegetation emissivity, respectively.
is the cavity effect due to surface roughness as in the previous model (
= 0 for flat surfaces). F is a geometrical shape factor assumed as the mean value of 0.55 [
70].
Table 4 presents the expressions of NDVI
THM for all models mentioned above.
In Li and Jiang’s LSE model,
is the apparent reflectance in the OLI band j and
– are coefficients obtained from [
76]. The LSE models of Band 11 were just utilized in the SWA method. It is important to point out again that the USGS announced caution in the use of Band 11 of Landsat 8 due to the calibration uncertainties [
75]. However, some researchers published satisfactory results by using SWA [
46,
76].
5. LST Computation Using Ground-Based SURFRAD Data
As stated in
Section 2.2, image-based LST results were validated using the data of five ground-based SURFRAD stations. Since these stations do not provide LST measurements directly, LST is calculated from the upwelling and downwelling longwave radiation measurements using the following Equation (22) with regard to the Stefan–Boltzmann law:
where
and
represent upwelling and dowelling thermal infrared (3–50 μm) irradiance in W/m
2, respectively, measured during satellite passages.
is the Stefan–Boltzmann constant (5.670367 × 10
−8 W∙m
−2∙K
−4), and
represents the broadband longwave surface emissivity, which is not measured by the station instruments. In previous studies on SURFRAD stations [
53,
56,
65], the broadband emissivity was computed as reported in [
104,
105] by regression from narrowband emissivity of MODIS thermal bands, which are available through the MODIS monthly emissivity data set. The results in [
104,
105] proved that the longwave broadband emissivity for the SURFRAD sites could be considered 0.97, as also assumed in [
64] and [
53].
Therefore, in this study, the broadband emissivity was assumed 0.97. This assumption impacts only the SURFRAD LST estimation, not the satellite-derived estimation. Heidinger et al. [
66] investigated the impact of changing the assumed broadband emissivity from 0.97 to 0.98 on the SURFRAD LST observation. The results indicated that a 0.01 error in broadband emissivity produces a SURFRAD LST error that rarely exceeds 0.25 K. In addition, Wang and Liang [
105] proved that the sensitivity of the SURFRAD LST to broadband emissivity ranged from 0.1K/0.01 to 0.35K/0.01, which means the accuracy of LST varies between 0.1 K to 0.4 K when the broadband emissivity error is about ±0.01. While this error is not negligible, it does not appear to be a dominant source of uncertainty in the SURFRAD-based performance metrics considering the magnitude of the other uncertainties [
66].
Satellite-based LST and SURFRAD-based LST were compared using statistical criteria, namely, the Root Mean Square Error (RMSE). RMSE, in Equation (23), is a widely used statistical metric evaluating the efficiency of the models.
where
and
are the satellite-based LST and SURFRAD-based LST, respectively, and n represents the pixel count.
7. Discussion
As stated in
Section 4, CBEM and NDVI-based LSE models are two appropriate models for Landsat data; CBEM can be used if emissivity measurements are obtained from in-situ campaigns, but it is not practical if the land cover information is not known accurately. Thus, we evaluated the impact of different NDVI-based LSE models, introduced in previous works, on LST retrieval methods over rural areas. It should be noted that the parameters and coefficients in NDVI-based LSE models were used as proposed in the original articles, and they can also be adapted to any study area with field campaigns. Valor and Caselles [
82] stated that the error of their methodology ranges from 0.5% (due to the experimental limitations of the field methods) to 2% (considering the case in which there is no information about the study area). Van de Griend and Owe [
83] did not conduct any sensitivity/error analysis but indicated that the correlation coefficient between NDVI and thermal emissivity was 0.941 at a 0.01 level of significance. One of the limitations of NDVI-based LSE models is its ineffectiveness in estimating LSE values for water and urban environments [
114,
115]. In this study, we just investigated the validation of daytime LST images. For nighttime LST evaluation, the LSE image can be estimated using CBEM derived from in-situ measurements or daytime NDVI-based LSE acquired on close dates. Overall, the proposed LST retrieval methods and LSE models can be implemented for regions other than the US, as well as for nighttime, non-rural, and winter data in clear sky conditions.
Considering the LST validation, error sources come from both satellite-based LST and ground-based LST. Satellite-based LST retrieval is still a challenging process due to the great variability of Earth surfaces and the necessary a priori knowledge about several parameters such as the atmosphere, the LSE, the meteorological conditions and the sensor specifications (spectral responses, signal to noise ratio, spectral resolution, spatial resolution, and viewing angle) [
7,
32,
48,
116,
117,
118]. Moreover, LST retrieval methods for satellite data are generally proposed considering different conditions and assumptions. Therefore, there is no universal method that always provides accurate LSTs from all satellite TIR data, and it is not easy to say which algorithm is superior to others [
7]. The accuracy of the radiometric measurements and emissivity is the primary uncertainty for ground-based LST retrievals [
119,
120,
121,
122,
123]. Sobrino and Skoković [
119,
122] presented an example of an error budget for The Global Change Unit (GCU) sites at the University of Valencia, and
Table 8 indicates the impact of the parameter uncertainty ranges on ground-based LST.
It is interesting to discuss our results in comparison with those of other studies that utilized SURFRAD LST measurements and Landsat data for LST retrieval. Meng et al. [
52] estimated LST from Landsat-8 data using the NOAA Joint Polar Satellite System (JPSS) Enterprise algorithm and a hybrid LSE model [
82,
124]. At the SURFRAD sites, the LST RMSE by the Enterprise algorithm was 3.22 K. Considering our analyses, SWA presented close results to the above analysis under three different LSE models ranging from 2.79 K to 3.02 K. Yu et al. [
46] compared RTE, SWA, and SCA methods using Landsat 8 data with their LSE models reported in
Section 4.3. They obtained satisfying RMSE values, i.e., 0.9 K, 1.39 K, and 1.03 K for RTE, SCA, and SWA, respectively. However, in this study, using Yu et al.’s LSE model, we obtained the RMSEs as 3.07 K, 3.18 K, and 3.02 K for RTE, SCA, and SWA, respectively. Zhang et al. [
57] used Sobrino et al.’s LSE model and SCA method for LST retrieval from Landsat 8 data and compared four Landsat 8 LST images with SURFRAD measurements. Their results showed 1.11 K RMSE with reference to four LST images, whilst we computed 2.94 K RMSE using 15 LST images of Landsat 8 for the same LSE model and retrieval method. In addition to the previous study, Zhang et al. [
53] also investigated the accuracy of SCA using Landsat 8 imagery and SURFRAD measurements using 40 Landsat 8 scenes acquired in different seasons and different years, and they obtained 1.96 K RMSE. Wang et al. [
54] reported that Practical Single-Channel Algorithm (PSCA) and generalized SCA provided 1.77 K and 2.24 K RMSE, respectively, in line with our SCA results based on Landsat 8 and Sobrino et al.’s LSE model. Sekertekin [
59] computed 3.12 K RMSE from 20 Landsat 8 images, close to the RTE-based Landsat 8 LST accuracy found in this test (2.73 K RMSE).
The limitations of this study and future investigations can be reported as follows: (1) Thermal bands have a native spatial resolution of 120 m, 60 m and 100 m for Landsat 5 TM, 7 ETM+, and 8 TIRS, respectively, but they are delivered by USGS at 30-m after cubic convolution resampling. Therefore, we also considered 30 m resampled TIR images which may lead to an error source when conducting pixel-scale validation. Different downscaling methods for TIR or LST data can be utilized as future work to examine the LST accuracy. (2) Although previous work proved that the accuracy of SURFRAD LST varies between 0.1 K to 0.4 K when the broadband emissivity error is about ±0.01, the use of fixed broadband emissivity (0.97) in this study may influence the ground-based LST calculation, but not dominantly. Broadband emissivity estimation models can be implemented in the future to show the optimal model for ground-based LST retrieval. (3) The LST toolbox, presented as a user facility in this study, does not include error analysis. Thus, users should carry out accuracy analysis after obtaining LST images. Besides, it can be improved and generated in an open-source environment as future work.
8. Conclusions
In this study, three LST retrieval algorithms (RTE, SCA, and MWA) were evaluated using Landsat 5 TM, 7 ETM+, and 8 OLI/TIRS data, and additionally, SWA were assessed for Landsat 8 OLI/TIRS data. Since LSE is one of the most important factors affecting the accuracy of LST retrieval methods, the effects of different NDVI-based LSE models on satellite-based LST accuracy were also investigated. Forty-five images acquired in the Spring-Summer-Autumn period over rural areas in the mid-latitude region in the Northern Hemisphere were obtained over five SURFRAD stations and simultaneous in-situ LST data were utilized for accuracy analyses. To get rid of step-by-step calculation for all LST methods and LSE models as well as for time consuming in processing of the images, an enhanced toolbox was generated for automated LST extraction. This toolbox can be utilized by all GIS users to obtain LST in an easy and practical way.
Three NDVI-based LSE models, namely, Sobrino et al.’s, Valor & Caselles’ and Van De Griend & Owe’s LSE model, were considered for Landsat 5 TM and 7 ETM+ data to investigate their effects on LST methods. In addition to these three LSE models, three more NDVI-based LSE models (Skoković et al.’s, Yu et al.’s, and Li and Jiang’s LSE models) were added to the analyses of Landsat 8 based LST methods. That is, the effects of six LSE models on the performance of LST methods from Landsat 8 data were investigated. To sum up, this study only considered NDVI-based LSE models for the evaluation of LST retrieval methods. Two different approaches were considered: 1) Sensor types of Landsat missions (Landsat 5, 7, and 8) were evaluated separately. 2) LST retrieval methods were compared with each other independently of sensor type, i.e., considering all Landsat missions together. In the toolbox, users can decide which LST method and LSE model they can utilize if they are dealing with the use of Landsat data. Furthermore, if they have their own LSE image, the toolbox makes it possible to use any external LSE image.
The obtained results showed that Sobrino et al.’s LSE model provided the best performance to extract LST for all Landsat missions and LST methods. Although all LST retrieval methods with Sobrino et al.’s LSE model presented satisfying and close results when using Landsat 5 TM data, RTE offered the best accuracy (2.35 K RMSE). The same would apply to Landsat 7 ETM+ data, even if MWA presented the best results (2.24 K RMSE). Again, Sobrino et al.’s LSE model provided higher accuracy for all LST retrieval methods from Landsat 8 data, with MWA as the best method (2.52 K RMSE). Considering all Landsat missions, MWA offered slightly better accuracy than RTE and SCA. Concerning the analyses above, it is hard to say which method is globally the best one, since the accuracy of the input parameters largely affects the performance of the methods. In addition, the spatio-temporal and seasonal comparison among LST retrieval methods revealed that RTE and SCA have a high level of agreement with each other regardless of the season. Instead, MWA presented different results than RTE and SCA, especially in summer.
The results indicated that LSE models have a great impact on the accuracy of satellite-based LST retrieval methods. This study also revealed that Sobrino et al.’s LSE model was the most appropriate model for all Landsat missions and LST retrieval methods over rural areas. Moreover, validation of LST retrieval methods with different LSE models over urban areas is a further challenge to be faced that deserves future investigations.