Measuring the Directional Ocean Spectrum from Simulated Bistatic HF Radar Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Bistatic Radar Cross Section of the Ocean Surface
- The Fourier coefficients are normally distributed about zero; hence
- As the surface is real, is equal to , which is true when
- The surface roughness spectrum , found by utilising the Wiener–Khinchin theorem, is related to the surface height Fourier coefficients bywhere and .
2.1.1. First Order
2.1.2. Second Order
2.1.3. Monostatic Conditions
2.2. Numerical Solution
2.2.1. First Order
2.2.2. Second Order
- When and , the solution of is
- When and , the solution is
2.2.3. Electromagnetic Singularities
2.2.4. Currents
3. Inversion of to Measure the Directional Wave Spectrum
The Seaview Inversion Method
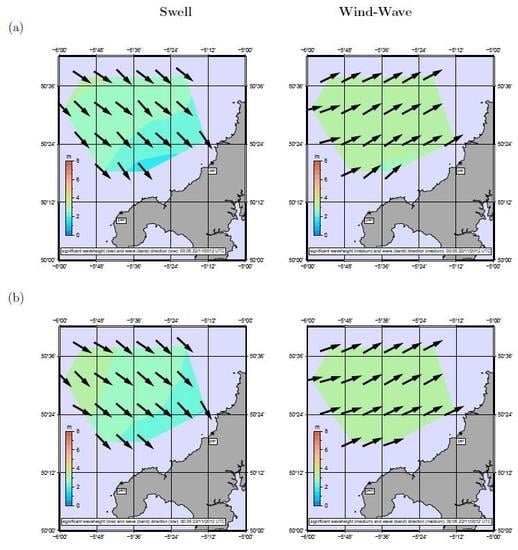
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Crombie, D.D. Doppler spectrum of sea echo at 13.56 Mc./s. Nature 1955, 175, 681–682. [Google Scholar] [CrossRef]
- Wyatt, L.R. Wave and Tidal Power measurement using HF radar. In Proceedings of the Oceans 2007-Europe, Aberdeen, UK, 18–21 June 2007; pp. 1–5. [Google Scholar]
- Paduan, J.D.; Washburn, L. High-frequency radar observations of ocean surface currents. Annu. Rev. Mar. Sci. 2013, 5, 115–136. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wyatt, L.R.; Ledgard, L.; Anderson, C. Maximum-likelihood estimation of the directional distribution of 0.53-Hz ocean waves. J. Atmos. Ocean. Technol. 1997, 14, 591–603. [Google Scholar] [CrossRef]
- Wyatt, L.R. Limits to the inversion of HF radar backscatter for ocean wave measurement. J. Atmos. Ocean. Technol. 2000, 17, 1651–1666. [Google Scholar] [CrossRef]
- Lipa, B.J. Derivation of directional ocean-wave spectra by integral inversion of second-order radar echoes. Radio Sci. 1977, 12, 425–434. [Google Scholar] [CrossRef]
- Lipa, B.J. Inversion of second-order radar echoes from the sea. J. Geophys. Res. Ocean. 1978, 83, 959–962. [Google Scholar] [CrossRef]
- Howell, R.; Walsh, J. Measurement of ocean wave spectra using narrow-beam HE radar. IEEE J. Ocean. Eng. 1993, 18, 296–305. [Google Scholar] [CrossRef]
- Hisaki, Y. Nonlinear inversion of the integral equation to estimate ocean wave spectra from HF radar. Radio Sci. 1996, 31, 25–39. [Google Scholar] [CrossRef]
- Wyatt, L.R. A relaxation method for integral inversion applied to HF radar measurement of the ocean wave directional spectrum. Int. J. Remote Sens. 1990, 11, 1481–1494. [Google Scholar] [CrossRef]
- Green, J.J.; Wyatt, L.R. Row-action inversion of the Barrick–Weber equations. J. Atmos. Ocean. Technol. 2006, 23, 501–510. [Google Scholar] [CrossRef]
- Barrick, D.E. First-order theory and analysis of MF/HF/VHF scatter from the sea. IEEE Trans. Antennas Propag. 1972, 20, 2–10. [Google Scholar] [CrossRef] [Green Version]
- Barrick, D.E. Remote Sensing of Sea State by Radar. In Remote Sensing of the Troposphere; Derr, V.E., Ed.; GPO: Washington, DC, USA, 1972; Chapter 12. [Google Scholar]
- Rice, S.O. Reflection of electromagnetic waves from slightly rough surfaces. Commun. Pure Appl. Math. 1951, 4, 351–378. [Google Scholar] [CrossRef]
- Lipa, B.J.; Barrick, D.E. Extraction of sea state from HF radar sea echo: Mathematical theory and modeling. Radio Sci. 1986, 21, 81–100. [Google Scholar] [CrossRef]
- Holden, G.J.; Wyatt, L.R. Extraction of sea state in shallow water using HF radar. In IEE Proceedings F (Radar and Signal Processing); IET: London, UK, 1992; Volume 139, pp. 175–181. [Google Scholar]
- Whelan, C.; Hubbard, M. Benefits of multi-static on HF Radar networks. In Proceedings of the OCEANS’15 MTS/IEEE Washington, Washington, DC, USA, 19–22 October 2015; pp. 1–5. [Google Scholar]
- Zhang, J.; Gill, E.W. Extraction of ocean wave spectra from simulated noisy bistatic high-frequency radar data. IEEE J. Ocean. Eng. 2006, 31, 779–796. [Google Scholar] [CrossRef]
- Silva, M.T. A Nonlinear Approach to Ocean Wave Spectrum Extraction From Bistatic HF-Radar Data. Master’s Thesis, Faculty of Engineering and Applied Science, Memorial University of Newfoundland, St. John’s, NL, Canada, 2017. [Google Scholar]
- Anderson, S. Directional wave spectrum measurement with multistatic HF surface wave radar. In Proceedings of the IEEE 2000 International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 24–28 July 2000; Volume 7, pp. 2946–2948. [Google Scholar]
- Johnstone, D.L. Second-Order Electromagnetic and Hydrodynamic Effects in High-Frequency Radio-Wave Scattering from the Sea; Technical Report, DTIC Document; Stanford University: Stanford, CA, USA, 1975. [Google Scholar]
- Gill, E.; Walsh, J. High-frequency bistatic cross sections of the ocean surface. Radio Sci. 2001, 36, 1459–1475. [Google Scholar] [CrossRef]
- Chen, Z.; Li, J.; Zhao, C.; Ding, F.; Chen, X. The Scattering Coefficient for Shore-to-Air Bistatic High Frequency (HF) Radar Configurations as Applied to Ocean Observations. Remote Sens. 2019, 11, 2978. [Google Scholar] [CrossRef] [Green Version]
- Hisaki, Y.; Tokuda, M. VHF and HF sea echo Doppler spectrum for a finite illuminated area. Radio Sci. 2001, 36, 425–440. [Google Scholar]
- Hardman, R.L. Remote Sensing of Ocean Winds and Waves With Bistatic HF Radar. Ph.D. Thesis, School of Mathematics and Statistics, University of Sheffield, Sheffield, UK, 2019. [Google Scholar]
- Stratton, J.A. Electromagnetic Theory; John Wiley Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Barrick, D.E.; Lipa, B.J. The second-order shallow-water hydrodynamic coupling coefficient in interpretation of HF radar sea echo. IEEE J. Ocean. Eng. 1986, 11, 310–315. [Google Scholar] [CrossRef]
- Thomas, J.B. An Introduction to Statistical Communication Theory; Wiley: Hoboken, NJ, USA, 1969. [Google Scholar]
- Barrick, D.E. Theory of HF and VHF propagation across the rough sea, 1, The effective surface impedance for a slightly rough highly conducting medium at grazing incidence. Radio Sci. 1971, 6, 517–526. [Google Scholar] [CrossRef]
- Hashimoto, N.; Tokuda, M. A Bayesian approach for estimating directional spectra with HF radar. Coast. Eng. J. 1999, 41, 137–149. [Google Scholar] [CrossRef]
- Pierson, W.J.; Moskowitz, L. A proposed spectral form for fully developed wind seas based on the similarity theory of SA Kitaigorodskii. J. Geophys. Res. 1964, 69, 5181–5190. [Google Scholar] [CrossRef]
- Wyatt, L.R. An evaluation of wave parameters measured using a single HF radar system. Can. J. Remote Sens. 2002, 28, 205–218. [Google Scholar] [CrossRef]
- Donelan, M.A.; Hamilton, J.; Hui, W. Directional spectra of wind-generated ocean waves. Phil. Trans. R. Soc. Lond. A 1985, 315, 509–562. [Google Scholar] [CrossRef]
- Wyatt, L.R.; Green, J.J.; Middleditch, A. HF radar data quality requirements for wave measurement. Coast. Eng. 2011, 58, 327–336. [Google Scholar] [CrossRef]
- Lopez, G.; Conley, D.C. Comparison of HF Radar Fields of Directional Wave Spectra against in Situ Measurements at Multiple Locations. J. Mar. Sci. Eng. 2019, 7, 217. [Google Scholar] [CrossRef] [Green Version]
- Lopez, G.; Conley, D.C.; Greaves, D. Calibration, validation and analysis of an empirical algorithm for the retrieval of wave spectru from HF radar sea echo. J. Atmos. Ocean. Technol. 2016, 33, 245–261. [Google Scholar] [CrossRef]
- Hardman, R.; Wyatt, L. Inversion of HF radar Doppler spectrum using a neural network. J. Mar. Sci. Eng. 2019, 7, 255. [Google Scholar] [CrossRef] [Green Version]
- Wyatt, L.R.; Holden, G.J. Limits in direction and frequency resolution for HF radar ocean wave directional spectra measurement. Glob. Atmos. Ocean. Syst. 1994, 2, 265–290. [Google Scholar]
- Wyatt, L.R. Measuring the ocean wave directional spectrum ‘First Five’ with HF radar. Ocean. Dyn. 2019, 69, 123–144. [Google Scholar] [CrossRef] [Green Version]























| Case | Type | Wind–Wave Hs m | Spread | Wind Speed m/s | Current Speed m/s | Swell Hs m | Tp s | Spread | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Model | 3.07 | 0.0 | 3.0 | 12.0 | 1.4 | 70.0 | ||||
| 2 | Model | 3.07 | 30.0 | 2.0 | 12.0 | 1.8 | 90.0 | 3.0 | 140.0 | 13.2 | 10.0 |
| 3 | Buoy | 1.72 | 1.8 | 90.0 | 68.24 | 12.8 | |||||
| 4 | Buoy | 1.72 | 1.8 | 90.0 | 148.16 | 6.74 | |||||
| 5 | Buoy | 2.70 | 1.8 | 90.0 | 109.01 | 14.22 | |||||
| 6 | Buoy | 5.87 | 1.0 | 245.0 | 162.36 | 9.85 |
| Cell Number | Configuration | Bistatic Angle | Angle between Braggs |
|---|---|---|---|
| 1664 | monostatic | 0 | 40.6 |
| 1 mono, 1 bistatic | 20.4 | 20.3 | |
| 3116 | monostatic | 0 | 60.0 |
| 1 mono, 1 bistatic | 30.1 | 29.9 | |
| 3128 | monostatic | 0 | 77.8 |
| 1 mono, 1 bistatic | 39.1 | 38.8 | |
| 3140 | monostatic | 0 | 99.6 |
| 1 mono, 1 bistatic | 50.1 | 49.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hardman, R.L.; Wyatt, L.R.; Engleback, C.C. Measuring the Directional Ocean Spectrum from Simulated Bistatic HF Radar Data. Remote Sens. 2020, 12, 313. https://0-doi-org.brum.beds.ac.uk/10.3390/rs12020313
Hardman RL, Wyatt LR, Engleback CC. Measuring the Directional Ocean Spectrum from Simulated Bistatic HF Radar Data. Remote Sensing. 2020; 12(2):313. https://0-doi-org.brum.beds.ac.uk/10.3390/rs12020313
Chicago/Turabian StyleHardman, Rachael L., Lucy R. Wyatt, and Charles C. Engleback. 2020. "Measuring the Directional Ocean Spectrum from Simulated Bistatic HF Radar Data" Remote Sensing 12, no. 2: 313. https://0-doi-org.brum.beds.ac.uk/10.3390/rs12020313