A More Reliable Orbit Initialization Method for LEO Precise Orbit Determination Using GNSS
Abstract
:1. Introduction
2. Orbit Initialization Methods
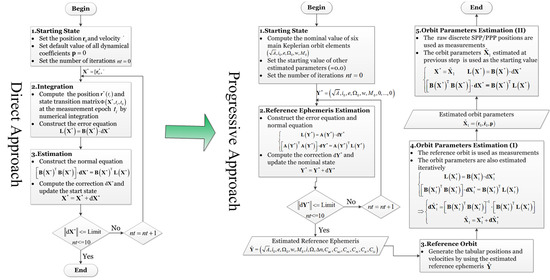
2.1. The Direct Approach
2.2. The Progressive Approach
3. Stability Analyses
3.1. Effect of the Starting State Error
3.2. Stability Analysis Tests
4. Experiments and Analysis
4.1. Orbit Initialization Experiements
4.2. Analysis and Discussion
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Montenbruck, O.; Ramos-Bosch, P. Precision real-time navigation of LEO satellites using global positioning system measurements. GPS Solut. 2008, 12, 187–198. [Google Scholar] [CrossRef]
- Wang, F.; Gong, X.; Sang, J.; Zhang, X. A novel method for precise onboard real-time orbit determination with a standalone GPS receiver. Sensors 2015, 15, 30403–34018. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jérôme, L. The Use of GPS/GNSS on Earth and in Space; Montreal Space Symposium: Montreal, QC, Canada, 2018. [Google Scholar]
- Montenbruck, O.; Hackel, S.; Jäggi, A. Precise orbit determination of the Sentinel-3A altimetry satellite using ambiguity-fixed GPS carrier phase observations. J. Geod. 2018, 92, 711–726. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Zhang, K.; Meng, X.; Zhang, W.; Zhang, Q.; Zhang, X.; Li, X. Precise orbit determination for the FY-3C satellite using onboard BDS and GPS observations from 2013, 2015, and 2017. Engineering 2019. [Google Scholar] [CrossRef]
- Li, X.; Wu, J.; Zhang, K.; Li, X.; Xiong, Y.; Zhang, Q. Real-Time kinematic precise orbit determination for LEO satellites using zero-differenced ambiguity resolution. Remote Sens. 2019, 11, 2815. [Google Scholar] [CrossRef] [Green Version]
- Gooding, R.H. A New Procedure for Orbit Determination Based on Three Lines of Sight (Angles Only); Defence Research Agency Farnborough: Hampshire, UK, 1993.
- Fujimoto, K.; Scheeres, D.J. Short-arc correlation and initial orbit determination for space-based observations. In Proceedings of the 2011 Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 13–16 September 2011. [Google Scholar]
- Weisman, R.M.; Majji, M.; Alfriend, K.T. Analytic characterization of measurement uncertainty and initial orbit determination on orbital element representations. Celest. Mech. Dyn. Astron. 2014, 118, 165–195. [Google Scholar] [CrossRef]
- Lei, X.; Wang, K.; Zhang, P.; Pan, T.; Li, H.; Sang, J.; He, D. A geometrical approach to association of space-based very short-arc LEO tracks. Adv. Space Res. 2018, 62, 542–553. [Google Scholar] [CrossRef]
- Li, X.; Ma, F.; Li, X.; Lv, H.; Bian, L.; Jiang, Z.; Zhang, X. LEO constellation-augmented multi-GNSS for rapid PPP convergence. J. Geod. 2019, 93, 749–764. [Google Scholar] [CrossRef]
- Ardito, C.T.; Morales, J.J.; Khalife, J.; Abdallah, A.A.; Kassas, Z. Performance evaluation of navigation using LEO satellite signals with periodically transmitted satellite positions. In Proceedings of the 2019 International Technical Meeting of The Institute of Navigation, Reston, VA, USA, 28–31 January 2019; pp. 306–318. [Google Scholar]
- Wang, L.; Chen, R.; Xu, B.; Zhang, X.; Li, T.; Wu, C. The challenges of LEO based navigation augmentation system–lessons learned from Luojia-1A satellite. In Proceedings of the China Satellite Navigation Conference (CSNC) 2019 Proceedings, Beijing, China, 22–25 May 2019; pp. 298–310. [Google Scholar]
- Li, X.; Zhang, K.; Ma, F.; Zhang, W.; Zhang, Q.; Qin, Y.; Zhang, H.; Meng, Y.; Bian, L. Integrated precise orbit determination of multi-GNSS and large LEO constellations. Remote Sens. 2019, 11, 2514. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Zhang, K.; Meng, X.; Zhang, Q.; Zhang, W.; Li, X.; Yuan, Y. LEO–BDS–GPS integrated precise orbit modeling using FengYun-3D, FengYun-3C onboard and ground observations. GPS Solut. 2020, 24, 1–13. [Google Scholar] [CrossRef]
- Borio, D.; Sokolova, N.; Lachapelle, G. Doppler measurements and velocity estimation: A theoretical framework with software receiver implementation. In Proceedings of the ION GNSS 2009, Savannah, GA, USA, 23–25 September 2009; pp. 23–25. [Google Scholar]
- Colombo, O.L. The dynamics of Global Positioning System orbits and the determination of precise ephemerides. J. Geophys. Res. 1989, 94, 9167–9182. [Google Scholar] [CrossRef]
- Montenbruck, O.; Gill, E. Satellite Orbits: Models, Methods and Application; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Anthony Flores, R.E. NAVSTAR GPS Space Segment/Navigation User Segment Interfaces (IS-GPS-200L). 2020. Available online: https://www.gps.gov/technical/icwg/IS-GPS-200L.pdf (accessed on 14 May 2020).
- Fu, X.; Wu, M. Optimal design of broadcast ephemeris parameters for a navigation satellite system. GPS Solut. 2012, 16, 439–448. [Google Scholar] [CrossRef]
- Földváry, L. Determination of satellite velocity and acceleration from kinematic LEO orbits. Acta Geod. Geophys. Hung. 2007, 42, 399–419. [Google Scholar] [CrossRef]
- Hwang, Y.; Lee, B.S.; Kim, Y.R.; Roh, K.M.; Jung, O.C.; Kim, H. GPS-based orbit determination for KOMPSAT-5 satellite. ETRI J. 2011, 33, 487–496. [Google Scholar] [CrossRef]
- Li, M.; Li, W.; Shi, C.; Jiang, K.; Guo, X.; Dai, X.; Meng, X.; Yang, Z.; Yang, G.; Liao, M. Precise orbit determination of the Fengyun-3C satellite using onboard GPS and BDS observations. J. Geod. 2017, 91, 1313–1327. [Google Scholar] [CrossRef] [Green Version]







| Date | KOMPSAT-5 | Date | FY3C | ||
|---|---|---|---|---|---|
| DA | PA | DA | PA | ||
| 2016/42 | √ | √ | 2013/285 | √ | √ |
| 2016/43 | × | √ | 2013/286 | √ | √ |
| 2016/44 | × | √ | 2013/287 | × | √ |
| 2016/45 | × | √ | 2013/288 | × | √ |
| 2016/46 | √ | √ | 2013/289 | √ | √ |
| 2016/47 | √ | √ | 2013/290 | √ | √ |
| 2016/48 | √ | √ | 2013/291 | √ | √ |
| 2016/49 | × | √ | 2013/292 | √ | √ |
| 2016/50 | × | √ | 2013/293 | √ | √ |
| 2016/51 | √ | √ | 2013/294 | √ | √ |
| Iterations | KOMPSAT-5 | FY3C | ||||||
|---|---|---|---|---|---|---|---|---|
| 2016/43 | 2016/44 | 2016/45 | 2016/49 | 2016/50 | 2013/287 | 2013/288 | ||
| Mean position error/m | 1.37 | 3.23 | 1.97 | 2.55 | 1.42 | 2.13 | 1.66 | |
| Mean velocity error/m/s | 2.73 | 2.44 | 2.43 | 3.67 | 1.95 | 2.85 | 1.76 | |
| DA/m | 1 | 64,450.8 | 20,124.5 | 2229.1 | 8672.6 | 3186.9 | 194,731.9 | 151,436.3 |
| 2 | 187,660.3 | Diverge | 5358.6 | 45,891.1 | 2282.1 | Diverge | 352,364.8 | |
| 3 | Diverge | 21,577.4 | Diverge | 3774.3 | Diverge | |||
| 4 | Diverge | 13,163.1 | ||||||
| 5 | 51,953.5 | |||||||
| 6 | Diverge | |||||||
| PA/m | 2.1 | 18,653.5 | 47,787.9 | 81,857.9 | 49,213.3 | 18,536.2 | 19,918.5 | 51,806.7 |
| 2.2 | 562.3 | 567.7 | 885.56 | 573.0 | 564.6 | 532.0 | 525.0 | |
| 2.3 | 562.4 | 575.1 | 1124.2 | 581.7 | 564.7 | 532.1 | 534.8 | |
| 2.4 | 562.4 | 563.1 | 566.4 | 566.8 | 564.6 | 532.0 | 518.4 | |
| 2.5 | 562.4 | 563.1 | 566.4 | 566.8 | 564.6 | 532.0 | 518.4 | |
| 4.1 | 540.5 | 488.9 | 439.2 | 508.4 | 456.5 | 498.8 | 491.6 | |
| 4.2 | 540.5 | 488.7 | 435.9 | 508.2 | 456.7 | 498.8 | 491.7 | |
| 4.3 | 540.5 | 488.7 | 435.8 | 508.2 | 456.7 | 498.8 | 491.7 | |
| 5.1 | 5.6 | 5.4 | 6.1 | 7.3 | 6.1 | 12.5 | 10.5 | |
| 5.2 | 5.6 | 5.4 | 6.1 | 7.3 | 6.1 | 12.5 | 10.5 | |
| 5.3 | 5.6 | 5.4 | 6.1 | 7.3 | 6.1 | 12.5 | 10.5 | |
| Iterations | R/m | T/m | N/m | 3D/m |
|---|---|---|---|---|
| 1 | 3137.55 | 558.00 | 20.98 | 3186.85 |
| 2 | 2199.16 | 608.68 | 32.88 | 2282.07 |
| 3 | 3623.94 | 1054.26 | 29.63 | 3774.29 |
| 4 | 12,550.51 | 3967.17 | 120.29 | 13,163.14 |
| 5 | 51,131.22 | 9198.94 | 373.86 | 51,953.46 |
| 6 | Diverge... | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, X.; Sang, J.; Wang, F.; Li, X. A More Reliable Orbit Initialization Method for LEO Precise Orbit Determination Using GNSS. Remote Sens. 2020, 12, 3646. https://0-doi-org.brum.beds.ac.uk/10.3390/rs12213646
Gong X, Sang J, Wang F, Li X. A More Reliable Orbit Initialization Method for LEO Precise Orbit Determination Using GNSS. Remote Sensing. 2020; 12(21):3646. https://0-doi-org.brum.beds.ac.uk/10.3390/rs12213646
Chicago/Turabian StyleGong, Xuewen, Jizhang Sang, Fuhong Wang, and Xingxing Li. 2020. "A More Reliable Orbit Initialization Method for LEO Precise Orbit Determination Using GNSS" Remote Sensing 12, no. 21: 3646. https://0-doi-org.brum.beds.ac.uk/10.3390/rs12213646