Gated Autoencoder Network for Spectral–Spatial Hyperspectral Unmixing
Abstract
:1. Introduction
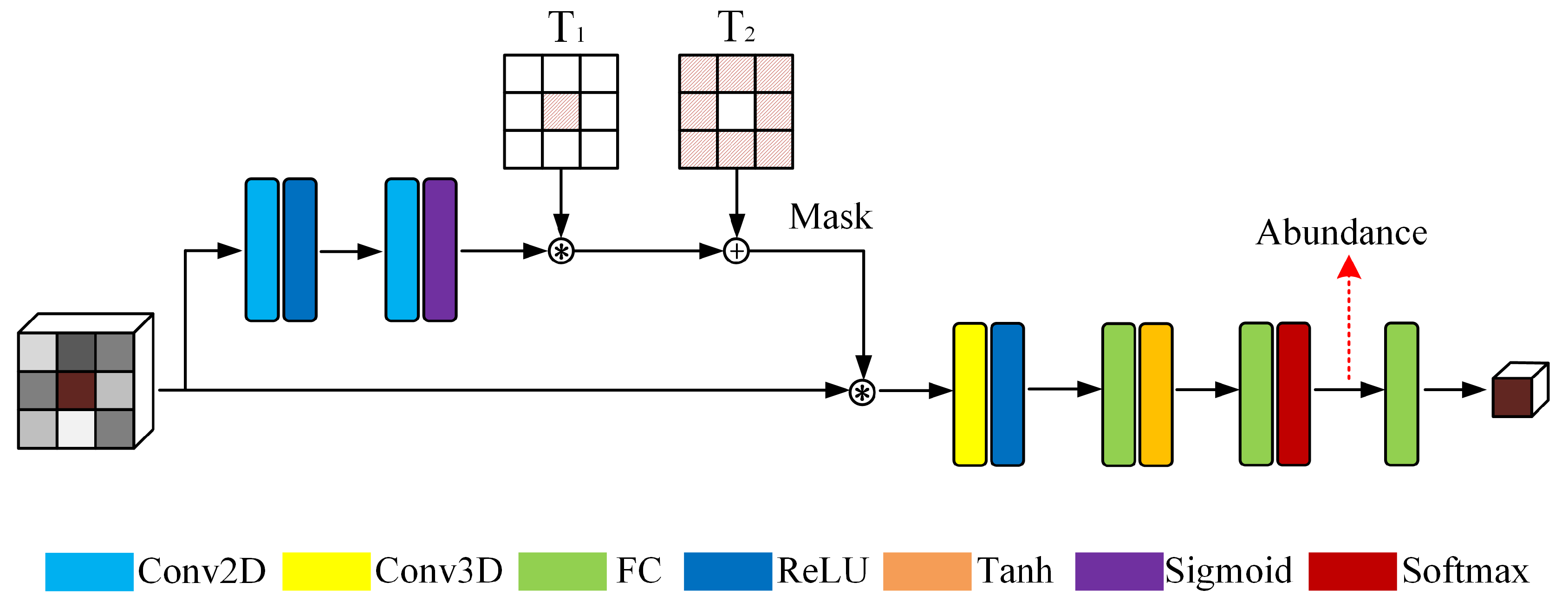
- We propose a gated three-dimensional convolutional autoencoder network to extract spectral and spatial features simultaneously. The architecture is constituted by a gated network that produces the attention weights assigned to neighboring pixels and an autoencoder backbone network that performs the unmixing procedure.
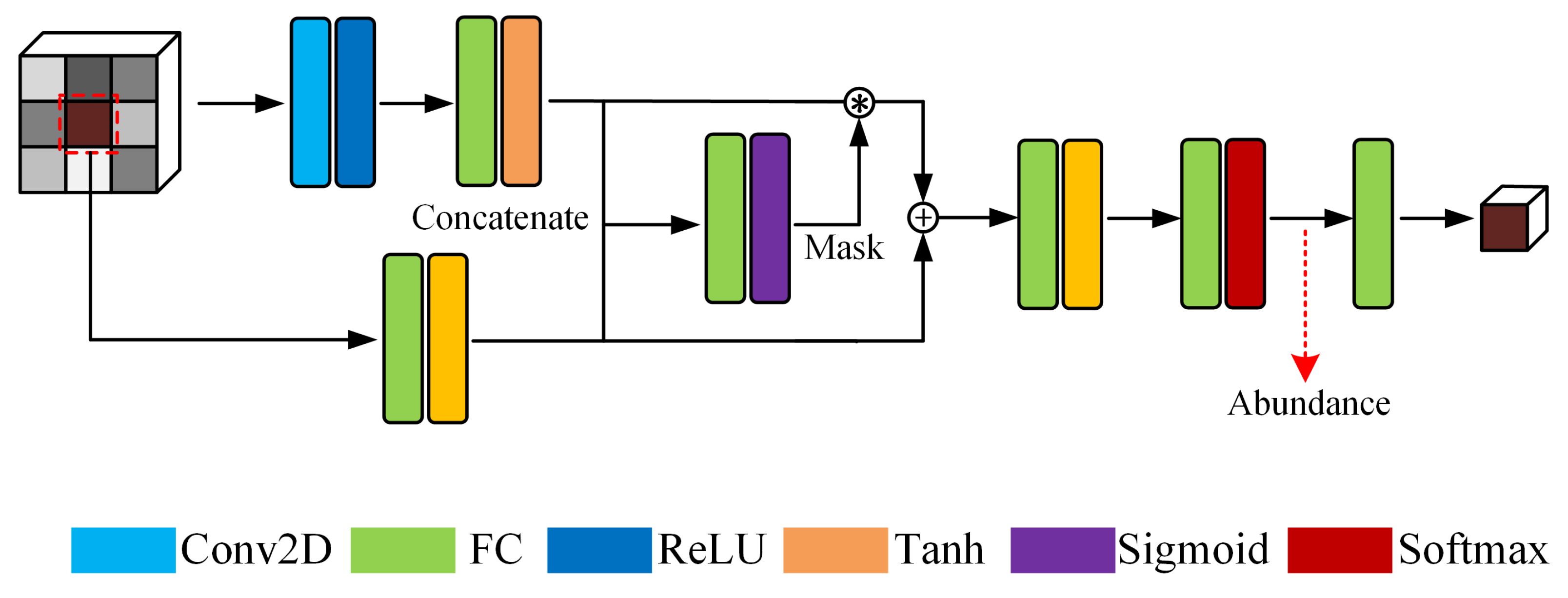
- We propose a gated dual branch autoencoder network to improve the exploitation efficiency of spatial and spectral information, respectively. The fully connected branch takes advantages of extracting spectral features, and the two-dimensional convolutional branch leverages the structural convenience of exploring inherent spatial correlation.
- Two regularizers, the gating regularization and abundance sparsity regularization, are imposed on the attention mask generated by the gated network and abundances, respectively, to enhance the accuracy of unmixing results and facilitate physically meaningful interpretation.
2. Related Works
2.1. Linear Mixing Model
2.2. Gating Mechanism
3. Methodology
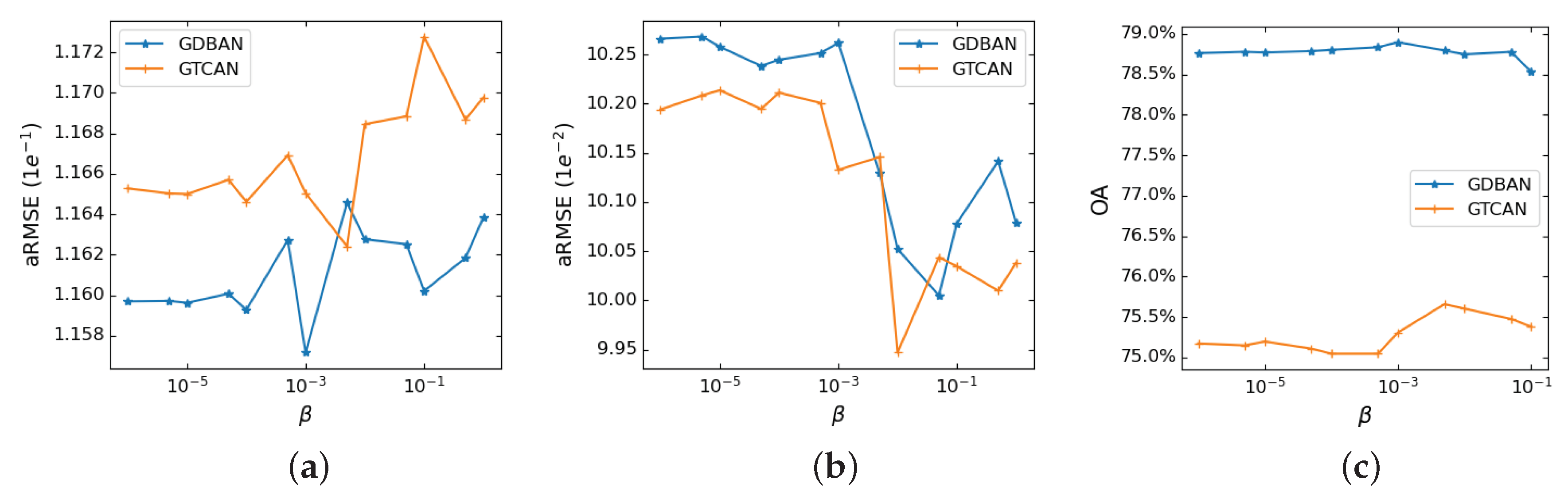
3.1. Gated Three-Dimensional Convolutional Autoencoder Network (GTCAN)
3.2. Gated Dual Branch Autoencoder Network (GDBAN)
4. Experiments
- SCLSU [36]. Scaled constrained least squares unmixing, equivalent to the non-negative least squares with normalized abundance, was proposed to address spectral scaling effects.
- CNNAEU [29]. Convolutional neural network autoencoder unmixing is a technique with fully two-dimensional convolutional architecture. Spatial information is used in this method.
- DCAE [28]. Deep convolutional autoencoder uses multiple one-dimensional convolutional layers to encode the spectral information and a fully connected layer to reconstruct the data. Spatial information is not incorporated in this method.
- AAS [22]. Autoencoder with adaptive abundance smoothing is a fully connected network, and an abundance spatial regularization is included in the loss function to exploit spatial correlation.
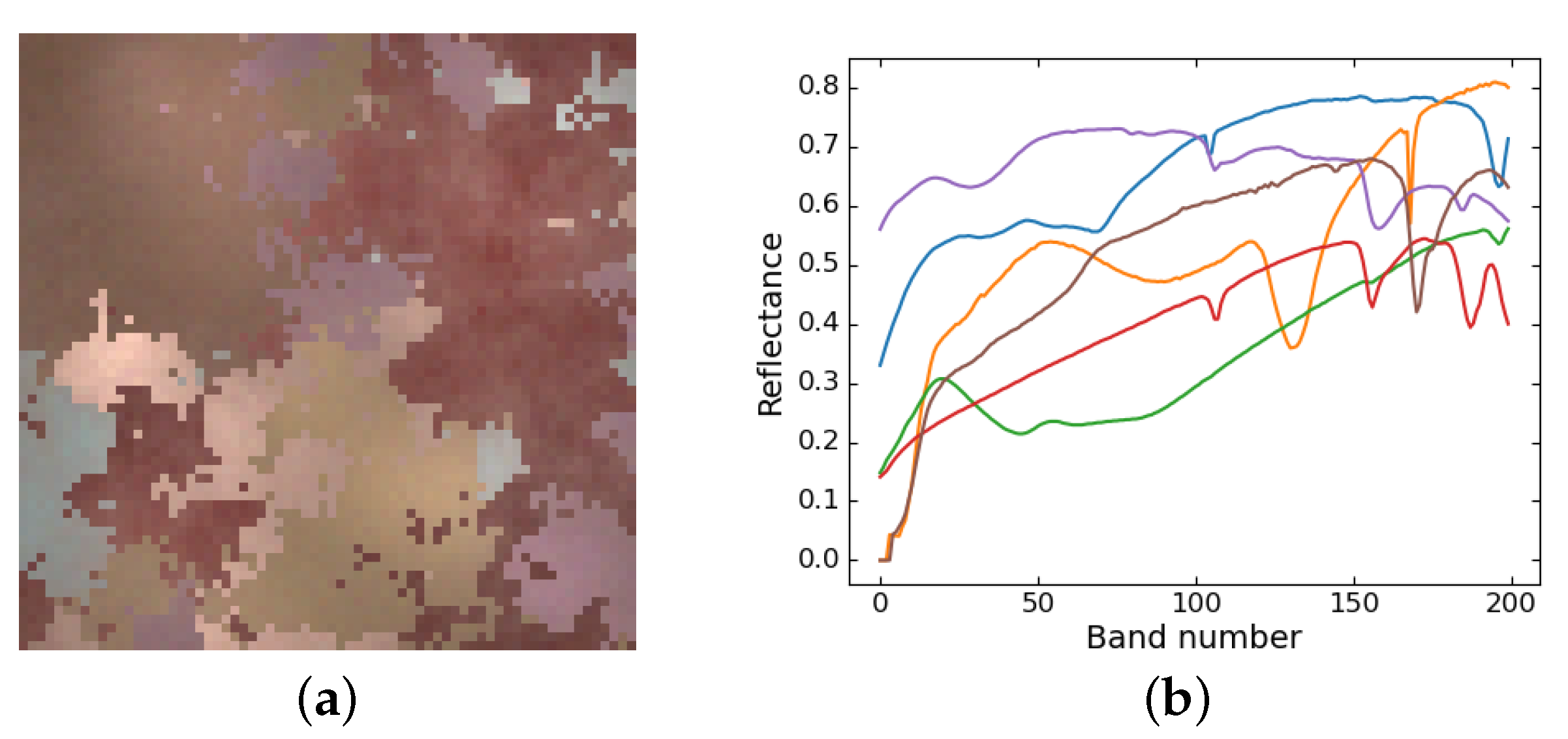
- Synthetic data. Six spectra were collected from the USGS library [37] and sampled into 200 bands as the endmembers. The abundances were generated by Gaussian fields using the toolbox at [38]. Then, to take the spatial–contextual correlation into account and model irregular illumination, we used normalized two-dimensional Gaussian distribution ranging from 0.75 to 1.25 to scale the synthetic abundances. Lastly, we synthesized the data following the LMM with random perturbations to simulate the noises. The shape of the synthetic image is , and the image is shown in Figure 3.
- Houston [29]. The raw data was used in the 2013 IEEE GRSS Data Fusion Contest, and we considered a subimage in this study. Four spectra are manually selected from the data as the endmembers. The ground truth is determined that if the spectral angle distance between a pixel and one of the reference endmembers is the closest, the pixel will be classified into the endmember category.
4.1. Experimental Setup
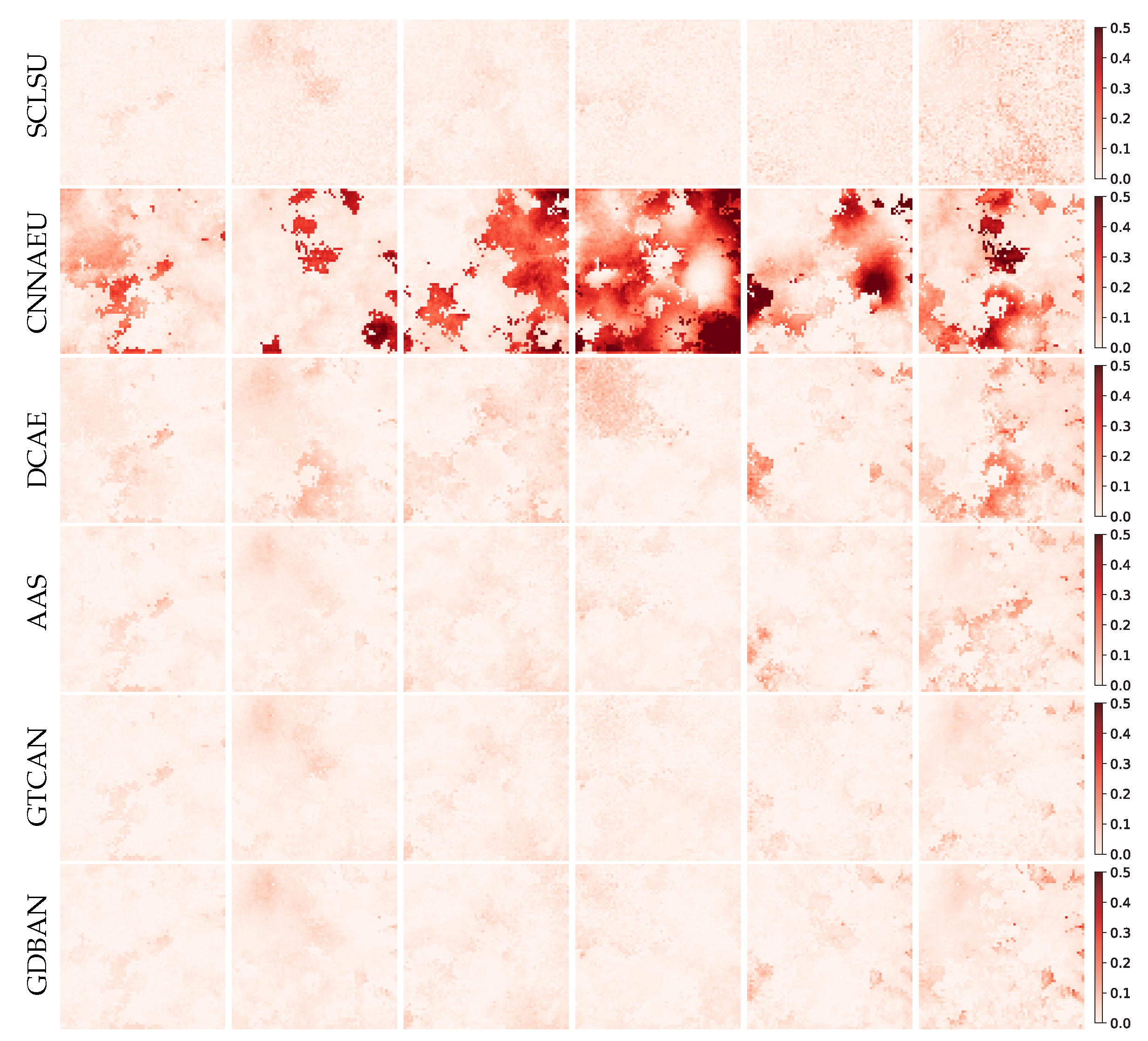
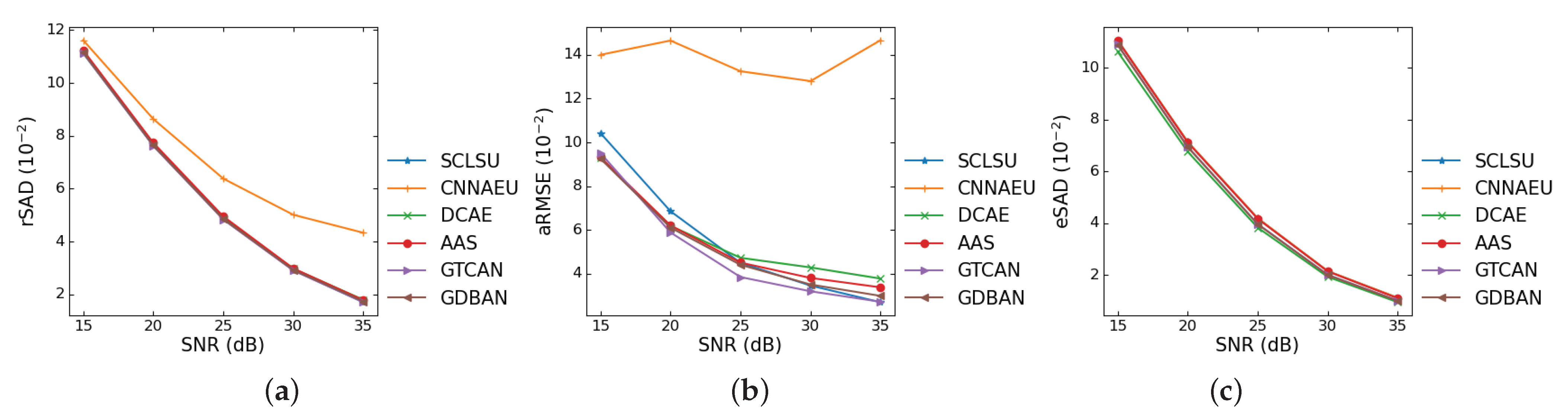
4.2. Experiments on Synthetic Data
4.3. Experiments on Real-World Data
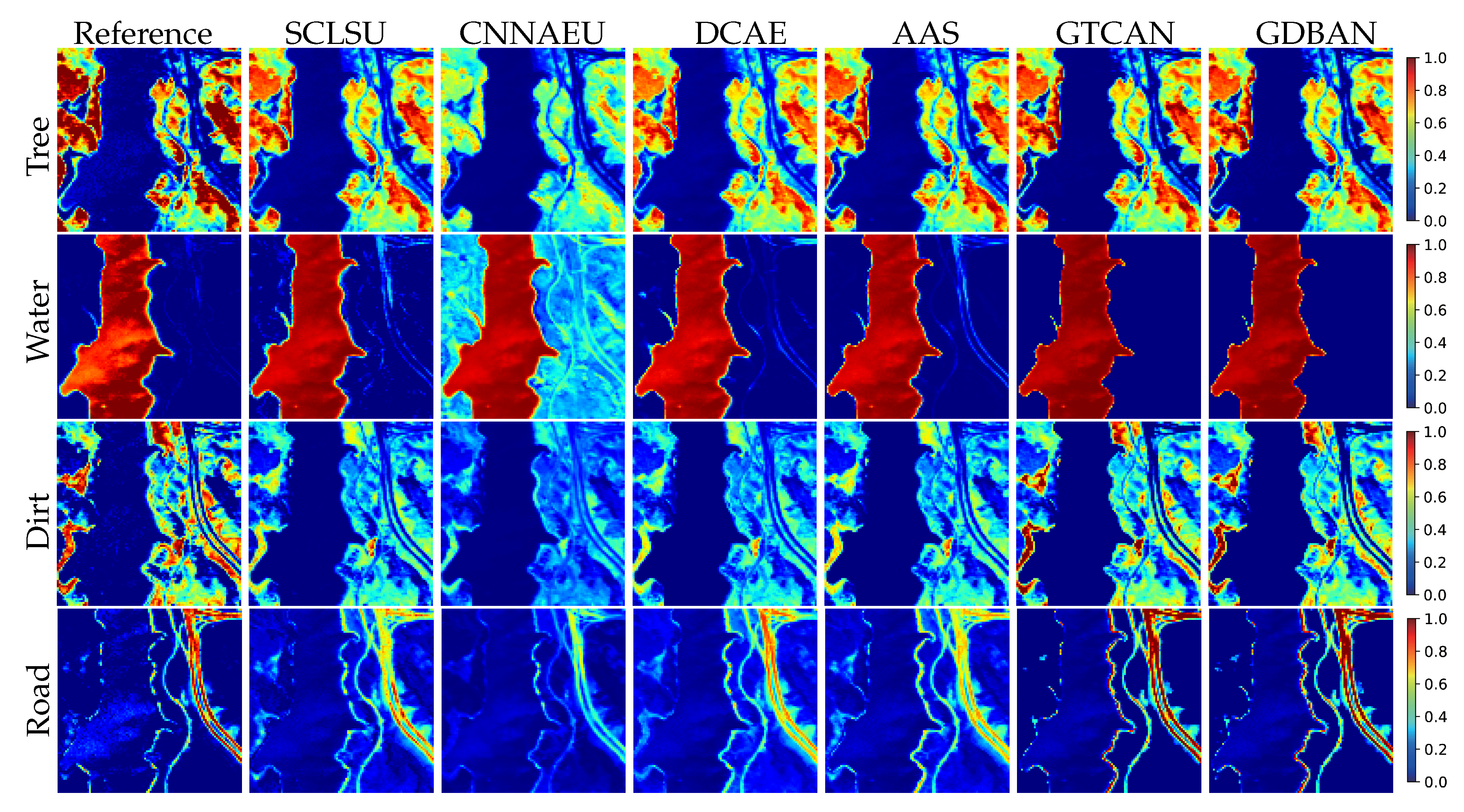
4.3.1. Experiments on Samson Data
4.3.2. Experiments on Jasper Ridge Data
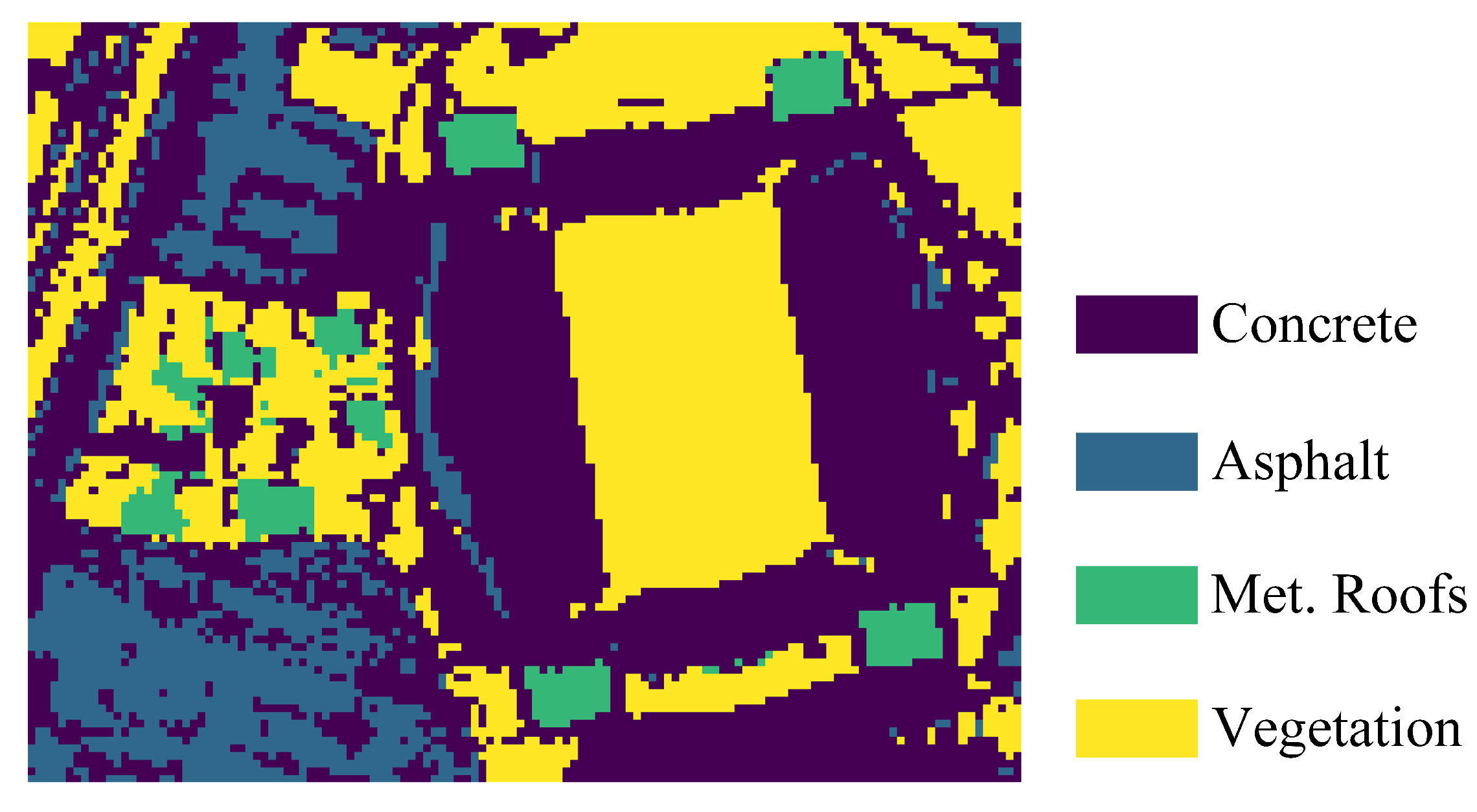
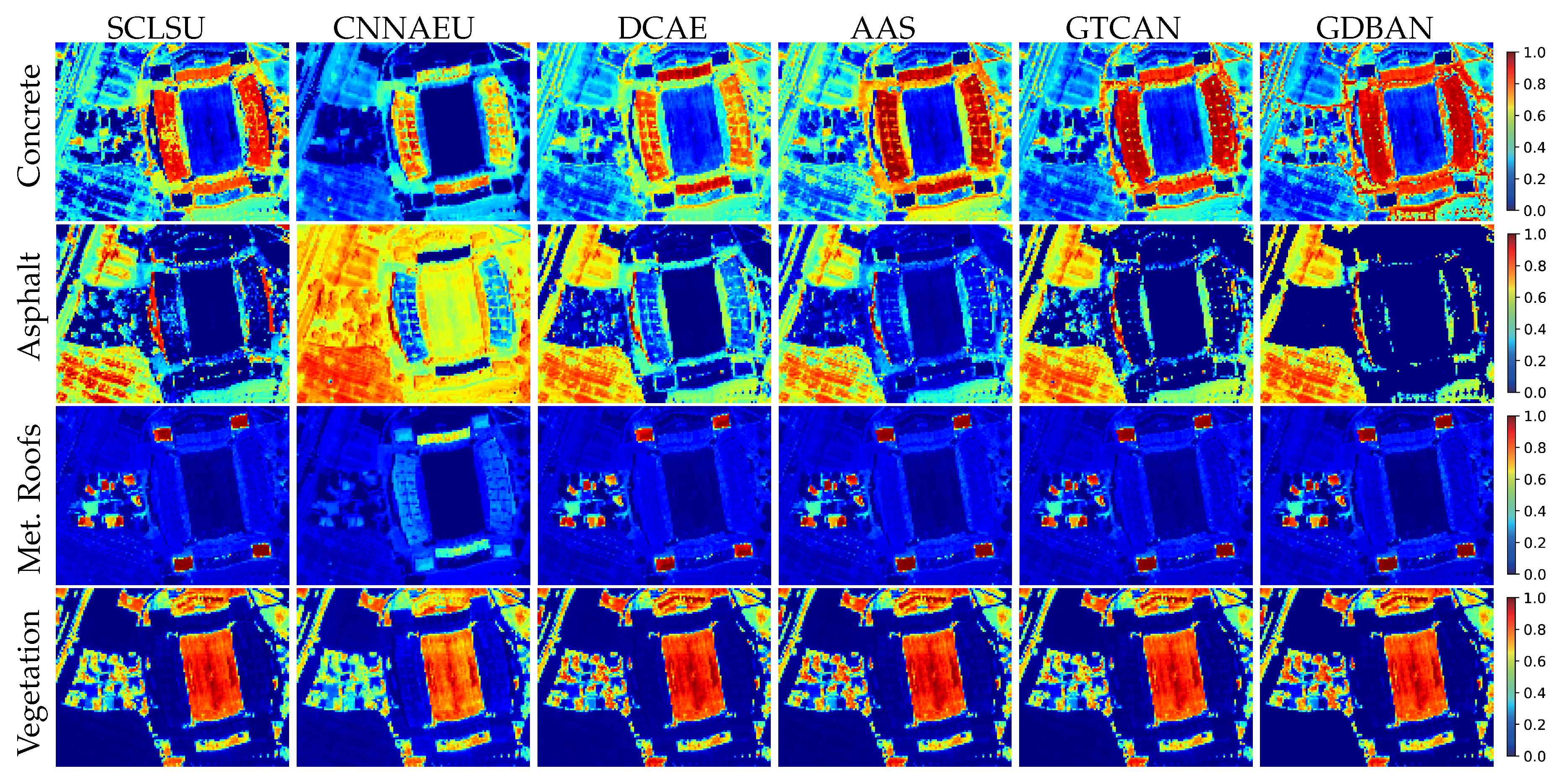
4.3.3. Experiments on Houston Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Keshava, N.; Mustard, J.F. Spectral unmixing. IEEE Signal Process. Mag. 2002, 19, 44–57. [Google Scholar] [CrossRef]
- Bhatt, J.S.; Joshi, M.V. Deep Learning in Hyperspectral Unmixing: A Review. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 2189–2192. [Google Scholar] [CrossRef]
- Heylen, R.; Parente, M.; Gader, P. A Review of Nonlinear Hyperspectral Unmixing Methods. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1844–1868. [Google Scholar] [CrossRef]
- Shi, C.; Wang, L. Incorporating spatial information in spectral unmixing: A review. Remote Sens. Environ. 2014, 149, 70–87. [Google Scholar] [CrossRef]
- Borsoi, R.A.; Imbiriba, T.; Bermudez, J.C.M.; Richard, C.; Chanussot, J.; Drumetz, L.; Tourneret, J.Y.; Zare, A.; Jutten, C. Spectral Variability in Hyperspectral Data Unmixing: A Comprehensive Review. arXiv 2020, arXiv:2001.07307. [Google Scholar]
- Ibarrola-Ulzurrun, E.; Drumetz, L.; Marcello, J.; Gonzalo-Martín, C.; Chanussot, J. Hyperspectral Classification Through Unmixing Abundance Maps Addressing Spectral Variability. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4775–4788. [Google Scholar] [CrossRef]
- Guo, A.J.; Zhu, F. Improving deep hyperspectral image classification performance with spectral unmixing. Signal Process. 2021, 183, 107949. [Google Scholar] [CrossRef]
- Zou, C.; Huang, X. Hyperspectral image super-resolution combining with deep learning and spectral unmixing. Signal Process. Image Commun. 2020, 84, 115833. [Google Scholar] [CrossRef]
- Li, J.; Peng, Y.; Jiang, T.; Zhang, L.; Long, J. Hyperspectral Image Super-Resolution Based on Spatial Group Sparsity Regularization Unmixing. Appl. Sci. 2020, 10. [Google Scholar] [CrossRef]
- Hasan, A.F.; Laurent, F.; Messner, F.; Bourgoin, C.; Blanc, L. Cumulative disturbances to assess forest degradation using spectral unmixing in the northeastern Amazon. Appl. Veg. Sci. 2019, 22, 394–408. [Google Scholar] [CrossRef]
- Li, H.; Zhang, L. A Hybrid Automatic Endmember Extraction Algorithm Based on a Local Window. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4223–4238. [Google Scholar] [CrossRef]
- Deng, C.; Wu, C. A spatially adaptive spectral mixture analysis for mapping subpixel urban impervious surface distribution. Remote Sens. Environ. 2013, 133, 62–70. [Google Scholar] [CrossRef]
- Jia, S.; Qian, Y. Constrained Nonnegative Matrix Factorization for Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2009, 47, 161–173. [Google Scholar] [CrossRef]
- Castrodad, A.; Xing, Z.; Greer, J.B.; Bosch, E.; Carin, L.; Sapiro, G. Learning Discriminative Sparse Representations for Modeling, Source Separation, and Mapping of Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4263–4281. [Google Scholar] [CrossRef]
- Iordache, M.; Bioucas-Dias, J.M.; Plaza, A. Total Variation Spatial Regularization for Sparse Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4484–4502. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Zhang, J.; Gao, Y.; Zhang, C.; Li, Z. Enhancing Spectral Unmixing by Local Neighborhood Weights. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1545–1552. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Zhang, L. Total Variation Regularized Reweighted Sparse Nonnegative Matrix Factorization for Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3909–3921. [Google Scholar] [CrossRef]
- Borsoi, R.A.; Imbiriba, T.; Bermudez, J.C.M.; Richard, C. A Fast Multiscale Spatial Regularization for Sparse Hyperspectral Unmixing. IEEE Geosci. Remote Sens. Lett. 2019, 16, 598–602. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Zhang, Z.; Wang, Q. Improved Collaborative Non-Negative Matrix Factorization and Total Variation for Hyperspectral Unmixing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 998–1010. [Google Scholar] [CrossRef]
- Li, H.; Feng, R.; Wang, L.; Zhong, Y.; Zhang, L. Superpixel-Based Reweighted Low-Rank and Total Variation Sparse Unmixing for Hyperspectral Remote Sensing Imagery. IEEE Trans. Geosci. Remote Sens. 2021, 59, 629–647. [Google Scholar] [CrossRef]
- Wang, J.J.; Huang, T.Z.; Huang, J.; Deng, L.J. A two-step iterative algorithm for sparse hyperspectral unmixing via total variation. Appl. Math. Comput. 2021, 401, 126059. [Google Scholar] [CrossRef]
- Hua, Z.; Li, X.; Qiu, Q.; Zhao, L. Autoencoder Network for Hyperspectral Unmixing with Adaptive Abundance Smoothing. IEEE Geosci. Remote Sens. Lett. 2020, 1–5. [Google Scholar] [CrossRef]
- Su, Y.; Marinoni, A.; Li, J.; Plaza, J.; Gamba, P. Stacked Nonnegative Sparse Autoencoders for Robust Hyperspectral Unmixing. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1427–1431. [Google Scholar] [CrossRef]
- Ozkan, S.; Kaya, B.; Akar, G.B. EndNet: Sparse AutoEncoder Network for Endmember Extraction and Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2019, 57, 482–496. [Google Scholar] [CrossRef] [Green Version]
- Qu, Y.; Qi, H. uDAS: An Untied Denoising Autoencoder With Sparsity for Spectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1698–1712. [Google Scholar] [CrossRef]
- Zhao, Z.; Hu, D.; Wang, H.; Yu, X. Minimum distance constrained sparse autoencoder network for hyperspectral unmixing. J. Appl. Remote Sens. 2020, 14, 1–15. [Google Scholar] [CrossRef]
- Dou, Z.; Gao, K.; Zhang, X.; Wang, H.; Wang, J. Hyperspectral Unmixing Using Orthogonal Sparse Prior-Based Autoencoder With Hyper-Laplacian Loss and Data-Driven Outlier Detection. IEEE Trans. Geosci. Remote Sens 2020, 58, 6550–6564. [Google Scholar] [CrossRef]
- Elkholy, M.M.; Mostafa, M.; Ebied, H.M.; Tolba, M.F. Hyperspectral unmixing using deep convolutional autoencoder. Int. J. Remote Sens. 2020, 41, 4799–4819. [Google Scholar] [CrossRef]
- Palsson, B.; Ulfarsson, M.O.; Sveinsson, J.R. Convolutional Autoencoder for Spectral–Spatial Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2021, 59, 535–549. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; van Merrienboer, B.; Gülçehre, Ç.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual Attention Network for Scene Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Xu, Z.; Zhang, H.; Wang, Y.; Chang, X.; Liang, Y. L1/2 regularization. Sci. China Inf. Sci. 2010, 53, 1159–1169. [Google Scholar] [CrossRef] [Green Version]
- Qian, Y.; Jia, S.; Zhou, J.; Robles-Kelly, A. Hyperspectral Unmixing via L1/2 Sparsity-Constrained Nonnegative Matrix Factorization. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4282–4297. [Google Scholar] [CrossRef] [Green Version]
- Hong, D.; Yokoya, N.; Chanussot, J.; Zhu, X.X. An Augmented Linear Mixing Model to Address Spectral Variability for Hyperspectral Unmixing. IEEE Trans. Image Process. 2019, 28, 1923–1938. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Clark, R.N.; Swayze, G.A.; Wise, R.A.; Livo, K.E.; Hoefen, T.M.; Kokaly, R.F.; Sutley, S.J. USGS Digital Spectral Library splib06a; Technical Report; US Geological Survey: Reston, VA, USA, 2007. [Google Scholar]
- Grupo de Inteligencia Computacional, Universidad del País Vasco/Euskal Herriko Unibertsitatea. Hyperspectral Imagery Synthesis Toolbox; Universidad del País Vasco/Euskal Herriko Unibertsitatea (UPV/EHU): Leioa, Spain, 2021. [Google Scholar]
- Zhu, F.; Wang, Y.; Fan, B.; Xiang, S.; Meng, G.; Pan, C. Spectral Unmixing via Data-Guided Sparsity. IEEE Trans. Image Process. 2014, 23, 5412–5427. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nascimento, J.M.P.; Dias, J.M.B. Vertex component analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef] [Green Version]

| GTDAN | GDBAN |
|---|---|
| Gated Net | First Branch |
| Conv2D, size = , channel = 16, padding = 1 | Conv2D, size = , channel = 128 |
| Conv2D, size = , channel = 1, padding = 1 | FC, length = 64 |
| AE Net | Second Branch |
| Conv3D, size = , channel = 16 | FC, length = 64 |
| FC, length = 64 | Gated Net |
| FC, length = P | FC, length = 1 |
| FC, length = L, bias = false | The Rest |
| FC, length = 32 | |
| FC, length = P | |
| FC, length = L, bias = false |
| Methods | rSAD | aRMSE | eSAD |
|---|---|---|---|
| SCLSU | 2.90 ± 0.12 | 3.17 ± 0.25 | 1.89 ± 0.23 |
| CNNAEU | 5.01 ± 0.67 | 12.79 ± 4.66 | 1.88 ± 0.23 |
| DCAE | 2.95 ± 0.12 | 3.88 ± 0.40 | 1.63 ± 0.23 |
| AAS | 2.96 ± 0.12 | 3.55 ± 0.25 | 1.87 ± 0.23 |
| GTCAN | 2.88 ± 0.12 | 2.85 ± 0.21 | 1.66 ± 0.24 |
| GDBAN | 2.90 ± 0.12 | 3.18 ± 0.21 | 1.65 ± 0.23 |
| Methods | SCLSU | CNNAEU | DCAE | AAS | GTCAN | GDBAN |
|---|---|---|---|---|---|---|
| Time (s) | 1 | 34 | 99 | 38 | 86 | 72 |
| Data | Methods | rSAD | aRMSE | eSAD |
|---|---|---|---|---|
| Samson | SCLSU | 5.22 ± 0.25 | 13.27 ± 2.34 | 6.61 ± 0.26 |
| CNNAEU | 10.35 ± 1.02 | 24.13 ± 0.65 | 6.59 ± 0.26 | |
| DCAE | 3.76 ± 0.08 | 14.94 ± 1.68 | 6.57 ± 1.40 | |
| AAS | 5.30 ± 0.25 | 13.11 ± 2.35 | 6.54 ± 0.29 | |
| GTCAN | 3.45 ± 0.03 | 10.94 ± 1.35 | 6.56 ± 1.04 | |
| GDBAN | 3.45 ± 0.04 | 11.04 ± 1.41 | 6.51 ± 1.08 | |
| Jasper Ridge | SCLSU | 12.55 ± 5.82 | 18.41 ± 3.01 | 24.43 ± 5.73 |
| CNNAEU | 16.19 ± 6.21 | 17.90 ± 1.80 | 24.43 ± 5.73 | |
| DCAE | 8.92 ± 3.42 | 17.08 ± 3.39 | 22.76 ± 4.95 | |
| AAS | 12.49 ± 5.91 | 17.68 ± 3.36 | 24.18 ± 5.72 | |
| GTCAN | 6.60 ± 0.46 | 16.24 ± 3.39 | 21.27 ± 5.08 | |
| GDBAN | 6.51 ± 0.45 | 16.23 ± 3.24 | 23.20 ± 7.25 |
| Methods | rSAD | OA | eSAD |
|---|---|---|---|
| SCLSU | 4.04 ± 0.84 | 71.33 ± 13.85 | 7.59 ± 0.68 |
| CNNAEU | 11.56 ± 1.81 | 59.23 ± 6.71 | 7.55 ± 0.68 |
| DCAE | 3.08 ± 0.65 | 73.51 ± 12.70 | 7.35 ± 0.71 |
| AAS | 4.10 ± 0.74 | 74.72 ± 15.59 | 7.55 ± 0.67 |
| GTCAN | 2.48 ± 0.43 | 75.71 ± 16.26 | 7.39 ± 0.77 |
| GDBAN | 2.76 ± 0.33 | 78.62 ± 16.41 | 6.06 ± 1.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hua, Z.; Li, X.; Jiang, J.; Zhao, L. Gated Autoencoder Network for Spectral–Spatial Hyperspectral Unmixing. Remote Sens. 2021, 13, 3147. https://0-doi-org.brum.beds.ac.uk/10.3390/rs13163147
Hua Z, Li X, Jiang J, Zhao L. Gated Autoencoder Network for Spectral–Spatial Hyperspectral Unmixing. Remote Sensing. 2021; 13(16):3147. https://0-doi-org.brum.beds.ac.uk/10.3390/rs13163147
Chicago/Turabian StyleHua, Ziqiang, Xiaorun Li, Jianfeng Jiang, and Liaoying Zhao. 2021. "Gated Autoencoder Network for Spectral–Spatial Hyperspectral Unmixing" Remote Sensing 13, no. 16: 3147. https://0-doi-org.brum.beds.ac.uk/10.3390/rs13163147






