Figure 1.
A flow-chart describing the AIRTop algorithm. Red box is stage 1 (feature extraction), blue box is stage 2 (topology map matching), orange box is stage 3 (matching process), green box is stage 4 (validation and accuracy).
2.1. Significant Features
CP identification is the key step in image registration. There are two main methods to detect CPs: area-based and feature-based. In feature-based algorithms, an image is represented in a compact form by a set of features. The common features are edges, regions, lines, line endings, line intersections, or region centroids. Thus, the feature-based methods are adopted when objects’ features are distinct. These methods are relatively more powerful for the registration of different types of images with distortions.
Because the image scenes studied in this research have a large area, region of interest (ROI) selection, which contains relatively large radiometric variation (grayscale contrasts), is conducted prior to feature detection. The idea of addressing the registration problem by applying a global-to-local level strategy has proven to be an elegant way of speeding up the whole process, while enhancing the accuracy of the registration procedure [
11]. Thus, we expected this method to greatly reduce false alarms in the subsequent feature extraction and CP identification steps. To select the distinct areas, an image is divided into adjacent small blocks (10% × 10% of image pixels with no overlap between blocks). Then, entropy is calculated for each block (with a filter size of 20% × 20% of the pixel block), which can be used to measure the local variation within the block.
Figure 2 shows the entropy map of an image (subset of one block) of 420 × 420 pixels, where the blocks with large entropies correspond to the areas with relatively high variation, such as buildings (two roofs in the center of the image) and roads (located in the upper right part of the image). A threshold η is set to choose the blocks with large entropies as ROIs for CP detection. This ensures that at least one ROI will be selected from each patch, which may result in a wider distribution of CPs.
Significant features are then extracted by SURF algorithm. First, the fast-Hessian corner detector [
16], which is based on integral image and approximation, is performed. The Hessian matrix is responsible for primary image rotation (
Figure 3) using principal points that are identified as being of interest. The next stage is to make a descriptor of local gray level geometry features. The vector representing the local feature is created by a combination of the Haar wavelet response. The values of dominant directions are defined relative to the principal point.
The approximated determinant of the Hessian represents the blob response in the image. These responses are saved in a blob response map over different scales, and local maxima are detected. An integral image (Equation (1)) at a location
represents the sum of all pixels in the input image
within a rectangular region formed by the origin and
. The sum of intensities inside a rectangular region (e.g., roofs) is calculated using integral images [
17]:
The Haar wavelet of the integral image is calculated. The responses are represented as points in a space with the horizontal response strength along the abscissa and the vertical response strength along the ordinate. The dominant orientation is estimated by calculating the sum of all responses within a sliding orientation window. The horizontal and vertical responses within the window are summed, yielding a local orientation vector. The longest vector defines the orientation of the point of interest [
18].
The results of the SURF algorithm are three additional images (integral image, primary rotated image, and feature orientation image) of the reference and sensed images. The next stage is feature extraction from both the reference and sensed images, by applying two algorithms supported by the SURF algorithm images: The Hough Transform [
19] used for long (global) edge extraction and the Canny detector [
20] used for extraction of shorter (local) edges.
Figure 2.
ROI selection. (A) Original image. (B) Entropy map of 10 adjacent blocks.
Figure 2.
ROI selection. (A) Original image. (B) Entropy map of 10 adjacent blocks.
Figure 3.
Repeatability score for image rotation of up to 180°.
Figure 3.
Repeatability score for image rotation of up to 180°.
The suggested process extracts long edges related to road features with the Hough Transform prior to the Canny operator. Since SURF integral (magnitude) and orientation images are applied as the base layer for feature detection, we propose modifying several stages of the Canny operator. First, the process of non-maximal suppression (NMS), also known as non-maximum, is imposed on the integral SURF image. Second, the edge-tracking process is controlled by a predefined threshold. The traditional Canny operator carries out the edge tracking according to a high and low (two) thresholds. The tracking of one edge begins at a pixel whose gradient is larger than the high threshold, and tracking continues in both directions from that pixel until there are no more pixels with gradients larger than the low threshold. However, it is usually difficult to set the two thresholds properly, especially for remotely sensed images, in view of the frequent nonuniformity of illumination and contrast in the different pixels [
21]. In our method, the short (local) edges can be implemented without two predefined thresholds, as shown after using Hough Transform, relatively long edges are related to roof features.
Since it is difficult to detect continuous and stable edges solely from the images (reference and sensed), the morphological closing operation, produced by the combination of dilation and erosion operations, is employed. During this process, the edge detected areas are integrated into individual features. Finally, all of the extracted features are converted from raster to vector format and saved as a GIS project. While roofs are converted into polygons, roads are converted into polylines that cross along the central line of the detected (long edged) features.
The extracted features are enhanced using a thresholding program that creates a binary raster image. Vectors are then extracted from this binary image by use of a simplified chord test [
22]. A pixel is considered to be part of the vector if the distance from its center to the vector being created is less than one pixel width. Modifications of the features include smoothing the vectors to remove or reduce the amount of aliasing so that they will have a more “real” appearance, or reducing the number of vertices (within vectors) produced during the initial translation.
A measure of the displacement between vector and initial raster feature provides more accurate information about the translations (
Table 1). As the area of this study is large, representing mixed land uses and complex structures and shapes, we examined the accuracy of the vectorization/rasterization models (ArcMap 9.3, ESRI) based on simulated geometric data. This test quantified the amount of area committed/omitted/correctly assigned to the converted feature (from raster to vector and
vice versa). This analysis was represented as an area error matrix.
Table 1.
The error matrix for simulated geometric features (raster resolution 0.25 m; size 60 m × 60 m; square area is 9 m2; shape area is 7 m2; circle radius is 0.75 m with area of 1.77 m2) and commission/omission of errors (in m2).
Table 1.
The error matrix for simulated geometric features (raster resolution 0.25 m; size 60 m × 60 m; square area is 9 m2; shape area is 7 m2; circle radius is 0.75 m with area of 1.77 m2) and commission/omission of errors (in m2).
| | Vector Data | |
| Raster Data | | Background | Square | Shape | Circle | |
| Background | 42.49284 | 0.005 | 0.002 | 0.00016 | 42.5 |
| Square | 0.002 | 8.998 | 0.000 | 0.000 | 9 |
| Shape | 0.004 | 0.000 | 6.996 | 0.000 | 7 |
| Circle | 0.00116 | 0.000 | 0.000 | 1.7684 | 1.77 |
| | 42.5 | 9.003 | 7.016 | 1.76856 | |
2.2. Topology Matching
Topological matching is used to reduce the search range or check the results of geometric matching since it is seldom used alone. Topological methods can spread the matching into the whole network, but this requires high topological similarity of the two datasets, as in topological transfer method [
23].
The data pre-processing stage standardizes input data sets, and ensures that conflation data sets have the same data format and the same north direction (SURF-rotated image). As part of the preparation, the search key on the shapes must be defined. In a real data set, the features extracted from reference and sensed images are biased by noises and retained artifacts. Thus, out of the many possible methods for defining a search key, the selected method must include a succinct representation of the shape, and must not be sensitive to noise or small errors on the feature surface. We propose to use the Multiresolution Reeb Graph (MRG) skeleton structure method [
24]. The Reeb graph uses a continuous scalar function on an object by the equivalence relation that identifies the points belonging to the same connected component [
25].
In the topology-matching process, the Reeb graph is used as a search key that represents feature shapes. A node of the Reeb graph represents a connected component in a particular region, and adjacent nodes are linked by an edge if the corresponding connected components of the object are contiguous. The Reeb graph is constructed by repartitioning each region in a binary manner.
The output of the resampling process is a hierarchical design of nodes (base and support) for each extracted feature. Then, the integral of the geodetic distance is calculated using Dijkstra’s algorithm, which evaluates approximated values, as suggested by Hilaga
et al. [
26].
The construction of the MRG is illustrated in
Figure 4. The following notations were defined: (1) R-node (red points are MRG node for s
0 level, blue points for s
1 level, green points for s
3 level, orange points for s
4 level); (2) R-edge (the thick lines connecting R-nodes of different resolutions); (3) T-set (the thin lines corresponding to each R-node in triangle connection); (4) μn-range (connecting function of R-node or T-set).
Figure 4.
Multiresolution Reeb graph in 2D for a roof as the selected feature. (A) Original image; (B) map of extracted features; (C) selected feature with respect to the corner detection function; and (D) corresponding Reeb graph.
Figure 4.
Multiresolution Reeb graph in 2D for a roof as the selected feature. (A) Original image; (B) map of extracted features; (C) selected feature with respect to the corner detection function; and (D) corresponding Reeb graph.
Topology matching follows coarse-to-fine resolution levels to estimate similarities between features. The comparison between reference and sensed images is based on the vertex attributes (R-node, R-edge, T-set, and μn-range) of each feature in these images. The most influential R-node is selected based on hierarchy design for each feature separately. The record of these nodes is compared by attributes and summarizes to the matching list of candidate R-nodes. The matching process is guided by two rules for similarity: (1) How the final similarity is reduced by the matching; (2) adjacent effect of nearest R-nodes.
2.3. Weight-Based Topological Map-Matching
The MRG based approach has major limitations when used with airborne and spaceborne image registration and processing. This method is affected by connectivity within the feature surface and is not bound to represent the true skeleton of the features. Furthermore, it is sensitive to the geometry of the feature, and thus is not faithful to subgraph matching.
To overcome these limitations, we suggested formulating topology relations (connectivity and contiguity) between extracted features within reference and sensed images individually. According to the topology relation of polygon to polygon, polygon to polyline, and polyline to polyline, matching can be deduced. The topology rules that control the interaction between features are performed at two levels. In the first level, each feature is globally aware and related to all features within the image. In the second level, each feature is introduced to the nearest neighborhood and has knowledge of its local surroundings. This level overlaps with the ROI that was selected by adjacent small blocks during the feature-extraction stage.
Consider first how to formulate the spatial dependency and relation of a single image having n features. Since any error in the initial matching process will lead to mismatching of the CP positions, a robust three-stage approach is introduced. The first stage is identification of a set of candidate CPs. The following stages involve both reference and sensed images. The second stage is identification of correct CPs among candidate CPs using heading weight (Hw) and proximity weight (Pw). The final stage is to estimate similarity between selected features supported by the MRG skeleton structure.
First, the AIRTop algorithm creates an error tolerance around features, the radius of which is primarily based on spatial resolution of given image. All candidate CPs that are either within, crossing or tangent to the tolerance of a certain point are related to it and considered a suitable candidate. Identification of candidate CPs is established on the R-node for the s0 level (MRG nodes) of each feature. A set of candidate CPs is represented by the nodes and vertices of polygons (features related to roofs) and polylines (features related to roads).
Next, a square proximity matrix of the distances between features is created. We employ the Gaussian-weighted matrix using Chord Length Distribution (CLD) as suggested by Taylor and Cooper [
27]. The heading is considered a cosine angle between features that has been included in a set of candidate CPs, in reference and sensed orientation (SURF result) maps. This parameter measures the angle difference between orientation maps with respect to the primary image rotation (SURF).
Finally, the similarity of the features is evaluated by MRG skeleton structure. The comparison includes all of the MRG parameters (R-node, R-edge, T-set and μn-range) for the features in both reference and sensed images.
The values of three weight coefficients (heading weight, proximity weight and MRG similarity) are estimated and summed to give the total weight score. The weight-optimization process parallels the map-matching (
MM). The first feature is selected from a set of candidate CPs on the sensed image and compared to features on a set of reference images by the three spatial descriptions/attributes of the features. The process initiates with the first-level topology rules (in which features are related to an entire image), where feature attributes are global connectivity and contiguity matrices. The comparison at this level provides a temporal list of fitting CPs candidates from reference image for each feature in the sensed image. The process continues at the local level using the second level of topology rules (in which features are related to the nearest neighborhood), where feature attributes are local connectivity and contiguity matrices, proximity matrix, heading matrix and MRG parameters (for each feature individually). For a specific feature (in the sensed image), the optimization process starts with the map-matching of a positioning-fixed CP between sensed and reference images. If no fixed CPs are found, the algorithm continues to the next region of interest and candidate CPs are listed in the temporal file. In the case of fixed CPs, the random values for the three coefficients (heading weight (
Hw), proximity weight (
Pw) and MRG similarity) are generated between 1 and 100 (so that the sum of all coefficients equals 100). Using these values, the process then calculates the total weight score (
MMtotal) for all features at the local level and indentifies the correct CPs based on the highest total weight score value (Equation (2)):
The relationship between percentage of wrong CPs identified and the weight coefficients (heading weight (
Hw), proximity weight (
Pw) and MRG similarity) is developed using a regression analysis. Since the functional relationship between the weights and the map-matching error is an internal test for accuracy, various specifications are considered. We assumed that the map-matching depends on the individual weights (
Hw,
Pw,
MRG), their square terms and their inverse terms. In Equation (3),
is a selected point,
are the regression coefficients to be estimated and
is the error of rasterization/vectorization conversion that has been assumed to be independently and identically distributed with constant variance:
To minimize the error, some restrictions have to be imposed. As discussed, the sum of all weight coefficients is set to 100 and the minimum and maximum values of each weight coefficient are set at 1 and 100, respectively. The optimization function obtained from the
MMerror analysis is given in Equation (4):
subject to:
Equation (4) was optimized using the nonlinear minimization method proposed by Michael
et al. [
28]. The values of the weight coefficients were calculated by identifying the global minimum of the map‑matching stage.
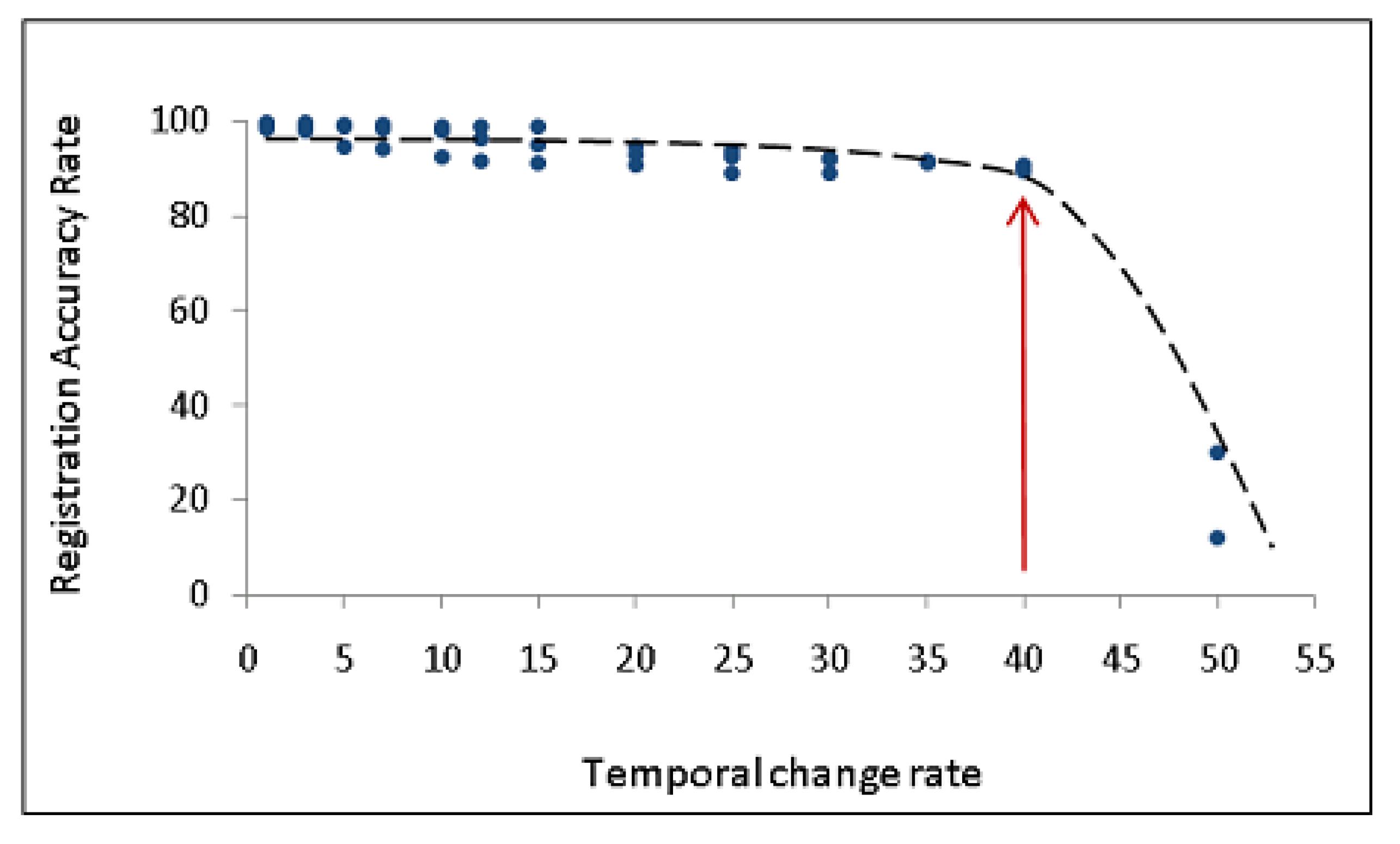
The accuracy of the map-matching procedure is estimated by mathematical representation of RMSE value. The results of the local map-matching are determined by a predefined RMSE threshold that is dependent on the spatial resolution of the images in question. If the algorithm fails to identify the correct CPs among the candidate features and the RMSE exceeds the threshold, then the algorithm regenerates another set of random values of coefficients and repeats the map-matching. This process continues by optional loop procedure until the algorithm selects the correct CPs.
To determine the accuracy of the map-matching procedure, we modified the commonly used test Point Error (TPE) method [
15]. TPE defines the test set by excluding groups of CPs from the map‑matching procedure and measures the accuracy of the registration process. Our modification of the TPE uses marked features rather than fixed CPs. These features are randomly chosen from the extracted-features map according to ROI. As a result, no regions are marked due random selection mode. Our scoring method does not allow setting TPE to zero due to overfitting. In our algorithm, 10% of all CPs are excluded as a test set from TPE evaluation. Again, if the algorithm fails to transform and resample the sensed image and TPE exceeds the threshold, then the algorithm regenerates by optional loop procedure.
For a given level of detail, the inner loop of the algorithm, as indicated in
Figure 1, optimizes the registration process in the global and local image domains. By globally optimizing the corresponding ROIs, the optimization process can rapidly converge or even skip areas that do not contain a required feature, leading to considerable savings in execution time. The strategy of local registration by global optimization can be justified by the following facts. If the CPs are already close to their optimal position within the selected ROI, the separated optimization of each CP leads to the same solution as the optimization of all points within the selected ROI. The optimal value of the similarity is achieved by maximizing the local topological relation of each component to the global similarity of the ROIs. The contributions of topological relation to each ROI are independent of each other because they are achieved by small rearrangements of the CPs, which adjust the registration of both images in local areas.