Image-Based Delineation and Classification of Built Heritage Masonry
Abstract
:1. Introduction
2. Problem Statement: Automatic Image-Based Delineation and Classification of Masonry
2.1. General Context
2.2. Automatic Delineation of Masonry: Challenges
2.3. Built Heritage Element Classification
3. Existing Approaches for Automatic Delineation
3.1. General Purpose Image Processing Tools
3.2. Image-Based Granulometry
3.3. Building Modeling and Segmentation
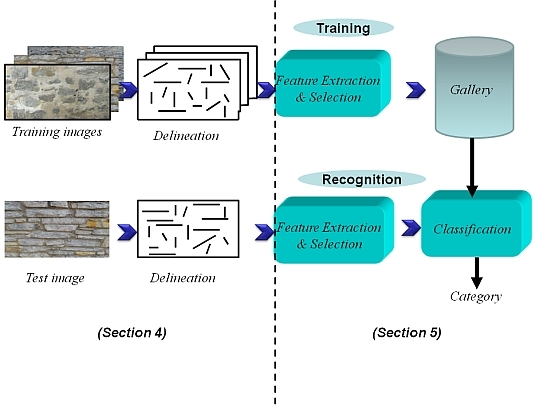
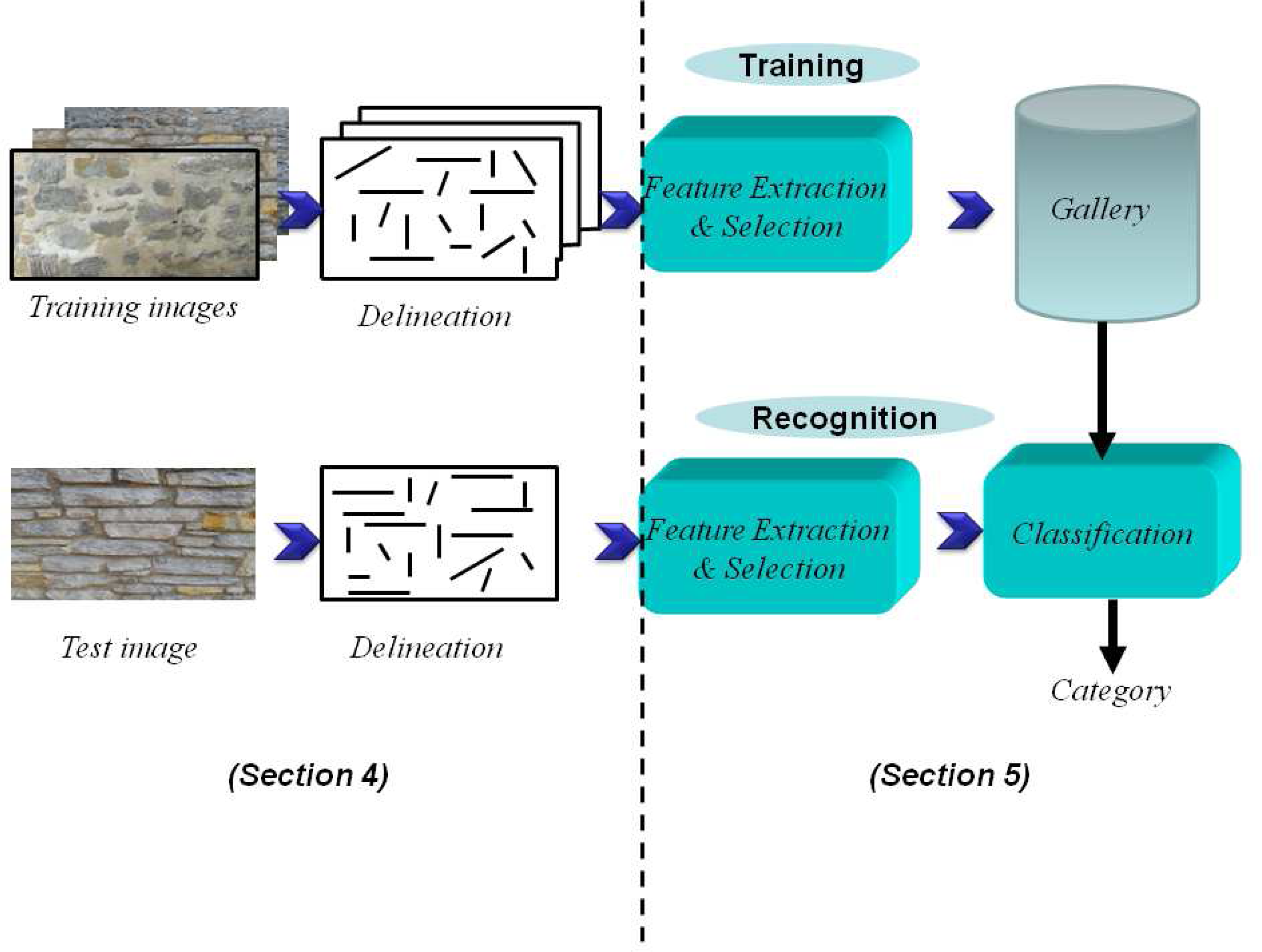
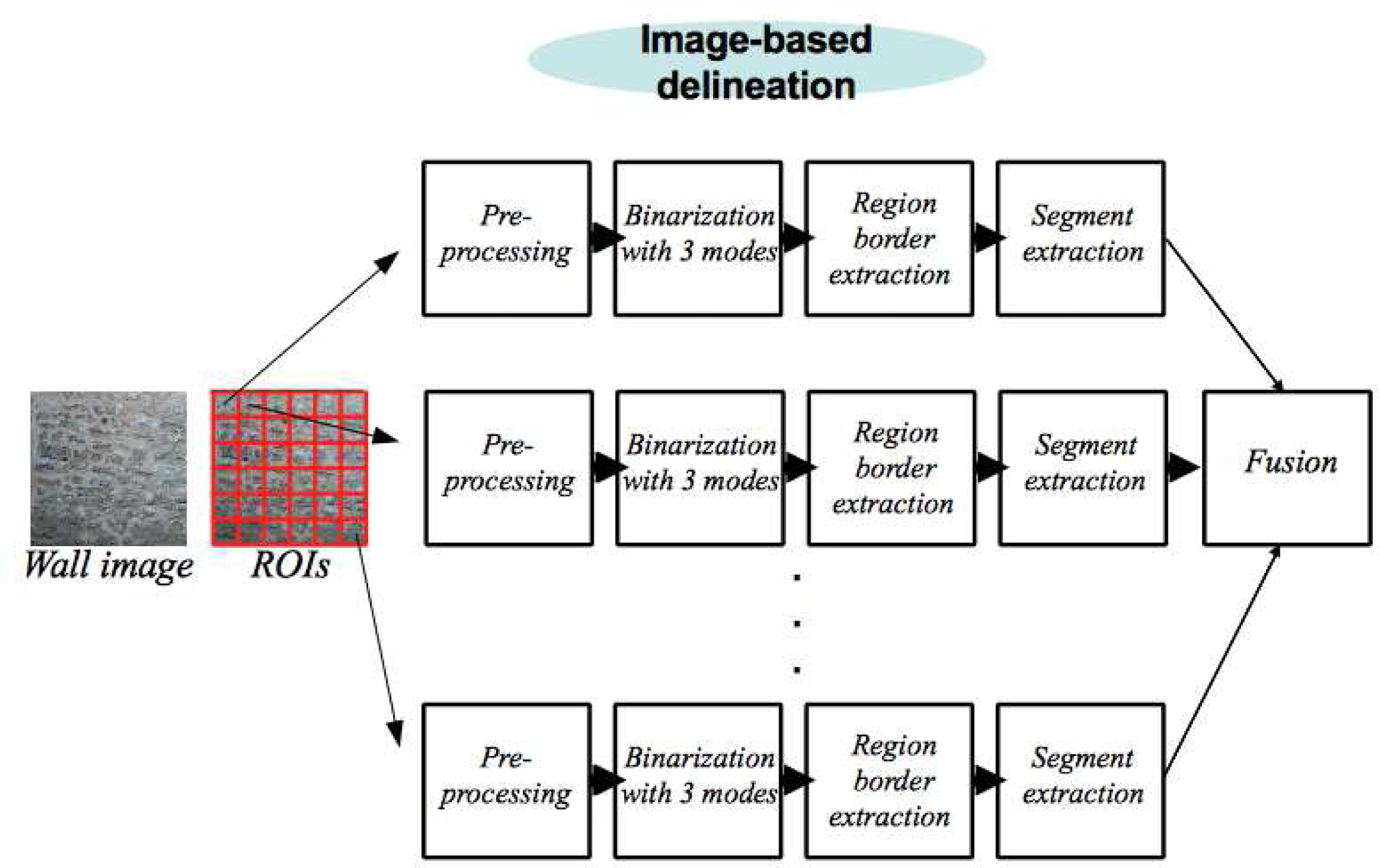
4. Proposed Delineation Framework
4.1. Preprocessing of an ROI
4.2. Processing of an ROI
4.2.1. Region Segmentation Using Most Frequent Intensities
4.2.2. Extracting Boundaries by Removing Inner Patches
4.2.3. Straight Segment Extraction
4.3. Fusion of ROI Delineations and Post-Processing
5. Results and Performance Evaluation
5.1. Automatic Delineation Results
5.2. Performance Evaluation: Masonry Classification
5.2.1. Machine Learning Approaches
5.2.2. Feature Selection
5.2.3. Experimental Results
- Regarding the lengths, these statistics are the minimum, maximum, least frequent, most frequent, mean and standard deviation.
- Regarding the slopes, the statistics used are the maximum, least frequent, most frequent, mean, standard deviation and percentage of slopes that are vertical (or very nearly vertical, i.e., a 90-degree slope).
- For slope differences, the statistics used are the least frequent, most frequent, mean, standard deviation, percentage of differences between zero and four degrees (pairs of segments that are parallel or nearly parallel) and percentage of differences between 86 and 94 degrees (pairs of segments that are perpendicular or nearly perpendicular).
- For the horizontal accumulation, the maximum (expressed as the percentage of the width), least frequent, mean and standard deviation are used.
- For the vertical accumulation, the minimum (expressed as the percentage of the height), maximum, least frequent, most frequent, mean and standard deviation are used.
6. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kersten, T.P.; Lindstaedt, M. Image-based low-cost systems for automatic 3D recording and modeling of archaeological finds and objects. Lect. Note. Comput. Sci 2012, 7616, 1–10. [Google Scholar]
- Moussa, W.; Abdel-Wahab, M.; Fritsch, D. Automatic fusion of digital images and laser scanner data for heritage preservation. Lect. Note. Comput. Sci 2012, 7616, 76–85. [Google Scholar]
- Stanco, F. Digital Imaging for Cultural Heritage Preservation: Analysis, Restoration, and Reconstruction of Ancient Artworks; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Izkara, J.; Mediavilla, A.; Rodriguez-Maribona, I. Information Technologies and Cultural Heritage: Innovative Tools for The Support in the Participative Management of Historical Centres. Proceedings of the Conference on Sustaining Europe’s Cultural Heritage, Ljubljana, Slovenia, 10–12 November 2008.
- Calabrò, E. Applying photogrammetric techniques to determine facade decays: The case study of zisa palace, Italy. Engineering 2012, 4, 707–712. [Google Scholar]
- Zaccarini, M.; Iannucci, A.; Orlandi, M.; Vandini, M.; Zambruno, S. A Multi-Disciplinary Approach to the Preservation of Cultural Heritage: A Case Study on the Piazzetta Degli Ariani, Ravenna. Proceedings of IEEE Digital Heritage, Marseille, France, 28 October–1 November 2013.
- Alshawabkeh, Y.; El-Khalili, M. Detection and quantification of material displacements at historical structures using photogrammetry and laser scanning techniques. Mediterr. Archaeol. Archaeom 2013, 13, 57–67. [Google Scholar]
- Stefani, C.; Brunetaud, X.; Janvier-Badosa, S.; Beck, K.; Luca, L.D.; Al-Mukhtar, M. 3D information system for the digital documentation and the monitoring of stone alteration. Lect. Note. Comput. Sci 2012, 7616, 330–339. [Google Scholar]
- Godin, G.; Beraldin, J.A.; Taylor, J.; Cournoyer, L.; Rioux, M.; El-Hackim, S.; Baribeau, R.; Blais, F.; Boulanger, P.; Domey, J.; et al. Active optical 3-D imaging for heritage applications. IEEE Comput. Graph. Appl 2002, 22, 24–36. [Google Scholar]
- Muller, P.; Wonka, P.; Haegler, S.; Ulmer, A.; Gool, L.V. Procedural modeling of buildings. ACM Trans. Graph 2006, 25, 614–623. [Google Scholar]
- Pasko, G.; Pasko, A.; Vilbrandt, T.; Filho, A.; da Silva, J. Digital interpretation of cultural heritage: 3D modeling and materialization of 2D artworks for future museums. Int. J. Incl. Mus. 3, 63–80.
- Remondino, F. Heritage recording and 3D modeling with photogrammetry and 3D scanning. Remote Sens 2011, 3, 1104–1138. [Google Scholar]
- Levoy, M.; Pulli, K.; Curless, B.; Rusinkiewicz, S.; Koller, D.; Pereira, L.; Ginzton, M.; Anderson, S.; Davis, J.; Ginsberg, J.; et al. The Digital Michelangelo Project: 3D Scanning of Large Statues. Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH ’00, New York, USA, 23–28 July 2000; pp. 131–144.
- Ikeuchi, K.; Oishi, T.; Takamatsu, J.; Sagawa, R.; Nakazawa, A.; Kurazume, R.; Nishino, K.; Kamakura, M.; Okamoto, Y. The great buddha project: Digitally archiving, restoring, and analyzing cultural heritage objects. Int. J. Comput. Vision 2007, 75, 189–208. [Google Scholar]
- Riveiro, B.; Morer, P.; Arias, P.; de Arteaga, I. Terrestrial laser scanning and limit analysis of masonry arch bridges. Constr. Build. Mater 2011, 25, 1726–1735. [Google Scholar]
- Laefer, D.F.; Truong-Hong, L.; Carr, H.; Singh, M. Crack detection limits in unit based masonry with terrestrial laser scanning. NDT & E Int 2014, 62, 66–76. [Google Scholar]
- Tapete, D.; Casagli, N.; Luzi, G.; Fanti, R.; Gigli, G.; Leva, D. Integrating radar and laser-based remote sensing techniques for monitoring structural deformation of archaeological monuments. J. Archaeol. Sci 2013, 40, 176–189. [Google Scholar] [Green Version]
- Rodríguez, A.; Valle, J.; Martínez, J. 3D Line Drawing from Point Clouds Using Chromatic Stereo and Shading. Proceedings of the 14th International Conference on Virtual Systems and Multimedia, Limassol, Cyprus, 20–25 October 2008; pp. 77–84.
- Arias, P.; Ordóñez, C.; Lorenzo, H.; Herraez, J. Methods for documenting historical agro-industrial buildings: A comparative study and a simple photogrammetric method. J. Cult. Herit 2006, 7, 350–354. [Google Scholar]
- Fuentes, J.M. Methodological bases for documenting and reusing vernacular farm architecture. J. Cult. Herit 2010, 11, 119–129. [Google Scholar]
- Alba, M.I.; Barazzetti, L.; Scaioni, M.; Rosina, E.; Previtali, M. Mapping infrared data on terrestrial laser scanning 3D models of buildings. Remote Sens 2011, 3, 1847–1870. [Google Scholar]
- De Luca, L.; Busayarat, C.; Stefani, C.; Véron, P.; Florenzano, M. A semantic-based platform for the digital analysis of architectural heritage. Comput. Graph 2011, 35, 227–241. [Google Scholar]
- Oses, N.; Dornaika, F. Image-based delineation of built heritage masonry for automatic classification. Lect. Note. Comput. Sci 2013, 7950, 782–789. [Google Scholar]
- Oses, N.; Azkarate, A. New Protocols for Built Heritage Protection in the Basque Country: Towards an Automatic Analysis Tool for Built Heritage. In Science and Technology for the Conservation of Cultural Heritage; Lazzari, M., Cano, E., Rogerio-Candelera, M., Eds.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- ICOMOS-International Scientific Committee for Stone (ISCS). Illustrated Glossary on Stone Deterioration Patterns; Monuments and Sites Volume XV; ICOMOS: Paris, France, 2008. [Google Scholar]
- Kimmel, R.; Bruckstein, A. On regularized Laplacian zero crossings and other optimal edge integrators. Int. J. Comput. Vision 2003, 53, 225–243. [Google Scholar]
- Zhang, W.; Qin, Z.; Wan, T. Image Scene Categorization Using Multi-Bag-of-Features. Proceedings of the International Conference on Machine Learning and Cybernetics, Guilin, China, 10–13 July 2011.
- Duan, K.; Parikh, D.; Crandall, D.; Grauman, K. Discovering Localized Attributes for Fine-Grained Recognition. Proceedings of the 2012 Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012.
- Yao, B.; Bradski, G.; Fei-Fei, L. A. Codebook-Free and Annotation-Free Approach for Fine-Grained Image Categorization. Proceedings of the 2012 Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012.
- Chen, L.; Yan, L. LBP Displacement Local Matching Approach for Human Face Recognition. Proceedings of the International Workshop on Computer Vision with Local Binary Pattern Variants, ACCV, Daejeon, Korea, 5–6 November 2012.
- He, S.; Sang, N.; Gao, C. Pyramid-Based Multi-Structure Local Binary Pattern for Texture Classification. Proceedings of the Asian Conference on Computer Vision, Queenstown, New Zealand, 8–12 November 2010.
- Wang, W. Rock Particle Image Segmentation and Systems. In Pattern Recognition Techniques, Technology and Applications; I-Tech: Vienna, Austria, 2008; pp. 197–226. [Google Scholar]
- Schleifer, J.; Tessier, B. FRAGSCAN: A Tool to Measure Fragmentation of Blasted Rock. In Measurement of Blast Fragmentation; Balkema: Rotterdam, The Netherlands, 1996; pp. 73–78. [Google Scholar]
- Maerz, N.H.; Palangio, T.C.; Franklin, J.A. WipFrag Image Based Granulometry System. Proceedings of the FRAGBLAST 5 Workshop on Measurement of Blast Fragmentation, Montreal, QC, Canada, 23–24 August 1996.
- Raina, A.K.; Choudhury, P.B.; Ramulu, M.; Chrakraborty, A.K.; Dudhankar, A.S. Fragalyst—An indigenous digital image analysis system for grain size measurement in mines. J. Geol. Soc. India 2002, 59, 561–569. [Google Scholar]
- Wendel, A.; Donoser, M.; Bischof, H. Unsupervised Facade Segmentation Using Repetitive Patterns. Proceedings of the 32th Annual Symposium of the German Association for Pattern Recognition (DAGM), Darmstadt, Germany, 21 September 2010.
- Briese, C.; Pfeifer, N. Towards automatic feature line modeling from terrestrial laser scanner data. Int. Arch. Photogr. Remote Sens. Spat. Inf. Sci 2008, XXXVII, 463–468. [Google Scholar]
- Boulaassal, H.; Landes, T.; Grussenmeyer, P. Reconstruction of 3D vector models of buildings by combination of ALS, TLS and VLS data. Int. Arch. Photogr. Remote Sens. Spat. Inf. Sci 2011, XXXVIII, 239–244. [Google Scholar]
- Bienert, A. Vectorization, Edge Preserving Smoothing and Dimensioning of Profiles in Laser Scanner Point Clouds. Proceedings of XXIst ISPRS Congress, Beijing, China, 3–11 July 2008.
- Sithole, G. Detection of bricks in a masonry wall. Int. Arch. Photogr. Remote Sens. Spat. Inf. Sci 2008, XXXVII, 567–572. [Google Scholar]
- Demarsin, K. Extraction of Closed Feature Lines from Point Clouds Based on Graph Theory. Ph.D. Thesis, Katholieke Universiteit Leuven, Leuven, Belgium. 2009. [Google Scholar]
- Hammoudi, K.; Dornaika, F.; Paparoditis, N. Generating Virtual 3D Model of Urban Street Facades by Fusing Terrestrial Multi-Source Data. Proceedings of the IEEE International Conference on Intelligent Environments, Nottingham, UK, 25–28 July 2011.
- Burochin, J.; Tournaire, O.; Paparoditis, N. An Unsupervised Hierarchical Segmentation of a Facade Building Image in Elementary 2D Models. Proceedings of the ISPRS Workshop on Object Extraction for 3D City Models, Road Databases and Traffic Monitoring, Paris, France, 3–4 September 2009.
- Hernandez, J.; Marcotegui, B. Morphological Segmentation of Building Facade Images. Proceedings of the 16th IEEE International Conference on Image Processing, Cairo, Egypt, 7–10 November 2009.
- Bradski, G. The OpenCV library. Dr. Dobb’s J. Softw. Tools. 2000, 120, pp. 122–125. Available online: http://www.drdobbs.com/open-source/the-opencv-library/184404319 (accessed on 18 February 2014).
- Telea, A. An image inpainting technique based on the fast marching method. J. Graph. Tools 2004, 9, 25–36. [Google Scholar]
- Kiryati, N.; Eldar, Y.; Bruckstein, A. A probabilistic Hough transform. Pattern Recognit 1991, 24, 303–316. [Google Scholar]
- Mark, H.; Eibe, F.; Geoffrey, H.; Bernhard, P.; Peter, R.; Ian, H.W. The WEKA data mining software: An update. SIGKDD Explor 2009, 11, 10–18. [Google Scholar]
- Aha, D.; Kibler, D.; Albert, M. Instance-based learning algorithms. Mach. Learn 1991, 6, 37–66. [Google Scholar]
- Mena-Torres, D.; Aguilar-Ruiz, J.; Rodriguez, Y. An Instance Based Learning Model for Classification in Data Streams with Concept Change. Proceedings of the 2012 11th Mexican International Conference on Artificial Intelligence (MICAI), San Luis Potosi, Mexico, 27 Octobe–4 November 2012; pp. 58–62.
- Meyer, D.; Leisch, F.; Hornik, K. The support vector machine under test. Neurocomputing 2003, 55, 169–186. [Google Scholar]
- Zhang, H. The Optimality of Naive Bayes. Proceedings of FLAIRS Conference, Miami Beach, FL, USA, 17–19 May 2004.
- Quinlan, J. C4.5: Programs for Machine Learning; Morgan Kaufmann Publishers Inc: San Francisco, CA, USA, 2003; Volume 55, pp. 169–186. [Google Scholar]
- Liua, H.; Suna, J.; Liua, L.; Zhang, H. Feature selection with dynamic mutual information. Pattern Recognit 2009, 43, 1330–1339. [Google Scholar]
- ElAlami, M. A filter model for feature subset selection based on genetic algorithm. Knowl.-Based Syst 2009, 22, 356–362. [Google Scholar]
- Mitchell, M. An Introduction to Genetics Algorithms; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour detection and hierarchical image segmentation. IEEE Trans. Pattern Anal. Mach. Intell 2011, 33, 898–916. [Google Scholar]











| 28 Features | 19 Features | ||||
|---|---|---|---|---|---|
| Classifier | Cases | No. of Errors | Accuracy | No. of Errors | Accuracy |
| 1-NN | 86 | 24 | 72.1% | 17 | 80.2% |
| 3-NN | 86 | 22 | 74.4% | 21 | 75.6% |
| NB | 86 | 25 | 70.9% | 25 | 70.9% |
| J48 | 86 | 26 | 69.8% | 23 | 73.3% |
| SVM | 86 | 21 | 75.6% | 19 | 78.3% |
| Classifier | Cases | No. of Errors | Accuracy |
|---|---|---|---|
| 1-NN | 86 | 13 | 84.9% |
| 3-NN | 86 | 14 | 83.7% |
| NB | 86 | 14 | 83.7% |
| J48 | 86 | 12 | 86.0% |
| SVM | 86 | 11 | 87.2% |
| Class 1 | Class 2 | Class 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Classifier | Rec. | Prec. | F1 | Rec. | Prec. | F1 | Rec. | Prec. | F1 |
| 1-NN | 84.8% | 87.5% | 86.2% | 80.0% | 66.7% | 72.7% | 86.6% | 91.7% | 89.2% |
| 3-NN | 97.0% | 78.0% | 86.5% | 53.3% | 80.0% | 64.0% | 84.2% | 91.4% | 87.7% |
| NB | 97.0% | 84.2% | 90.1% | 60.0% | 64.3% | 62.1% | 81.6% | 91.2% | 86.1% |
| J48 | 90.9% | 96.8% | 93.7% | 73.3% | 68.8% | 71.0% | 86.8% | 84.6% | 85.7% |
| SVM | 97.0% | 82.1% | 88.9% | 73.3% | 78.6% | 75.9% | 84.2% | 97.0% | 90.1% |
| Classified as | |||
|---|---|---|---|
| Class | Class 2 | Class | |
| Class 1 | 32 | 1 | 0 |
| Class 2 | 3 | 11 | 1 |
| Class 3 | 4 | 2 | 32 |
| Feature | Selected/Not Selected |
|---|---|
| 1 minimum length | 00010 |
| 2 maximum length | 10100 |
| 3 least frequent length | 00010 |
| 4 most frequent length | 00110 |
| 5 length mean | 11010 |
| 6 length standard deviation | 01011 |
| 7 maximum slope | 00110 |
| 8 least frequent slope | 10101 |
| 9 most frequent slope | 01010 |
| 10 slope mean | 00011 |
| 11 slope standard deviation | 01100 |
| 12 percentage of vertical slopes | 00100 |
| 13 least frequent slope difference | 00001 |
| 14 most frequent slope difference | 00010 |
| 15 slope difference mean | 00011 |
| 16 slope difference standard deviation | 00110 |
| 17 percentage of pairs of segments nearly parallel | 11111 |
| 18 percentage of pairs of segments nearly perpendicular | 11101 |
| 19 maximum row count | 00101 |
| 20 least frequent row count | 10010 |
| 21 row count mean | 10001 |
| 22 row count SD | 01000 |
| 23 minimum column count | 01011 |
| 24 maximum column count | 10010 |
| 25 least frequent column count | 10101 |
| 26 most frequent column count | 11101 |
| 27 column count mean | 10000 |
| 28 column count SD | 01000 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Oses, N.; Dornaika, F.; Moujahid, A. Image-Based Delineation and Classification of Built Heritage Masonry. Remote Sens. 2014, 6, 1863-1889. https://0-doi-org.brum.beds.ac.uk/10.3390/rs6031863
Oses N, Dornaika F, Moujahid A. Image-Based Delineation and Classification of Built Heritage Masonry. Remote Sensing. 2014; 6(3):1863-1889. https://0-doi-org.brum.beds.ac.uk/10.3390/rs6031863
Chicago/Turabian StyleOses, Noelia, Fadi Dornaika, and Abdelmalik Moujahid. 2014. "Image-Based Delineation and Classification of Built Heritage Masonry" Remote Sensing 6, no. 3: 1863-1889. https://0-doi-org.brum.beds.ac.uk/10.3390/rs6031863