Mass Flux Solution in the Tibetan Plateau Using Mascon Modeling
Abstract
:1. Introduction
2. Materials and Methodology
2.1. Research Area
2.2. Data
2.2.1. GRACE Monthly Solutions
2.2.2. GIA Models
2.3. Mascon Modeling
2.4. Regularization Solution
2.5. Leakage Problem
3. Mass Flux Solution in Tibetan Plateau
3.1. Spatial Sampling Strategy
3.2. Regularization Parameter
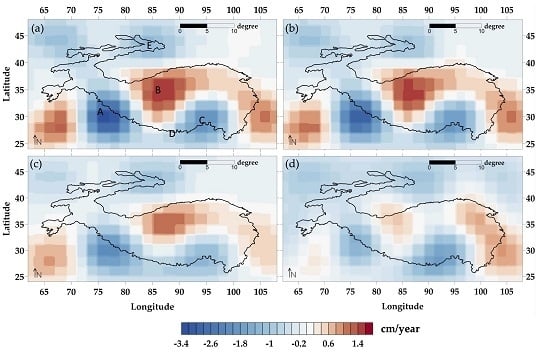
3.3. Spatial Distribution of Tibet
3.4. Trend of Total Mass Variations
4. Discussion
4.1. Mass Variations Distribution
4.2. Total Mass Variation
4.3. Tongji-GRACE02 Monthly Solutions
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Jekeli, C. Alternative Methods to Smooth the Earth’s Gravity Field; Report 327 of Geodetic Science and Surveying; Ohio Ohio State University: Columbus, OH, USA, 1981. [Google Scholar]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. 1998, 103, 30205. [Google Scholar] [CrossRef]
- Zhang, Z.Z.; Chao, B.F.; Lu, Y.; Hsu, H.T. An effective filtering for GRACE time-variable gravity: Fan filter. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Luo, Z.; Li, Q.; Zhang, K.; Wang, H. Trend of mass change in the Antarctic ice sheet recovered from the GRACE temporal gravity field. Sci. China Earth Sci. 2011, 55, 76–82. [Google Scholar] [CrossRef]
- Sasgen, I.; Martinec, Z.; Fleming, K. Wiener optimal filtering of GRACE data. Stud. Geophys. Geod. 2006, 50, 499–508. [Google Scholar] [CrossRef]
- Muller, P.M.; Sjogren, W.L. Mascons: Lunar mass concentrations. Science 1968, 161, 680–684. [Google Scholar] [CrossRef] [PubMed]
- Koch, K.-R.; Morrison, F. A simple layer model of the geopotential from a combination of satellite and gravity data. J. Geophys. Res. 1970, 75, 1483–1492. [Google Scholar] [CrossRef]
- Koch, K.-R.; Witte, B.U. Earth’s gravity field represented by a simple-layer potential from Doppler tracking of satellites. J. Geophys. Res. 1971, 76, 8471–8479. [Google Scholar] [CrossRef]
- Koch, K.R. Simple layer model of the geopotential in satellite geodesy. In The Use of Artificial Satellites for Geodesy; Geophysics Monography Series; Henriksen, S.W., Mancini, A., Chovitz, B.H., Eds.; American Geophysical Union: Washington, DC, USA, 1972; Volume 15, pp. 107–109. [Google Scholar]
- Wong, L.; Buechler, G.; Downs, W.; Sjogren, W.; Muller, P.; Gottlieb, P. A surface-layer representation of the lunar gravitational field. J. Geophys. Res. 1971, 76, 6220–6236. [Google Scholar] [CrossRef]
- Morrison, F. Algorithms for computing the geopotential using a simple density layer. J. Geophys. Res. 1976, 81, 4933–4936. [Google Scholar] [CrossRef]
- Russell, R.P.; Arora, N. Global point mascon models for simple, accurate, and parallel geopotential computation. J. Guid. Control Dyn. 2012, 35, 1568–1581. [Google Scholar] [CrossRef]
- Forsberg, R.; Reeh, N. Mass change of the Greenland ice sheet from GRACE. In Proceedings of the 1st Meeting of the International Gravity Field Service, Istanbul, Turkey, 28 August–1 September 2006.
- Baur, O.; Sneeuw, N. Assessing Greenland ice mass loss by means of point-mass modeling: A viable methodology. J. Geod. 2011, 85, 607–615. [Google Scholar] [CrossRef]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W. Improved methods for observing earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Zwally, H.J.; Abdalati, W.; Rowlands, D.D.; Ray, R.D.; Nerem, R.S.; Lemoine, F.G.; McCarthy, J.J.; Chinn, D.S. Recent Greenland ice mass loss by drainage system from satellite gravity observations. Science 2006, 314, 1286–1289. [Google Scholar] [CrossRef] [PubMed]
- Luthcke, S.B.; Rowlands, D.D.; Lemoine, F.G.; Klosko, S.M.; Chinn, D.; McCarthy, J.J. Monthly spherical harmonic gravity field solutions determined from GRACE inter-satellite range-rate data alone. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Rowlands, D.D.; Luthcke, S.B.; McCarthy, J.J.; Klosko, S.M.; Chinn, D.S.; Lemoine, F.G.; Boy, J.P.; Sabaka, T.J. Global mass flux solutions from GRACE: A comparison of parameter estimation strategies—Mass concentrations versus Stokes coefficients. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Sabaka, T.J.; Rowlands, D.D.; Luthcke, S.B.; Boy, J.P. Improving global mass flux solutions from gravity recovery and climate experiment (GRACE) through forward modeling and continuous time correlation. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Sabaka, T.J.; Loomis, B.D.; Arendt, A.A.; McCarthy, J.J.; Camp, J. Antarctica, Greenland and Gulf of Alaska land-ice evolution from an iterated GRACE global mascon solution. J. Glaciol. 2013, 59, 613–631. [Google Scholar] [CrossRef]
- Rowlands, D.D.; Luthcke, S.B.; Klosko, S.M.; Lemoine, F.G.R.; Chinn, D.S.; McCarthy, J.J.; Cox, C.M.; Anderson, O.B. Resolving mass flux at high spatial and temporal resolution using GRACE intersatellite measurements. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Qiu, J. China: The third pole. Nature 2008, 454, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Krause, P.; Biskop, S.; Helmschrot, J.; Flügel, W.A.; Kang, S.; Gao, T. Hydrological system analysis and modelling of the Nam Co basin in Tibet. Adv. Geosci. 2010, 27, 29–36. [Google Scholar] [CrossRef]
- Song, C.; Huang, B.; Ke, L. Modeling and analysis of lake water storage changes on the Tibetan Plateau using multi-mission satellite data. Remote Sens. Environ. 2013, 135, 25–35. [Google Scholar] [CrossRef]
- Yi, S.; Sun, W. Evaluation of glacier changes in high-mountain Asia based on 10 year GRACE RL05 models. J. Geophys. Res. Solid Earth 2014, 119, 2504–2517. [Google Scholar] [CrossRef]
- Jacob, T.; Wahr, J.; Pfeffer, W.T.; Swenson, S. Recent contributions of glaciers and ice caps to sea level rise. Nature 2012, 482, 514–518. [Google Scholar] [CrossRef] [PubMed]
- International Centre for Global Earth Models. Available online: http://icgem.gfz-potsdam.de/ICGEM/ (accessed on 19 May 2016).
- Bettadpur, S. Gravity Recovery and Climate Experiment UTCSR Level-2 Processing Standards Document for Level-2 Product Release 0005; Center for Space Research, University of Texas at Austin: Austin, TX, USA, 2012. [Google Scholar]
- Watkins, M.M.; Yuan, D.-N. JPL Level-2 Processing Standards Document for Level-2 Product Release 05; GRACE 327-741, Rev. 4.0; Jet Propulsion Laboratory: Pasadena, CA, USA, 2012. [Google Scholar]
- Dahle, C.; Flechtner, F.; Gruber, C.; König, D.; König, R.; Michalak, G.; Neumayer, K.-H.; Gfz, D.G. GFZ GRACE Level-2 Processing Standards Document for Level-2 Product Release 0005; Deutsches GeoForschungsZentrum GFZ: Potsdam, Germany, 2013. [Google Scholar]
- Chen, Q.; Shen, Y.; Zhang, X.; Hsu, H.; Chen, W.; Ju, X.; Lou, L. Monthly gravity field models derived from GRACE level 1b data using a modified short-arc approach. J. Geophys. Res. Solid Earth 2015, 120, 1804–1819. [Google Scholar] [CrossRef]
- Cheng, M.; Tapley, B.D. Variations in the earth’s oblateness during the past 28 years. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Moritz, H. Physical Geodesy, 2nd ed.; Springer-Verlag Wien: New York, NY, USA, 2006. [Google Scholar]
- Wu, X.; Ray, J.; van Dam, T. Geocenter motion and its geodetic and geophysical implications. J. Geodyn. 2012, 58, 44–61. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Cheng, M.K.; Ries, J.C.; Tapley, B.D. Geocenter Variations from Analysis of SLR Data; Springer: Heidelberg, Germany, 2013. [Google Scholar]
- Peltier, W.R. Ice Age Paleotopography. Science 1994, 265, 195–201. [Google Scholar] [CrossRef] [PubMed]
- Peltier, W.R. Global glacial isostasy and the surface of the ice-age earth: The ICE-5G (VM2) model and GRACE. Ann. Rev. Earth Planet. Sci. 2004, 32, 111–149. [Google Scholar] [CrossRef]
- Paulson, A.; Zhong, S.; Wahr, J. Inference of mantle viscosity from GRACE and relative sea level data. Geophys. J. Int. 2007, 171, 497–508. [Google Scholar] [CrossRef]
- Baur, O.; Kuhn, M.; Featherstone, W.E. GRACE-derived ice-mass variations over Greenland by accounting for leakage effects. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Wang, H.; Wu, P. Effects of lateral variations in lithospheric thickness and mantle viscosity on glacially induced surface motion on a spherical, self-gravitating Maxwell Earth. Earth Planet. Sci. Lett. 2006, 244, 576–589. [Google Scholar] [CrossRef]
- Tikhonov, A.N. Solution of incorrectly formulated problems and the regularization method. Sov. Math. Dokl. 1963, 5, 1035–1038. [Google Scholar]
- Tikhonov, A.N. Regularization of incorrectly posed problems. Sov. Math. Dokl. 1963, 4, 1624–1627. [Google Scholar]
- Golub, G.H.; Heath, M.; Wahba, G. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics 1979, 21, 215–223. [Google Scholar] [CrossRef]
- Xu, P.; Shen, Y.; Fukuda, Y.; Liu, Y. Variance component estimation in linear inverse ill-posed models. J. Geod. 2006, 80, 69–81. [Google Scholar] [CrossRef]
- Shen, Y.; Xu, P.; Li, B. Bias-corrected regularized solution to inverse ill-posed models. J. Geod. 2012, 86, 597–608. [Google Scholar] [CrossRef]
- Kusche, J.; Klees, R. Regularization of gravity field estimation from satellite gravity gradients. J. Geod. 2002, 76, 359–368. [Google Scholar] [CrossRef]
- Ran, J.; Ditmar, P.; Klees, R.; Vizcaino, M. Advanced analysis of mass balance of the Greenland ice sheet from GRACE and surface mass balance modelling. In Proceedings of the 26th IUGG General Assembly, Prague, Czech Republic, 22 June–2 July 2015.
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, V.M.; Wahr, J.; Swenson, S. Dwindling groundwater resources in northern India, from satellite gravity observations. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, K.; Qin, J.; Zhao, L.; Tang, W.; Han, M. Evaluation of AMSR-E retrievals and GLDAS simulations against observations of a soil moisture network on the central Tibetan Plateau. J. Geophys. Res. Atmos. 2013, 118, 4466–4475. [Google Scholar] [CrossRef]
- Wang, W.; Gao, Y.; Xu, J. Applicability of GLDAS and climate change in the Qinghai-Xizang Plateau and its surrounding arid area. Plateau Meteorol. 2013, 32, 635–645. (In Chinese) [Google Scholar]
- Chen, J.L.; Wilson, C.R.; Blankenship, D.; Tapley, B.D. Accelerated Antarctic ice loss from satellite gravity measurements. Nat. Geosci. 2009, 2, 859–862. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Seo, K.-W. S2 tide aliasing in GRACE time-variable gravity solutions. J. Geod. 2008, 83, 679–687. [Google Scholar] [CrossRef]
- Ran, J.; Zhong, M.; Xu, H.Z.; Zhou, Z.; Wan, X. Analysis of the gravity field recovery accuracy from the low-low satellite-to-satellite tracking mission. Chin. J. Geophys. 2015, 58, 3487–3495. [Google Scholar]
- Lelin, X.; Hui, L.; Songbai, X.; Kaixuan, K.; Xiaoling, L. Long-term gravity changes in Chinese mainland from GRACE and ground-based gravity measurements. Geod. Geodyn. 2011, 2, 61–70. [Google Scholar] [CrossRef]
- Scherler, D.; Bookhagen, B.; Strecker, M.R. Spatially variable response of Himalayan glaciers to climate change affected by debris cover. Nat. Geosci. 2011, 4, 156–159. [Google Scholar] [CrossRef]
- Gardelle, J.; Berthier, E.; Arnaud, Y.; Kääb, A. Region-wide glacier mass balances over the Pamir-Karakoram-Himalaya during 1999–2011. Cryosphere 2013, 7, 1263–1286. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Yao, T.; Xie, H.; Kang, S.; Lei, Y. Increased mass over the Tibetan Plateau: From lakes or glaciers? Geophys. Res. Lett. 2013, 40, 2125–2130. [Google Scholar] [CrossRef]
- Ge, S.; McKenzie, J.; Voss, C.; Wu, Q. Exchange of groundwater and surface-water mediated by permafrost response to seasonal and long term air temperature variation. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Cheng, G.; Jin, H. Permafrost and groundwater on the Qinghai-Tibet Plateau and in Northeast China. Hydrogeol. J. 2012, 21, 5–23. [Google Scholar] [CrossRef]
- Jin, H.; He, R.; Cheng, G.; Wu, Q.; Wang, S.; Lü, L.; Chang, X. Changes in frozen ground in the source area of the yellow river on the Qinghai-Tibet Plateau, China, and their eco-environmental impacts. Environ. Res. Lett. 2009, 4. [Google Scholar] [CrossRef]
- Gardelle, J.; Berthier, E.; Arnaud, Y. Slight mass gain of Karakoram glaciers in the early twenty-first century. Nat. Geosci. 2012, 5, 322–325. [Google Scholar] [CrossRef]
- Chen, Q.; Shen, Y.; Chen, W.; Zhang, X.; Hsu, H. An improved GRACE monthly gravity field solution by modeling the non-conservative acceleration and attitude observation errors. J. Geod. 2016. [Google Scholar] [CrossRef]
- Dyurgerov, M.B. Reanalysis of glacier changes: From the IGY to the IPY, 1960–2008. Data Glaciol. Stud. 2010, 108, 1–116. [Google Scholar]














| Gravity Model | Time Period | Numbers of Months without Data |
|---|---|---|
| CSR RL05 | April 2002–October 2014 | 12 |
| JPL RL05 | April 2002–September 2014 | 12 |
| GFZ RL05a | April 2002–August 2014 | 12 |
| Tongji-GRACE02 | January 2003–April 2015 | 11 |
| Models | Annual Amplitude (cm) | Annual Phase (°) | Semiannual Amplitude (cm) | Semiannual Phase (°) |
|---|---|---|---|---|
| CSR RL05 | 2.33 ± 0.21 | 204.83 ± 5.04 | 0.21 ± 0.17 | 102.33 ± 49.57 |
| JPL RL05 | 1.96 ± 0.26 | 201.74 ± 7.45 | 0.25 ± 0.10 | 84.05 ± 74.38 |
| GFZ RL05a | 2.19 ± 0.21 | 208.01 ± 5.16 | 0.21 ± 0.24 | 107.30 ± 30.14 |
| Tongji-GRACE02 | 2.15 ± 0.22 | 209.93 ± 5.79 | 0.22 ± 0.28 | 117.11 ± 31.00 |
| GLDAS | 0.56 ± 0.13 | 167.70 ± 12.83 | 0.13 ± 0.07 | 136.84 ± 39.48 |
| Models | 161-Day Amplitude (cm) | 161-Day Phase (°) | Trend (Gt/year) |
|---|---|---|---|
| CSR RL05 | 0.17 ± 0.20 | 341.00 ± 70.04 | −6.41 ± 4.74 |
| JPL RL05 | 0.10 ± 0.26 | 277.55 ± 142.72 | −5.87 ± 4.88 |
| GFZ RL05a | 0.24 ± 0.22 | 250.04 ± 49.96 | −6.08 ± 4.65 |
| Tongji-GRACE02 | 0.28 ± 0.23 | 269.42 ± 44.12 | −11.50 ± 4.79 |
| GLDAS | 0.07 ± 0.13 | 285.63 ± 249.36 | 1.90 ± 0.98 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Shen, Y.; Chen, Q. Mass Flux Solution in the Tibetan Plateau Using Mascon Modeling. Remote Sens. 2016, 8, 439. https://0-doi-org.brum.beds.ac.uk/10.3390/rs8050439
Chen T, Shen Y, Chen Q. Mass Flux Solution in the Tibetan Plateau Using Mascon Modeling. Remote Sensing. 2016; 8(5):439. https://0-doi-org.brum.beds.ac.uk/10.3390/rs8050439
Chicago/Turabian StyleChen, Tianyi, Yunzhong Shen, and Qiujie Chen. 2016. "Mass Flux Solution in the Tibetan Plateau Using Mascon Modeling" Remote Sensing 8, no. 5: 439. https://0-doi-org.brum.beds.ac.uk/10.3390/rs8050439