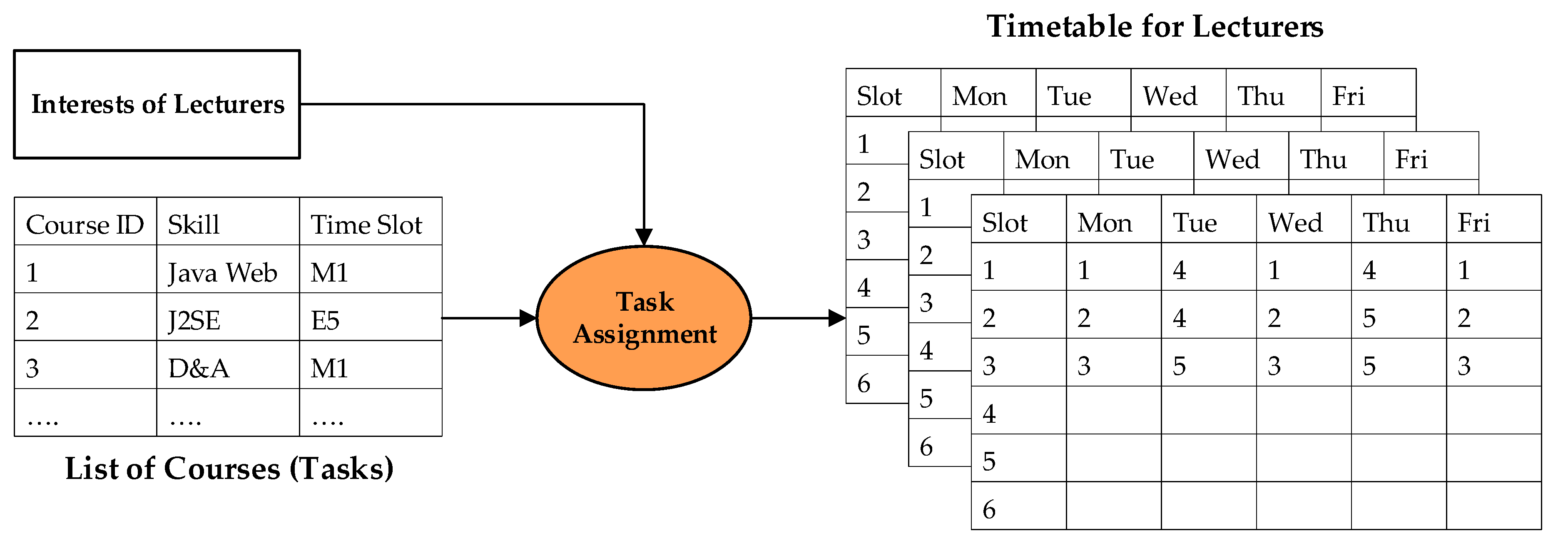
2. Mathematical Problem
2.1. Multi-Objective Task Assignment Problem
In this research, we also define our timetable problem in the form of IP as follows:
Let is the number of lecturers.
Denote is the number of subjects.
is the number of available time slots, in our case,
as described in
Table 1.
is the number of section, a section represents a particular class studies a specific subject at a timeslot.
are class, subject, and time slot of section -th respectively.
is a number of classes that lecturer -th prefers to teach.
is a minimum number of classes that the lecturer -th has to teach.
as integer for every represent the rating of the lecturer -th to teach subject -th. The value indicates that the lecturer does not want to teach the subject. Other values respectively mean “like a little” to “like very much”.
as integer for every denote the rating of the lecturer -th to teach at time slot -th. The value indicates that the lecturer does not want to teach at the time slot. Other values respectively mean “like a little” to “like very much.”
is the decision variable for every . if the lecturer -th is assigned to section -th, otherwise.
We define several constraints to the problem as follows:
All section must be assigned lecturer and at most one lecturer is assigned to a section.
A particular lecturer does not teach the subject that he/she does not have skill.
A particular lecturer does not teach at the time-slot that he/she is not available.
All lecturers have to satisfy the quota for the number of sections they have to teach.
In this research, we have defined some objectives functions that maximize the lecturer’s preference level on time-slots, subjects, and the number of classes that the lecturer expects to teach. The objective functions described as follows:
Maximize the expectations of the lecturers on the subject they want to teach.
Maximize the expectations of the lecturers on the time slots they want to teach.
Minimize the errors on the number of classes that the lecturers want to teach.
Minimize the number of parts of the day, which lecturers must work (morning, afternoon every day). The lecturer would register three classes, even if he expressed his interest in all of the time-slots. It is better to assign him/her to work in the slot-times (E1, E2, E3) instead of (E1, E4, M1):
where
is a fuzzy logic membership function that returns the rating for the number of parts of the day, which lecturers have to work, the detailed implementation can be different in different situations. We show our implementation in the part of the experiment to suit the context of FPT University.
The proposed model is in the form of a multi-objective programming problem (MOP) [
24]. Since there are often many Pareto optimization solutions for MOP problems, solving such a problem is not as simple as a typical single goal optimization problem. In the following sections, we present an approach to transform the optimal problem into a more suitable form to find the optimal solution in the decision space.
2.2. Compromise Programming for MOP
Our proposed scheduling problem becomes MOP. There are two main approaches to solving the MOP problem: preference method and non-preference method, as mentioned in Hwang’s survey [
24]. The most useful solution is found using different philosophies that depending on the subjective preferences of the decision-makers. In the decision-making process, decision-makers can place interest in each criterion according to his/her subjective preferences. Here, the decision-maker should be an expert in the domain. It is challenging to find the desired weights for different objectives. This section of this paper discusses the compromise programming approach that requires no pre-defined decision-maker preferences.
The problem of 4*
objective functions is complicated for decision-makers to define the weights corresponding to each lecturer. There are many proposed methods to solve multi-objective problems. Zeleny [
25] introduced the ideal solution defined as the best-compromise solution that is the nearest to perfection. Ngo et al. [
26,
27,
28] applied compromise programming to solve the problem of the binary objective in team selection, where they introduced the idea point E and try to find the solution that has minimum distance to E. Mahmudova used a variant of compromise programming called TOPSIS to identify the criteria and alternatives for software. They chose an alternate variant that has to be at the shortest Euclidean distance from the positive ideal solution and the farthest Euclidean distance from the negative ideal solution. The value of best and worst alternatives to software efficiency was found using the estimates of professional programmers [
29]. Xu et al. determined the best compromise solution using a linear fuzzy membership function that represents the degree of achievement of an objective function as a value between 0 and 1. The best compromise solution is the one that archived the highest value of the normalized membership function
calculated at the
-th solution [
30]. Wei and Tian used a fuzzy statistic algorithm to select the best compromise solutions after obtaining Pareto-optimal solutions [
31].
When the decision-maker stands in the view of lecturers, they declare their preferences on subjects and time-slots. It is hard to find the solution to archive the best, but we can define the best schedule they expect. The only goal left is to find a solution that is closest to this predefined point. The question we may ask decision-maker and predictable answer for them is as follows:
The decision-maker mostly provides this pair of the above question and answer for the time-slot, skill, number of courses, and part of the days they have to work. The objective function is now expressed as follow:
Where
is the vector of expected timetable for lecturer
-th, such that
The denotes the normalization function, is max rating for the number of parts of the days that a lecturer has to work.
Let
is the matrix of the solution.
where
is the vector of final timetable for lecturer
-th, such that:
is the matrix of the worse possible solution.
where
is the vector of the worse timetable for lecturer
-th, such that:
The original multi-objective functions (O1), (O2), (O3), and (O4) are rewritten in the form of compromise problem (CP):
4. Experiment and Result
To evaluate the proposed model and algorithm, we use the data collected in the spring semester of 2020 of the Computing Fundamental department at FPT University. A total of H = 139 sections of S = 17 subjects were assigned to G = 27 lecturers. The
function’s returned values were collected depending on the different business settings.
Table 1 illustrates the definition of the timeslots at the institution. The merged cells described that two real-life slots are marked as the same time slot in the mathematical model.
We construct a fuzzy function to fit the definition of the timeslots as the following algorithms. Our goal is to determine the number of sessions per day that the instructor must be in college and rate it. A good schedule that is matching the number of sections to teach with the number of part of days that lecturer has to present at the school gain 100% satisfaction (points). Satisfaction is inversely proportional to the instructor’s waiting time. For some situations, when hiring qualified lecturers is not easy work, a compact schedule in the aspect of time may give more flexibility to the human resources organizing process.
| Function: |
| Input: |
| 1: | |
| 2: | = |
| 3: | |
| 4: | If and () Return |
| 5: | If and () Return |
| 6: | If and () Return |
| 7: | If and () Return |
| 8: | If and () Return |
| 9: | If and () Return |
| 10: | If and () Return |
| 11: | If and () Return |
| 12: | If and () Return |
| 13: | If Return |
| The function defined as: |
| Function: |
| Input: |
| 1: | |
| 2: | If () Then |
| 3: | If () Then |
| 4: | If () Then |
| 5: | If () Then |
| 6: | Return |
We built a webpage to collect lecturer preferences of the subjects, time-slots, and the number of time-slots they want to teach, as shown in
Figure 3. The preferences gathering process needs to be done before starting the scheduler triggered. The lecturers use their personal accounts to make declarations with the system. In this experiment, we set the preferences received the values in the range of
and
.
The developed system described in this report was deployed on a computer configured as follows: Processor: Intel(R) Xeon(R) CPU X5650 @2.67 GHz (4 CPUs), ~2.3 GHz; Memory: 8096 MB RAM; all code implemented in java 8.
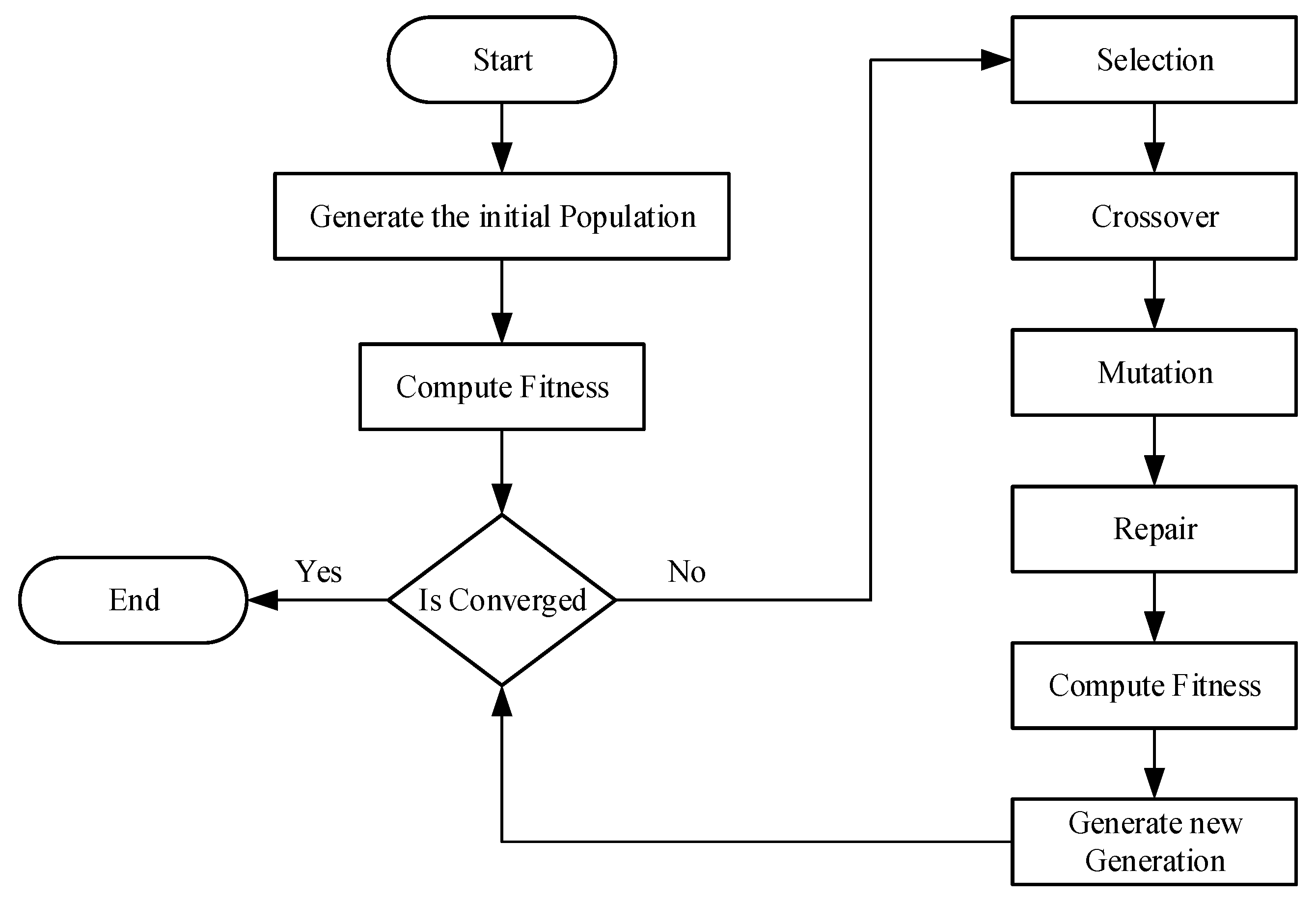
The designed genetic algorithm operated based on several parameters. They have a significant influence on the results of the algorithm. In this section, we describe how the values of this parameter are selected. To select the most suitable parameters for the genetic algorithm, we execute the algorithm multiple times. Observed effects on the corresponding MOP approaches are listed in
Table 2.
The tested ranges of the importance of the parameters show good results. The small tournament size makes the crossover loses diversity. It negatively affects the algorithm results as well as the time of convergence. The tournament size = 7 seems to generate good results for the scalarizing approach, and tournament size > 9 increases the processing time even though it maintains an excellent fitness value. Population size > 100 gets worse for both fitness values and processing time. Based on the observed results, we selected the parameter set to run the algorithm according to
Table 3.
To evaluate the proposed algorithm. We have run the algorithm multiple times with the same initial value.
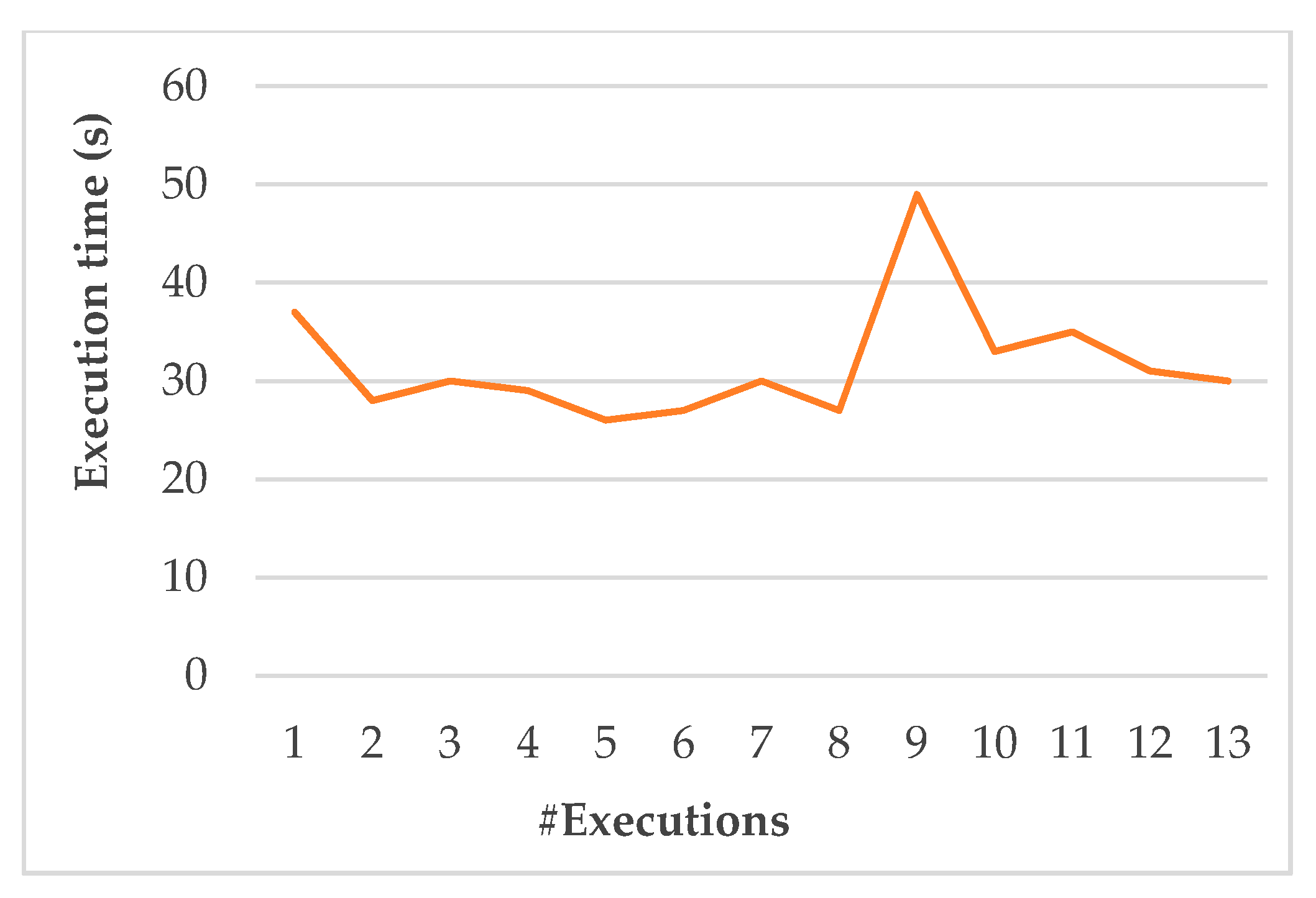
Figure 4 shows the fitness values over 13 executions. It shows that the result is nearing expected values (approximately 1) on tested data. The average time execution is around 33 s, as shown in
Figure 5. In fact, the teaching assignment process accounts for an average of 1 working day of the head of department. In many cases when the number of sections is too large, it is even more time-consuming.
The fitness values change during each generation of the Genetic Algorithm is shown in
Figure 6. After about the first 20 generations, the fitness value came very close to the convergence value. The proposed model allows faculty preferences for four aspects: skills, timeslots, number of classes, and working time. It considers more aspects of stakeholders’ needs than the simple “sum of favorites on the particular wish of lecturers” model introduced by previous research [
17,
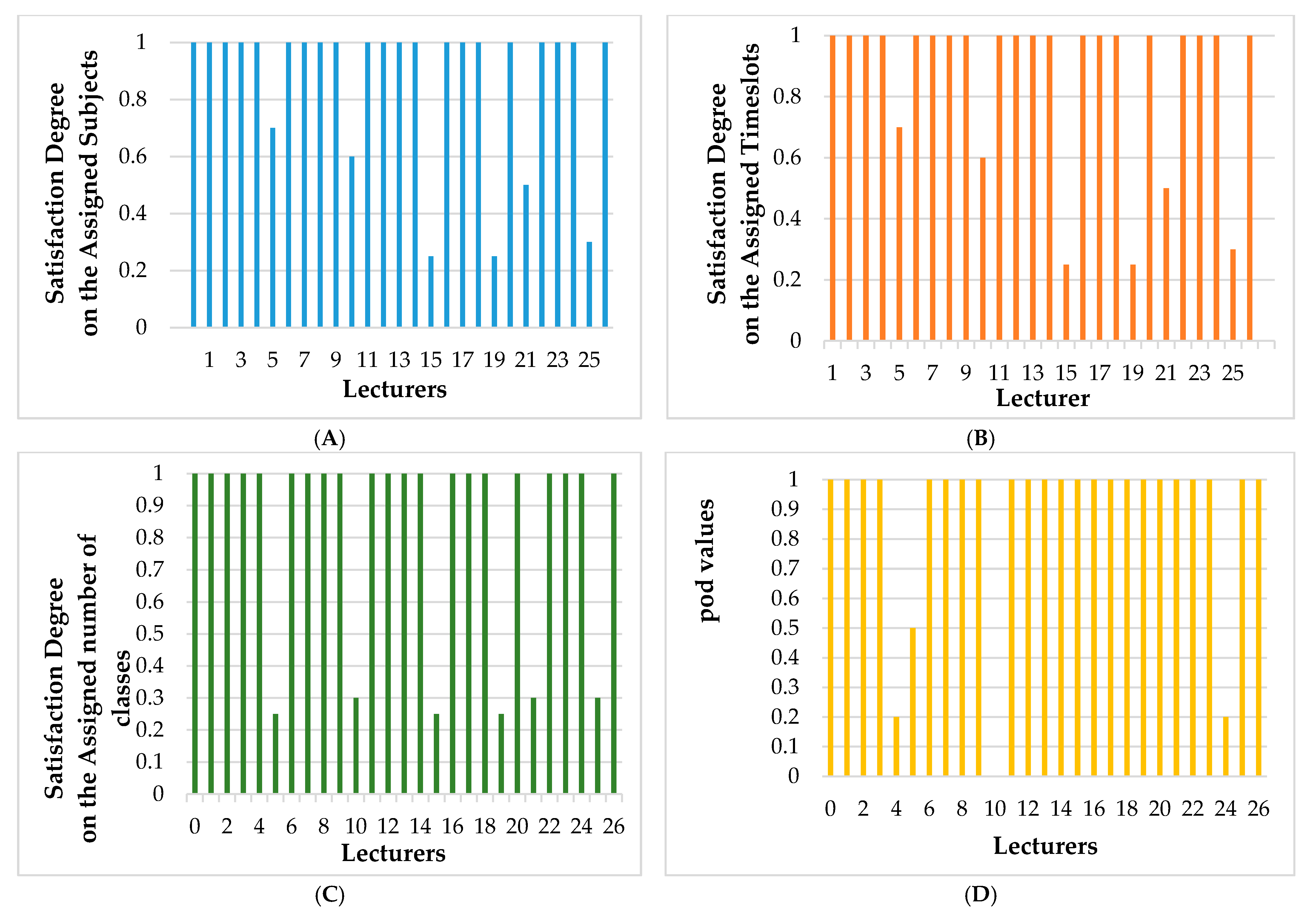
21]. We use a non-preference approach for the multi-objective problem. Compromise programming gives a satisfactory answer in cases where there is not any priority assigned. The lecturer’s satisfaction degrees corresponding to the groups of objective functions were obtained by executing GA displayed in
Figure 7. It observed that teachers who are registered to teach many subjects could guide in many different time frames and naturally prioritize various topics. Meanwhile, with the target function’s current scoring: 100%~5 stars of subjects * 5 stars of time slots, which leads to those who can teach few items or more constrained about time constraints may receive a less-satisfied schedule.
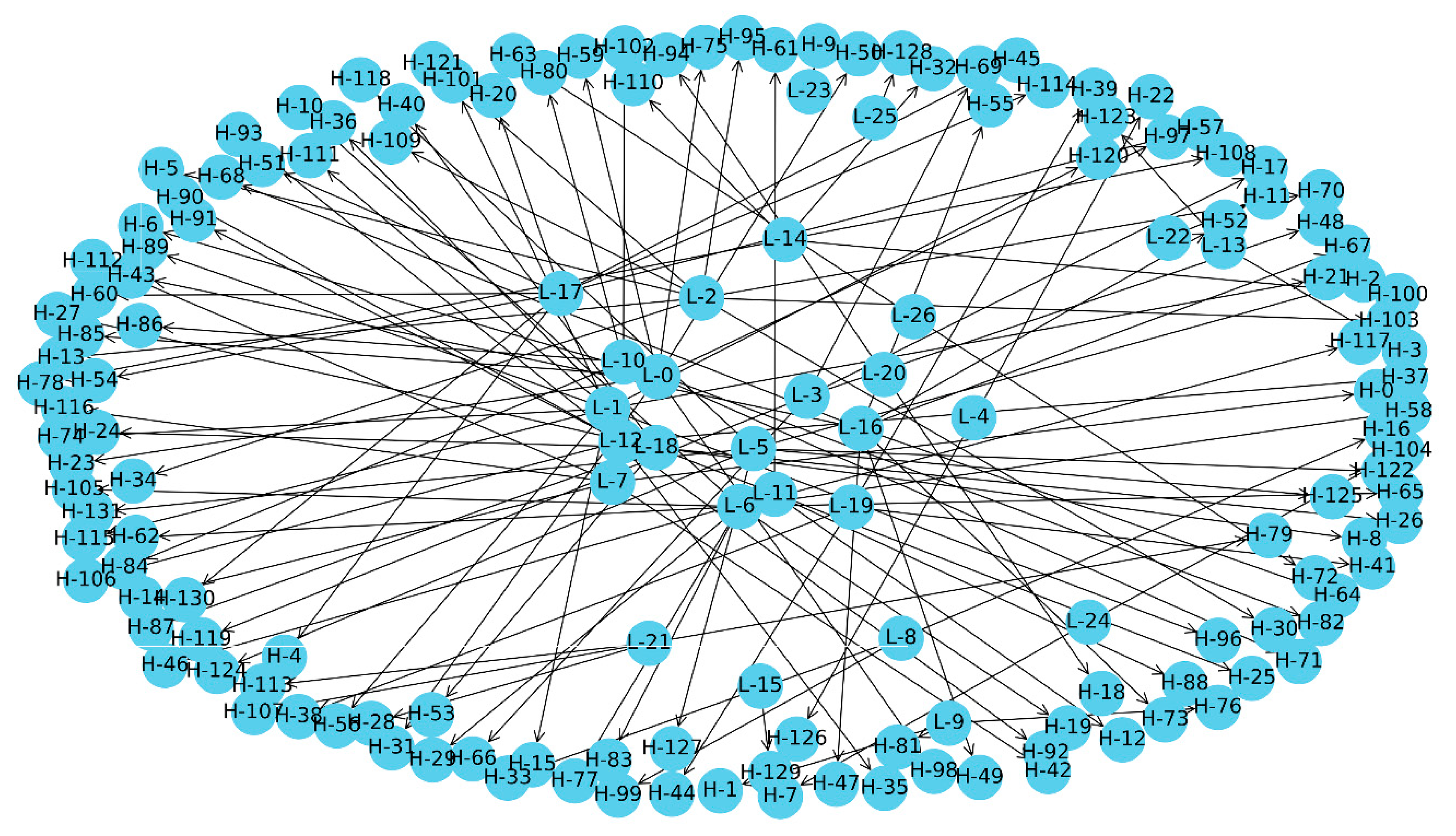
We illustrate the optimal solution in
Figure 8. A directed graph is used to represent matching between instructor and sections. Each section node will only associate with one node trainer. In this situation, the arrow comes from a trainer node and points to the corresponding section node.
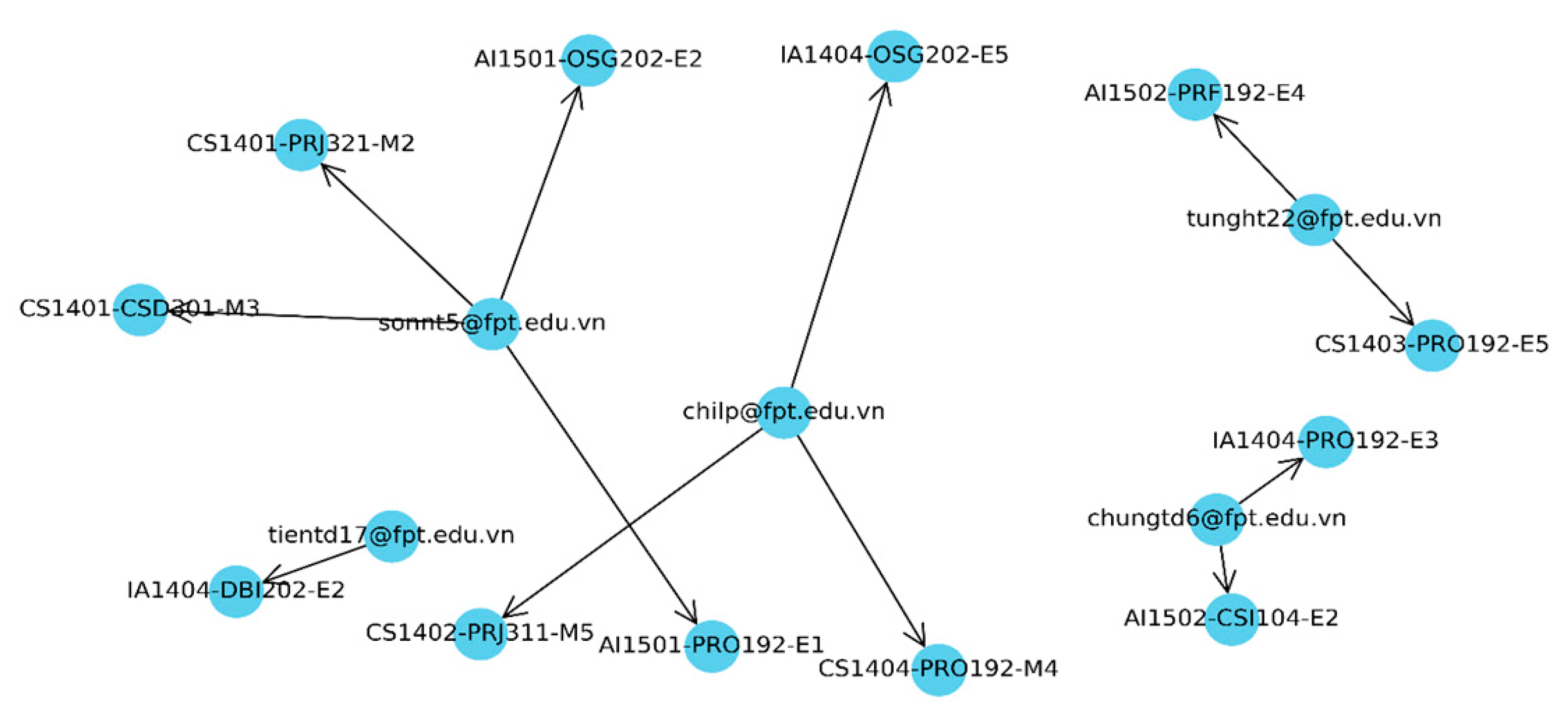
The Genetic Algorithm (and also other approximation algorithms) does not guarantee to find the global solution. The obtained solutions may be local optima. Since our model is different from previous models, it is not feasible to compare the proposed algorithm with the available settings. However, we can evaluate whether the algorithm works well in terms of a smaller search space. We extracted a data set from 5 lecturers, and 12 sections then found the global solution using exhaustive search. The proposed scheme’s comparison results with the implementation of the Brute Force algorithm are shown in
Table 4, and the optimal solution is illustrated in
Figure 9.
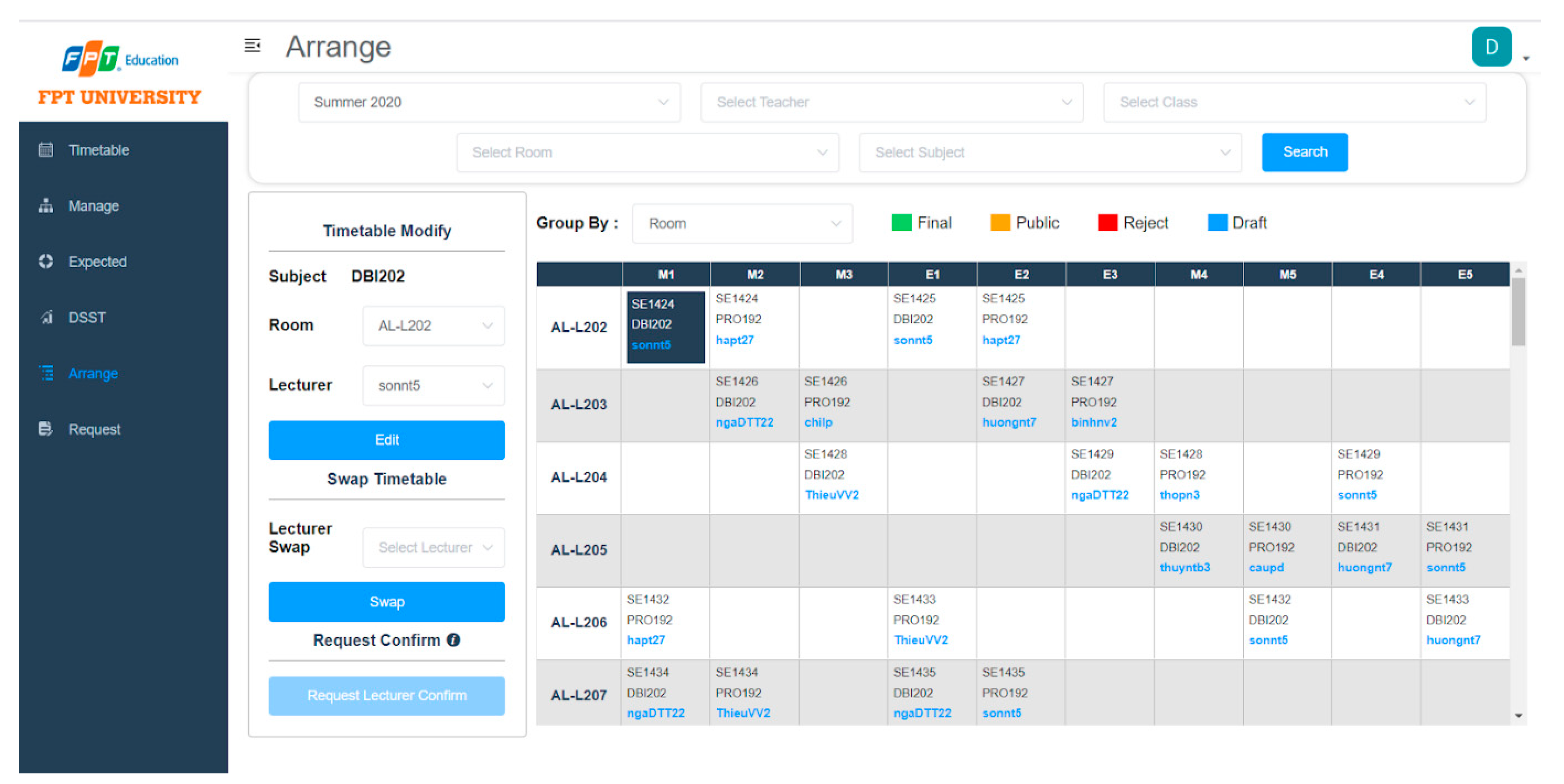
Decision-maker may have their customization on the provided schedule in this situation. To support them, modify the plan quickly, we design a web page to help drag and drop, as shown in
Figure 10. The decision-maker can choose any course and assign it to another instructor by dropping the item in the corresponding line. The information systems part plays a vital role in compensating for the shortcomings of the proposed algorithm.
5. Conclusions
In this study, we have proposed a multi-objective optimization model for the assignment task. The proposed model satisfies the lecturers’ preferences regarding skills, time, and the number of jobs while ensuring related constraints. Our model was applied to the FPT University lecturers scheduling problem and defined a generic solution for multi-objective task assignment problems. We use compromise programming to turn the multi-objective problem into a single-objective problem. Although in the preferred approach, users can set different values for each weight of the target function. It is flexible, but in a multi-dimensional space, the visualization of the results corresponding to a parameter set is difficult. It leads decision-makers to explore parameter sets in an ample search space. On the other hand, a compromise model is a single-shot solution for decision-makers. It avoids them having to define preference information for the objectives. The model itself has found a way to the best. However, the low use of parameters reduces the ability to interact with the model of a decision-maker. The proposed scheme for genetic algorithm shows that it works effectively; the repair step has removed all binding violation solutions without affecting crossovers’ diversity. Shortly, we are looking to build an integrated model with lecturers and students’ scheduling simultaneously. Refining the parameters of the algorithm is also a job in our plan.