1. Introduction
Creating logs is a common practice in programming, which is used to store runtime information of a software system. It is carried out by the developers who insert logging statements into the source code of the applications. Since log files contain all the important information, they can be used for numerous purposes, such as outlier detection [
1,
2], performance monitoring [
3,
4], fault localization [
5], office tracking [
6], business model mining [
7], or reliability engineering [
8].
Outlier detection (also known as anomaly detection) is done by detecting unusual log messages that differ significantly from the rest of the messages, thus raising suspicion. These messages can be used to pinpoint the cause of the problem such as errors in a text, structural defects, or network intrusion. For example, a log message with high temperature values could indicate a misfunctioning ventilator. The authors of “Anomaly Detection from Log Files Using Data Mining Techniques” [
1] proposed an anomaly-based approach using data mining of logs, and the overall error rates of their method were below 10%. There are three main types of anomaly detection methods, such as K-Means+ID3 (supervised) [
9], DeepAnT (unsupervised) [
10] or GANomally (semi-supervised) [
11]. Supervised techniques work based on data sets that have been labeled “normal” and “abnormal”. Unsupervised algorithms use unlabeled datasets. Semi-supervised detection creates a model that represents normal behavior [
2].
With the appearance of large-scale systems, performance monitoring has become a vital task. Since these systems produce numerous log messages every minute, it is impossible to monitor the data by hand. For these reasons, various tools have been created to aid the developer tasked with the monitoring of the performance. One such tool was proposed by the authors of “Structured Comparative Analysis of Systems Logs to Diagnose Performance Problems” [
3] that uses machine learning to find the relations between the performance and different modules of the system. Another such tool has been proposed in “Personalized Ranking for Digital Libraries Based on Log Analysis” [
4], where the authors analyzed user feedback from access logs and predicted user preferences.
The authors of “Scalable Offline Monitoring” [
6] proposed an approach to monitor IT systems offline, where system actions are logged in a distributed file system and subsequently checked for compliance against policies formulated in an expressive temporal logic.
Log files also contain information of the preference of the users, which can be used to create business models. Such models can be later used for example to provide better deals for the customers of a webshop that generated the log files. For example, authors of “An e-customer behavior model with online analytical mining for internet marketing planning” [
7] developed constructs for measuring the online movement of e-customers to identify important dimensions of their behavior and abstract changes in their behavior by developing an e-customer behavioral graph.
Automated log analysis can also be used for reliability engineering. In “A Survey on Automated Log Analysis for Reliability Engineering” [
8], the authors provided a survey on this topic.
The volume of the software logs has escalated rapidly due to the evolution of computers and the wide usage of different types of software. More and more storage space is needed to store these files. The authors of “Loghub: a large collection of system log datasets towards automated log analytics” [
12] provide a large collection of log datasets. To handle such datasets, compression of these files is necessary. A comprehensive comparison between the general compressing algorithms can be seen in “A study of the performance of general compressors on log files” [
13].
Numerous techniques that take different aspects of log files into account have been developed to decrease the size of these files. A compression algorithm for CAN traffic log files is proposed by the authors of “Efficient lossless compression of CAN traffic logs” [
14]. It uses semantic compression to retain precise information, which is needed for forensic purposes. Operational profiles, containing the most common usage scenarios of different softwares, are used to compress log files in “An industrial case study of customizing operational profiles using log compression [
15]. Since creating a profile could be time- and resource-consuming, they use an approach that converts log files into log signals, which are then used to easily create profiles.
In “SEAL: Storage-efficient Causality Analysis on Enterprise Logs with Query-friendly Compression” [
16], the authors created a dependency graph from the log files, which was then compressed. Hidden structures can also be used to compress log files. In “Logzip: Extracting Hidden Structures via Iterative Clustering for Log Compression” [
17] the authors provide a tool that uses such items to compress log files. In “Improving State-of-the-art Compression Techniques for Log Management Tools” [
18], a method is proposed by the authors that pre-processes small log blocks. After the pre-processing, a general compressor is applied on the data.
Many times, choosing the best data compressor of a given set is done by the empirical comparison of the compressors. One of the goals of “Time-universal data compression and prediction” [
19] was to turn this process into a part of the compression method, automating and optimizing it.
In “Lossless Compression of Time Series Data with Generalized Deduplication” [
20], the authors presented a new strategy for data deduplication to provide compressed data storage for large amounts of time series data. In their approach, they split each data chunk into a part that must be stored directly and a part worth deduplicating. This enables greater compression than the classic deduplication based on their analysis.
Shared dictionary compression has been shown to reduce data usage in pub/sub networks, but it requires manual configuration. A new dictionary maintenance algorithm by the authors of “PreDict: Predictive Dictionary Maintenance for Message Compression in Publish/Subscribe” [
21] adjusts its operation over time by adapting its parameters to the message stream and enabling high compression ratios.
Learning categorical features with large vocabularies has become a challenge for machine learning. In “Categorical Feature Compression via Submodular Optimization” [
22], the authors designed a vocabulary compression algorithm, a novel parametrization of mutual information objective, a data structure to query submodular functions and a distributed implementation. They also provided an analysis of simple alternative heuristic compression methods.
The authors of “Integer Discrete Flows and Lossless Compression” [
23] introduced Integer Discrete Flow (IDF), a flow-based generative model, an integer map that can learn transformation on high-dimensional discrete data. They also demonstrate that IDF-based compression achieves state-of-the-art lossless compression rates.
In “On the Feasibility of Parser-based Log Compression in Large-Scale Cloud Systems” [
24] the authors built LogReducer based on three techniques to compress numerical values in system logs: delta timestamps, correlation identification, and elastic encoding. Their evaluation showed that it achieved high compression ratio on large logs, with comparable speed to the general-purpose compression algorithm.
The authors of “Pattern-Guided File Compression with User-Experience Enhancement for Log-Structured File System on Mobile Devices” [
25] introduced file access pattern guided compression (FPC). It is optimized for the random-writes and fragmented-reads of mobile applications, featuring dual-mode compression: foreground and background compression to reduce write stress on write-mostly files and to pack random-reading file blocks.
The raw log messages are usually unstructured, but all the previously mentioned techniques require a structured input. Because of that, the use of log parsing is necessary. It is used to transform the raw messages into structured events. These events can be later used to encode the log messages and decrease the size of the log files. Several algorithms have been introduced to address this problem [
26,
27,
28]. Since log files can contain sensitive user data, it is important to encrypt the files. Up to this date, various encrypting methods have been proposed [
29,
30].
2. Materials and Methods
In this paper, we propose a method that uses a dictionary and employs different template miners to extract message types from raw log lines. The utilized algorithms are IPLoM, LenMa, Spell, Drain, and MoLFI. We then use these message types to build a dictionary where each ID represents a template/message type. This dictionary is used to encode the raw lines into entries that consist of the corresponding ID and the parameters of the specific line.
We compare the size of the encoded messages and their corresponding dictionary with the size of the raw messages. We do not evaluate the performance or accuracy of the algorithms. Since parameters could be sensitive user data, we use encryption methods on the encoded messages. Specifically, these methods are AES, Blowfish, and FFX. The size of the encrypted messages is also compared to the size of the original raw messages. Lastly, we study the speed of the template miners.
The structure of the paper is as follows.
Section 3 gives a brief overview of log parsing and how the individual template miners work. A high-level definition of the encryption methods is explained in
Section 4.
Section 5 contains the description of the performed experiments. Numerical examples based on log lines generated by real-life networking devices are represented to evaluate the compression capacity of the different algorithms. The possible future work about the issue in question and the conclusion we draw can be read in
Section 6.
3. Concepts and Problems
3.1. Log Parsing
To gather run-time information of a software, logging is used as a programming routine. This is carried out by programmers by inserting commands into the source code to print the desired information into log file entries. One line of the log file is referred to as a log record, which is created by a log print statement.
Since developers are allowed to write free-text messages, the entries are usually raw, unstructured messages. They typically describe an event that occurs in the form of raw messages (free text explanation) such as restarts, system updates, or flash messages. These unstructured entries usually contain more than just a message, but also include other information, like the
Timestamp (containing the time of the event occurrence), the
Module (which generated the message), or the
Performed action. An example from our log lines can be seen in
Figure 1.
A word delimited by a space in the message part of the entry is called a
Token. For example, in
Figure 1, the word “APU” is a token. A log message is always made up of two parts. The first is the fixed part, which is called
Template and is the same for all appearances. The template contains the
Constant tokens. These are the words that cannot be expressed by a wildcard value in its associated message type; for example, the “restart” token in the example is a constant. The other part is the variable part which may alter at different occurrences. This part incorporates the
variable tokens, which can be represented by a wildcard value in its associated message type. The “241” and “6” and “cold” values in
Figure 1 are variable tokens.
Parsing each log record
r into a set of message types (and the belonging parameter values) is the objective of log parsing. More formally, in the case of an ordered list of log records, log
containing
M different message types generated by
P different processes, where these values are not known, a
Structured log parser parses the log entries and returns all
M different message types. Using such a parser is necessary for almost any log analysis technique. Log parsers are powerful tools; however, they do not apply to all cases, which means pre- and post-processing are also necessary. There are guidelines for pre-processing in “ An Evaluation Study on Log Parsing and Its Use in Log Mining” [
31] like the use of regex to identify trivial constant parts or deleting duplicate lines.
3.2. Iplom
IPLoM is a log data clustering algorithm introduced in “ Lightweight Algorithm for Message Type Extraction in System Application Logs” [
32] that iteratively partitions a set of log messages that are used as training examples. The algorithm is divided into four steps.
The first step partitions the messages by event size (the number of tokens in the message part). The algorithm assumes that log messages belonging to the same message type have equal event sizes. It uses this heuristic to partition the messages into nonoverlapping batches of messages.
The second step is to partition by token position. Since all messages have the same length, they can be viewed as n-tuples where n is the length of the messages. This step also uses a heuristic, which is that the column with the minimum number of unique words is likely to contain constant words at that position in the message type. The messages are again partitioned by these unique words in a way that the result partitions will only contain one of the previously discovered unique values at that position.
In the third step, new partitions are created by bijection. To determine the most frequently appearing token count amidst the positions, the number of unique tokens at each position is calculated. This implies the number of message types in the partition. After this, the first two positions with the same number of unique tokens as the most frequent token count are chosen to partition again the log messages containing these tokens at the given positions.
Finally, in the fourth step, message types are created for each cluster by counting the unique tokens in all positions. If a position has multiple values, then it is treated as a variable, otherwise, it is considered to be a constant.
3.3. Lenma
LenMa was proposed in “Clustering system log messages using length of words” [
28] and uses the assumption that messages belonging to the same message type have words of equal length in the same positions. First, a word length vector
is created from the message. For example, the word length vector of “APU error, slot 6 (npu cold restart)” would be encoded as the following:
The tokens of the message are also stored in a new word vector
. This vector contains the template of the message. After this, an
similarity value is calculated between the actual message and all clusters with the same event size by the use of cosine similarity. More formally,
where
is the word length vector of cluster
c and
is the word length cluster of the actual message, while
and
are the length of the
ith word in both the cluster and the actual message. This, however, is not enough to correctly cluster all the messages. The comparison between the constant tokens in the same position is also important. This is done by calculating the positional similarity index
, which was also introduced in [
28]. The
is defined as:
where
and
are the word vectors and
i is the position in them. If the message’s
value is higher than the threshold the message is considered to be in the cluster. Afterward, two things can happen. If there is no cluster with a similarity score greater than the threshold, the message is used to create a new cluster. It is important to note that higher threshold values could result in an increased cluster production. Otherwise, the word length vector of the cluster with the highest score is updated. If there is a word in the cluster whose length does not equal to the length of the word in the new message at the same position, the value is updated to the length of the word in the new message. For example, if we take the message “APU error, slot 6 (device cold restart)”, and the previous example as our
c cluster, the new
vector would be:
The word vector is also updated in a similar fashion. If there is a word in the cluster that is different from the word in the actual message at the same position, the word is changed to a wildcard mask, indicating that it is a variable token. In the end, each cluster represents a message type.
3.4. Spell
Spell views log messages as sequences and uses
LCS (Longest Common Subsequence) to extract message types [
33]. Every word is considered to be a token. Log lines are then converted into token sequences, and a unique ID is assigned to them.
A special data structure called LCSObject is created to store LCSseq, which is the LCS of numerous log messages. It is also seen as a possible message type for these log messages. That said, LCSObject also contains a list of the line IDs of the corresponding lines. The already parsed LCSObjects are stored in a list called LCSMap.
The algorithm works as follows. When a new log line is parsed, token sequence is created from it, and a search through the LCSMap is initiated. Consider the LCSseq in the ith LCSObject as and calculate , indicating the length of LCS(). During the search, (the largest ) and , the index of the LCSObject that resulted in , are stored. In the end, the LCSseq of and are believed to have the same message type, if is greater than the given threshold. In the case of multiple LCSObjects with , the one with the smallest value is chosen. After that, the new LCS sequence describing the message type for and all entries in the jth LCSObject is created via backtracking. While backtracking, the positions where two sequences are different are denoted with the “*” wildcard mask. After this, ’s line ID is added to the line IDs of the jth LCSObject and its is changed to LCS(). If there is no such LCSObject that has an LCS with larger than , then a new LCSObject is created with as its LCSseq and ’s line ID as its line ID list.
3.5. Drain
Drain is a fixed-depth tree-based online log parsing method that was introduced in “An online log parsing approach with fixed depth tree” [
26]. The parse tree consists of three types of nodes. At the top of the parse tree is the
root node, which is connected to the
internal nodes. They do not involve any log groups since they are designed to contain specially constructed rules that control the search process. The bottom layer of the parse tree is made from the
leaf nodes. These nodes hold the log groups, and they can be reached by a path from the root node. The log groups are made log line IDs and log events. The log event is used to indicate the message type that is best suited for the log messages in the group. The name suggests that all leaf nodes have a fixed predefined depth, and Drain only traverses through
internal nodes before reaching a leaf node.
The first step is to search by the length of the log message that is equal to the number of words in the message. Log groups with a different number of tokens are expressed by the first-layer nodes. A path to the first node representing the same length as the actual log line length is selected. For example, in the case of “NPU cold restart” the internal node representing “Length-3” is chosen.
The second step uses the presumption that log messages that have the same message type usually have the same constant token in the first position of the message. The next node is selected by this assumption. For example, in the case of the previous “NPU cold restart” message, the 2nd layer node encoding that the message starts with “NPU” is picked. Messages beginning with a parameter can lead to branch explosion. Tokens that only contain digits are considered to be special. In the case of such messages, a special “*” node is selected in this step.
The third step is to search by token similarity. By this step, the search has already reached a leaf node containing multiple log groups. The most appropriate log group is selected based on the similarity of the actual message and the log event of each group. The similarity,
, is defined as:
where
n is the number of tokens in the message and
is the actual log message,
is the log event of the group and
denotes the
ith token in the message. The function
is defined as the following:
where
and
are the two tokens. If the greatest similarity reaches the predefined threshold, the log group that reached the largest similarity is returned; otherwise, a flag is returned to indicate that the message does not fit into any log group.
The last step is to update the parse tree. If the output of the previous step is a log group, the ID of the actual log line is added to its ID list and the log event of the group is updated. This is done by checking if the tokens are the same in the different positions of the actual message and the log event. If they differ, a wildcard mask “*” is set in the log event at that position; otherwise, nothing happens. If a previous step resulted in the flag, a new log group is created from the actual message, only with the ID of the actual log line.
3.6. MoLFI
MoLFI was proposed in “A search-based approach for accurate identification of log message formats” [
34] and employs the standard NSGA-II for the log parsing problem. While pre-processing the data, trivial constants are replaced with a unique #spec# token that cannot be changed in the later steps. The messages are also sorted into buckets based on their token count.
A new two-level encoding schema is applied: each chromosome C is a set of groups where each group is a collection of templates (message types) with the token count N. This schema ensures that only messages and templates of the same length are matched in the later steps.
In the first step, the initial population is created. Let M denote the pre-processed log messages. After a chromosome is created, it is filled with groups of templates. Each group contains pre-processed log messages with the same N length. Initially, all messages are in a special set called unmatched. In every turn, a message is randomly selected from here, and a template t is created based on it. The template is identical to the message except for a randomly selected token, which is changed to “*”. This is then added to the group , and the unmatched set is updated (the message is removed). This loop stops when the unmatched set becomes empty.
The next step is to Crossover, which is achieved by the use of the uniform crossover [
35] operator. Two parents are taken and two offsprings are created by this operator by mixing the attributes of the parents. The templates between the parents are exchanged without changing the set of templates constructing each group. The offsprings contain all the already-processed messages and do not overlap on any template.
The next step is to mutate the offsprings. This is done by randomly altering a template in each of its groups. Let be the selected template. Each token has chance to be changed. If a token is modified, the following can happen: If it is a variable token, it is changed to a constant token randomly selected from the fixed tokens at that position in the messages that match . If it is a constant token, it is replaced by a wildcard “*” token. If it is the special #spec# token, nothing happens. At this point, a correction algorithm is used to remove overlapping templates and to add random templates to groups that do not match all of their messages. In the end, the variable tokens that do not influence the frequency scores are removed by inspecting if their deletion changes the messages that match their template or not. If there is a change, they are added back to the template; otherwise, the template remains unchanged. This algorithm results in numerous optimal solutions, from which the knee point is chosen as the final output.
4. Encryption Techniques
Encryption is a basic term in cryptography that stands for the process of encoding information. The original human-readable data, plaintext, are transformed into an incomprehensible text, a ciphertext that appears to be random. The process requires the use of a secret key that both the sender and the recipient know. These keys are usually pseudo-random generated keys. Ideally, with the use of the key, only authorized parties can decode the ciphertext and access the initial message. While it is possible to decrypt the message without the key, it requires a computing capacity that modern computers cannot deal with.
4.1. AES
The Advanced Encryption Standard (AES) is a symmetric encryption that is a subset of the Rijndael block cipher introduced in “AES proposal: Rijndael” [
29]. It is considered to be one of the best encrypting algorithms. It has a key size of either 128, 192, or 256 bits and a fixed block size of 128 bit and encrypts only one block at a time. It operates on the
state, which is a
column-major order array of bytes. The algorithm’s input is the plaintext, which is converted into the output (ciphertext) via a number of transformation rounds. The number of rounds
depends on the size of the key. In the case of 128-bit keys, 10 round is used, 12 rounds in case of 192-bit keys and 14 rounds for 256-bit keys. A high-level description of the operation of the method is the following.
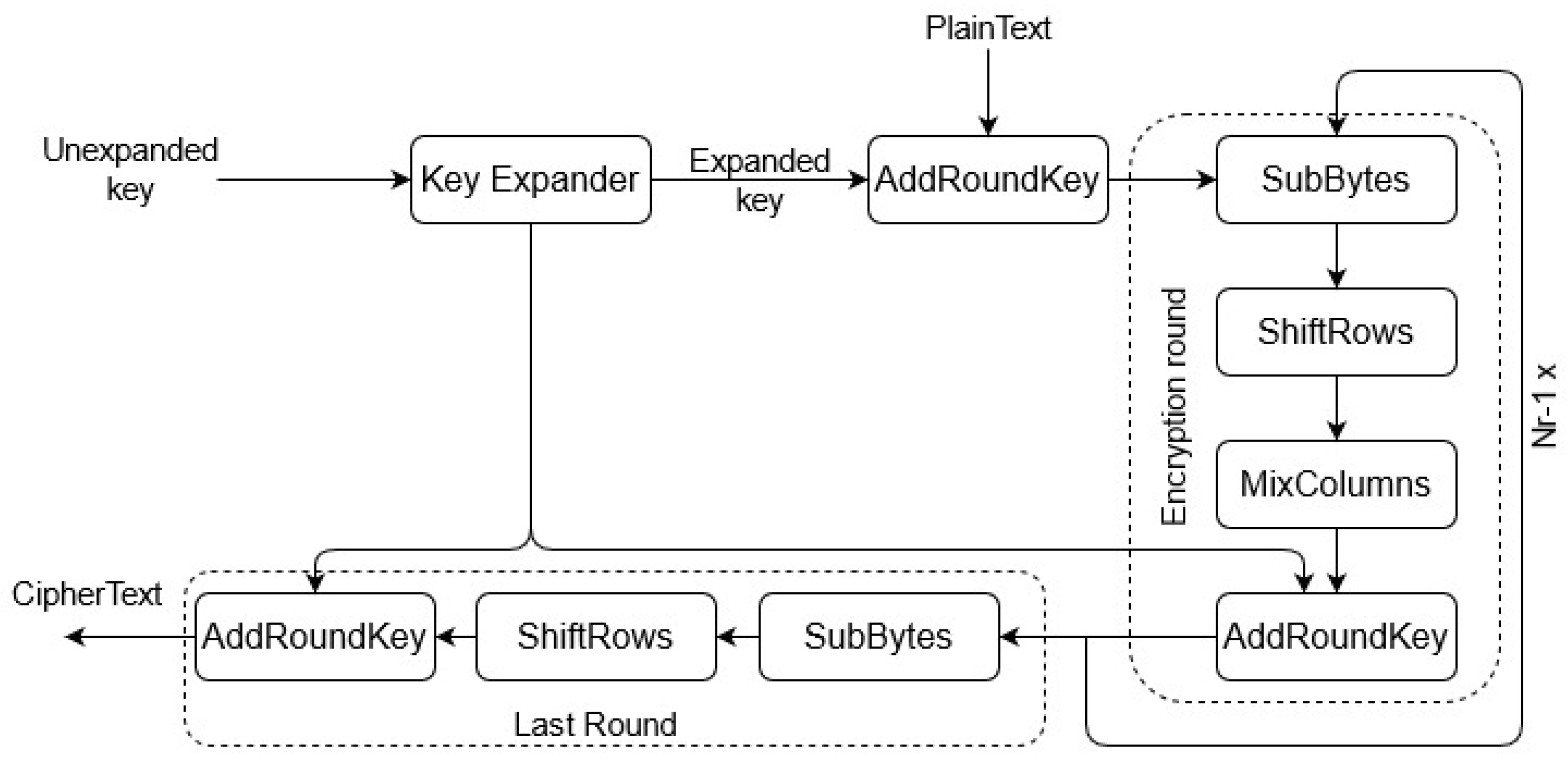
The first step is the KeyExpansion that derives round keys from the cipher key based on the AES key schedule. This is followed by an initial AddRoundKey that uses bitwise xor to combine each byte of the state with a byte of the round key.
This is followed by
rounds consisting of four phases. The first is
SubBytes, which replaces each byte with another based on a lookup table in a non-linear fashion. This is followed by
ShiftRows, a cyclical shift in the last three rows of the state. After this, the four bytes in each column of the state are combined by the
MixColumns operation. Lastly, another AddRoundKey is used. The
rounds are followed with a final round, which is composed of SubBytes, ShiftRows, and AddRoundKey. To decode the ciphertext with the use of the same encryption key, a set of reverse rounds is used. The algorithm can be seen in
Figure 2.
4.2. Blowfish
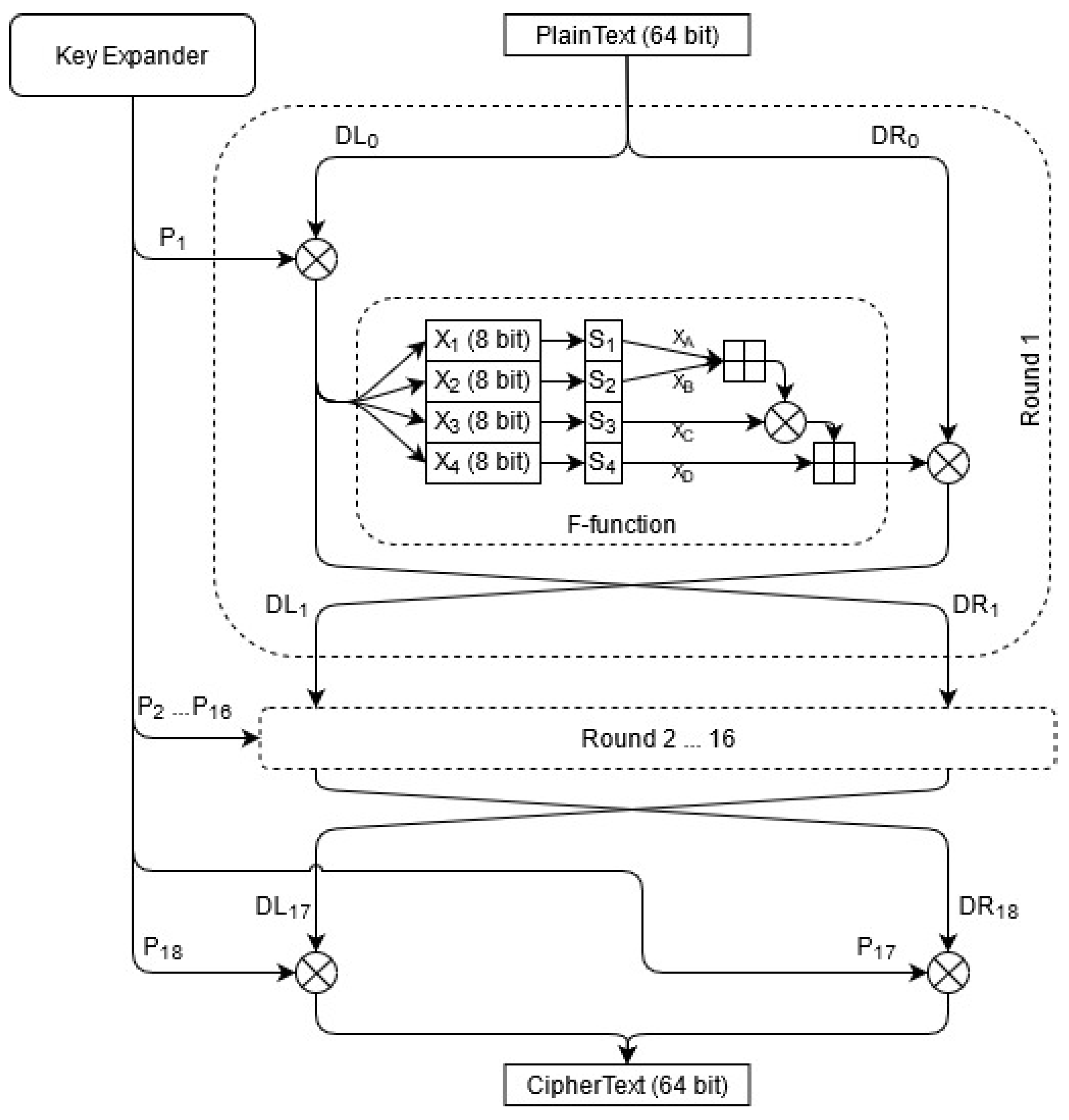
Blowfish was designed by Bruce Schneier in “Description of a new variable-length key, 64-bit block cipher (Blowfish)” [
30], 1993, to replace DES. It is a fast and free public encryption software; therefore, it is neither licensed nor patented. It is also a Feistel cipher [
36]. Blowfish is a symmetric block cipher with a fixed block size of 64 bits, which means that it divides the input into fixed 64-bit blocks while encrypting and decrypting. It has a variable key length that can vary from 32 bits up to 448 bits. The encryption schedule of Blowfish can be seen in
Figure 3. There are 18 subkeys stored in a
P-array, with each being a 32-bit entry. Four
Substitution boxes (S-box) ,
,
,
are used by the algorithm, each consisting of 256 entries with a size of 32 bits.
First, the P-array and the S-boxes are initialized with the use of Blowfish’s key schedule: values are generated from the hexadecimal digits of pi. This is followed by 16 rounds, each consisting of four operations. Each round takes two inputs, the corresponding subkey and the plaintext (data), from the output of the previous round. Let and denote the left and right sides of the data. The first step is to XOR the ith subkey in the P-array, , with .
The second step is to use this XORed data as the input of the F-function. The function works as follows: four 8-bit quarters , , , are created from the 32-bit input and are used as the input of the S-boxes, which then creates 32-bit values , , , from them. and are added modulo ; next, the result is XORed with . This value is added with , generating the output of the F-function.
In the third step, the is XORed with the output of the function. The final step swaps the left side and the right side. The output of the 16th round is then post-processed (output whitening). The last swap is undone and is XORed with , while is XORed with . Decryption works in the same way as encryption, except that the subkeys in P-array are used in reverse order.
4.3. FFX
FFX is a
Format-preserving, Feistel-based encryption method that was introduced in “Format-Preserving Feistel-Based Encryption Mode” [
37]. Format-preserving encryption means that the ciphertext has the same format as the plaintext input. For example, the encryption of a 16-digit credit card number would result in a ciphertext consisting of 16 digits. FFX takes three parameters as its input, the plaintext that is to be encoded, the key that will be used as the round key, and a tweak [
38]. A tweak is a nonempty set of strings that are used to modify the round key. As its name suggests, the algorithm is based on the use of a Feistel network [
36].
The core of each Feistel network is a round function that takes a subkey and a data block as its inputs and returns an output with the same size of the data block. Each round in the network consists of two main operations. The first one is to run the round function on half of the data, and the second is to XOR the output of the function with the other half. FFX uses AES as the round function for its Feistel network. Only one secret key is used as the round keys of AES; however, it is marginally tweaked every round.
6. Discussion and Conclusions
In this paper, we evaluated the compression capacity of our dictionary method with the use of various template miners. These measures acquire message events from log files. Events consist of variable tokens (parameters) and constant tokens. We use these templates to create a dictionary where each ID represents a message event. The ID of the corresponding template is assigned to each log line. We then use the dictionary to encode the messages based on the principle that we only store the ID and the parameter list. Since parameters could contain confidential information, the compressed files are encrypted as well.
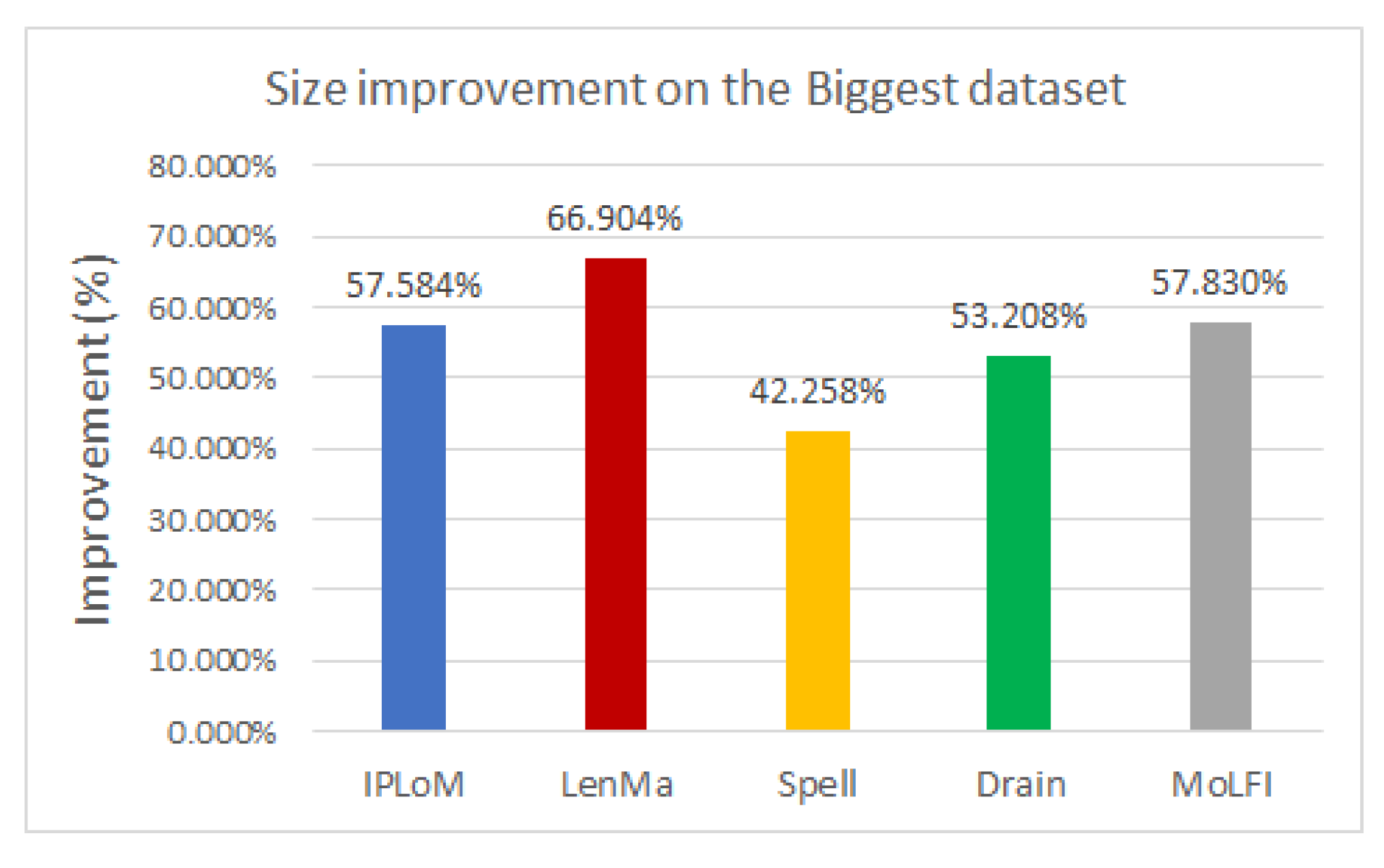
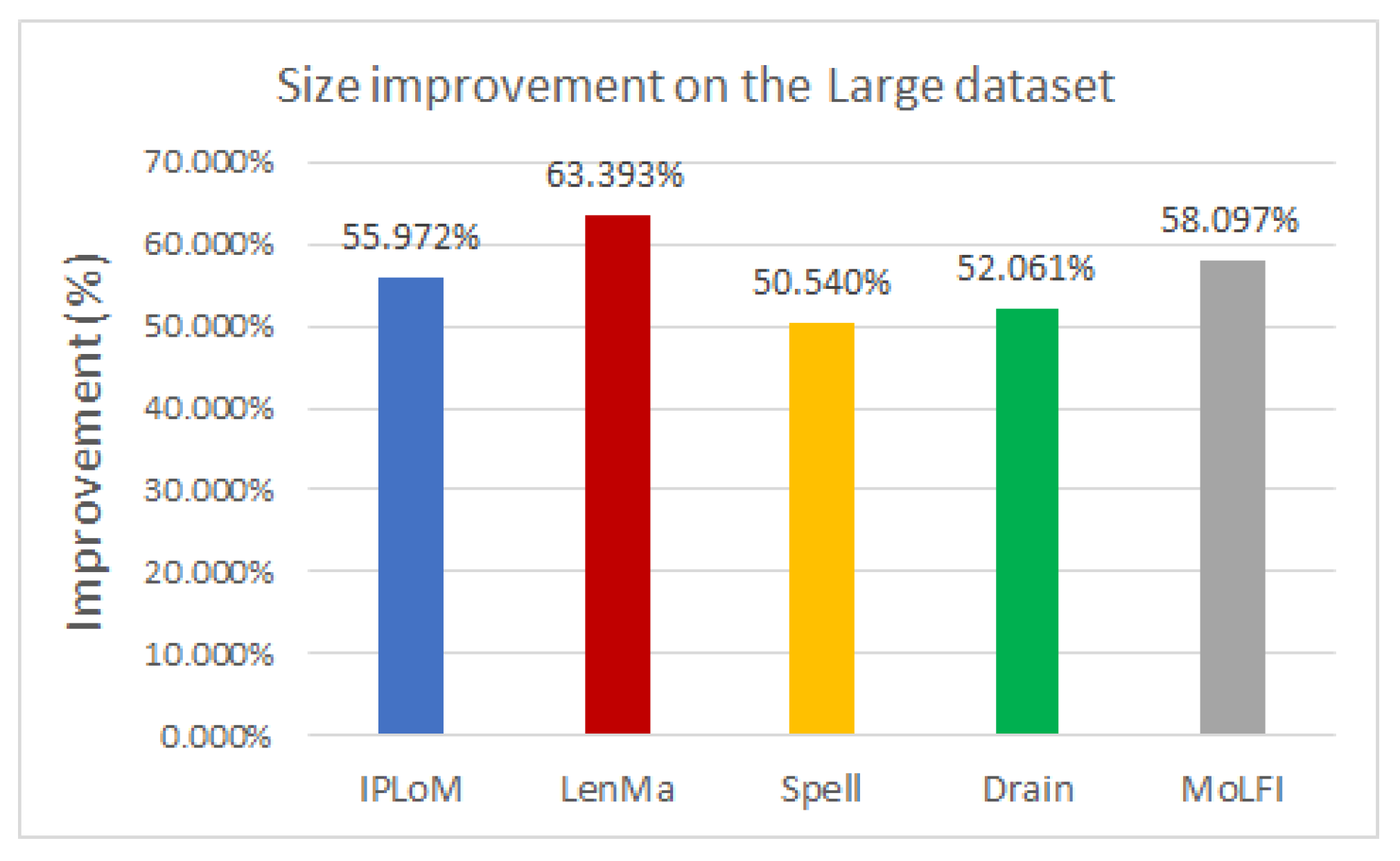
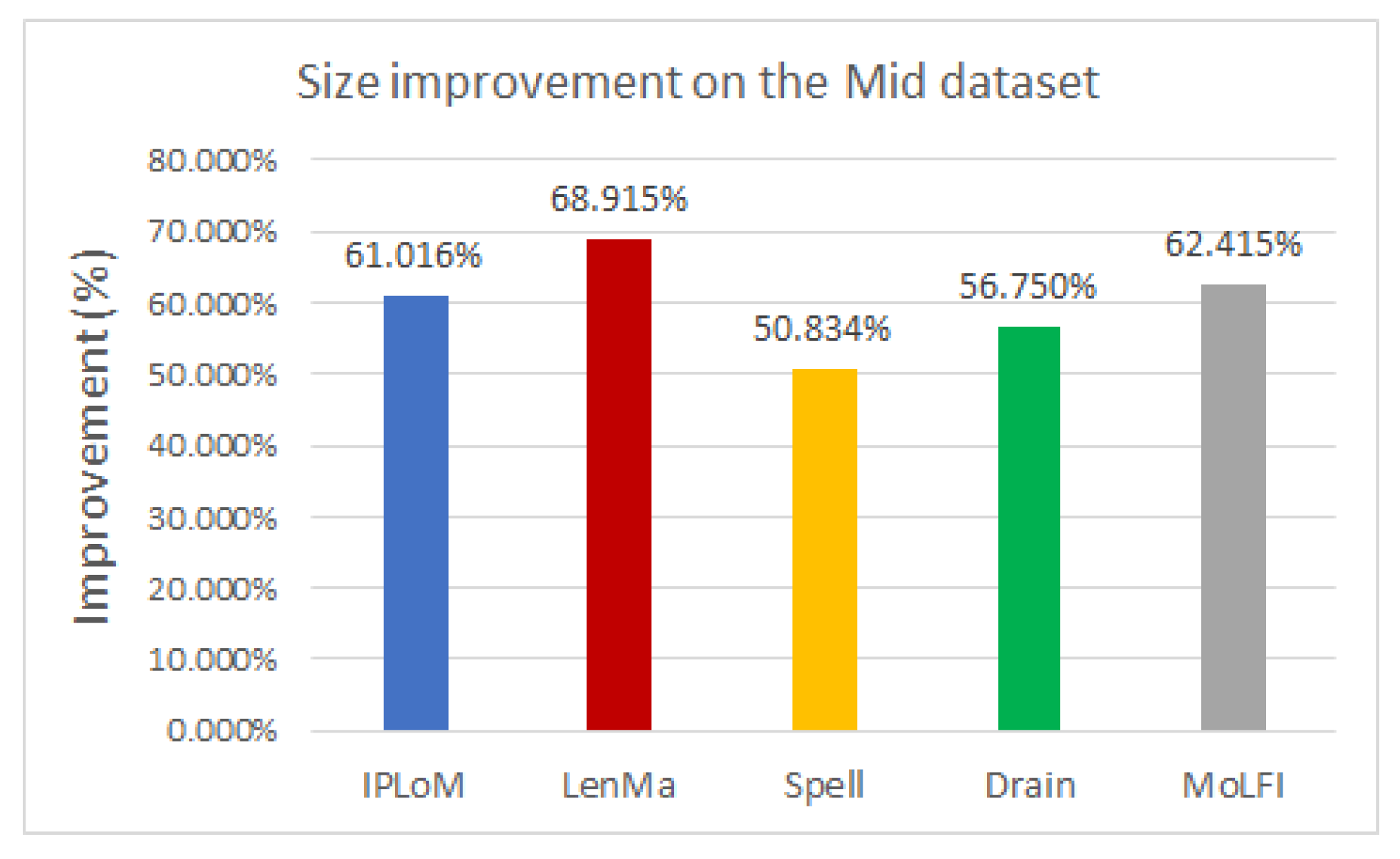
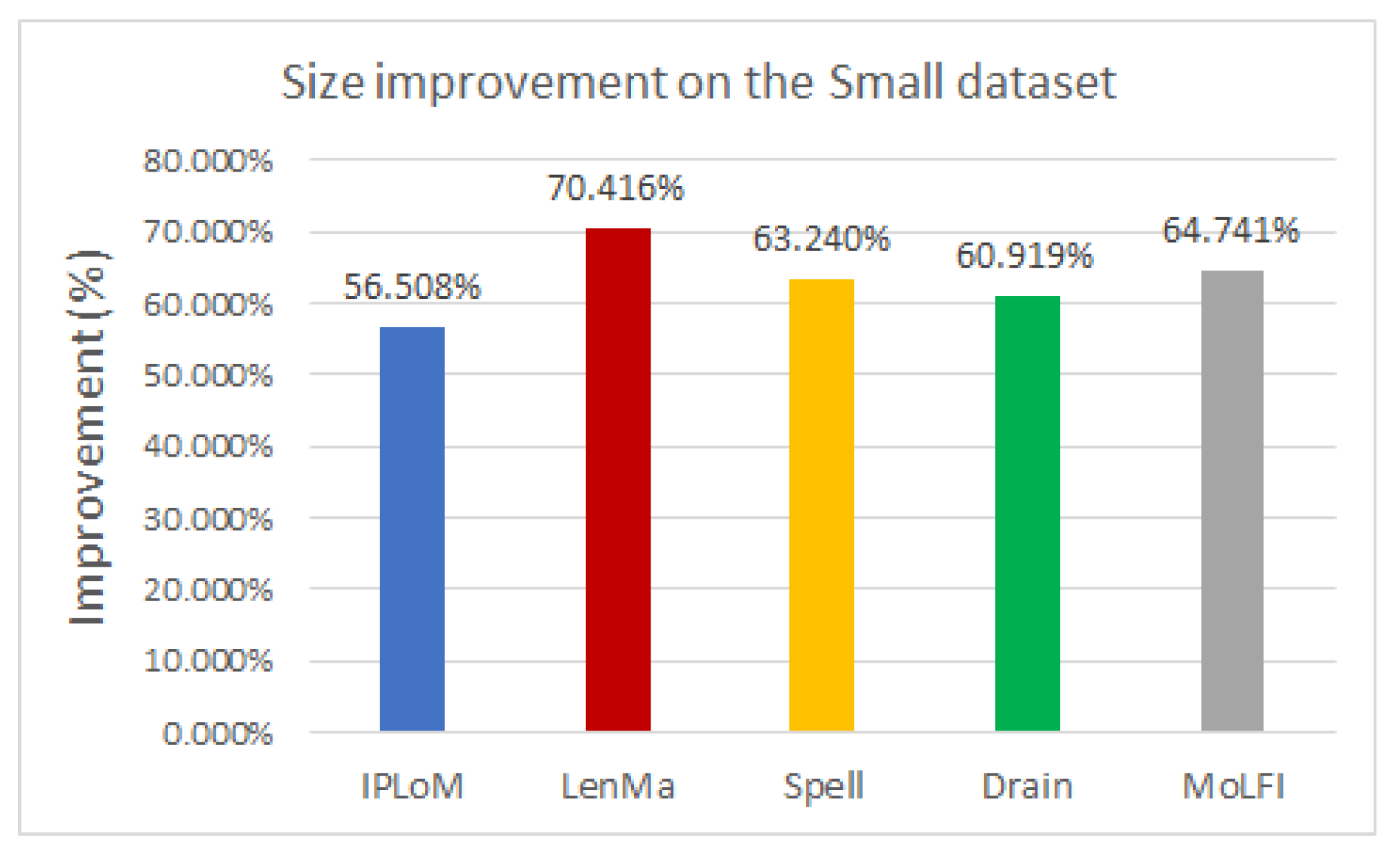
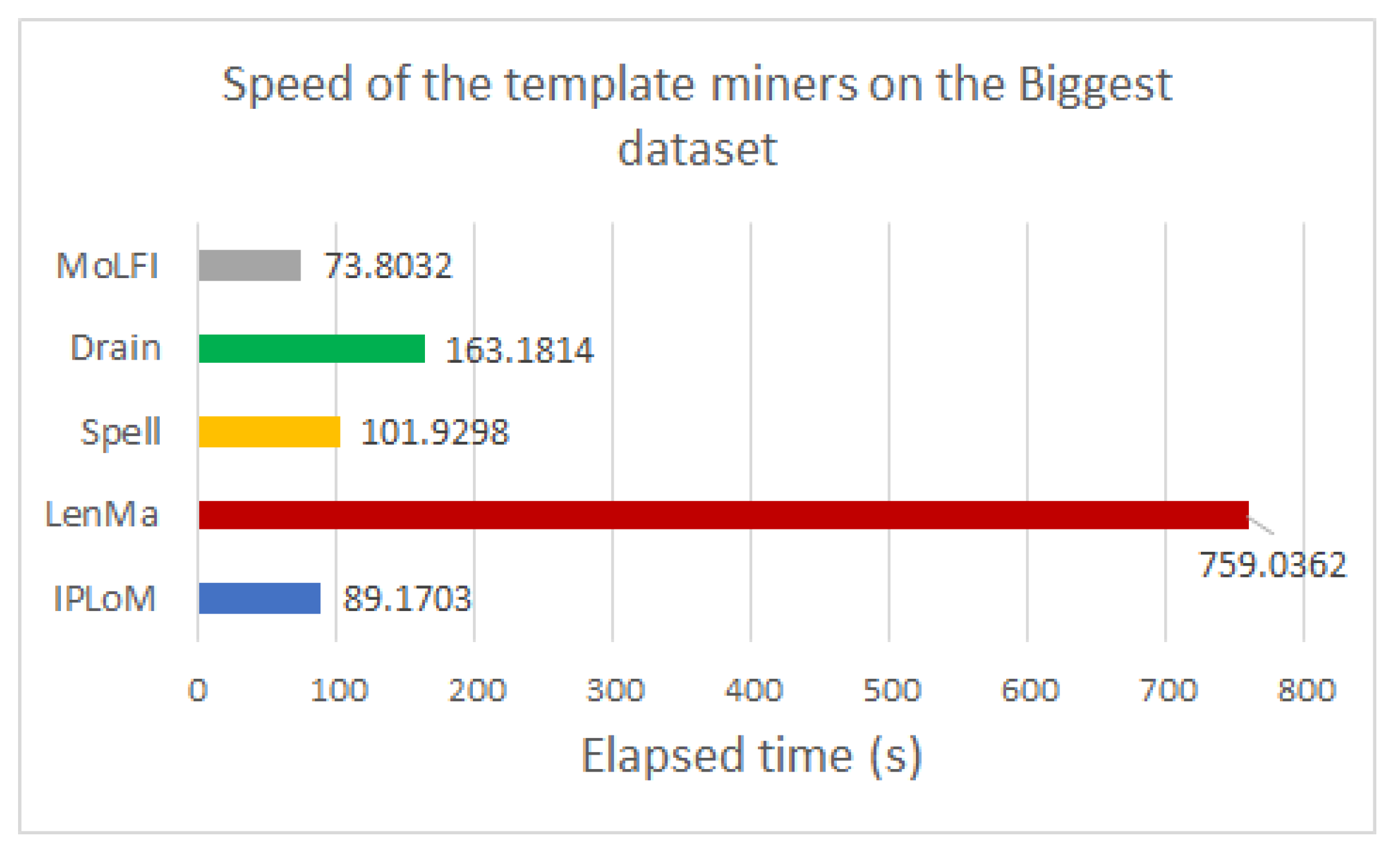
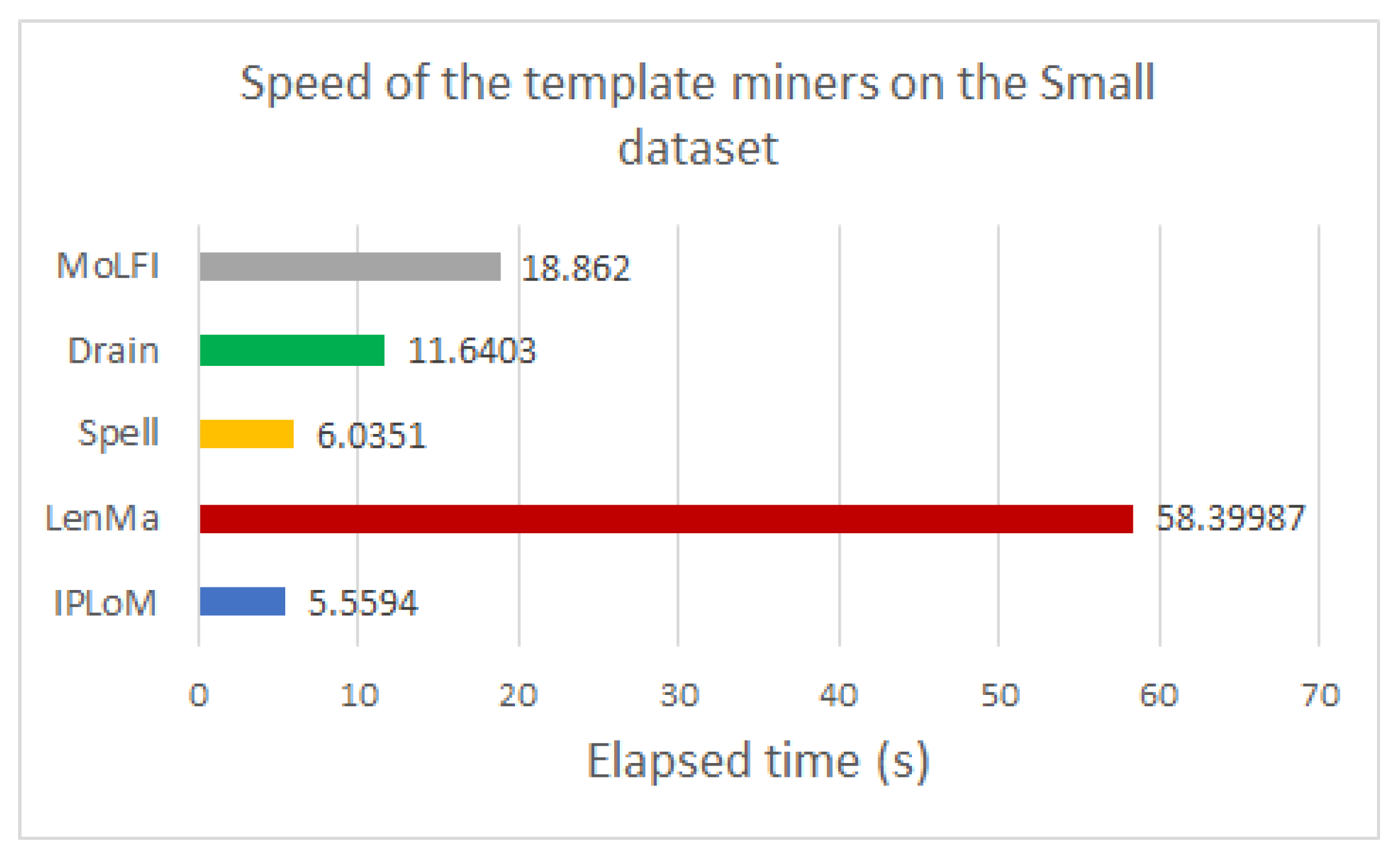
To analyze the performance of the template miners in pair with this encoding method, several experiments were conducted. The experimental results showed that using any type of template miner with the generated directory results in around 50% compression. Out of all the investigated measures, LenMa proved to be the best with an average of 67.407%. It produced a bigger dictionary, and because of that, fewer parameters had to be encoded, which resulted in smaller file sizes. In the case of the encryption methods, the results showed that the use of FFX slightly decreases the size of the compressed file. The speed of the template miners was also compared. Based on our experiments, LenMa was outstandingly slower than the other methods, despite its good performance at compression. Our results yielded that IPLoM is the fastest among the examined methods.
Based on our experiments, we would suggest the combination of IPLoM and FFX to achieve the best results; however, using any of the log miners with the dictionary method greatly reduces the size of the log file.
While we only investigated these five template miners, it is possible that other methods could yield better results. We only evaluated the performance on log files, and it would be interesting to measure the performance in the case of stream-like data. It would be also beneficial to compare the performance of our method and the performance of the existing general compressors. The compression rate achieved by the combination of our algorithm and the general compressors could be also investigated.