2. Motivation and Examples
In the journey of refinements, perfecting belief formulation became an objective in itself, and perhaps, we lost sight of the reason why we need those beliefs.
Specifying off-equilibrium choices is certainly very useful for eliminating “incredible threats” and keeping strategies dynamically consistent.
4 The conventional thinking was that in order to determine whether an action at an off-equilibrium information set is optimal, we need beliefs; and then, given those beliefs, the player making the choice can consider his/her expected payoff to make the optimal choice. Actions at unreached information sets that constitute an “incredible threat” are instances where a player is deliberately not maximizing at his/her decision point; the purpose being to thereby steer an earlier player away from that decision point for the threatening party’s own advantage, when instead with the appropriate choice, the earlier player may have preferred to go to that decision point. Any other instances of non-optimal behaviour at unreached information sets does not constitute a threat. For the no threat information sets, non-optimal behaviour is not problematic and should not influence our understanding of what is a valid equilibrium. To illustrate this, some examples will be considered.
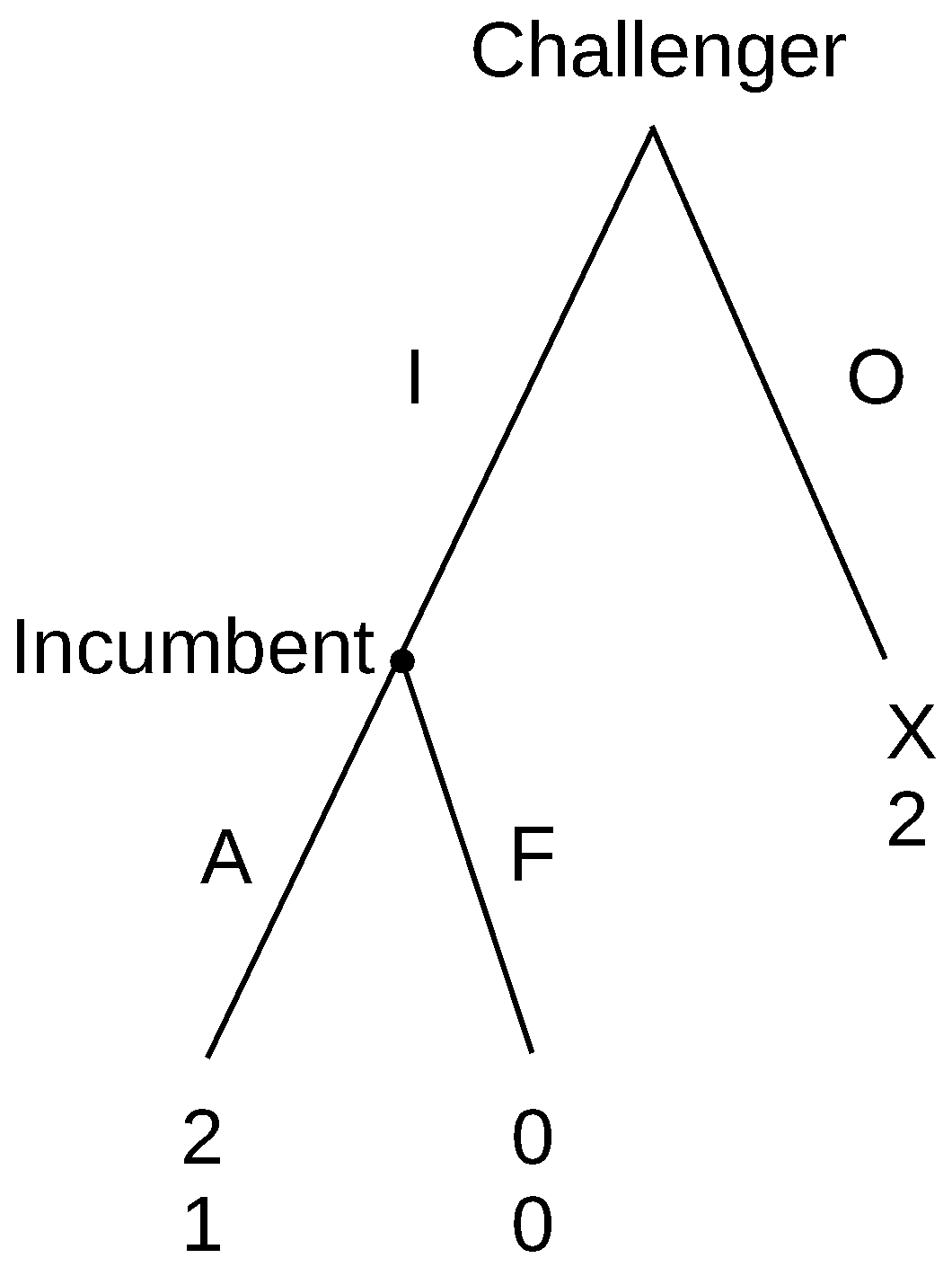
For simplicity, start with a full information game, the entry game in
Figure 1, where x
. The entrant has two actions, I (opt In) or O (stay Out), and if he/she enters, the incumbent can either F (Fight) or A (Accommodate). Notice that there are two Nash equilibria, IA and OF. Fight (F) is an incredible threat,
5 invalidating the OF equilibrium. We will call such an information set, or single decision point, where a player can make an incredible threat, pivotal. Now, if we alter the payoffs for the challenger at Out (O) to x
, it becomes weakly dominant for the challenger to just staying out. It is not so important to specify the incumbent’s behaviour because it is not relevant to the challenger’s decision to stay out. Fight is no longer a threat that influences the challenger. The decision point is no longer pivotal. The incumbent’s behaviour is not relevant to the challenger’s decision to stay out. It would be fine to think that the incumbent plans to fight, or indeed not to think about the incumbent’s choice at all, as in this game, it makes no difference.
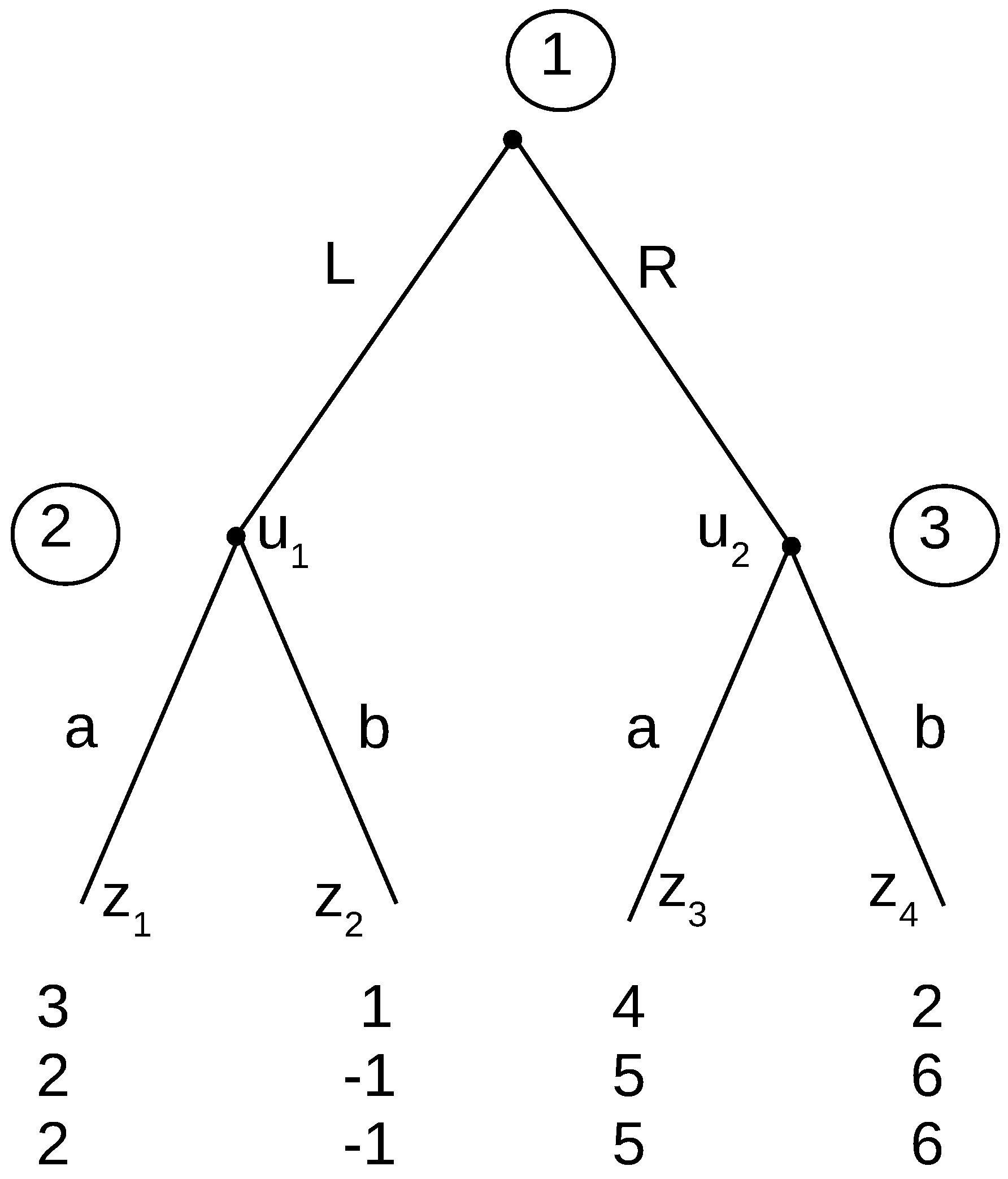
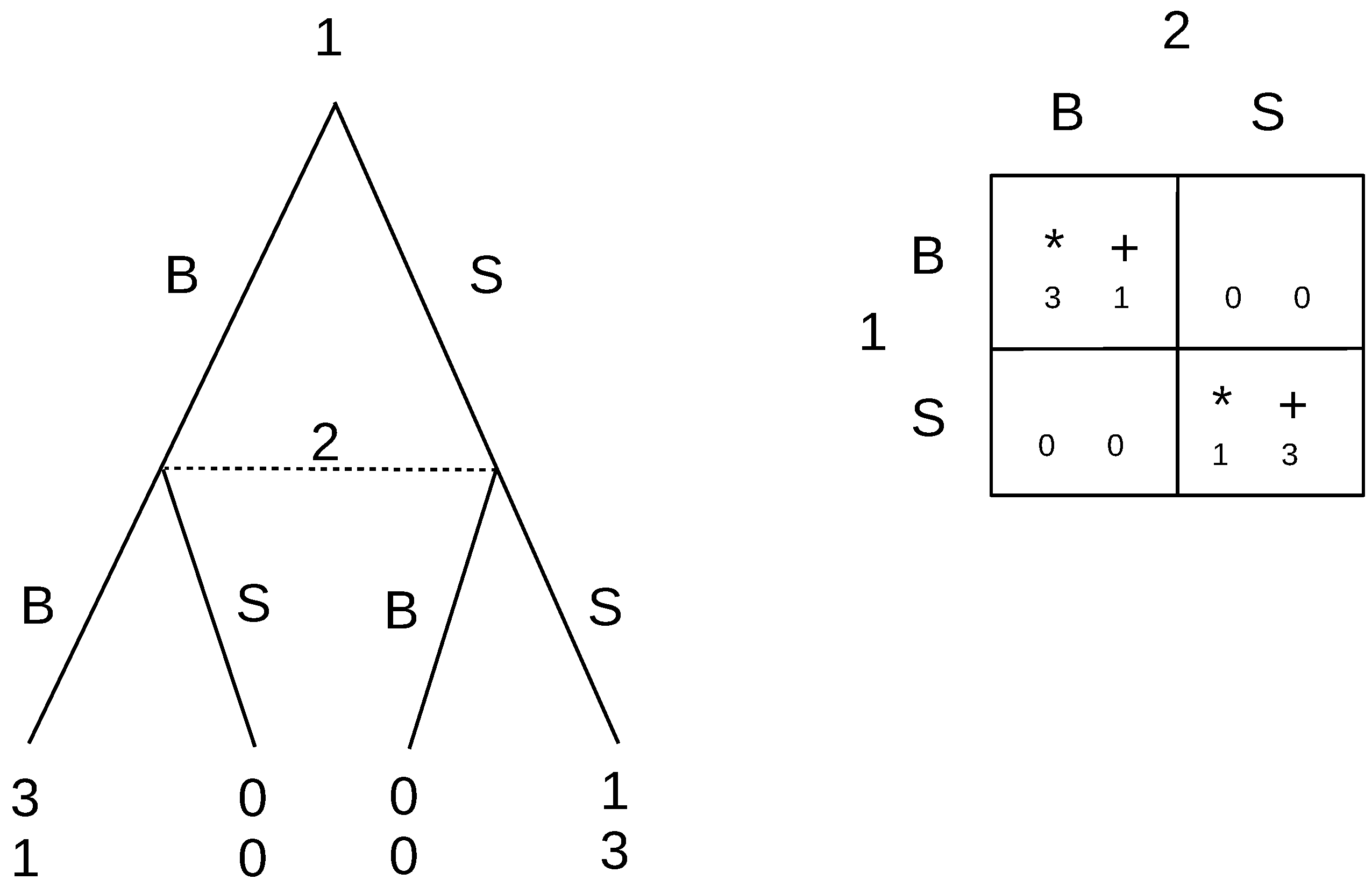
Consider the three-player game in
Figure 2. Nash equilibria are Lab and Rbb. Here, we can agree that we should eliminate Rbb because Player 2 is using an incredible threat by saying that he/she plans to play b. By saying this, he/she is preventing Player 1 from choosing L, which he/she would have preferred. Therefore, in this instance, subgame perfection is important, and we do need Player 2 to make a rational choice at his/her decision point.
Now, let us see a game without full information.
6 Consider the game in
Figure 3, with
,
and
.
There are two pure strategy equilibria here: (L, L’) and (R, R’). If we include beliefs that rationalize Player 2’s actions, we find the perfect Bayesian equilibria: (L, L’,
) and (R, R’,
). Furthermore, the second is problematic because the associated beliefs put much weight on action M, which is strictly dominated by R and weakly dominated by L, so it is not ever going to be played by Player 1. To solve this problem, a further restriction that is placed on beliefs is that there should be no probability weight put on the outcome of an action if it is strictly dominated at an earlier information set, if this is possible.
7 This eliminates the (R, R’) equilibrium, since now, Player 2 is not maximizing by choosing R’. While it is clear that the equilibrium needs eliminating, this seems like a complicated way to do it.
Consider some variations of this game. Suppose the payoff from the outside option R changed to . Now, action M is only weakly dominated , and if strictly less, it is not dominated at all. How can we eliminate the equilibrium (R, R’, ), and do we want to eliminate it? A further modification to consider is that in addition to reducing the outside option payoff to , suppose that the payoffs after M for Player 1 are exchanged, so that and . Does that change how we think about the (R, R’) equilibrium? For all these versions of this game, with current refinements, we get different answers depending on the modification, but in each case, the only ideal reactive equilibrium is (L, L’).
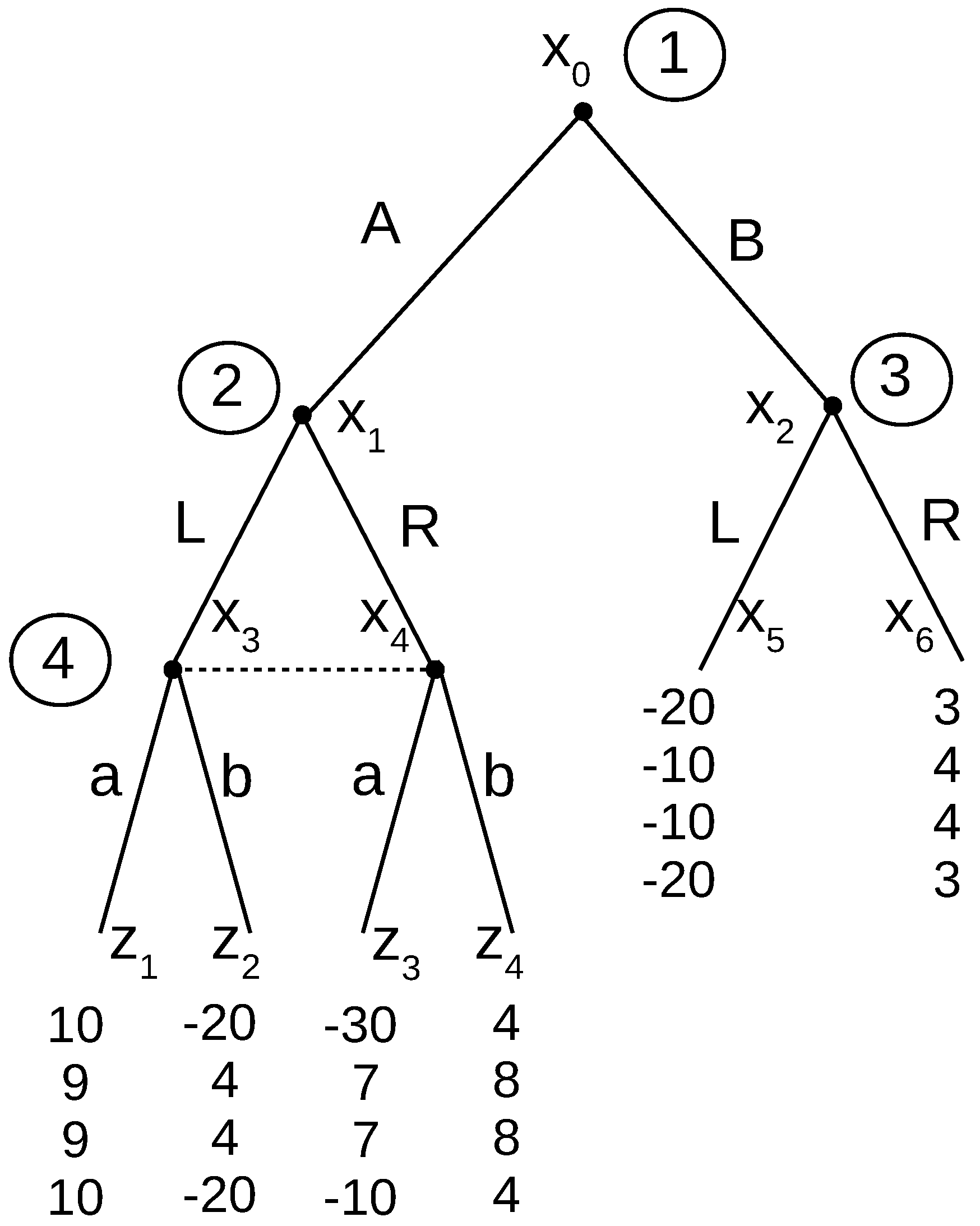
Before we define ideal reactive equilibrium, consider a final example, given in
Figure 4. Consider the two pure strategy Nash equilibria ALRa and ALLa. Conventional refinements would eliminate ALRa because Player 3’s action is not rational; never mind that Player 3’s action does not in any way constitute an incredible threat that influences the equilibrium path. Here is an instance where conventional theory requires too much rationality. In a sense, both are valid, because it does not matter what Player 3 plans to do. He/she could threaten by moving L, and it would be incredible; however, that is not what is motivating Player 1 to move A. With ideal reactive equilibrium, only the equilibrium path is relevant, because all the thinking that goes into the thought process dynamics has already distilled the incredible threats, and they are being ignored.
These are just a few examples. In what follows, we explore how to remove incredible threats without appealing to beliefs.
3. Ideal Reactive Equilibrium
Ideal reactive equilibrium utilizes the novel idea of the manipulated Nash thought process found in Amershi, Sadanand and Sadanand [
1,
2,
3,
4]. Although this work builds on that concept, it is distinct and involves much further development and investigation. Specifically, thought process dynamics itself is developed further here and in particular operationalized for signalling games. It is also analysed in greater detail from the perspective of first and second mover advantage games. Moreover, equilibrium is defined somewhat differently and shown to always exist for finite games.
To give a formal definition of ideal reactive equilibrium, we first need to define some terms that culminate in the definition of IRE.
Deliberate deviation of order n, : Starting from any set of initial choices for all the players, a deliberate deviation of order n by a particular player at a particular information set is a departure by that player from his/her initial choice to another of his/her available choices (pure action, no randomization), and he/she supposes that n of his/her immediate followers can observe the deviation. That is, we erase the information sets (if there are any) for those n players’ choices that follow the particular player.
After a deliberate deviation, any player may respond with his/her best response to any changes that have occurred. This includes the original player. After that, any other player may respond with his/her best response to all the changes that have occurred thus far, and so on, until everyone is using a best response and we are at a (possibly different) Nash equilibrium.
Successful deliberate deviation: A deliberate deviation of any order is said to be successful if after the deviation and after all players are allowed to respond using best responses, the final outcome results in an increase in the payoff for the deviating player.
If a deliberate deviation is successful, then the outcome is that we remain at the final Nash equilibrium after deviation and best responses. If it is not successful, then the original deviator retracts his/her deviation, and we are back at the original starting point.
Thought process: A thought process is a sequence of outcomes starting with a deliberate deviation and then tracking all the best responses until we arrive at the resolution of that deviation. If the deviation is unsuccessful, then no movement occurs under the thought process; if it is successful, then the thought process tracks all the various stages of outcomes until we reach the final Nash equilibrium. Then, another deliberate deviation may be be undertaken by any player, and the thought process continues to track the outcomes of that deviation and all the best responses that follow, as before. This continues until either there are no more successful deviations available or until we observe that the thought process is cycling indefinitely through a subset of the terminal nodes.
Ideal reactive equilibrium: A Nash equilibrium is an ideal reactive equilibrium if:
all thought processes end with no change in the players’ choices,
or if all thought processes cycle endlessly through the same subset of terminal nodes, then the original Nash equilibrium is IRE if either its outcome is part of the subset through which the thought process cycles or, in the case of the original Nash equilibrium being a mixed strategy Nash equilibrium, if the cycling utilizes all the actions with positive probability weights in the mixed strategy.
As is evident from the definitions, the thought process gives importance to order of play, and earlier movers enjoy an advantageous position relative to later movers. Each player goes through successive orders of thinking
8 and revising his/her choices, by imagining that arbitrary numbers of immediate followers can actually observe their moves even if in the original game, they could not. Upon “virtually observing”,
9 the followers may want to change their response.
This is all a thought process only. Players do not actually take any actions; it is only in the mind of the original player that began this line of thinking. Since all this thinking is simply based on the knowledge of the game tree, which all players possess, they can all anticipate each others’ thinking. As indicated in the definitions, the original player may retract his/her deviation if he/she finds that he/she is actually worse off. Throughout the thought process dynamics, order of play is respected, and so by deviating, players can only influence their followers by supposing that they can observe the deviation, and not players preceding them. In case there are any nature moves, which are not strategic and cannot be influenced, players simply use expected payoffs in their thinking.
It may seem very strong to suppose that in a deliberate deviation of order n, the n follower players have a sudden and complete revelation of the deviator’s new action. However, it should not be taken literally that the information is actually revealed, but rather, it is the deviator pondering: What if these n followers could figure out what I have done? Assuming they could figure it out, what would they then do? Then, what would everyone else do? At the end of it, if the deviator is indeed better off, then those n followers (who can also replicate the deviator’s thought process) would expect the deviator to deviate, because he/she can and he/she is better off by doing it.
As we see from the definitions, beliefs are not necessary in defining and finding IRE. Payoffs depend only on the actions chosen by the players, as those are the only arguments of a payoff function. Probabilities can enter into the picture, and expected payoffs can be involved, but only to the extent that there are moves by nature. As we follow what happens to the original deviator, when we work though a thought process, as each stage, the actions chosen by everyone are well defined, and therefore, the payoffs for all players including the deviator can be computed, again without the need for any beliefs. Therefore, we can compute the deviator’s payoffs due to the deviation and be certain whether he/she will find the deviation worthwhile. Similarly, we can compute payoffs at every stage of a thought process and finally determine which Nash equilibria are IRE, without ever appealing to beliefs.
Yet, we will see that in most instances, IRE achieves the same or a stronger refinement of Nash equilibrium, as compared to conventional belief-based refinements. The main intuition of how this is possible is the thought process dynamics. Recall that one of the features of any trembling hand refinement was to utilise completely mixed strategies. The idea was that every feasible action must have some probability weight so that the impact of that action on the whole game was not lost by focusing on some Nash equilibrium that put no weight on that action. Here, with IRE, instead of putting some weight on each action, the thought process dynamics allows each player to put all of his/her weight on each particular action by making a deliberate deviation towards that action. In doing so, the full effect of each possible action is considered, without requiring any beliefs.
A particular initial Nash action profile can be immune to deliberate deviation if all such forays into thinking eventually fail and all players retract their deliberate deviations to return to the original action profile. The other possible way that a deliberate deviation can be unsuccessful is if it does not lead anywhere because it keeps cycling. If every thought process fails because the deliberate deviations contained in it either return to the original action profile or cycle endlessly, then the original action profile becomes an ideal reactive equilibrium, because all deliberate deviations have failed to give the deviator a permanent improvement. Although an appealing feature of IRE is the simplicity of the thinking required and the similarity to how an uninitiated novice may approach the problem, it is very important to recognize that a fully-exhaustive search must be done over all possible thought processes. IRE is conceptually simpler, but since in most instances, it achieves a level of refinement that equals or exceeds conventional refinements, we should expect that this simplicity is balanced by the magnitude of the task of exhaustively searching through all possible thought processes.
To motivate the intuition of IRE, consider the following situation. Suppose two competitors discover two new markets where they can expand, market
A and market
B. They also learn that they each have resources to enter only one of the markets, and if both were in the same new market, they would compete away the profits and earn
; however, if only one firm was in market
A, it would earn three, and if only one firm was in market
B, it would earn one. Firm 1 comes to know of this first and knows that he/she is first; and by the time Firm 2 learns, Firm 1 has has already made secret and irreversible moves to enter one of the markets. The timing is very important, and the game tree is depicted in
Figure 5.
10How should Firm 2 think about this? We know that if we solved for all the Nash equilibria, there are three: , , and a mixed strategy solution with each firm choosing A with probability 0.25. For to happen, Firm 1 thinks: Suppose I took the better market (A), would Firm 2 realize that that is what I would do, because being first, I would take the best thing available, and then figuring this out, Firm 2 would move to the other market (B)? Or should I take the worse market (B) in spite of being first, because when Firm 2 realizes all that has happened, he/she will think that I would leave the good market for him/her? Or should I randomize, and Firm 2 would be sure to figure that out and respond appropriately?
I would think it is quite obvious that the only thing Firm 2 can believe is that Firm 1 has taken the lucrative market, and so, it should make plans to enter the other market. This is essentially the battle of the sexes game. If we turn to the experimental evidence, Cooper, DeJong, Forsythe and Ross [
16,
17,
18] found that when experimental subjects play the sequential unobserved battle of the sexes (without outside option, with outside option that is credible, with outside option that is not credible), they invariably choose the Player 1 preferred solution.
11 IRE predicts that Firm 1 would pick
A and Firm 2 would pick
B.
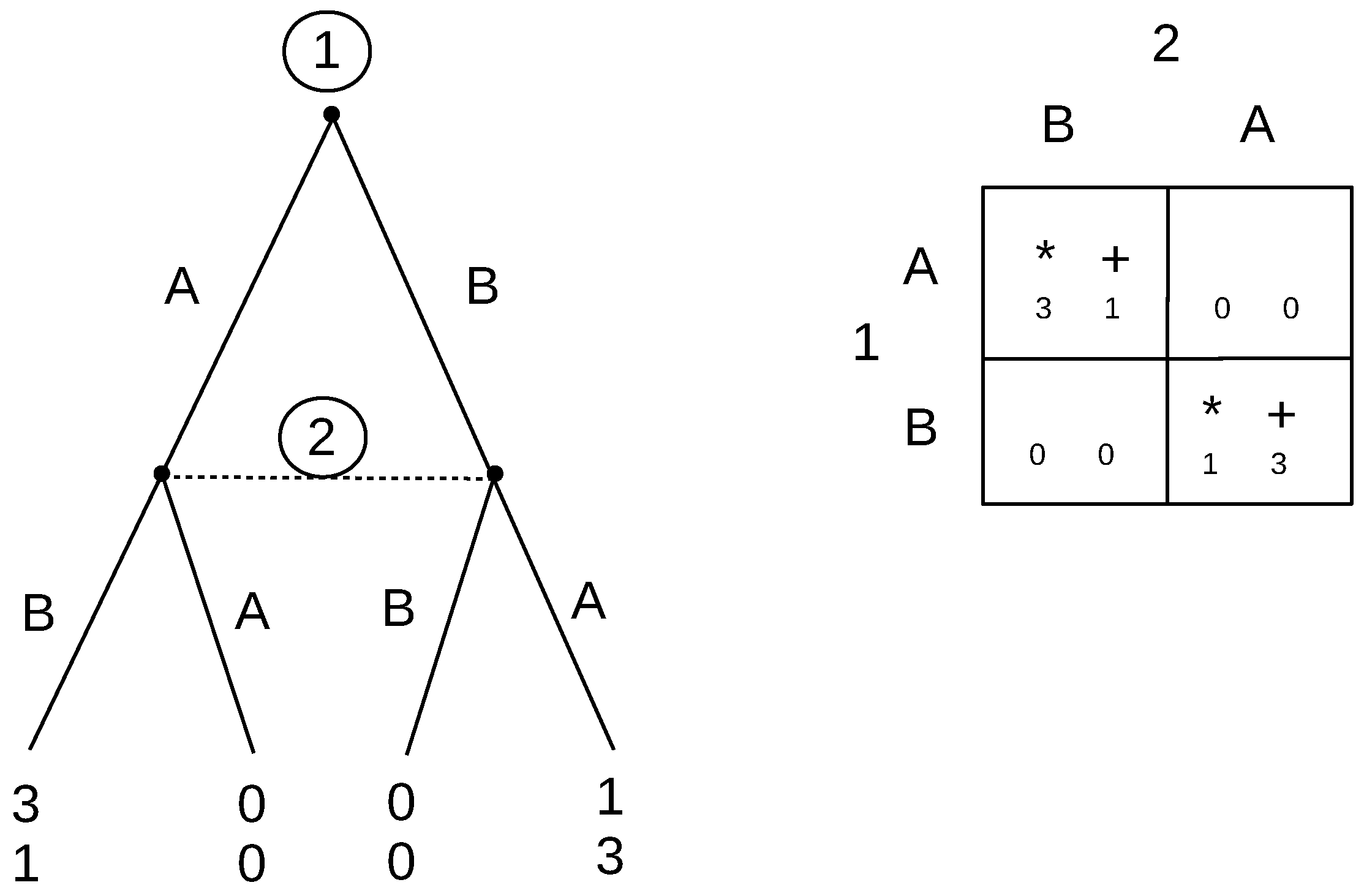
Accordingly, in the battle of the sexes game given in
Figure 6, there are two pure strategy Nash equilibria, BB and SS, and a mixed strategy solution. The ideal reactive equilibrium, given that specific order of play, is only the BB solution. This is because SS is not immune to deliberate deviations, namely a first order deviation by Player 1 to B would be responded with B, and Player 1 would be better off, so he/she would undertake such a deviation. Instead, if we begin with the mixed strategy solution, again a first order deviation by Player 1 to B would be responded with B, and Player 1 would be better off, so he/she would undertake such a deviation. Therefore, both of these Nash equilibria are not IRE. Looking at the BB equilibrium, there is no deliberate deviation that any player can take that would make him/her better off. Player 2 cannot make any deliberate deviations, because he/she has no followers. Player 1 could deliberately deviate to S, but then, that would be met with a best response of S by Player 2, which would give Player 1 a payoff of only one, which is worse. Therefore, he/she would retract his/her deliberate deviation, confirming that BB is an IRE.
In effect, this equilibrium refinement extends the notion of forward induction to games where there is actually no signal, except the knowledge that earlier players move first and that confers an advantage to them. The order of play itself acts as a signal identifying which action a leader player must have taken.
It should be noted that the thought process does not always simply result in Player 1’s preferred equilibrium being selected. There are advantages in playing earlier in the game, namely that an early player can rule out large parts of the game by his/her choices. However, the disadvantage is that after moving, each player relinquishes control of the game to the players that remain. We see this in the three-player game in
Figure 7.
There are two pure strategy Nash equilibria: LAa and RBb. In the spirit of virtual observability, it is almost as if Player 1’s move can be seen by the other players. We will argue that although LAa has a higher payoff for Player 1, RBb is the only ideal reactive equilibrium.
Suppose we start at RBb and Player 1 considered a deviation to L. The players that follow would quite correctly anticipate it, as they should in the thought process dynamics. Given that Player 1 has already moved, he/she has committed to playing L and given up further control of the game. The other players would have anticipated Player 1’s move; therefore, they would behave as if they were playing the “subgame” after Player 1’s move L. By playing L, Player 1 has relinquished control of the game, and Players 2 and 3 no longer need to worry about the Nash conditions that bind Player 1 to choosing L. He/she has already moved, it is finished; once moved, he/she cannot take it back. Therefore, now focusing on their “subgame”, Players 2 and 3 would figure out that it is in their best interest to play Bb, which is Nash in the “subgame.” This gives Player 1 a payoff of two, which is lower than his/her original payoff of four, under RBb. Player 1 can figure out all of this and would not make the deviation to L in the first place.
Exactly the same basic argument can be used to show that starting from LAa, there will be a successful deviation by Player 1 to R, and so, it is not an ideal reactive equilibrium.
The next example of ideal reactive equilibrium illustrates an instance where the thought process is not able to refine the Nash equilibria because the thought process dynamics in each case goes on endlessly without resolution, and so, the deliberate deviations are unsuccessful. Therefore, all of the Nash equilibria that can be reached in an endless thought process cycle are ideal reactive equilibria in this game.
Consider the game in
Figure 8. There are two pure strategy Nash equilibria here: Lra and Rrb. However, any thought process dynamics from either starting point does not resolve. Lra brings us to terminal node
, and from there, Player 2 could do an order one deviation to l, bringing us to
. Then, Player 3’s best response would bring us to
. However, if that is what he/she is doing, Player 1 would make a best response bringing us to
. Now, Player 3 would prefer to change, leaving us at
, causing a change by Player 1 to
, and then, Player 2 brings us back to
, then the cycle could repeat again. This is of course not path independent, but as can easily be seen, all alternative paths also cycle endlessly, rendering all deliberate deviations unsuccessful. A similar result of unending cycling occurs for thought processes originating from Rrb, the other Nash equilibrium.
One important test of whether an equilibrium concept is valid is whether real people play according to it. There is mounting experimental evidence that order of play makes a difference in sequential games where some or all of the moves by earlier players are not observed by follower players. It is well established in the experimental literature that, contrary to conventional game theory, order of play affects how games are played. Normal form invariance is refuted.
12The first experimental results that suggested an order of play effect was the work by Cooper, DeJong, Forsythe and Ross [
16,
17,
18]. There, they investigated the battle of the sexes game to see how experimental subjects dealt with outside options. They presented subjects with sequential unobserved battle of the sexes games without outside options, with outside options that were credible, and with outside options that were not credible. They expected to find that only in the games where the outside option was credible would you find a large propensity toward the Player 1 preferred equilibrium. They were puzzled to find that it did not matter whether the outside option was credible, or whether there even was an outside option. Players seemed to predominantly play the Player 1 preferred Nash equilibrium, which is exactly what IRE predicts. Camerer, Knez and Weber [
15] set out to test whether real subjects played according to the Amershi, Sadanand and Sadanand [
1,
2,
3,
4] Mapnash equilibrium for weak link games such as the stag hunt. They found that in later rounds, their results confirmed a first mover advantage, which they called “virtual observability”. Muller and Sadanand [
21] have found that subjects often choose in accordance with “virtual observability,” particularly for simple games. Brandts and Holt [
24] and Rapoport [
25] have also found order of play effects. In addition Schotter, Wegelt and Wilson [
26] gave important results on how experimental subjects perceive order of play based on the presentation of the games.
The question that this growing strand of the experimental literature poses is: Exactly how does order of play affect outcomes? Indeed, Hammond [
27] stated that the conventional assumption of normal form invariance may be “unduly restrictive” and emphasized the need for a systematic theory of how order of play affects outcomes.
13 Huck and Müller [
28] conducted some experiments and found that the opportunity to burn money confers a substantial advantage to first movers, and they too urge that “we make theoretical advances to understand the role of physical timing and first-mover advantages in games.” I believe that IRE is a good beginning at filling this void.
4. Properties and More Examples
There are four properties to notice about the ideal reactive equilibrium. First, the whole process happens without any need for beliefs. For unreached information sets that are not pivotal, it is not important to even specify behaviour for these counterfactual contingencies. Even when unreached information sets are pivotal, all players realize that they are so, and by working through all possible thought processes, they have already disallowed incredible threats, so again, it is not important to indicate choices there. Thus, the specification of what constitutes an equilibrium is simplified to almost the novice student’s approach of just providing the equilibrium path. Moreover, because sequential rationality-based refinements impose a blanket condition of rationality everywhere in the game, these conventional refinements can in some instances impose too much rationality and as a result make different predictions than what is predicted by IRE. The games where we see this are quite knife-edge, and for the most part except for such examples, IRE agrees with conventional belief-based refinements or further refines them. The example where we illustrate an instance of too much rationality is Selten’s horse, which will be discussed in detail in this section.
The second point is not a very precise one and will be illustrated in some of the examples to follow. The rough intuition is that if we can identify parts of games where preferences of players are aligned and where they are in conflict, then as long as the conflict payoffs are not higher, earlier players will, if possible, steer the game towards the parts where there is alignment, rather than conflict. The intuition for this is straightforward: the parts where there is conflict are second mover advantage situations where leader players hold no particular power and so can often result in randomization; the aligned portions are where leader players can exert some first mover advantage.
Next, because there exist knife-edge games where IRE and conventional refinements make completely different predictions, it will not be possible to show that one refines the other. However, except for the knife-edge games, in many instances, IRE actually refines belief-based refinements. Naturally, I will not be able to prove that IRE refines sequential rationality-based refinements, since there are examples where predictions differ. Instead, many examples, particularly of signalling games, will be provided to demonstrate that IRE refines belief-based equilibrium concepts. The examples of signalling games are mainly found in the next section.
Finally, I will show that IRE always exists for finite games. This is fairly easy to show by first noticing that since these are finite games, there is only a finite number of terminal nodes. Therefore, any thought process can only take a finite number of values, and therefore, they can only either cycle indefinitely or settle to a Nash equilibrium. From the definition, we know that if the thought process cycles indefinitely, there is an IRE. Therefore, we are left with the case where all thought processes settle to a Nash equilibrium. However, then, there must be an IRE at the Nash equilibrium where any one of them settles, because by definition, the settling point is where no more deliberate deviations are successful. If we started with such a Nash equilibrium, it would not be possible for any player to make any deliberate deviations that could be successful, and so, it would by definition be an IRE.
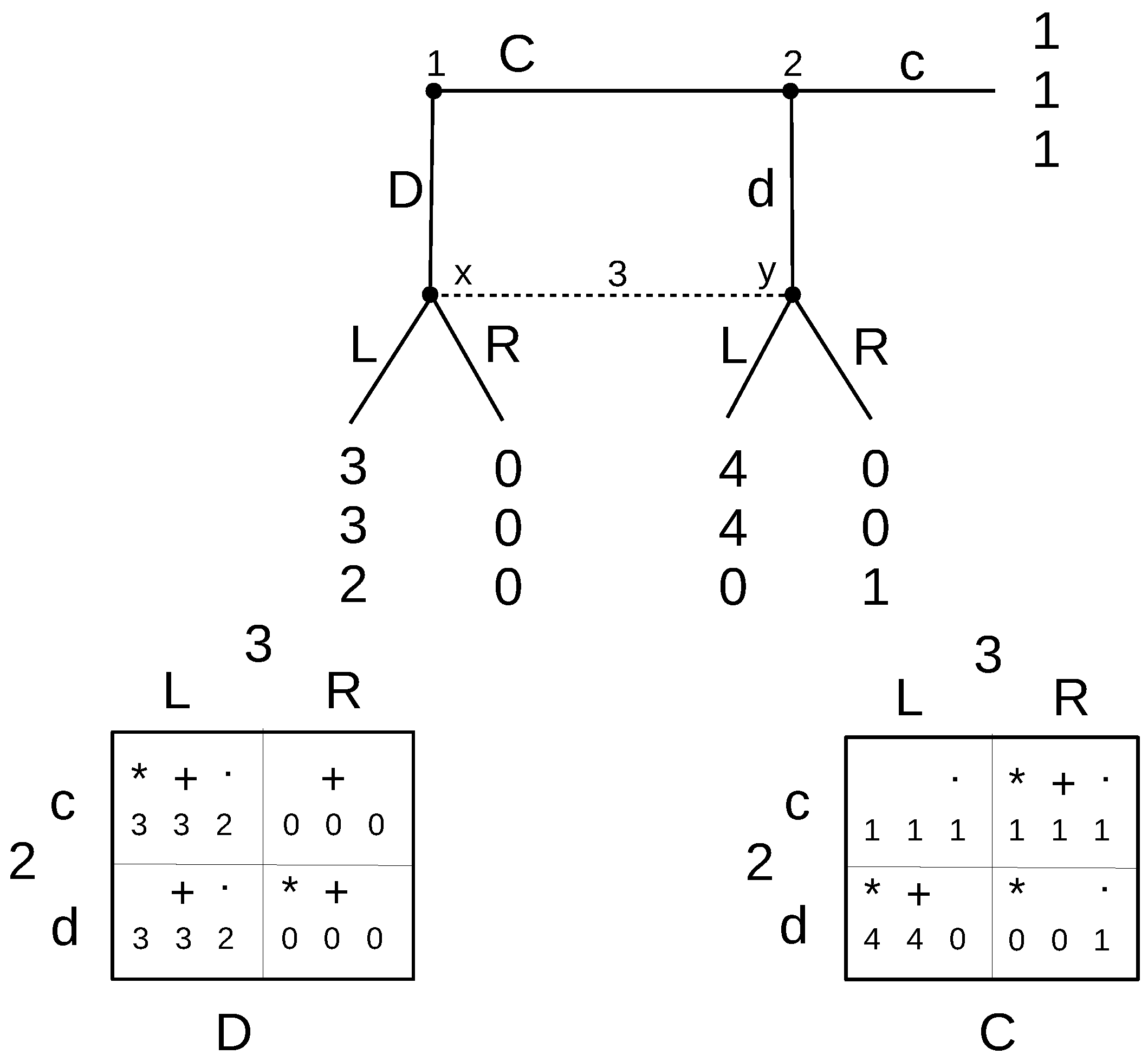
Returning now to the first property, consider Selten’s horse in
Figure 9. There are two equilibria DcL and CcR. Conventional theory argues that DcL should not be considered a valid outcome, because it requires Player 2 to choose c, which is not optimal when Player 3 is choosing L. However, the thing is that Player 2 is fully informed and knows perfectly well that he/she does not get a turn in the DL outcome, since Player 1 is playing D. Even Player 3 knows this and sets his/her beliefs correctly to prob(x) = 1 at his/her information set. If everyone were to use these correct beliefs, Player 2’s action of playing c or d would be considered totally inconsequential. Moreover, we realize that Player 2’s action c poses no “incredible threat” since switching to d (the “rational” choice) does not induce Player 1 to change his/her decision to exclude Player 2’s decision node from the equilibrium path. This is because Player 1 would have worked out the entire thought process and realized that any change toward Player 2’s decision node would trigger Player 3 to revise his/her choice from L to R, giving Player 1 a payoff of zero. Therefore, Player 1 would not entertain such a deviation in the first place.
Therefore, really, there is no need for Player 2’s decision to be rational. Player 2’s decision is unimportant, and this redeems the validity of DcL. Moreover, as it is the preferred outcome for Player 1, DcL is the equilibrium outcome selected by the ideal reactive equilibrium, which is contrary to most existing notions of equilibrium.
14 This is an instance where conventional sequential rationality-based refinements impose too much rationality.
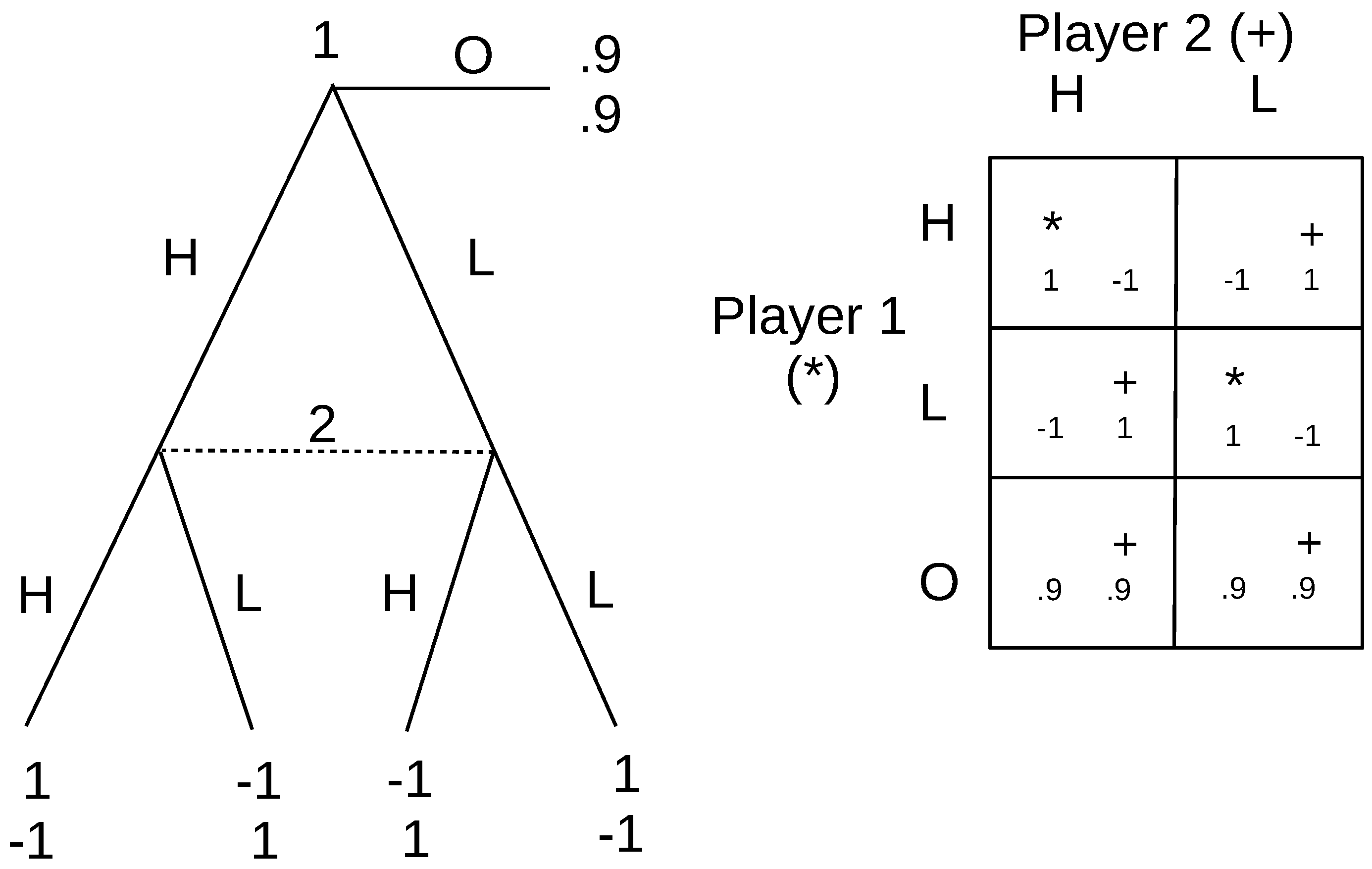
Consider the game of matching pennies in
Figure 10, with an outside option paying (0.9,0.9), which being a second mover advantage game, illustrates the second point. The Nash equilibrium here is a mixed strategy equilibrium. Player 1 chooses O with certainty, and Player 2 mixes with any probability,
prob(H)
. In order to make these choices optimal for Player 2, the conventional approach is that we need beliefs on Player 2’s information set that conform to Player 2’s choice being optimal. We thus would have to assign the probabilities
to each node. These beliefs, though quite plausible, are actually unnecessary, since if Player 2 held some other beliefs, that would result in no randomization, but as those beliefs themselves are unknown, Player 2’s choice could still appear to be randomized (similar to Harsanyi’s argument about mixed strategies). Player 1 is taking the outside option because it pays more, and so, he/she prefers to avoid the second mover advantage interaction with Player 2.
If instead, the outside option had paid the first player some negative amount, say −0.1, then the game would play out differently. Now, although there is still an outside option, it is worse than what Player 1 expects to get from the second mover advantage interaction. The Nash equilibrium in this modified game will be that each randomizes with probability between H and T, and this is the IRE. To see that, consider all the possible deliberate deviations. Player 2 cannot make deliberate deviations since he/she has no followers, only Player 1 can. If Player 1 deviates to the outside option, he/she immediately retreats, since his/her expected payoff is lower. If instead, he/she deviates to H (or T), Player 2’s best response will be T (or H), and this will be an endless cycle involving the actions over which they are randomizing, confirming that the original mixed strategy solution is IRE.
In games with a first mover advantage, it is beneficial to the first mover if the second mover could observe his/her move. We see that in many games where the first move cannot be completely observed, forward induction arguments often steer us to the first mover preferred outcome. If instead, it is a second mover advantage game, then forward induction is not very helpful in sorting out multiple equilibria, if there are any. Ideal reactive equilibrium also shares this tendency of other forward induction concepts.
The beer and quiche game [
30], given in
Figure 11, pairs both first and second mover advantage games with the two types of senders. We notice that the strong (
) Player 1 plays a first mover advantage game (both with Beer (B) and with Quiche (Q), but prefers beer), while the weak (
) Player 1 plays a second mover advantage game (again in both instances). In first mover advantage games, first players always want to reveal themselves as such, while in second mover advantage games, first players never want to reveal themselves. Therefore, it is not surprising that the chosen equilibrium is pooling, as the weak does not want to reveal himself, and the strong Player 1 gets his/her way with beer; if the weak were to try his/her way by choosing quiche, he/she would end up disclosing his/her identity. Then, the responder will clearly not duel for beer (N) and will duel (D) for quiche, which makes the weak sender worse off. The equilibrium response to both pooling with beer is no duel (N).
We can go through the thought process dynamics to show that the Nash equilibrium where both senders pool at quiche is not an IRE. If we were in the pooling equilibrium at quiche, the strong sender would deviate to beer and will suppose that the receiver (follower) observes that he/she has done this. The receiver would then respond to beer by choosing N (no duel) and also realize that if anyone is signalling quiche, he/she must be the weak sender, and so also modify his/her response to quiche by D (duelling). Now, the weak sender will quickly change his/her choice to beer also. The thought process settles here because there are no more deliberate deviations that can be successful.
5. Signalling Games
In the previous section, we saw the beer and quiche game, which is a signalling game. We applied ideal reactive equilibrium informally there to show how we arrive at the same conclusion as the intuitive criterion, but in a much simpler fashion. In this section, we will discuss in more detail how to apply ideal reactive equilibrium to signalling games. We will see that in some instances, IRE can refine further as compared to some standard sequential rationality-based signalling game refinements. For simplicity, we will suppose the game is a basic two-player game with the sender moving first and then the receiver.
To check whether a Nash equilibrium is ideal reactive, we begin a thought process where the sender of a particular type deviates deliberately and changes his/her message. Then, we follow all the possible best responses if the responder knew which type of sender it was. If any subgroup of senders is better off under the best responses for their type, then we continue the thought process. We also have to check whether the responder may change his/her reply to any of the other original signals being used in the Nash equilibrium, in light of this change. We also need to check whether any other sender types want to change their signal, and so on. This continues until all avenues have been explored. If none of the thought experiments lead to a change, the original Nash equilibrium is an ideal reactive equilibrium.
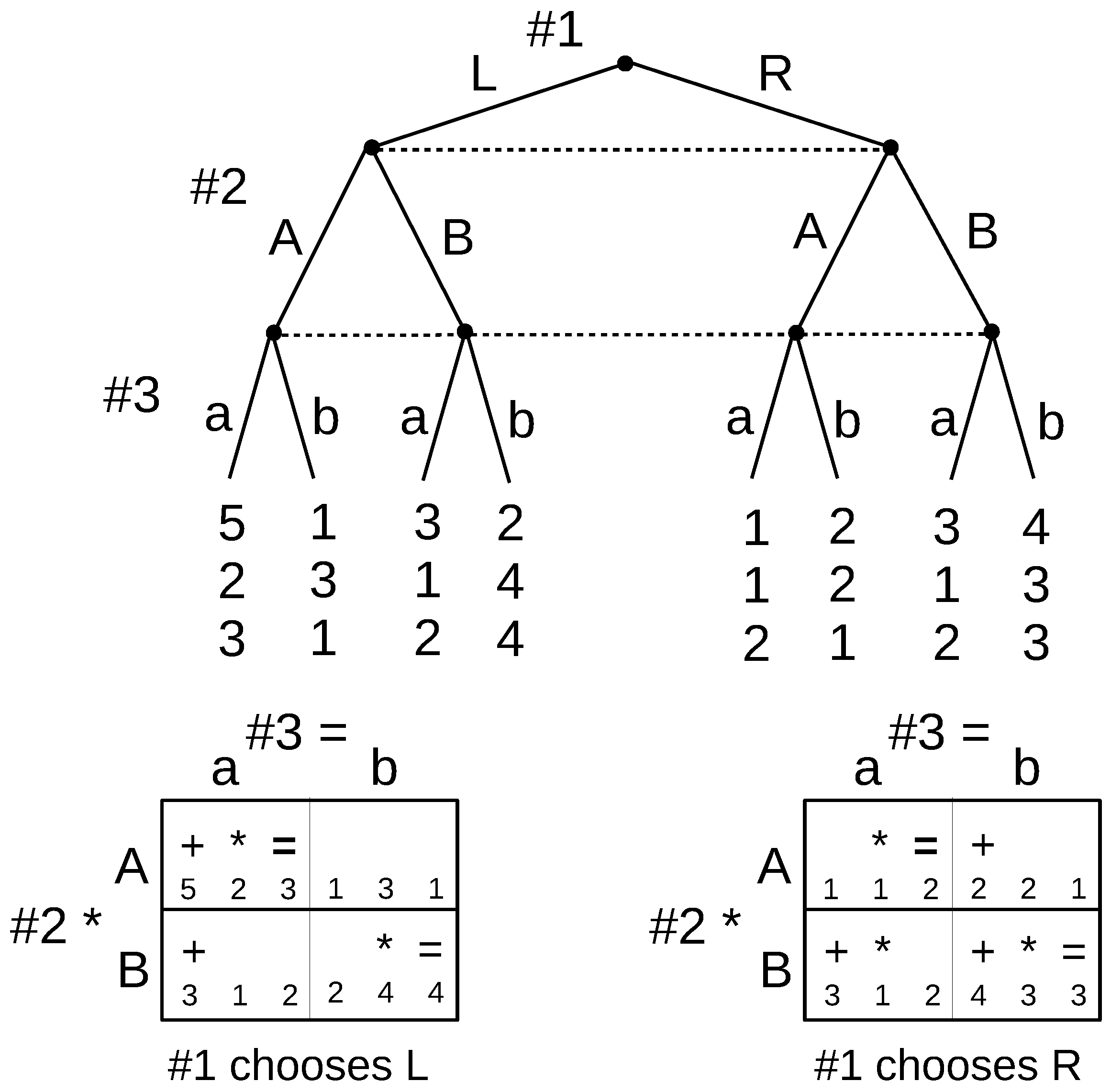
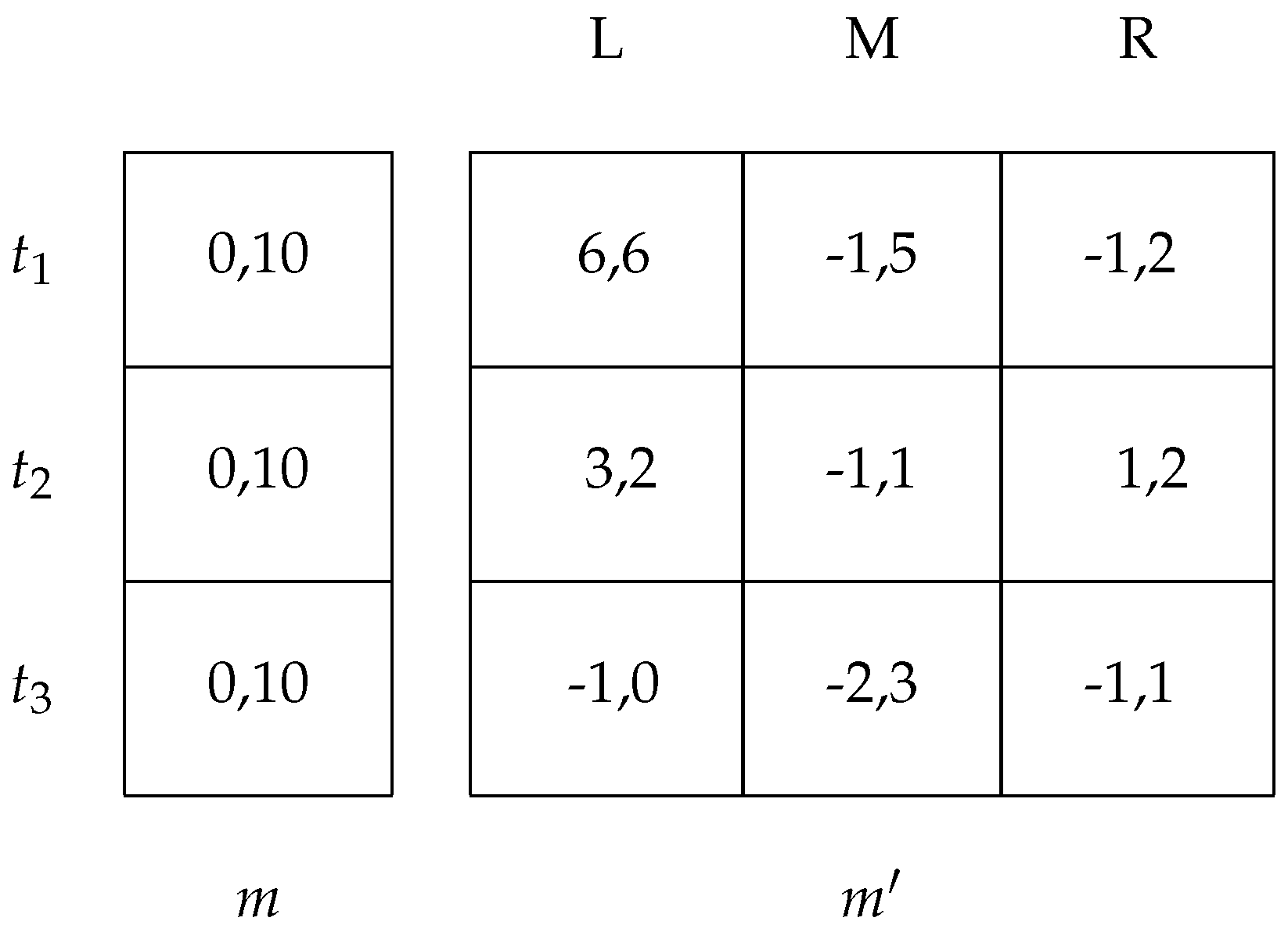
Consider the example in
Figure 12. Each type is equally likely. The Nash equilibria are
,
, and
. From these, only
is an ideal reactive equilibrium.
To see this, we will start with a Nash equilibrium that is not an IRE and go through the thought process to see how it arrives at the IRE. Suppose we start with , and suppose there is a deviation to possibly by . Now, let us look at the best responses for the receiver. BR, BR, BR, BR, BR, and BR. All players and types can immediately see that the deviator is not , since he/she is worse off with every response (equilibrium dominance). Therefore, it can only be or . Suppose that the responder thought it was just and the responder chose R as his/her response. Now, we are at , which itself is a Nash equilibrium. However, the thought process does not end there. Type could do a first order deviation where he/she also deviates to , and now, the responder will be better off responding with L, rather than R. The thought process ends here, since no one wants to make a further deviation. Therefore, the original equilibrium is not an ideal reactive equilibrium, nor is . The only ideal reactive equilibrium is .
If we apply the Cho–Kreps intuitive criterion to this game, we can eliminate the pooling equilibrium . Notice that the beliefs supporting this pooling equilibrium at require that the receiver believes that the probability of . However, equilibrium dominance indicates that this probability should be zero, which rules out the pooling equilibrium. However, beyond that, the Cho–Kreps intuitive criterion cannot refine any further, because it requires an off-equilibrium message in order to apply equilibrium dominance, and in the remaining two equilibria, all messages are used, so there is no out-of-equilibrium message. Similarly, divine equilibrium can also only eliminate the pooling equilibrium, because it too requires out of equilibrium messages to be able to assign sensible beliefs at unreached information sets. Thus, we see that IRE refines both the intuitive criterion and divine equilibrium.
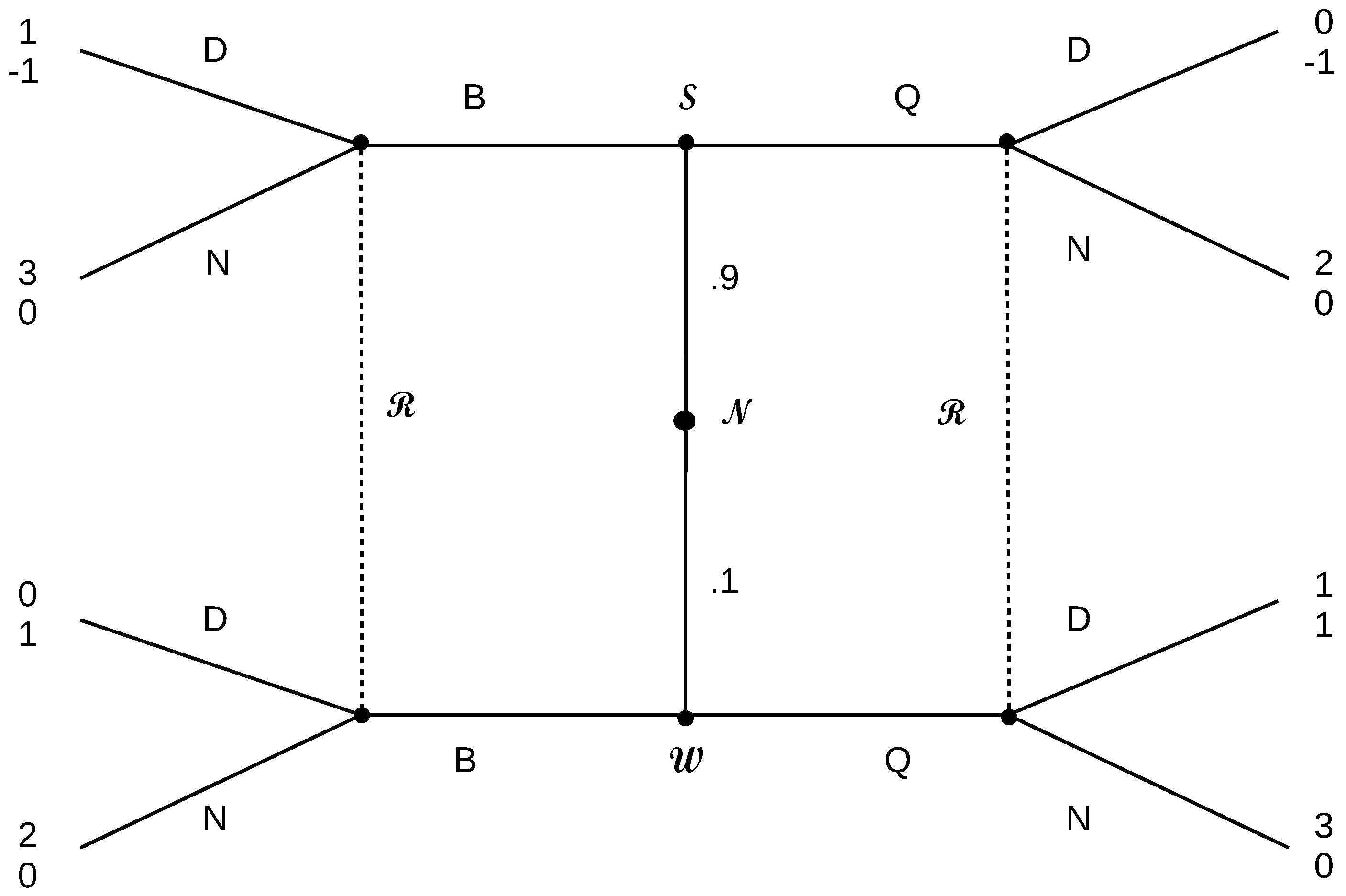
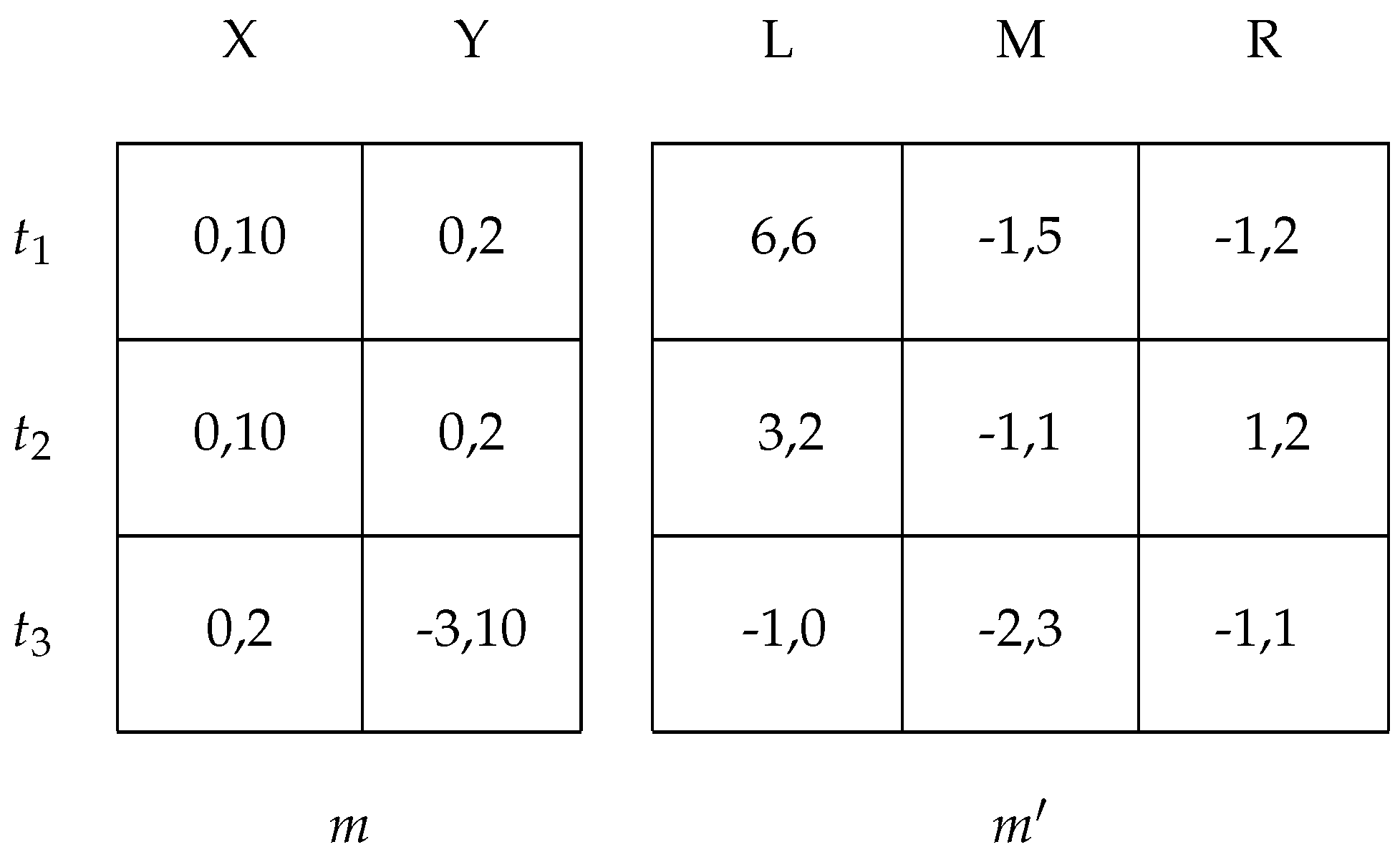
Now, let us modify the example to allow the responder a move after
m also, as seen in
Figure 13. This example illustrates how it is not enough to simply follow what happens to the deviator and deviating message, but we must also see whether changes occur in the responder’s choices for types that do not deviate.
Here, the Nash equilibria are and , and only the latter is an ideal reactive equilibrium.
Notice that the game after the message is identical to the last example. The only modification is that there is a choice between X and Y after the message m; the payoffs under X are almost the same as before, and some new payoffs have been added for the response Y.
We want to show that the pooling equilibrium is not an ideal reactive equilibrium. We follow the same thought process for the previous example, with deviating to , and then , also trying to make that deviation, and the responder will choose L. It all seems good for the two deviating types.
However, notice now that if only
is left signalling
m, then the responder will change his/her response after
m to
Y.
15 However, now,
wants to deviate as well. Then, the responder’s best action after
becomes
M, which causes all of the types to retreat back to
m. Since
can anticipate all this,
would not deviate to
in the first place. Therefore, the thought process would rest at
, which is the ideal reactive equilibrium. In this instance, IRE, the intuitive criterion and divine equilibrium all agree on
.
These two examples serve to demonstrate how we conduct the thought process dynamics for signalling games. Essentially, it is the same requirement: a Nash equilibrium is ideal reactive if there is no successful deviation using thought process dynamics (or if all thought processes result in endless cycles). Only care must be taken to explore all possible avenues. They also illustrate how IRE compares with other conventional refinements.