Necessary Optimality Conditions for a Class of Control Problems with State Constraint
Abstract
:1. Introduction
- (i)
- it has a finite number of inclusion-maximal boundary intervals,
- (ii)
- an implication holds that if for a certain t, then t belongs to the closure of some boundary interval of u, 2
- (iii)
- the conditions of nontangentiality
- (iv)
- there is an open set containing all points such that , and there is a function such that
2. The One-Spike Control Variation and Trajectory Variation
- (i)
- if for some , and u has no exit points in ,
- (ii)
- if and , where is the greatest entry point of u less than or equal to t,
- (iii)
- otherwise.
3. The Adjoint Function and The One-Spike Necessary Optimality Condition
- (i)
- for everyand every,
- (ii)
- the functionis constant.
4. The Two-Spike Necessary Optimality Condition
- (i)
- ifand, then,
- (ii)
- ifand, then,
- (iii)
- ifand, thenand
5. A Geometrical Interpretation and a Minimum Condition
- (i)
- for every,
- (ii)
- for every pairsuch that.
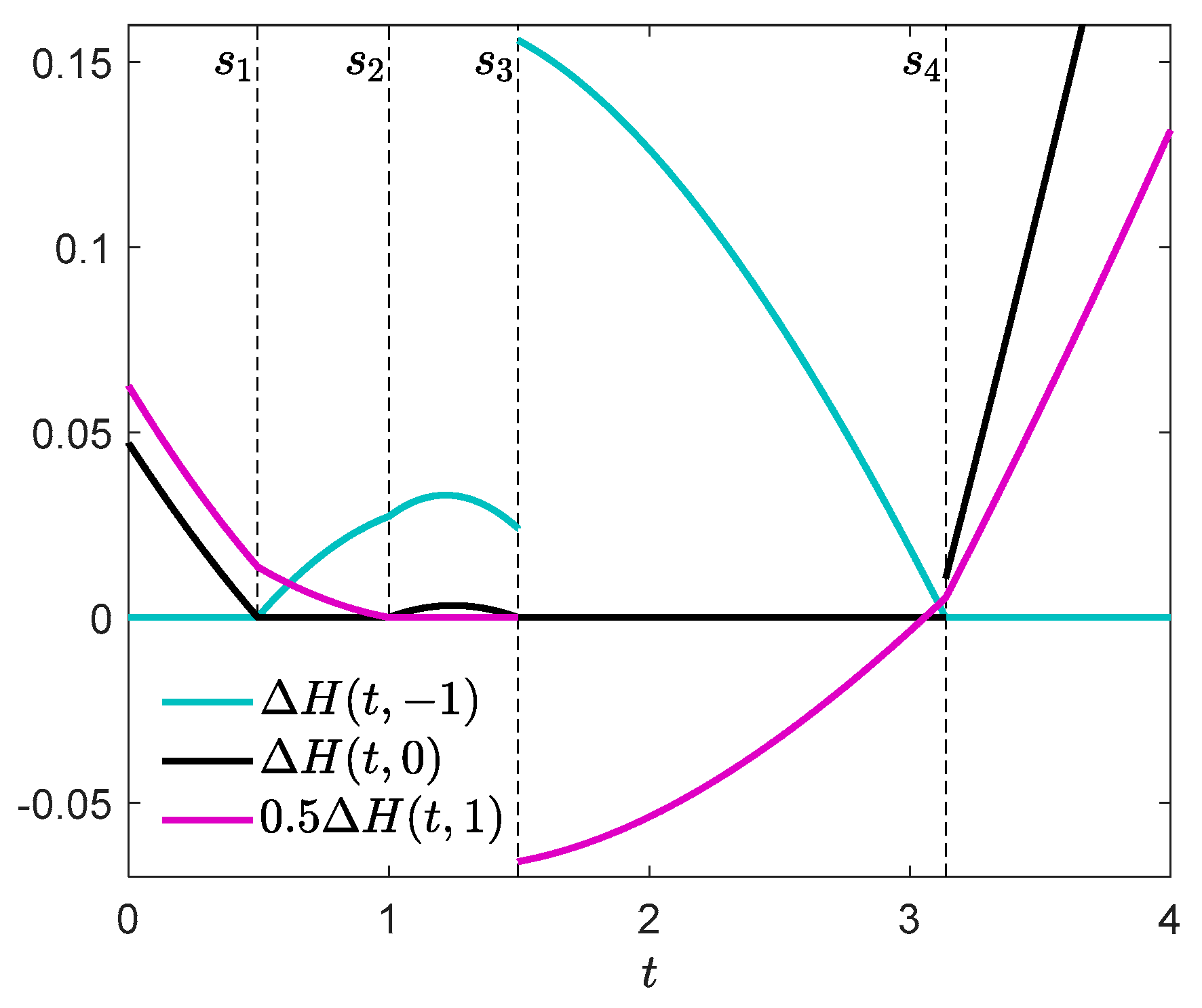
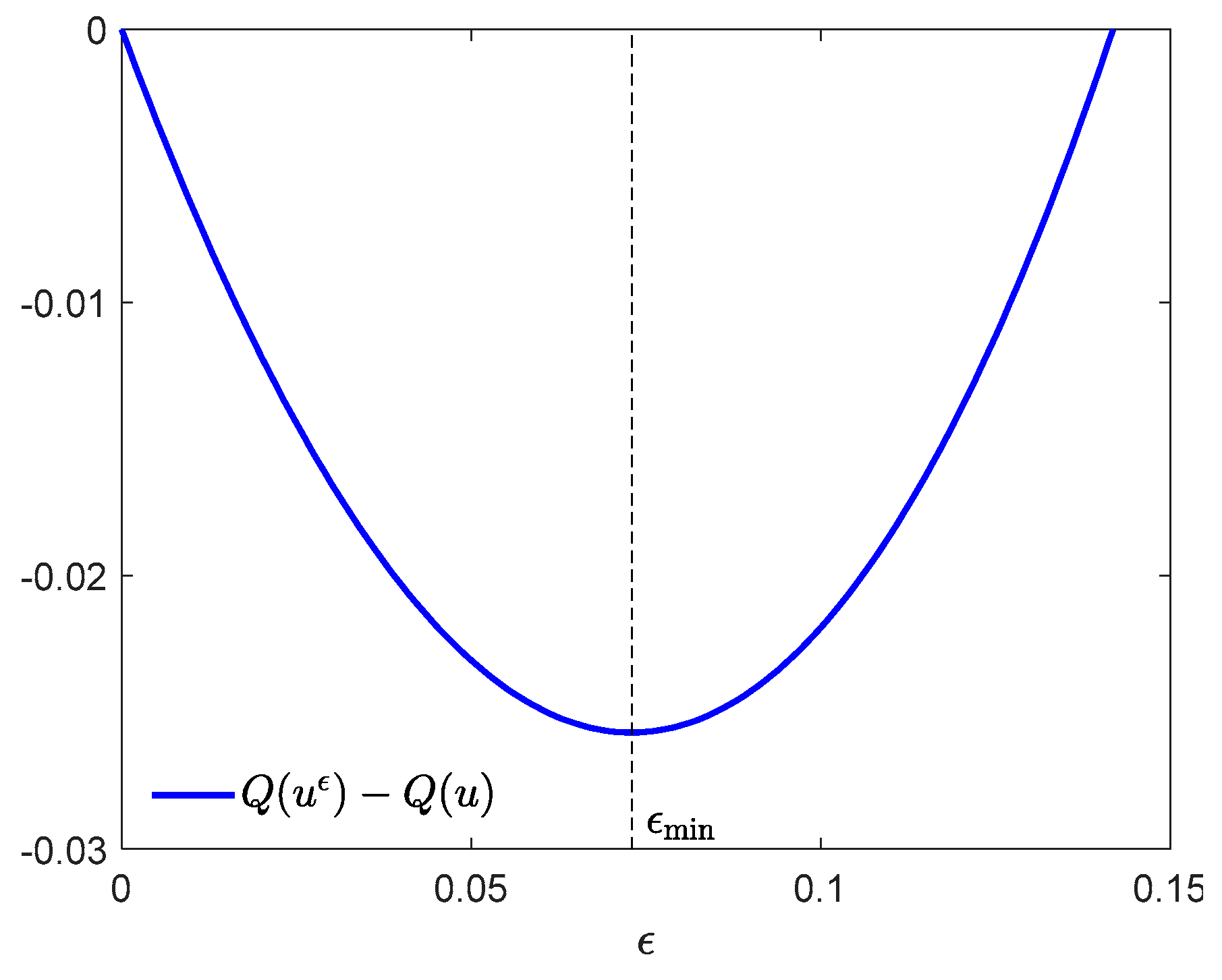
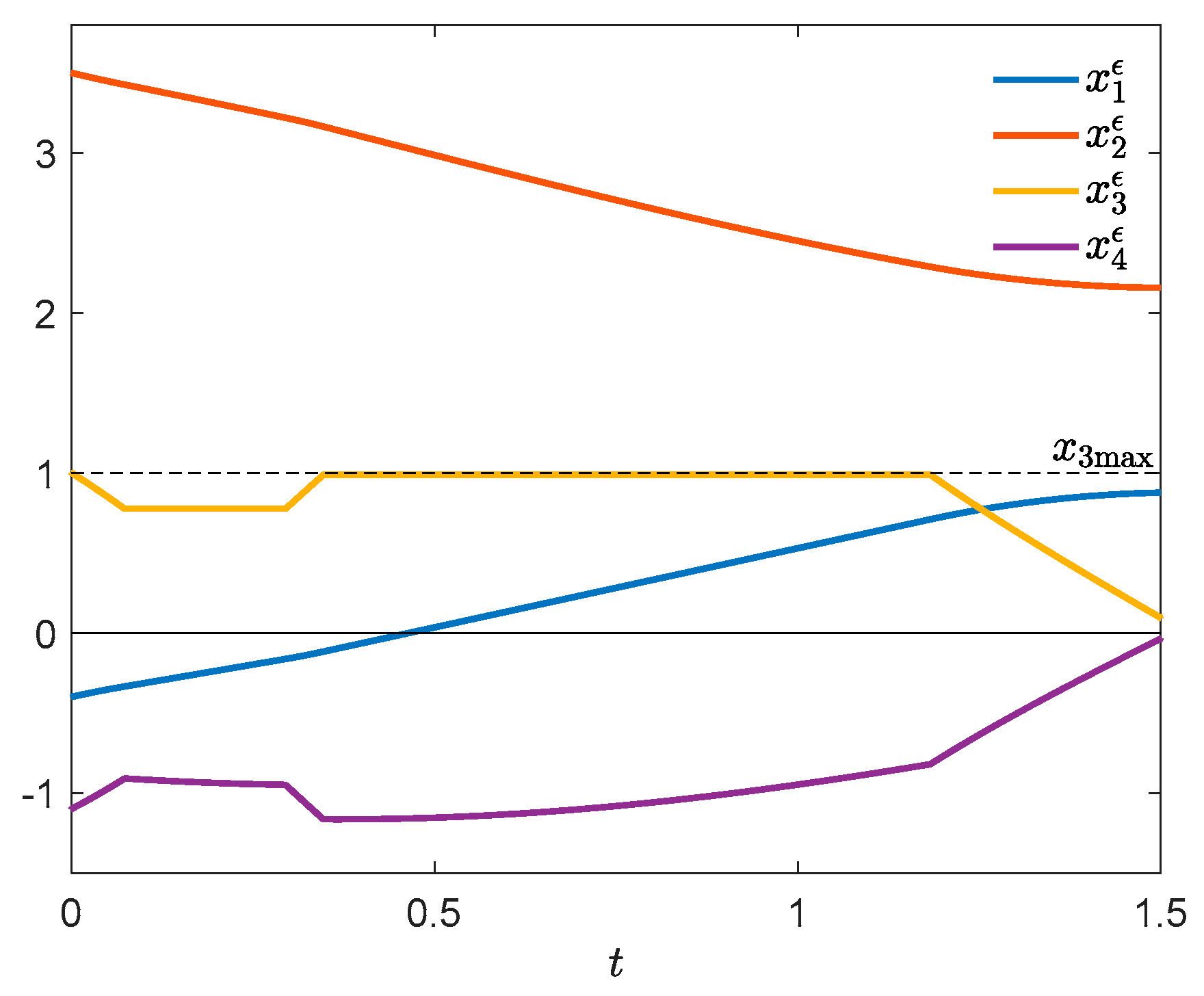
6. Example 1
7. The Control Affine Case
- (i)
- ifor, thenexists and,
- (ii)
- ifor, thenexists and.
- (i)
- ifand, then,
- (ii)
- ifand, then,
- (iii)
- ifand, thenand.
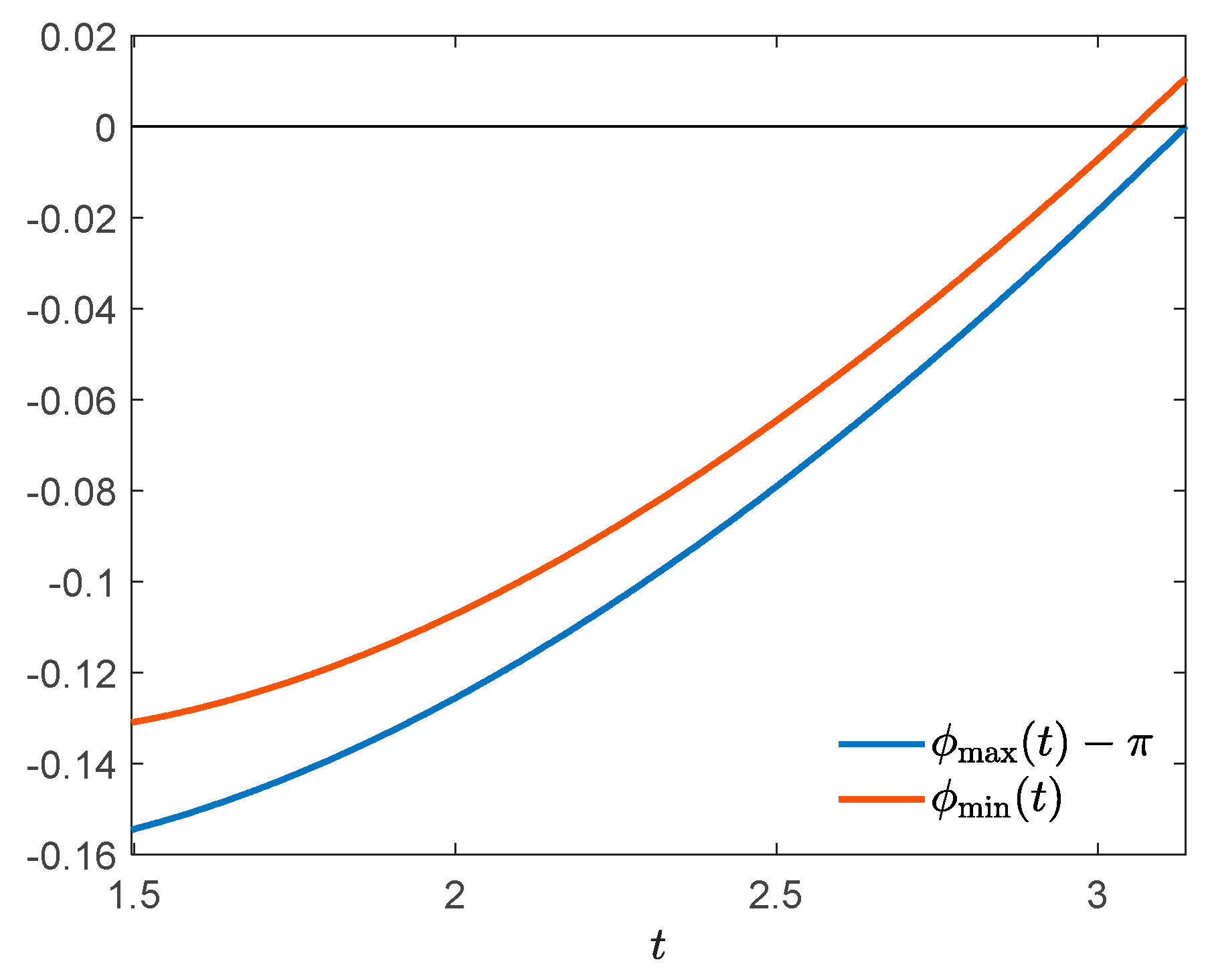
8. Example 2: The Pendulum on a Cart
- (i)
- if and ,
- (ii)
- if and ,
- (iii)
- if and .
9. Connections with Some Classical Results
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pontryagin, L.S.; Boltyanskii, V.G.; Gamkrelidze, R.V.; Mishchenko, E.F. The Mathematical Theory of Optimal Processes; Nauka: Moscow, Russia, 1961; (in Russian, first English language edition: Wiley & Sons, Inc., New York, 1962). [Google Scholar]
- Karamzin, D.; Pereira, F.L. On a Few Questions Regarding the Study of State-Constrained Problems in Optimal Control. J. Optimiz. Theory App. 2019, 180, 235–255. [Google Scholar] [CrossRef]
- Maurer, H. On the Minimum Principle for Optimal Control Problems with State Constraints; Universität Münster: Münster, Germany, 1979. [Google Scholar]
- Hartl, R.F.; Sethi, S.P.; Vickson, R.G. A survey of the maximum principles for optimal control problems with state constraints. SIAM Rev. 1995, 37, 181–218. [Google Scholar] [CrossRef]
- Arutyunov, A.V.; Karamzin, D.Y.; Pereira, F.L. The maximum principle for optimal control problems with state constraints by R.V. Gamkrelidze: Revisited. J. Optimiz. Theory Appl. 2011, 149, 474–493. [Google Scholar] [CrossRef]
- Bonnans, J.F. Course on Optimal Control. Part I: The Pontryagin approach (Version of 21 August 2019). Available online: http://www.cmap.polytechnique.fr/~bonnans/notes/oc/ocbook.pdf (accessed on 30 December 2020).
- Bourdin, L. Note on Pontryagin Maximum Principle with Running State Constraints and Smooth Dynamics—Proof based on the Ekeland Variational Principle; University of Limoges: Limoges, France, 2016; Available online: https://arxiv.org/pdf/1604.04051v1.pdf (accessed on 30 December 2020).
- Dmitruk, A.; Samylovskiy, I. On the relation between two approaches to necessary optimality conditions in problems with state constraints. J. Optimiz. Theory Appl. 2017, 173, 391–420. [Google Scholar] [CrossRef]
- Vinter, R. Optimal Control; Birkhäuser: Boston, MA, USA, 2000. [Google Scholar]
- Korytowski, A.; Szymkat, M. On convergence of the Monotone Structural Evolution. Control Cybern. 2016, 45, 483–512. [Google Scholar]
- Bonnans, J.F. The shooting approach to optimal control problems. IFAC Proc. Vol. 2013, 46, 281–292. [Google Scholar] [CrossRef] [Green Version]
- Bonnans, J.F.; Hermant, A. Well-posedness of the shooting algorithm for state constrained optimal control problems with a single constraint and control. SIAM J. Control Optim. 2007, 46, 1398–1430. [Google Scholar] [CrossRef] [Green Version]
- Chertovskih, R.; Karamzin, D.; Khalil, N.T.; Pereira, F.L. Regular path-constrained time-optimal control problems in three-dimensional flow fields. Eur. J. Control 2020, 56, 98–106. [Google Scholar] [CrossRef] [Green Version]
- Cortez, K.; de Pinho, M.R.; Matos, A. Necessary conditions for a class of optimal multiprocess with state constraints. Int. J. Robust Nonlinear Control 2020, 30, 6021–6041. [Google Scholar] [CrossRef]
| 1 | PC(0,T; U) is the space of all functions [0,T] → U which have a finite number of discontinuities, are right-continuous in [0,T[, left-continuous at T, and have a finite left-hand limit at every point. |
| 2 | Controls leading to state trajectories with boundary touch points are not verifiable. |

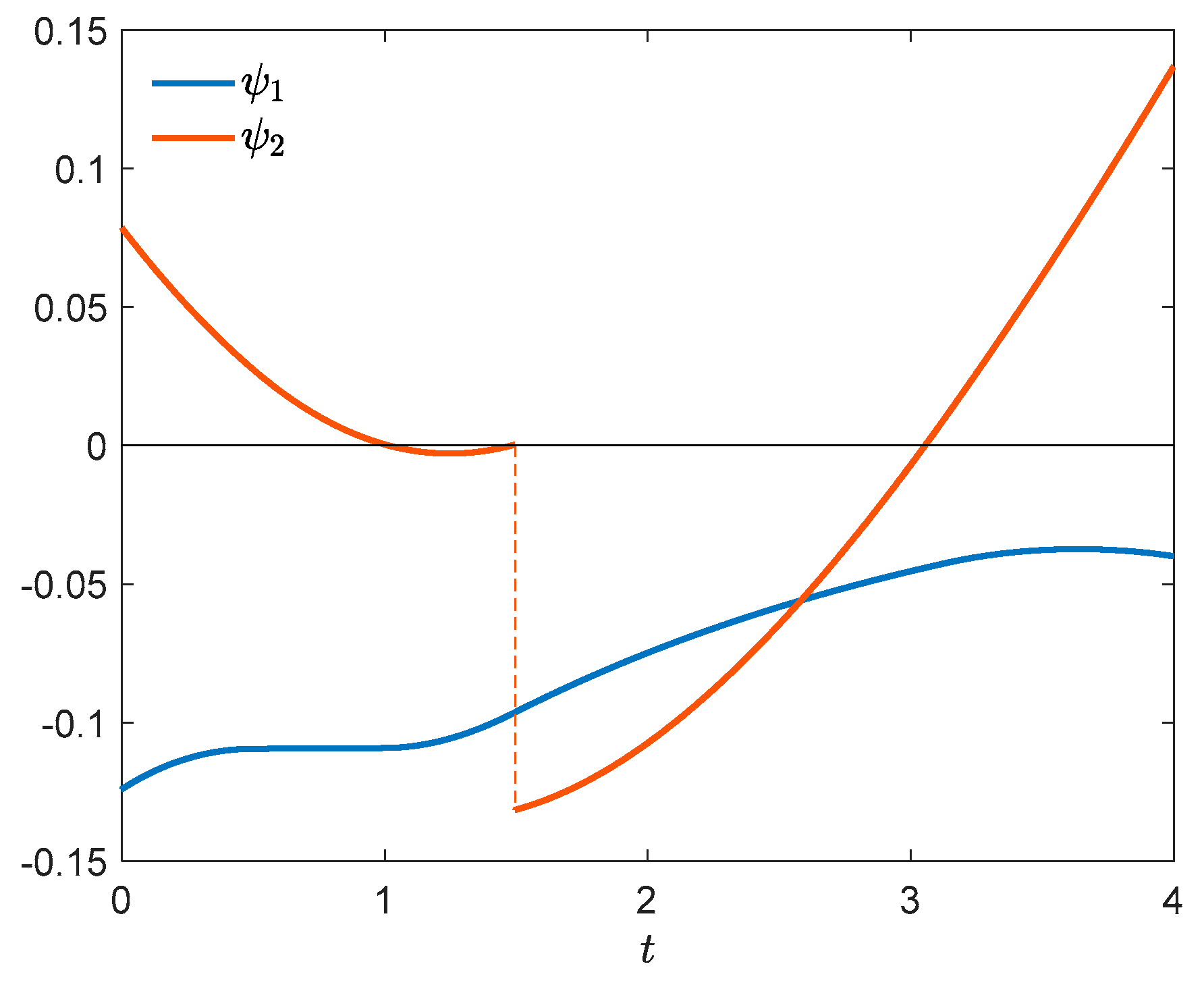







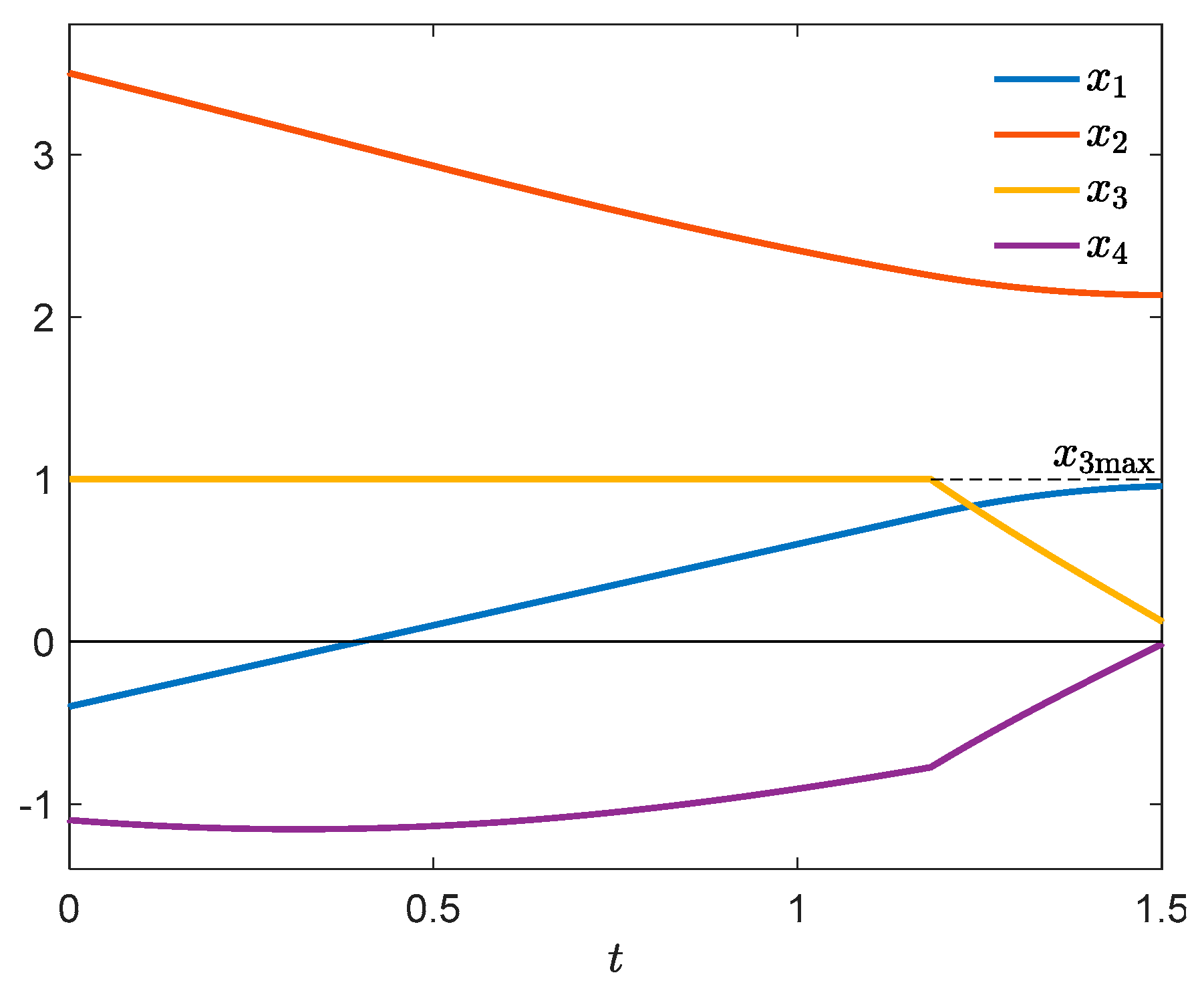

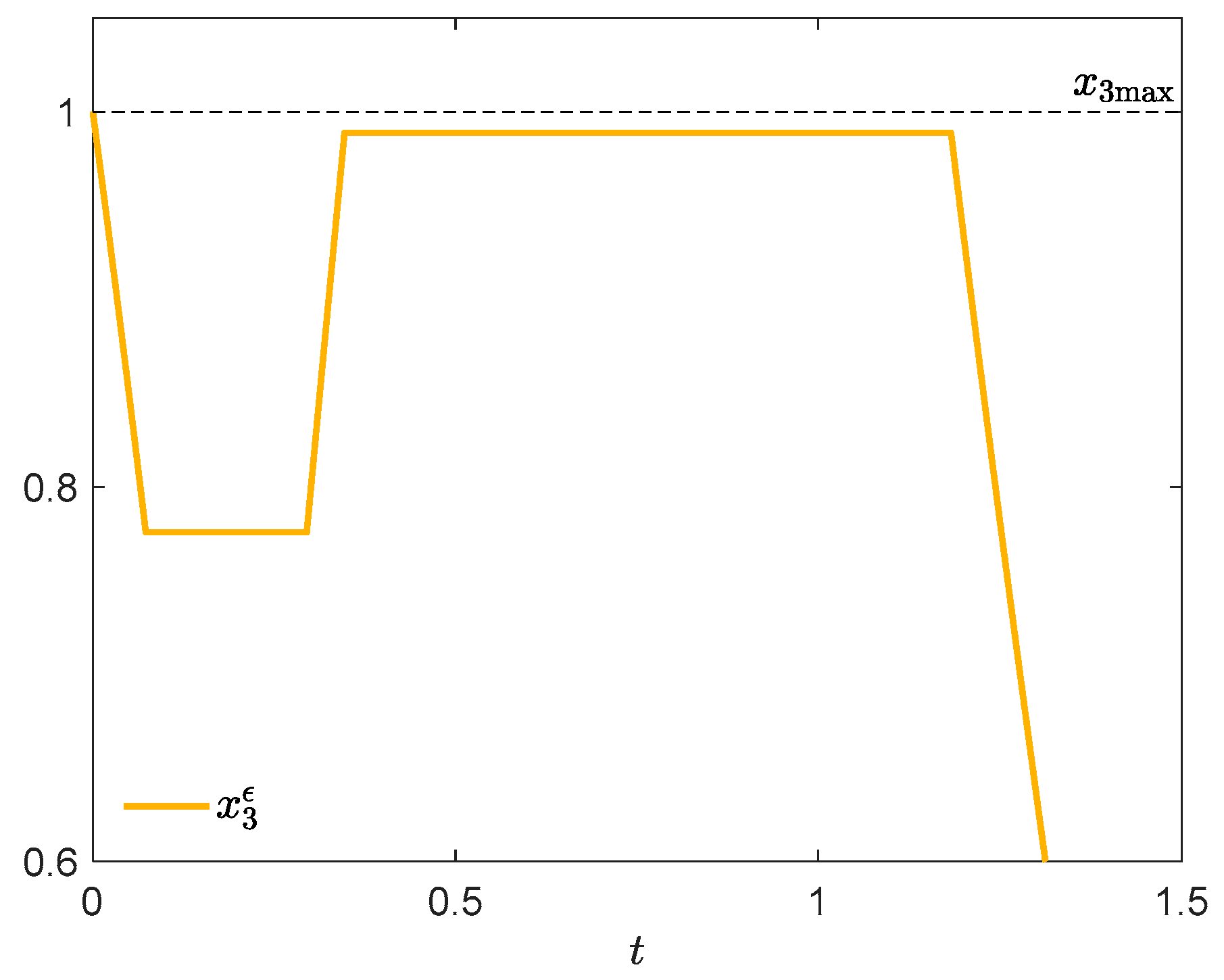
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korytowski, A.; Szymkat, M. Necessary Optimality Conditions for a Class of Control Problems with State Constraint. Games 2021, 12, 9. https://0-doi-org.brum.beds.ac.uk/10.3390/g12010009
Korytowski A, Szymkat M. Necessary Optimality Conditions for a Class of Control Problems with State Constraint. Games. 2021; 12(1):9. https://0-doi-org.brum.beds.ac.uk/10.3390/g12010009
Chicago/Turabian StyleKorytowski, Adam, and Maciej Szymkat. 2021. "Necessary Optimality Conditions for a Class of Control Problems with State Constraint" Games 12, no. 1: 9. https://0-doi-org.brum.beds.ac.uk/10.3390/g12010009




