1. Introduction
Can an employer distinguish between moral and altruistic employees? Ref. [
1] explores a moral hazard in teams problem where an employer has to choose between hiring a team of altruistic agents or a team of moral agents (as in [
2,
3,
4]). The key finding is that the principal sometimes prefers the team of moral agents over the team of altruistic ones depending on the production technology and the common degree of morality or altruism. The author then argues that firms may have incentives to collect information about their prospective employees’ preferences in order to benefit from offering less costly contracts.
This last point, however, is not developed there. In particular, Ref. [
1] assumes that the agents’ preferences are common knowledge, i.e. the principal knows not only which kind of prosocial preferences the prospective employees have, but also what is the common degree of morality or altruism displayed by the agents.
The objective of this paper is to relax that strong assumption: in what follows, it is assumed that the degree of altruism or morality is known to all parties, but the utility function specification is private knowledge of the agents. The principal then seeks to distinguish the two groups by offering menus of contracts that induce participation, effort provision, and revelation of private information by the employees.
This class of adverse selection followed by moral hazard problems has been analyzed before. RefS. [
5,
6] have dedicated sections to this broad class of problems, and provide more references to the literature. To cite but a few articles exploring screening preferences, Ref. [
7] considers the problem of screening risk-averse agents under moral hazard under the strong assumption that the utility function satisfies single-crossing and CARA properties. As a result, they find that the power of incentives is decreasing with respect to risk-aversion. Ref. [
8] study a two-output model with risk-neutral agent protected by limited liability and ex-post participation constraints, and find that a fully pooling contract is optimal. Ref. [
9] build upon the previous model by assuming that the agent is risk-averse, and also finds that pooling contracts are difficult to avoid.
All the papers cited above differ from the environment studied here in one important way: they assume that preferences are common knowledge, but that either the degree of risk-aversion or a productivity parameter is private information of the single agent. Here, as stated before, the utility function rather than the common degree of altruism or morality is private information of the agents. The main results, however, are in line with [
8,
9]: separation is difficult to achieve by the principal if she desires the agents to exert effort in equilibrium. Intuitively, this is a consequence of the utility functions not displaying a single-crossing-like property, an assumption that is imposed in [
7].
Screening prosocial preferences has been the central issue in some studies, both theoretically and empirically. Ref. [
10] studies an environment with a single principal screening a continuum of workers that have private information about their ability and preferences over social comparisons. In particular, Ref. [
10] contrasts the optimal employment contracts for selfish and inequity-averse agents, and finds that it is impossible to screen workers of similar ability with respect to their social preferences within the firm, a result that is line with the ones found here. The main difference between [
10] and the model in this study is that the former considers only the adverse selection problem faced by the principal when hiring a single agent, while the latter assumes teamwork and moral hazard. Closer in essence to this paper are the works of [
11,
12], who consider screening followed by moral hazard when agents’ prosocial preferences are characterized by inequity aversion. Their results also suggest that screening agents according to their social preferences is not feasible.
The approach here developed is close in essence to [
13]. In the first step, I search for the set of feasible contracts, that is, those that satisfy the participation constraints plus the moral hazard incentive compatibility constraints for each preference group. In the second step, the principal selects the least costly menu of feasible contracts that also induce the preference groups to truthfully reveal their types. As a consequence, I obtain a
no-distortion-at-the-top-like result: the principal offers the second-best moral hazard contract to the least costly to hire preference group, and distorts the allocation to the costlier one either by excluding it from the relationship or by demanding a different level of effort.
The paper goes as follows.
Section 2 presents the environment and the concept of separating equilibrium to be considered.
Section 3 discusses screening and existence of separating equilibria, while
Section 4 characterizes contracts that support pooling equilibria.
Section 5 concludes. For ease of exposition, all proofs are relegated to
Appendix A.
2. The Model
This model builds upon the model in [
1]. Consider a single risk-neutral principal (she/firm) who faces a continuum of potential employees with total mass normalized to one. Alternatively, the model can be restated by considering
n pairs of potential employees, without loss. The firm seeks to hire a pair of agents to work on a common task that yields output
to the principal, with
. The probability
p of the high outcome being achieved depends on the binary choices of effort made by the agents employed in the firm,
for
. In particular,
where I assume that
. The cost of exerting effort is identical to every agent,
, for
.
Output is contractible, and the principal posts wage schedules
in order to attract the teams of agents. If the firm successfully attracts a pair of employees, her realized profit is
Denoted by
, the expected
material payoff accruing to agent
i from the effort choices
and wage schedule
, for
. I restrict attention to wage schedules pairs
determining the payments following good and bad realizations of revenues. This is in line with [
8,
9], where the schedules are composed of a fixed plus a variable part. In what follows, the
material payoff function takes the expected additively separable form
where
is the function that associates the agent’s consumption utility to each wage realization
w. The agents are risk averse towards wages:
is assumed to be twice-continuously differentiable, strictly increasing and strictly concave.
Each pair of agents belongs to one class of preference group: altruistic or moral. More precisely, each team is composed of two agents drawn from the same preference group, as in [
1]. The principal only knows the proportion of the population that each group corresponds to:
for altruist, and
for moral. The agents’ preferences in each group are represented by the utility functions
for the altruists and
for the moral agents, where
and
represent the agents’ degrees of altruism and morality, respectively. While subtle, the difference in the utility functions is crucial. For both preference groups, the first term captures the individual’s material payoff, given the strategy profile effectively used. For altruistic agents, the second term captures the impact of agent
j’s material payoff given the strategy profile
on agent
i’s utility, weighted by the degree of altruism
. Meanwhile, for moral agents, the second term captures the Kantian moral concern. In other words, each moral individual considers what his material payoff would be if, hypothetically, the other agent were to mimic him. Extended discussions on the interpretations of moral preferences can be found in [
2,
3,
4].
In what follows, as discussed in [
1], I assume that
, and focus on the comparable functions
As pointed out in [
2] and also explored in [
14], this is the formulation that gives rise to the behavioral equivalence between
homo moralis and altruistic preferences. Under an appropriate change of variables, the altruistic utility function could be rewritten as
, for
.
Throughout the exposition, I use the superscripts to denote equations and variables relevant to moral agents, and to refer to altruistic ones.
The timing of the game is depicted in
Figure 1.
3. Screening
Due to the assumption of a common degree of morality or altruism, I restrict attention to symmetric contracts offered to each team. These assumptions simplify the problem in the sense that both the incentive compatibility and individual rationality constraints are similar to the ones studied in the literature with a single agent, save for their dependence on the common degree of morality/altruism. For the pure moral hazard problem, these constraints are
for altruistic agents, and
for moral agents.
In contrast to [
1], I allow the different groups to have different reservation utilities. Two particular cases deserve a special mention. First, as in [
1], agents in each group may have exactly the same reservation utility
, which generates different utility levels for the participating agents whenever
due to the utility function representing each prosocial preference. The second particular case is
, so that the participation constraints for both moral and altruistic agents are identical for any common degree of prosociality
. If
, then both moral and altruistic agents behave as purely selfish individuals, and the screening problem becomes irrelevant.
Let denote the set of contracts that satisfy the participation and incentive compatibility constraints of altruistic agents, and similarly define the set for moral agents. The principal’s screening problem is to choose and such that neither group has an incentive to pick the contract designed for the other group. This is akin to the incentive compatibility constraint in the adverse selection problem, and it can be seen as an additional set of constraints in the principal’s maximization program. The issue, however, is that the intersection between these two sets of feasible contracts is not empty, and thus one can always construct a separating equilibrium by selecting two contracts, and , in , and arguing that each group will self-select into one, and only one, of these contracts.
I will, therefore, focus on a stronger form of separation: I will require that a menu of contracts has at most one element in the intersection of the feasible sets. This will ensure that at least one group has no incentives to deviate and accept the contract designed for the other group.
Let
, which is uniquely defined for each
since
u is strictly increasing by assumption. I can therefore rewrite the sets of feasible contracts using the linear constraints
for altruistic agents and
for moral agents. I can easily draw the sets of feasible contracts for the cases in which the production technology displays decreasing or increasing returns to efforts, by appropriately choosing the reservation utilities
and
. In
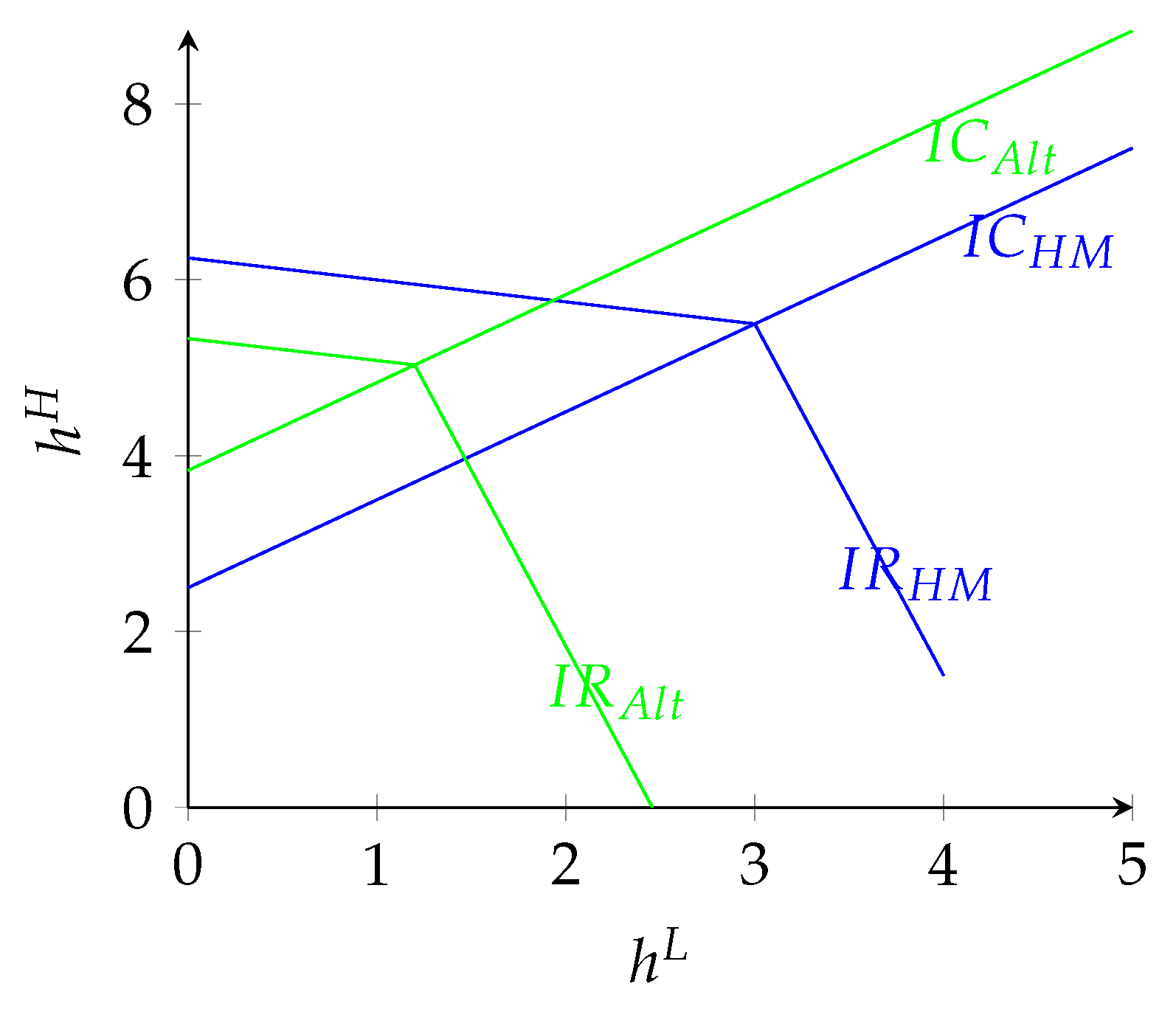
Figure 2 and
Figure 3, I assume that
. Notice, in
Figure 2, that
, which implies that any feasible contract offered to moral agents is also accepted by altruistic ones at the same time that it also provides the latter with incentives to exert high effort. Meanwhile, in
Figure 3, a contract in
is also accepted by altruistic agents, but it may not necessarily induce them to exert the high effort.
Lemma 1. Suppose that . There exists no strictly separating menu of contracts that induces both agents to exert high effort. Similarly, if , no strictly separating equilibrium exists that induces all agents to exert effort.
Lemma 1 states that a separating equilibrium does not exist if the reservation utility of both groups is such that the participation constraints are never identical and contracts incentivize agents to exert the high effort. Then, for each case, one can find a profitable deviation for a group, i.e. either the moral agents are better off taking the contract designed for the altruistic teams, or altruists like the moral contracts better than their own.
Lemma 2. Suppose that . There exists no strictly separating menu of contracts that induces both agents to exert high effort.
The negative results in Lemmas 1 and 2 can be linked to the fact that the isoutility curves of moral and altruistic agents never cross in the region where both groups are incentivized to exert the high effort. Indeed, under the assumptions of each statement, the indifference curves of each kind of prosocial agent are either identical to one another, or they are parallel. It is this violation of a single-crossing-like property that prevents the principal from finding schedules that elicit the agents’ preferences.
Proposition 1. There exists no strictly separating menu of contracts that induces both types of agents to accept a contract and exert high effort for any .
3.1. Separating Equilibria with Low Effort
A separating equilibrium also does not exist if the principal requires both types of agents to exert low effort. Indeed, due to risk aversion by the agents, the principal can induce participation by offering the constant schedules
and
for the altruistic and moral groups, respectively, satisfying the individual rationality constraints
By standard arguments, these constraints must bind in an equilibrium. However, if , one preference group always has incentives to deviate and accept the contract designed for the second group. On the other hand, if , then since u is strictly increasing, which implies that all workers accept exactly the same contract, and thus picking them apart is impossible for the principal. This argument is collected in the following result.
Proposition 2. No separating equilibrium exists if the principal wishes to induce both preference groups to accept the contract and exert low effort.
3.2. Screening Preference Groups through Exclusion
Propositions 1 and 2 have shown that the principal cannot screen moral agents from altruistic ones when she must induce both participation and high effort. However, the principal might be able to screen the different preference groups by offering a single (non-null) contract.
Turn once more to
Figure 2, by assuming identical reservation utilities and increasing returns to effort. If the principal offers a menu with a single contract that satisfies both the participation and incentive compatibility constraint of the altruistic agent with equality (the intersection of the green lines), she will ensure that: (i) altruistic agents accept the offer and exert high effort, and (ii) moral agents choose not to participate in the relationship with the principal. The same can be achieved under decreasing returns to effort by offering a similar contract (
Figure 3).
More generally, the principal can screen the preference groups by offering a singleton menu, where the contract offered necessarily satisfies with equality the participation constraint of the preference group with the lowest reservation utility.
Proposition 3. Suppose that . The principal can screen different preference groups by offering a single contract that excludes the agents with the highest reservation utility.
Proposition 3 holds either when the principal wishes to induce high or low effort. For the latter case, the argument behind Proposition 3 is even more compelling since the principal will offer a constant wage schedule to the risk-averse agents to exert zero effort, and therefore she can simply choose to employ the cheapest of the preference groups in terms of reservation utilities.
3.3. Screening with Different Efforts
So far, my analysis has focused on the case where both groups of agents are required by the principal to exert the same level of effort, either high or low. The negative results are basically a consequence of the indifference curves for the two groups being parallel to one another when efforts are the same: this implies that the contract offered to the group with the highest outside option also attracts the other team.
Although excluding one preference group from participating in the relationship with the principal is one way to screen agents, a second one exists, namely, requiring that only one group exerts high effort.
If only one group is expected to exert effort, the incentive compatibility constraint with respect to effort can be neglected for that group. Moreover, a constant schedule should be offered to that same group due to the agents’ risk-aversion. In what follows, I will denote by 1 the preference group that should exert effort, and by 2 the preference group who should not exert effort. The feasible set of contracts for the principal will be given by all values of satisfying the incentive compatibility and individual rationality constraints for group 1, and the participation constraint for group 2.
One must, however, notice an important difference between the participation constraints for both groups. For group 1, which is bound by the incentive compatibility constraint, the
is given by
On the other hand, for group 2, participation must satisfy
If the individual rationality curves never intersect, i.e. if either or , then a separating equilibrium does not exist, for the simple reason that the contract offered to the group with the highest outside option also attracts the agents of the other group, in much a similar manner to the case where the principal induces no group to high effort.
This is not true if the participation constraints intersect (which requires that
). Using the linearization
, the feasible set of contracts can be represented as in
Figure 4 below.
The contract offered to the agents in group 2 is given by the intersection of the line with the participation constraint for said group, since such a point has the principal proposing a constant schedule to the agents who are not expected to exert effort. On the other hand, agents in group 1 are offered the contract lying in the intersection between the two participation constraints, which they strictly prefer to the constant schedule of group 1 (while the latter is indifferent between the two contracts). The assumption that the participation constraints intersect also implies that the incentive compatibility constraint for group 1 is satisfied.
One remark is in order here: the principal leaves group 1 agents some rent for exerting the high effort, in the sense that the incentive compatibility constraint is not necessarily satisfied with equality (i.e. the pair does not lie in ). This can be interpreted as a no distortion at the top result: the principal’s offer does not distort (downward) the effort demanded from the least costly group, but she must still pay a rent to that group.
Proposition 4. Suppose that and are such that and the individual rationality constraints from both groups cross each other once. Then, a separating equilibrium exists if the principal induces only one preference group to exert the high effort.
4. Pooling Equilibria
Let be the contract that satisfies both conditions in with equality, and similarly, define . Additionally, denote by the contract that satisfies both the participation constraint for moral agents and the incentive compatibility constraint for altruistic agents with equality. The following proposition states the result formally.
Proposition 5. Suppose that . constitutes a pooling equilibrium with both groups of agents exerting the high effort under increasing returns to efforts, while constitutes such an equilibrium under decreasing returns to efforts.
I do not claim in Proposition 5 that and are the unique pooling equilibrium contracts under increasing and decreasing returns to efforts, respectively. Indeed, in the former case, any contract in indeed constitutes a pooling equilibrium. These two contracts, however, are completely characterized by a simple linear system of two equations. They also characterize one pooling equilibrium when : in this case, the participation constraints for both groups are identical, and characterizing the feasible sets for the contracts depends only on comparisons of the incentive compatibility constraints. Moreover, they are the least costly for the principal to offer among all pooling contracts.
However, one must stress that the principal is better off by offering a menu of contracts that screens different preference groups through exclusion. Indeed, since the principal always favors one preference group over the other for any degree of prosociality different than zero (where both moral and altruistic agents would be identical to purely selfish ones), the principal maximizes expected profits by hiring only the cheapest group he can incentivize to participate and exert the high effort, while excluding the more expensive group from partaking in any relationship with himself.
5. Discussion
The results presented above, in line with the literature on screening prosocial preferences, imply that the principal may be unable to construct a menu of contracts that is successful in screening teams of agents belonging to different preference groups. As a consequence, developing experiments to infer agents’ preferences in a static environment would present the same difficulties.
However, one possible strategy would be to offer the contracts sequentially. To fix ideas, suppose that the production technology exhibits increasing returns to efforts, and that . Under these circumstances, , as was argued in the proof of Lemma 1. If agents are perfectly patient, then the principal could offer in the first period, which would be accepted by all the altruistic agents but not by the moral ones, and only then offer to the remaining agents. Such sequential mechanism would make use of time to screen the agents, a channel that is not available in the static model described above.
There are two main issues with such an approach, at least from a theoretical viewpoint. First, if all the potential employees are aware that the employer would utilize the sequential offer mechanism above, altruistic agents would not accept in the first period in order to contract under in the second period and therefore enjoy a higher utility. Clearly, such deviation by altruistic agents would again leave the principal unable to screen between the two preference groups.
Secondly, the sequential approach relies on the agents being infinitely patient and the two preference groups displaying the same reservation utility. The mechanism could still be employed in the situation where and , where denotes group discount factor. In this case, if the altruistic group discounts the future much more than its moral counterpart, the mechanism could indeed lead to full screening. Unfortunately, to the best of my knowledge, I do not know any research establishing conditions under which different prosocial preferences lead to heterogeneous discount factors.