Modeling the Shape of Ions in Pyrite-Type Crystals

Abstract

The geometrical shape of ions in crystals and the concept of ionic radii are re-considered. The re-investigation is motivated by the fact that a spherical modelling is justified for p valence shell ions on cubic lattice sites only. For the majority of point groups, however, the ionic radius must be assumed to be an anisotropic quantity. An appropriate modelling of p valence ions then has to be performed by ellipsoids. The approach is tested for pyrite-structured dichalcogenides MX₂, with chalcogen ions X = O, S, Se and Te. The latter are found to exhibit the shape of ellipsoids being compressed along the <111> symmetry axes, with two radii r_|| and r_⊥ describing their spatial extension. Based on this ansatz, accurate interatomic M–X distances can be derived and a consistent geometrical model emerges for pyrite-structured compounds. Remarkably, the volumes of chalcogen ions are found to vary only little in different MX₂ compounds, suggesting the ionic volume rather than the ionic radius to behave as a crystal-chemical constant.

1. Introduction

The geometrical conception of atoms and ions has offered a straightforward approach for the physical modelling of hetero-polar crystals. In particular, the model of spherical ions having a constant radius has been widely disseminated [1,2], and numerous applications have been noted in diverse fields, such as high-T_c superconductors [3], multiferroic compounds [4] or the modelling of technical devices, like high-k field-effect transistors [5], to mention only a few examples. The approach assumes that ions of a chemical element and specific valence attain the same spherical volume in distinct crystalline compounds AB, such that the interatomic distance d_AB between the nearest neighbors is determined by the addition of radii r_A + r_B.

The concept celebrated its greatest success in applying it to rock salt- or sphalerite-structured compounds, where the ions occupy lattice sites of point groups m3m (O_h) or 43m (T_d). Here, consistent ionic radii could be derived that are exhibited in all of those crystals with only little variations [6]. It was the concept’s tempting promise that one geometric parameter would be conserved in all crystal surroundings, establishing a crystal-chemical conservation law. As it turned out, however, the respective ionic radii had to be split into different values according to bonding geometry, coordination number, etc., in order to arrive at sufficiently accurate interatomic distances. The extensive analysis of some hundred oxide and fluoride compounds led Shannon and Prewitt (1969) and Shannon (1976) to a set of ionic radii from the majority of relevant ions that still represent the state-of-the-art data [7,8]. Although these tables allowed for an accurate modelling of bond distances for the compounds from which they derive, many bond distances could only be predicted with little accuracy, in particular, when crystals with highly polarizable ions or complex crystallographic structures were considered.

The question arises whether more accurate results can be obtained when more general shapes than spheres would be used. In fact, since the crystal potential is superimposed to the spherical potential of the ion’s nucleus, there is no reason to stipulate a spherical shape for ions in crystal lattices. In the first attempt, it might be assumed that ions have to be modelled by ellipsoids instead of spheres, which should yield interatomic distances of improved accuracy for ions on polar lattice sites [9,10]. Koch and Fischer equally emphasized that the ellipsoidal modelling would appear more appropriate in certain crystal lattices with particularly convincing results to be expected for intermetallic compounds, like MgCu₂ [2]. Later, Birkholz and Rudert fully exploited the formalism to transition metal disulfides crystallizing in the pyrite structure. They showed that the sulfur ion in the MS₂ series, with M = Mn, Fe, Co, Ni, Cu, can consistently be described by a rotational ellipsoid with varying main axes r_|| and r_⊥ [11]. The significance of this more complex consideration of bonding geometry for the T_c maximum in solid solution of superconducting pyrite-type di-selenides and di-tellurides has recently been demonstrated by Guo and co-workers [12,13]. In order to study more crystals with respect to the applicability of the approach, the complete set of pyrite-type compounds MX₂ with monovalent chalcogenide ions X⁻ will be investigated in this work.

2. Motivation of Ellipsoidally Shaped Ions in Crystals

The starting point of the approach is the Neumann principle, according to which any observable quantity of a quantum mechanical system has to obey the same symmetry as the system itself [14]. Here, ionic multi-electron atoms located on crystal lattice sites obeying one of the 32 crystallographic point groups (PG) will be associated with the system, while their electron densities and bond distances will be regarded as observables. The notion of the crystalline field will be followed in this work, as already introduced by Bethe [15]. However, the emphasis will not be on the splitting of atomic terms, but on the splitting of orbital energies and the consequences for their spatial extension.

It will be assumed that the electronic levels of ions in crystals can be described within the orbital approximation [16]. Furthermore, the crystalline lattice will be supposed to be static, and dynamic effects will be neglected. It will be assumed for the charge density of ions that a possible asphericity is only related to their valence electrons, while inner shell electrons are fully accounted for by a spherical density function, ρ(r,θ,φ) = ρ_core(r) + ρ_val(r,θ,φ). The approach shares common aspects with techniques for the determination of electron densities (ED) from X-ray diffraction [17,18,19]. The question of ionic shape, however, is substantially easier than a full ED determination, since it only seeks the course of the outermost iso-contour surface of the electron density instead of its entire distribution in the unit cell.

Use will be made of the self-consistent Hartree–Fock formalism, since it allows writing the electron density of a many electron system as a sum of squares of basis functions. The latter are accounted for by , with principal quantum number n [20]. R_nl stands for the radial function that determines the ions spatial extension and κ_nl is the contraction-expansion parameter having the dimensionality of an inverse length. Strictly speaking, R_nl does not only depend on the radial coordinate r, but on its product with κ_nl having R_nl = R_nl(κ_nlr). The parameter κ is usually associated with an effective nuclear charge Z_eff via κ = Z_effmq²/(2πε₀ћ²n) in order to account for screening (m electron mass, q elementary charge, ε₀ permittivity of vacuum). Moreover, κ is related to the bonding energy of the electronic level via En = −κ²ћ²/(8m) [20].

The geometric significance of κ lies in the fact that it determines the radial extension until to which the particular orbital extends in space. In general, the radial part R_nl of electronic state nl is given by the sum over a small number of basis functions of the form:

N_nl(κ_nlr)ⁿ exp(−κ_nlr/2)

(1)

where N_nl is a normalization factor depending only on n and l. The determination of the set of κ parameters and their relative weights in the sum over all Equation (1) terms is the central task of the Hartree–Fock procedure [16,21,22,23,24]. Since this work is only concerned with the outermost course of the electron density of an ion, it will be assumed that considering one single term suffices to describe the ED at large distances from the nucleus. This will be the term with the smallest κ value.

The basis functions are assumed to be affected by the crystal field, which may lead to a splitting of levels with the same l that were considered degenerate in case of the free ion [14]. The angular parts 43m of the symmetry-adapted basis functions derive from basis functions spanning the irreducible representations (irrep) of the full rotation group D^l, which are the spherical harmonics:

(2)

In this expression, the index µ is used instead of m in order to numerate the different irreps [24]. The set of is unequivocally defined for each of the 32 PG; for a tabulation, see [25]. The symmetry-adapted basis functions of l = 1 states can be represented for most cases by p orbitals or real spherical harmonics y_lm± that derive from spherical harmonics via for |m| = 1 and y_l0 = for m = 0. Then, the Cartesian coordinate system has to be oriented along the main symmetry axes of the lattice site, like the z-axis along the major axes of rotation, etc.

The basic ansatz of this work is that the splitting of levels with the same l will not affect the angular functions alone, but also the radial functions, causing R_nl → R_nlµ. This becomes evident from the observation that symmetry adapted basis functions spanning different irreps, like and , are not transformed into each other under the symmetry operations allowed by the PG. For instance, a p_z orbital extending along the symmetry axis of a 3 (C₃) lattice site does not transform to p_x or p_y under any symmetry operation contained in the group.

In order to arrive at appropriate wave functions, it would thus be allowed to multiply the spanning different irreps by different radial functions R_nlµ without violating the constraint of length conservation under symmetry operations. Accordingly, fully symmetry-adapted basis functions are given by the product function R_nlμ , and there are various possibilities by which a distinction of radial functions may be introduced. In the framework used in self-consistent field theories and as given in Equation (1), the natural choice is to allow for different κ_µ for basis functions of different irreps R_nlµ(κ_µr). The κ splitting would correspond to a splitting of formerly degenerate levels into states of different bonding energy, since both are related as given above. No assumption will be made on the magnitude of the splitting; however, it will just be allowed for basis functions of different irreps in accordance with lattice site symmetry.

The derivation of the number of different κ to occur in the valence ED simply follows from the number of different irreps or symmetry species. The degeneracy of p states appears only for ions on cubic lattice sites. However, for all trigonal, tetragonal and hexagonal PGs, a splitting into two different states becomes allowed. This would affect the majority of site symmetries in crystals, i.e., 19 of 32 PGs [25]. For lower symmetry sites, l = 1 states would even split into three different levels. The electron density of the valence shell (with the largest principal quantum number n) then becomes:

(3)

where q is the elementary charge, and the occupation number of the different states h_lµ may amount to zero, one or two. The sum over all h_lµ gives the number of valence electrons, Σh_lµ = N_val. The consequences of κ splitting upon the shape of ions are straightforward. While only one average radial parameter r_s had to be used in the concept of ionic radii, in the approach outlined here, an envelope function r_s(θ,φ) must be introduced that derives from identifying a surface of constant charge density:

ρ_val(r_s,θ,φ) = ρ_s

(4)

Performing the volume integration over the charge density up to this limit:

(5)

gives the fraction f of valence charge density N_valq enclosed by the r_s(θ,φ) surface. The magnitude of f is typically set to values around 90%. For the concept proposed here, it is assumed that the precise value of f is chosen such that it assures the iso-density surface r_s(θ,φ) of neighboring ions to touch at a common point in the space between them. These points will be named contact points in the following.

The κ splitting will cause the spatial extension of the electron density to vary in different directions. This becomes obvious by re-writing Equation (3) for an ion at a triclinic, monoclinic or orthorhombic lattice site in Cartesian coordinates:

(6)

where the summation i = 1…3 stands for x, y and z. Insertion of Equation (1) yields for large r values:

(7)

where r_s and x_s,i now stand for the radial and Cartesian coordinates of the iso-density surface. It is easily shown that Equation (7) describes a general ellipsoid for κ₁ ≠ κ₂ ≠ κ₃. In addition, a careful analysis of Equation (7) reveals that the spherical character of the r_s(θ,φ) should increase with quantum number n, i.e., the period of the ion within the periodic table. The iso-contour surface of electron density in the outermost regions of a p valence shell ion at triclinic, monoclinic and orthorhombic lattice sites accordingly is that of a general ellipsoid.

The shape simplifies to that of a rotational ellipsoid for κ₁ = κ₂ ≠ κ₃, which is obeyed by p valence ions on trigonal, tetragonal and hexagonal lattice sites. It simplifies further to a sphere on cubic lattice sites, where κ₁ = κ₂ = κ₃ holds. In the latter case, all terms in Equation (7) can be placed before the sum that ends up with Σ(x² + y² + z²), such that the whole equation just depends on the radial coordinate r and, thus, describes the shape of the sphere. Strictly speaking, these results would be valid only for either closed shell systems, all h_i = 2, or half-closed shells, all h_i = 1. It is realized from Equation (7) that any aspherical deformation would be amplified by a mixed occupation, i.e., valence shells with varying occupation numbers.

It can be concluded that the general shape Equation (7), firstly, motivates the success of the concept of ionic radii for the alkali halides and sphalerites, where ions occupy cubic sites of PG m3m and 43m. Secondly, it becomes evident why the ionic radii derived from these compounds do not apply to ions on lower symmetry sites. It may be understood that for the majority of bond distances, only rough approximations of the true bonding geometry were obtained with a single radius value, when, in fact, two or three radial parameters were required.

It is concluded that the general shape Equation (7) may yield a more accurate geometrical picture when applied to p valence ions on crystal positions of non-cubic symmetry. That was the basics for the application of the approach in [11], and its expansion will be tested in the following part for an extended set of compounds having the same crystal structure.

A pragmatic distinction seems helpful before starting the test. It will be supposed in the following that aspherical charge densities are more significant for anions than for cations. This is motivated by the smaller ionization energies of anions compared to cations. Hence, the difference of the anionic volume V₋ compared to that of the neutral atom V_at is larger than for cations: |V₋ − V_at| > |V_at − V₊|. This rule holds at least for the most important ions of the second to fourth period, although the asphericity of cations may become equally important for higher periods.

3. Application to Pyrite-Structure Dichalcogenides

The approach will now be applied to metal dioxides, disulfides, diselenides and ditellurides MX₂ that crystallize in the pyrite structure; see Table 1. It will not be endeavored to give a theoretical calculation of ionic wave functions according to the rules outlined in the previous section. Nor will the numerical values of κ parameters or the fraction f of enclosed valence electrons be determined. Instead, the ellipsoidal modelling of anions will be investigated by making use of highly precise structural data that have been determined for these compounds by diffraction experiments and which are also listed in Table 1. As in the crystal radii approach, the ionic shapes will be chosen such that neighboring ions share a common contact point via their iso-density surfaces.

Table 1. Lattice parameters of pyrite-type compounds MX₂. Unit cell edges a and positional parameters u were taken from cited references and used to calculate X–X and M–X bond length d_XX and d_MX. Metal ionic radii r_MSP were selected from SPS tables for VI-fold coordinated divalent metal ions [7,8]; spin-states were chosen in agreement with experimental data, i.e., high-spin for Mn²⁺ and low-spin for Fe²⁺, etc. Ellipsoidal radii r_||, r_⊥ and ionic volume V_X are given in the last columns as calculated from d_XX and Equations (8) and (9). Lengths are given in nm and volumes in nm³.

MX2	a	u	Ref.	dMX	dXX	rMSP	r||	r⊥	VX
MgO2	0.48441	0.4114	[26]	0.2083	0.1487	0.072	0.0743	0.1415	0.00623
ZnO2	0.4871	0.413	[27]	0.2099	0.1468	0.074	0.0734	0.1413	0.00614
CdO2	0.5313	0.4192	[28]	0.2308	0.1487	0.095	0.0744	0.142	0.00628
FeS2	0.54160	0.38484	[29]	0.2263	0.2161	0.061	0.1080	0.1676	0.0127
CoS2	0.55385	0.38987	[30]	0.2325	0.2113	0.065	0.1056	0.1704	0.0129
NiS2	0.56852	0.39454	[31]	0.2398	0.2077	0.069	0.1038	0.1744	0.0132
CuS2	0.57891	0.39878	[32]	0.2453	0.2030	0.073	0.1015	0.1766	0.0133
MnS2	0.6104	0.4011	[33]	0.2593	0.2091	0.083	0.1046	0.1810	0.0143
FeSe2	0.5783	0.386	[34]	0.2419	0.2284	0.061	0.1142	0.1836	0.0161
CoSe2	0.58593	0.379	[35]	0.2437	0.2456	0.065	0.1228	0.1804	0.0167
NiSe2	0.59629	0.383	[35]	0.2488	0.2417	0.069	0.1208	0.1820	0.0168
MnSe2	0.6417	0.393	[36]	0.2702	0.2379	0.083	0.1189	0.1908	0.0181
MgTe2	0.70212	0.3875	[26]	0.2941	0.2736	0.072	0.1368	0.2257	0.0292
MnTe2	0.6943	0.386	[36]	0.2904	0.2742	0.083	0.1371	0.2103	0.0254

Table 1. Lattice parameters of pyrite-type compounds MX₂. Unit cell edges a and positional parameters u were taken from cited references and used to calculate X–X and M–X bond length d_XX and d_MX. Metal ionic radii r_MSP were selected from SPS tables for VI-fold coordinated divalent metal ions [7,8]; spin-states were chosen in agreement with experimental data, i.e., high-spin for Mn²⁺ and low-spin for Fe²⁺, etc. Ellipsoidal radii r_||, r_⊥ and ionic volume V_X are given in the last columns as calculated from d_XX and Equations (8) and (9). Lengths are given in nm and volumes in nm³.

MX2	a	u	Ref.	dMX	dXX	rMSP	r||	r⊥	VX
MgO2	0.48441	0.4114	[26]	0.2083	0.1487	0.072	0.0743	0.1415	0.00623
ZnO2	0.4871	0.413	[27]	0.2099	0.1468	0.074	0.0734	0.1413	0.00614
CdO2	0.5313	0.4192	[28]	0.2308	0.1487	0.095	0.0744	0.142	0.00628
FeS2	0.54160	0.38484	[29]	0.2263	0.2161	0.061	0.1080	0.1676	0.0127
CoS2	0.55385	0.38987	[30]	0.2325	0.2113	0.065	0.1056	0.1704	0.0129
NiS2	0.56852	0.39454	[31]	0.2398	0.2077	0.069	0.1038	0.1744	0.0132
CuS2	0.57891	0.39878	[32]	0.2453	0.2030	0.073	0.1015	0.1766	0.0133
MnS2	0.6104	0.4011	[33]	0.2593	0.2091	0.083	0.1046	0.1810	0.0143
FeSe2	0.5783	0.386	[34]	0.2419	0.2284	0.061	0.1142	0.1836	0.0161
CoSe2	0.58593	0.379	[35]	0.2437	0.2456	0.065	0.1228	0.1804	0.0167
NiSe2	0.59629	0.383	[35]	0.2488	0.2417	0.069	0.1208	0.1820	0.0168
MnSe2	0.6417	0.393	[36]	0.2702	0.2379	0.083	0.1189	0.1908	0.0181
MgTe2	0.70212	0.3875	[26]	0.2941	0.2736	0.072	0.1368	0.2257	0.0292
MnTe2	0.6943	0.386	[36]	0.2904	0.2742	0.083	0.1371	0.2103	0.0254

The geometry of bonding in pyrite-type disulfides has recently been modelled under the assumption of spherical ion shapes [11]. This is visualized by a 3D plot for the prototype compound FeS₂ in Figure 1. The cubic pyrite structure contains four formula units MX₂ per unit cell with anions residing on three (C₃) and cations on 3 (C_3i) lattice sites; further structural details are given in the figure legend and [37]. For plotting Figure 1, cation radii r_MSP were taken from the SPS listing [7,8], while the radius of sulfur anions was naturally chosen as half the sulfur dumbbell distance, r_S = d_SS/2. It turned out that the calculation of the interatomic Fe–S distance d_Fe–S by simply summing up r_MSP and r_S resulted in a 25% deviation from the experimental value. This insufficiency of the spherical model was not only obtained for FeS₂, but equally observed for all compounds listed in Table 1. It demonstrates the inadequacy of the spherical modelling for pyrite-type crystals.

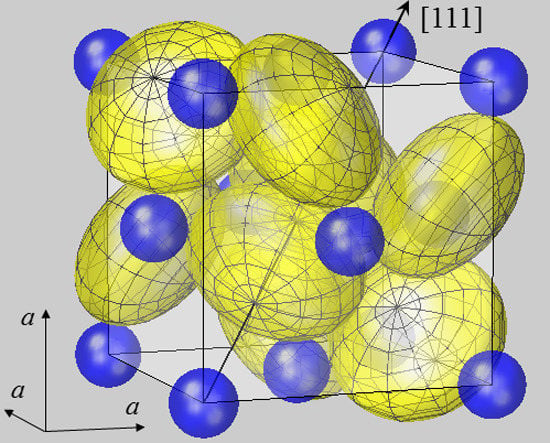
Figure 1. Spherical modelling of the pyrite unit cell (space group Pa3). While Fe²⁺ ions (blue) form an fcc lattice, sulfur ions (yellow) reside on <111> axes, as described by positional parameter u. In FeS₂ u amounts to 0.38484 in fractional coordinates of the unit cell [38]. The body diagonal is shown as an arrow. S ions form dumbbells, and there are four S₂ dumbbells in the unit cell. Only the dumbbell at (uuu) and (ūūū) appears undivided, while the remaining S₂ dimers all extend from the cell shown into neighboring cells. In order to visualize the different site symmetries, a mesh is inscribed into S ion spheres with poles lying on <111> symmetry axes. All ions are modelled by spheres with radii r_MSP for Fe²⁺ and half the S–S bond distance d_SS/2 for S⁻. With this setting, Fe and S spheres have contacts with none or only one neighbor, respectively. This result also holds for the other compounds listed in Table 1. Such a spherical packing would be unstable in terms of packing theory [2], demonstrating the failure of the ionic radius concept in the case of pyrite-type compounds.

Figure 1. Spherical modelling of the pyrite unit cell (space group Pa3). While Fe²⁺ ions (blue) form an fcc lattice, sulfur ions (yellow) reside on <111> axes, as described by positional parameter u. In FeS₂ u amounts to 0.38484 in fractional coordinates of the unit cell [38]. The body diagonal is shown as an arrow. S ions form dumbbells, and there are four S₂ dumbbells in the unit cell. Only the dumbbell at (uuu) and (ūūū) appears undivided, while the remaining S₂ dimers all extend from the cell shown into neighboring cells. In order to visualize the different site symmetries, a mesh is inscribed into S ion spheres with poles lying on <111> symmetry axes. All ions are modelled by spheres with radii r_MSP for Fe²⁺ and half the S–S bond distance d_SS/2 for S⁻. With this setting, Fe and S spheres have contacts with none or only one neighbor, respectively. This result also holds for the other compounds listed in Table 1. Such a spherical packing would be unstable in terms of packing theory [2], demonstrating the failure of the ionic radius concept in the case of pyrite-type compounds.

As mentioned before, a possible asphericity of cations will be neglected. Therefore, metal ions in the pyrite structure are assumed to exhibit the shape of spheres, and r_MSP values were again taken from the SPS listing [7,8]. Only those pyrite-structure dichalcogenides were selected to enter into Table 1, for which a radius value for a six-fold-coordinated M²⁺ was given in the SPS listing. Hence, the availability of these data served as a selection criterion for the compounds to be investigated here.

Charge densities of monovalent X anions, however, have to be modelled by ellipsoids. A nearly sp³ hybridization was assumed to account for their electronic configuration as deduced from their tetrahedral coordination. Since the electron density is assumed to scale with the square of electron wave functions, the hybridization does not affect the splitting of p levels into symmetry-adapted states. It is well known that the p orbitals in a three symmetry span a one-dimensional A and a two-dimensional E representation. Accordingly, two contraction-expansion parameters κ_|| and r_⊥ are needed to describe the spatial extension of chalcogen ion ellipsoids, which correspond to one radius r_|| along the <111> symmetry axis and another radius κ_⊥ perpendicular to it. Rotational ellipsoids of initially unknown principal extension where accordingly placed on X lattice sites in the second step of the geometrical construction.

The lengths of the major axes of X ellipsoids were determined in the third step by varying r_|| and r_⊥ until the first contact with the iso-surfaces of lattice neighbors was obtained. This construction is easily performed for r_||, since its magnitude is simply given by half the dumbbell distance, r_|| = d_XX/2. The geometrical derivation of r_⊥, however, is more complex. It can be seen from the bonding geometry shown in Figure 2 that the metal-chalcogen distance d_MX should be decomposed in the metal radius r_MSP and half of the diameter of the chalcogen ellipsoid, with the diameter chosen to lie in the direction of the M–X internuclear axis [11]. Since the ellipsoid diameter depends on both r_|| and r_⊥, the equation:

(8)

holds, where α is the M–X–X bond angle, and cosα = 3 is valid in the pyrite structure. From this equation, r_⊥ can be derived, if the other quantities are known. From a geometric point of view, the solution of Equation (8) for known values of d_MX, r_MSP, r_|| and α corresponds to varying r_⊥ until the X ellipsoid comes in contact with the neighboring M spheres. The obtained X ellipsoid with the radii r_|| and r_⊥ is visualized in Figure 2 for FeS₂, where the neighbors of the first bonding spheres of an S₂ dumbbell are shown.

Figure 2. Bonding coordination of the sulfur dumbbell in FeS₂ at (uuu) and (ūūū). (a) Within the crystallographic unit cell and (b) as S₂Fe₆ cluster with internuclear axes. According to the presented approach, ellipsoidal deformations are allowed to occur for S anions on three (C₃) symmetry sites, but might be neglected for Fe cations. The bond partner of sulfur dimers S₂ form two interpenetrating tetrahedrons with the neighbor S residing on top and three Fe²⁺ forming the basis. The tetrahedrons itself are compressed as are the sulfur ellipsoids. The latter exhibit a smaller radius parallel to the <111> axis r_|| compared to the perpendicular radius r_⊥. Comparable geometries are found for the other pyrite-type compounds listed in Table 1.

Figure 2. Bonding coordination of the sulfur dumbbell in FeS₂ at (uuu) and (ūūū). (a) Within the crystallographic unit cell and (b) as S₂Fe₆ cluster with internuclear axes. According to the presented approach, ellipsoidal deformations are allowed to occur for S anions on three (C₃) symmetry sites, but might be neglected for Fe cations. The bond partner of sulfur dimers S₂ form two interpenetrating tetrahedrons with the neighbor S residing on top and three Fe²⁺ forming the basis. The tetrahedrons itself are compressed as are the sulfur ellipsoids. The latter exhibit a smaller radius parallel to the <111> axis r_|| compared to the perpendicular radius r_⊥. Comparable geometries are found for the other pyrite-type compounds listed in Table 1.

Equation (8) re-establishes the additivity of the interatomic distance by decomposing it into the metal ionic radius plus a weighted sum of ellipsoidal radii with weighting factors given by the direction cosine and direction sine with respect to the inter-nuclear axis. The formula exemplarily shows that interatomic distances in crystals indeed exhibit an additivity rule. However, bond distances d are not simply obtained by adding two ionic radii, like r_M and r_X, but derive from a geometrically more complex scheme that has to comply with the crystal symmetry and the relative orientation of valence orbitals. Only this procedure is in accordance with Neumann’s principle.

Finally, also the volume of chalcogen ellipsoids can be derived from:

(9)

with r_⊥ entering quadratically, as both perpendicular directions are equivalent.

4. Results and Discussion

The three parameters of interest, r_||, r_⊥ and V_X, were analyzed with this ansatz for all MX₂ investigated in this work, and the results are also compiled in Table 1. It can be seen that the magnitude of the equatorial radius r_⊥ exceeds that of the polar radius r_|| in all cases. In terms of contraction-expansion parameters, this result is equivalent to κ_|| > κ_⊥. Accordingly, chalcogen ions exhibit the shape of oblate ellipsoids being compressed along <111> axes.

The compression of chalcogen ellipsoids towards X anions and their elongation in the perpendicular direction appears very plausible from an electrostatic point of view. This suggests that electrons of one anion in the vicinity of the X–X internuclear axis are repelled by the negative charge of the neighboring anion. In addition, they are also attracted towards the cations, the combination of both effects causing the oblate appearance.

The deformation ratio of chalcogen ions r_⊥/r_|| is seen in Table 1 to increase in the sequence O > S > Se > Te. This development is fully in accordance with the statement that r_⊥/r_|| should diminish with principal quantum number n for an otherwise unchanged energy splitting, as may occur for a nearly constant crystal-structure surrounding when going from one pyrite-structured dichalcogenide to another. Figure 3 displays the aspherical modelling for the prototype compound of the pyrite structure, which is the first visualization of the FeS₂ crystallographic unit cell that is adequately modelled with ellipsoidal sulfur ions.

The presented modelling appears unfamiliar, since we have got acquainted to consider ionic shapes along bond distances, as in molecules. In the new approach, however, the shape is decomposed along symmetry axes and perpendicular axes because of the orthonormality of p orbitals. For the chalcogen ions in pyrite crystals, the second ellipsoidal axis is not directed along the M–X bond axis, but perpendicular to C₃. This procedure makes the new picture difficult to grasp. On the other hand, the model is more in accordance with the crystalline state, where chemical bonding is not a phenomenon between neighboring atoms, but between one ion and all other ions of the crystallite.

Derived data appear also interesting with respect to the volume of chalcogen ions V_X. Their values, as calculated from r_|| and r_⊥ according to Equation (8), are given in Table 1. It can be seen that ionic volumes compare very well, when compounds with equal chalcogen ions are compared (O⁻, S⁻, Se⁻ and Te⁻). It must be remembered that the accuracy of metal ionic radii is only on the order of some percent [7,8], which suggests that the scatter in V_X values may practically vanish, if small corrections on r_MSP would apply.

Figure 3. A new look at the pyrite structure: crystallographic unit cell of pyrite FeS₂ with Fe and S ions modelled by spheres and ellipsoids, respectively. Radial parameters r_MSP for Fe²⁺ and r_|| and r_⊥ for S⁻ were used as given for FeS₂ in Table 1. The mesh inscribed into the sulfur ions now reveals the ellipsoidal compression along <111> directions. In this model, the number of contact points of S and Fe ions become four and six, respectively, and the ellipsoidal deformation is concluded to enable a stable packing.

Figure 3. A new look at the pyrite structure: crystallographic unit cell of pyrite FeS₂ with Fe and S ions modelled by spheres and ellipsoids, respectively. Radial parameters r_MSP for Fe²⁺ and r_|| and r_⊥ for S⁻ were used as given for FeS₂ in Table 1. The mesh inscribed into the sulfur ions now reveals the ellipsoidal compression along <111> directions. In this model, the number of contact points of S and Fe ions become four and six, respectively, and the ellipsoidal deformation is concluded to enable a stable packing.

Table 2 lists the average values of V_X as obtained from each group of MX₂. The data are found to exhibit a monotonic increase from O to Te, as expected. The respective standard deviations δV_X have also been given, which are perceived to be on the order of 1.7%. These variations are rather small when compared to other approaches for the geometrical modelling of pyrite-type compounds. They will even diminish when transformed from a volume scale to a length scale to compare their accuracy with data derived from the ionic radius concept.

Such an appropriate length scale is given by the sphere-equivalent radius r_x of chalcogen ions, which is derived from and stands for the radius a spherical X⁻ ion would have. Sphere-equivalent radii r_x were calculated for each compound investigated here, and averages were formed for the groups of dioxides, disulfides, etc.

The data are also given in Table 2, and their respective standard deviations δr_x are seen to range from 0.3% to 2.3%. This is a rather small scatter compared to the conventional crystal radii approach [7,8] and again signifies the reliability of the approach introduced here. Furthermore, the calculation of interatomic distances now yields only small deviations from experimental data in the few percent range, when their calculation is based on V_X values given in Table 2 and the d_MX decomposition according to Equation (8).

The physical significance of the ionic volume data V_X is underlined by a comparison with the volumes of chalcogen atoms V_at and divalent ions V_di. Accurate data for them can be obtained from the literature, where they were either obtained through theoretical calculation or were determined from sphalerite-type compounds [7,8,39].

Table 2. Spherically-averaged radii and volumes of chalcogen atoms and ions with radii given in nm, volumes in 10⁻³ nm³ and relative errors δr_x and δV_X in %. Numbers in parenthesis give the standard deviations for the last digit(s) of the preceding value. Averaged data of monovalent ions r_x and V_X were derived as outlined in the text, while spherical volumes of chalcogen atoms V_at and tetrahedrally coordinated divalent ions V_di were calculated from their radii given in [39] and [7,8], respectively.

X	rx	δrx	VX	δVX	Vat	Vdi
O	0.1141(4)	0.3	6.22(6)	1.0	1.2	11.0
S	0.1469(21)	1.4	13.3(6)	4.3	4.71	26.1
Se	0.1593(15)	1.0	16.9(7)	4.3	6.71	32.5
Te	0.1867(43)	2.3	27(2)	7	10.77	45.2

Table 2. Spherically-averaged radii and volumes of chalcogen atoms and ions with radii given in nm, volumes in 10⁻³ nm³ and relative errors δr_x and δV_X in %. Numbers in parenthesis give the standard deviations for the last digit(s) of the preceding value. Averaged data of monovalent ions r_x and V_X were derived as outlined in the text, while spherical volumes of chalcogen atoms V_at and tetrahedrally coordinated divalent ions V_di were calculated from their radii given in [39] and [7,8], respectively.

X	rx	δrx	VX	δVX	Vat	Vdi
O	0.1141(4)	0.3	6.22(6)	1.0	1.2	11.0
S	0.1469(21)	1.4	13.3(6)	4.3	4.71	26.1
Se	0.1593(15)	1.0	16.9(7)	4.3	6.71	32.5
Te	0.1867(43)	2.3	27(2)	7	10.77	45.2

The comparison is visualized in Figure 4, where the three different volumes are displayed as a function of atomic number Z. In regard to many details, such as substantial increases between O and S or Se and Te, etc., the volume of monovalent ions V_X is seen to follow the same trend as V_at and V_di. Moreover, V_X values consistently range between 50% and 60% of divalent ions V_di. The trend in V_X and the absolute values can thus be considered to be very reliable.

The results imply considering the derived V_X values rather than a single radius as a crystal-chemical constant, which are attained by the specific ion in different crystalline solids. The distinction is irrelevant for ions on cubic lattice sites for which the concept of crystal radii has initially been developed. It becomes important, however, when ions on positions with lower site symmetry are considered. In these cases, rather, the crystal volume seems to be conserved, while the ion’s extension in different directions will depend on existing symmetry axes and their relative orientation. The shape of a p valence shell ion has to be modelled by a general ellipsoid for ions on low-symmetry sites. Monovalent chalcogen ions O⁻, S⁻, Se⁻ and Te⁻ in pyrite-type compounds exhibit remarkably consistent volumes when modelled by ellipsoids in accordance with the presented formalism.

Figure 4. The volume of chalcogen atoms and ions as a function of atomic number Z (data are given in Table 2). In the plot, V_at stands for the volume of covalent atoms (from [39], MW), V_X for monovalent ions as derived in this work and V_di for divalent ions (from [7,8], SPS). Continuous and dashed lines merely serve as a visual guide.

Figure 4. The volume of chalcogen atoms and ions as a function of atomic number Z (data are given in Table 2). In the plot, V_at stands for the volume of covalent atoms (from [39], MW), V_X for monovalent ions as derived in this work and V_di for divalent ions (from [7,8], SPS). Continuous and dashed lines merely serve as a visual guide.

5. Conclusions

A geometrical approach has been derived that allows one to cure the inaccurate modelling of crystal structures by the ionic radius concept. It turns out for p valence shell ions that an isotropic ionic radius only occurs on cubic lattice sites. For all other site symmetries, however, two or three radial parameters will apply. Appropriate geometric shapes for p valence shell ions are thus given by ellipsoids instead of spheres.

The application of the approach to pyrite-type compounds MX₂ gave two remarkable results. First, re-establishing an additivity rule for interatomic distances d_MX has succeeded. However, d does not simply derive from the addition of two radial parameters r_|| and r_⊥, but a decomposition of d in accordance with the lattice site symmetry must be performed. Equation (8) exemplarily shows how this ensues in the case of the pyrite structure. In addition, the ionic volume, as in rock salt and sphalerite structures, re-appeared as a conserved quantity by applying the geometrically correct bond distance decomposition. A possible conservation of ionic volume seems of fundamental importance for crystalline bonding in general and would allow the prediction of crystal structures from a finite set of parameters.