Wetting of Nematic Liquid Crystals on Crenellated Substrates: A Frank–Oseen Approach

Abstract

We revisit the wetting of nematic liquid crystals in contact with crenellated substrates, studied previously using the Landau–de Gennes formalism. However, due to computational limitations, the characteristic length scales of the substrate relief considered in that study limited to less than 100 nematic correlation lengths. The current work uses an extended Frank–Oseen formalism, which includes not only the free-energy contribution due to the elastic deformations but also the surface tension contributions and, if disclinations or other orientational field singularities are present, their core contributions. Within this framework, which was successfully applied to the anchoring transitions of a nematic liquid crystal in contact with structured substrates, we extended the study to much larger length scales including the macroscopic scale. In particular, we analyzed the interfacial states and the transitions between them at the nematic–isotropic coexistence.

1. Introduction

The study of nematic liquid crystals in contact with microstructured substrates has been an active area of research in the last decades [1,2,3], with practical applications such as zenithally bistable devices [4,5,6,7,8,9] and tailoring of soft rails for colloidal transport on surfaces [10,11,12,13,14,15,16]. Structured substrates frustrate the nematic orientational order, and thus elastic distortions of the nematic and, in some cases, topological defects arise driven by the substrate relief. When the substrate has cusps, disclination-like singularities nucleate at or very close to them [17,18,19,20,21,22]. These play an essential role in the multistability resulting from the existence of distinct interfacial states of the nematic in contact with a microstructured substrate, with different nematic textures [23].

Nematic wetting of structured substrates has attracted much less attention [24,25]. At planar substrates, a first-order orientational wetting transition is predicted by the Landau–de Gennes theory, where a macroscopic nematic layer intrudes at the substrate–isotropic liquid interface [26,27], and has been observed experimentally [28,29,30,31,32]. Macroscopically, wetting of a planar substrate is described by Young’s equation

$$cos{\theta }_{\pi }=\frac{{\sigma }_{si}-{\sigma }_{sn}}{{\sigma }_{ni}}$$

(1)

where ${\theta }_{\pi }$ is the contact angle between the planar substrate and a large nematic droplet at coexistence with the isotropic phase. Equation (1) can be understood as the force balance applied to the nematic–isotropic–substrate contact line. When the substrate is rough, the effective surface area increases. Simple thermodynamic arguments show that, under these conditions, the wetting transition should occur for a contact angle which obeys Wenzel’s law [33]

$$cos\theta =rcos{\theta }_{\pi }$$

(2)

where the roughness parameter r is defined as $r=\mathcal{S}/\mathcal{A}$, with $\mathcal{S}$ the true substrate area and $\mathcal{A}$ its projected area. This result is based on the assumption that the wetting transition involves the same interfacial states as the planar case, denoted by dry and complete wet states. However, even for simple fluids, roughness leads to the stabilization of intermediate states where the substrate grooves are partially filled while the substrate is still in contact with the bulk phase, which are denoted by filled states. In this framework, wetting phenomena become more complex, and new transitions such as filling may precede the wetting transition [34,35]. This is also expected to occur for liquid crystals. In addition, the interplay between interfacial configurations (as well as the substrate relief) and the orientational order in the nematic phase generates a plethora of distinct interfacial states, leading to rather complex interfacial phase diagrams [36]. In this context, systematic studies of the wetting for sawtooth [36,37], sinusoidal [38,39] and crenellated substrates [40,41] have been reported within the Landau–de Gennes theory. These studies revealed complex phase diagrams which differ considerably from their simple fluids counterparts. This can be ascribed to the role played by elastic deformations and the presence of topological defects in the free energy of the interfacial states. These studies were, however, restricted to substrate periodicities smaller than $100\xi$, where $\xi$ is the bulk nematic correlation length, owing to computational limitations. Thus, it is desirable to extend the analysis of the wetting phase diagrams to larger values of the substrate period to understand in detail the differences between the phenomenology for simple fluids and in nematic liquid crystals. In this paper, we extend the modified Frank–Oseen model [22] to study wetting phenomena on microstructured substrates. As an example, we apply this model to the study of the wetting phase diagram of crenellated substrates, although the methodology can be readily applied to other substrates.The modified Frank–Oseen model has been successfully applied to characterize the behavior of bulk nematic liquid crystals in contact with microstructured substrates, with results in line with those of the Landau–de Gennes theory [22,23]. This approach will bridge the gap between the macroscopic scale and the mesoscopic scale described by the Landau–de Gennes theory, shedding light on the physical mechanisms that drive wetting by nematic liquid crystals.

2. Theoretical Model and Methods

Wetting of a nematic, at equilibrium with the isotropic liquid, on a crenellated substrate with homeotropic anchoring is considered within the modified Frank–Oseen model [21,22,23]. In this model, the free energy of an interfacial configuration of the nematogen in contact with the substrate is given by three contributions. First, the surface contribution associated to the different interfaces. There are three distinct interfaces: substrate–nematic, substrate–isotropic and nematic–isotropic. We assume that the substrate anchoring is homeotropic for both nematic and isotropic phases, i.e., nematogen molecules orient preferentially perpendicular to the substrate when close to it. On the other hand, random planar anchoring at the nematic–isotropic interface is considered, that is, molecules are oriented parallel to the interface but there is no privileged orientation in the interfacial plane. We denote by ${\sigma }_{sn}$, ${\sigma }_{si}$ and ${\sigma }_{ni}$ the surface tension associated to the substrate–nematic, substrate–isotropic and nematic–isotropic interface, respectively, with the anchoring conditions mentioned above. Thus, the surface contribution ${\mathcal{F}}_s$ can be written as

$${\mathcal{F}}_s=\sum _{\alpha }\sum _{\beta }{\sigma }_{\alpha \beta }{\mathcal{S}}_{\alpha \beta },$$

(3)

where $\alpha$ and $\beta$ stand for the phases (isotropic, nematic and substrate) and ${\mathcal{S}}_{\alpha \beta }$ is the total interfacial area between phases $\alpha$ and $\beta$. The second contribution is associated to the elastic distortions of the director field in the nematic phase. For this purpose, we suppose that anchoring is strong, i.e., the director field is fixed at the substrate and at the interface. This condition is valid if the relevant length scales at the surface and at the interface are much larger than the extrapolation length [42]. Under these conditions, the elastic contribution ${\mathcal{F}}_e$ is given by the Frank–Oseen model [43,44]

$${\mathcal{F}}_e=\frac{1}{2}{\int }_{\mathcal{V}}d\mathbf{r}\left[K_1{(\nabla ·\mathbf{n})}^2+K_2{(\mathbf{n}·\nabla \times \mathbf{n})}^2+K_3{(\mathbf{n}\times \nabla \times \mathbf{n})}^2+K_{24}\nabla ·[(\mathbf{n}·\nabla )\mathbf{n}-\mathbf{n}(\nabla ·\mathbf{n})]\right],$$

(4)

where $\mathcal{V}$ is the volume occupied by the nematic; $K_1$, $K_2$ and $K_3$ are the splay, twist and bend bulk elastic constants, respectively; and $K_{24}$ is the saddle-splay elastic constant. Finally, if disclinations and/or director field singularities associated to cusps in the substrate topography appear in the nematic texture, a third contribution ${\mathcal{F}}_d$ associated to the nematic order distortions in the defect or singularity cores must be included. Thus, the total free energy $\mathcal{F}$ can be written as

$$\mathcal{F}={\mathcal{F}}_s+{\mathcal{F}}_e+{\mathcal{F}}_d.$$

(5)

We consider a crenellated substrate with grooves of depth and width h and $l_2$, respectively, separated horizontally by a distance $l_1$ (see Figure 1), so that the period of the substrate relief is $\lambda =l_1+l_2$. The substrate is translationally invariant along the z axis. The substrate promotes the nematic phase (with homeotropic anchoring, as previously stated) and is in contact with a bulk isotropic phase. Under appropriate conditions, a wetting nematic layer is formed between the substrate and the isotropic bulk phase. In general, the profile of the nematic–isotropic interface is unknown and should be obtained by the minimization of Equation (5). However, in what follows, we assume that it is planar and parallel to the $xz$ plane. This approximation is valid for wide grooves, since the Laplace equation dictates that at nematic–isotropic coexistence the interfacial curvature must vanish. Within this approximation, the interfacial configuration is determined by the nematic layer thickness d, as shown in Figure 1. Furthermore, we suppose that the director field in the nematic phase is in the $xy$ plane and, consequently, only splay and bend deformations are allowed. Under these simplifying assumptions, the director field $\mathbf{n}$ can be parameterized as $\mathbf{n}=(-sin\theta (x,y),cos\theta (x,y),0)$, and Equation (4) can be recast as [17,23]

$${\mathcal{F}}_e=\frac{K_1}{2}{\int }_{\mathcal{V}}\left({|\nabla \theta |}^2+\left(\frac{K_3-K_1}{K_1}\right){(\mathbf{n}·\nabla \theta )}^2\right)d\mathbf{r}.$$

(6)

Our goal is to obtain the wetting phase diagram of the Landau–de Gennes theory in the limit of wide grooves or large-scale surface relief. In this sense, the model outlined above can be understood as an approximation to the Landau–de Gennes theory in this limit [21,22,23]. In particular, and in order to make contact with previous results [40], we consider the following Landau–de Gennes free energy $F_{LdG}={\int }_{\mathcal{V}}d\mathbf{r}\left({\mathcal{F}}_b^{LdG}\left(\mathbf{Q}\right)+{\mathcal{F}}_e^{LdG}\left(\partial \mathbf{Q}\right)\right)+{\int }_{\mathcal{S}}{\mathcal{F}}_s^{LdG}\left(\mathbf{Q}\right)$, where the bulk and elastic free energy densities are, respectively,

$$\begin{array}{ccc}\hfill {\mathcal{F}}_b^{LdG}& =& a_o\left(T-T^{*}\right)\mathrm{Tr}{\mathbf{Q}}^2-b\mathrm{Tr}{\mathbf{Q}}^3+c{\left(\mathrm{Tr}{\mathbf{Q}}^2\right)}^2\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill {\mathcal{F}}_e^{LdG}& =& \frac{L_1}{2}{\partial }_{\gamma }{Q}_{\alpha \beta }{\partial }_{\gamma }{Q}_{\beta \alpha }+\frac{L_2}{2}{\partial }_{\gamma }{Q}_{\alpha \gamma }{\partial }_{\delta }{Q}_{\delta \alpha }.\hfill \end{array}$$

(8)

Here, $\mathbf{Q}$ is the traceless symmetric nematic order tensor with matrix elements $Q_{\alpha \beta }$ [42]; $\mathrm{Tr}$ denotes the trace operation; T is the temperature; $a_o$, b, $T^{*}$, $L_1$ and $L_2$ are phenomenological constants; ${\partial }_{\alpha }\equiv \partial /\partial x_{\alpha }$ is the partial derivative with respect to the Cartesian coordinate $x_{\alpha }$; and Einstein summation convention in Equation (8) is used. The bulk term ${\mathcal{F}}_b^{LdG}$, which accounts for the contribution to the free energy of the local molecular alignment, determines the bulk nematic order parameter: $S=0$ (isotropic phase) if $\tau =24a_o(T-T^{*})c/b^2>1$, and $S=\left(b/8c\right)\left(1+\sqrt{1-8\tau /9}\right)$ (nematic phase) if $\tau <1$. The elastic term ${\mathcal{F}}_e^{LdG}$ penalizes distortions of the orientational field, with two elastic constants $L_1$ and $L_2$ related to the Frank–Oseen elastic constants: $K_1=K_3=9S^2{L}_1\left(2+L_2/L_1\right)/4$ and $K_2=9S^2{L}_1/2$. The correlation length is defined as $\xi =\sqrt{8c(3L_1+2L_2)/b^2}$. In addition, we consider the surface free energy density used in Refs. [21,22,23,36,37,38,40]

$${\mathcal{F}}_s^{LdG}=-w\mathrm{Tr}\mathbf{Q}·{\mathbf{Q}}_s,$$

(9)

where w is a parameter related to the anchoring strength [22] and ${\mathbf{Q}}_s$ is the reference tensor order parameter on the substrate with Cartesian components ${\left(Q_s\right)}_{ij}=(3{\nu }_i{\nu }_j-{\delta }_{ij})/2$, with ${\nu }_i$ the Cartesian components of the unit vector normal to the substrate $\mathit{\nu }$. In this paper, we use units where $b=8/3$, $c=4/9$ and $\xi =1$, and thus the nematic order parameter S is measured relative to its value at coexistence with the isotropic liquid at ($\tau =1$) [21]. We fix the temperature at $\tau =1$ and as in previous works choose $\kappa =L_2/L_1=2$. If the relevant length scales of the substrate are large enough, inhomogeneities in the nematic order parameter S are restricted to surfaces, interfaces and defect cores. For the remaining nematic domain where S takes the bulk value the Landau–de Gennes free energy reduces to the Frank–Oseen elastic model [21]. In addition, the relevant surface tensions can be obtained analytically within the Landau–de Gennes formalism. With these parameters, the nematic–isotropic surface tension is ${\sigma }_{ni}\approx 0.178$ [37], the substrate–nematic surface tension is [21,22]

$${\sigma }_{sn}=\frac{\sqrt{2}(2S^n\left(0\right)+1){(S^n\left(0\right)-1)}^2}{6}-w{S}^n\left(0\right),$$

(10)

where $S^n\left(0\right)=(1+\sqrt{1+2\sqrt{2}w})/2$, and likewise the substrate–isotropic surface tension is

$${\sigma }_{si}=\frac{\sqrt{2}(3-2S^i\left(0\right)){\left(S^i\left(0\right)\right)}^2}{6}-w{S}^i\left(0\right),$$

(11)

where $S^i\left(0\right)=(1-\sqrt{1-2\sqrt{2}w})/2$. The latter expression is valid for $w\lesssim 0.24$ [26], since at larger values of the anchoring strength the minimum free energy configuration corresponds to a microscopically thick layer of uniform nematic oriented homeotropically. Under these conditions, ${\sigma }_{si}={\sigma }_{sn}+{\sigma }_{ni}^{\perp }$, where ${\sigma }_{ni}^{\perp }=\sqrt{2}/6$ is the surface tension associated to the interface between the isotropic liquid and the nematic phase oriented homeotropically far from it [37]. The width of this nematic layer must be smaller than $K{\pi }^2/8({\sigma }_{ni}^{\perp }-{\sigma }_{ni})\approx 55$, which is the critical width beyond which the cost of the elastic deformation is lower than the anchoring mismatch at the nematic–isotropic interface [27].

The elastic contribution, ${\mathcal{F}}_e$, is calculated using Equation (6) with $K_1=K_3\equiv K=18/7$ and $\kappa =2$ [21]. Finally, for the evaluation of ${\mathcal{F}}_d$, we proceed to a full minimization of the Landau–de Gennes free energy $F_{LdG}$ with appropriate geometries and boundary conditions. Details of this procedure are given in Appendix A. In general, ${\mathcal{F}}_d=f_d\left(w\right)L_z$, where $f_d$ is a function which depends on the anchoring strength w and the type of disclinations and singularities present in the nematic texture, but not on their position or on the director distortions away from the disclination core or the substrate cusp. Finally $L_z$ is the length along the z axis of the substrate.

To obtain the free energy of an interfacial configuration with a nematic layer of thickness d at a given anchoring strength w, we start by placing the required nematic director singularities and disclinations in the texture to satisfy the boundary conditions for $\theta$. Note that multiple configurations are compatible with the same physical boundary conditions, due to the top-bottom symmetry of the nematic [23]. Once this is done, both ${\mathcal{F}}_s$ and ${\mathcal{F}}_d$ are given. Then, we evaluate ${\mathcal{F}}_e$ in the mean-field approximation by minimizing Equation (6) for $K_1=K_3$. The field $\theta$ corresponding to the minimum of that Equation is a solution of the Laplace equation

$${\nabla }^2\theta =0$$

(12)

subject to the corresponding boundary conditions on $\theta$: $\theta =0$ or $\pi$ on horizontal sections of the substrate; and $\theta =\pm \pi /2$ on vertical sections of the substrate and nematic–isotropic interface. This degeneracy of the boundary values of $\theta$ results from the nematic top-bottom symmetry. By periodicity in the x direction and translational invariance along the z axis, the problem is restricted to a 2D domain associated to one period of the substrate. Substitution of $\theta$ into Equation (6) leads to the value of ${\mathcal{F}}_e$. In this study, we obtained numerically both $\theta (x,y)$ and ${\mathcal{F}}_e$ by the boundary element method proposed in Ref. [23]. Using the divergence theorem and Green’s second identity, ${\mathcal{F}}_e$ can be recast as

$${\mathcal{F}}_e=\frac{K}{2}{\int }_{\mathcal{V}}{|\nabla \theta |}^{2}d\mathbf{r}=\frac{K{L}_z}{2}\oint \theta (\nu ·\nabla \theta )d\mathbf{s},$$

(13)

where the second integral is over the boundary and $\mathit{\nu }$ is the outward normal to the boundary at $\mathbf{s}$. To obtain the normal derivative of $\theta$ on the boundary, we split $\mathit{\nu }·\nabla \theta =\mathit{\nu }·\nabla {\theta }_s+\mathit{\nu }·\nabla {\theta }_{ns}$, where the singular term ${\theta }_s$ is associated to director singularities of winding numbers $I_i$ located at positions $(x_i,y_i)$

$${\theta }_s=\sum _i{I}_i\left[arctan\left(\frac{tanh\frac{q}{2}(y-y_i)}{tan\frac{q}{2}(x-x_i)}\right)-arctan\left(\frac{1}{tan\frac{q}{2}(x-x_i)}\right)\right],$$

(14)

with $q=2\pi /\lambda$, and the non-singular term ${\theta }_{ns}$ satisfies the integral equation

$${\int }_{\mathcal{L}}d\mathbf{s}(\mathit{\nu }·\nabla {\theta }_{ns})G(\mathbf{s},{\mathbf{s}}_0)=\frac{{\theta }_{ns}\left({\mathbf{s}}_0\right)}{2}+{\int }_{\mathcal{L}}d\mathbf{s}{\theta }_{ns}(\mathit{\nu }·{\nabla }_{\mathbf{s}}G(\mathbf{s},{\mathbf{s}}_0)).$$

(15)

Here, $\mathcal{L}$ is the union of the substrate and nematic–isotropic interfacial profile in the $x-y$ plane and $G(\mathbf{r},{\mathbf{r}}_0)$ is the fundamental solution of the Laplace equation in the infinite strip $-\lambda /2\le x\le \lambda /2$ and $-\infty <y<\infty$ with periodic boundary conditions on x

$$G(\mathbf{r},{\mathbf{r}}_0)=-\frac{1}{4\pi }ln(coshq(y-y_0)-cosq(y-y_0)),$$

(16)

where $\mathbf{r}=(x,y)$ and ${\mathbf{r}}_0=(x_0,y_0)$. To solve Equation (15) and evaluate ${\mathcal{F}}_e$ from Equation (13), we discretize the boundary $\mathcal{L}$ in a number of straight segments, typically of order of 100. Then, Equation (15) reduces to a set of linear equations where the unknowns are the values of $\mathit{\nu }·\nabla {\theta }_{ns}$, which are supposed to be constant on each segment. In some cases, however, ${\mathcal{F}}_e$ may be obtained analytically using conformal mapping techniques [22,23,45,46,47,48].

The interfacial phase diagram for a substrate geometry is obtained by evaluation of the free energy branches as a function of w for the relevant interfacial configurations, where the equilibrium state corresponds to the configuration with the lowest free energy. The phase boundaries where first-order phase transitions occur are determined by the crossing of the two free-energy branches with the lowest energies.

3. Results

First, we identify the relevant interfacial configurations. We note that these configurations can be classified in terms of the nematic layer thickness d. If $d=0$, i.e., there is no nematic layer, we denote the state by dry (D). For $0<d\le h$, the substrates grooves are partially filled by nematic, thus we denote these states by filled (F). Finally, for $d>h$, a thick nematic layer forms between the substrate and the isotropic phase; we denote these states by wet (W). However, for a given d, there is not only one F or W state, but different states with distinct textures of the nematic phase. Figure 2 illustrates the most relevant ones for this paper, as we checked that other interfacial states have higher free energies than at least one of these. We identify two filled states: a symmetric $F_s$ and an asymmetric $F_a$ state. For the latter, there are two distinct textures, the mirror image of each other with the same free energy, which are regarded as the same interfacial state. The $F_s$ state is characterized by two singularities of topological charge $+1$ along the bottom corners of the substrate, and a disclination line of topological charge $+1$ located at the midpoint of the nematic–isotropic interface. On the other hand, the $F_a$ state is characterized by singularities of opposite charge $+1$ and $-1$ located at the bottom corners. Similarly, there are two wetting states: a symmetric $W_s$ and an asymmetric $W_a$ state (again, there are two $W_a$ states with the same free energy with nematic textures which are related by a mirror symmetry). The $W_s$ state, in addition to the singularities of the $F_s$ state, has two additional singularities of topological charge $-1/3$ on the top corners of the substrate. Finally, the $W_a$ state has singularities of topological charges $+1$, $-1$, $+1/3$ and $-1/3$ arranged as shown in Figure 2d. We note that these states are analogous to those obtained in Reference [40]: $W_a$ and $W_s$ correspond to the wetting states of the Landau–de Gennes theory, $F_a$ corresponds to the unbent filled state $F_u$ in that reference, and $F_s$ resembles the bent filled state $F_b$ of Reference [40]. We come back to this point below.

For a given substrate geometry and anchoring strength w, we have to obtain the value of d that minimizes Equation (5). As ${\mathcal{F}}_d$ only depends on w and the set of nematic director singularities present in the texture, the value of d for a given interfacial state is determined by the surface and elastic contributions to the filled states. Furthermore, only the elastic contribution is relevant to obtain the value of d for the wet states. However, we found that in all cases the minimum free energy configuration for filled states (either $F_s$ or $F_a$) corresponds to $d=h$, and for wetting states (either symmetric or asymmetric) to the $d\to \infty$ limit. These observations can be rationalized by the fact that ${\sigma }_{sn}<{\sigma }_{si}$ and, consequently, the surface term favors large values of d in the filled states. On the other hand, the higher the confinement of the nematic is, the larger the elastic distortions are and, consequently, the elastic free energy increases with the confinement. As an example, Figure 3 shows the decay of the elastic contribution to the free energy per substrate period and unit length along the z axis as a function of d for the asymmetric states ($F_a$ if $d<h$, $W_a$ otherwise). It is also clear in this figure that the numerical results for the elastic free energy of the $F_a$ state are in excellent agreement with the analytical expression Equation (A8) (with h replaced by d), and thus we used the latter for the calculations in this study. On the other hand, the limiting elastic free energy for the $W_a$ state at large d is given by the elastic free energy of a bulk nematic with the corresponding asymmetric texture in contact with the substrate [23], even when the angular field away from the substrate does not match the anchoring condition at the nematic–isotropic interface. This is due to the fact that the angular profile $\theta$ at large d and well above the substrate is linear in y as in a slit pore with an effective thickness $d-d_0$, with $d_0$ a constant. Thus, the elastic free energy is inversely proportional to the effective thickness and, consequently, vanishes as $d\to \infty$.

We now proceed to calculate the interfacial phase diagram. To make contact with the previous Landau–de Gennes results [40], we consider substrates with $l_1=l_2$, $l_1=2l_2$ and $l_2=2l_1$. We start with large values of the substrate period $\lambda$, where the elastic and singularity cores contributions to the free energy are expected to be negligible with respect to ${\mathcal{F}}_s$. Under this assumption, we find that the D state is the most stable at small w, the F state is most stable at intermediate w and the W state is the most stable state at large w, irrespective of the substrate geometry. The phase boundary between the D and F states can be obtained by equating the surface free energies of both states, leading to the condition

$$\frac{{\sigma }_{si}-{\sigma }_{sn}}{{\sigma }_{ni}}\approx w=\frac{1}{1+\frac{2h}{l_2}}$$

(17)

which corresponds to the prediction of Wenzel’s law Equation (2) for $\theta =0$. This approximation is valid for small w [37]. By contrast, the wetting transition between the F and the W states occurs exactly at the same value of w as for the planar case $w_{\pi }\approx 0.178$. We note that the phase boundaries depend on w and $h/l_2$, but not on $l_1/l_2$. Thus, we represent the phase diagrams in the $w-h/l_2$ representation.

This large-scale approximation does not distinguish between the F or W states with different nematic textures. However, as shown in Reference [23], the free energy difference between the $W_s$ and $W_a$ is due exclusively to ${\mathcal{F}}_d$. In addition, for the intermediate values of w that are relevant, $W_s$ is the most stable state at small h, while $W_a$ is the most stable state at large h. The phase boundary between the $W_s$ and $W_a$ states depends on w, $h/l_2$ and $l_1/l_2$, and it is independent of the substrate period $\lambda$. Regarding the F states, the next-to-leading order contribution to the free energy is the logarithmic term of $l_2$ which arises from the director singularities. Equations (A8) and (A11) in Appendix B show that, for large $l_2$, the logarithmic term of the $F_s$ state is twice that of the $F_a$ state. Thus, at large $\lambda$, only the $F_a$ states are stable.

Figure 4 depicts the interfacial phase diagram for $\lambda ={10}^5$. First, we note that it is very similar to the phase diagram of the infinite period substrate, $\lambda \to \infty$, considered previously. In addition, the phase boundaries are quite insensitive to the value of $l_1/l_2$, with the exception of the $W_s-W_a$ boundary, which shifts to the left as $l_1/l_2$ decreases. The most distinctive features with respect to the $\lambda \to \infty$ case, are the emergence of a $D-W_s$ wetting transition at small $h/l_2$ and the increase of w at the $F_a-W_a$ wetting transition above $w_{\pi }$, although it seems to saturate when $h/l_2>0.2$. The existence of an asymptotic limit for large $h/l_2$ is not unexpected, and may be rationalized by the fact that the nematic texture deep in the groove becomes independent of h and resembles that of a bulk nematic in a rectangular well [23]. Thus, the elastic and defect free energy contributions of the distortions and singularities of this region of the groove will be the same in the $F_a$ and $W_a$ states and, consequently, a change in h will not affect the wetting transition. If $\lambda$ is decreased to $\lambda ={10}^4$, the deviations with respect to the $\lambda \to \infty$ phase diagram increase (see Figure 5). We note that the relative stability of the D state with respect to the $F_a$ state is increased (the larger the ratio $l_1/l_2$ is, the more stable the D state becomes). On the other hand, the $F_a-W_a$ phase boundary moves to higher values of w, with a shift that increases with decreasing $l_1/l_2$. However, the topology of the phase diagram is unchanged.

If we decrease the value of $\lambda$ further, dramatic changes are observed in the phase diagram. As an example, Figure 6 shows the interfacial phase diagram for $\lambda ={10}^3$. As a first observation the shift of the $D-F_a$ phase boundary to larger values of $h/l_2$ leads to the disappearance of the coexistence between the $F_a$ and $W_s$ states and the emergence of a $D-W_a$ phase boundary. The most striking feature, however, is observed at the $F_a-W_a$ wetting transition. At $l_1/l_2=1$ and 2, the $F_a-W_a$ phase boundary shifts towards much larger values of w (larger for $l_1/l_2=1$ than for $l_1/l_2=2$), reaching the asymptotic value at higher values of $h/l_2$ than for the higher values of $\lambda$. Finally, at $l_1/l_2=0.5$, we see a major change in the topology of the phase diagram: the $W_a$ state is suppressed at large $h/l_2$, being replaced by $F_a$ states. Thus, the $F_a-W_a$ phase boundary becomes almost vertical. For $w>0.24$ the isotropic-substrate configuration changes from a microscopic thin paranematic layer to a configuration in which a microscopically thick layer of homeotropically-oriented nematic phase intrudes between the substrate and the bulk isotropic liquid phase. This is similar to the $F^{+}$ states in Reference [40], where a nematic droplet phase nucleates on the upper surface of the substrate. By analogy, we denote this state by $F_a^{+}$.

The suppression of the wetting states at large $h/l_2$ was also reported for the Landau–de Gennes theory in Reference [40]. For small $\lambda$, the elastic and core contributions to the free energy, which favor the $F_a$ state, are lower than the difference between the top substrate surface contributions between $W_a$ and $F_a$. This also explains why this is first observed at small values of $l_1/l_2$.

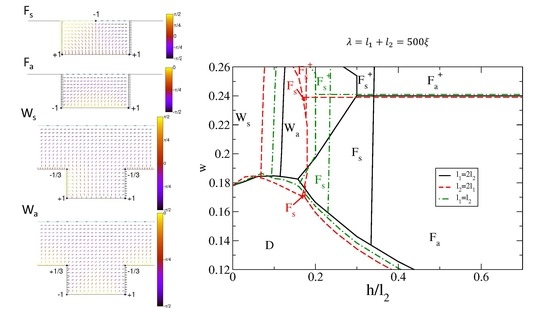
As $\lambda$ is further reduced, the suppression of the wetting states at large $h/l_2$ is extended to larger values of $l_1/l_2$. Furthermore, new features appear in the phase diagram. Figure 7 illustrates the interfacial phase diagram for $\lambda =500$. At intermediate values of $h/l_2$, the $F_a$ state is suppressed in favor of the $F_s$ state, indicating that the difference between core contributions to the free energy in the filled states, which favors the $F_s$ state, overcomes the difference of the logarithmic contributions in $l_2$ which favors the $F_a$ state. As for the asymmetric filled states at large $h/l_2$, we can distinguish between $F_s$ and $F_s^{+}$ depending on w, being smaller or larger than $0.24$, the value above which a thick layer of nematic is formed on the top substrate surface. However, at this length scale, the nematic texture differs from that depicted in Figure 2a. As described in Appendix A, the isotropic–nematic interface exhibits a significant distortion near the disclination core. Thus, the microscopic length scale associated to the interfacial deformation, which is of order 10, becomes comparable to h (note that $F_s$ appears for h in the range 40–60). As a result, the true interfacial configuration of the symmetric filled states resembles that of the $F_b$ and $F_b^{+}$ states reported in Reference [40]. As a conclusion, the topology of the phase diagram for $\lambda =500$ starts to exhibit features similar to those of the small period substrates reported for the Landau–de Gennes theory.

4. Discussion and Conclusions

We studied the interfacial phase diagram of a bulk isotropic liquid in contact with a crenellated substrate which favors the nematic with homeotropic anchoring. This study was based on the modified Frank–Oseen formalism, which separates surface, elastic and singularity cores contributions. We selected parameters in line with those of the Landau–de Gennes theory reported in Reference [40] to facilitate the comparison between the two approaches. First, we identified the relevant interfacial states and their features. We found that, in addition to the dry D state, there are two filled states $F_s$ and $F_a$ and two wet states $W_s$ and $W_a$ characterized by different nematic textures. The different contributions to the free energy were evaluated either numerically or analytically. We calculated the interfacial phase diagram in terms of the anchoring strength w and the grooves depth-to-width aspect ratio $h/l_2$ for values of the periodicity $\lambda$ ranging from 500 to ${10}^5$ bulk correlation lengths. For large values of $\lambda ={10}^4$ and ${10}^5$, we obtained a phase diagram with a topology similar to that of simple fluids. In general, wetting of a substrate with a given geometry occurs in two steps as w increases: first from a dry to an asymmetric filled state, and then to a completely wet state. A direct transition from dry to a completely wet state is observed only for very shallow substrates. Furthermore, the rougher the substrate is, the lower the value of w at the $D-F$ transition. Finally, the completely wet state exhibits symmetric textures for shallow substrates, and asymmetric ones otherwise.

As $\lambda$ decreases to ${10}^3$, we observed significant changes in the topology of the phase diagram, in particular the suppression of the completely wet state $W_a$ and its substitution by a filled $F_a$ state for rough substrates and large w. This result is at odds with the expectation, based on Wenzel’s law [33], that the roughness of hydrophilic substrates favors wetting. This feature is more prominent as $\lambda$ is decreased to 500 and, in addition, the $F_s$ state is stabilized for intermediate values of $h/l_2$. This $\lambda$ is one order of magnitude larger than the largest $\lambda$ considered in the Landau–de Gennes study of Reference [40], but we observed the same qualitative features of the phase diagrams reported there.

We may be tempted to push the calculations reported here to lower values of $\lambda$, but it is clear that $\lambda =500$ is already at limit of validity of the modified Frank–Oseen approach, which is based on the separation of length scales, which determine distinct additive contributions to the free energy [22]. While surface contributions are determined by the order parameter profiles, which vary in the range of a few correlation lengths around the substrate or at the interface, the elastic contribution assumes that the nematic tensor is bulk-like in most of the nematic region. Finally, the presence of triple isotropic–nematic–substrate or disclination lines at the isotropic–nematic interface introduces new microscopic length scales of the order of tens of correlation lengths in filled F states, as shown in Appendix A. Thus, our approximation will breakdown for smaller values of $\lambda$ (especially in the regions involving F states) and our predictions will not be reliable.

Finally, it would be interesting to check our results by experiment. The nematic correlation length of 5CB at the nematic–isotropic transition is around 17 nm [49]. Thus, the values of $\lambda$ considered here correspond to values in the range of 10–1000 $\mathsf{\mu }$m, which are accessible experimentally [14].