A Guideline for Successful Calibration and Uncertainty Analysis for Soil and Water Assessment: A Review of Papers from the 2016 International SWAT Conference
Abstract
:1. Introduction
2. Outstanding Calibration and Uncertainty Analysis Issues
2.1. Inadequate Definition of the Base Model
2.2. Parameterization
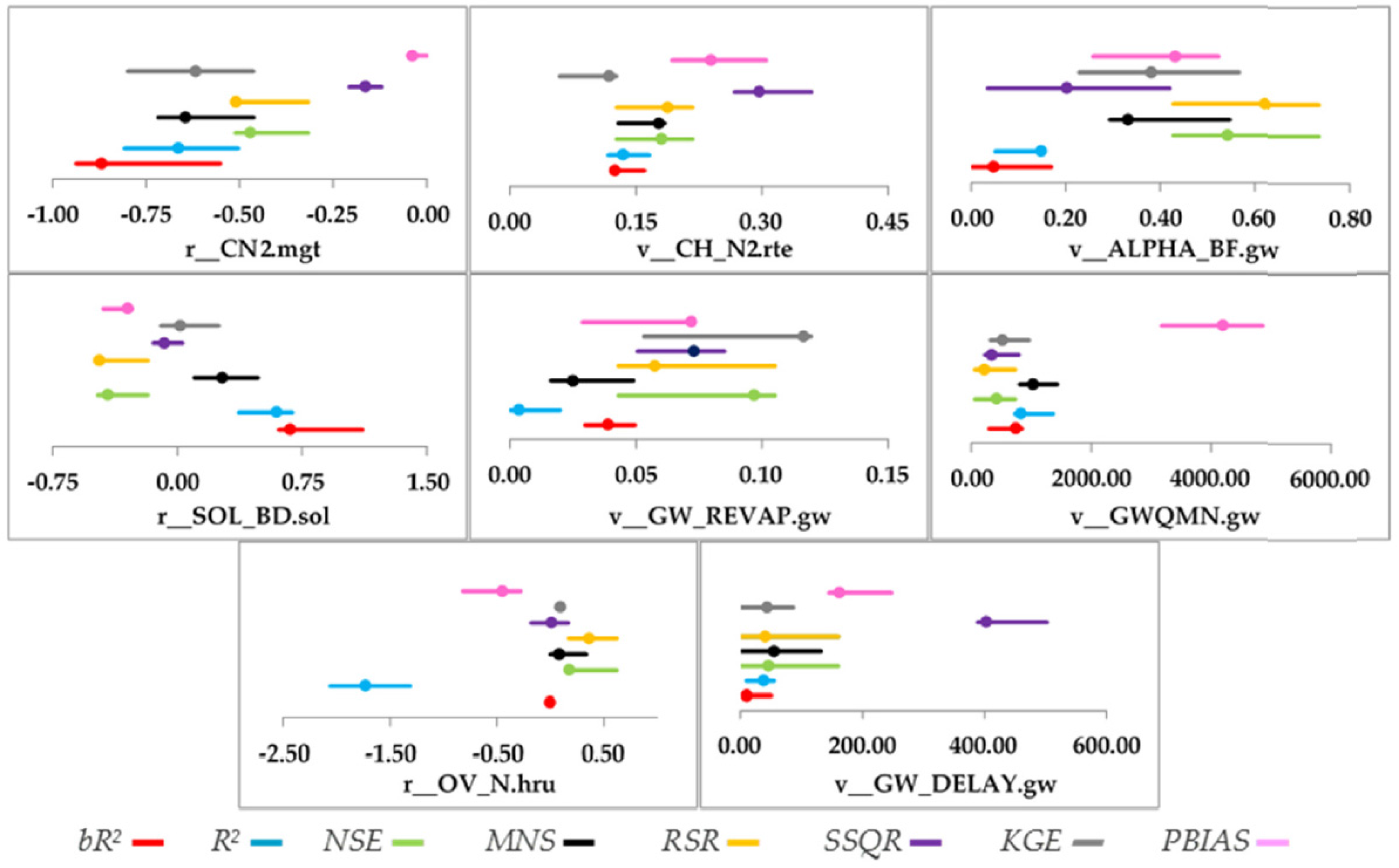
2.3. Use of Different Objective Functions
2.4. Use of Different Optimization Algorithms
2.5. Calibration Uncertainty or Model Non-Uniqueness
2.6. Calibrated Model Conditionality
2.7. Time Constraint
2.8. Experience of the Modeler
3. A Protocol for Calibration of Soil and Water Assessment Tools (SWAT) Models
3.1. Pre-Calibration Input Data and Model Structure Improvement
3.2. Identify the Parameters to Optimize
3.3. Identify Other Sensitive Parameters
3.4. Running the Model
3.5. Perform Post-Processing
3.6. Modifying the Suggested New Parameters
Author Contributions
Conflicts of Interest
Appendix A
| Important Processes | Location | Country | Calibration | Water Quality | Crop | Author | |
|---|---|---|---|---|---|---|---|
| 1 | Thermal stress | Rhode Island | USA | SWAT-CUP | Temp. | Chambers et al. | |
| 2 | Fish Habitat | Rhode Island | USA | SWAT-CUP | Temp. | Chambers et al. | |
| 3 | Leaching | North China Plain | China | NO3 | Maize | Chen et al. | |
| 4 | Water resources | Istanbul | Turkey | SWAT-CUP | Cuceloglu et al. | ||
| 5 | TN loss | Yangtze River | China | TN | Ding et al. | ||
| 6 | Permafrost | Central Siberia | Russia | SWAT-CUP | Fabre et al. | ||
| 7 | Climate change | Continental US | USA | WT, DO, TN, TP | Fant et al. | ||
| 8 | Flooding | Alberta | Canada | SWAT-CUP | Gharib et al. | ||
| 9 | Gridded rainfall | Garonne River watershed | France | SWAT-CUP | Grusson et al. | ||
| 10 | Uncertainty issues | Karkheh River Basin | Iran | SWAT-CUP | Houshmand et al. | ||
| 11 | Drought, Climate change | Karkheh River Basin | Iran | SWAT-CUP | Kamali et al. | ||
| 12 | Uncertainty | Karkheh River Basin | Iran | SWAT-CUP | Kamali et al. | ||
| 13 | Flooding | Paldang Dam | Korea | manual | Lee et al. | ||
| 14 | Non-point source pollution | Baoding City | China | manual | TN, TP | Li et al. | |
| 15 | Pesticide | Pagsanjan-Lumban Basin, | Philippines | SWAT-CUP | Ligaray et al. | ||
| 16 | Buffer strip | Itumbiara city | Braziil | manual | sediment | Lutz et al. | |
| 17 | Climate change | Upper Narew, Barycz | Poland | SWAT-CUP | Sediment, TN | Marcinkowski et al. | |
| 18 | Non-point source pollution | Hunt River Rhode Island | USA | SWAT-CUP | TN | Paul et al. | |
| 19 | SWAT, GWLF comparison | Tunxi and the Hanjiaying basins | China | SWAT-CUP | Sediment, TN | Qi et al. | |
| 20 | Climate–Land-use Change | Black Sea Basin | Europe | SWAT-CUP | Rouholahnejad et al. | ||
| 21 | Climate change | Segura River Basin | Spain | SWAT-CUP | Senent-Aparicio et al. | ||
| 22 | Optimal design | Clear Creek watershed (TX) | USA | SWAT-CUP | Seo et al. | ||
| 23 | Water quality | Clear Creek watershed (TX) | USA | SWAT-CUP | Seo et al. | ||
| 24 | Gridded rainfall | Kelantan River Basin | Malaysia | SWAT-CUP | Tan et al. | ||
| 25 | Coupling SWAT-MODSIM | Karkheh River Basin | Iran | SWAT-CUP | Wheat, maize | Vaghefi et al. | |
| 26 | Water balance | Loei Province | Thailand | SWAT-CUP | Para-rubber | Wangpimool et al. | |
| 27 | Climate data | USA | USA | White et al. |
References
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment. Part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Klove, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Johnson, A.; van Genuchten, M.T. Estimating uncertain flow and transport parameters using a sequential uncertainty fitting procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
- Dechen, F.; Carmela, S.; Telles, T.S.; Guimaraes, M.D.; de Fatima, M.; De Maria, I.C. Losses and costs associated with water erosion according to soil cover rate. Bragantia 2015, 74, 224–233. [Google Scholar] [CrossRef]
- Gulati, A.; Rai, S.C. Cost estimation of soil erosion and nutrient loss from a watershed of the Chotanagpur Plateau, India. Curr. Sci. 2014, 107, 670–674. [Google Scholar]
- Mcqueen, A.D.; Shulstad, R.N.; Osborn, C.T. Controlling agricultural soil loss in Arkansas north lake Chicot watershed—A cost-analysis. J. Soil Water Conserv. 1982, 37, 182–185. [Google Scholar]
- Kamali, B.; Houshmand Kouchi, D.; Yang, H.; Abbaspour, K.C. Multilevel Drought Hazard Assessment under Climate Change Scenarios in Semi-Arid Regions—A Case Study of the Karkheh River Basin in Iran. Water 2017, 9, 241. [Google Scholar] [CrossRef]
- Pagliero, L.; Bouraoui, F.; Willems, P.; Diels, J. Large-Scale Hydrological Simulations Using the Soil Water Assessment Tool, Protocol Development, and Application in the Danube Basin. J. Environ. Qual. 2014, 4, 145–154. [Google Scholar] [CrossRef]
- Whittaker, G.; Confesor, R.; Di Luzio, M.; Arnold, J.G. Detection of overparameterization and overfitting in an automatic calibration of swat. Trans. ASABE 2010, 53, 1487–1499. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Houshmand Kouchi, D.; Esmaili, K.; Faridhosseini, A.; Sanaeinejad, S.H.; Khalili, D.; Abbaspour, K.C. Sensitivity of Calibrated Parameters and Water Resource Estimates on Different Objective Functions and Optimization Algorithms. Water 2017, 9, 384. [Google Scholar] [CrossRef]
- Yang, J.; Abbaspour, K.C.; Reichert, P.; Yang, H. Comparing uncertainty analysis techniques for a SWAT application to Chaohe Basin in China. J. Hydrol. 2008, 358, 1–23. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Van Griensven, A.; Meixner, T. Methods to quantify and identify the sources of uncertainty for river basin water quality models. Water Sci. Technol. 2006, 53, 51–59. [Google Scholar] [CrossRef] [PubMed]
- Kuczera, G.; Parent, E. Monte Carlo assessment of parameter uncertainty in conceptual catchment models: The Metropolis algorithm. J. Hydrol. 1998, 211, 69–85. [Google Scholar] [CrossRef]
- Marshall, L.; Nott, D.; Sharma, A. A comparative study of Markov chain Monte Carlo methods for conceptual rainfall–runoff modeling. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Yang, J.; Reichert, P.; Abbaspour, K.C.; Yang, H. Hydrological Modelling of the Chaohe Basin in China: Statistical Model Formulation and Bayesian Inference. J. Hydrol. 2007, 340, 167–182. [Google Scholar] [CrossRef]
- Rouholahnejad, E.; Abbaspour, K.C.; Vejdani, M.; Srinivasan, R; Schulin, R.; Lehmann, A. Parallelization framework for calibration of hydrological models. Environ. Model. Softw. 2012, 31, 28–36. [Google Scholar] [CrossRef]
- Ostfeld, A.; Salomons, E.; Ormsbee, L.; Uber, J.; Bros, C.M.; Kalungi, P.; Burd, R.; Zazula-Coetzee, B.; Belrain, T.; Kang, D.; et al. Battle of the Water Calibration Networks. J. Water Resour. Plan. Manag. 2012, 138, 523–532. [Google Scholar] [CrossRef]
- Hollaender, H.M.; Bormann, H.; Blume, T.; Buytaert, W.; Chirico, G.B.; Exbrayat, J.F.; Gustafsson, D.; Hoelzel, H.; Krausse, T.; Kraft, P.; et al. Impact of modellers’ decisions on hydrological a priori predictions. Hydrol. Earth Syst. Sci. 2014, 18, 2065–2085. [Google Scholar] [CrossRef]
- Freni, G.; Mannina, G.; Viviani, G. Uncertainty in urban stormwater quality modelling: The effect of acceptability threshold in the GLUE methodology. Water Res. 2008, 42. [Google Scholar] [CrossRef] [PubMed]
- Whittemore, R. Is the time right for consensus on model calibration guidance? J. Environ. Eng. 2001, 127, 95–96. [Google Scholar] [CrossRef]
- Chambers, B.M.; Pradhanang, S.M.; Gold, A.J. Assessing Thermally Stressful Events in a Rhode Island Coldwater Fish Habitat Using the SWAT Model. Water 2017, 9, 667. [Google Scholar] [CrossRef]
- Chambers, B.M.; Pradhanang, S.M.; Gold, A.J. Simulating Climate Change Induced Thermal Stress in Coldwater Fish Habitat Using SWAT Model. Water 2017, 9, 732. [Google Scholar] [CrossRef]
- Chen, S.; Sun, C.; Wu, W.; Sun, C. Water Leakage and Nitrate Leaching Characteristics in the Winter Wheat–Summer Maize Rotation System in the North China Plain under Different Irrigation and Fertilization Management Practices. Water 2017, 9, 141. [Google Scholar] [CrossRef]
- Cuceloglu, G.; Abbaspour, K.C.; Ozturk, I. Assessing the Water-Resources Potential of Istanbul by Using a Soil and Water Assessment Tool (SWAT) Hydrological Model. Water 2017, 9, 814. [Google Scholar] [CrossRef]
- Ding, X.; Xue, Y.; Lin, M.; Jiang, G. Influence Mechanisms of Rainfall and Terrain Characteristics on Total Nitrogen Losses from Regosol. Water 2017, 9, 167. [Google Scholar] [CrossRef]
- Fabre, C.; Sauvage, S.; Tananaev, N.; Srinivasan, R.; Teisserenc, R.; Miguel Sánchez Pérez, J. Using Modeling Tools to Better Understand Permafrost Hydrology. Water 2017, 9, 418. [Google Scholar] [CrossRef]
- Fant, C.; Srinivasan, R.; Boehlert, B.; Rennels, L.; Chapra, S.C.; Strzepek, K.M.; Corona, J.; Allen, A.; Martinich, J. Climate Change Impacts on US Water Quality Using Two Models: HAWQS and US Basins. Water 2017, 9, 118. [Google Scholar] [CrossRef]
- Gharib, A.; Davies, E.G.R.; Goss, G.G.; Faramarzi, M. Assessment of the Combined Effects of Threshold Selection and Parameter Estimation of Generalized Pareto Distribution with Applications to Flood Frequency Analysis. Water 2017, 9, 692. [Google Scholar] [CrossRef]
- Grusson, Y.; Anctil, F.; Sauvage, S.; Miguel Sánchez Pérez, J. Testing the SWAT Model with GriddedWeather Data of Different Spatial Resolutions. Water 2017, 9, 54. [Google Scholar] [CrossRef]
- Kamali, B.; Abbaspour, K.C.; Yang, H. Assessing the Uncertainty of Multiple Input Datasets in the Prediction of Water Resource Components. Water 2017, 9, 709. [Google Scholar] [CrossRef]
- Lee, J.E.; Heo, J.H.; Lee, J.; Kim, N.W. Assessment of Flood Frequency Alteration by Dam Construction via SWAT Simulation. Water 2017, 9, 264. [Google Scholar] [CrossRef]
- Li, C.; Zheng, X.; Zhao, F.; Wang, X.; Cai, Y.; Zhang, N. Effects of Urban Non-Point Source Pollution from Baoding City on Baiyangdian Lake, China. Water 2017, 9, 249. [Google Scholar] [CrossRef]
- Ligaray, M.; Kim, M.; Baek, S.; Ra, J.S.; Chun, J.A.; Park, Y.; Boithias, L.; Ribolzi, O.; Chon, K.; Cho, K.H. Modeling the Fate and Transport of Malathion in the Pagsanjan-Lumban Basin, Philippines. Water 2017, 9, 451. [Google Scholar] [CrossRef]
- Luz, M.P.; Beevers, L.C.; Cuthbertson, A.J.S.; Medero, G.M.; Dias, V.S.; Nascimento, D.T.F. The Mitigation Potential of Buffer Strips for Reservoir Sediment Yields: The Itumbiara Hydroelectric Power Plant in Brazil. Water 2016, 8, 489. [Google Scholar] [CrossRef]
- Marcinkowski, P.; Piniewski, M.; Kardel, I.; Szcześniak, M.; Benestad, R.; Srinivasan, R.; Ignar, S.; Okruszko, T. Effect of Climate Change on Hydrology, Sediment and Nutrient Losses in Two Lowland Catchments in Poland. Water 2017, 9, 156. [Google Scholar] [CrossRef]
- Paul, S.; Cashman, M.A.; Szura, K.; Pradhanang, S.M. Assessment of Nitrogen Inputs into Hunt River by OnsiteWastewater Treatment Systems via SWAT Simulation. Water 2017, 9, 610. [Google Scholar] [CrossRef]
- Qi, Z.; Kang, G.; Chu, C.; Qiu, Y.; Xu, Z.; Wang, Y. Comparison of SWAT and GWLF Model Simulation Performance in Humid South and Semi-Arid North of China. Water 2017, 9, 567. [Google Scholar] [CrossRef]
- Rouholahnejad, E.; Abbaspour, K.C.; Lehmann, A. Water Resources of the Black Sea Catchment under Future Climate and Landuse Change Projections. Water 2017, 9, 598. [Google Scholar] [CrossRef]
- Senent-Aparicio, J.; Pérez-Sánchez, J.; Carrillo-García, J.; Soto, J. Using SWAT and Fuzzy TOPSIS to Assess the Impact of Climate Change in the Headwaters of the Segura River Basin (SE Spain). Water 2017, 9, 149. [Google Scholar] [CrossRef]
- Seo, M.; Jaber, F.; Srinivasan, R.; Jeong, J. Evaluating the Impact of Low Impact Development (LID) Practices on Water Quantity and Quality under Different Development Designs Using SWAT. Water 2017, 9, 193. [Google Scholar] [CrossRef]
- Seo, M.; Jaber, F.; Srinivasan, R. Evaluating Various Low-Impact Development Scenarios for Optimal Design Criteria Development. Water 2017, 9, 270. [Google Scholar] [CrossRef]
- Tan, M.L.; Gassman, P.W.; Cracknell, A.P. Assessment of Three Long-Term Gridded Climate Products for Hydro-Climatic Simulations in Tropical River Basins. Water 2017, 9, 229. [Google Scholar] [CrossRef]
- Vaghefi, S.A.; Abbaspour, K.C.; Faramarzi, M.; Srinivasan, R.; Arnold, J.G. Modeling Crop Water Productivity Using a Coupled SWAT–MODSIM Model. Water 2017, 9, 157. [Google Scholar] [CrossRef]
- Wangpimoo, W.; Pongput, K.; Tangtham, N.; Prachansri, S.; Gassman, P.W. The Impact of Para Rubber Expansion on Streamflow and OtherWater Balance Components of the Nam Loei River Basin, Thailand. Water 2017, 9, 1. [Google Scholar] [CrossRef]
- White, M.J.; Gambone, M.; Haney, E.; Arnold, J.; Gao, J. Development of a Station Based Climate Database for SWAT and APEX Assessments in the US. Water 2017, 9, 437. [Google Scholar] [CrossRef]
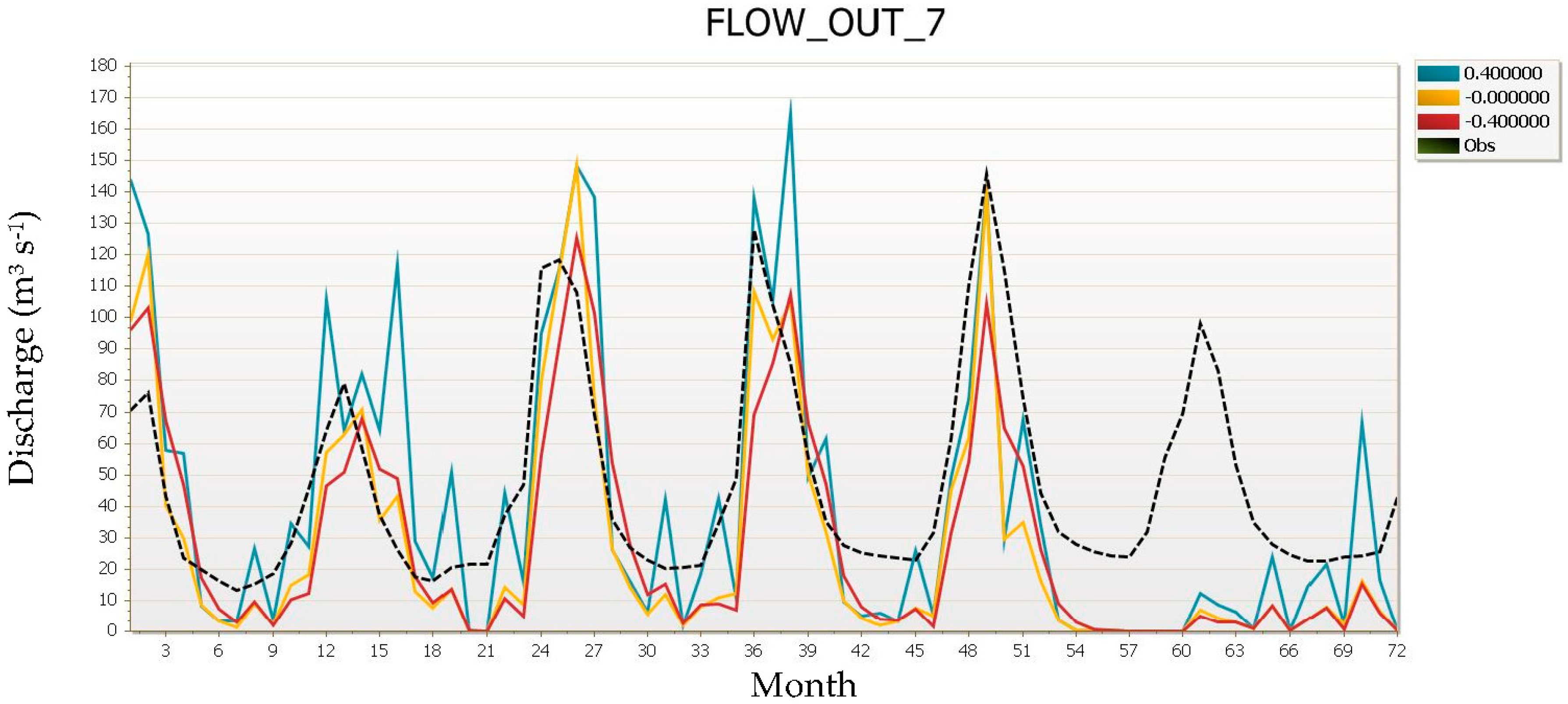
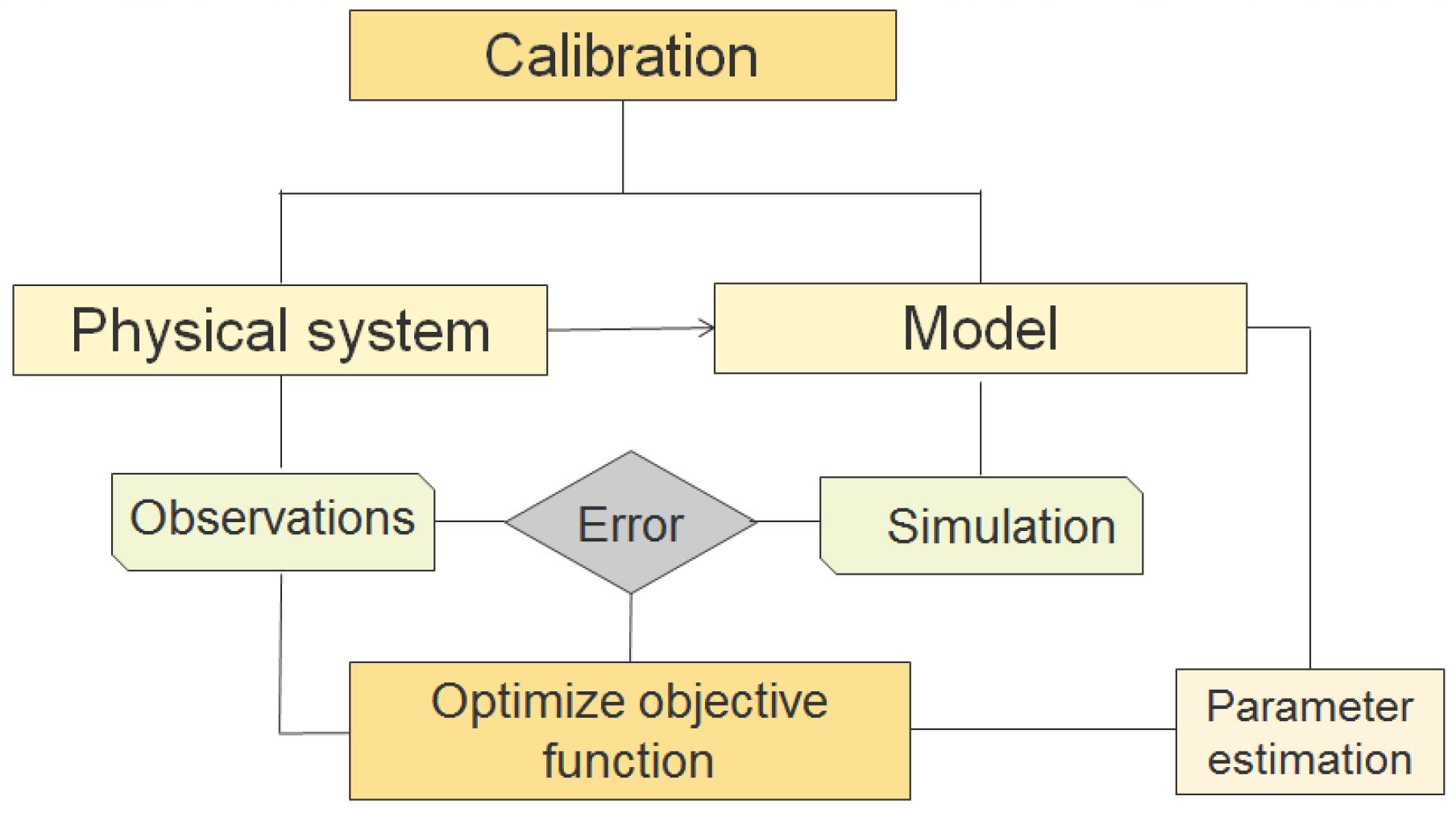
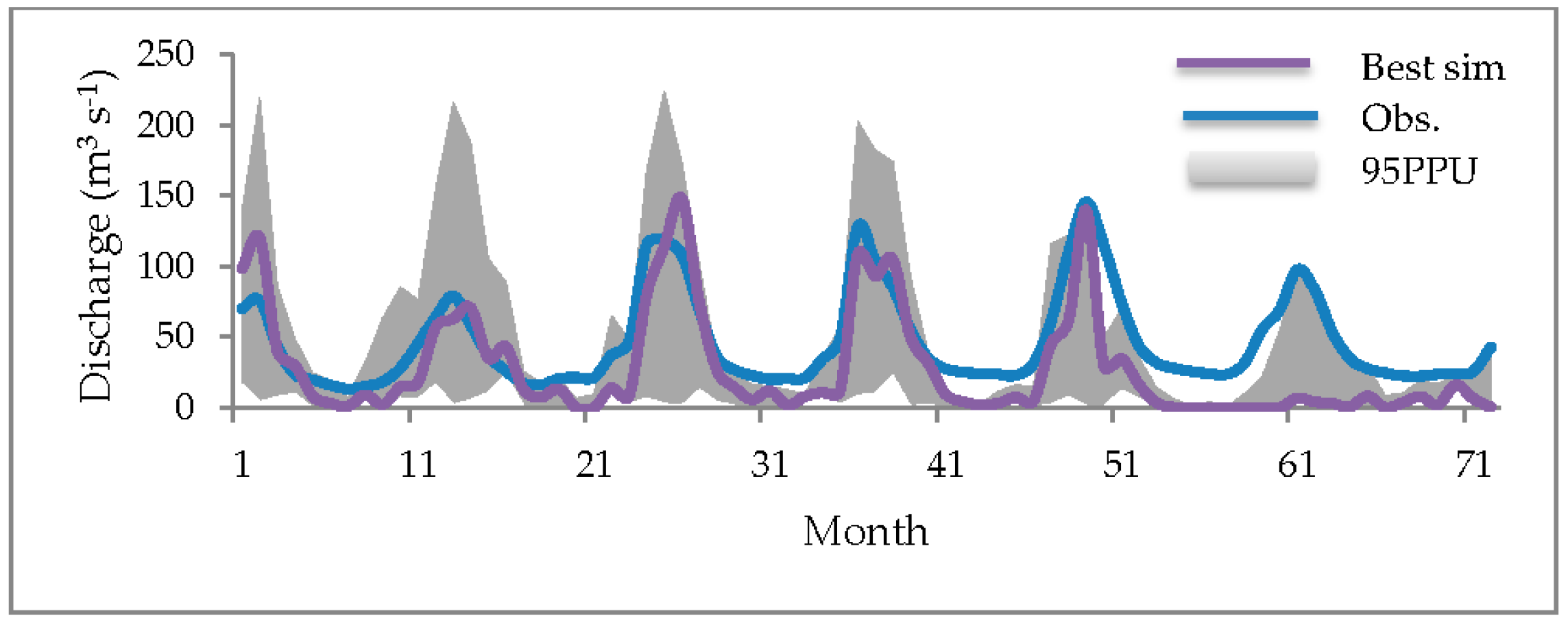
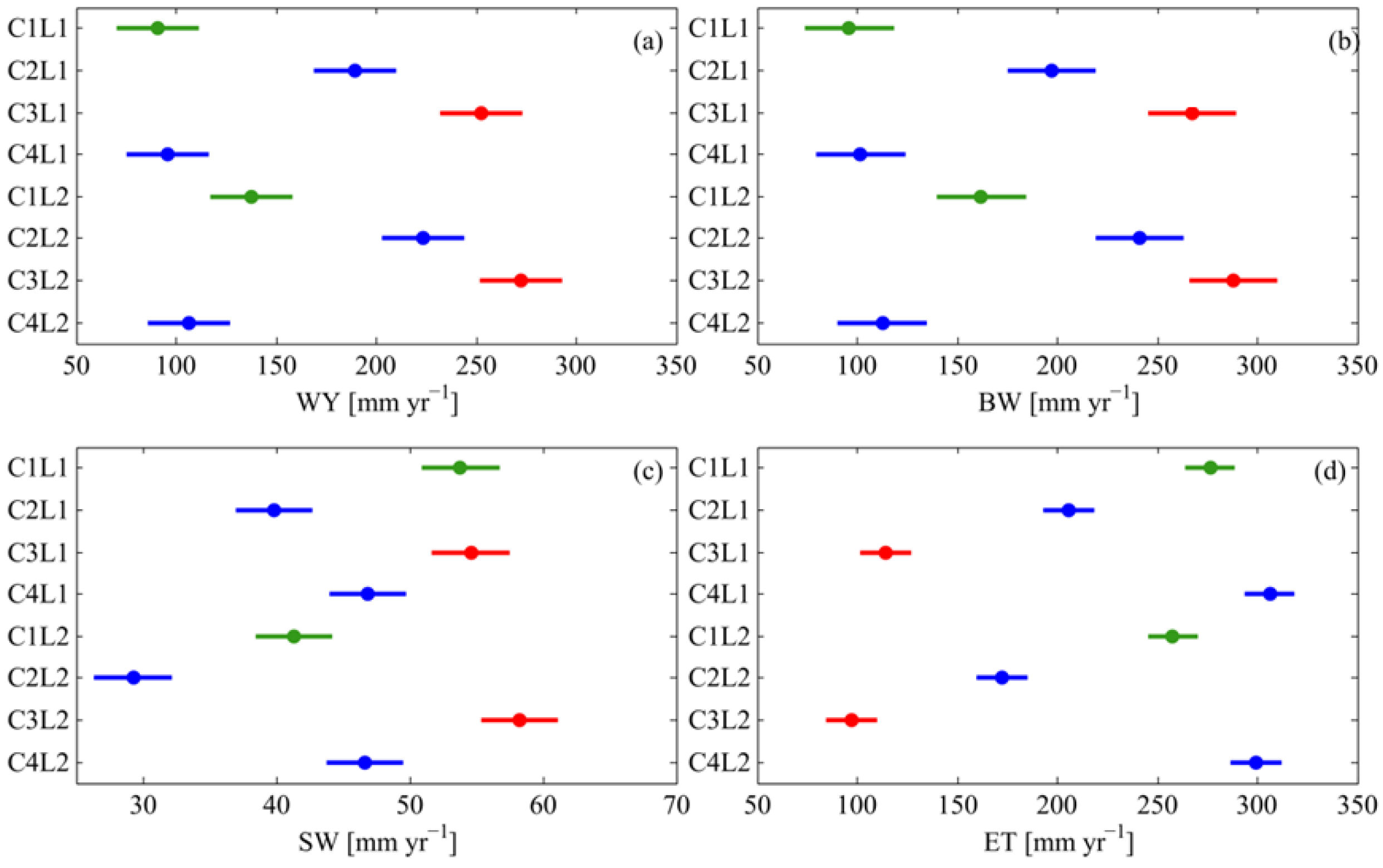





| Terminology | Definition |
|---|---|
| SWAT | An agro-hydrological program for watershed management. |
| Model | A hydrologic program like SWAT becomes a model only when it reflects specifications and processes of a region. |
| Watershed | A hydrologically isolated region. |
| Sub-basin | A unit of land within a watershed delineated by an outlet. |
| Hydrologic response unit (HRU) | The smallest unit of calculation in SWAT made up of overlying elevation, soil, land-use, and slope. |
| Parameter | A model input representing a process in the watershed. |
| Variable | A model output. |
| Deterministic model | A model that takes a single-valued input and produces a single-valued output. |
| Stochastic model | A model that takes parameters in the form of a distribution and produces output variables in the form of a distribution also. SWAT and most other hydrologic models are deterministic models. |
| Before Terracing | After Terracing | |||||||
|---|---|---|---|---|---|---|---|---|
| Soil Loss (tn ha−1) | Cost of Soil Loss ($ ha−1) | Prob. of Soil Loss | Risk of Soil Loss ($ ha−1) | Soil Loss (tn ha−1) | Cost of Soil Loss ($ ha−1) | Prob. of Soil Loss | Risk of Soil Loss ($ ha−1) | Gain ($ ha−1) |
| 513 | 5130 | 0.29 | 1501 | 209 | 2090 | 0.41 | 460 | 1041 |
| 534 | 5340 | 0.14 | 747 | 219 | 2190 | 0.59 | 241 | 506 |
| 601 | 6010 | 0.14 | 841 | 258 | 2580 | 0.72 | 464 | 376 |
| 668 | 6680 | 0.09 | 601 | 296 | 2960 | 0.78 | 414 | 187 |
| 735 | 7350 | 0.06 | 441 | 335 | 3350 | 0.86 | 335 | 106 |
| 802 | 8020 | 0.05 | 481 | 373 | 3730 | 0.91 | 261 | 220 |
| 869 | 8690 | 0.05 | 434 | 411 | 4110 | 0.94 | 206 | 229 |
| 936 | 9360 | 0.06 | 562 | 450 | 4500 | 0.95 | 180 | 382 |
| 1003 | 10,030 | 0.05 | 502 | 488 | 4880 | 0.98 | 244 | 258 |
| 1070 | 10,700 | 0.06 | 642 | 527 | 5270 | 1.00 | 211 | 431 |
| Expectation | 6751 | 3016 | 3735 | |||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbaspour, K.C.; Vaghefi, S.A.; Srinivasan, R. A Guideline for Successful Calibration and Uncertainty Analysis for Soil and Water Assessment: A Review of Papers from the 2016 International SWAT Conference. Water 2018, 10, 6. https://0-doi-org.brum.beds.ac.uk/10.3390/w10010006
Abbaspour KC, Vaghefi SA, Srinivasan R. A Guideline for Successful Calibration and Uncertainty Analysis for Soil and Water Assessment: A Review of Papers from the 2016 International SWAT Conference. Water. 2018; 10(1):6. https://0-doi-org.brum.beds.ac.uk/10.3390/w10010006
Chicago/Turabian StyleAbbaspour, Karim C., Saeid Ashraf Vaghefi, and Raghvan Srinivasan. 2018. "A Guideline for Successful Calibration and Uncertainty Analysis for Soil and Water Assessment: A Review of Papers from the 2016 International SWAT Conference" Water 10, no. 1: 6. https://0-doi-org.brum.beds.ac.uk/10.3390/w10010006






