Ultrafast Dynamics of High-Harmonic Generation in Terms of Complex Floquet Spectral Analysis
Abstract
:1. Introduction
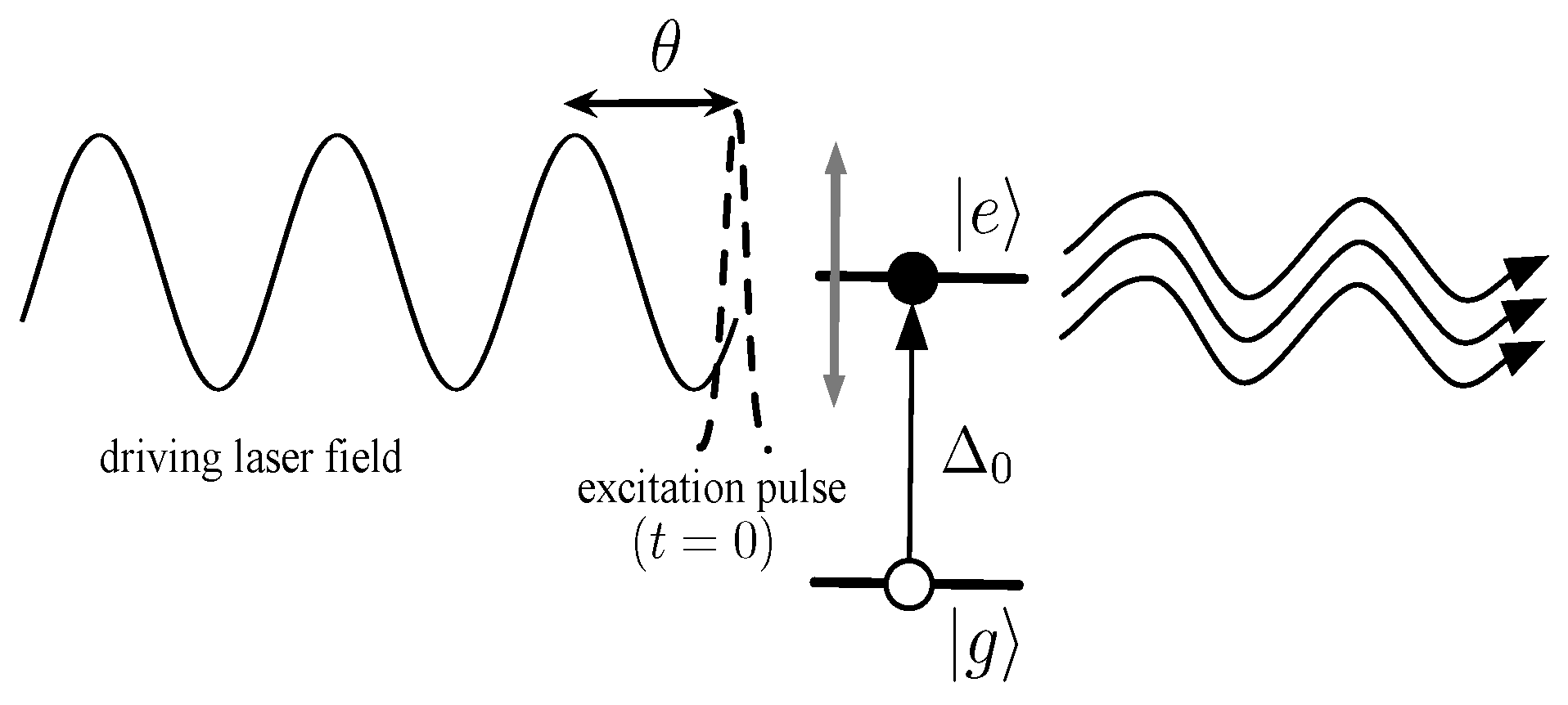
2. Model
3. Complex Eigenvalue Problem of the Floquet Hamiltonian
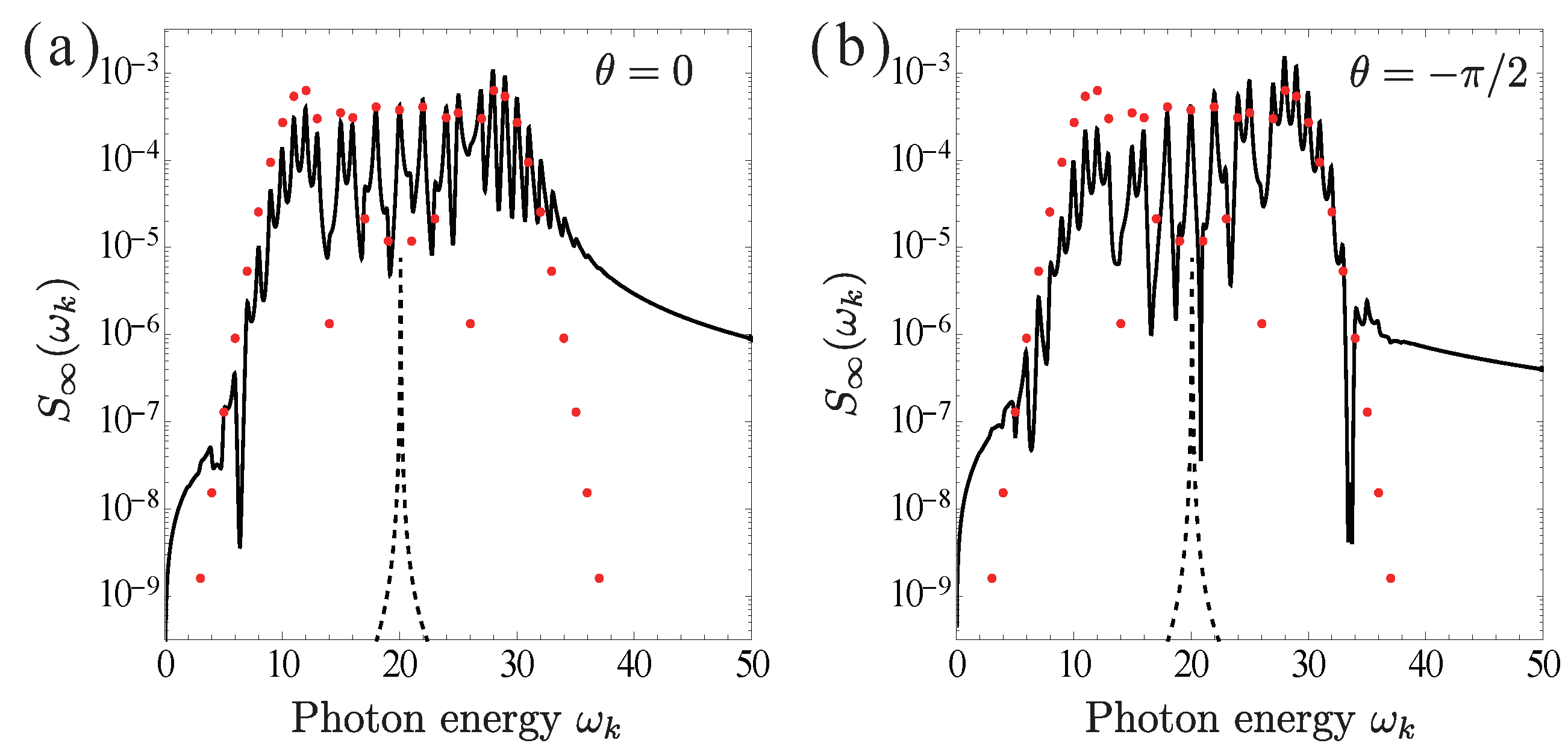
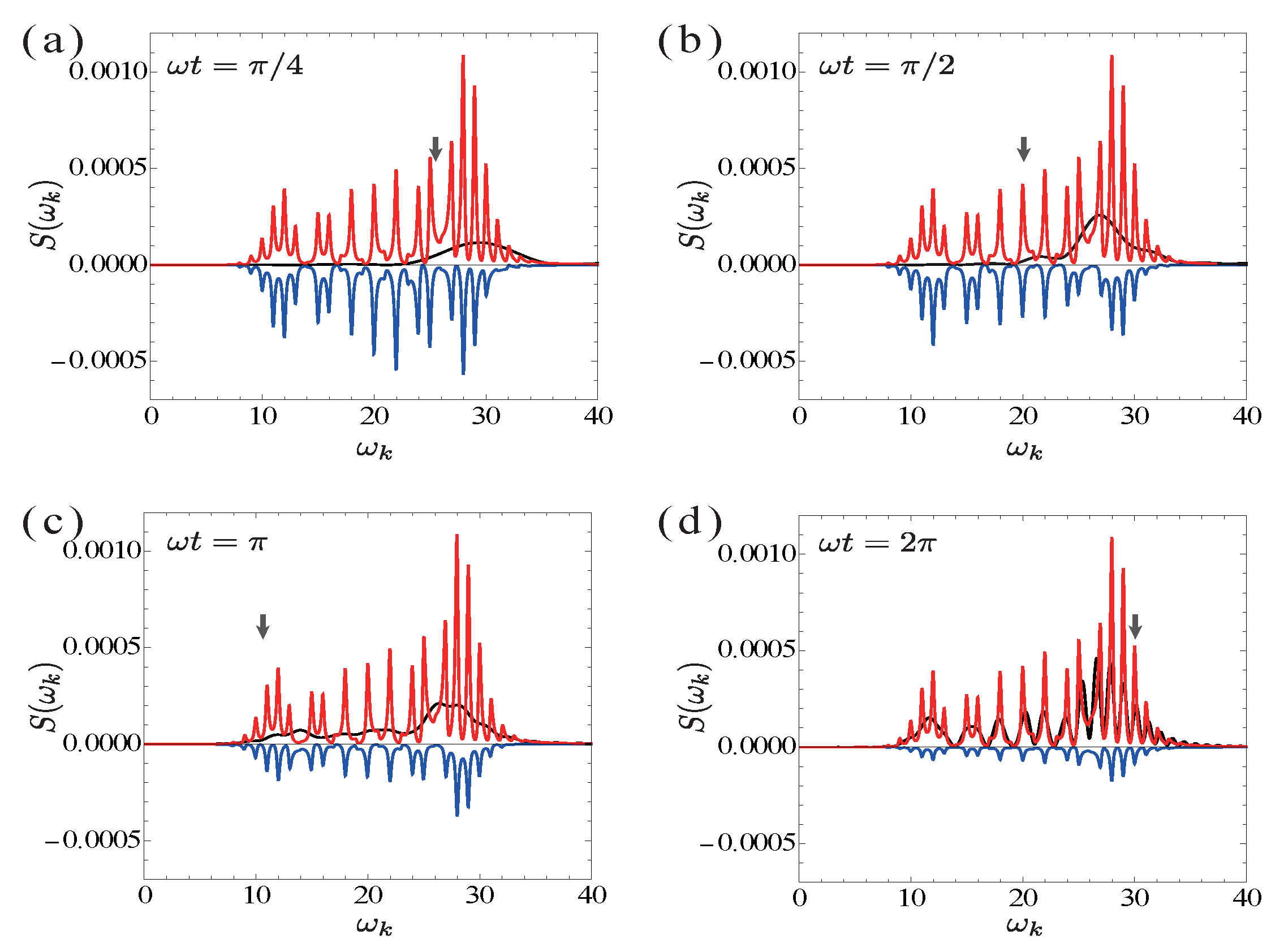
4. HHG Spectrum
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| HHG | High-Harmonic Generation |
| TLS | Two-Level System |
| CEP | Carrier-Envelope-Phase |
Appendix A. Hamiltonian of the Driven TLS
Appendix B. Complex Eigenvalue Problem of the Floquet Hamiltonian
Appendix B.1. Discrete Floquet Resonance State
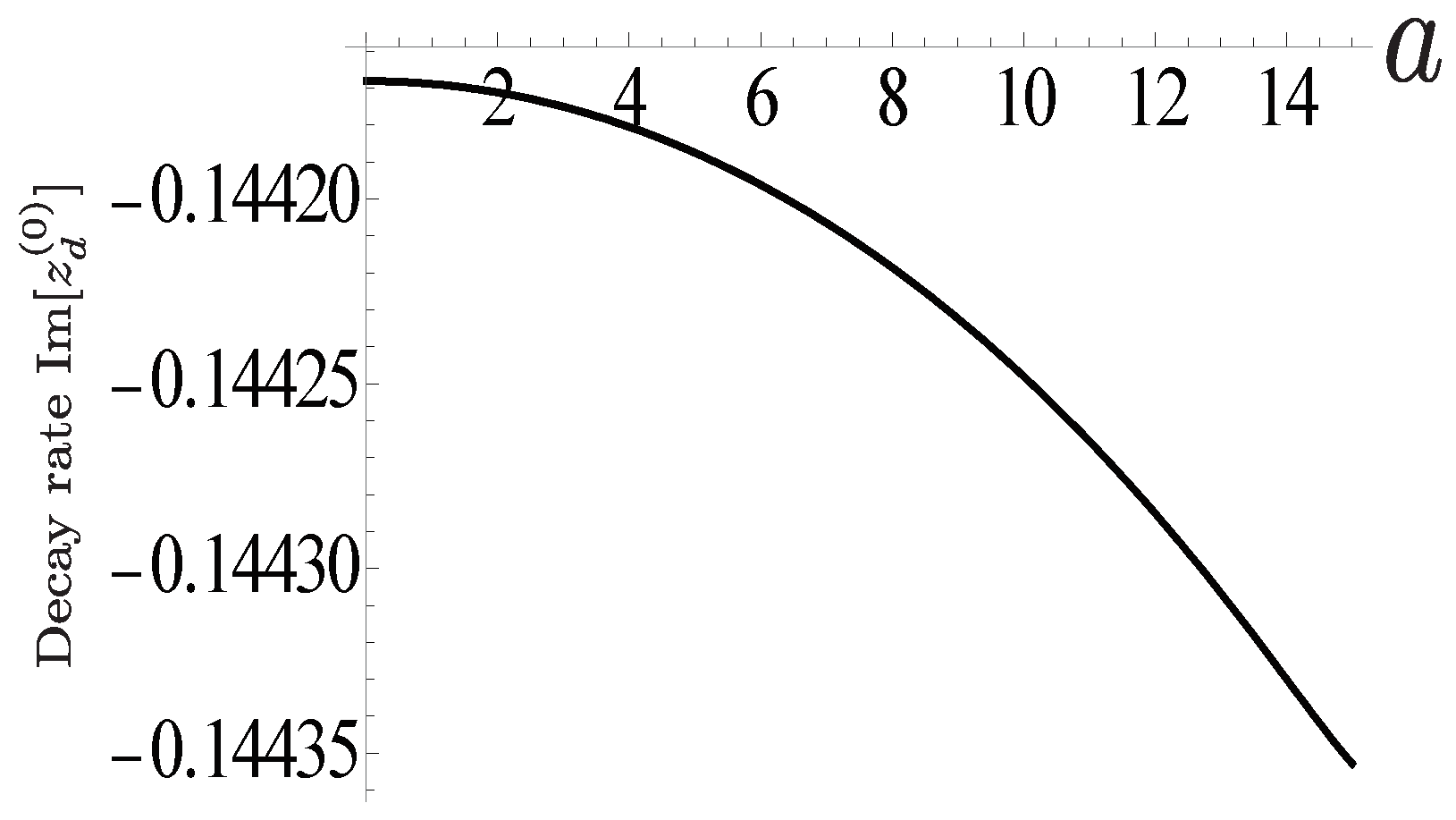
Appendix B.2. Dressed Radiation Field
References
- Corkum, P.B.; Krausz, F. Attosecond science. Nat. Phys. 2007, 3, 381–387. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar] [CrossRef]
- Corkum, P.; Burnett, N.; Brunel, F. Above-threshold ionization in the long-wavelength limit. Phys. Rev. Lett. 1989, 62, 1259–1262. [Google Scholar] [CrossRef] [PubMed]
- Mohideen, U.; Sher, M.; Tom, H.; Aumiller, G.; Wood, O.; Freeman, R.; Boker, J.; Bucksbaum, P. High intensity above-threshold ionization of He. Phys. Rev. Lett. 1993, 71, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schafer, K.J.; Kulander, K.C. High Harmonic Generation from Ultrafast Pump Lasers. Phys. Rev. Lett. 1997, 78, 638–641. [Google Scholar] [CrossRef] [Green Version]
- Krause, J.; Schafer, K.; Kulander, K. High-order harmonic generation from atoms and ions in the high intensity regime. Phys. Rev. Lett. 1992, 68, 3535–3538. [Google Scholar] [CrossRef] [PubMed]
- Brabec, T.; Krausz, F. Intense few-cycle laser fields: Frontiers of nonlinear optics. Rev. Mod. Phys. 2000, 72, 545–591. [Google Scholar] [CrossRef]
- Popmintchev, T.; Chen, M.C.; Arpin, P.; Murnane, M.M.; Kapteyn, H.C. The attosecond nonlinear optics of bright coherent X-ray generation. Nat. Photonics 2010, 4, 822–832. [Google Scholar] [CrossRef]
- Popmintchev, T.; Chen, M.C.; Popmintchev, D.; Arpin, P.; Brown, S.; Ališauskas, S.; Andriukaitis, G.; Balčiunas, T.; Mücke, O.D.; Pugzlys, A.; et al. Bright Coherent Ultrahigh Harmonics in the keV X-ray Regime from Mid-Infrared Femtosecond Lasers. Science 2012, 336, 1287–1291. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.T.; Zhang, C.; Ruchon, T.; Hergott, J.F.; Auguste, T.; Villeneuve, D.M.; Corkum, P.B.; Quéré, F. Photonic streaking of attosecond pulse trains. Nat. Photonics 2013, 7, 651–656. [Google Scholar] [CrossRef]
- Gruson, V.; Barreau, L.; Jiménez-Galan, Á.; Risoud, F.; Caillat, J.; Maquet, A.; Carré, B.; Lepetit, F.; Hergott, J.F.; Ruchon, T.; et al. Attosecond dynamics through a Fano resonance: Monitoring the birth of a photoelectron. Science 2016, 354, 734–738. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kaldun, A.; Blättermann, A.; Stooß, V.; Donsa, S.; Wei, H.; Pazourek, R.; Nagele, S.; Ott, C.; Lin, C.D.; Burgdörfer, J.; et al. Observing the ultrafast buildup of a Fano resonance in the time domain. Science 2016, 354, 738–741. [Google Scholar] [CrossRef] [PubMed]
- Cirelli, C.; Marante, C.; Heuser, S.; Petersson, C.; Galán, Á.; Argenti, L.; Zhong, S.; Busto, D.; Isinger, M.; Nandi, S.; et al. Anisotropic photoemission time delays close to a Fano resonance. Nat. Commun. 2018, 9. [Google Scholar] [CrossRef] [PubMed]
- Nisoli, M.; Decleva, P.; Calegari, F.; Palacios, A.; Martín, F. Attosecond Electron Dynamics in Molecules. Chem. Rev. 2017, 117, 10760–10825. [Google Scholar] [CrossRef] [PubMed]
- Young, L.; Ueda, K.; Gühr, M.; Bucksbaum, P.; Simon, M.; Mukamel, S.; Rohringer, N.; Prince, K.; Masciovecchio, C.; Meyer, M.; et al. Roadmap of ultrafast x-ray atomic and molecular physics. J. Phys. B 2018, 51. [Google Scholar] [CrossRef]
- Ghimire, S.; Dichiara, A.; Sistrunk, E.; Agostini, P.; Dimauro, L.; Reis, D. Observation of high-order harmonic generation in a bulk crystal. Nat. Phys. 2011, 7, 138–141. [Google Scholar] [CrossRef]
- Schubert, O.; Hohenleutner, M.; Langer, F.; Urbanek, B.; Lange, C.; Huttner, U.; Golde, D.; Meier, T.; Kira, M.; Koch, S.W.; et al. Sub-cycle control of terahertz high-harmonic generation by dynamical Bloch oscillations. Nat. Photonics 2014, 8, 119–123. [Google Scholar] [CrossRef] [Green Version]
- Hohenleutner, M.; Langer, F.; Schubert, O.; Knorr, M.; Huttner, U.; Koch, S.; Kira, M.; Huber, R. Real-time observation of interfering crystal electrons in high-harmonic generation. Nature 2015, 523, 572–575. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vampa, G.; Hammond, T.; Thiré, N.; Schmidt, B.; Légaré, F.; McDonald, C.; Brabec, T.; Corkum, P. Linking high harmonics from gases and solids. Nature 2015, 522, 462–464. [Google Scholar] [CrossRef] [PubMed]
- Ndabashimiye, G.; Ghimire, S.; Wu, M.; Browne, D.A.; Schafer, K.J.; Gaarde, M.B.; Reis, D.A. Solid-state harmonics beyond the atomic limit. Nature 2016, 534, 520–523. [Google Scholar] [CrossRef] [PubMed]
- Bauer, D.; Hansen, K.K. High-Harmonic Generation in Solids with and without Topological Edge States. Phys. Rev. Lett. 2018, 120, 177401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McDonald, C.R.; Amin, K.S.; Aalmalki, S.; Brabec, T. Enhancing High Harmonic Output in Solids through Quantum Confinement. Phys. Rev. Lett. 2017, 119, 183902. [Google Scholar] [CrossRef] [PubMed]
- Luu, T.T.; Garg, M.; Kruchinin, S.Y.; Moulet, A.; Hassan, M.T.; Goulielmakis, E. Extreme ultraviolet high-harmonic spectroscopy of solids. Nature 2015, 521, 498–502. [Google Scholar] [CrossRef] [PubMed]
- You, Y.S.; Yin, Y.; Wu, Y.; Chew, A.; Ren, X.; Zhuang, F.; Gholam-Mirzaei, S.; Chini, M.; Chang, Z.; Ghimire, S. High-harmonic generation in amorphous solids. Nat. Commun. 2017, 8, 724. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zaks, B.; Liu, R.B.; Sherwin, M.S. Experimental observation of electron–hole recollisions. Nature 2012, 483, 580–583. [Google Scholar] [CrossRef] [PubMed]
- Langer, F.; Hohenleutner, M.; Schmid, C.P.; Poellmann, C.; Nagler, P.; Korn, T.; Schüller, C.; Sherwin, M.S.; Huttner, U.; Steiner, J.T.; et al. Lightwave-driven quasiparticle collisions on a subcycle timescale. Nature 2016, 533, 225–229. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uchida, K.; Otobe, T.; Mochizuki, T.; Kim, C.; Yoshita, M.; Akiyama, H.; Pfeiffer, L.N.; West, K.W.; Tanaka, K.; Hirori, H. Subcycle Optical Response Caused by a Terahertz Dressed State with Phase-Locked Wave Functions. Phys. Rev. Lett. 2016, 117, 277402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uchida, K.; Otobe, T.; Mochizuki, T.; Kim, C.; Yoshita, M.; Tanaka, K.; Akiyama, H.; Pfeiffer, L.N.; West, K.W.; Hirori, H. Coherent detection of THz-induced sideband emission from excitons in the nonperturbative regime. Phys. Rev. B 2018, 97, 165122. [Google Scholar] [CrossRef]
- Luu, T.; Wörner, H. High-order harmonic generation in solids: A unifying approach. Phys. Rev. B 2016, 94. [Google Scholar] [CrossRef] [Green Version]
- Milonni, P.W. The Quantum Vacuum: An Introduction to Quantum Electrodynamics; Academic Press: New York, NY, USA, 1994. [Google Scholar]
- Mukamel, S. Principles of Nonlinear Optical Spectroscopy; Oxford Series in Optical and Imaging Sciences; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Kulander, K.C.; Schafer, K.J. Time-dependent calculations of electron and photon emission from an atom in an intense laser field. In Atoms and Molecules in Intense Fields; Springer: Berlin/Heidelberg, Germany, 1997; pp. 149–172. [Google Scholar]
- Tancogne-Dejean, N.; Mücke, O.D.; Kärtner, F.X.; Rubio, A. Impact of the Electronic Band Structure in High-Harmonic Generation Spectra of Solids. Phys. Rev. Lett. 2017, 118, 087403. [Google Scholar] [CrossRef] [PubMed]
- Vampa, G.; McDonald, C.R.; Orlando, G.; Corkum, P.B.; Brabec, T. Semiclassical analysis of high harmonic generation in bulk crystals. Phys. Rev. B 2015, 91, 064302. [Google Scholar] [CrossRef] [Green Version]
- Golde, D.; Meier, T.; Koch, S.W. High harmonics generated in semiconductor nanostructures by the coupled dynamics of optical inter- and intraband excitations. Phys. Rev. B 2008, 77, 075330. [Google Scholar] [CrossRef]
- Weisskopf, V.; Wigner, E. Berechnung der natürlichen Linienbreite auf Grund der Diracschen Lichttheorie. Zeitschrift für Physik 1930, 63, 54–73. [Google Scholar] [CrossRef]
- Heitler, W. The Quantum Theory of Radiation; International Series of Monographs on Physics; Oxford University Press: Oxford, UK, 1947. [Google Scholar]
- Compagno, G.; Passante, R.; Persico, F. Atom-Field Interactions and Dressed Atoms; Cambridge Studies in Modern Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Cohen-Tannoudji, C.; Dupont-Roc, J.; Grynberg, G. Atom—Photon Interactions: Basic Process and Applications. In Atom—Photon Interactions; Wiley: Weinheim, Germany, 2008. [Google Scholar]
- Petrosky, T.; Prigogine, I.; Tasaki, S. Quantum theory of non-integrable systems. Phys. A Stat. Mech. Appl. 1991, 173, 175–242. [Google Scholar] [CrossRef]
- Petrosky, T.; Prigogine, I. The Liouville space extension of quantum mechanics. Adv. Chem. Phys. 1997, 99, 1–120. [Google Scholar]
- Ordonez, G.; Petrosky, T.; Prigogine, I. Quantum transitions and dressed unstable states. Phys. Rev. A 2001, 63, 052106. [Google Scholar] [CrossRef]
- Petrosky, T.; Ordonez, G.; Prigogine, I. Space-time formulation of quantum transitions. Phys. Rev. A 2001, 64, 062101/1–062101/21. [Google Scholar] [CrossRef]
- Tanaka, S.; Garmon, S.; Petrosky, T. Nonanalytic enhancement of the charge transfer from adatom to one-dimensional semiconductor superlattice and optical absorption spectrum. Phys. Rev. B 2006, 73, 115340. [Google Scholar] [CrossRef]
- Yamada, N.; Noba, K.I.; Tanaka, S.; Petrosky, T. Dynamical suppression and enhancement of instability for an unstable state by a periodic external field. Phys. Rev. B 2012, 86. [Google Scholar] [CrossRef]
- Tanaka, S.; Garmon, S.; Kanki, K.; Petrosky, T. Higher-order time-symmetry-breaking phase transition due to meeting of an exceptional point and a Fano resonance. Phys. Rev. A 2016, 94, 022105. [Google Scholar] [CrossRef]
- Fukuta, T.; Garmon, S.; Kanki, K.; Noba, K.i.; Tanaka, S. Fano absorption spectrum with the complex spectral analysis. Phys. Rev. A 2017, 96, 052511. [Google Scholar] [CrossRef]
- Cohen-Tannoudji, C.; Dupont-Roc, J.; Grynberg, G. Atom-Photon Interactions: Basic Processes and Applications; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
- Grifoni, M.; Hänggi, P. Driven quantum tunneling. Phys. Rep. 1998, 304, 229–354. [Google Scholar] [CrossRef] [Green Version]
- Shirley, J. Solution of the schrödinger equation with a hamiltonian periodic in time. Phys. Rev. 1965, 138, B979–B987. [Google Scholar] [CrossRef]
- Sambe, H. Steady states and quasienergies of a quantum-mechanical system in an oscillating field. Phys. Rev. A 1973, 7, 2203–2213. [Google Scholar] [CrossRef]
- Yamane, H.; Tanaka, S.; Domina, M.; Passante, R.; Petrosky, T. Analysis of high-harmonic generation in terms of complex Floquet spectral analysis. In Proceedings of the 2017 Progress in Electromagnetics Research Symposium, Singapore, 19–22 November 2017; pp. 1437–1444. [Google Scholar]
- Friedrichs, K. On the perturbation of continuous spectra. Commun. Pure Appl. Math. 1948, 1, 361–406. [Google Scholar] [CrossRef]
- Petrosky, T.; Ordonez, G.; Prigogine, I. Quantum transitions and nonlocality. Phys. Rev. A 2000, 62, 042106. [Google Scholar] [CrossRef]
- Glauber, R.J. Optical Coherence and Photon Statistics. In Quantum Theory of Optical Coherence; de Witt, C., Blandin, A., Cohen-Tannoudji, C., Eds.; WileyWiley: Hoboken, NJ, USA, 2007; Chapter 2; pp. 23–182. [Google Scholar]
- Carmichael, H. Statistical Methods in Quantum Optics 1: Master Equations and Fokker-Planck Equations; Theoretical and Mathematical Physics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Korbman, M.; Kruchinin, S.Y.; Yakovlev, V.S. Quantum beats in the polarization response of a dielectric to intense few-cycle laser pulses. New J. Phys. 2013, 15, 013006. [Google Scholar] [CrossRef] [Green Version]
- Wu, M.; Browne, D.A.; Schafer, K.J.; Gaarde, M.B. Multilevel perspective on high-order harmonic generation in solids. Phys. Rev. A 2016, 94, 063403. [Google Scholar] [CrossRef]
- Clemmen, S.; Farsi, A.; Ramelow, S.; Gaeta, A.L. Ramsey Interference with Single Photons. Phys. Rev. Lett. 2016, 117, 223601. [Google Scholar] [CrossRef] [PubMed]
- Whiting, D.J.; Šibalić, N.; Keaveney, J.; Adams, C.S.; Hughes, I.G. Single-Photon Interference due to Motion in an Atomic Collective Excitation. Phys. Rev. Lett. 2017, 118, 253601. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, L.N.; Iff, O.; Betzold, S.; Dusanowski, Ł.; Emmerling, M.; Moon, K.; Lee, Y.J.; Kwon, S.H.; Höfling, S.; Schneider, C. Spontaneous Emission Enhancement in Strain-Induced WSe2 Monolayer-Based Quantum Light Sources on Metallic Surfaces. ACS Photonics 2018, 5, 1919–1926. [Google Scholar] [CrossRef] [Green Version]
- Browne, D.E.; Keitel, C.H. Resonance fluorescence in intense laser fields. J. Mod. Opt. 2000, 47, 1307–1337. [Google Scholar] [CrossRef]
- Hizhyakov, V.; Tehver, I. Theory of Resonant Secondary Radiation due to Impurity Centres in Crystals. Phys. Status Solidi B 1967, 21, 755–768. [Google Scholar] [CrossRef]
- Toyozawa, Y. Resonance and Relaxation in Light Scattering. J. Phys. Soc. Jpn. 1976, 41, 400–411. [Google Scholar] [CrossRef]
- Kotani, A. On the Relationship between Resonant Light Scattering and Luminescence—A Singular Aspect in Localized Electron-Phonon System with Linear Interaction. J. Phys. Soc. Jpn. 1978, 44, 965–972. [Google Scholar] [CrossRef]
- Kayamura, Y. Resonant Secondary Radiation in Strongly Coupled Localized Electron-Phonon System. J. Phys. Soc. Jpn. 1988, 57, 292–301. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamane, H.; Tanaka, S. Ultrafast Dynamics of High-Harmonic Generation in Terms of Complex Floquet Spectral Analysis. Symmetry 2018, 10, 313. https://0-doi-org.brum.beds.ac.uk/10.3390/sym10080313
Yamane H, Tanaka S. Ultrafast Dynamics of High-Harmonic Generation in Terms of Complex Floquet Spectral Analysis. Symmetry. 2018; 10(8):313. https://0-doi-org.brum.beds.ac.uk/10.3390/sym10080313
Chicago/Turabian StyleYamane, Hidemasa, and Satoshi Tanaka. 2018. "Ultrafast Dynamics of High-Harmonic Generation in Terms of Complex Floquet Spectral Analysis" Symmetry 10, no. 8: 313. https://0-doi-org.brum.beds.ac.uk/10.3390/sym10080313




