A New Strategy to Integrate Heath–Carter Somatotype Assessment with Bioelectrical Impedance Analysis in Elite Soccer Players
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Procedures
- PhA = Xc/R × 180°/π.
- FFM, FM, and FM% using a specific equation for athletes as follow [24]:
- FFM = −2.261 + 0.327 × stature2/R + 0.525 × body weight + 5.462 × 1;
- FM = Body weight − FFM;
- FM% = FM/body weight × 100.
2.3. Statistical Analysis
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Devlin, B.L.; Leveritt, M.D.; Kingsley, M.; Belski, R. Dietary Intake, Body Composition, and Nutrition Knowledge of Australian Football and Soccer Players: Implications for Sports Nutrition Professionals in Practice. Int. J. Sport Nutr. Exerc. Metab. 2017, 27, 130–138. [Google Scholar] [CrossRef]
- Bongiovanni, T.; Trecroci, A.; Cavaggioni, L.; Rossi, A.; Perri, E.; Pasta, G.; Iaia, F.M.; Alberti, G. Importance of anthropometric features to predict physical performance in elite youth soccer: A machine learning approach. Res. Sports Med. 2020, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Campa, F.; Semprini, G.; Júdice, P.B.; Messina, G.; Toselli, S. Anthropometry, physical and movement features, and repeated-sprint ability in soccer players. Int. J. Sports Med. 2019, 40, 100–109. [Google Scholar] [CrossRef]
- Nescolarde, L.; Yanguas, J.; Lukaski, H.; Alomar, X.; Rosell-Ferrer, J.; Rodas, G. Effects of muscle injury severity on localized bioimpedance measurements. Physiol. Meas. 2015, 36, 27–42. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.M.; Pierson, R.N., Jr.; Heymsfield, S.B. The five-level model: A new approach to organizing body-composition research. Am. J. Clin. Nutr. 1992, 56, 19–28. [Google Scholar] [CrossRef] [PubMed]
- Silva, A.M. Structural and functional body components in athletic health and performance phenotypes. Eur. J. Clin. Nutr. 2019, 73, 215–224. [Google Scholar] [CrossRef] [PubMed]
- Carter, J.E.L. The Heath-Carter Somatotype Method, 3rd ed.; San Diego State University Syllabus Service: San Diego, CA, USA, 1980. [Google Scholar]
- Campa, F.; Silva, A.M.; Talluri, J.; Matias, C.N.; Badicu, G.; Toselli, S. Somatotype and Bioimpedance Vector Analysis: A New Target Zone for Male Athletes. Sustainability 2020, 12, 4365. [Google Scholar] [CrossRef]
- Cárdenas-Fernández, V.; Chinchilla-Minguet, J.L.; Castillo-Rodríguez, A. Somatotype and Body Composition in Young Soccer Players According to the Playing Position and Sport Success. J. Strength Cond. Res. 2019, 33, 1904–1911. [Google Scholar] [CrossRef]
- Sánchez Muñoz, C.; Muros, J.J.; López Belmonte, Ó.; Zabala, M. Anthropometric characteristics, body composition and somatotype of elite male young runners. Int. J. Environ. Res. Public Health 2020, 17, 674. [Google Scholar] [CrossRef] [Green Version]
- American Dietetic Association; Dietitians of Canada; American College of Sports Medicine; Rodriguez, N.R.; Di Marco, N.M.; Langley, S. American College of Sports Medicine position stand. Nutrition and athletic performance. Med. Sci. Sports Exerc. 2009, 41, 709–731. [Google Scholar]
- Santos, D.A.; Dawson, J.A.; Matias, C.N.; Rocha, P.M.; Minderico, C.S.; Allison, D.B.; Sardinha, L.B.; Silva, A.M. Reference values for body composition and anthropometric measurements in athletes. PLoS ONE 2014, 9, e97846. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Castizo-Olier, J.; Irurtia, A.; Jemni, M.; Carrasco-Marginet, M.; Fernández-García, R.; Rodríguez, F.A. Bioelectrical impedance vector analysis (BIVA) in sport and exercise: Systematic review and future perspectives. PLoS ONE 2018, 13, e0197957. [Google Scholar] [CrossRef]
- Marini, E.; Campa, F.; Buffa, R.; Stagi, S.; Matias, C.N.; Toselli, S.; Sardinha, L.B.; Silva, A.M. Phase angle and bioelectrical impedance vector analysis in the evaluation of body composition in athletes. Clin. Nutr. 2020, 39, 447–454. [Google Scholar] [CrossRef]
- Katch, F.I.; Katch, V.L. Measurement and prediction errors in body composition assessment and the search for the perfect prediction equation. Res. Q. Exerc. Sport. 1980, 51, 249–260. [Google Scholar] [CrossRef]
- Bongiovanni, T.; Mascherini, G.; Genovesi, F.; Pasta, G.; Iaia, F.M.; Trecroci, A.; Ventimiglia, M.; Alberti, A.; Campa, F. Bioimpedance Vector References Need to Be Period-Specific for Assessing Body Composition and Cellular Health in Elite Soccer Players: A Brief Repor. J. Funct. Morphol. Kinesiol. 2020, 5, 73. [Google Scholar] [CrossRef]
- Levi Micheli, M.; Pagani, L.; Marella, M.; Gulisano, M.; Piccoli, A.; Angelini, F.; Burtscher, M.; Gatterer, H. Bioimpedance and impedance vector patterns as predictors of league level in male soccer players. Int. J. Sports Physiol. Perform. 2014, 9, 532–539. [Google Scholar] [CrossRef]
- Mascherini, G.; Gatterer, H.; Lukaski, H.; Burtscher, M.; Galanti, G. Changes in hydration, body-cell mass and endurance performance of professional soccer players through a competitive season. J. Sports Med. Phys. Fit. 2015, 55, 749–755. [Google Scholar]
- Campa, F.; Silva, A.M.; Matias, C.N.; Monteiro, C.P.; Paoli, A.; Nunes, J.P.; Talluri, J.; Lukaski, H.C.; Toselli, S. Body Water Content and Morphological Characteristics Modify Bioimpedance Vector Patterns in Volleyball, Soccer, and Rugby Players. Int. J. Environ. Res. Public Health 2020, 17, 6604. [Google Scholar] [CrossRef] [PubMed]
- Kim, C.H.; Park, J.H.; Kim, H.; Chung, S.; Park, S.H. Modeling the human body shape in bioimpedance vector measurements. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 3872–3874. [Google Scholar]
- Steward, A.; Marfell-Jones, M. International Standards for Anthropometric Assessment; International Society for the Advancement of Kinanthropometry: Lower Hutt, New Zealand, 2014. [Google Scholar]
- Campa, F.; Matias, C.; Gatterer, H.; Toselli, S.; Koury, J.C.; Andreoli, A.; Melchiorri, G.; Sardinha, L.B.; Silva, A.M. Classic bioelectrical impedance vector reference values for assessing body composition in male and female athletes. Int. J. Environ. Res. Public Health 2019, 16, 5066. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lukaski, H.C.; Piccoli, A. Bioelectrical impedance vector analysis for assessment of hydration in physiological states and clinical conditions. In Handbook of Anthropometry; Preedy, V., Ed.; Springer: Berlin, Germany, 2012; pp. 287–305. [Google Scholar]
- Matias, C.N.; Campa, F.; Santos, D.A.; Lukaski, H.C.; Sardinha, L.B.; Silva, A.M. Fat-free Mass BIA Predictive Equation for Athletes Using a 4-Compartment Model. Int. J. Sports Med. 2020. [Google Scholar] [CrossRef]
- Guo, S.S.; Chumlea, W.C.; Cockram, D.B. Use of statistical methods to estimate body composition. Am. J. Clin. Nutr. 1996, 64, 428S–435S. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, S.S.; Chumlea, W.C. Statistical methods for the development and testing of predictive equations. In Human Body Composition; Roche, A.F., Heymsfield, S.B., Lohman, T.G., Eds.; Human Kinetics: Champaign, IL, USA, 1996; pp. 191–202. [Google Scholar]
- Li, L. A concordance correlation coefficient to evaluate reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar]
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 1, 307–310. [Google Scholar] [CrossRef]
- McBride, G.B. A Proposal fo Strength-of-Agreement Criteria for Lin.s.Concordance Correlation Coefficient; National Institute of Water & Atmospheric Research Ltd.: Auckland, New Zealand, 2005. [Google Scholar]
- Campa, F.; Matias, C.N.; Marini, E.; Heymsfield, S.B.; Toselli, S.; Sardinha, L.B.; Silva, A.M. Identifying athlete body-fluid changes during a competitive season with bioelectrical impedance vector analysis. Int. J. Sports Physiol. Perform. 2020, 15, 361–367. [Google Scholar] [CrossRef]
- Vucetić, V.; Matković, B.R.; Sentija, D. Morphological differences of elite Croatian track-and-field athletes. Coll. Antropol. 2008, 32, 863–868. [Google Scholar]
- Massidda, M.; Toselli, S.; Brasili, P.; Calò, C.M. Somatotype of elite Italian gymnasts. Coll. Antropol. 2013, 37, 853–857. [Google Scholar]
- Bourgois, J.; Claessens, A.L.; Vrijens, J.; Philippaerts, R.; Van Renterghem, B.; Thomis, M.; Janssens, M.; Loos, R.; Lefevre, J. Anthropometric characteristics of elite male junior rowers. Br. J. Sports Med. 2000, 34, 213–217. [Google Scholar] [CrossRef] [Green Version]
- Reilly, T.; Bangsbo, J.; Franks, A. Anthropometric and physiological predispositions for elite soccer. J. Sports Sci. 2000, 18, 669–683. [Google Scholar] [CrossRef]
- Fuster, V.; Jerez, A.; Ortega, A. Anthropometry and strength relationship: Male-female differences. Anthropol. Anz. 1998, 56, 49–56. [Google Scholar] [CrossRef]
- Lewandowska, J.; Buśko, K.; Pastuszak, A.; Boguszewska, K. Somatotype variables related to muscle torque and power in judoists. J. Hum. Kinet. 2011, 30, 21–28. [Google Scholar] [CrossRef]
- Ryan-Stewart, H.; Faulkner, J.; Jobson, S. The influence of somatotype on anaerobic performance. PLoS ONE 2018, 13, e0197761. [Google Scholar] [CrossRef] [PubMed]
- Silva, A.M.; Matias, C.N.; Nunes, C.L.; Santos, D.A.; Marini, E.; Lukaski, H.C.; Sardinha, L.B. Lack of agreement of in vivo raw bioimpedance measurements obtained from two single and multi-frequency bioelectrical impedance devices. Eur. J. Clin. Nutr. 2019, 73, 1077–1083. [Google Scholar] [CrossRef] [PubMed]
| Variable | Development Group (n = 117) | Cross-Validation Group (n = 59) |
|---|---|---|
| Mean ± Standard Deviation | Mean ± Standard Deviation | |
| Age (years) | 27.4 ± 4.3 | 28.0 ± 5.0 |
| Weight (kg) | 79.5 ± 6.1 | 78.9 ± 6.5 |
| Stature (cm) | 183.8 ± 0.5 | 182.9 ± 0.5 |
| Body mass index (kg/m2) | 23.5 ± 1.2 | 23.6 ± 1.3 |
| Resistance (ohm) | 464.3 ± 37.1 | 456.8 ± 33.3 |
| Reactance (ohm) | 63.8 ± 5.7 | 64.6 ± 6.6 |
| Phase angle (degree) | 7.9 ± 0.5 | 8.1 ± 0.9 |
| Fat-free mass (kg) Fat mass (kg) Fat mass (%) | 68.8 ± 5.4 | 68.7 ± 5.7 |
| 10.6 ± 1.7 | 10.2 ± 1.9 | |
| 13.3 ± 1.9 | 12.9 ± 1.9 | |
| Triceps skinfold (mm) | 6.1 ± 1.7 | 5.6 ± 1.2 |
| Subscapular skinfold (mm) | 9.5 ± 1.7 | 9.6 ± 1.7 |
| Supraspinal skinfold (mm) | 6.7 ± 1.8 | 6.4 ± 1.7 |
| Medial calf skinfold (mm) | 5.4 ± 1.4 | 5.0 ± 0.9 |
| Contracted arm circumference (cm) | 33.1 ± 1.7 | 33.3 ± 1.5 |
| Calf circumference (cm) | 37.9 ± 1.7 | 38.2 ± 3.4 |
| Humerus width (cm) | 7.2 ± 0.4 | 7.2 ± 0.3 |
| Femur width (cm) | 10.2 ± 0.5 | 10.3 ± 0.5 |
| Endomorphy | 2.0 ± 0.4 | 1.9 ± 0.4 |
| Mesomorphy | 4.9 ± 0.8 | 5.2 ± 0.8 |
| Ectomorphy | 2.7 ± 0.6 | 2.7 ± 0.6 |
| Variable | Predictors | R | R2 | SEE | VIF | Prediction Equation |
|---|---|---|---|---|---|---|
| Endomorphy | FM% S2/R Triceps skinfold Supraspinal skinfold Stature | 0.91 | 0.83 | 0.16 | 2.12 3.45 1.06 1.15 2.29 | y = 4.292 + 0.050 × FM% + 0.012 × S2/R + 0.092 × triceps skinfold + 0.139 × supraspinal skinfold − 0.029 × stature |
| Mesomorphy | CAC CC FFM Stature | 0.89 | 0.80 | 0.36 | 1.58 2.11 4.80 2.54 | y = 10.351 + 0.212 × CAC + 0.187 × CC + 0.048 × FFM − 0.125 × stature |
| Ectomorphy | FFM/S Stature | 0.94 | 0.87 | 0.22 | 1.29 1.29 | y = −7.945 − 25.021 × FFM/S + 0.109 × Stature |
| Variable | Regression Analysis | CCC Analysis | Agreement Analysis | |||||
|---|---|---|---|---|---|---|---|---|
| R2 | PE | CCC | ρ | Cb | Bias | 95% LoA | Trend | |
| Cross-Validation | ||||||||
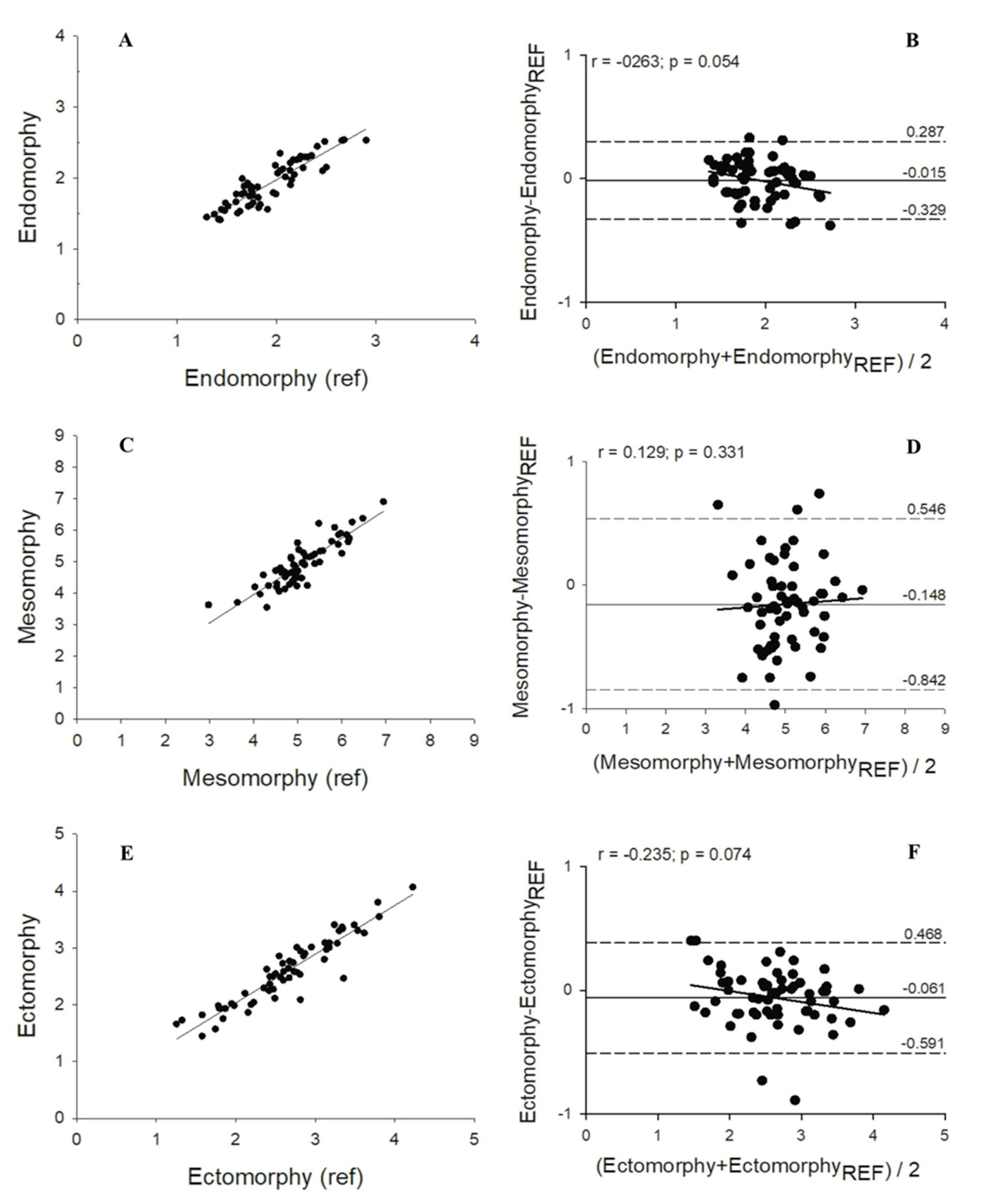
| Endomorph | 0.80 | 0.162 | 0.89 | 0.8957 | 0.9917 | −0.0149 | −0.329; 0.287 | r = −0.263 (p = 0.054) |
| Mesomorph | 0.84 | 0.338 | 0.90 | 0.9173 | 0.9940 | −0.1479 | −0.842; 0.546 | r = −0.129 (p = 0.331) |
| Ectomorph | 0.87 | 0.229 | 0.93 | 0.9346 | 0.9973 | −0.0613 | −0.591; 0.468 | r = −0.235 (p = 0.074) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campa, F.; Bongiovanni, T.; Matias, C.N.; Genovesi, F.; Trecroci, A.; Rossi, A.; Iaia, F.M.; Alberti, G.; Pasta, G.; Toselli, S. A New Strategy to Integrate Heath–Carter Somatotype Assessment with Bioelectrical Impedance Analysis in Elite Soccer Players. Sports 2020, 8, 142. https://0-doi-org.brum.beds.ac.uk/10.3390/sports8110142
Campa F, Bongiovanni T, Matias CN, Genovesi F, Trecroci A, Rossi A, Iaia FM, Alberti G, Pasta G, Toselli S. A New Strategy to Integrate Heath–Carter Somatotype Assessment with Bioelectrical Impedance Analysis in Elite Soccer Players. Sports. 2020; 8(11):142. https://0-doi-org.brum.beds.ac.uk/10.3390/sports8110142
Chicago/Turabian StyleCampa, Francesco, Tindaro Bongiovanni, Catarina N. Matias, Federico Genovesi, Athos Trecroci, Alessio Rossi, F. Marcello Iaia, Giampietro Alberti, Giulio Pasta, and Stefania Toselli. 2020. "A New Strategy to Integrate Heath–Carter Somatotype Assessment with Bioelectrical Impedance Analysis in Elite Soccer Players" Sports 8, no. 11: 142. https://0-doi-org.brum.beds.ac.uk/10.3390/sports8110142








