Spatiotemporal Variability in Phytoplankton Bloom Phenology in Eastern Canadian Lakes Related to Physiographic, Morphologic, and Climatic Drivers
Abstract
:1. Introduction
2. Materials and Methods
3. Results
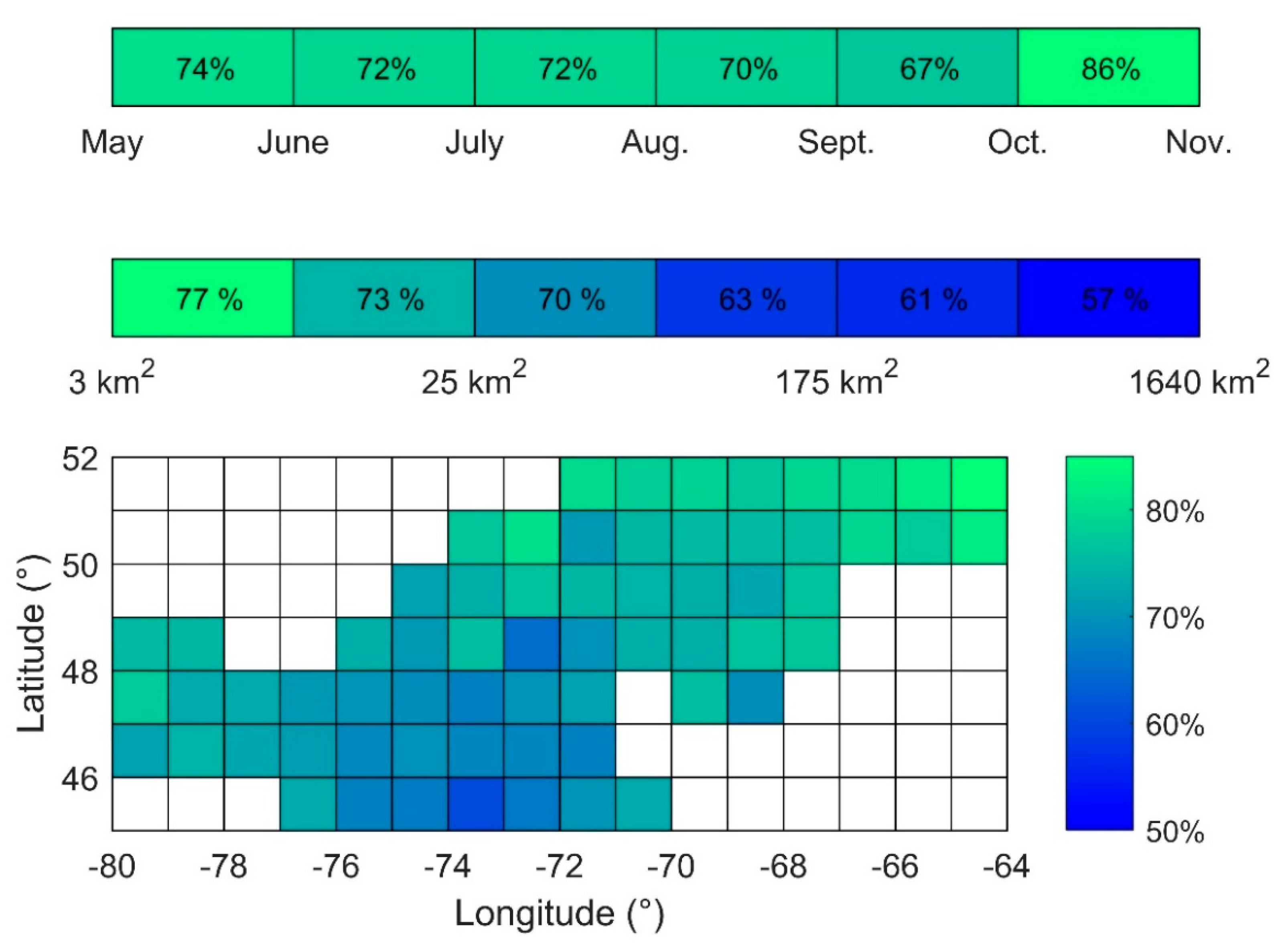
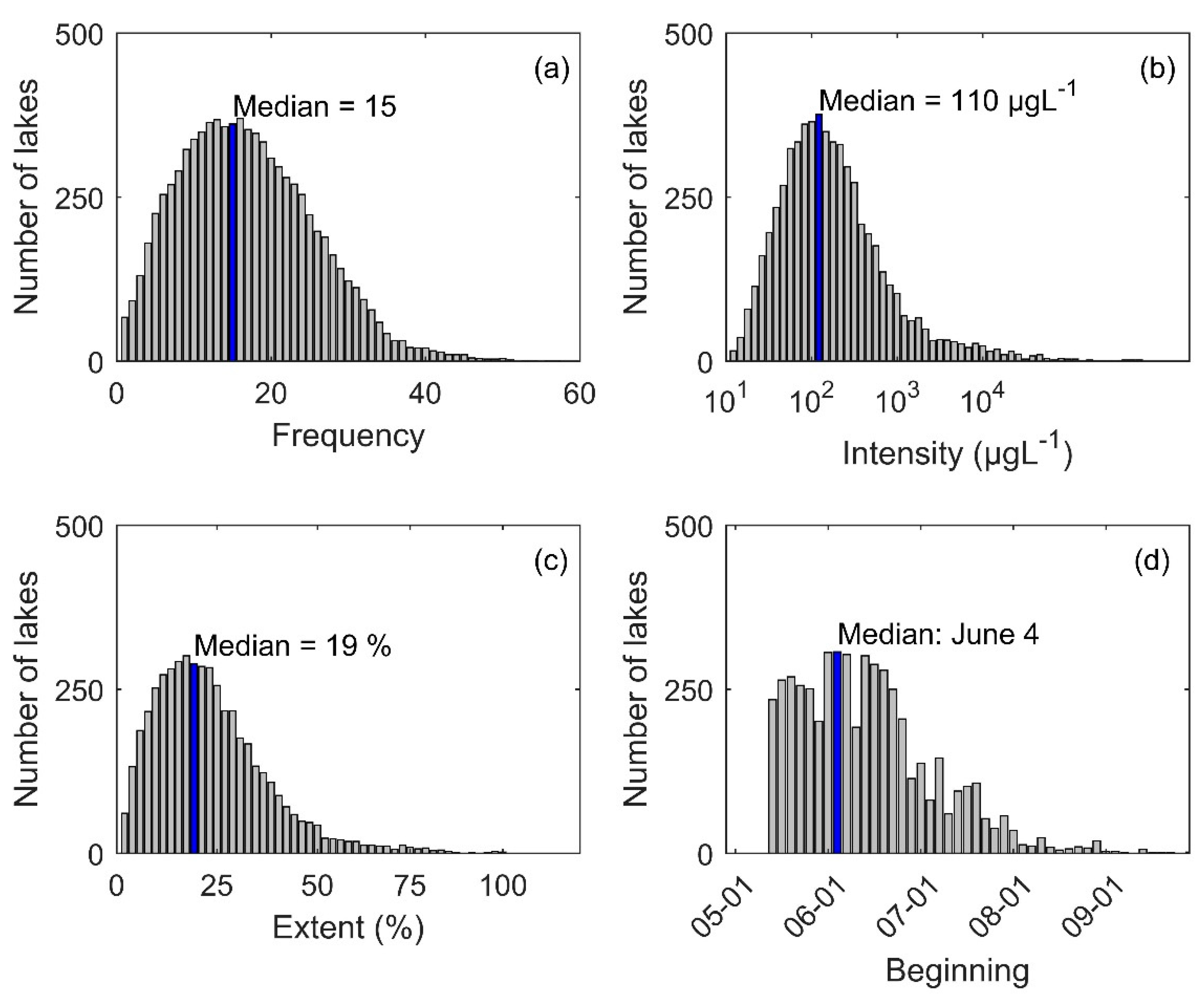
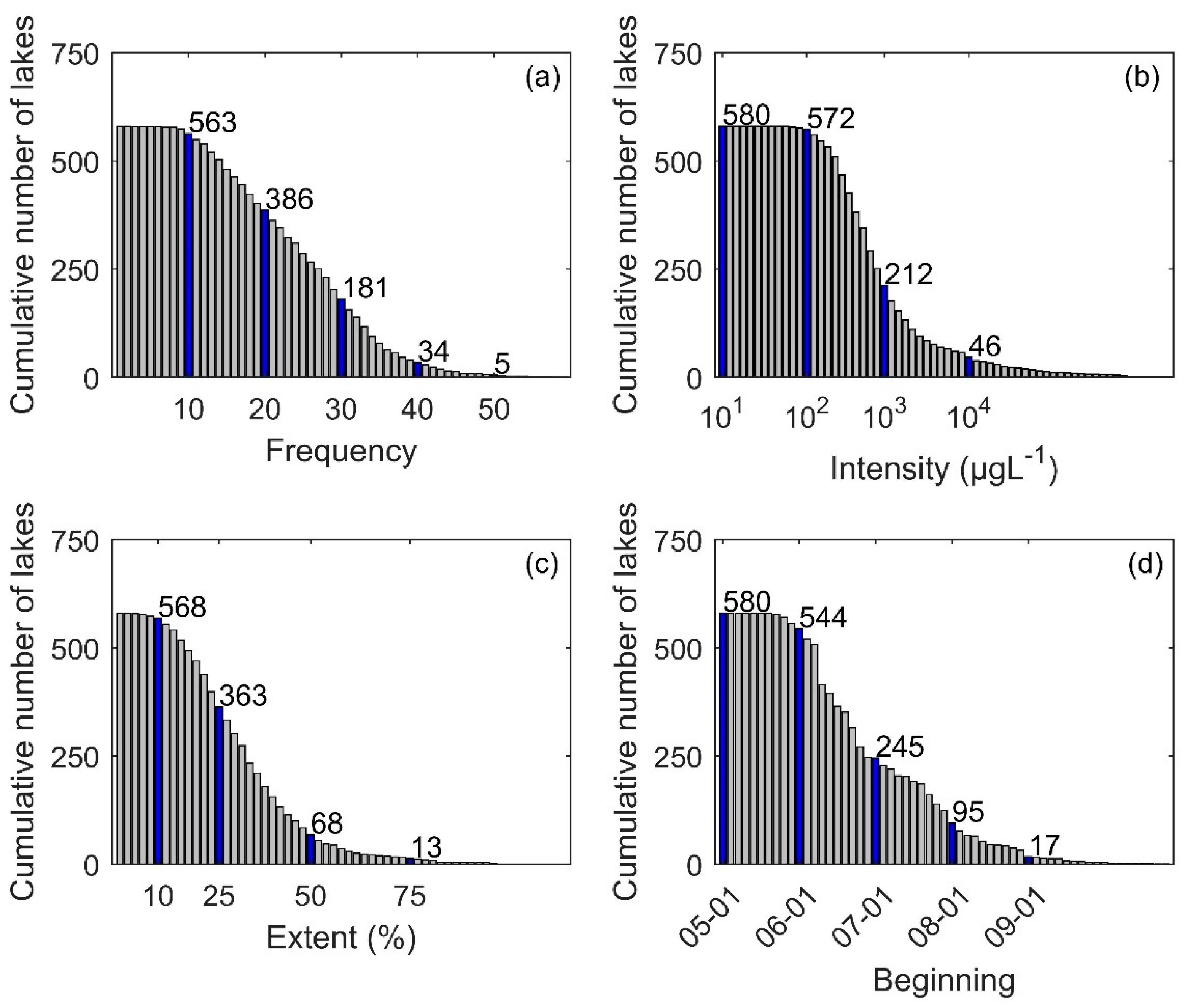
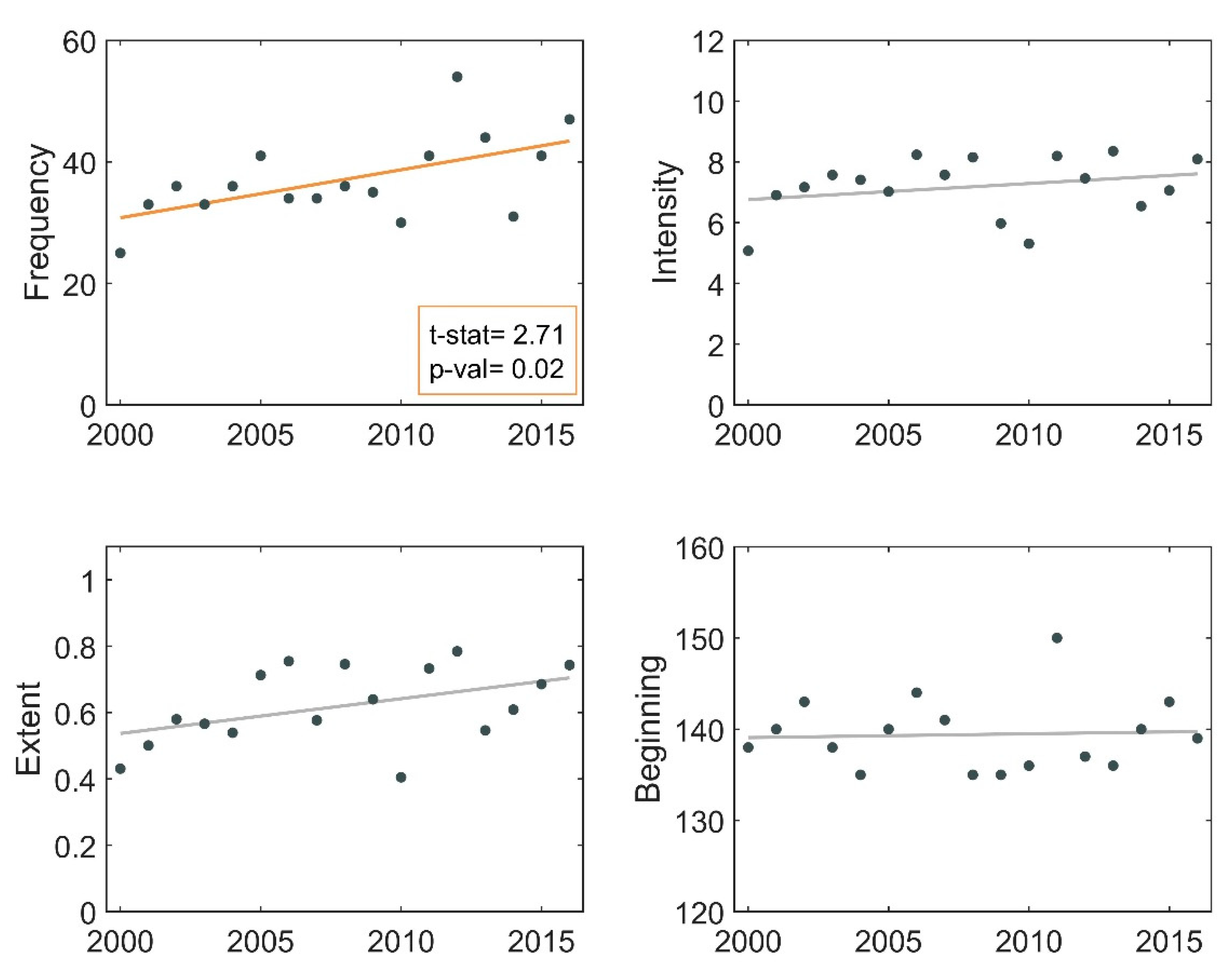
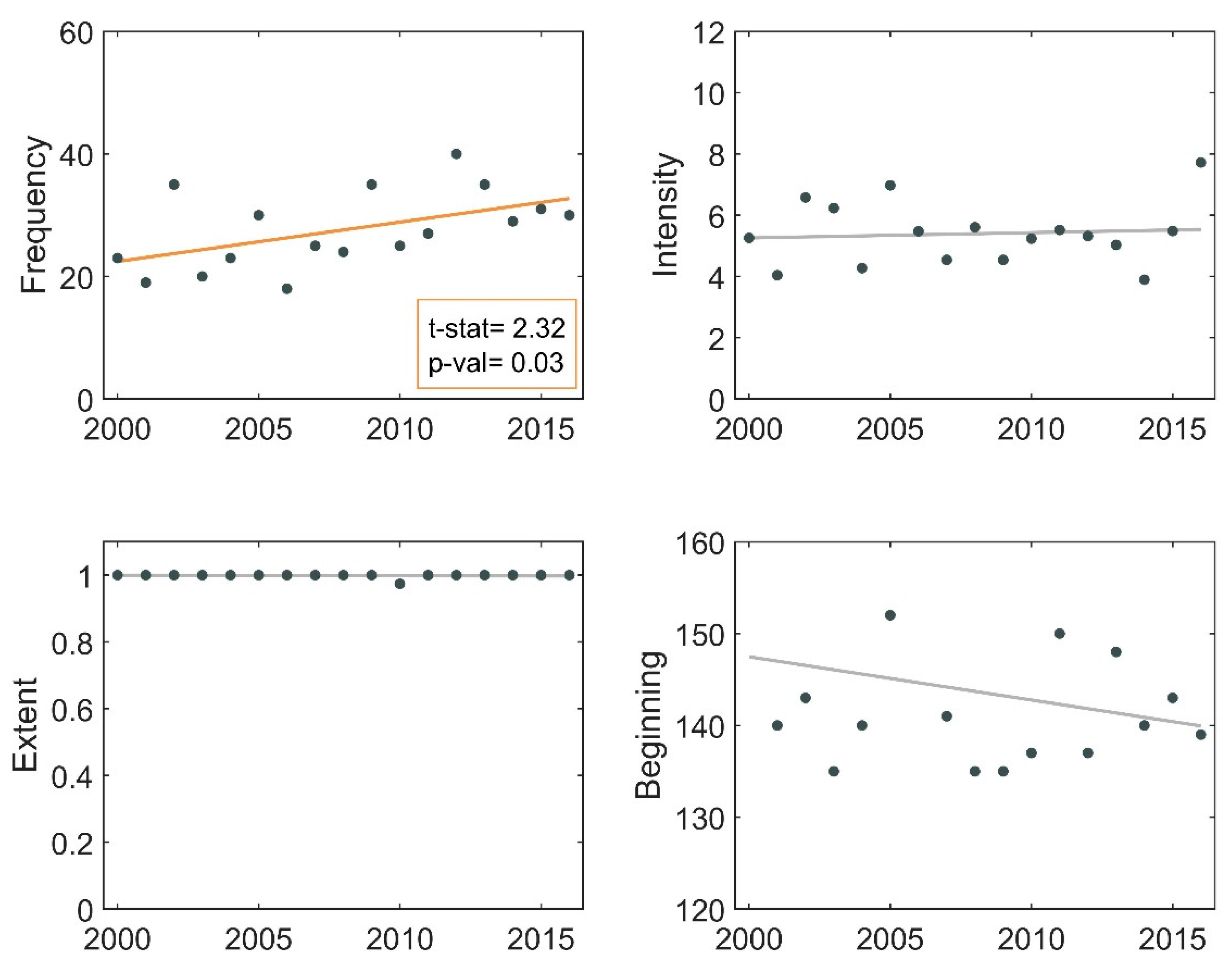
3.1. Descriptive Analysis of Bloom Events
3.2. Frequency of Blooms
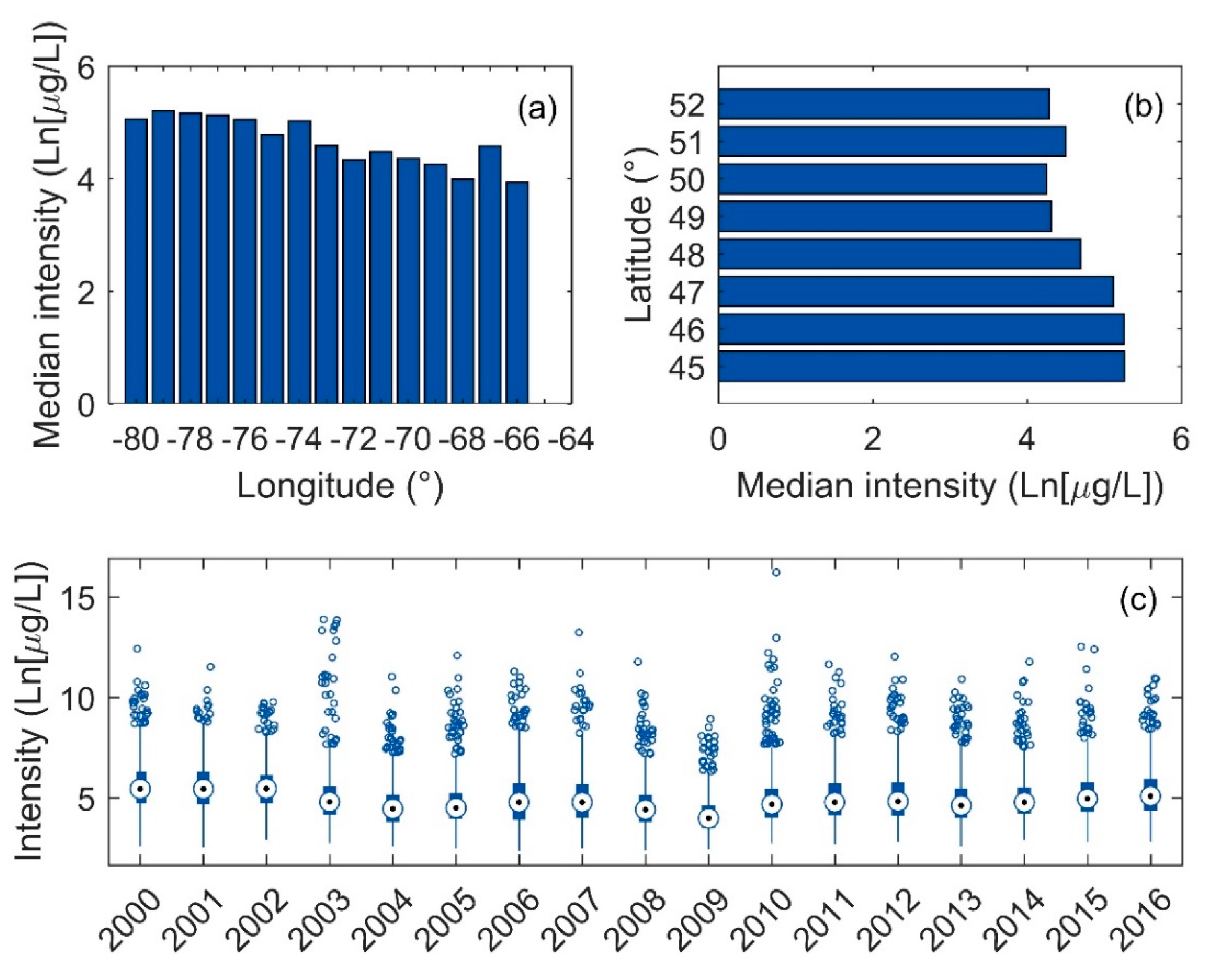
3.3. Intensity of Blooms
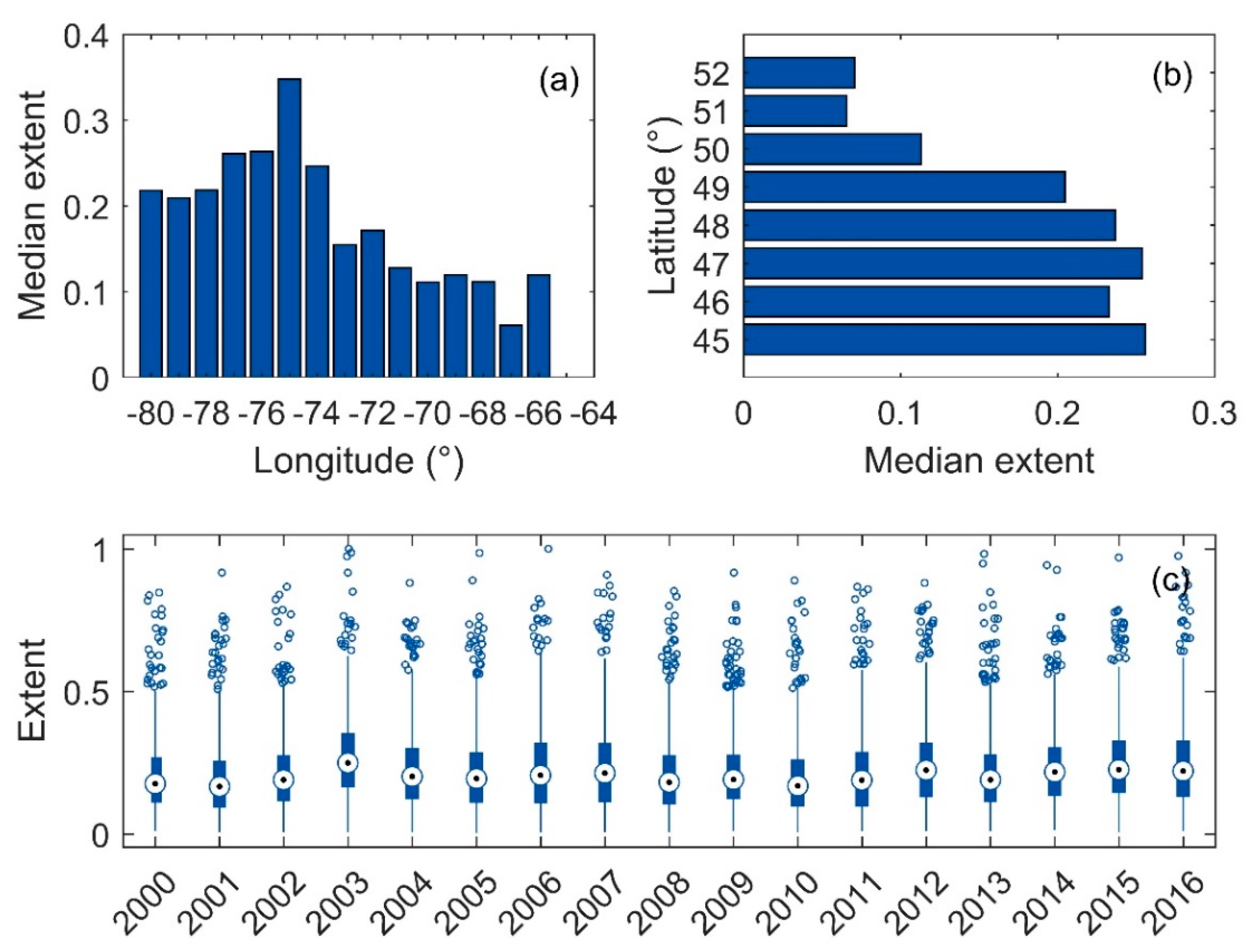
3.4. Surface Area of Blooms
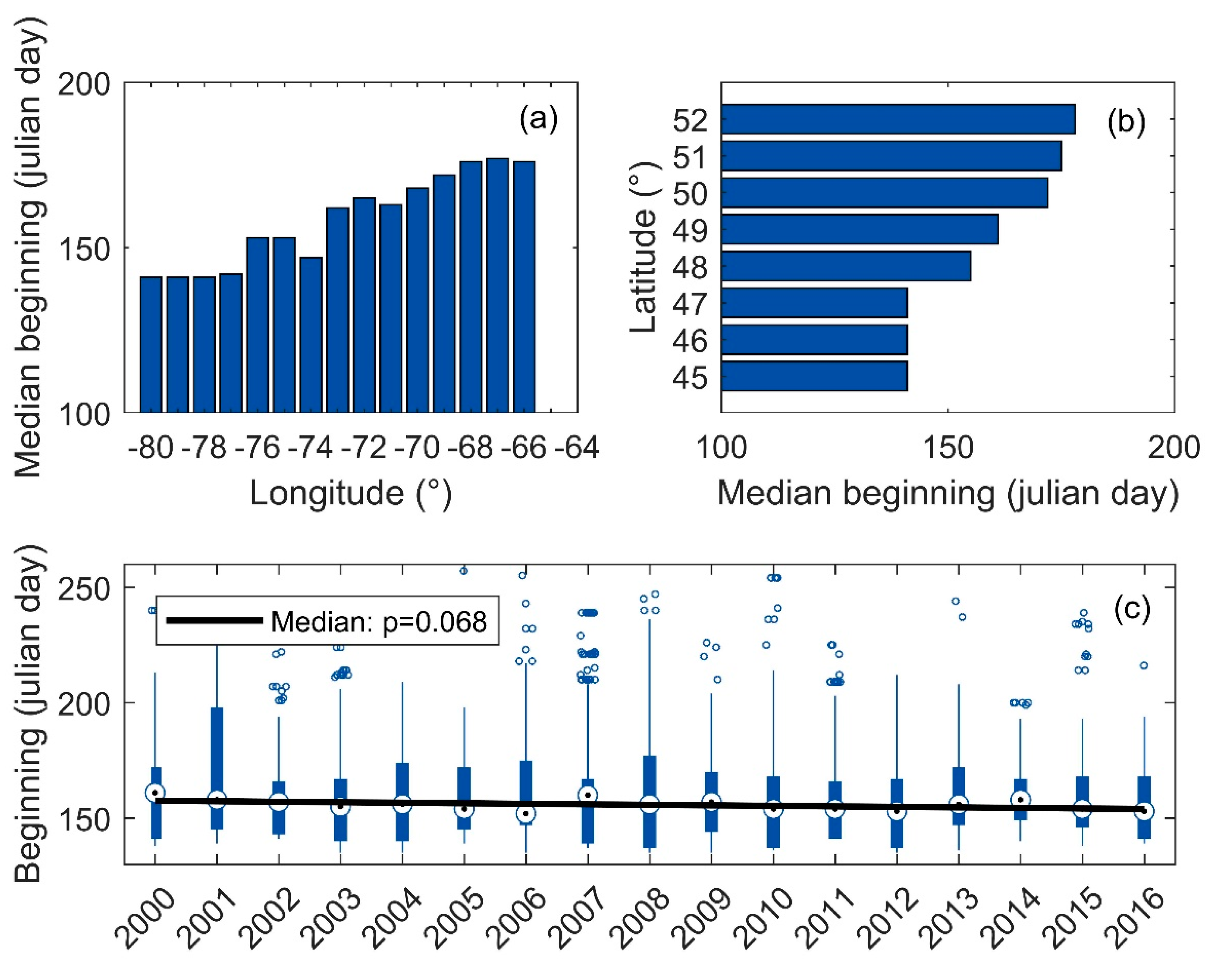
3.5. Onset Date of Blooms
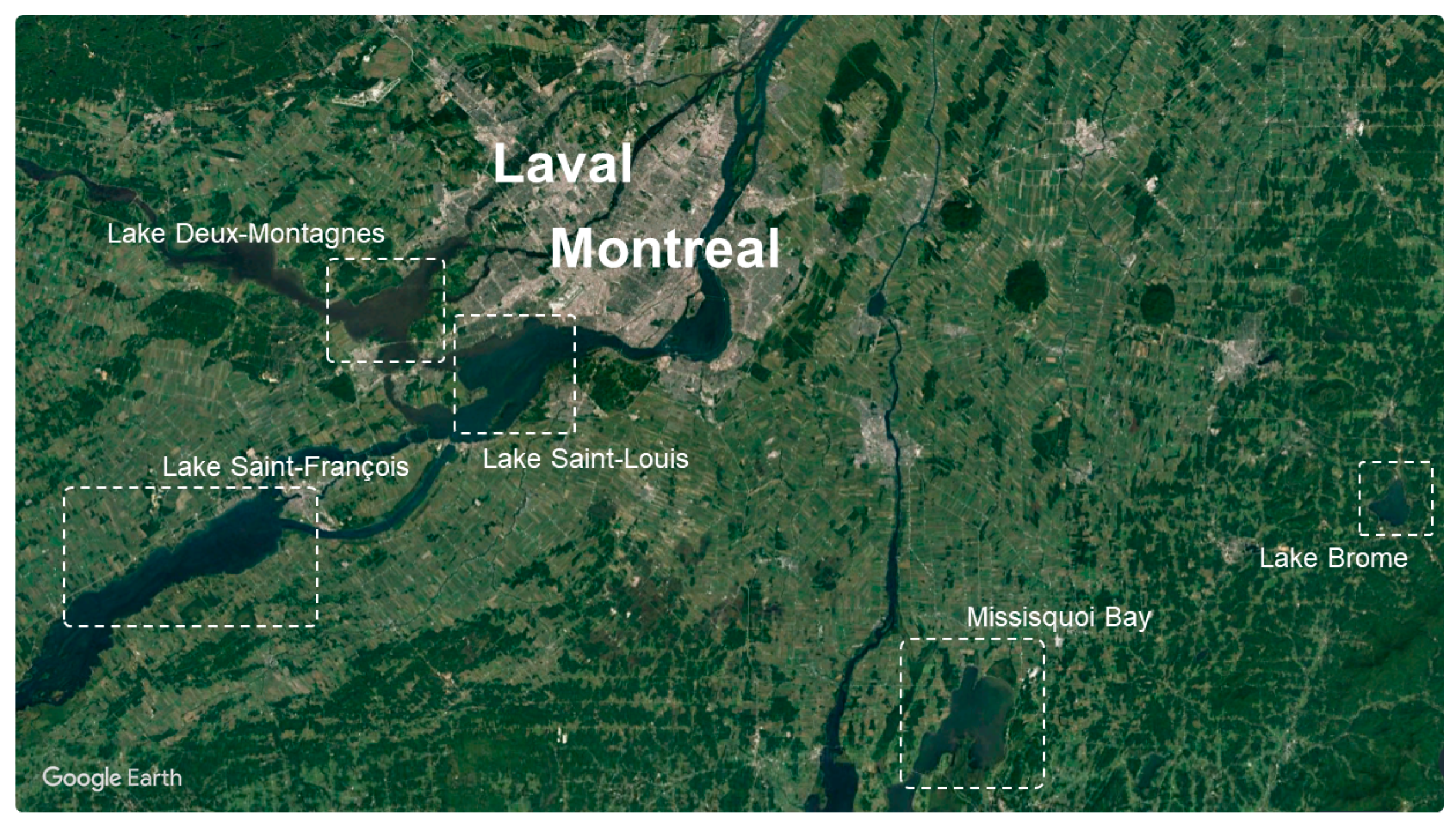
3.6. Phenological Trends of Missisquoi Bay and Lake Brome
3.7. Correlation Analysis
3.8. Canonical Correlation Analysis
3.8.1. Phenological Variables
3.8.2. Environmental Variables
4. Discussion
4.1. Phenological Trends
4.2. Links to Climate and Environmental Physiography
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Uncertainties on the Estimation of Pytoplankton Biomass and Global Trends
Appendix B
| Frequency | Intensity | Surface Area | Onset | ||
|---|---|---|---|---|---|
| Lake morphology | Area | 0.09 | 0.21 | −0.01 | −0.02 |
| Perimeter | 0.16 | 0.54 | −0.10 | −0.05 | |
| Gravelius coefficient | 0.22 | 0.50 | −0.18 | −0.11 | |
| Length of the Gravelius’s rectangle | 0.16 | 0.54 | −0.10 | −0.05 | |
| Width of the Gravelius’s rectangle | 0.15 | 0.25 | −0.01 | −0.03 | |
| Watershed morphology | Area | 0.16 | 0.27 | 0.06 | −0.05 |
| Perimeter | 0.18 | 0.37 | −0.03 | −0.06 | |
| Gravelius coefficient | 0.21 | 0.34 | −0.12 | -0.12 | |
| Length of the Gravelius’s rectangle | 0.18 | 0.37 | −0.03 | −0.06 | |
| Width of the Gravelius’s rectangle | 0.21 | 0.46 | −0.04 | −0.05 | |
| Slope—mean | 0.10 | 0.04 | 0.09 | −0.04 | |
| Slope—standard deviation | −0.24 | −0.09 | −0.14 | 0.22 | |
| Physiography | Land cover—Forest | 0.16 | 0.28 | 0.04 | −0.05 |
| Land cover—Settlement | 0.17 | 0.13 | 0.16 | −0.07 | |
| Land cover—Cropland | 0.20 | 0.16 | 0.21 | −0.08 | |
| Land cover—Forest (relative) | −0.33 | −0.10 | −0.21 | 0.17 | |
| Land cover—Settlement (relative) | 0.29 | 0.07 | 0.16 | −0.22 | |
| Land cover—Cropland (relative) | 0.30 | 0.10 | 0.20 | −0.13 | |
| Population ecumene | 0.32 | 0.06 | 0.25 | −0.30 | |
| Agriculture ecumene | 0.28 | 0.09 | 0.19 | −0.14 | |
| Climate | Total precipitation—annual | −0.23 | −0.43 | 0.02 | 0.11 |
| Total precipitation—summer | −0.22 | −0.35 | 0.01 | 0.09 | |
| Mean temperature—annual | −0.13 | −0.47 | 0.03 | 0.00 | |
| Mean temperature—summer | −0.13 | −0.47 | 0.03 | 0.01 | |
| Wind speed—annual | 0.02 | 0.02 | 0.08 | −0.04 | |
| Wind speed—summer | 0.09 | 0.06 | 0.08 | −0.08 | |
| Degree-days above 20 °C | 0.61 | 0.16 | 0.35 | −0.55 |
Appendix C
| Frequency | Intensity | Extent | Onset Date | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L Area | 1 | 1 | 0.32 | 0.29 | −0.66 | Frequency | ||||||||||||||||||||||
| L Perimeter | 0.50 | 1 | 1 | 0.03 | −0.16 | Intensity | ||||||||||||||||||||||
| L Shape index | 0.13 | 0.79 | 1 | 1 | −0.32 | Extent | ||||||||||||||||||||||
| L Length | 0.48 | 1.00 | 0.80 | 1 | 1 | Onset date | ||||||||||||||||||||||
| L Width | 0.90 | 0.39 | 0.00 | 0.37 | 1 | |||||||||||||||||||||||
| W Area | 0.57 | 0.52 | 0.29 | 0.51 | 0.60 | 1 | ||||||||||||||||||||||
| W Perimeter | 0.57 | 0.62 | 0.44 | 0.61 | 0.59 | 0.89 | 1 | |||||||||||||||||||||
| W Shape index | 0.26 | 0.43 | 0.50 | 0.43 | 0.24 | 0.41 | 0.69 | 1 | ||||||||||||||||||||
| W Length | 0.57 | 0.61 | 0.44 | 0.60 | 0.59 | 0.89 | 1.00 | 0.69 | 1 | |||||||||||||||||||
| W Width | 0.47 | 0.72 | 0.54 | 0.71 | 0.52 | 0.85 | 0.87 | 0.50 | 0.86 | 1 | ||||||||||||||||||
| Slope—mean | 0.01 | 0.11 | 0.13 | 0.11 | 0.01 | 0.59 | 0.37 | 0.10 | 0.37 | 0.43 | 1 | |||||||||||||||||
| Slope—std | 0.05 | −0.04 | −0.04 | −0.04 | 0.01 | −0.08 | −0.03 | 0.08 | −0.03 | −0.08 | −0.11 | 1 | ||||||||||||||||
| Forest | 0.55 | 0.52 | 0.30 | 0.51 | 0.59 | 1.00 | 0.90 | 0.42 | 0.90 | 0.86 | 0.57 | −0.08 | 1 | |||||||||||||||
| Settlement | 0.22 | 0.24 | 0.16 | 0.24 | 0.23 | 0.81 | 0.60 | 0.20 | 0.59 | 0.65 | 0.88 | −0.14 | 0.78 | 1 | ||||||||||||||
| Cropland | 0.21 | 0.24 | 0.15 | 0.24 | 0.25 | 0.77 | 0.59 | 0.20 | 0.59 | 0.66 | 0.72 | −0.15 | 0.75 | 0.95 | 1 | |||||||||||||
| Forest (rel) | −0.06 | −0.06 | 0.01 | −0.06 | −0.17 | −0.13 | −0.13 | −0.04 | −0.13 | −0.24 | −0.09 | 0.20 | −0.11 | −0.21 | −0.30 | 1 | ||||||||||||
| Settlement (rel) | 0.03 | 0.02 | −0.04 | 0.02 | 0.11 | 0.08 | 0.06 | 0.01 | 0.06 | 0.11 | 0.08 | −0.10 | 0.07 | 0.15 | 0.18 | −0.76 | 1 | |||||||||||
| Cropland (rel) | 0.06 | 0.07 | 0.01 | 0.07 | 0.17 | 0.13 | 0.14 | 0.05 | 0.14 | 0.26 | 0.07 | −0.22 | 0.11 | 0.21 | 0.31 | −0.96 | 0.55 | 1 | ||||||||||
| Population ecumene | 0.04 | 0.01 | −0.04 | 0.00 | 0.11 | 0.07 | 0.06 | 0.00 | 0.06 | 0.12 | 0.05 | −0.04 | 0.06 | 0.11 | 0.14 | −0.54 | 0.62 | 0.43 | 1 | |||||||||
| Agriculture ecumene | 0.08 | 0.07 | 0.01 | 0.07 | 0.17 | 0.13 | 0.14 | 0.05 | 0.14 | 0.24 | 0.06 | −0.20 | 0.11 | 0.19 | 0.27 | −0.87 | 0.63 | 0.85 | 0.48 | 1 | ||||||||
| Total pcp—annual | −0.29 | −0.54 | −0.40 | −0.54 | −0.30 | −0.41 | −0.42 | −0.22 | −0.42 | −0.54 | −0.14 | 0.04 | −0.41 | −0.27 | −0.30 | 0.21 | −0.18 | −0.20 | −0.13 | −0.18 | 1 | |||||||
| Total pcp—summer | −0.22 | −0.41 | −0.30 | −0.40 | −0.22 | −0.31 | −0.31 | −0.16 | −0.31 | −0.40 | −0.11 | −0.03 | −0.30 | −0.20 | −0.23 | 0.16 | −0.14 | −0.15 | −0.12 | −0.14 | 0.88 | 1 | ||||||
| Mean temp—annual | −0.43 | −0.79 | −0.56 | −0.79 | −0.44 | −0.60 | −0.62 | −0.30 | −0.62 | −0.79 | −0.21 | 0.05 | −0.60 | −0.39 | −0.43 | 0.13 | −0.04 | −0.15 | −0.01 | −0.12 | 0.67 | 0.50 | 1 | |||||
| Mean temp—summer | −0.43 | −0.79 | −0.56 | −0.79 | −0.44 | −0.60 | −0.62 | −0.30 | −0.62 | −0.79 | −0.21 | 0.05 | −0.60 | −0.39 | −0.43 | 0.14 | −0.04 | −0.16 | −0.02 | −0.12 | 0.67 | 0.51 | 1.00 | 1 | ||||
| Wind—annual | −0.01 | −0.01 | −0.02 | −0.01 | 0.00 | −0.03 | −0.04 | −0.07 | −0.04 | −0.02 | −0.01 | −0.12 | −0.02 | −0.02 | −0.02 | −0.11 | 0.13 | 0.08 | 0.04 | 0.04 | 0.00 | 0.04 | 0.01 | 0.02 | 1 | |||
| Wind—summer | −0.06 | −0.01 | 0.01 | −0.01 | −0.04 | −0.06 | −0.08 | −0.08 | −0.08 | −0.04 | −0.02 | −0.25 | −0.06 | −0.04 | −0.04 | −0.04 | 0.04 | 0.03 | −0.05 | −0.01 | 0.04 | 0.06 | 0.02 | 0.02 | 0.73 | 1 | ||
| Degree days | −0.09 | 0.00 | 0.06 | 0.00 | −0.06 | 0.01 | 0.01 | 0.08 | 0.01 | 0.02 | 0.07 | −0.26 | 0.01 | 0.08 | 0.09 | −0.24 | 0.26 | 0.20 | 0.27 | 0.21 | −0.13 | −0.13 | 0.02 | 0.02 | 0.10 | 0.18 | 1 | |
| L Area | L Perimeter | L Shape index | L Length | L Width | W Area | W Perimeter | W Shape index | W Length | W Width | Slope—mean | Slope—std | Forest | Settlement | Cropland | Forest (rel) | Settlement (rel) | Cropland (rel) | Pop ecumene | Agr ecumene | Pcp—annual | Pcp—summer | Temp—annual | Temp—summer | Wind—annual | Wind—summer | Degree days |
Appendix D
References
- Michalak, A.M.; Anderson, E.J.; Beletsky, D.; Boland, S.; Bosch, N.S.; Bridgeman, T.B.; Chaffin, J.D.; Cho, K.; Confesor, R.; Daloglu, I. Record-setting algal bloom in Lake Erie caused by agricultural and meteorological trends consistent with expected future conditions. Proc. Natl. Acad. Sci. USA 2013, 110, 6448–6452. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Higgins, S.N.; Pennuto, C.M.; Howell, E.T.; Lewis, T.W.; Makarewicz, J.C. Urban influences on Cladophora blooms in Lake Ontario. J. Great Lakes Res. 2012, 38, 116–123. [Google Scholar] [CrossRef]
- Duan, H.; Loiselle, S.A.; Zhu, L.; Feng, L.; Zhang, Y.; Ma, R. Distribution and incidence of algal blooms in Lake Taihu. Aquat. Sci. 2015, 77, 9–16. [Google Scholar] [CrossRef]
- Rosen, B.H.; Davis, T.W.; Gobler, C.J.; Kramer, B.J.; Loftin, K.A. Cyanobacteria of the 2016 Lake Okeechobee and Okeechobee Waterway Harmful Algal Bloom; No. 2017-1054; US Geological Survey: Reston, VA, USA, 2017. [CrossRef] [Green Version]
- Simiyu, B.M.; Oduor, S.O.; Rohrlack, T.; Sitoki, L.; Kurmayer, R. Microcystin Content in Phytoplankton and in Small Fish from Eutrophic Nyanza Gulf, Lake Victoria, Kenya. Toxins 2018, 10, 275. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chorus, I.; Bartram, J. Toxic Cyanobacteria in Water: A Guide to Their Public Health Consequences, Monitoring and Management; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Steffensen, D.A. Economic cost of cyanobacterial blooms. In Cyanobacterial Harmful Algal Blooms: State of the Science and Research Needs; Springer: New York, NY, USA, 2008; Volume 619. [Google Scholar] [CrossRef]
- Zamyadi, A.; McQuaid, N.; Prévost, M.; Dorner, S. Monitoring of potentially toxic cyanobacteria using an online multi-probe in drinking water sources. J. Environ. Monit. 2012, 14, 579–588. [Google Scholar] [CrossRef] [PubMed]
- Hozumi, A.; Ostrovsky, I.; Sukenik, A.; Gildor, H. Turbulence regulation of Microcystis surface scum formation and dispersion during a cyanobacteria bloom event. Inland Waters 2020, 10, 51–70. [Google Scholar] [CrossRef]
- Wheeler, S.M.; Morrissey, L.A.; Levine, S.N.; Livingston, G.P.; Vincent, W.F. Mapping cyanobacterial blooms in Lake Champlain’s Missisquoi Bay using QuickBird and MERIS satellite data. J. Great Lakes Res. 2012, 38, 68–75. [Google Scholar] [CrossRef]
- Bonnet, M.; Poulin, M. DyLEM-1D: A 1D physical and biochemical model for planktonic succession, nutrients and dissolved oxygen cycling: Application to a hyper-eutrophic reservoir. Ecol. Model. 2004, 180, 317–344. [Google Scholar] [CrossRef]
- Janssen, F.; Neumann, T.; Schmidt, M. Inter-annual variability in cyanobacteria blooms in the Baltic Sea controlled by wintertime hydrographic conditions. Mar. Ecol. Prog. Ser. 2004, 275, 59–68. [Google Scholar] [CrossRef]
- Laanemets, J.; Lilover, M.-J.; Raudsepp, U.; Autio, R.; Vahtera, E.; Lips, I.; Lips, U. A fuzzy logic model to describe the cyanobacteria Nodularia spumigena blooms in the Gulf of Finland, Baltic Sea. Hydrobiologia 2006, 554, 31–45. [Google Scholar] [CrossRef]
- Onderka, M. Correlations between several environmental factors affecting the bloom events of cyanobacteria in Liptovska Mara reservoir (Slovakia)—A simple regression model. Ecol. Model. 2007, 209, 412–416. [Google Scholar] [CrossRef]
- Garnier, J.; Nemery, J.; Billen, G.; Théry, S. Nutrient dynamics and control of eutrophication in the Marne River system: Modelling the role of exchangeable phosphorus. J. Hydrol. 2005, 304, 397–412. [Google Scholar] [CrossRef]
- Couture, R.-M.; Tominaga, K.; Starrfelt, J.; Moe, S.J.; Kaste, Ø.; Wright, R.F. Modelling phosphorus loading and algal blooms in a Nordic agricultural catchment-lake system under changing land-use and climate. Environ. Sci. Process. Impacts 2014, 16, 1588–1599. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cremona, F.; Vilbaste, S.; Couture, R.-M.; Nõges, P.; Nõges, T. Is the future of large shallow lakes blue-green? Comparing the response of a catchment-lake model chain to climate predictions. Clim. Chang. 2017, 141, 347–361. [Google Scholar] [CrossRef]
- Couture, R.-M.; Moe, S.J.; Lin, Y.; Kaste, Ø.; Haande, S.; Solheim, A.L. Simulating water quality and ecological status of Lake Vansjø, Norway, under land-use and climate change by linking process-oriented models with a Bayesian network. Sci. Total Environ. 2018, 621, 713–724. [Google Scholar] [CrossRef]
- Hu, W.; Connell, D.; Mengersen, K.; Tong, S. Weather variability, sunspots, and the blooms of cyanobacteria. EcoHealth 2009, 6, 71–78. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.; Guo, H.; Yu, S.; Sheng, H. Modelling the effect of weather conditions on cyanobacterial bloom outbreaks in Lake Dianchi: A rough decision-adjusted logistic regression model. Environ. Model. Assess. 2013, 18, 199–207. [Google Scholar] [CrossRef]
- Paerl, H.W. Controlling eutrophication along the freshwater–marine continuum: Dual nutrient (N and P) reductions are essential. Estuaries Coasts 2009, 32, 593–601. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Ma, H.; Sheng, D.; Wang, D. Assessing the interactions between chlorophyll a and environmental variables using copula method. J. Hydrol. Eng. 2011, 17, 495–506. [Google Scholar] [CrossRef]
- Davis, T.W.; Berry, D.L.; Boyer, G.L.; Gobler, C.J. The effects of temperature and nutrients on the growth and dynamics of toxic and non-toxic strains of Microcystis during cyanobacteria blooms. Harmful Algae 2009, 8, 715–725. [Google Scholar] [CrossRef]
- Guildford, S.J.; Hecky, R.E.; Smith, R.E.; Taylor, W.D.; Charlton, M.N.; Barlow-Busch, L.; North, R.L. Phytoplankton nutrient status in Lake Erie in 1997. J. Great Lakes Res. 2005, 31, 72–88. [Google Scholar] [CrossRef]
- Steffen, M.M.; Belisle, B.S.; Watson, S.B.; Boyer, G.L.; Wilhelm, S.W. Status, causes and controls of cyanobacterial blooms in Lake Erie. J. Great Lakes Res. 2014, 40, 215–225. [Google Scholar] [CrossRef]
- Chaffin, J.D.; Bridgeman, T.B.; Bade, D.L. Nitrogen constrains the growth of late summer cyanobacterial blooms in Lake Erie. Adv. Microbiol. 2013, 3, 16. [Google Scholar] [CrossRef] [Green Version]
- Duan, H.; Ma, R.; Zhang, Y.; Loiselle, S.A. Are algal blooms occurring later in Lake Taihu? Climate local effects outcompete mitigation prevention. J. Plankton Res. 2014, 36, 866–871. [Google Scholar] [CrossRef] [Green Version]
- Havens, K.E.; James, R.T.; East, T.L.; Smith, V.H. N: P ratios, light limitation, and cyanobacterial dominance in a subtropical lake impacted by non-point source nutrient pollution. Environ. Pollut. 2003, 122, 379–390. [Google Scholar] [CrossRef]
- Lilover, M.-J.; Stips, A. The variability of parameters controlling the cyanobacteria bloom biomass in the Baltic Sea. J. Mar. Syst. 2008, 74, 108–115. [Google Scholar] [CrossRef]
- Bergström, A.-K. The use of TN:TP and DIN:TP ratios as indicators for phytoplankton nutrient limitation in oligotrophic lakes affected by N deposition. Aquat. Sci. 2010, 72, 277–281. [Google Scholar] [CrossRef]
- Ptacnik, R.; Andersen, T.; Tamminen, T. Performance of the Redfield ratio and a family of nutrient limitation indicators as thresholds for phytoplankton N vs. P limitation. Ecosystems 2010, 13, 1201–1214. [Google Scholar] [CrossRef]
- Winder, M.; Berger, S.A.; Lewandowska, A.; Aberle, N.; Lengfellner, K.; Sommer, U.; Diehl, S. Spring phenological responses of marine and freshwater plankton to changing temperature and light conditions. Mar. Biol. 2012, 159, 2491–2501. [Google Scholar] [CrossRef]
- Mehnert, G.; Leunert, F.; Cirés, S.; Jöhnk, K.D.; Rücker, J.; Nixdorf, B.; Wiedner, C. Competitiveness of invasive and native cyanobacteria from temperate freshwaters under various light and temperature conditions. J. Plankton Res. 2010, 32, 1009–1021. [Google Scholar] [CrossRef]
- Paerl, H.W.; Hall, N.S.; Calandrino, E.S. Controlling harmful cyanobacterial blooms in a world experiencing anthropogenic and climatic-induced change. Sci. Total Environ. 2011, 409, 1739–1745. [Google Scholar] [CrossRef] [PubMed]
- Huisman, J.; Hulot, F.D. Population dynamics of harmful cyanobacteria. In Harmful Cyanobacteria; Springer: Berlin/Heidelberg, Germany, 2005; pp. 143–176. [Google Scholar] [CrossRef]
- Janssen, A.B.; Janse, J.H.; Beusen, A.H.; Chang, M.; Harrison, J.A.; Huttunen, I.; Kong, X.; Rost, J.; Teurlincx, S.; Troost, T.A. How to model algal blooms in any lake on earth. Curr. Opin. Environ. Sustain. 2019, 36, 1–10. [Google Scholar] [CrossRef]
- Reichwaldt, E.S.; Ghadouani, A. Effects of rainfall patterns on toxic cyanobacterial blooms in a changing climate: Between simplistic scenarios and complex dynamics. Water Res. 2012, 46, 1372–1393. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Duan, H.; Shi, X.; Yu, Y.; Kong, F. Contributions of meteorology to the phenology of cyanobacterial blooms: Implications for future climate change. Water Res. 2012, 46, 442–452. [Google Scholar] [CrossRef]
- Moss, B. Cogs in the endless machine: Lakes, climate change and nutrient cycles: A review. Sci. Total Environ. 2012, 434, 130–142. [Google Scholar] [CrossRef] [PubMed]
- Wagner, C.; Adrian, R. Cyanobacteria dominance: Quantifying the effects of climate change. Limnol. Oceanogr. 2009, 54, 2460–2468. [Google Scholar] [CrossRef]
- Bartosiewicz, M.; Przytulska, A.; Deshpande, B.N.; Antoniades, D.; Cortes, A.; MacIntyre, S.; Lehmann, M.F.; Laurion, I. Effects of climate change and episodic heat events on cyanobacteria in a eutrophic polymictic lake. Sci. Total Environ. 2019, 693, 133414. [Google Scholar] [CrossRef]
- Ho, J.C.; Michalak, A.M.; Pahlevan, N. Widespread global increase in intense lake phytoplankton blooms since the 1980s. Nature 2019, 574, 667–670. [Google Scholar] [CrossRef]
- Chapra, S.C.; Boehlert, B.; Fant, C.; Bierman Jr, V.J.; Henderson, J.; Mills, D.; Mas, D.M.; Rennels, L.; Jantarasami, L.; Martinich, J. Climate change impacts on harmful algal blooms in US freshwaters: A screening-level assessment. Environ. Sci. Technol. 2017, 51, 8933–8943. [Google Scholar] [CrossRef]
- Edwards, M.; Richardson, A.J. Impact of climate change on marine pelagic phenology and trophic mismatch. Nature 2004, 430, 881. [Google Scholar] [CrossRef]
- Winder, M.; Sommer, U. Phytoplankton response to a changing climate. Hydrobiologia 2012, 698, 5–16. [Google Scholar] [CrossRef]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S-PLUS; Springer Science & Business Media: Berlin, Germany, 2013; p. 487. [Google Scholar]
- Trishchenko, A.; Luo, Y.; Khlopenkov, K. A method for downscaling MODIS land channels to 250 m spatial resolution using adaptive regression and normalization. In Remote Sensing for Environmental Monitoring; International Society for Optics and Photonics: Bellingham, WA, USA, 2006; Volume 6366, p. 36607. [Google Scholar] [CrossRef]
- El-Alem, A.; Chokmani, K.; Laurion, I.; El-Adlouni, S.E.; Raymond, S.; Ratte-Fortin, C. Ensemble-Based Systems to Monitor Algal Bloom With Remote Sensing. IEEE Trans. Geosci. Remote. Sens. 2019, 57, 7955–7971. [Google Scholar] [CrossRef]
- Ratte-Fortin, C.; Chokmani, K.; El Alem, A. A novel algorithm for cloud detection over inland water bodies using 250m downscaled MODIS imagery. Int. J. Remote Sens. 2018, 39, 6429–6439. [Google Scholar] [CrossRef]
- World Health Organization. Guidelines for Safe Recreational Water Environments: Coastal and Fresh Waters; World Health Organization: Geneva, Switzerland, 2003; Volume 1, p. 253. [Google Scholar]
- Ministère du Développement durable, de l’Environnement, de la Faune & des Parcs. L’Eau. La Vie. L’Avenir. Politique Nationale De L’Eau; Bibliothèque nationale du Québec: Montréal, QC, Canada, 2002. [Google Scholar]
- Natural Resources Canada. Canadian Digital Elevation Model [Computer File]; Natural Resources Canada: Ottawa, ON, Canada, 2015. Available online: http://ouvert.canada.ca/data/fr/dataset/7f245e4d-76c2-4caa-951a-45d1d2051333 (accessed on 26 May 2017).
- Mesinger, F.; DiMego, G.; Kalnay, E.; Mitchell, K.; Shafran, P.C.; Ebisuzaki, W.; Jović, D.; Woollen, J.; Rogers, E.; Berbery, E.H. North American regional reanalysis. Bull. Am. Meteorol. Soc. 2006, 87, 343–360. [Google Scholar] [CrossRef] [Green Version]
- Dupuis, A.P.; Hann, B.J. Warm spring and summer water temperatures in small eutrophic lakes of the Canadian prairies: Potential implications for phytoplankton and zooplankton. J. Plankton Res. 2009, 31, 489–502. [Google Scholar] [CrossRef] [Green Version]
- Neuheimer, A.B.; Taggart, C.T. The growing degree-day and fish size-at-age: The overlooked metric. Can. J. Fish. Aquat. Sci. 2007, 64, 375–385. [Google Scholar] [CrossRef]
- Natural Resources Canada. Land Use 1990, 2000 & 2010. [Computer File]; Natural Resources Canada: Ottawa, ON, Canada, 2015. Available online: https://open.canada.ca/data/en/dataset/18e3ef1a-497c-40c6-8326-aac1a34a0dec (accessed on 17 August 2017).
- Natural Resources Canada. Population Ecumene Census Division. [Computer File]; Natural Resources Canada: Ottawa, ON, Canada, 2016. Available online: https://open.canada.ca/data/en/dataset/8498f9b4-4914-456c-9223-4260ea3bea4d (accessed on 17 August 2017).
- Kruskal, W.H.; Wallis, W.A. Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Bradley, J.V. Distribution-Free Statistical Tests; Prentice-Hall: Upper Saddle River, NJ, USA, 1968; p. 388. [Google Scholar]
- Jarque, C.M.; Bera, A.K. Efficient tests for normality, homoscedasticity and serial independence of regression residuals. Econ. Lett. 1980, 6, 255–259. [Google Scholar] [CrossRef]
- Bartlett, M.S. A note on tests of significance in multivariate analysis. Math. Proc. Camb. Philos. Soc. 1939, 35, 180–185. [Google Scholar] [CrossRef]
- Johnson, R.; Wichern, D. Applied Multivariate Statistical Analysis, 6th ed.; Pearson Prentice Hall: London, UK, 2007; p. 265. [Google Scholar]
- Thompson, B. A primer on the logic and use of canonical correlation analysis. Meas. Eval. Couns. Dev. 1991, 24, 80–93. [Google Scholar]
- Zientek, L.; Thompson, B. Commonality analysis: Partitioning variance to facilitate better understanding of data. J. Early Interv. 2006, 28, 299–307. [Google Scholar] [CrossRef]
- Henson, R.K. The Logic and Interpretation of Structure Coefficients in Multivariate General Linear Model Analyses. In Proceedings of the Annual Meeting of the American Educational Research Association, New Orleans, LA, USA, 1–5 April 2002; p. 35. [Google Scholar]
- Ministère de l’Environnement et de la Lutte contre les Changements Climatiques. Portrait global de la qualité des eaux au Québec: État et tendances de la qualité de l’eau en 2000. Direction des politiques du secteur agricole, ministère de l’Environnement, Québec, Envirodoq ENV/2003/0025. 2000, p. 143. Available online: http://www.environnement.gouv.qc.ca/eau/sys-image/global/global2.htm (accessed on 17 January 2019).
- Ministère de l’Environnement et de la Lutte contre les Changements Climatiques. Bilan de la gestion des épisodes de fleurs d’eau d’algues bleu-vert au Québec, de 2007 à 2012. Direction du suivi de l’état de l’environnement. 2014, p. 32. Available online: http://www.environnement.gouv.qc.ca/eau/algues-bv/bilan/Bilan_ABV_2007-2012.pdf (accessed on 17 January 2019).
- Ministère de l’Environnement et de la Lutte contre les Changements Climatiques. Bilan final des plans d’eau touchés par une fleur d’eau d’algues bleu-vert en 2009. Direction du suivi de l’état de l’environnement. 2010, p. 11. Available online: http://www.grobec.org/pdf/action/bilan_cyanobacteries_quebec_2009.pdf (accessed on 17 January 2019).
- Winter, J.G.; DeSellas, A.M.; Fletcher, R.; Heintsch, L.; Morley, A.; Nakamoto, L.; Utsumi, K. Algal blooms in Ontario, Canada: Increases in reports since 1994. Lake Reserv. Manag. 2011, 27, 107–114. [Google Scholar] [CrossRef] [Green Version]
- Huisman, J.; Codd, G.A.; Paerl, H.W.; Ibelings, B.W.; Verspagen, J.M.; Visser, P.M. Cyanobacterial blooms. Nat. Rev. Microbiol. 2018, 16, 471. [Google Scholar] [CrossRef] [PubMed]
- Taranu, Z.E.; Gregory-Eaves, I.; Leavitt, P.R.; Bunting, L.; Buchaca, T.; Catalan, J.; Domaizon, I.; Guilizzoni, P.; Lami, A.; McGowan, S.; et al. Acceleration of cyanobacterial dominance in north temperate-subarctic lakes during the Anthropocene. Ecol. Lett. 2015, 18, 375–384. [Google Scholar] [CrossRef] [PubMed]
- Weber, S.J.; Mishra, D.R.; Wilde, S.B.; Kramer, E. Risks for cyanobacterial harmful algal blooms due to land management and climate interactions. Sci. Total Environ. 2020, 703, 134608. [Google Scholar] [CrossRef] [PubMed]
- Fortin, N.; Aranda-Rodriguez, R.; Jing, H.; Pick, F.; Bird, D.; Greer, C.W. Detection of microcystin-producing cyanobacteria in Missisquoi Bay, Quebec, Canada, using quantitative PCR. Appl. Environ. Microbiol. 2010, 76, 5105–5112. [Google Scholar] [CrossRef] [Green Version]
- Rashidan, K.; Bird, D. Role of predatory bacteria in the termination of a cyanobacterial bloom. Microb. Ecol. 2001, 41, 97–105. [Google Scholar] [CrossRef]
- Rolland, A.; Bird, D.F.; Giani, A. Seasonal changes in composition of the cyanobacterial community and the occurrence of hepatotoxic blooms in the eastern townships, Québec, Canada. J. Plankton Res. 2005, 27, 683–694. [Google Scholar] [CrossRef] [Green Version]
- Smeltzer, E.; d Shambaugh, A.; Stangel, P. Environmental change in Lake Champlain revealed by long-term monitoring. J. Great Lakes Res. 2012, 38, 6–18. [Google Scholar] [CrossRef]
- Duan, H.; Ma, R.; Xu, X.; Kong, F.; Zhang, S.; Kong, W.; Hao, J.; Shang, L. Two-decade reconstruction of algal blooms in China’s Lake Taihu. Environ. Sci. Technol. 2009, 43, 3522–3528. [Google Scholar] [CrossRef]
- Dibike, Y.; Prowse, T.; Saloranta, T.; Ahmed, R. Response of Northern Hemisphere lake-ice cover and lake-water thermal structure patterns to a changing climate. Hydrol. Process. 2011, 25, 2942–2953. [Google Scholar] [CrossRef]
- Kraemer, B.M.; Mehner, T.; Adrian, R. Reconciling the opposing effects of warming on phytoplankton biomass in 188 large lakes. Sci. Rep. 2017, 7, 10762. [Google Scholar] [CrossRef] [PubMed]
- Anderson, D.M.; Glibert, P.M.; Burkholder, J.M. Harmful algal blooms and eutrophication: Nutrient sources, composition, and consequences. Estuaries 2002, 25, 704–726. [Google Scholar] [CrossRef]
- Paerl, H.W.; Scott, J.T. Throwing Fuel on the Fire: Synergistic Effects of Excessive Nitrogen Inputs and Global Warming on Harmful Algal Blooms; ACS Publications: Washington, DC, USA, 2010. [Google Scholar] [CrossRef]
- Schreurs, H. Cyanobacterial Dominance Relations to Eutrophication and Lake Morphology. Ph.D. Thesis, University of Amsterdam, Amsterdam, The Netherlands, 1992; p. 198. [Google Scholar]
- Elliott, J.A. The seasonal sensitivity of cyanobacteria and other phytoplankton to changes in flushing rate and water temperature. Glob. Chang. Boil. 2010, 16, 864–876. [Google Scholar] [CrossRef]
- Carvalho, L.; Miller, C.A.; Scott, E.M.; Codd, G.A.; Davies, P.S.; Tyler, A.N. Cyanobacterial blooms: Statistical models describing risk factors for national-scale lake assessment and lake management. Sci. Total Environ. 2011, 409, 5353–5358. [Google Scholar] [CrossRef] [Green Version]
- Elliott, J.A. Is the future blue-green? A review of the current model predictions of how climate change could affect pelagic freshwater cyanobacteria. Water Res. 2012, 46, 1364–1371. [Google Scholar] [CrossRef] [Green Version]
- Larson, J.H.; Evans, M.A.; Kennedy, R.J.; Bailey, S.W.; Loftin, K.A.; Laughrey, Z.R.; Femmer, R.A.; Schaeffer, J.S.; Richardson, W.B.; Wynne, T.T. Associations between cyanobacteria and indices of secondary production in the western basin of Lake Erie. Limnol. Oceanogr. 2018, 63, 232–243. [Google Scholar] [CrossRef]
- Ralston, D.K.; Keafer, B.A.; Brosnahan, M.L.; Anderson, D.M. Temperature dependence of an estuarine harmful algal bloom: Resolving interannual variability in bloom dynamics using a degree-day approach. Limnol. Oceanogr. 2014, 59, 1112–1126. [Google Scholar] [CrossRef]
- Trudgill, D.L.; Honek, A.; Li, D.; Straalen, N.M. Thermal time—Concepts and utility. Ann. Appl. Boil. 2005, 146, 1–14. [Google Scholar] [CrossRef]
- Trombetta, T.; Vidussi, F.; Mas, S.; Parin, D.; Simier, M.; Mostajir, B. Water temperature drives phytoplankton blooms in coastal waters. PLoS ONE 2019, 14, e0214933. [Google Scholar] [CrossRef] [Green Version]
- Ho, J.C.; Michalak, A.M. Exploring temperature and precipitation impacts on harmful algal blooms across continental US lakes. Limnol. Oceanogr. 2020, 65, 992–1009. [Google Scholar] [CrossRef] [Green Version]
- Pick, F.R. Blooming algae: A Canadian perspective on the rise of toxic cyanobacteria. Can. J. Fish. Aquat. Sci. 2016, 73, 1149–1158. [Google Scholar] [CrossRef] [Green Version]
- De Jong, S.; Auping, W.L.; Oosterveld, W.T.; Usanov, A.; Abdalla, M.; van de Bovenkamp, A.; della Frattina, C.F. The Geopolitical Impact of Climate Mitigation Policies. How Hydrocarbon Exporting Rentier States and Developing Nations can Prepare for a More Sustainable Future; The Hague Centre for Strategic Studies: Hague, The Netherlands, 2017; p. 99. [Google Scholar]
- Canadian Geographic. Extreme of Weather. 2018. Available online: http://www.canadiangeographic.com/atlas/themes.aspx?id=weather&sub=weather_power_solarpower&lang=En (accessed on 21 September 2018).
- Cole, H.; Henson, S.; Martin, A.; Yool, A. Mind the gap: The impact of missing data on the calculation of phytoplankton phenology metrics. J. Geophys. Res. Ocean. 2012, 117, 1–8. [Google Scholar] [CrossRef]

| Phenological Variables | Environmental Variables |
|---|---|
| 1—Frequency | 1—Lake area |
| 2—Intensity | 2—Lake shape index |
| 3—Surface area | 3—Watershed area |
| 4—Onset date | 4—Watershed shape index |
| 5—Watershed slope—standard deviation | |
| 6—Land cover—Forest (%) | |
| 7—Land cover—Settlement (%) | |
| 8—Land cover—Cropland (%) | |
| 9—Population ecumene | |
| 10—Agriculture ecumene | |
| 11—Total precipitation—annual | |
| 12—Mean temperature—annual | |
| 13—Degree-days above 20 °C | |
| 14—Wind speed—summer |
| Observed Test Statistic | Degrees of Freedom | |||||
|---|---|---|---|---|---|---|
| 1 | 0.77 | 0.53 | 0.15 | 16,067 | 56 | 83.51 |
| 2 | 0.71 | 0.24 | 0.17 | 7470 | 39 | 62.43 |
| 3 | 0.23 | 0.14 | 0.07 | 697 | 24 | 42.98 |
| 4 | 0.13 | 0.09 | 0.05 | 167 | 11 | 24.72 |
| Total | 1 | 0.44 |
| Phenology | Morphology | Physiography | Climate | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Frequency (x1,1) | Intensity (x1,2) | Surface Area (x1,3) | Onset Date (x1,4) | Lake Area (x2,1) | Lake Shape Index (x2,2) | Watershed Area (x2,3) | Watershed Shape Index (x2,4) | Slope (x2,5) | Forest (x2,6) | Settlement (x2,7) | Cropland (x2,8) | Population Ecumene (x2,9) | Agriculture Ecumene (x2,10) | Precipitation (x2,11) | Temperature (x2,12) | Degree-Days (x2,13) | Wind Speed (x2,14) | |
| Function 1 | ||||||||||||||||||
| a1,i, b1,j: | −0.54 | −0.20 | −0.06 | 0.41 | −0.36 | −0.05 | 0.21 | −0.13 | 0.14 | −0.20 | −0.37 | 0.16 | −0.22 | −0.11 | 0.15 | −0.10 | −0.56 | 0.05 |
| ,: | −0.94 | −0.49 | −0.46 | 0.89 | −0.38 | −0.27 | −0.19 | −0.27 | 0.27 | 0.38 | −0.65 | −0.10 | −0.48 | −0.32 | 0.27 | 0.02 | −0.84 | −0.10 |
| Function 2 | ||||||||||||||||||
| a2,i, b2,j: | −0.21 | −0.69 | 0.73 | −0.22 | −0.89 | 0.21 | −0.15 | 0.02 | −0.05 | 0.08 | 0.13 | −0.05 | 0.20 | 0.17 | 0.26 | 0.08 | 0.18 | −0.05 |
| ,: | 0.00 | −0.66 | 0.70 | −0.22 | −0.86 | −0.55 | −0.67 | −0.41 | −0.05 | −0.06 | 0.17 | −0.36 | 0.19 | 0.03 | 0.44 | 0.54 | 0.26 | 0.01 |
| h2: | 88.3% | 67.2% | 70.2% | 84.1% | 88.4% | 37.8% | 48.9% | 24.6% | 7.8% | 14.6% | 45.4% | 14.2% | 26.4% | 10.3% | 26.5% | 29.4% | 77.6% | 1.0% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ratté-Fortin, C.; Chokmani, K.; Laurion, I. Spatiotemporal Variability in Phytoplankton Bloom Phenology in Eastern Canadian Lakes Related to Physiographic, Morphologic, and Climatic Drivers. Environments 2020, 7, 77. https://0-doi-org.brum.beds.ac.uk/10.3390/environments7100077
Ratté-Fortin C, Chokmani K, Laurion I. Spatiotemporal Variability in Phytoplankton Bloom Phenology in Eastern Canadian Lakes Related to Physiographic, Morphologic, and Climatic Drivers. Environments. 2020; 7(10):77. https://0-doi-org.brum.beds.ac.uk/10.3390/environments7100077
Chicago/Turabian StyleRatté-Fortin, Claudie, Karem Chokmani, and Isabelle Laurion. 2020. "Spatiotemporal Variability in Phytoplankton Bloom Phenology in Eastern Canadian Lakes Related to Physiographic, Morphologic, and Climatic Drivers" Environments 7, no. 10: 77. https://0-doi-org.brum.beds.ac.uk/10.3390/environments7100077






