A Novel Approach to Shadow Boundary Detection Based on an Adaptive Direction-Tracking Filter for Brain-Machine Interface Applications
Abstract
:1. Introduction
- Development of a BMI prototype-based on a novel shadow detection system for controlling wheelchairs
- Development of an adaptive direction tracking filter to extract more effective feature information with less redundancy and time
- Development of a machine learning based system able to automatically detect shadows in an image
2. Related Works
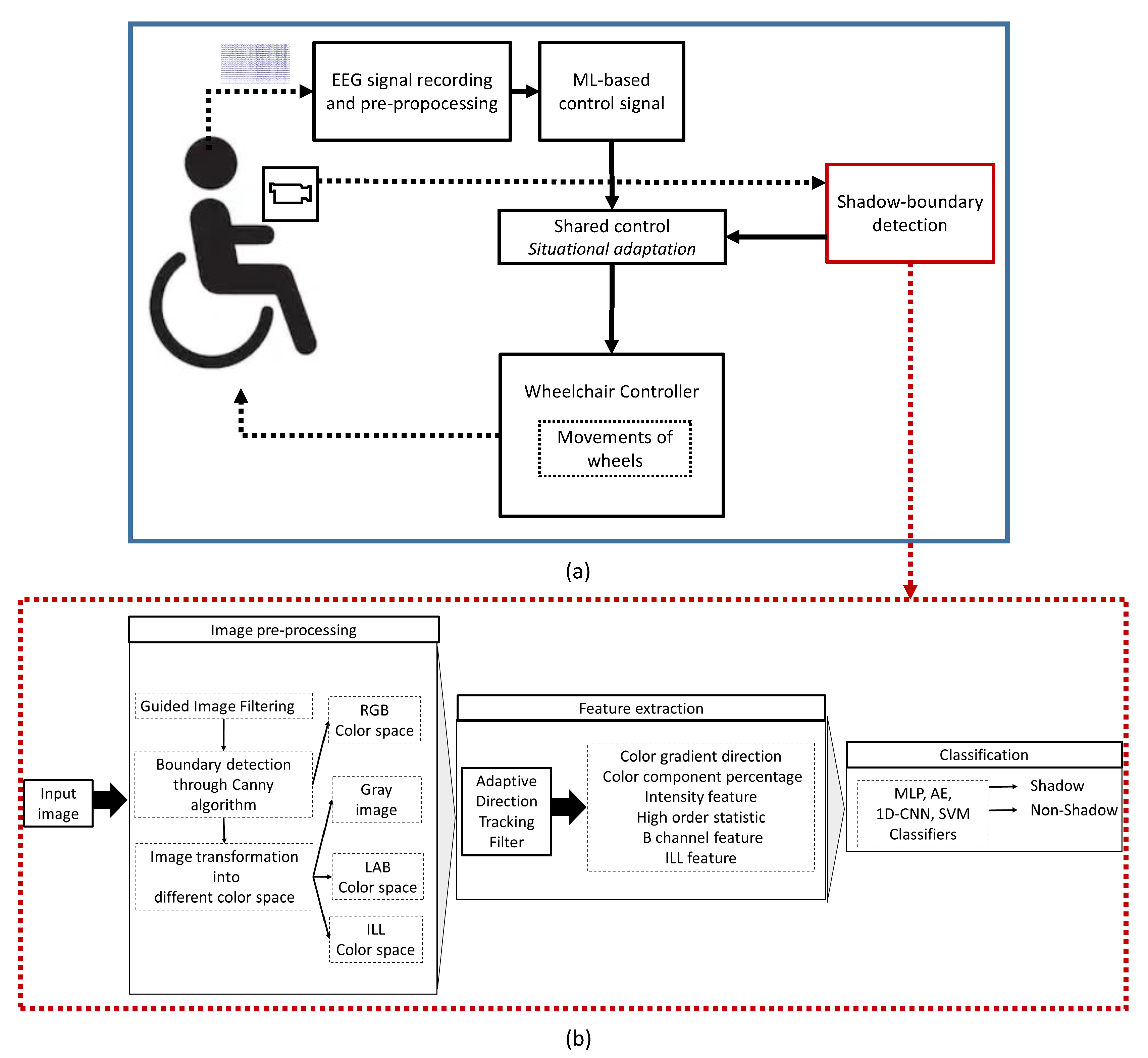
3. Proposed BMI System
3.1. Dataset Description
3.2. Image Pre-Processing
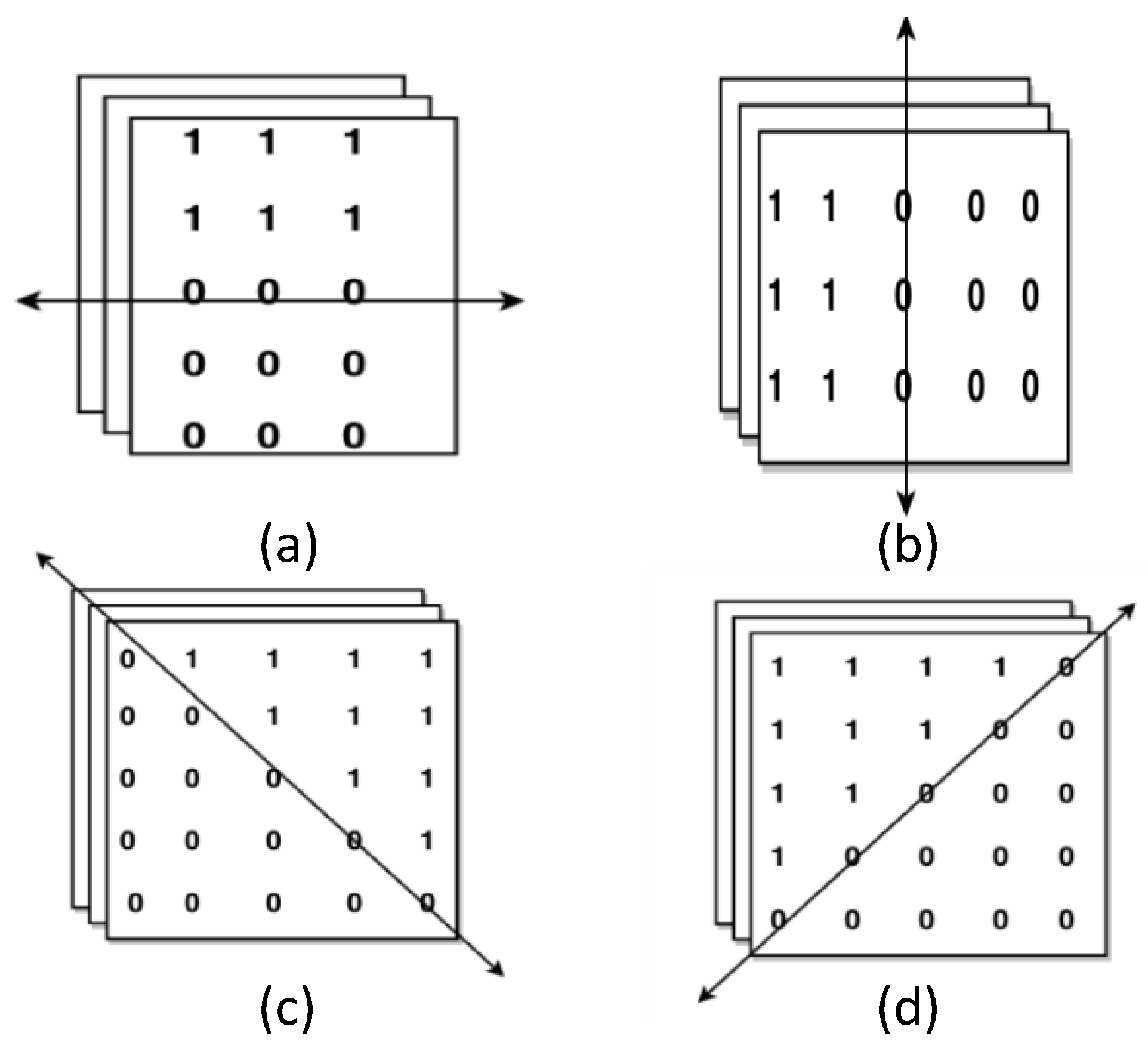
3.3. Design of Adaptive Direction Tracking (ADT) Filter
3.4. Feature Extraction
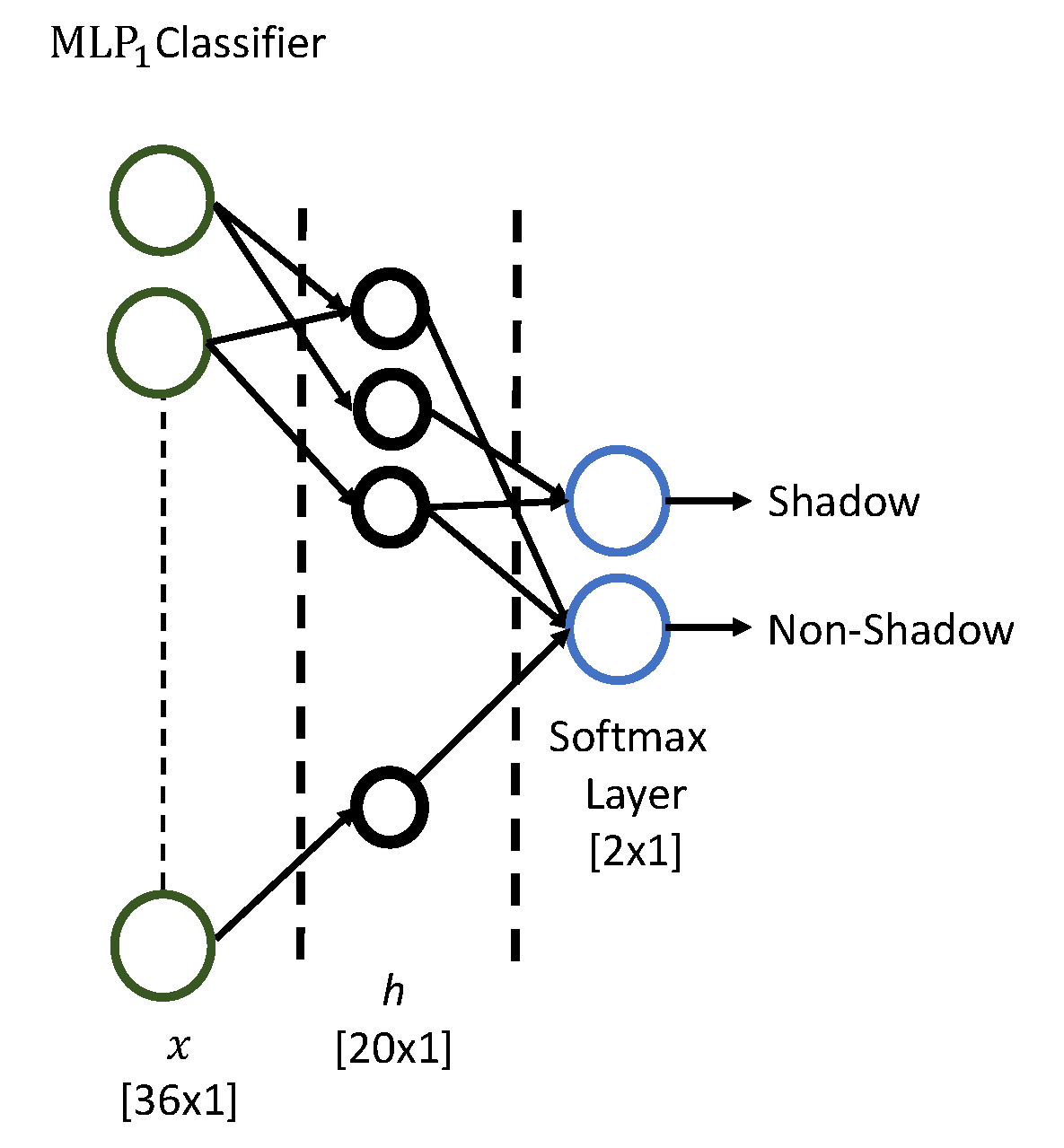
3.5. Machine Learning Models
4. Results and Discussion
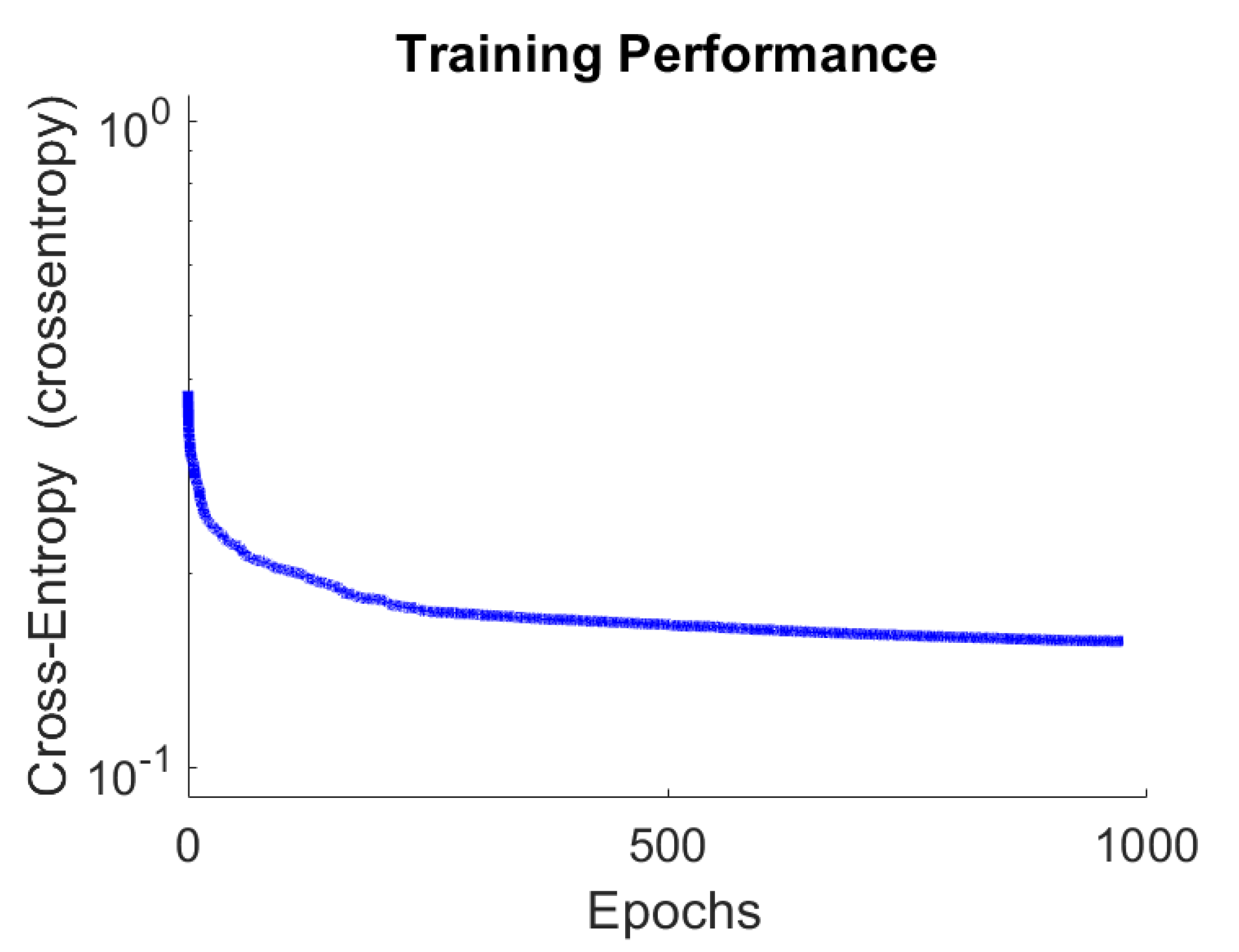
4.1. Performance of the Proposed System
4.2. Permutation Analysis
4.3. Comparison of Shadow Detection Models
5. Summary and Future Works
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Carmena, J.M.; Lebedev, M.A.; Crist, R.E.; O’Doherty, J.E.; Santucci, D.M.; Dimitrov, D.F.; Patil, P.G.; Henriquez, C.S.; Nicolelis, M.A. Learning to control a brain–machine interface for reaching and grasping by primates. PLoS Biol. 2003, 1, e42. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Solé-Casals, J.; Caiafa, C.F.; Zhao, Q.; Cichocki, A. Brain-Computer Interface with Corrupted EEG Data: A Tensor Completion Approach. Cogn. Comput. 2018, 10, 1062–1074. [Google Scholar] [CrossRef] [Green Version]
- Ullman, S. High-Level Vision: Object Recognition and Visual Cognition; MIT Press: Cambridge, MA, USA, 1996; Volume 2. [Google Scholar]
- Russell, M.; Zou, J.J.; Fang, G. An evaluation of moving shadow detection techniques. Comput. Vis. Media 2016, 2, 195–217. [Google Scholar] [CrossRef] [Green Version]
- Xiang, J.; Fan, H.; Liao, H.; Xu, J.; Sun, W.; Yu, S. Moving object detection and shadow removing under changing illumination condition. Math. Probl. Eng. 2014, 2014, 827461. [Google Scholar] [CrossRef] [Green Version]
- Liasis, G.; Stavrou, S. Satellite images analysis for shadow detection and building height estimation. ISPRS J. Photogramm. Remote Sens. 2016, 119, 437–450. [Google Scholar] [CrossRef]
- Okabe, T.; Sato, I.; Sato, Y. Attached shadow coding: Estimating surface normals from shadows under unknown reflectance and lighting conditions. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 1693–1700. [Google Scholar]
- Wei, H.; Liu, Y.; Xing, G.; Zhang, Y.; Huang, W. Simulating Shadow Interactions for Outdoor Augmented Reality with RGBD Data. IEEE Access 2019, 7, 75292–75304. [Google Scholar] [CrossRef]
- Huang, X.; Hua, G.; Tumblin, J.; Williams, L. What characterizes a shadow boundary under the sun and sky? In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 898–905. [Google Scholar]
- Zhu, J.; Samuel, K.G.; Masood, S.Z.; Tappen, M.F. Learning to recognize shadows in monochromatic natural images. In Proceedings of the 2010 IEEE Computer Society conference on computer vision and pattern recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 223–230. [Google Scholar]
- Lalonde, J.F.; Efros, A.A.; Narasimhan, S.G. Detecting ground shadows in outdoor consumer photographs. In Proceedings of the European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2010; pp. 322–335. [Google Scholar]
- Ieracitano, C.; Mammone, N.; Hussain, A.; Morabito, F.C. A novel multi-modal machine learning based approach for automatic classification of EEG recordings in dementia. Neural Netw. 2020, 123, 176–190. [Google Scholar] [CrossRef] [PubMed]
- Ieracitano, C.; Adeel, A.; Morabito, F.C.; Hussain, A. A novel statistical analysis and autoencoder driven intelligent intrusion detection approach. Neurocomputing 2020, 387, 51–62. [Google Scholar] [CrossRef]
- Hou, B.; Kang, G.; Zhang, N.; Liu, K. Multi-target Interactive Neural Network for Automated Segmentation of the Hippocampus in Magnetic Resonance Imaging. Cogn. Comput. 2019, 11, 630–643. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, Z. Optimal Feature Selection for Learning-Based Algorithms for Sentiment Classification. Cogn. Comput. 2019, 12, 238–248. [Google Scholar] [CrossRef]
- Lee, D.H. One-shot scale and angle estimation for fast visual object tracking. IEEE Access 2019, 7, 55477–55484. [Google Scholar] [CrossRef]
- Yao, C.; Sun, P.; Zhi, R.; Shen, Y. Learning coexistence discriminative features for multi-class object detection. IEEE Access 2018, 6, 37676–37684. [Google Scholar] [CrossRef]
- Mahmood, A.; Uzair, M.; Al-Maadeed, S. Multi-order statistical descriptors for real-time face recognition and object classification. IEEE Access 2018, 6, 12993–13004. [Google Scholar] [CrossRef]
- Zhai, S.; Shang, D.; Wang, S.; Dong, S. DF-SSD: An Improved SSD Object Detection Algorithm Based on DenseNet and Feature Fusion. IEEE Access 2020, 8, 24344–24357. [Google Scholar] [CrossRef]
- Hamad, E.M.; Al-Gharabli, S.I.; Saket, M.M.; Jubran, O. A Brain Machine Interface for command based control of a wheelchair using conditioning of oscillatory brain activity. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Seogwipo, Korea, 11–15 July 2017; pp. 1002–1005. [Google Scholar]
- Xin, L.; Gao, S.; Tang, J.; Xu, X. Design of a Brain Controlled Wheelchair. In Proceedings of the 2018 IEEE 4th International Conference on Control Science and Systems Engineering (ICCSSE), Wuhan, China, 21–23 August 2018; pp. 112–116. [Google Scholar]
- Deng, X.; Yu, Z.L.; Lin, C.; Gu, Z.; Li, Y. A Bayesian Shared Control Approach for Wheelchair Robot with Brain Machine Interface. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 28, 328–338. [Google Scholar] [CrossRef]
- Ruhunage, I.; Perera, C.J.; Munasinghe, I.; Lalitharatne, T.D. EEG-SSVEP based Brain Machine Interface for Controlling of a Wheelchair and Home Appliances with Bluetooth Localization System. In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 2520–2525. [Google Scholar]
- Abiyev, R.H.; Akkaya, N.; Aytac, E.; Günsel, I.; Çağman, A. Brain-computer interface for control of wheelchair using fuzzy neural networks. BioMed Res. Int. 2016, 2016, 9359868. [Google Scholar] [CrossRef] [Green Version]
- Finlayson, G.D.; Hordley, S.D.; Drew, M.S. Removing shadows from images. In Proceedings of the European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2002; pp. 823–836. [Google Scholar]
- He, Q.; Chu, C.H.H. A new shadow removal method for color images. Adv. Remote Sens. 2013, 2, 32770. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Zhao, Y.; Chen, C.P. Moving Cast Shadows Segmentation Using Illumination Invariant Feature. IEEE Trans. Multimed. 2019, 22, 2221–2233. [Google Scholar] [CrossRef]
- Murali, S.; Govindan, V. Shadow detection and removal from a single image using LAB color space. Cybern. Inf. Technol. 2013, 13, 95–103. [Google Scholar] [CrossRef] [Green Version]
- Khan, E.A.; Reinhard, E. Evaluation of color spaces for edge classification in outdoor scenes. In Proceedings of the IEEE International Conference on Image Processing 2005, Genova, Italy, 14 September 2005; Volume 3, p. III-952. [Google Scholar]
- Xu, L.; Qi, F.; Jiang, R. Shadow removal from a single image. In Proceedings of the Sixth International Conference on Intelligent Systems Design and Applications, Jinan, China, 16–18 October 2006; Volume 2, pp. 1049–1054. [Google Scholar]
- Shao, Q.; Xu, C.; Zhou, Y.; Dong, H. Cast shadow detection based on the YCbCr color space and topological cuts. J. Supercomput. 2018, 76, 3308–3326. [Google Scholar] [CrossRef]
- Nielsen, M.; Madsen, C.B. Graph cut based segmentation of soft shadows for seamless removal and augmentation. In Proceedings of the Scandinavian Conference on Image Analysis; Springer: Berlin/Heidelberg, Germany, 2007; pp. 918–927. [Google Scholar]
- Shor, Y.; Lischinski, D. The shadow meets the mask: Pyramid-based shadow removal. Comput. Graph. Forum 2008, 27, 577–586. [Google Scholar] [CrossRef]
- Golchin, M.; Khalid, F.; Abdullah, L.N.; Davarpanah, S.H. Shadow Detection using Color and Edge Information. J. Comput. Sci. 2013, 9, 1575–1588. [Google Scholar] [CrossRef] [Green Version]
- Guo, R.; Dai, Q.; Hoiem, D. Single-image shadow detection and removal using paired regions. In Proceedings of the CVPR 2011, Providence, RI, USA, 20–25 June 2011; pp. 2033–2040. [Google Scholar]
- Yuan, X.; Ebner, M.; Wang, Z. Single-image shadow detection and removal using local colour constancy computation. IET Image Process. 2014, 9, 118–126. [Google Scholar] [CrossRef]
- Shen, L.; Wee Chua, T.; Leman, K. Shadow optimization from structured deep edge detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 2067–2074. [Google Scholar]
- Nguyen, V.; Vicente, Y.; Tomas, F.; Zhao, M.; Hoai, M.; Samaras, D. Shadow detection with conditional generative adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4510–4518. [Google Scholar]
- Chen, Q.; Zhang, G.; Yang, X.; Li, S.; Li, Y.; Wang, H.H. Single image shadow detection and removal based on feature fusion and multiple dictionary learning. Multimed. Tools Appl. 2018, 77, 18601–18624. [Google Scholar] [CrossRef]
- Hema, C.; Paulraj, M.; Yaacob, S.; Adom, A.H.; Nagarajan, R. Motor imagery signal classification for a four state brain machine interface. Int. J. Comput. Inf. Eng. 2007, 1, 1375–1380. [Google Scholar]
- Yousefnezhad, M.; Zhang, D. Anatomical pattern analysis for decoding visual stimuli in human brains. Cogn. Comput. 2018, 10, 284–295. [Google Scholar] [CrossRef] [Green Version]
- Russell, B.C.; Torralba, A.; Murphy, K.P.; Freeman, W.T. LabelMe: A database and web-based tool for image annotation. Int. J. Comput. Vis. 2008, 77, 157–173. [Google Scholar] [CrossRef]
- Torralba, A.; Murphy, K.P.; Freeman, W.T. Sharing features: Efficient boosting procedures for multiclass object detection. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR 2004, Washington, DC, USA, 27 June–2 July 2004; Volume 2, p. II. [Google Scholar]
- He, K.; Sun, J.; Tang, X. Guided image filtering. In Proceedings of the European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1–14. [Google Scholar]
- Green, B. Canny edge detection tutorial. Retrieved March 2002, 6, 2005. [Google Scholar]
- Chong, H.Y.; Gortler, S.J.; Zickler, T. A perception-based color space for illumination-invariant image processing. ACM Trans. Graph. (TOG) 2008, 27, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Tsai, V.J. A comparative study on shadow compensation of color aerial images in invariant color models. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1661–1671. [Google Scholar] [CrossRef]
- Finlayson, G.D.; Hordley, S.D.; Lu, C.; Drew, M.S. On the removal of shadows from images. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 28, 59–68. [Google Scholar] [CrossRef] [PubMed]
- Troscianko, T.; Baddeley, R.; Párraga, C.A.; Leonards, U.; Troscianko, J. Visual encoding of green leaves in primate vision. J. Vis. 2003, 3, 137. [Google Scholar] [CrossRef]
- Minnaert, M. The Nature of Light and Colour in the Open Air; Courier Corporation: Washington, DC, USA, 2013. [Google Scholar]
- Lynch, D.K.; Livingston, W.C.; Livingston, W. Color and Light in Nature; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Møller, M.F. A Scaled Conjugate Gradient Algorithm for Fast Supervised Learning; Computer Science Department, Aarhus University: Aarhus, Denmark, 1990. [Google Scholar]
- Pal, S.K.; Mitra, S. Multilayer perceptron, fuzzy sets, classifiaction. IEEE Trans. Neural Netw. 1992, 3, 683–697. [Google Scholar] [CrossRef] [PubMed]
- Baldi, P. Autoencoders, unsupervised learning, and deep architectures. In Proceedings of the ICML Workshop on Unsupervised and Transfer Learning, Bellevue, WA, USA, 28 June–2 July 2011; pp. 37–49. [Google Scholar]
- Gao, F.; Huang, T.; Sun, J.; Wang, J.; Hussain, A.; Yang, E. A new algorithm for SAR image target recognition based on an improved deep convolutional neural network. Cogn. Comput. 2019, 11, 809–824. [Google Scholar] [CrossRef] [Green Version]
- Yue, Z.; Gao, F.; Xiong, Q.; Wang, J.; Huang, T.; Yang, E.; Zhou, H. A novel semi-supervised convolutional neural network method for synthetic aperture radar image recognition. Cogn. Comput. 2019, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Mammone, N.; Ieracitano, C.; Morabito, F.C. A deep CNN approach to decode motor preparation of upper limbs from time–frequency maps of EEG signals at source level. Neural Netw. 2020, 124, 357–372. [Google Scholar] [CrossRef]
- Zhong, G.; Yan, S.; Huang, K.; Cai, Y.; Dong, J. Reducing and stretching deep convolutional activation features for accurate image classification. Cogn. Comput. 2018, 10, 179–186. [Google Scholar] [CrossRef]
- Feng, S.; Wang, Y.; Song, K.; Wang, D.; Yu, G. Detecting multiple coexisting emotions in microblogs with convolutional neural networks. Cogn. Comput. 2018, 10, 136–155. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Z.; He, H. Hierarchical convolutional neural networks for EEG-based emotion recognition. Cogn. Comput. 2018, 10, 368–380. [Google Scholar] [CrossRef]
- Peng, D.; Liu, Z.; Wang, H.; Qin, Y.; Jia, L. A novel deeper one-dimensional CNN with residual learning for fault diagnosis of wheelset bearings in high-speed trains. IEEE Access 2018, 7, 10278–10293. [Google Scholar] [CrossRef]
- Scherer, D.; Müller, A.; Behnke, S. Evaluation of pooling operations in convolutional architectures for object recognition. In Proceedings of the International Conference on Artificial Neural Networks; Springer: Berlin/Heidelberg, Germany, 2010; pp. 92–101. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Hsu, C.W.; Chang, C.C.; Lin, C.J. A Practical Guide to Support Vector Classification. 2003. Available online: https://www.csie.ntu.edu.tw/~cjlin/ (accessed on 20 September 2020).
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Ojala, M.; Garriga, G.C. Permutation tests for studying classifier performance. J. Mach. Learn. Res. 2010, 11, 1833–1863. [Google Scholar]
- Vasamsetti, S.; Mittal, N.; Neelapu, B.C.; Sardana, H.K. 3D Local Spatio-temporal Ternary Patterns for Moving Object Detection in Complex Scenes. Cogn. Comput. 2019, 11, 18–30. [Google Scholar] [CrossRef]
- Li, G.; Wang, Z.Y.; Luo, J.; Chen, X.; Li, H.B. Spatio-Context-Based Target Tracking with Adaptive Multi-Feature Fusion for Real-World Hazy Scenes. Cogn. Comput. 2018, 10, 545–557. [Google Scholar] [CrossRef]
- Aljarah, I.; Ala’M, A.Z.; Faris, H.; Hassonah, M.A.; Mirjalili, S.; Saadeh, H. Simultaneous feature selection and support vector machine optimization using the grasshopper optimization algorithm. Cogn. Comput. 2018, 10, 478–495. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Wang, S.; Gu, D. Ongoing Evolution of Visual SLAM from Geometry to Deep Learning: Challenges and Opportunities. Cogn. Comput. 2018, 10, 875–889. [Google Scholar] [CrossRef]
- Perera, A.G.; Law, Y.W.; Chahl, J. Human pose and path estimation from aerial video using dynamic classifier selection. Cogn. Comput. 2018, 10, 1019–1041. [Google Scholar] [CrossRef] [Green Version]
- Ning, Q.; Zhu, J.; Chen, C. Very fast semantic image segmentation using hierarchical dilation and feature refining. Cogn. Comput. 2018, 10, 62–72. [Google Scholar] [CrossRef]









| Model | Precision | Recall | F-Measure | Accuracy |
|---|---|---|---|---|
| MLP1 | 82.72 ± 0.77% | 87.52 ± 0.4% | 85.05 ± 0.57% | 84.63 ± 0.63% |
| MLP2 | 79.47 ± 0.97% | 85.55 ± 0.66% | 82.39 ± 0.69% | 81.71 ± 0.77% |
| MLP3 | 82.6 ± 0.66% | 86.6 ± 0.45% | 84.55 ± 0.53% | 84.19 ± 0.56% |
| AE1 | 74.27 ± 0.99% | 81.14 ± 1.47% | 77.55 ± 1.03% | 76.51 ± 1.04% |
| AE2 | 75.5 ± 1.99% | 81.44 ± 1.42% | 78.36 ± 1.71% | 77.51 ± 1.89% |
| AE3 | 75.67 ± 0.77% | 82.29 ± 0.75% | 78.84 ± 0.66% | 77.91 ± 0.72% |
| 1D-CNN | 73.5 ± 1.91% | 81.0 ± 2.3% | 76.90 ± 1% | 75.80 ± 1.2% |
| SVM | 62.5 ± 3.88% | 58.6 ± 9.64% | 59.93 ± 3.85% | 61.27 ± 2.18% |
| Model | Precision | Recall | F-Measure | Accuracy |
|---|---|---|---|---|
| MLP1 | 82.72 ± 0.77% | 87.52 ± 0.4% | 85.05 ± 0.57% | 84.63 ± 0.63% |
| Huang | 60 ± 4.91% | 77.17 ± 5.50% | 67.37 ± 4.10% | 62.52 ± 5.54% |
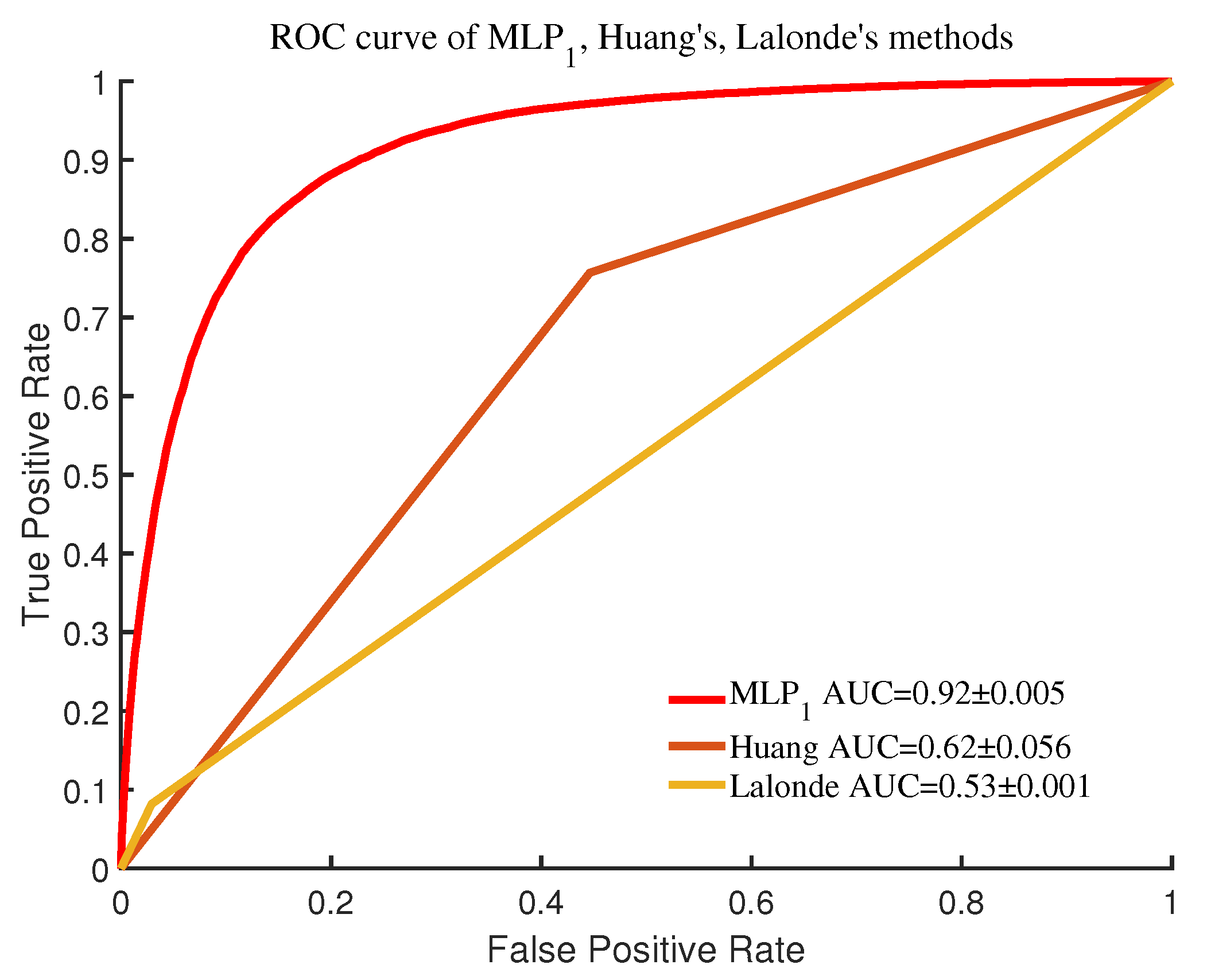
| Lalonde | 74.03 ± 0.75% | 8.19 ± 0.12% | 14.74 ± 0.21% | 52.67 ± 0.1% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ju, Z.; Gun, L.; Hussain, A.; Mahmud, M.; Ieracitano, C. A Novel Approach to Shadow Boundary Detection Based on an Adaptive Direction-Tracking Filter for Brain-Machine Interface Applications. Appl. Sci. 2020, 10, 6761. https://0-doi-org.brum.beds.ac.uk/10.3390/app10196761
Ju Z, Gun L, Hussain A, Mahmud M, Ieracitano C. A Novel Approach to Shadow Boundary Detection Based on an Adaptive Direction-Tracking Filter for Brain-Machine Interface Applications. Applied Sciences. 2020; 10(19):6761. https://0-doi-org.brum.beds.ac.uk/10.3390/app10196761
Chicago/Turabian StyleJu, Ziyi, Li Gun, Amir Hussain, Mufti Mahmud, and Cosimo Ieracitano. 2020. "A Novel Approach to Shadow Boundary Detection Based on an Adaptive Direction-Tracking Filter for Brain-Machine Interface Applications" Applied Sciences 10, no. 19: 6761. https://0-doi-org.brum.beds.ac.uk/10.3390/app10196761








