Comparison of Training Approaches for Photovoltaic Forecasts by Means of Machine Learning
Abstract
:1. Introduction
2. Training Database Composition Approaches
- the “training set” (or equally “training database”), which is used to adjust the weights among neurons by performing the forecast on the same samples,
- the “validation set”, which is used as a stopping criteria to avoid over-fitting and under-fitting. It proves the goodness of the trained network on additional samples which have not been previously included in the training set. The purpose of this step is to test the generalization capability of the neural network on a new data-set.
- error back-propagation (EBP)
- gradient descent
- conjugate gradient
- evolutionary algorithms (genetic algorithms, particle swarm optimization, etc.)
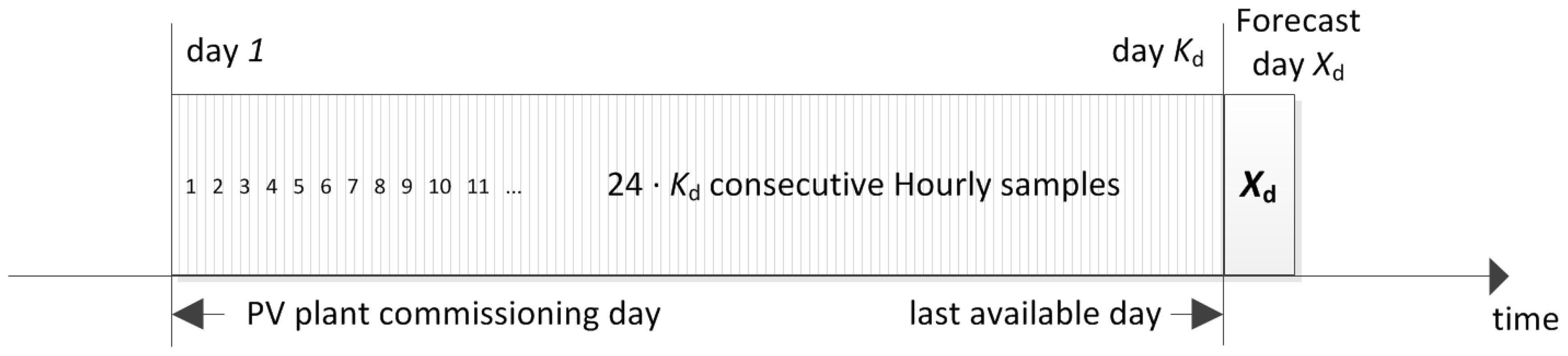
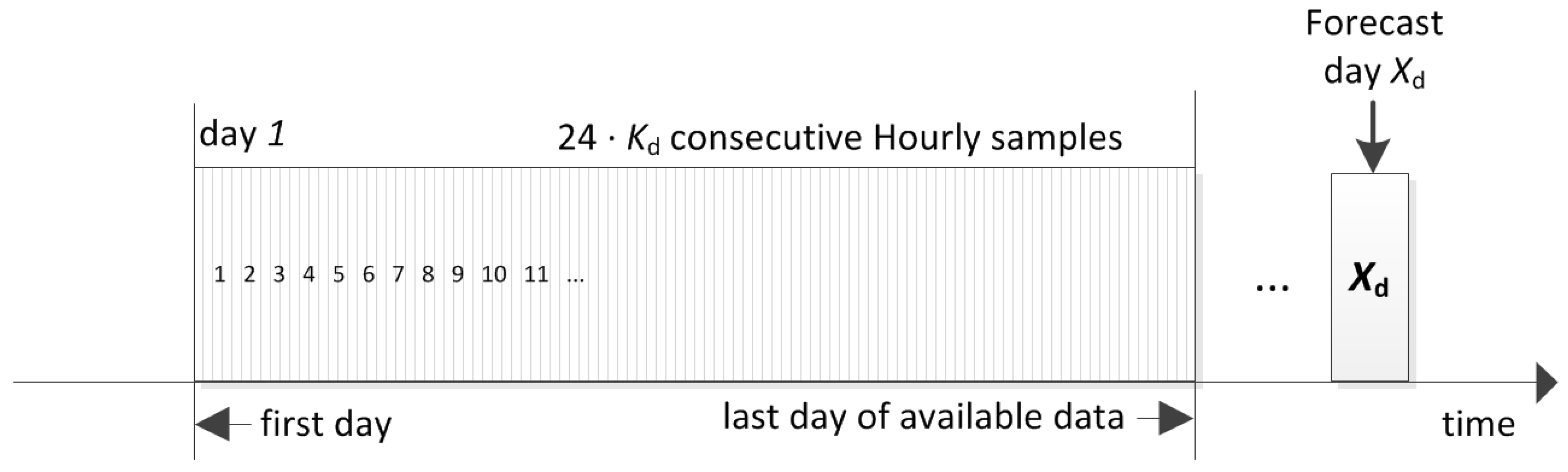
2.1. Incremental Training Data-Set
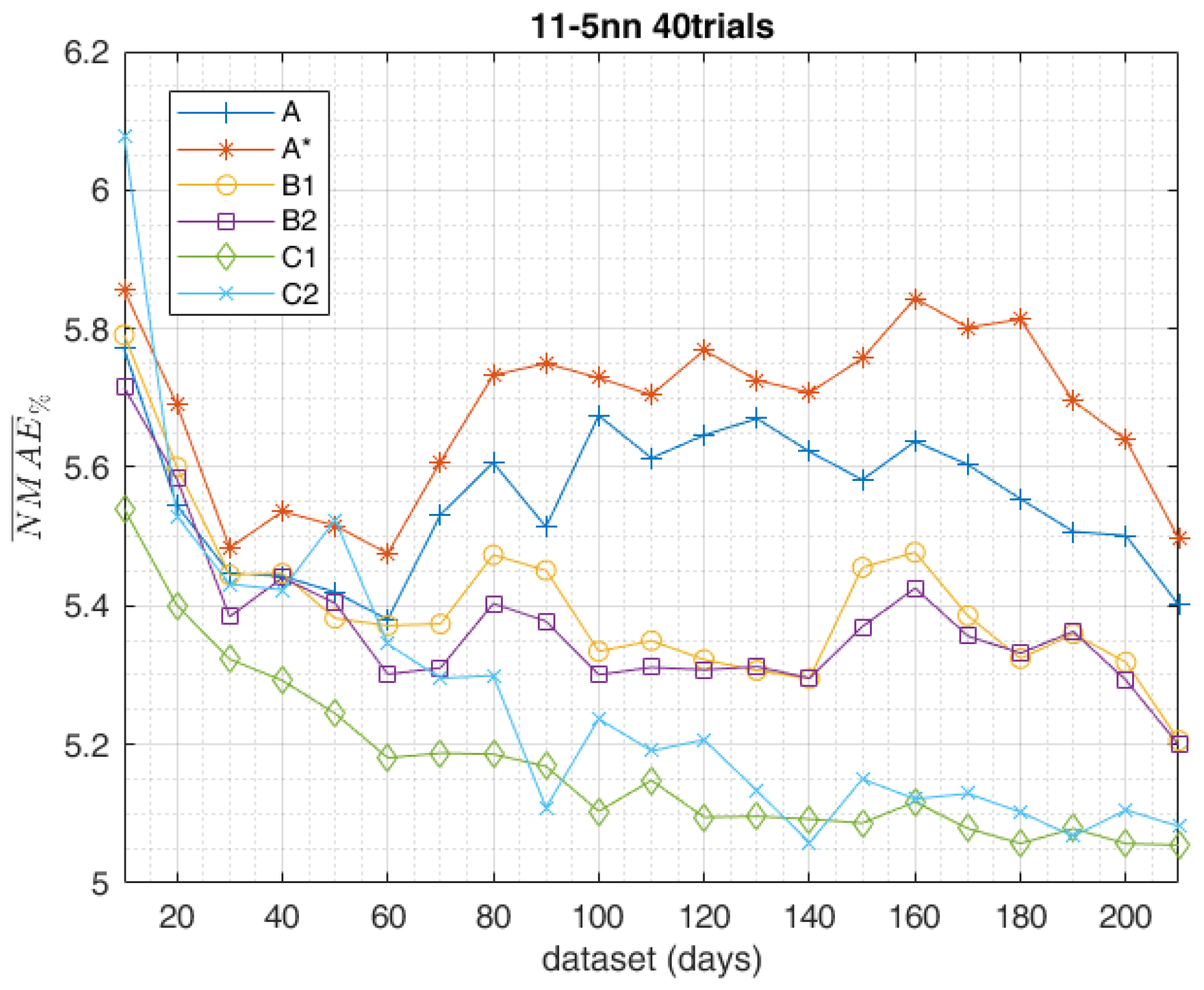
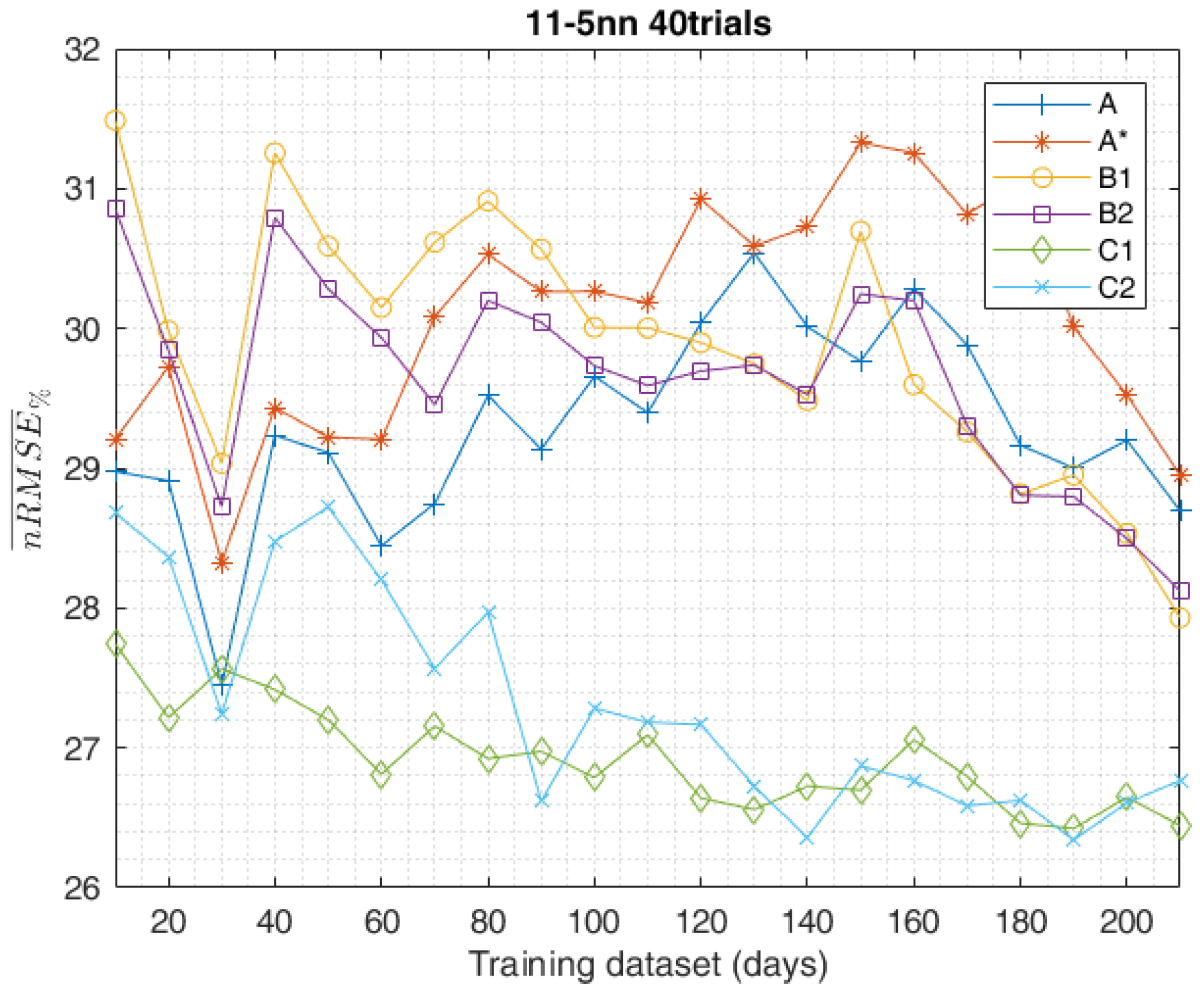
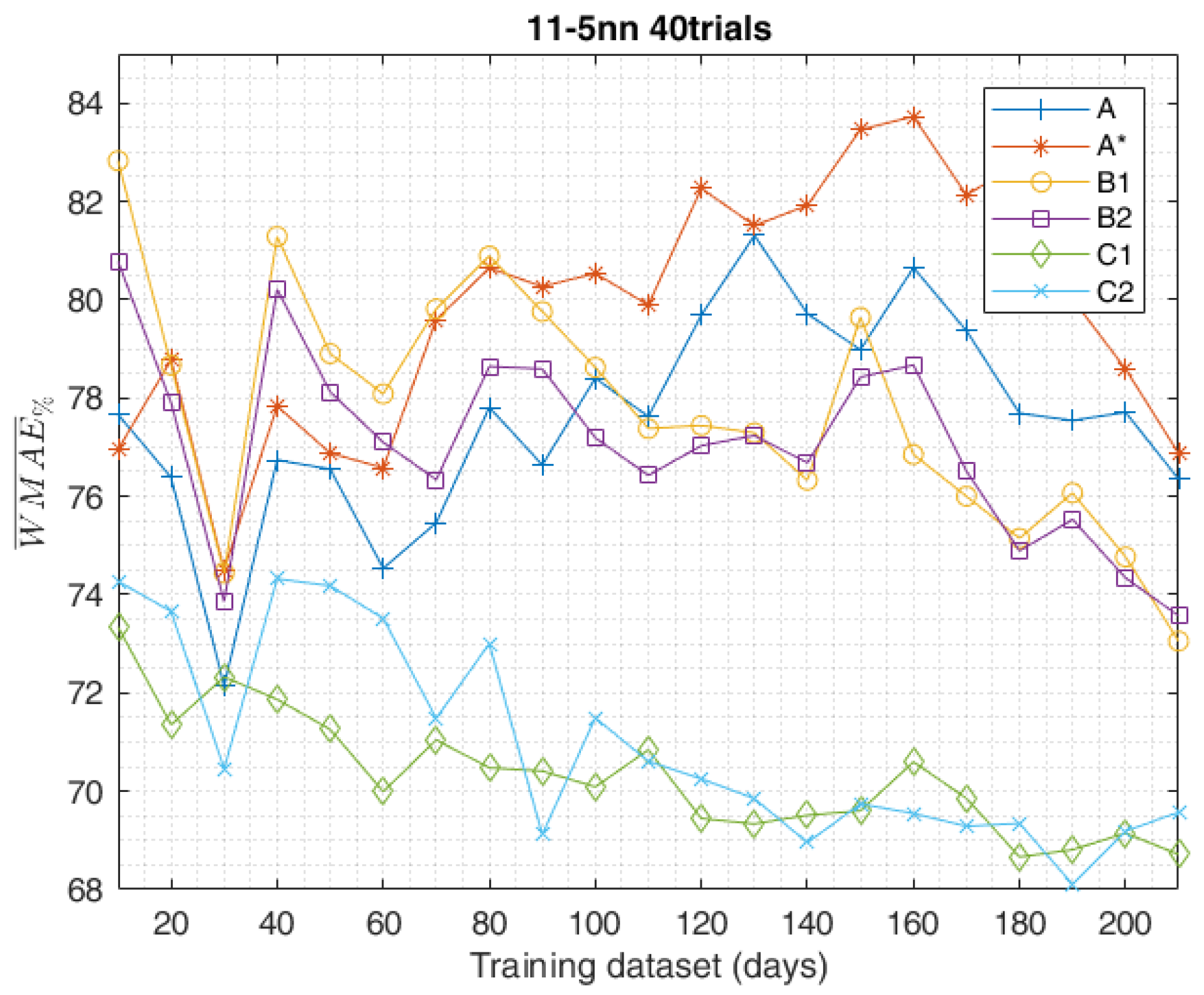
- Method A employs the same chronologically consecutive samples by grouping the 90% of the samples which are closest to the forecast day for the training set and the remaining 10% of the samples for the validation set.
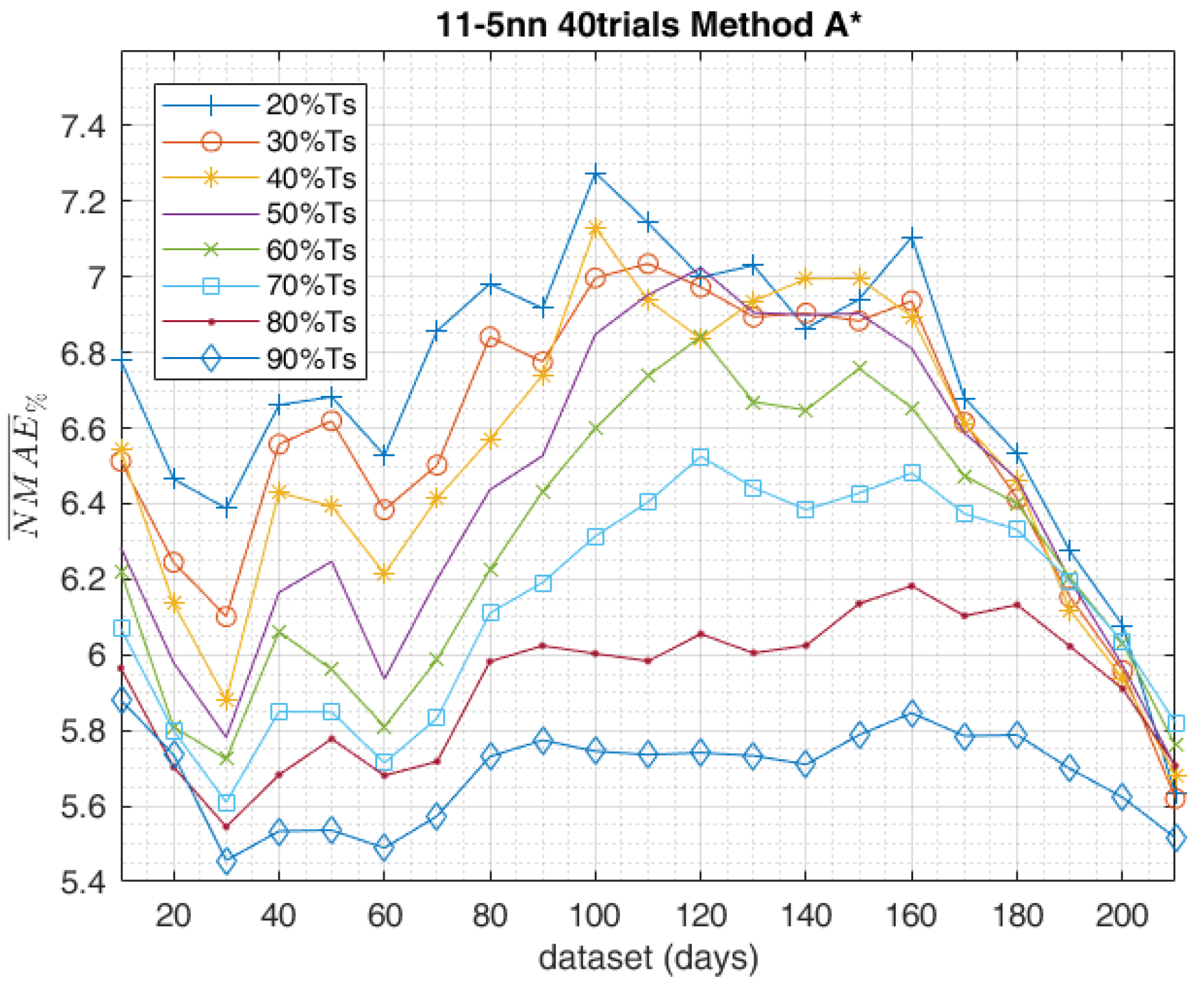
- Method A* employs the same chronologically consecutive samples by grouping the 90% of the samples for the training set and the 10% of the samples which are closest to the forecast day for the validation set.
- Method B employs the samples by randomly grouping them separately, 90% for the training set and 10% for the validation set.
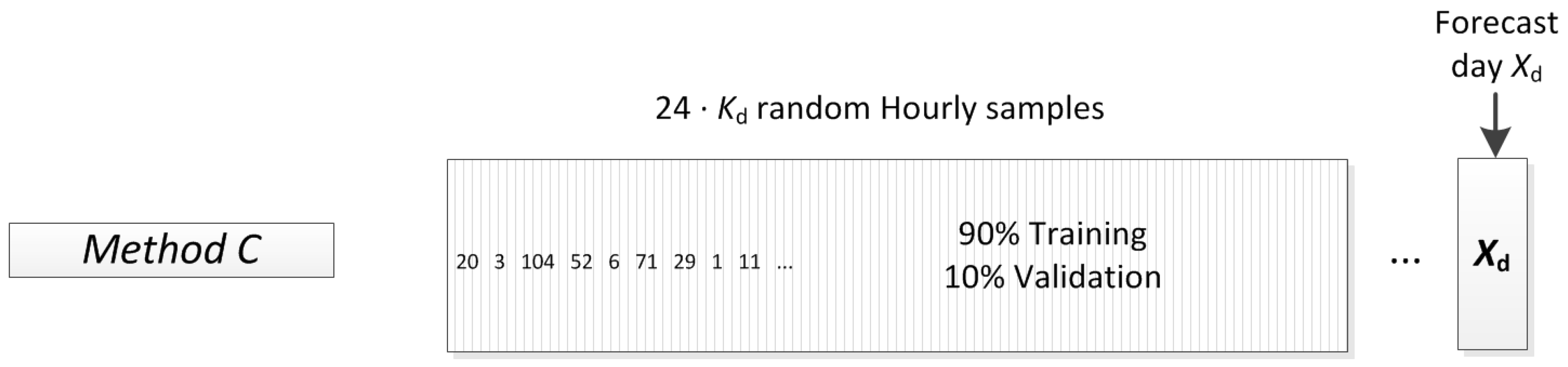
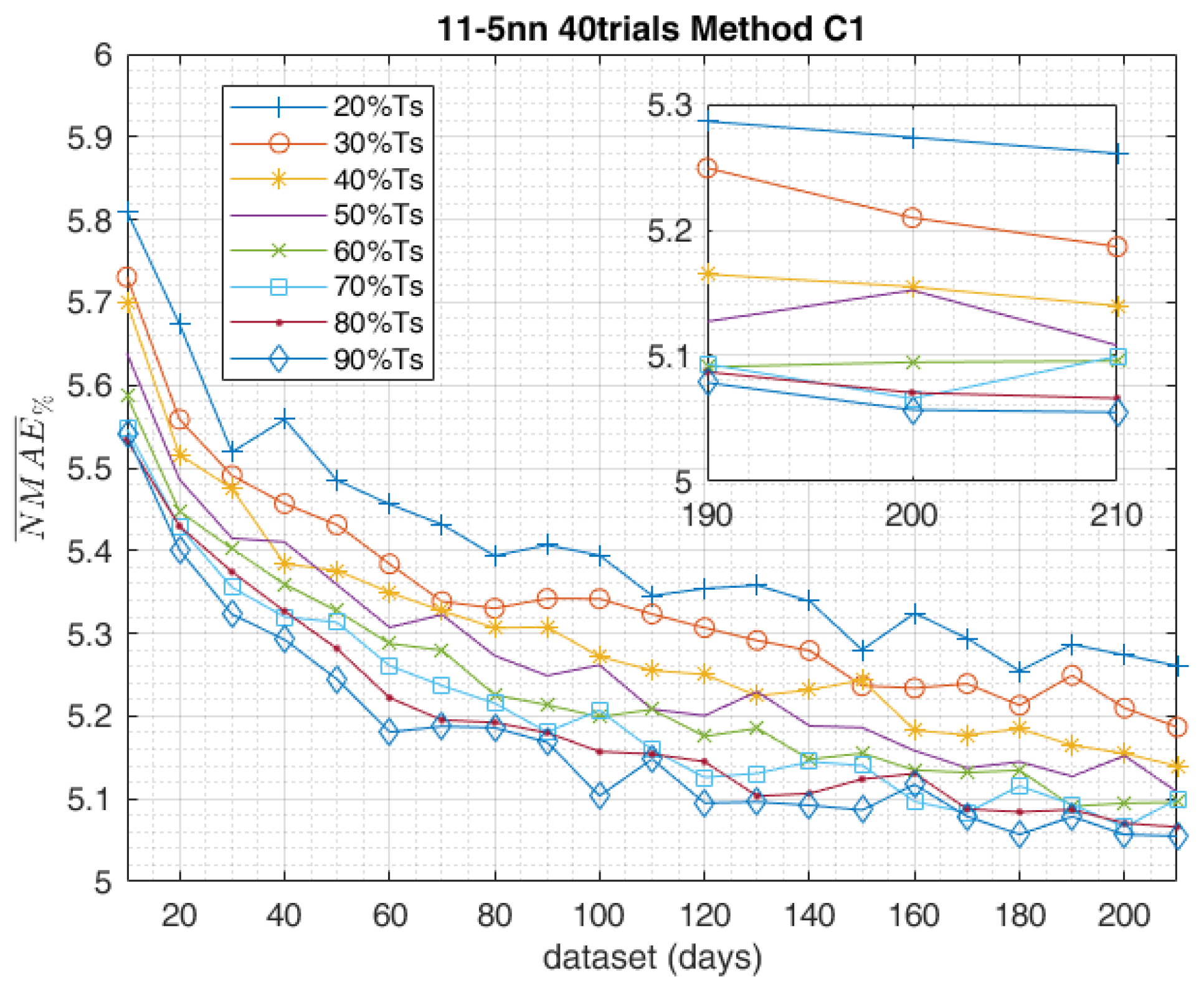
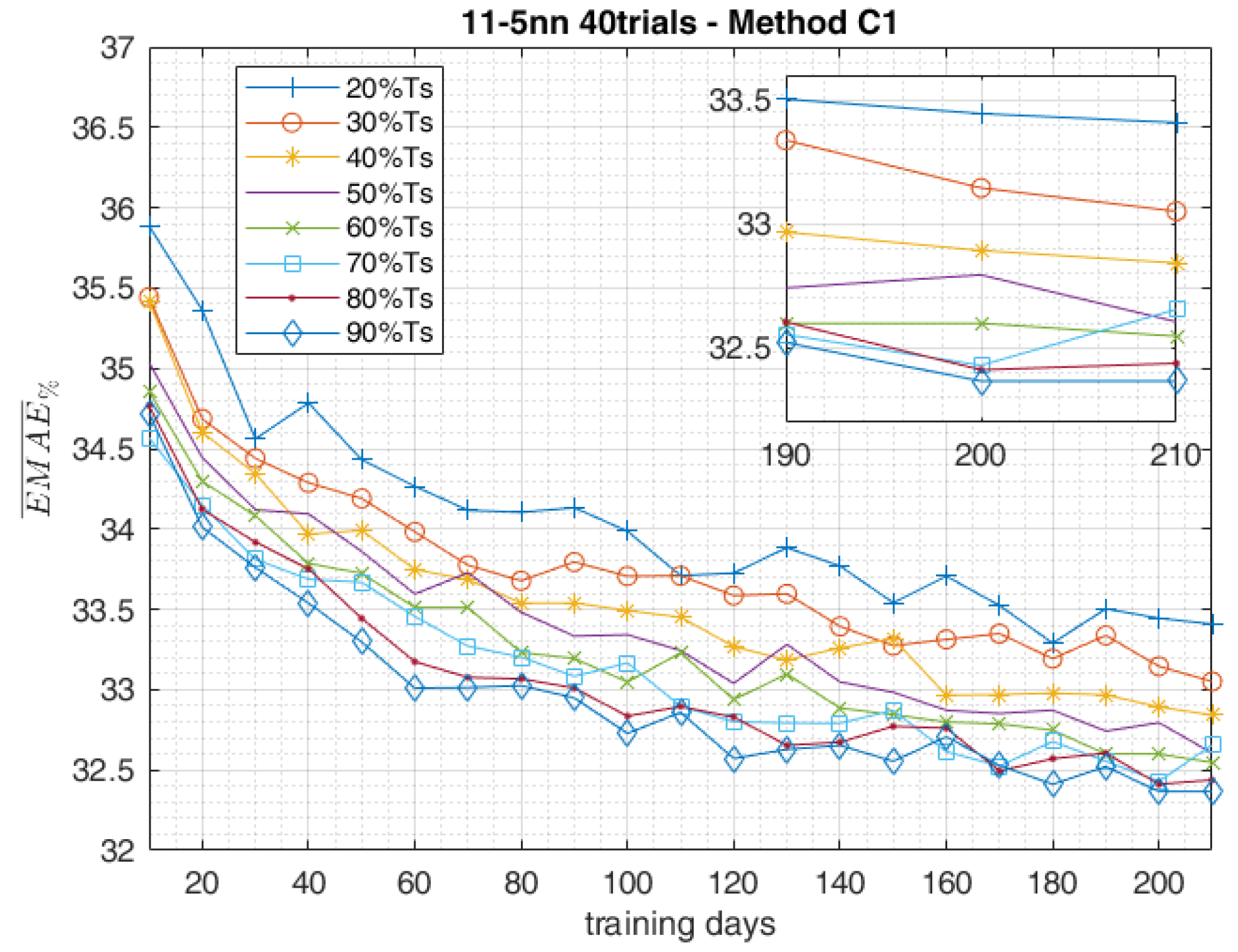
2.2. Complete Training Data-Set
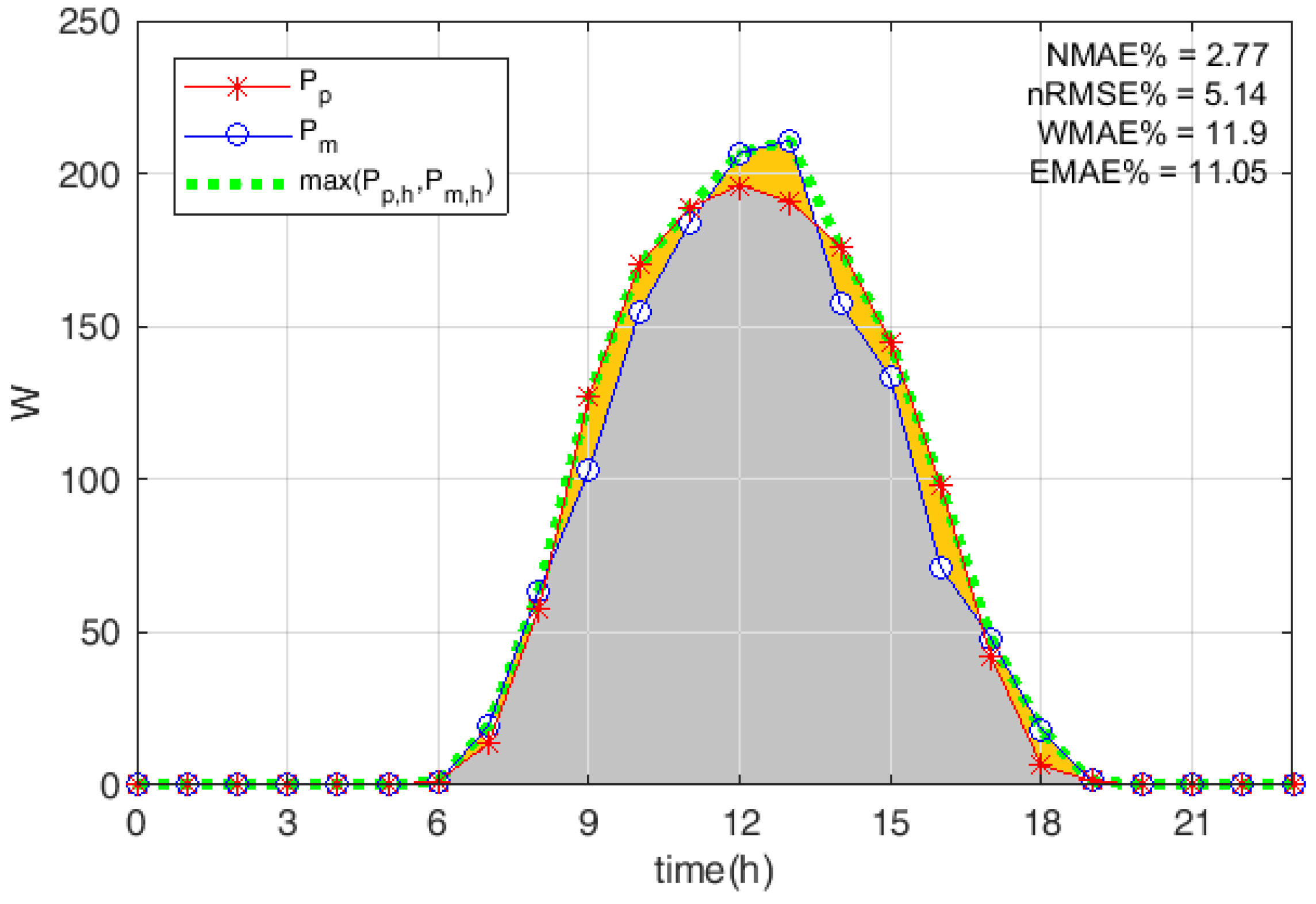
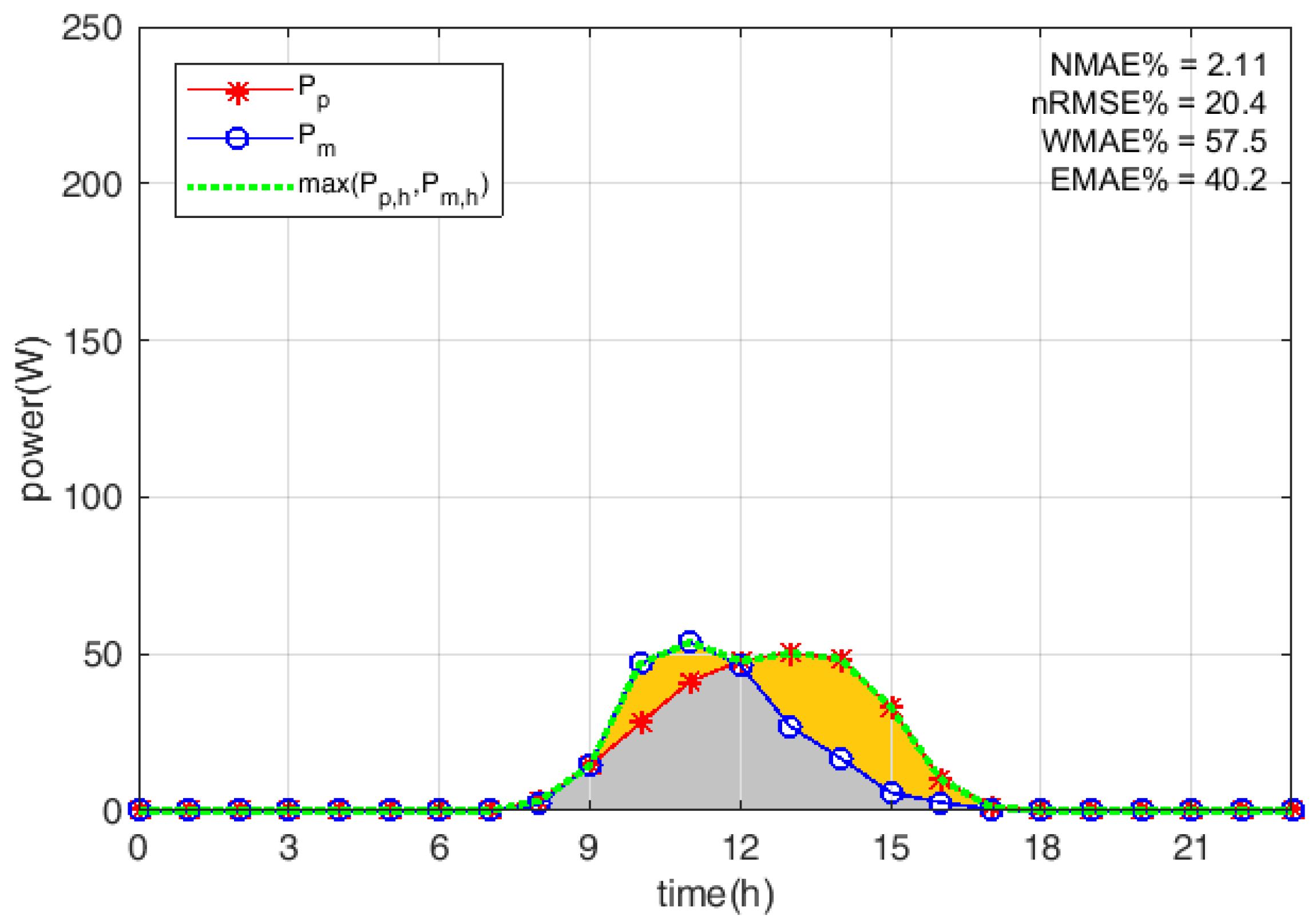
3. Evaluation Indexes
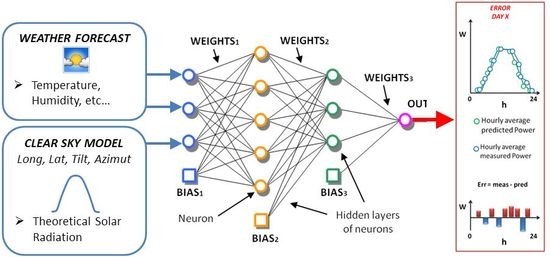
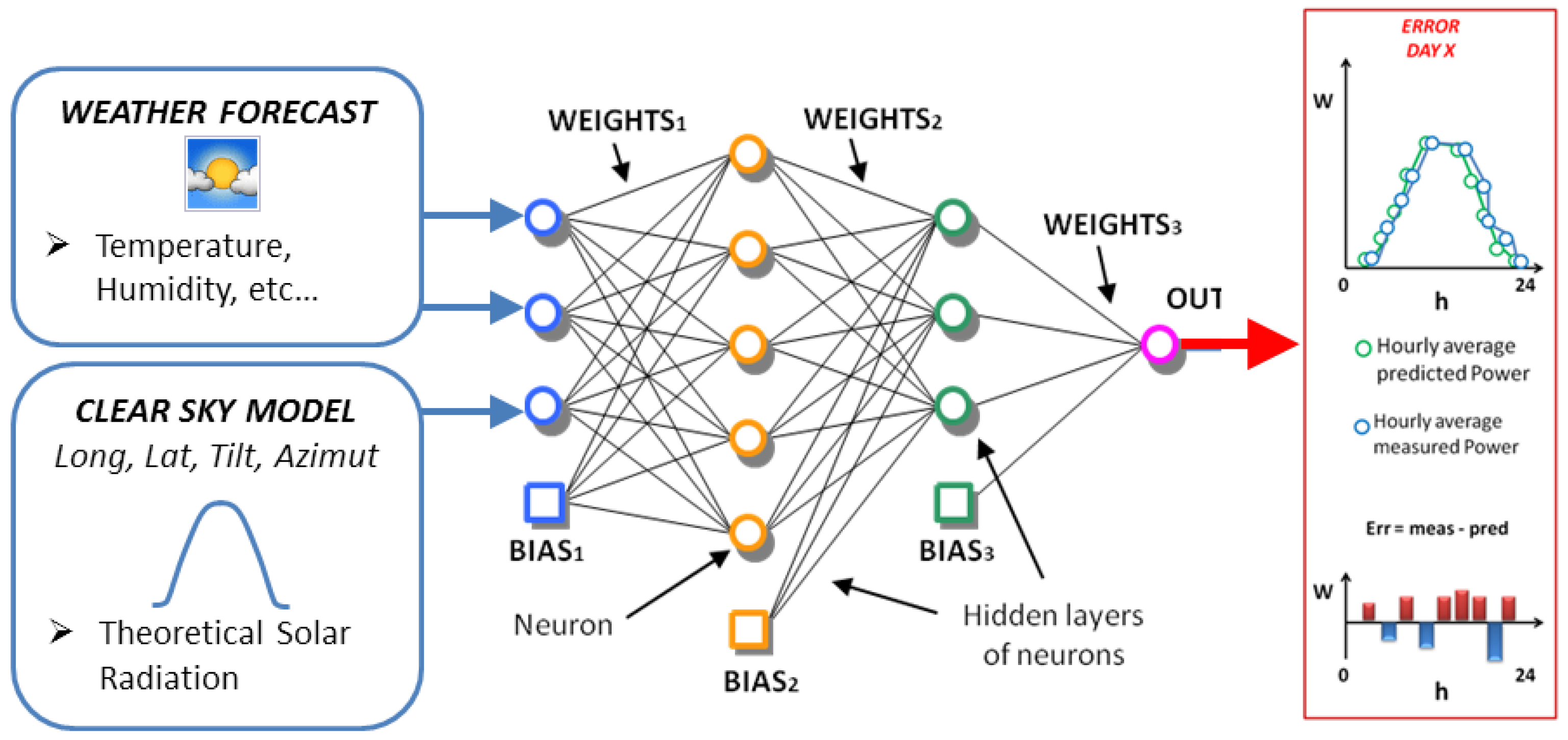
4. Case Study
- PV technology: Silicon mono crystalline,
- Rated power (Net capacity of the PV module): 245 Wp,
- Azimuth: (assuming as south direction and counting clockwise),
- Solar panel tilt angle (): ,
- ambient temperature (C),
- global horizontal irradiance (W/m),
- global irradiance on the plane of the array (W/m),
- wind speed (m/s),
- wind direction (),
- P pressure (hPa),
- R precipitation (mm),
- cloud cover (%),
- cloud type (Low/Medium/High).
- neurons in the input layer: 11,
- neurons in the first hidden layer: 11,
- neurons in the second hidden layer: 5,
- neurons in the output layer: 1,
- training algorithm: Levenberg–Marquardt,
- activation function: sigmoid,
- number of trials in the ensemble forecast: 40.
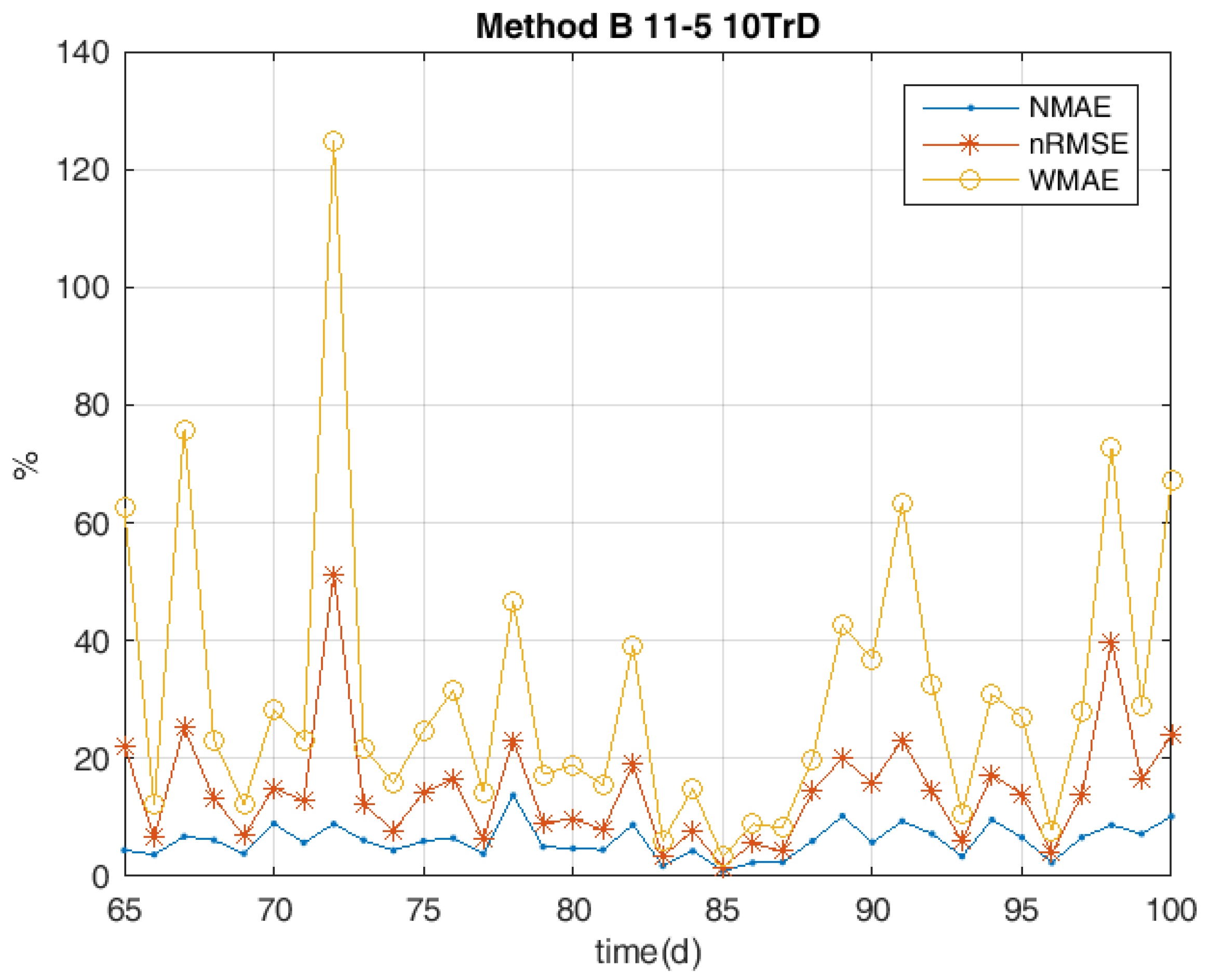
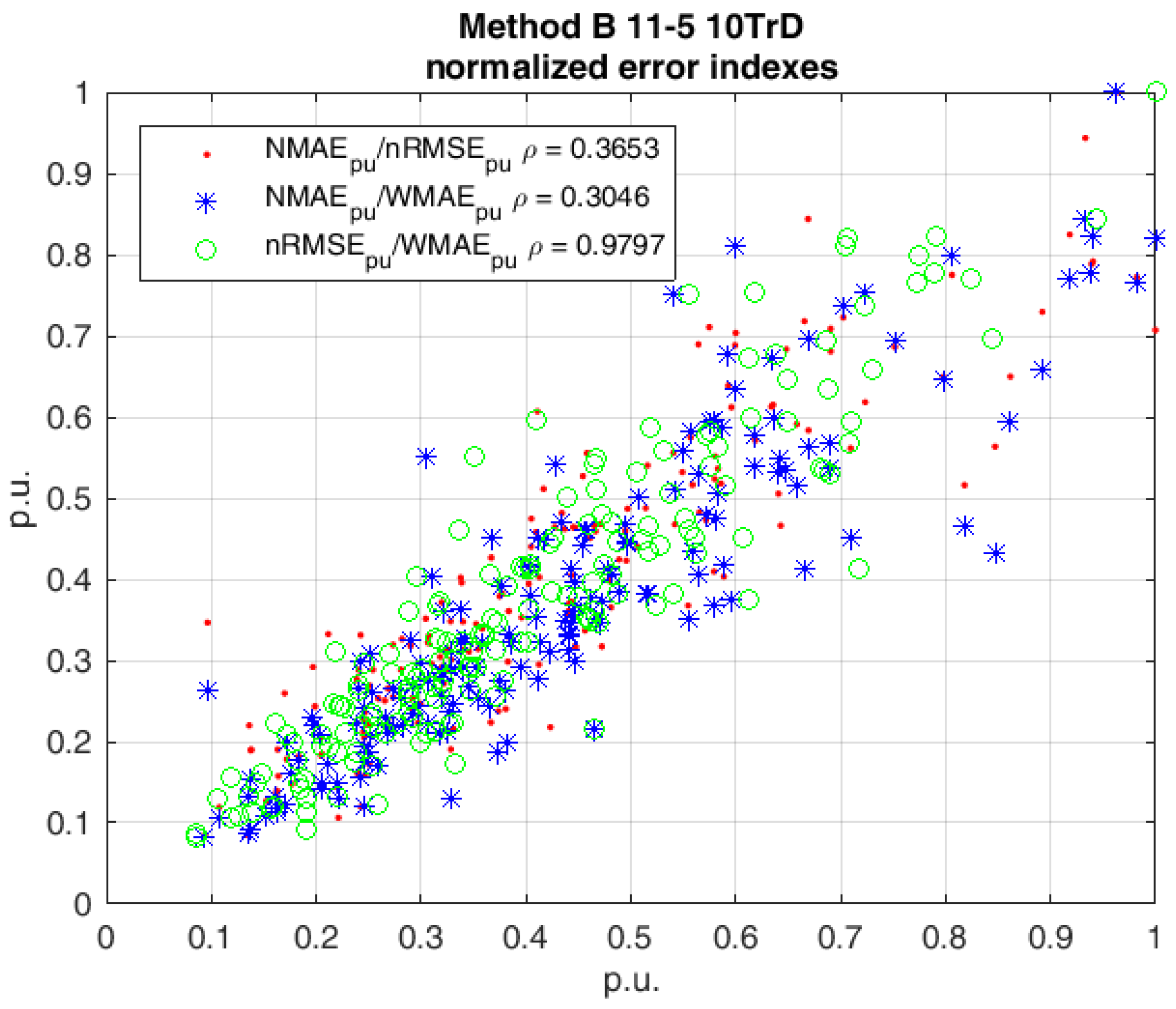
5. Results
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Pelland, S.; Remund, J.; Kleissl, J.; Oozeki, T.; De Brabandere, K. Photovoltaic and solar forecasting: State of the art. IEA PVPS Task 2013, 14, 1–36. [Google Scholar]
- Paulescu, M.; Paulescu, E.; Gravila, P.; Badescu, V. Weather Modeling and Forecasting of PV Systems Operation; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Raza, M.Q.; Nadarajah, M.; Ekanayake, C. On recent advances in PV output power forecast. Sol. Energy 2016, 136, 125–144. [Google Scholar] [CrossRef]
- Faranda, R.S.; Hafezi, H.; Leva, S.; Mussetta, M.; Ogliari, E. The Optimum PV Plant for a Given Solar DC/AC Converter. Energies 2015, 8, 4853–4870. [Google Scholar] [CrossRef] [Green Version]
- Dolara, A.; Lazaroiu, G.C.; Leva, S.; Manzolini, G.; Votta, L. Snail Trails and Cell Microcrack Impact on PV Module Maximum Power and Energy Production. IEEE J. Photovolt. 2016, 6, 1269–1277. [Google Scholar] [CrossRef]
- Omar, M.; Dolara, A.; Magistrati, G.; Mussetta, M.; Ogliari, E.; Viola, F. Day-ahead forecasting for photovoltaic power using artificial neural networks ensembles. In Proceedings of the 2016 IEEE International Conference on Renewable Energy Research and Applications (ICRERA), Birmingham, UK, 20–23 November 2016; pp. 1152–1157. [Google Scholar]
- Cali, Ü. Grid and Market Integration of Large-Scale Wind Farms Using Advanced Wind Power Forecasting: Technical and Energy Economic Aspects; Erneuerbare Energien und Energieeffizienz—Renewable Energies and Energy Efficiency; Kassel University Press: Kassel, Germany, 2011. [Google Scholar]
- Ni, Q.; Zhuang, S.; Sheng, H.; Kang, G.; Xiao, J. An ensemble prediction intervals approach for short-term PV power forecasting. Sol. Energy 2017, 155, 1072–1083. [Google Scholar] [CrossRef]
- Simonov, M.; Mussetta, M.; Grimaccia, F.; Leva, S.; Zich, R. Artificial intelligence forecast of PV plant production for integration in smart energy systems. Int. Rev. Electr. Eng. 2012, 7, 3454–3460. [Google Scholar]
- Duan, Q.; Shi, L.; Hu, B.; Duan, P.; Zhang, B. Power forecasting approach of PV plant based on similar time periods and Elman neural network. In Proceedings of the 2015 Chinese Automation Congress (CAC), Wuhan, China, 27–29 November 2015; pp. 1258–1262. [Google Scholar]
- Gardner, M.; Dorling, S. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Nelson, M.; Illingworth, W. A Practical Guide to Neural Nets; Physical Sciences; Addison-Wesley: Boston, MA, USA, 1991; 316p. [Google Scholar]
- Bose, B.K. Neural Network Applications in Power Electronics and Motor Drives—An Introduction and Perspective. IEEE Trans. Ind. Electron. 2007, 54, 14–33. [Google Scholar] [CrossRef]
- Ogliari, E.; Dolara, A.; Manzolini, G.; Leva, S. Physical and hybrid methods comparison for the day ahead PV output power forecast. Renew. Energy 2017, 113, 11–21. [Google Scholar] [CrossRef]
- Elder, J.F.; Abbott, D.W. A comparison of leading data mining tools. In Proceedings of the Fourth International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 27–31 August 1998; Volume 28. [Google Scholar]
- Bergstra, J.; Breuleux, O.; Bastien, F.; Lamblin, P.; Pascanu, R.; Desjardins, G.; Turian, J.; Warde-Farley, D.; Bengio, Y. Theano: A CPU and GPU math compiler in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 1–7. [Google Scholar]
- Collobert, R.; Kavukcuoglu, K.; Farabet, C. Torch7: A matlab-like environment for machine learning. In Proceedings of the BigLearn, NIPS Workshop, Sierra Nevada, Spain, 16–17 December 2011. Number EPFL-CONF-192376. [Google Scholar]
- Kalogirou, S. Artificial Intelligence in Energy and Renewable Energy Systems; Nova Publishers: Hauppauge, NY, USA, 2007. [Google Scholar]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Gandelli, A.; Grimaccia, F.; Leva, S.; Mussetta, M.; Ogliari, E. Hybrid model analysis and validation for PV energy production forecasting. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 1957–1962. [Google Scholar]
- Dolara, A.; Grimaccia, F.; Leva, S.; Mussetta, M.; Ogliari, E. A Physical Hybrid Artificial Neural Network for Short Term Forecasting of PV Plant Power Output. Energies 2015, 8, 1138–1153. [Google Scholar] [CrossRef] [Green Version]
- Rana, M.; Koprinska, I.; Agelidis, V.G. Forecasting solar power generated by grid connected PV systems using ensembles of neural networks. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–16 July 2015; pp. 1–8. [Google Scholar]
- Grimaccia, F.; Leva, S.; Mussetta, M.; Ogliari, E. ANN Sizing Procedure for the Day-Ahead Output Power Forecast of a PV Plant. Appl. Sci. 2017, 7, 622. [Google Scholar] [CrossRef]
- Netsanet, S.; Zhang, J.; Zheng, D.; Hui, M. Input parameters selection and accuracy enhancement techniques in PV forecasting using Artificial Neural Network. In Proceedings of the 2016 IEEE International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 21–23 October 2016; pp. 565–569. [Google Scholar]
- Panapakidis, I.P.; Christoforidis, G.C. A hybrid ANN/GA/ANFIS model for very short-term PV power forecasting. In Proceedings of the 2017 11th IEEE International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Cadiz, Spain, 4–6 April 2017; pp. 412–417. [Google Scholar]
- Tetko, I.V.; Livingstone, D.J.; Luik, A.I. Neural network studies. 1. Comparison of overfitting and overtraining. J. Chem. Inf. Comput. Sci. 1995, 35, 826–833. [Google Scholar] [CrossRef]
- Hansen, L.K.; Salamon, P. Neural network ensembles. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 993–1001. [Google Scholar] [CrossRef]
- Perrone, M.P. General averaging results for convex optimization. In Proceedings of the 1993 Connectionist Models Summer School; Psychology Press: London, UK, 1994; pp. 364–371. [Google Scholar]
- Odom, M.D.; Sharda, R. A neural network model for bankruptcy prediction. In Proceedings of the 1990 IJCNN International Joint Conference on Neural Networks, San Diego, CA, USA, 17–21 June 1990; pp. 163–168. [Google Scholar]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H. Neural Network Design; Campus Publishing Service, University of Colorado Bookstore: Boulder, CO, USA, 2014; ISBN 9780971732100. [Google Scholar]
- Chen, S.H.; Jakeman, A.J.; Norton, J.P. Artificial intelligence techniques: an introduction to their use for modelling environmental systems. Math. Comput. Simul. 2008, 78, 379–400. [Google Scholar] [CrossRef]
- Monteiro, C.; Fernandez-Jimenez, L.A.; Ramirez-Rosado, I.J.; Munoz-Jimenez, A.; Lara-Santillan, P.M. Short-Term Forecasting Models for Photovoltaic Plants: Analytical versus Soft-Computing Techniques. Math. Probl. Eng. 2013, 2013, 767284. [Google Scholar] [CrossRef]
- Ulbricht, R.; Fischer, U.; Lehner, W.; Donker, H. First Steps Towards a Systematical Optimized Strategy for Solar Energy Supply Forecasting. In Proceedings of the European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases (ECMLPKDD 2013), Riva del Garda, Italy, 23–27 September 2013. [Google Scholar]
- Kleissl, J. Solar Energy Forecasting and Resource Assessment; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Ogliari, E.; Grimaccia, F.; Leva, S.; Mussetta, M. Hybrid Predictive Models for Accurate Forecasting in PV Systems. Energies 2013, 6, 1918–1929. [Google Scholar] [CrossRef] [Green Version]
- Wolfram, M.; Bokhari, H.; Westermann, D. Factor influence and correlation of short term demand for control reserve. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–5. [Google Scholar]
- SolarTechLab Department of Energy. Available online: http://www.solartech.polimi.it/ (accessed on 30 September 2017).
- ABB MICRO-0.25-I-OUTD. Available online: https://library.e.abb.com/public/0ac164c3b03678c085257cbd0061a446/MICRO-CDD_BCD.00373_EN.pdf (accessed on 21 January 2018).
- Leva, S.; Dolara, A.; Grimaccia, F.; Mussetta, M.; Ogliari, E. Analysis and validation of 24 hours ahead neural network forecasting of photovoltaic output power. Math. Comput. Simul. 2017, 131, 88–100. [Google Scholar] [CrossRef] [Green Version]
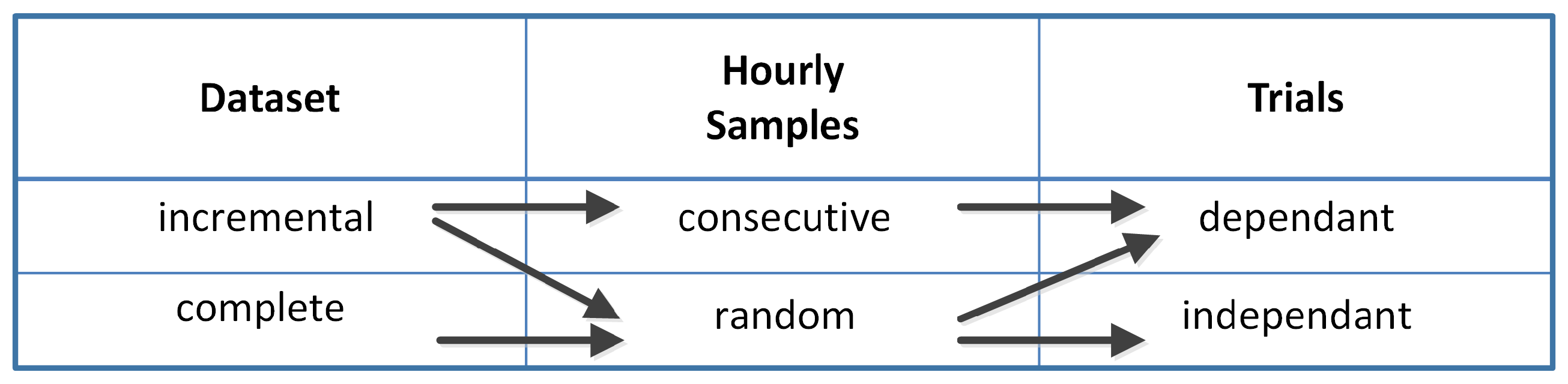


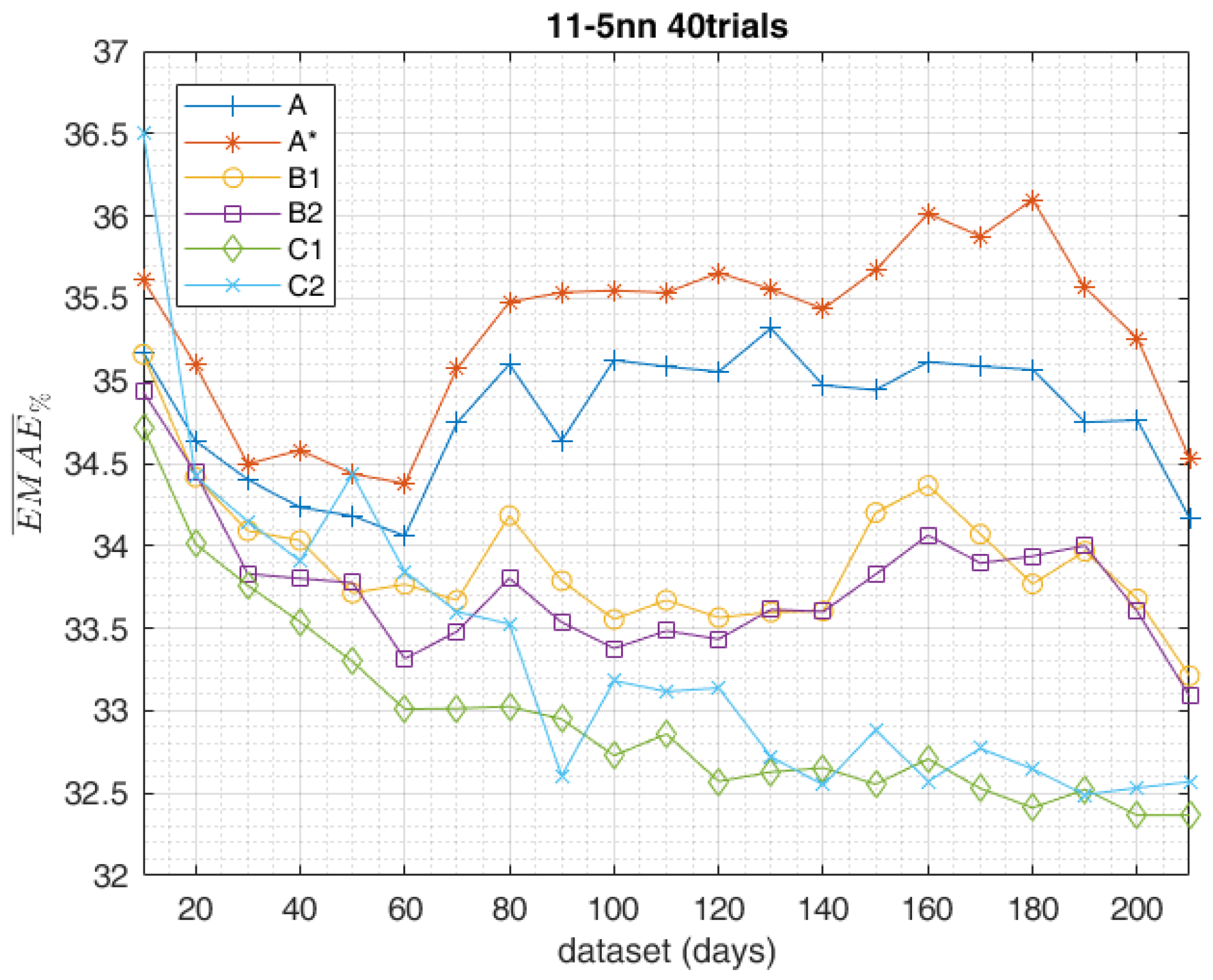
| Method | Data-Set | Trials | Samples |
|---|---|---|---|
| A | Incremental | Dependent | Consecutive (10% 90%) |
| A* | Incremental | Dependent | Consecutive (90% 10%) |
| B1 | Incremental | Independent | Random |
| B2 | Incremental | Dependent | Random |
| C1 | Complete | Independent | Random |
| C2 | Complete | Dependent | Random |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dolara, A.; Grimaccia, F.; Leva, S.; Mussetta, M.; Ogliari, E. Comparison of Training Approaches for Photovoltaic Forecasts by Means of Machine Learning. Appl. Sci. 2018, 8, 228. https://0-doi-org.brum.beds.ac.uk/10.3390/app8020228
Dolara A, Grimaccia F, Leva S, Mussetta M, Ogliari E. Comparison of Training Approaches for Photovoltaic Forecasts by Means of Machine Learning. Applied Sciences. 2018; 8(2):228. https://0-doi-org.brum.beds.ac.uk/10.3390/app8020228
Chicago/Turabian StyleDolara, Alberto, Francesco Grimaccia, Sonia Leva, Marco Mussetta, and Emanuele Ogliari. 2018. "Comparison of Training Approaches for Photovoltaic Forecasts by Means of Machine Learning" Applied Sciences 8, no. 2: 228. https://0-doi-org.brum.beds.ac.uk/10.3390/app8020228