Sliding-Mode Speed Control of PMSM with Fuzzy-Logic Chattering Minimization—Design and Implementation
Abstract
:1. Introduction

2. Permanent Magnet Synchronous Motor Model
3. Sliding Mode Controller Design and Chattering Minimization
3.1. The Basic Sliding Mode Controller Design
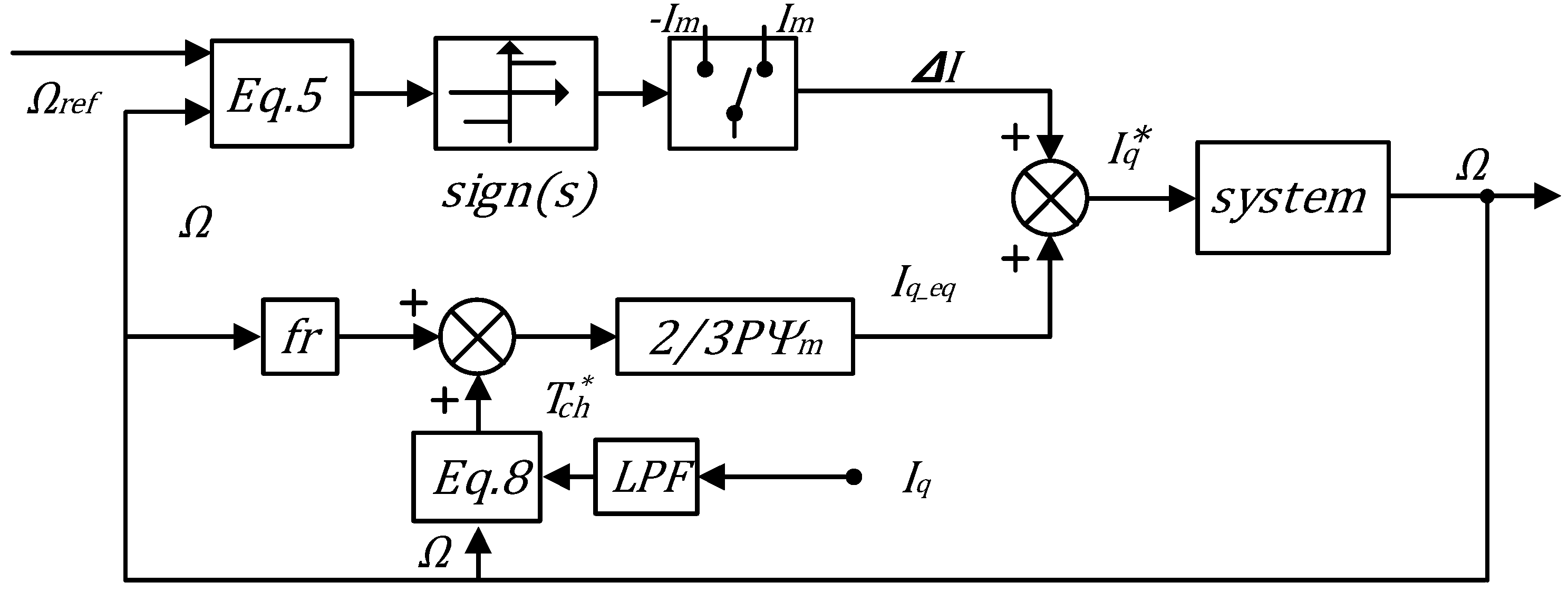
3.2. Chattering Minimization Using Fuzzy Logic Algorithm
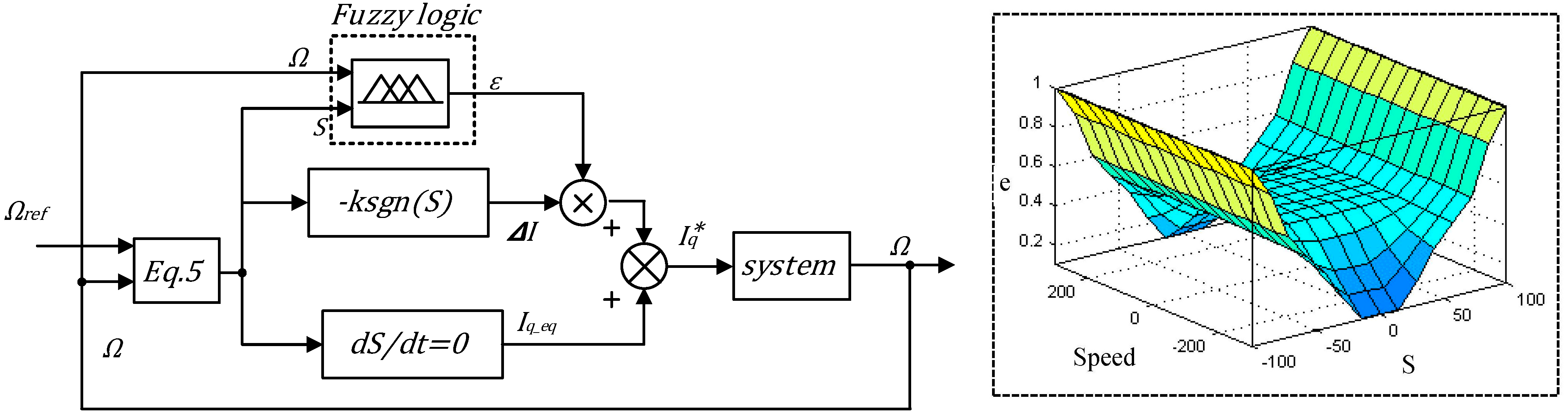
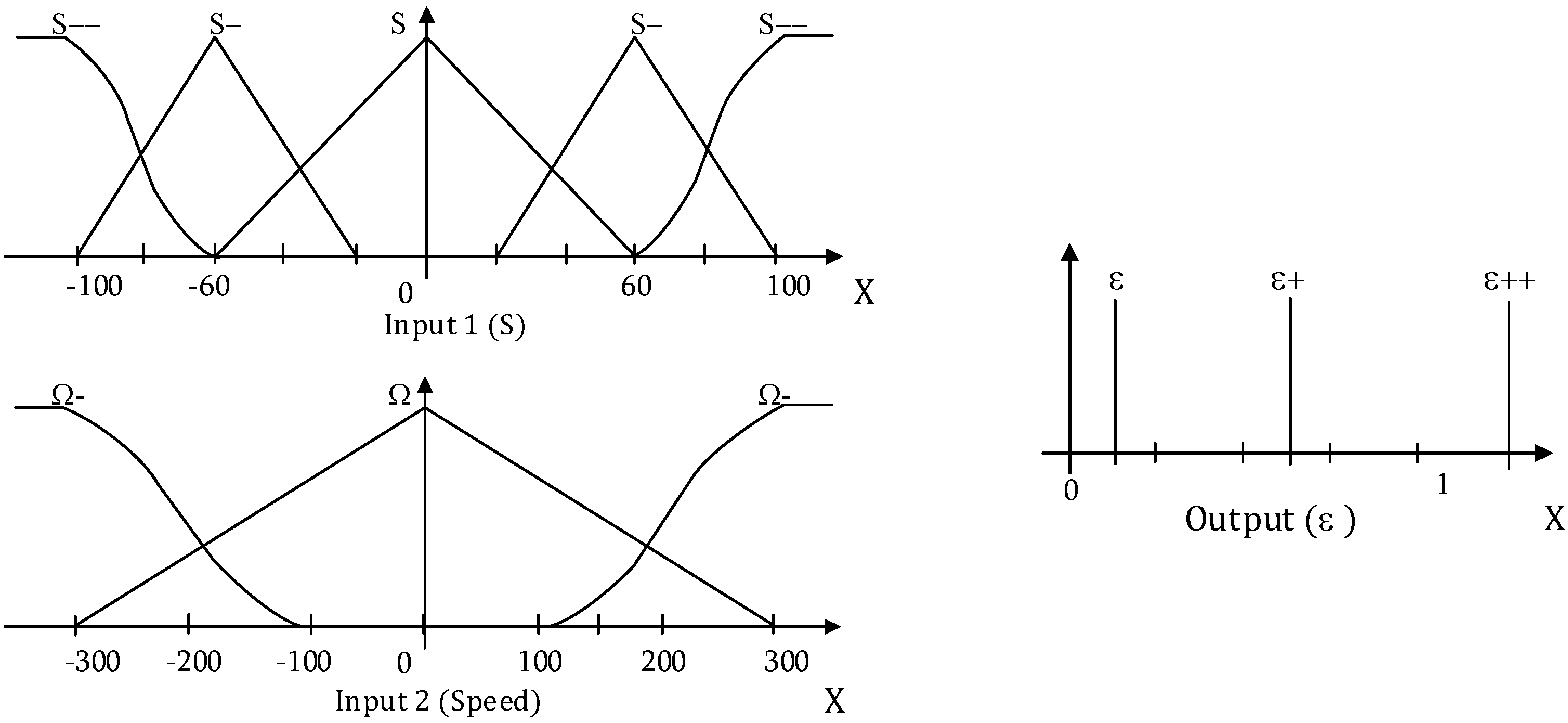
| Inputs | S-- | S- | S0 | S+ | S++ |
|---|---|---|---|---|---|
| Ω- | ε++ | ε+ | ε | ε+ | ε++ |
| Ω | ε++ | ε+ | ε | ε+ | ε++ |
| Ω+ | ε++ | ε+ | ε | ε+ | ε++ |
4. Simulation and Experimental Results
| Components | Values | Components | Values |
|---|---|---|---|
| Rated power | P = 80 W | Pole pairs | 4 |
| DC-voltage | 24 V | Viscous friction | fr = 0.04 10-3 Kgm2 |
| Rated speed | 4000 rpm | Rotation inertia | J = 0.5 10-3 Nm/rad |
| Resistance and inductance | R = 0.43 Ω, L = 1.35 mH | Sampling | fs = 10 kHz |
| Rated torque | 0.19 Nm | PWM frequency | FPWM = 10 kHz |

4.1. Simulation Results and Discussion
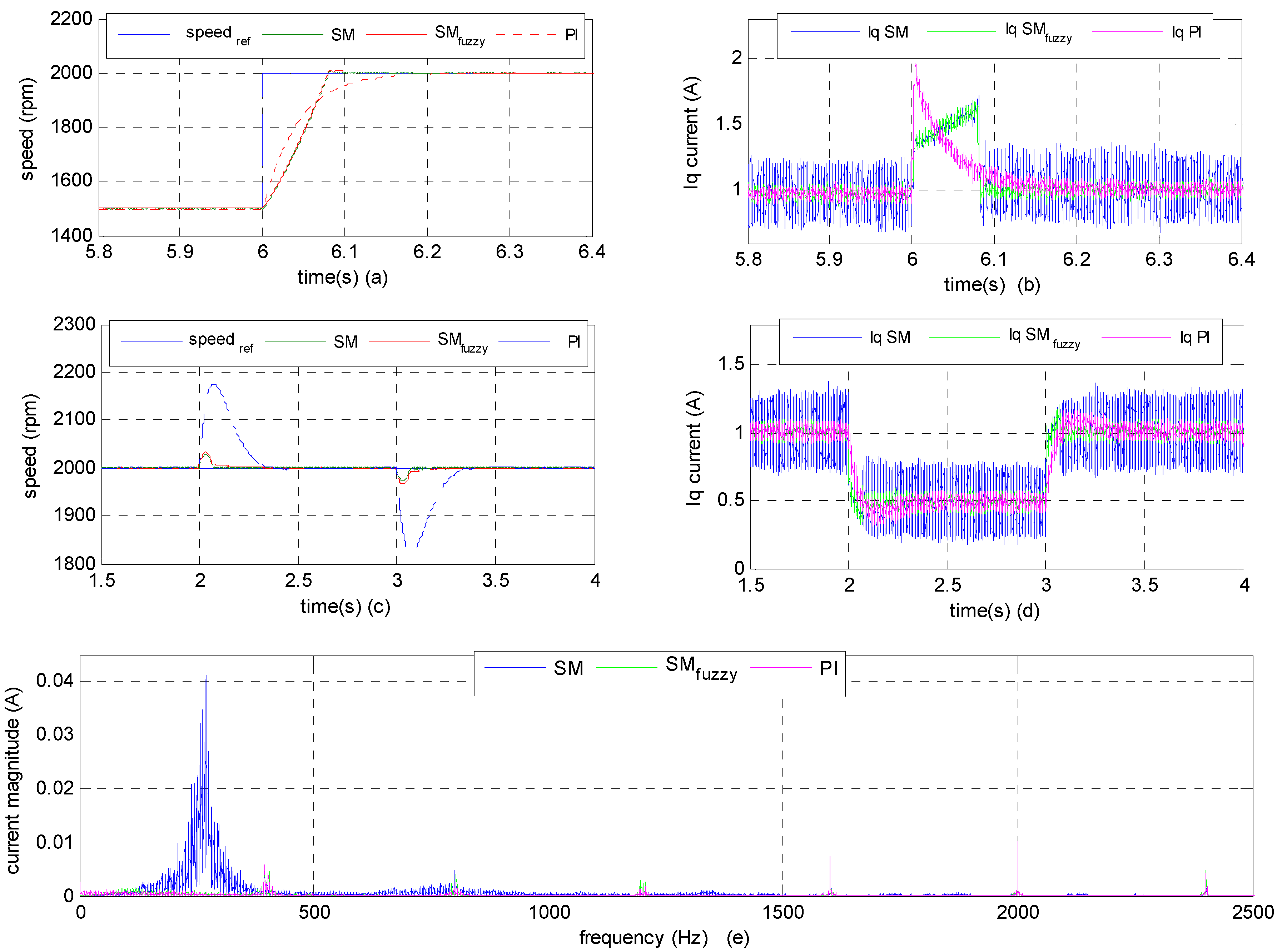
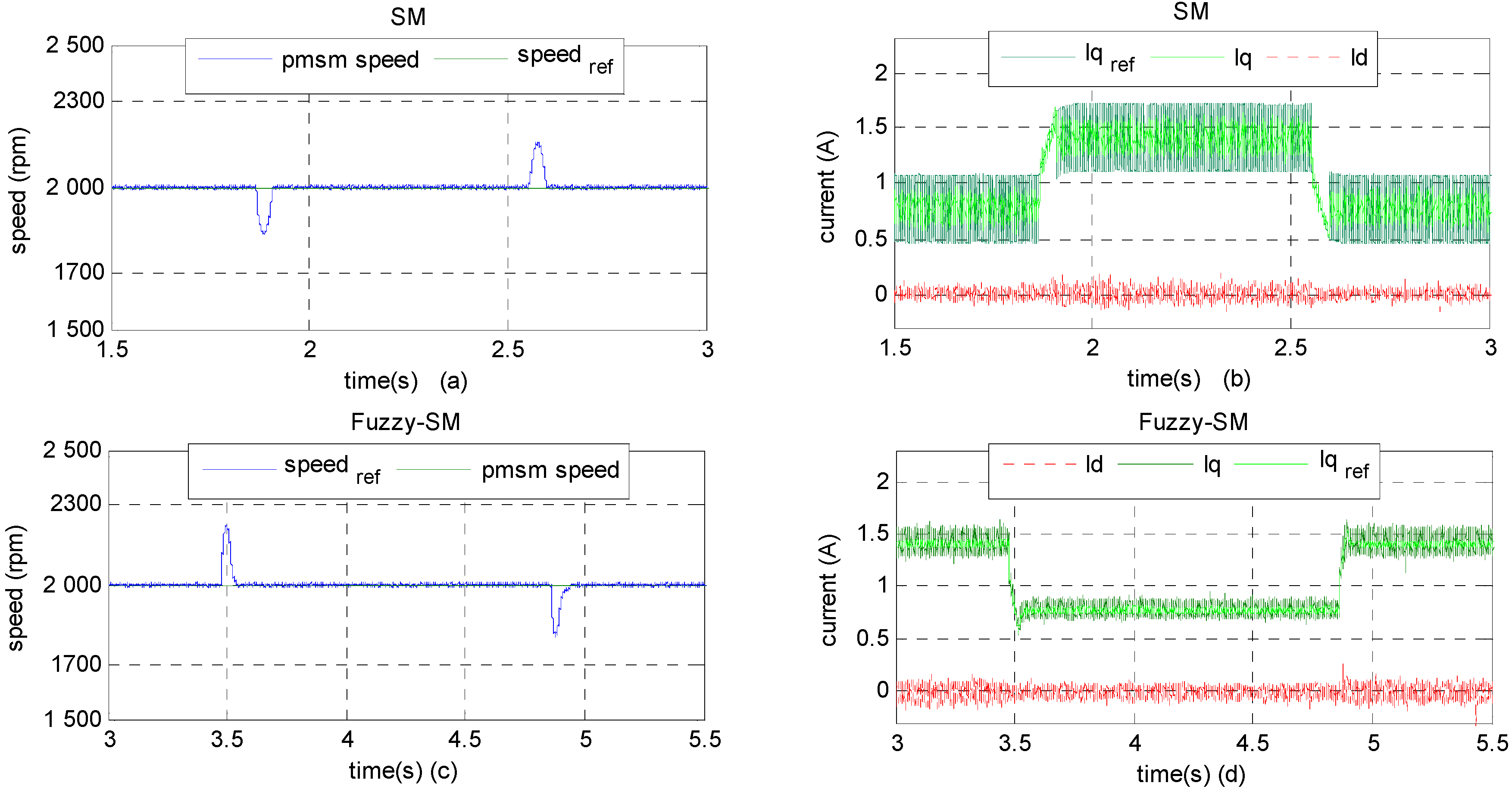
4.2. Implementation and Experimental Results

5. Conclusions
Author Contributions
Conflicts of Interest
References
- Abed, K. Techniques De Commande Avancees Appliquees Aux Machines De Type Asynchrone. Ph.D. Thesis, University Mentouri of Constantine, Constantine, Algeria, 22 Junuary 2010. [Google Scholar]
- Hsien, T.L.; Sun, Y.Y.; Tsai, M.C. H∞ control for a sensorless permanent-magnet synchronous drive. In Proceedings of the Power Conversion Conference, Yokohama, Japan, 19–21 April 1993.
- Foo, G.H.B.; Rahman, M.F. Direct torque control of an IPM synchronous motor drive at very low speed using a sliding-mode stator flux observer. IEEE Trans. Power Electron. 2010, 25, 933–942. [Google Scholar] [CrossRef]
- Casey, B.B.; Azizur Rahman, M. Intelligent Speed Control of Interior Permanent Magnet Motor Drives Using a Single Untrained Artificial Neuron. IEEE Trans. Ind. Appl. 2013, 49, 1836–1843. [Google Scholar]
- Fnaiech, M.A.; Betin, F.; Capolino, G.A.; Fnaiech, F. Fuzzy logic and sliding-mode controls applied to six-phase induction machine with open phases. IEEE Trans. Ind. Electron. 2010, 57, 354–364. [Google Scholar] [CrossRef]
- Wang, L.; Chai, T.; Zhai, L. Neural-network-based terminal sliding mode control of robotic manipulators including actuator dynamics. IEEE Trans. Ind. Electron. 2009, 56, 3296–3304. [Google Scholar] [CrossRef]
- Boubakir, A.; Boudjema, F.; Boubakir, C.; Ikhlef, N. Loi de Commande par Mode de Glissement avec Une Surface de Glissement Non Linéaire Appliquée au Système Hydraulique à Réservoirs Couplés. In Proceedings of the 4th International Conference on Computer Integrated Manufacturing, Algiers, Algeria, 3–4 November 2007.
- Fnaiech, M.A.; Betin, F.; Capolino, G.A. Sliding Mode Control applied to the Inner Loop Regulation of a Faulted Six Phase Induction Machine (6PIM). In Proceedings of the Electric Machines and Drives Conference, Miami, FL, USA, 3–6 May 2009; pp. 1305–1310.
- Lin, C.K. Nonsingular terminal sliding mode control of robot manipulators using fuzzy wavelet networks. IEEE Trans. Fuzzy Syst. 2006, 14, 849–859. [Google Scholar] [CrossRef]
- Shaocheng, T.; Han-Xiong, L. Fuzzy adaptive sliding-mode control for MIMO nonlinear systems. IEEE Trans. Fuzzy Syst. 2003, 11, 354–360. [Google Scholar] [CrossRef]
- Su, T.; Liaw, C.M. Adaptive positioning control for a LPMSM drive based on adapted inverse model and robust disturbance observer. IEEE Trans. Power Electron. 2006, 21, 505–517. [Google Scholar]
- Gao, W.; Hung, J.C. Variable structure control of nonlinear systems: A new approach. IEEE Trans. Power Electron. 1993, 40, 45–55. [Google Scholar]
- Lin, F.J.; Hwang, J.C.; Chou, P.H.; Hung, Y.C. FPGA-based intelligent-complementary sliding-mode control for PMLSM servo-drive system. IEEE Trans. Power Electron. 2010, 25, 2573–2587. [Google Scholar] [CrossRef]
- Zhang, X.G.; Zhao, K.; Sun, L. A PMSM sliding mode control system based on a novel reaching law. In Proceedings of the International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011.
- Chiu, J.Y.-C.; Leung, K.K.-S.; Chung, H.S.-H. High-order switching surface in boundary control of inverters. IEEE Trans. Power Electron. 2007, 22, 1753–1765. [Google Scholar] [CrossRef]
- Lin, C.-K.; Liu, T.-H.; Wei, M.-Y.; Fu, L.-C.; Hsiao, C.-F. Design and implementation of a chattering-free non-linear sliding-mode controller for interior permanent magnet synchronous drive systems. Electr. Power Appl. 2012, 6, 332–344. [Google Scholar] [CrossRef]
- Mohammad, R.S.; Pooria, O.; Mohammad, H.K. Robust control strategy for electrically driven robot manipulators: Adaptive fuzzy sliding mode. Electr. Power Appl. Sci. Meas. Technol. 2015, 9, 322–334. [Google Scholar]
- Zhao, K.; Zhang, X.G.; Sun, L.; Cheng, C. Sliding mode control of high-speed PMSM based on precision linearization control. In Proceedings of the Electrical Machines and Systems, Beijing, China, 20–23 August 2011; pp. 1–4.
- Fadil, H.; Yousfi, D.; Driss, Y.A.; Nasrudin, A.R. Synchronization techniques benchmarking of grid fault modes in single-phase systems. In Proceedings of the Renewable and Sustainable Energy Conference, Ouarzazate, Morocco, 17–19 October 2014; pp. 191–196.
- Li, S.; Zhou, M.; Yu, X. Design and Implementation of Terminal Sliding Mode Control Method for PMSM Speed Regulation System. IEEE Trans. Ind. Inform. 2013, 9, 1879–1891. [Google Scholar] [CrossRef]
- Lopez, P.; Nouri, A.S. Théorie Elémentaire et Pratique de la Commande par les Régimes Glissants; Mathématiques & Applications 55; Springer: New York, NY, USA, 2006; pp. 25–113. [Google Scholar]
- Bartoszewicz, A. (Ed.) Sliding Mode Control; InTech: Rijeka, Croatia, 2011; pp. 25–109.
- Fadil, H.; Yousfi, D.; Elhadiyani, M.L.; Driss, Y.A.; Nasrudin, A.R. Design and Experimental Evaluation of a Fuzzy-PI Controller applied to the PMSM Speed control. In Proceedings of the Mediterranean Green Energy Forum, Marrakech, Morocco, 26–28 March 2015.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hicham, F.; Yousfi, D.; Youness, A.D.; Larbi, E.M.; Rahim, N.A. Sliding-Mode Speed Control of PMSM with Fuzzy-Logic Chattering Minimization—Design and Implementation. Information 2015, 6, 432-442. https://0-doi-org.brum.beds.ac.uk/10.3390/info6030432
Hicham F, Yousfi D, Youness AD, Larbi EM, Rahim NA. Sliding-Mode Speed Control of PMSM with Fuzzy-Logic Chattering Minimization—Design and Implementation. Information. 2015; 6(3):432-442. https://0-doi-org.brum.beds.ac.uk/10.3390/info6030432
Chicago/Turabian StyleHicham, Fadil, Driss Yousfi, Aite Driss Youness, Elhafyani Mohamed Larbi, and Nasrudin Abd Rahim. 2015. "Sliding-Mode Speed Control of PMSM with Fuzzy-Logic Chattering Minimization—Design and Implementation" Information 6, no. 3: 432-442. https://0-doi-org.brum.beds.ac.uk/10.3390/info6030432






