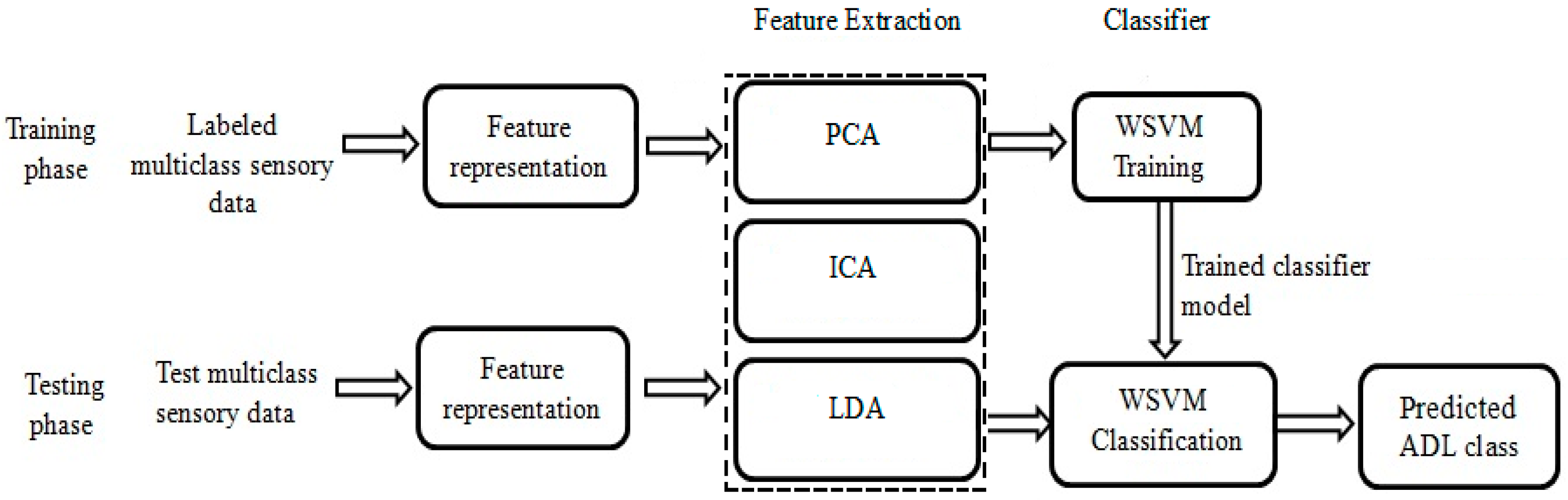
3.3. Results
In our experiments, the SVM algorithm is tested with a LibSVM implementation [
31]. It was used to implement the one-versus-one multiclass classifier [
5]. We used the radial basis kernel function as follows:
. Firstly, we optimized the SVM hyper-parameters (σ,
C) for all training sets in the range (0.1–2) and [0.1, 1, 10, 100], respectively, to maximize the class accuracy of the leave-one-day-out cross validation technique. The best pair parameters (σ
opt,
Copt) = (1.7, 1), (2, 1), (1.4, 1), and (1.2, 1) are used for the datasets TK26M, TK57M, TAP30F, and TAP80F respectively. Then, locally, we optimized the cost parameter
Ci, adapted for each activity class by using WSVM classifier with the common cost parameter is fixed
C = 1, see
Table 3,
Table 4,
Table 5 and
Table 6.
Table 3.
Selection of the weights wi using TK26M dataset.
| Activity | Id | Le | To | Sh | Sl | Br | Di | Dr |
|---|
| wi | 5 | 1 | 61 | 88 | 2 | 216 | 73 | 419 |
Table 4.
Selection of the weights wi using TK57M dataset.
| Activity | Id | Le | Ea | To | Sho | B.t | Sha | Sl | Dre |
|---|
| wi | 4 | 1 | 32 | 50 | 63 | 118 | 179 | 2 | 107 |
| Me | Br | Lu | Di | Sn | Dri | Re | - | - |
| 749 | 164 | 193 | 41 | 500 | 375 | 5 | - | - |
Table 5.
Selection of the weights wi using TAP30F dataset.
| Activity | Id | Le | To | Ba | Gr | Dr | P.b | P.l | P.d |
|---|
| wi | 1 | 220 | 24 | 40 | 38 | 126 | 82 | 28 | 101 |
| P.s | P.b | W.d | Cl | D.l | - | - | - | - |
| 131 | 128 | 307 | 96 | 73 | - | - | - | - |
Table 6.
Selection of the weights wi using TAP80F dataset.
| Activity | Id | To | T.m | P.b | P.l | P.d | P.s | W.d | W.TV | L.m |
|---|
| wi | 1 | 30 | 92 | 38 | 21 | 36 | 72 | 53 | 32 | 17 |
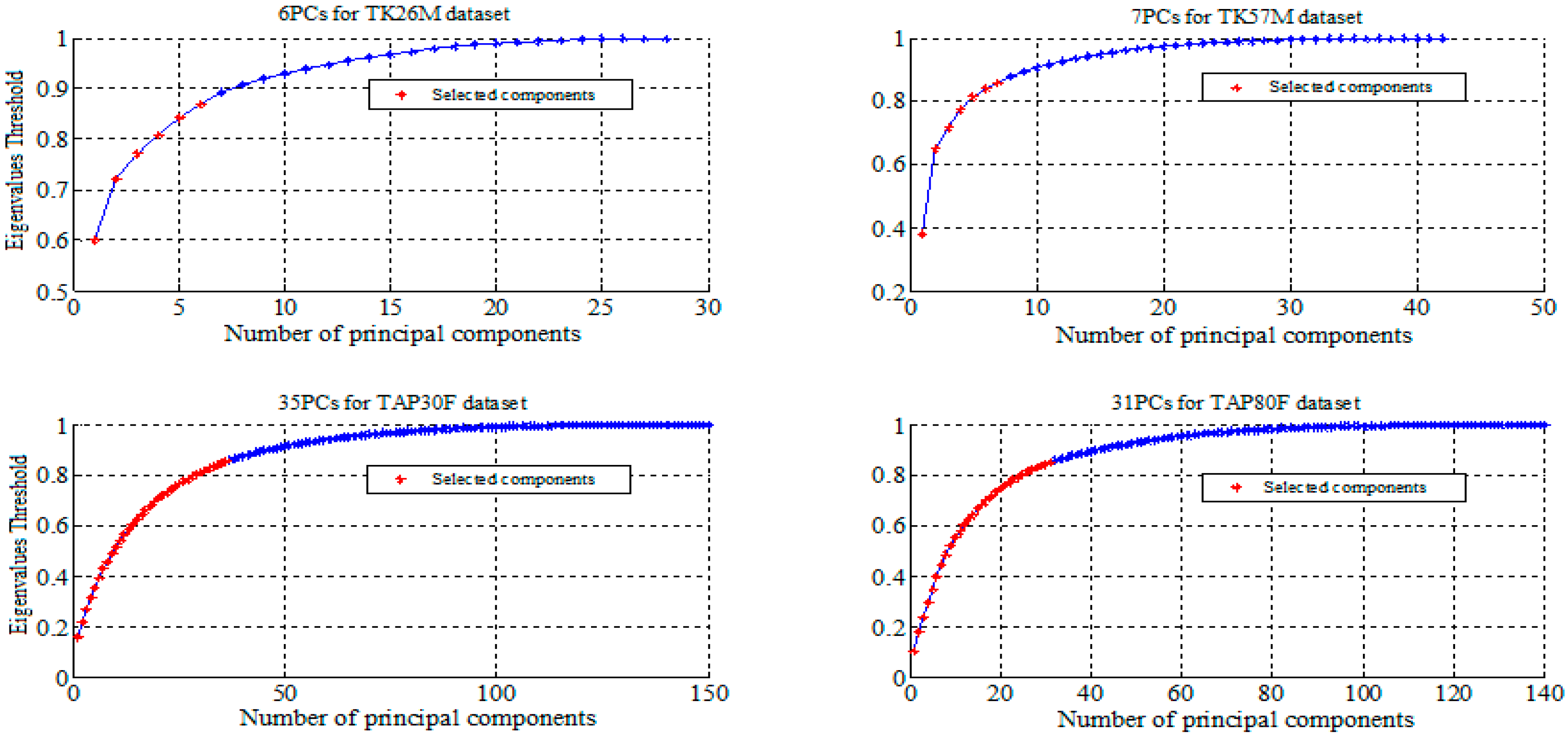
We reported in
Figure 2 and
Figure 3 the selected features using PCA and LDA for all datasets. The summary of the performance measures obtained for all classifiers are presented in
Table 7. For CRF results on these datasets, refer to [
3,
33,
34]. ICA differs from PCA in the fact that the low-dimensional signals do not necessarily correspond to the directions of maximum variance. We start with the first independent component and keep increasing the number until the cross-validation error reduces.
After the selection of the best parameters, we evaluated the performance of different algorithms using appropriate metrics for imbalanced classification. The classification results for CRF, SVM, WSVM, PCA+WSVM, ICA+WSVM, and LDA+WSVM are summarized in
Table 7 below.
Figure 2.
Feature selection by Principal Component Analysis (PCA).
Figure 3.
Feature selection by Linear Discriminant Analysis (LDA).
Table 7.
Recall (Rec.), Precision (Prec.), F-measure (F), and Accuracy (Acc.) results for all methods. The values are percentages.
| Dataset | Classifier | Rec. | Prec. | F | Acc. |
|---|
| TK26M | CRF [3] | 70.8 | 74.4 | 72.5 | 95.6 |
| SVM | 61.8 | 73.3 | 67.0 | 95.5 |
| WSVM | 72.8 | 74.6 | 73.7 | 92.5 |
| PCA+WSVM | 71.5 | 71.5 | 71.5 | 91.2 |
| ICA+WSVM | 71.2 | 73.3 | 72.2 | 92.7 |
| LDA+WSVM | 77.0 | 78.4 | 77.7 | 93.5 |
| TK57M | CRF [33] | 30.0 | 36.0 | 33.0 | 78.0 |
| SVM | 35.6 | 34.9 | 35.2 | 80.8 |
| WSVM | 40.8 | 37.8 | 39.2 | 77.1 |
| PCA+WSVM | 36.5 | 34.2 | 35.3 | 76.9 |
| ICA+WSVM | 36.2 | 38.1 | 37.1 | 76.6 |
| LDA+WSVM | 42.3 | 39.8 | 41.0 | 77.2 |
| TAP30F | CRF [34] | 26.3 | 31.9 | 28.8 | 83.7 |
| SVM | 22.3 | 34.0 | 26.9 | 83.3 |
| WSVM | 30.8 | 30.6 | 30.7 | 23.8 |
| PCA+WSVM | 32.1 | 31.6 | 31.8 | 20.8 |
| ICA+WSVM | 30.4 | 28.7 | 29.5 | 21.7 |
| LDA+WSVM | 38.2 | 52.9 | 44.3 | 33.8 |
| TAP80F | CRF [34] | 27.1 | 29.5 | 28.2 | 77.2 |
| SVM | 15.2 | 30.0 | 20.1 | 75.6 |
| WSVM | 29.2 | 29.4 | 29.3 | 28.7 |
| PCA+WSVM | 29.6 | 29.4 | 29.5 | 22.4 |
| ICA+WSVM | 26.5 | 27.9 | 27.2 | 22.1 |
| LDA+WSVM | 38.7 | 45.7 | 41.9 | 28.7 |
This table shows that LDA+WSVM method gives a clearly better F-measure performance, while CRF and SVM methods perform better in terms of accuracy for all datasets. As can be noted in this table, LDA outperforms PCA and ICA for recognizing activities with a WSVM classifier for all datasets. The PCA+WSVM method improves the classification results compared to CRF, SVM, WSVM, and ICA+WSVM for the TAP30F and TAP80F datasets, compared to other datasets.
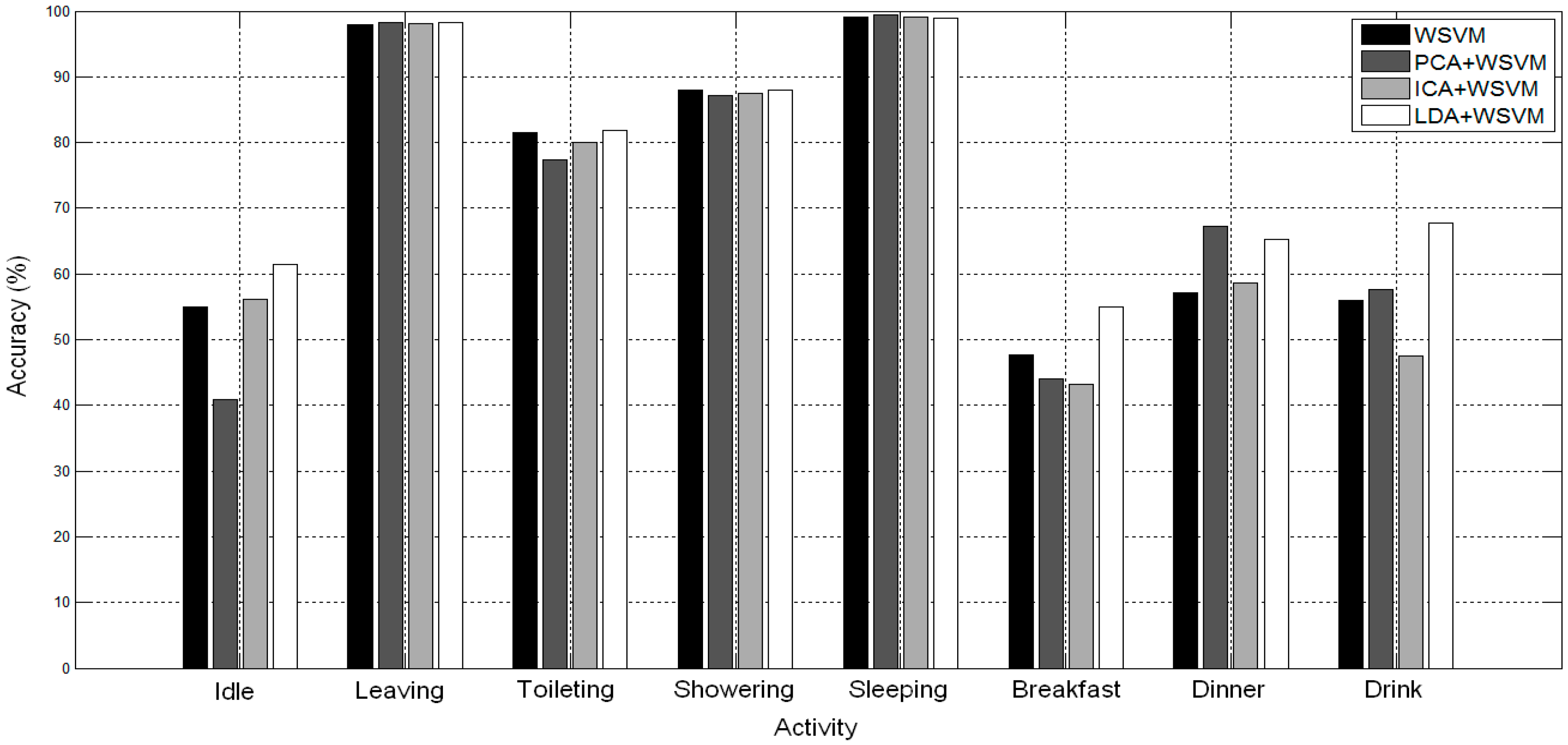
The
Figure 4 and
Figure 5 give the classification results in terms of the accuracy measure for each activity with WSVM, PCA+WSVM, ICA+WSVM, and LDA+WSVM methods.
In
Figure 4, for WSVM, PCA+WSVM, LDA+WSVM models, the minority activities “Toileting”, “Showering”, and the kitchen activities “Breakfast” and “Drink” are significantly better detected, compared to other methods. LDA+WSVM is an effective method for recognizing activities. The majority activities are better for all methods, while the “Idle” activity is more accurate for the LDA+WSVM method.
Figure 4.
Accuracy for each activity on TK26M dataset.
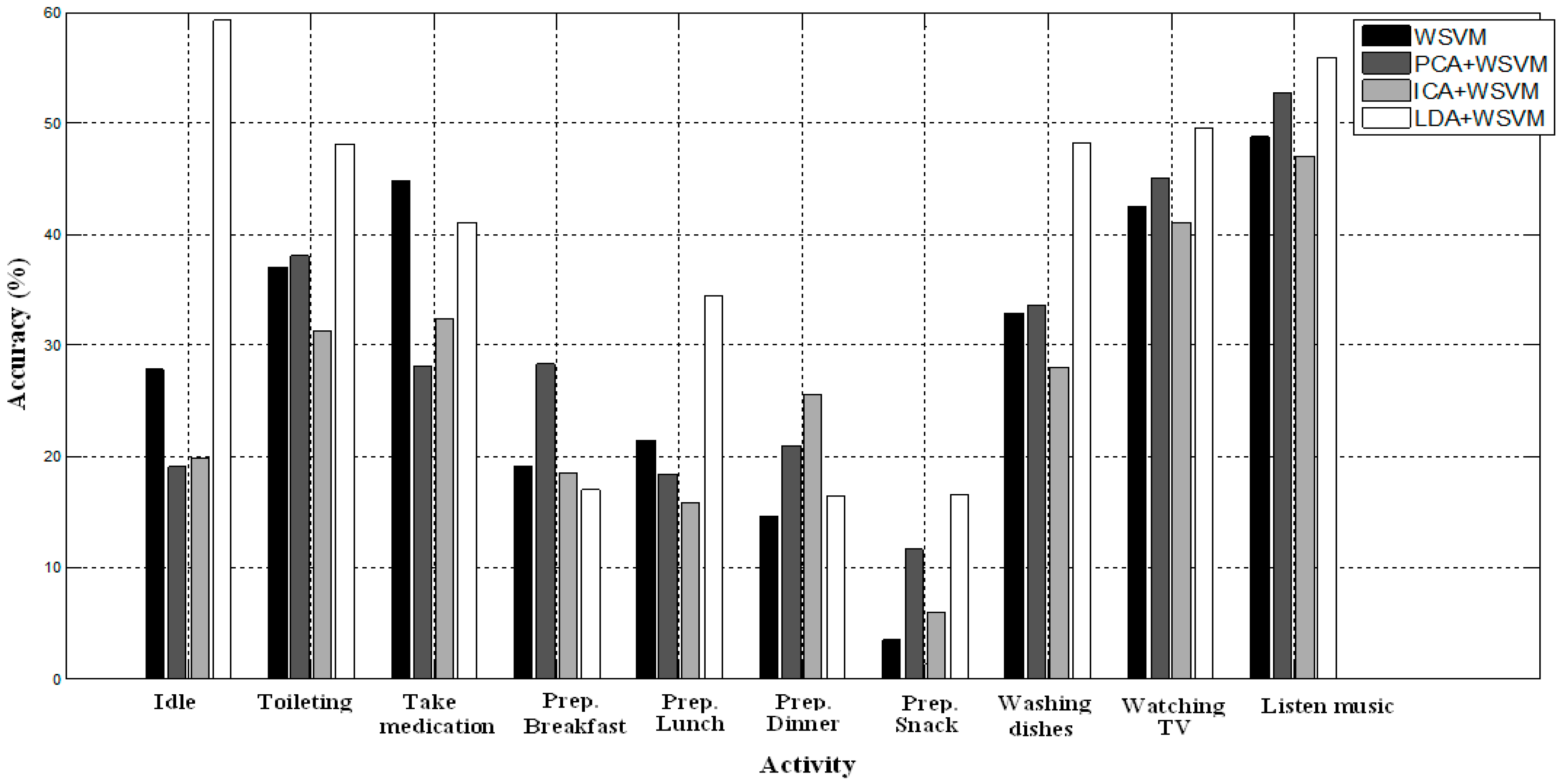
Figure 5.
Accuracy for each activity on TAP80F dataset.
We can see in
Figure 5 that the minority activities (“Toileting”, “Washing dishes”, “Watching TV”, “Listen music”, and the kitchen activities “Prep.Lunch”, “Prep.Snack”) are better recognized with LDA-WSVM. Additionally, the kitchen activities perform worst for all datasets. They are, in general, hard to recognize but they are better recognized with LDA-WSVM compared to others methods.
3.4. Discussion
Based on the experiments carried out in this work, a number of conclusions can be drawn. Using experiments on large real-world datasets, we showed the F-measure obtained with TK26M dataset is better compared to other datasets for all recognition methods because the TK57M, TAP30F, and TAP80F datasets include more activity classes. We supposed that the use of a hand-written diary in the TK57M house and PDA in TAP30F and TAP80F houses for annotating data is less accurate than using the Bluetooth headset as in TK26M house. For the TK26M dataset, a Bluetooth headset was used which communicated with the same server the sensor data was logged on. This means the timestamps of the annotation were synchronized with the timestamps of the sensors. In TK57M activity diaries were used, this is more error-prone because times might not always be written down correctly and the diaries have to be typed over afterwards.
In this section, we explain the difference in terms of performance between different recognition methods for imbalanced dataset. Our experimental results show that WSVM and LDA+WSVM methods work better for classifying activities; they consistently outperform the other methods in terms of the accuracy of the minority classes. In particular, LDA-WSVM is the best classification method for all datasets because the LDA method is more adapted for the features reduction in the datasets with consideration the discrimination between classes.
PCA-WSVM outperforms CRF, SVM, WSVM, and ICA-WSVM for TAP30F and TAP80F datasets. In other datasets ICA-WSVM surpasses PCA-WSVM. We conclude that the PCA method is more adapted for the features extraction in the datasets with large features vectors.
A multiclass SVM classifier does not take into consideration the differences (costs) between the class distributions during the learning process and optimizes with the cross-validation research the same cost parameter C for all classes. Not considering the weights in SVM formulation affects the classifiers’ performances and favors the classification of majority activities (“Idle”, “Leaving” and “Sleeping”). Although WSVM, including the individual setting of parameter C for each class, is significantly more effective than CRF and SVM methods, WSVM is not efficient compared to LDA+WSVM. The LDA method significantly improves the performance of the WSVM classifier. Thus, it follows that LDA-WSVM can be made more robust for classifying human activities.
The recognition of the minority activities in TK26M as “Toileting”, “Showering”, “Breakfast” “Dinner”, and “Drink” is lower compared to “Leaving” and “Sleeping” activities. This is mainly due to the fact that the minority activities are less represented in the training dataset. However, the activities “Idle” and the three kitchen activities gave the worst results compared to the others activities. Most confusion occurs between the “Idle” activity and the kitchen activities. In particular, the “Idle” is one of the most frequent activities but is usually not a very important activity to recognize. It might, therefore, be preferable to lose accuracy on this activity if it allows a better recognition of minority classes.
The kitchen activities are food-related tasks, they are worst recognized for all methods because most of the instances of these activities were performed in the same location (kitchen) using the same set of sensors. In other words, it is observed that groups of similar activities are more separable if performed in different locations. For example, “Toileting” and “Showering” are more separable because they are in two different locations in the TK26M dataset. Therefore, the location of the sensors is of great importance for the performance of the recognition system.