Computation of the Likelihood in Biallelic Diffusion Models Using Orthogonal Polynomials
Abstract
:1. Introduction
2. Mutation and Drift Diffusion
2.1. Moran and Diffusion Models
2.2. Solution of the Mutation-Drift Diffusion Using Modified Jacobi Polynomials
2.2.1. Relationship of the Forward and Backward Diffusion Equation; Sturm–Liouville Form
2.2.2. Modified Jacobi Polynomials
2.2.3. Series Expansion; Approximation of Functions by Orthogonal Polynomials
2.2.4. Example: A Change in the Scaled Mutation Rate with Modified Jacobi Polynomials
2.3. Statistics of Site Frequency Spectra
2.3.1. Equilibrium
2.3.2. Outside Equilibrium
3. Selection and Drift Diffusion with Mutations from the Boundaries
3.1. Pure Drift within the Polymorphic Region
3.1.1. Equilibrium of Mutations from the Boundaries and Drift; Outgroup Information
3.1.2. Equilibrium of Mutations from the Boundaries and Drift; No Outgroup Information
3.1.3. Example for the Use of Gegenbauer Polynomials: Evolve and Resequence
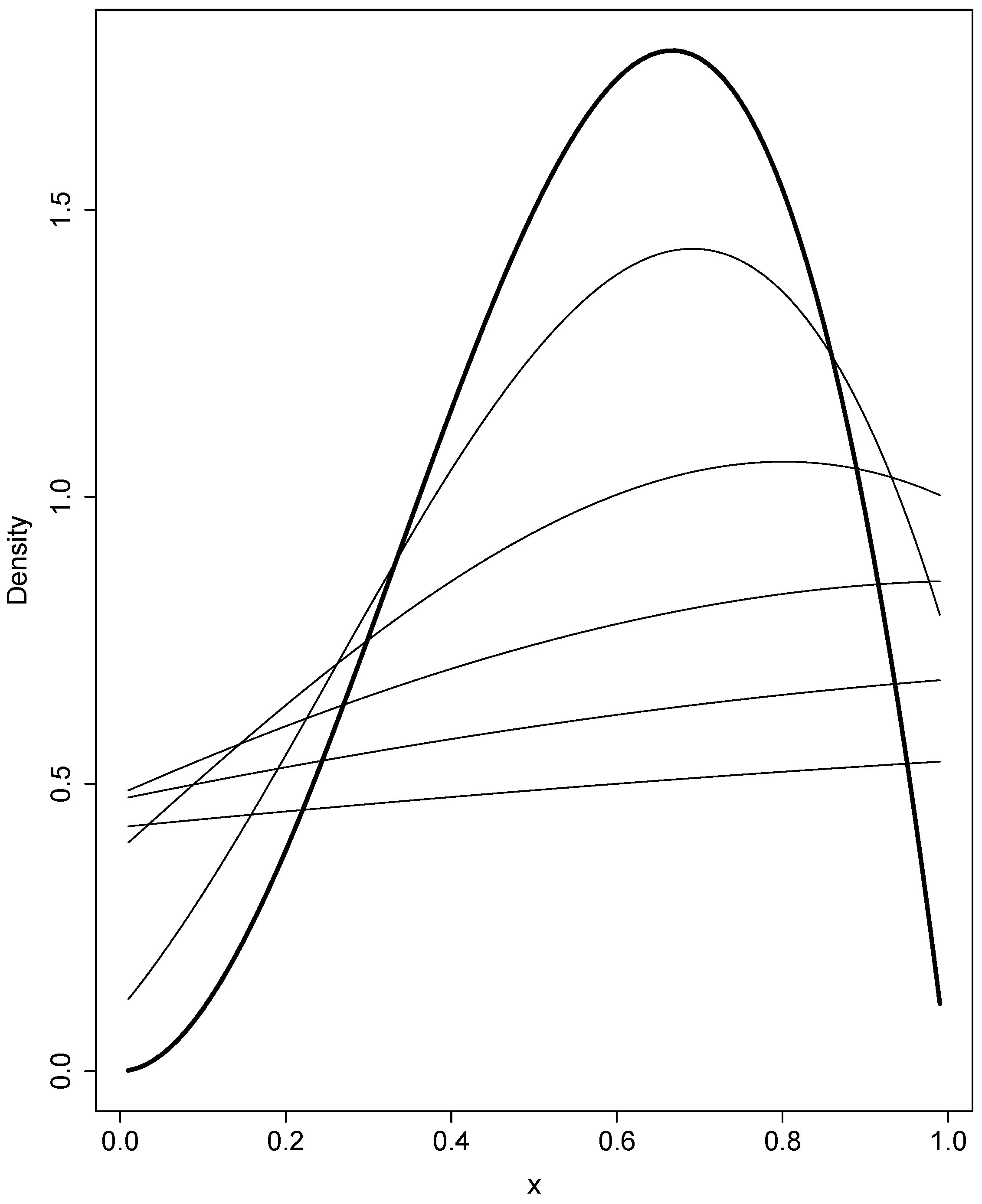
3.2. Selection and Drift
4. Conclusions
Acknowledgments
Appendix. The Oblate Spheroidal Wave Function
Conflicts of Interest
References
- Parsch, J.; Novozhilov, S.; Saminadin-Peter, S.; Wong, K.; Andolfatto, P. On the utility of short intron sequences as a reference for the detection of positive and negative selection in Drosophila. Mol. Biol. Evol. 2010, 27, 1226–1234. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R. The Genetical Theory of Natural Selection; Clarendon Press: Oxford, UK, 1930. [Google Scholar]
- Wright, S. Evolution in Mendelian populations. Genetics 1931, 16, 97–159. [Google Scholar] [PubMed]
- Moran, P. Random processes in genetics. Proc. Camb. Philos. Soc. 1958, 54, 60–71. [Google Scholar] [CrossRef]
- Kimura, M. The Neutral Theory of Molecular Evolution; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- Kimura, M. Population Genetics, Molecular Evolution, and the Neutral Theory: Selected Papers; University of Chicago Press: Chicago, IL, USA, 1994. [Google Scholar]
- Evans, S.; Shvets, Y.; Slatkin, M. Non-equilibrium theory of the allele frequency spectrum. Theor. Popul. Biol. 2007, 71, 109–119. [Google Scholar] [CrossRef] [PubMed]
- Zivkovic, D.; Stephan, W. Analytical results on the neutral non-equilibrium allele frequency spectrum based on diffusion theory. Theor. Popul. Biol. 2011, 79, 184–191. [Google Scholar] [CrossRef] [PubMed]
- Ewens, W. Mathematical Population Genetics, 2nd ed.; Springer: New York, NY, USA, 2004. [Google Scholar]
- Wolfram Research, Inc. Mathematica, Version 10.0. Champaign, IL, USA, 2014. Available online: http://wolfram.com/ (accessed on 6 November 2014).
- Matlab 8.4. The MathWorks Inc.: Natick, MA, USA, 2014. Available online: http://www.mathworks.de/ (accessed on 6 November 2014).
- Song, Y.; Steinrücken, M. A simple method for finding explicit analytic transition densities of diffusion processes with general diploid selection. Genetics 2012, 190, 1117–1129. [Google Scholar] [CrossRef] [PubMed]
- Baake, E.; Bialowons, R. Ancestral Processes with Selection: Branching and Moran Models; Banach Center Publications: Bielefeld, Germany, 2008; Volume 80, pp. 33–52. [Google Scholar]
- Etheridge, A.; Griffiths, R. A coalescent dual process in a Moran model with genic selectio. Theor. Popul. Biol. 2009, 75, 320–330. [Google Scholar] [CrossRef] [PubMed]
- Vogl, C.; Clemente, F. The allele-frequency spectrum in a decoupled Moran model with mutation, drift, and directional selection, assuming small mutation rates. Theor. Popul. Genet. 2012, 81, 197–209. [Google Scholar] [CrossRef] [PubMed]
- Hein, J.; Schierup, M.; Wiuf, C. Gene Genealogies, Variation, and Evolution: A Primer in Coalescent Theory; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Hazewinkel, M. Sturm-Liouville Theory. In Encyclopedia of Mathematics; Springer: New York, NY, USA, 2001. [Google Scholar]
- Griffiths, R.; Spanò, D. Diffusion processes and coalescent trees. In Probability and Mathematical Genetics: Papers in Honour of Sir John Kingman; Cambridge University Press: Cambridge, UK, 2010; pp. 358–375. [Google Scholar]
- Handbook of Mathematical Functions, 9th ed.; Abramowitz, M.; Stegun, I. (Eds.) Dover: New York, NY, USA, 1970.
- Kimura, M. Solution of a process of random genetic drift with a continuous model. Proc. Natl. Acad. Sci. USA 1955, 41, 144–150. [Google Scholar] [CrossRef] [PubMed]
- Vogl, C. Estimating the Scaled Mutation Rate and Mutation Bias with Site Frequency Data. Theor. Popul. Biol. 2014, in press. [Google Scholar] [CrossRef] [PubMed]
- McKane, A.; Waxman, D. Singular solutions of the diffusion equation of population genetics. J. Theor. Biol. 2007, 247, 849–858. [Google Scholar] [CrossRef] [PubMed]
- Tran, T.; Hofrichter, J.; Jost, J. An introduction to the mathematical structure of the Wright-Fisher model of population genetics. Theory Biosci. 2013, 132, 73–82. [Google Scholar] [CrossRef] [PubMed]
- Clemente, F.; Vogl, C. Unconstrained evolution in short introns?—An analysis of genome-wide polymorphism and divergence data from Drosophila. J. Evol. Biol. 2012, 25, 1975–1990. [Google Scholar] [PubMed]
- Clemente, F.; Vogl, C. Evidence for complex selection on four-fold degenerate sites in Drosophila melanogaster. J. Evol. Biol. 2012, 25, 2582–2595. [Google Scholar] [CrossRef] [PubMed]
- Ewens, W. A note on the sampling theory for infinite alleles and infinite sites models. Theor. Popul. Biol. 1974, 6, 143–148. [Google Scholar] [CrossRef]
- Watterson, G. On the number of segregating sites in genetical models without recombination. Theor. Popul. Biol. 1975, 7, 256–276. [Google Scholar] [CrossRef]
- Sawyer, S.; Hartl, D. Population genetics of polymorphism and divergence. Genetics 1992, 132, 1161–1176. [Google Scholar] [PubMed]
- RoyChoudhury, A.; Wakeley, J. Sufficiency of the number of segregating sites in the limit under finite-sites mutation. Theor. Popul. Biol. 2010, 78, 118–122. [Google Scholar] [CrossRef] [PubMed]
- Vogl, C. Biallelic Mutation-Drift Diffusion in the Limit of Small Scaled Mutation Rates. ArXiv E-Prints 2014. [Google Scholar]
- Gutenkunst, R.; Hernandez, R.; Williamson, S.; Bustamante, C. Inferring the Joint Demographic History of Multiple Populations from Multidimensional SNP Frequency Data. PLoS Genet. 2009, 5, e1000695. [Google Scholar] [CrossRef] [PubMed]
- Tobler, R.; Franssen, S.; Kofler, R.; Orozco-Terwengel, P.; Nolte, V.; Hermisson, J.; Schlötterer, C. Massive habitat-specific genomic response in D. melanogaster populations during experimental evolution in hot and cold environments. Mol. Biol. Evol. 2014, 31, 364–375. [Google Scholar] [PubMed]
- Williamson, E.; Slatkin, M. Using maximum likelihood to estimate population size from temporal changes in allele frequencies. Genetics 1999, 152, 755–761. [Google Scholar] [PubMed]
- Anderson, E.; Williamson, E.; Thompson, E. Monte Carlo evaluation of the likelihood for Ne from temporally spaced samples. Genetics 2000, 156, 2109–2118. [Google Scholar] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; ISBN 3-900051-07-0. R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Falloon, P.; Abbott, P.; Wang, J. Theory and computation of spheroidal wave functions. J. Phys. A Math. Gen. 2003, 36, 5477–5495. [Google Scholar] [CrossRef]
- Beaumont, M.; Zhang, W.; Balding, D. Approximate Bayesian Computation in Population Genetic. Genetics 2002, 162, 2025–2035. [Google Scholar] [PubMed]
- Stratton, J. Spheroidal Wave Functions; The Technology Press of the Massachusetts Institute of Technology: Cambridge, MA, USA, 1954. [Google Scholar]
- Meixner, J.; Schäfke, F. Mathieusche Funktionen und Sphäroidfunktionen; Springer: Berlin, Germany, 1954. (In German) [Google Scholar]
- Flammer, C. Spheroidal Wave Functions; Stanford University Press: Palo Alto, CA, USA, 1957. [Google Scholar]
- Li, L.W.; Leong, M.S.; Yeo, T.S.; Kooi, P.S.; Tan, K.Y. Computations of spheroidal harmonics with complex arguments: A review with an algorithm. Phys. Rev. E 1998, 58, 6792–6806. [Google Scholar] [CrossRef]
- Falloon, P.E. Theory and Computation of Spheroidal Harmonics with General Arguments. Master’s Thesis, Department of Physics, The University of Western Australia, Crawley, Australia, 2001. [Google Scholar]
© 2014 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vogl, C. Computation of the Likelihood in Biallelic Diffusion Models Using Orthogonal Polynomials. Computation 2014, 2, 199-220. https://0-doi-org.brum.beds.ac.uk/10.3390/computation2040199
Vogl C. Computation of the Likelihood in Biallelic Diffusion Models Using Orthogonal Polynomials. Computation. 2014; 2(4):199-220. https://0-doi-org.brum.beds.ac.uk/10.3390/computation2040199
Chicago/Turabian StyleVogl, Claus. 2014. "Computation of the Likelihood in Biallelic Diffusion Models Using Orthogonal Polynomials" Computation 2, no. 4: 199-220. https://0-doi-org.brum.beds.ac.uk/10.3390/computation2040199



