Next Article in Journal
Field Programmable Gate Array Applications—A Scientometric Review
Next Article in Special Issue
Efficient Evaluation of Molecular Electrostatic Potential in Large Systems
Previous Article in Journal
A DFT Study on Structure and Electronic Properties of BN Nanostructures Adsorbed with Dopamine
Previous Article in Special Issue
Coordinate Scaling in Time-Independent Excited-State Density Functional Theory for Coulomb Systems
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Computation
Volume 7
Issue 4
10.3390/computation7040062
computation-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Emerging DFT Methods and Their Importance for Challenging Molecular Systems with Orbital Degeneracy

by
Emilio San-Fabián Maroto
and
Juan-Carlos Sancho-García
*
Departamento de Química Física, Universidad de Alicante, E-03080 Alicante, Spain
*
Author to whom correspondence should be addressed.
Computation 2019, 7(4), 62; https://doi.org/10.3390/computation7040062
Submission received: 11 October 2019 / Revised: 26 October 2019 / Accepted: 2 November 2019 / Published: 3 November 2019
(This article belongs to the Special Issue New Advances in Density Functional Theory and Its Application)
Browse Figures
Versions Notes

Abstract

:
We briefly present some of the most modern and outstanding non-conventional density-functional theory (DFT) methods, which have largely broadened the field of applications with respect to more traditional calculations. The results of these ongoing efforts reveal that a DFT-inspired solution always exists even for pathological cases. Among the set of emerging methods, we specifically mention FT-DFT, OO-DFT, RSX-DFT, MC-PDFT, and FLOSIC-DFT, complementing the last generation of existing density functionals, such as local hybrid and double-hybrid expressions.

1. Introduction

In 1964, P. Hohenberg and W. Kohn (Walter Kohn received—shared with John A. Pople—the Nobel prize in Chemistry in 1998 for his work on DFT) published a pair of celebrated theorems forming the core for density-functional theory (DFT) [1]. Only one year later, the development of the Kohn–Sham (KS) scheme made DFT a practical theory for all kind of electronic structure calculations, as it is often implemented today (KS-DFT) [2]. These authors showed a one-to-one relation (correspondence) between the energy and the electron density of a system always exists, i.e., it is in principle possible to obtain directly the exact energy from this density through a universal functional. However, the mathematical formulation that delivers this energy is still unknown. This approach completely circumvented the paths that classically formed the core of quantum chemistry: the wavefunction is no longer needed and the associated Schrödinger equation does not need to be solved respectively.
The key to this longstanding success was to model or mimic the subtle effects dominating matter at the quantum scale by means of a functional of the electronic density only. The specific functional machinery should accurately include electron–electron exchange and correlation effects, in order to address the structure and bonding of molecules, and it should be more advantageous than ab initio methods, either by reducing the computational cost associated with any molecular or solid-state calculation or by introducing theoretical models that can rationalize chemical reactivity or physical concepts. It was not until the 1980s that modern and accurate approximations of that universal functional were proposed [3,4] beyond those initially used in solid-state physics. That meant having expressions that can calculate the stabilizing effects of matter for any system arising from a purely quantum-mechanical (non-classical) origin, after inserting the electronic density into that chosen mathematical form (i.e., the exchange-correlation functional). The development of these expressions is normally a laborious work, needing extensive calibrations and applications before its wide adoption by the community. Apart from the local density approximation (LDA), the extensions are known as generalized gradient approximation (GGA) and meta-GGA are currently available in most codes for computational simulations of any type. It should also be noted that the dispersion effects (i.e., weak intra- and inter-molecular interactions induced by dispersion forces) have been successfully incorporated into routine DFT calculations, leading to a significant increase in the accuracy of DFT methods [5].
Therefore, DFT has probably become the preferred electronic structure theory for molecular and extended systems, due to an initially favorable scaling with respect to the system size N, i.e., O(N3) for these non-hybrid methods, compared with other traditional ab initio methods including correlation effects. This success is largely due to the existing flavors for the exchange-correlation functional, thanks to intense and ongoing research in recent decades to develop expressions capturing many-body interelectronic effects through electronic density. The hierarchy of available expressions (LDA, GGA, meta-GGA) also consists of orbital-dependent hybrid and double-hybrid functionals, also allowing the step-by-step application of these forms, and then to bracket the expected errors and/or confirm the results obtained at a lower level by those at a higher level; however, at the expense of an increasing computational cost going from O(N3) (semi-local functionals) to O(N4) (hybrid functionals) or O(N5) (double-hybrid functionals). Fortunately, this formal scaling can be reduced in practice, thanks to integral decomposition techniques such as the resolution of identity (RI) or density fitting scheme [6], which expands the product of two Gaussian functions in the basis of an auxiliary Gaussian basis set. Finally, some approximate DFT-based methods have also appeared recently, like composite (and low-cost) DFT-3c expressions (e.g., B97-3c [7]) and the GFN1 [8] and GFNn-xTB [9] variants of the density functional tight-binding theory.
On the other hand, in recent years, we have also seen a revival of first-principle methods with a considerably reduced scaling with respect to their canonical variants, e.g., coupled-cluster with single, double, and perturbatively added triple excitations, or CCSD(T), keeping cost scaling as O(N7), and thus prohibitive for large systems. The approximated versions have become competitive with DFT and highlight the constantly needed trade-off between accuracy and computational cost. A prominent and promising example of the latter advances are local correlation methods, e.g., domain-based local pair natural orbitals (DLPNO), making it possible to perform highly accurate but initially very costly ab initio calculations like (DLPNO-)CCSD(T) [10] or (DLPNO-)NEVPT2 [11] on large systems such as small proteins. In this context, it is thus a good time to briefly present some of the most recent DFT advances paving the way towards the study of complex molecular systems, in the search of universal methods able to provide the right answer for the right reason, taking into account some lessons learnt from the past for systems for which standard DFT applications are historically known to fail [12,13].

2. Beyond a Hybrid Functional in DFT

The great success of hybrid functionals combining an exchange energy functional with a fixed fraction of EXact eXchange (EXX) has prompted the development of more sophisticated approaches. Instead of relying on a constant value for EXX, local hybrid functionals replace it by a real-space-dependent one, mediated by a local mixing function [14]. Note that the gauge problem for the corresponding exchange energy densities has also been solved recently [15], fostering definitively the application of these methods to ground- and excited-state systems.
Another possibility to go beyond the valuable answer provided by a global hybrid functional, with its pros and cons facing some relevant challenges, is provided by merging not only an exchange functional with its EXX counterpart, but also a correlation functional with some ab initio counterpart. If that is achieved by second-order Perturbation Theory (PT2), the resulting expression is known as double-hybrid functional [16] and seems to lead to a systematic improvement with respect to hybrid methods for ground- and excited-state properties [17].

3. Summary of Some Emerging DFT Methods

The improvements summarized in the following share some common features: They can be applied to any particular exchange-correlation functional of choice, and start to be available in some of the most globally employed computational codes (ORCA [18], Q-Chem [19], OpenMolcas [20], etc.) These methods still allow for accurate and conclusive results, providing new insights for all kinds of closed- and open-shell systems (including orbital degeneracy) and/or are less prone to the self-interaction error (SIE) affecting largely the DFT results for challenging systems [21]. Among the variety of existing methods, we (non-exhaustively) selected a sample of those which have been thoroughly and robustly benchmarked in the past, and are now available in a few distributed codes, thus, making it possible to anticipate their consolidation in the coming years among the theoretical community:
  • Finite-Temperature DFT (FT-DFT)
  • Orbital-Optimized DFT (OO-DFT)
  • Range-Separated eXchange DFT (RSX-DFT)
  • Multiconfigurational Pair-DFT (MC-PDFT)
  • Fermi-Löwdin Orbital Self-Interaction Corrected DFT (FLOSIC-DFT)
Finite-Temperature DFT, also called thermally assisted-occupation DFT [22], is a useful tool for systems with a complicated electronic structure [23,24]. Besides its utility to select active orbitals prone to partial occupation, as the first step for more sophisticated multiconfigurational or complete active space self-consistent field (MCSCF/CASSCF) treatments, it has been recently applied to a large set of radical and radicaloid systems [25,26,27,28,29]. It is also conceived as a low-cost tool to explore energy landscapes with varying biradical character, as it may happen in organic chemical reactions, and to discard pathological cases in datasets more effectively than using traditional descriptors [30].
Orbital-optimized DFT methods have been pioneeringly applied in recent years coupled with modern non-empirical double-hybrid functionals [31,32]. Since this family of functionals includes by default a correlation energy fraction arising from second-order perturbation theory, which often dominates the accuracy of the whole model due to long-range correlation effects, this term benefits from its own optimized orbitals analogous to the original MP2 method in its OO-MP2 form [33]. However, in standard applications of double-hybrid functionals, the KS optimized orbitals are used to also feed that energy term. If the MP2-optimized orbitals are used instead, one improves the results with respect to standard models, notably for electronically open-shell complicated systems, and through first-order properties obtained as derivatives of the energy.
Range-Separated eXchange DFT has become increasingly popularized, in recent years, thanks to, e.g., the CAM-B3LYP [34] and ωB97XD [35] expressions. For Ŵ = Σi<j υ(ri,rj), a two-body operator, it is possible to use an alternative based on the interelectronic distance rij and an arbitrary parameter ω such as υ(ri,rj) = erf(ωrij)/rij. That parameter (to be fitted against some training datasets) makes it possible to split the electron–electron interaction to a short-range and a long-range contribution, with the former treated by a conventional density functional. Recently, how to obtain a value of ω free of any empiricism was also determine, beyond the reproduction of the exact energy of the H atom [36], independently of the density functional (i.e., GGA, meta-GGA, and hybrid or double-hybrid) chosen.
Multiconfigurational Pair-DFT (MC-PDFT) [37] combines the advantages of wave function theory and DFT, translating any available functional depending on spin densities and their gradients (ρσ, ∇ρσ, σ = α,β) into a functional depending not only on the one-body electronic density, ρ(r), but also on the two-body on-top pair density ρ2(r). Since the latter magnitude is built from a multi-determinantal wave function, it includes by definition all many-body effects qualitatively. The selection of the active space is done automatically [38] and analytical gradients are also available [39], thus, perfectly complementing historical attempts to merge wave function and DFT methods for strongly correlated systems [40,41,42].
The Fermi-Löwdin Orbital Self-Interaction Corrected DFT (FLOSIC-DFT) is viewed as a further step in developing methods for more universal treatment of unphysical SIE in DFT [43]. The main difference with respect to former SIE-corrected versions relies on how energy-minimizing orbitals are variably obtained, towards SIE-free properties, with the present variant offering computational advantages and with analytical gradients also available [44].
Common to all these methods is the underlying interplay between various first-principle theories. For instance, FT-DFT relies on fractional orbital occupations produced by the Fermi-Dirac distribution, induced by a fictitious electronic temperature, a technique used extensively in condensed matter physics. On the other hand, OO-DFT borrows the orbital optimization technique primarily developed for the traditional MP2 method, while RSX-DFT makes use of the interelectronic dependence of two-electron integral historically used to switch from a non-interacting to an interacting particle system. Note also that RSX-DFT and FLOSIC-DFT are expected to yield to more accurate results than standard DFT calculations for properties dominated by the self-interaction-error of common functionals: charge-transfer excited-states, potential energy curves, and dissociation energies of charged systems, delocalized vs. localized electronic structures, etc.
We also mention here some other non-standard DFT-based methods, such as the adiabatic-connection fluctuation-dissipation (ACFD) towards the exact Kohn-Sham correlation energy [45], the spin-restricted ensemble-referenced Kohn–Sham (REKS) method [46], the reduced density matrix functional theory (RDMFT) [47], the density matrix renormalization group pair-density functional theory (DMRG-PDFT) [48], the combined DFT/MRCI method [49], the use of spin-flip (SF) techniques to tackle excited-state energies [50,51], or the localized orbital scaling correction (LOSC) [52]. The use of machine learning techniques is also a strongly raising field, not only in terms of new functionals forms but also for the accurate prediction of chemical properties [53]. Moreover, it has been also shown how localizing electronic density errors in real-space can contribute to further chemical insights [54].

4. Some Illustrative Cases

In the following, we will focus on some particularly challenging applications to a pair of diradicals taken as examples, with energetically close low- and high-spin solutions arising from orbital degeneracy, often dubbed as strongly correlated systems. All the calculations presented here are done with the ORCA 4.0.1.2. package, employing ultrafine integration grids (keywords: NoFinalGrid/Grid7) in all cases.
We will start by revisiting the automerization reaction of cyclobutadiene (Figure 1) between the rectangular (D2h) and square (D4h) forms. The rectangular structure (a well-behaved closed-shell molecule) is the minimum of the potential energy surface. The square structure is more problematic, in the sense that the highest occupied molecular orbital is a pair of two degenerate π(eg) orbitals ϕ2 and ϕ3 filled with two electrons. Thus, a two-determinant wavefunction, |ϕcoreϕ12ϕ22> and |ϕcoreϕ12ϕ32>, is at least needed to qualitatively describe this structure, with highly sophisticated multi-reference coupled-cluster method providing an energy difference (i.e., a barrier height) between both forms of 6.0-7.0 kcal/mol [55,56].
Standard DFT is, on the other hand, unable to provide a quantitative answer, with all methods tested here giving a highly overestimated barrier height around 23–25 kcal/mol since the energy gain due to the orbital degeneracy (static correlation energy) is missed in traditional KS-DFT, e.g., PBE0/cc-pVTZ gives an energy barrier of 25.1 kcal/mol and PBE-QIDH/cc-pVTZ a value of 23.8 kcal/mol. OO-PBE-QIDH gives a value of 23.1 kcal/mol, showing the intrinsic difficulties in dealing with degeneracy effects. However, those methods depending on ρ(r) and ρ2(r) are able to provide a barrier (with the cc-pVTZ basis set) between 6–9 kcal/mol, once a correlation energy functional is reformulated in such a way that it depends on the density mentioned above and also on the pair density [57], in perfect agreement with those ab initio calculations indicated previously. On the other hand, FT-PBE0/cc-pVTZ also provides a value between 3–6 kcal/mol if an electronic (fictitious) temperature is fixed around 8000–9000 K.
Another recent example of a traditionally challenging molecule is the triangulene diradical system, see Figure 2, which has been recently synthesized for the first time after many attempts [58], since it constitutes the smallest polycyclic aromatic hydrocarbon that possesses a triplet ground-state. Ovchinnikov’s rule [59] already predicts this high-spin ground-state due to the sublattice invariance, but DFT applications for radical(-like) systems are known to suffer from spin-contamination and other issues, with very costly high-level ab initio calculations being the alternative choice.
The energy difference between the triplet and (closed-shell) singlet amounts to 0.6–0.7 eV at the MR-CISD+Q/6-31G(d) level [60], with standard DFT applications leading to a broad range of results although always correctly yielding the triplet as the ground-state [61]. For instance, PBE0/6-31G(d) calculations predict a singlet-triplet energy difference of 1.2 eV, with spin-flip techniques reducing the value to 0.39 eV at the SF-PBE0/6-31G(d) level (0.34 eV after the corresponding Yamaguchi spin correction [62]). Going now from hybrid to double-hybrid methods, PBE-QIDH/6-31G(d) reduces the value to 0.68 eV. On the other hand, the application of FT-PBE/6-31G(d) (at 9000 K) produces an energy difference of 0.7 eV, also close to ab initio predictions.

5. Final Remarks

These examples illustrate the necessary and complex interrelationship between adjacent theoretical fields, used smartly in last years to form a virtuous cycle for chemistry and physics, and some of the large worldwide efforts to provide more accurate DFT-based methods. The shortcoming and limitations of semi-local (LDA, GGA, meta-GGA) and hybrid functionals are recognized for a long time, but a set of new methods have entered into the (specialized) DFT community to remedy this situation mostly in the last decade. There is hope that this trend will continue in the coming years, with developments and benchmarking of methods constituting a creative and fast-growing field interpenetrating cutting-edge applications.

Author Contributions

Both authors contributed equally to the manuscript.

Funding

This research was funded by “Generalitat Valenciana”, grant number AICO/2018/175, and by “Ministerio de Ciencia, Innovación y Universidades", project FIS2015-64222-C2-2-P.

Acknowledgments

We acknowledge discussions with current and former members of the Quantum Chemistry group of the University of Alicante, as well as with close colleagues and collaborators. We also gratefully acknowledge the participants at the “18th International Conference on Density-Functional Theory and its Applications” (Alicante, Spain) for their valuable contributions showing the rich state-of-the-art of DFT worldwide, as well as the whole Scientific and Organizing Committees.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef] [Green Version]
  2. Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef] [Green Version]
  3. Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
  4. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. 1988, 37, 785–789. [Google Scholar] [CrossRef] [Green Version]
  5. Grimme, S.; Hansen, A.; Brandenburg, J.G.; Bannwarth, C. Dispersion-Corrected Mean-Field Electronic Structure Methods. Chem. Rev. 2016, 116, 5105–5154. [Google Scholar] [CrossRef] [Green Version]
  6. Kossmann, S.; Neese, F. Comparison of two efficient approximate Hartee–Fock approaches. Chem. Phys. Lett. 2009, 48, 240–243. [Google Scholar] [CrossRef]
  7. Brandenburg, J.G.; Bannwarth, C.; Hansen, A.; Grimme, S. B97-3c: A revised low-cost variant of the B97-D density functional method. J. Chem. Phys. 2018, 148, 064104. [Google Scholar] [CrossRef]
  8. Grimme, S.; Bannwarth, C.; Shushkov, P. A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All spd-Block Elements (Z = 1–86). J. Chem. Theory Comput. 2017, 13, 1989–2009. [Google Scholar] [CrossRef]
  9. Bannwarth, C.; Ehlert, S.; Grimme, S. GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions. J. Chem. Theory Comput. 2019, 15, 1652–1671. [Google Scholar] [CrossRef]
  10. Riplinger, C.; Sandhoefer, B.; Hansen, A.; Neese, F. Natural triple excitations in local coupled cluster calculations with pair natural orbitals. J. Chem. Phys. 2013, 139, 134101. [Google Scholar] [CrossRef]
  11. Guo, Y.; Sivalingam, K.; Valeev, E.F.; Neese, F. SparseMaps—A systematic infrastructure for reduced-scaling electronic structure methods. III. Linear-scaling multireference domain-based pair natural orbital N-electron valence perturbation theory. J. Chem. Phys. 2016, 144, 094111. [Google Scholar] [CrossRef]
  12. Moscardó, F.; San-Fabián, E. Density-functional formalism and the two-body problem. Phys. Rev. A 1991, 44, 1549–1553. [Google Scholar] [CrossRef]
  13. Sancho-García, J.C.; Moscardó, F. Usefulness of the Colle-Salvetti model for the treatment of the non-dynamical correlation. J. Chem. Phys. 2003, 118, 1054–1058. [Google Scholar] [CrossRef]
  14. Maier, T.M.; Arbuznikov, A.V.; Kaupp, M. Local hybrid functionals: Theory, implementation, and performance of an emerging new tool in quantum chemistry and beyond. WIREs Comput. Mol. Sci. 2019, 9, e1378. [Google Scholar] [CrossRef]
  15. Maier, T.M.; Hassler, M.; Arbuznikov, A.V.; Kaupp, M. New approaches for the calibration of exchange-energy densities in local hybrid functionals. Phys. Chem. Chem. Phys. 2016, 31, 21133–21144. [Google Scholar] [CrossRef]
  16. Goerigk, L.; Grimme, S. Double-hybrid density functionals. WIREs Comput. Mol. Sci. 2014, 4, 576–600. [Google Scholar] [CrossRef]
  17. Brémond, É.; Ciofini, I.; Sancho-García, J.C.; Adamo, C. Nonempirical double-hybrid functionals: An effective tool for chemists. Acc. Chem. Res. 2016, 49, 1503–1513. [Google Scholar] [CrossRef]
  18. Neese, F. Software update: The ORCA program system, version 4.0. WIREs: Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
  19. Shao, Y.; Shao, Y.; Gan, Z.; Epifanovsky, E.; Gilbert, A.T.; Wormit, M.; Kussmann, J.; Lange, A.W.; Behn, A.; Deng, J.; et al. Advances in molecular quantum chemistry contained in the Q-Chem 4 program package. Mol Phys. 2015, 113, 184–215. [Google Scholar] [CrossRef]
  20. Fdez, I.G.; Vacher, M.; Alavi, A.; Angeli, C.; Aquilante, F.; Autschbach, J.; Bao, J.J.; Bokarev, S.I.; Bogdanov, N.A.; Carlson, R.K.; et al. OpenMolcas: From source code to insight. J. Chem. Theory Comput. 2019. [Google Scholar] [CrossRef]
  21. Bao, J.L.; Gagliardi, L.; Truhlar, D.G. Self-interaction error in density functional theory: An appraisal. J. Phys. Chem. Lett. 2018, 9, 2353–2358. [Google Scholar] [CrossRef]
  22. Chai, J.-D. Density functional theory with fractional orbital occupations. J. Chem. Phys. 2012, 136, 154104. [Google Scholar] [CrossRef]
  23. Grimme, S.; Hansen, A. A Practicable Real-Space Measure and Visualization of Static Electron-Correlation Effects. Angew. Chem. Int. Ed. 2015, 54, 12308–12313. [Google Scholar] [CrossRef]
  24. Bauer, C.A.; Hansen, A.; Grimme, S. The frational occupation number weighted density as a versatile analysis tool for molecules with a complicated electronic structure. Chem.: Eur. J. 2017, 23, 6150–6164. [Google Scholar] [CrossRef]
  25. Pérez-Guardiola, A.; Sandoval-Salinas, M.E.; Casanova, D.; San-Fabián, E.; Pérez-Jiménez, A.J.; Sancho-García, J.C. The role of topology in organic molecules: Origin and comparison of the radical character in linear and cyclic oligoacenes and related oligomers. Phys. Chem. Chem. Phys. 2018, 20, 7112–7124. [Google Scholar] [CrossRef]
  26. Pérez-Guardiola, A.; Ortiz-Cano, R.; Sandoval-Salinas, M.E.; Fernández-Rossier, J.; Casanova, D.; Pérez-Jiménez, A.J.; Sancho-García, J.C. From cyclic nanorings to single-walled carbon nanotubes: Disclosing the evolution of their electronic structure with the help of theoretical methods. Phys. Chem. Chem. Phys. 2019, 21, 2547–2557. [Google Scholar] [CrossRef]
  27. Seenithurai, S.; Chai, J.D. Electronic and hydrogen storage properties of Li-terminated linear boron chains studied by TAO-DFT. Sci. Rep. 2018, 8, 13538. [Google Scholar] [CrossRef]
  28. Chung, J.H.; Chai, J.D. Electronic properties of möbius cyclacenes studied by Thermally-Assisted-Occupation Density Functional Theory. Sci. Rep. 2019, 9, 2907. [Google Scholar] [CrossRef]
  29. Seenithurai, S.; Chai, J.D. Electronic properties of linear and cyclic boron nanoribbons from Thermally-Assisted-Occupation Density Functional Theory. Sci. Rep. 2019, 9, 12139. [Google Scholar] [CrossRef]
  30. Dohm, S.; Hansen, A.; Steinmetz, M.; Grimme, S.; Checinski, M.P. Comprehensive thermochemical benchmark set of realistic closed-shell metal organic reactions. J. Chem. Theory Comput. 2018, 14, 2596–2607. [Google Scholar] [CrossRef]
  31. Peverati, R.; Head-Gordon, M. Orbital optimized double-hybrid density functionals. J. Chem. Phys. 2013, 139, 024110. [Google Scholar] [CrossRef]
  32. Sancho-García, J.C.; Pérez-Jiménez, A.J.; Savarese, M.; Brémond, E.; Adamo, C. Importance of orbital optimization for double-hybrid density functionals: Application of the OO-PBE-QIDH model for closed- and open-shell systems. J. Phys. Chem. A 2016, 120, 1756–1762. [Google Scholar] [CrossRef]
  33. Bozkaya, U.; Turney, J.M.; Yamaguchi, Y.; Schaefer III, H.F.; Sherrill, C.D. Quadratically convergent algorithm for orbital optimization in the orbital-optimized coupled-cluster doubles method and in orbital-optimized second-order Møller-Plesset perturbation theory. J. Chem. Phys. 2011, 135, 104103. [Google Scholar] [CrossRef]
  34. Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
  35. Chai, J.D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
  36. Brémond, E.; Pérez-Jiménez, A.J.; Sancho-García, J.C.; Adamo, C. Range-separated hybrid density functionals made simple. J. Chem. Phys. 2019, 150, 201102. [Google Scholar] [CrossRef] [Green Version]
  37. Gagliardi, L.; Truhlar, D.G.; Li Manni, G.; Carlson, R.K.; Hoyer, C.E.; Bao, J.L. Multiconfiguration pair-density functional theory: A new way to treat strongly correlated systems. Acc. Chem. Res. 2017, 50, 66–73. [Google Scholar] [CrossRef]
  38. Bao, J.J.; Dong, S.S.; Gagliardi, L.; Truhlar, D.G. Automatic selection of an active space for calculating electronic excitation spectra by MS-CASPT2 or MC-PDFT. J. Chem. Theory Comput. 2018, 14, 2017–2025. [Google Scholar] [CrossRef]
  39. Sand, A.M.; Hoyer, C.D.; Sharkas, K.; Kidder, K.M.; Lindh, R.; Truhlar, D.G.; Gagliardi, L. Analytic gradients for complete active space pair-Density Functional Theory. J. Chem. Theory Comput. 2018, 14, 126–138. [Google Scholar] [CrossRef]
  40. Moscardó, F.; San-Fabián, E. A density functional for the correlation energy, deduced in the framework of the correlation factor approach. Int. J. Quantum Chem. 1991, 40, 23–32. [Google Scholar] [CrossRef]
  41. Becke, A.D.; Savin, A.; Stoll, H. Extension of the local-spin-density exchange-correlation approximation to multiplet states. Theor. Chem. Acta 1995, 91, 147–156. [Google Scholar] [CrossRef]
  42. Burke, K.; Perdew, J.P.; Ernzerhof, M. Extension of the local-spin-density exchange-correlation approximation to multiplet states. J. Chem. Phys. 1998, 109, 3760–3771. [Google Scholar] [CrossRef]
  43. Sharkas, K.; Li, L.; Trepte, K.; Withanage, K.P.K.; Joshi, R.P.; Zope, R.R.; Baruah, T.; Johnson, J.K.; Jackson, K.A.; Peralta, J.E. Shrinking self-interaction errors with the Fermi-Löwdin orbital self-interaction corrected density functional approximation. J. Phys. Chem. A 2018, 122, 9307. [Google Scholar] [CrossRef]
  44. Trepte, K.; Schwalbe, S.; Hahn, T.; Kortus, J.; Kao, D.-y.; Yamamoto, Y.; Baruah, T.; Zope, R.R.; Withanage, K.P.K.; Peralta, J.E.; et al. Analytic Atomic Gradients in the Fermi- Löwdin obital self-interaction correction. J. Comp. Chem. 2019, 40, 820–825. [Google Scholar] [CrossRef]
  45. Görling, A. Hierarchies of methods towards the exact Kohn-Sham correlation energy based on the adiabatic-connection fluctuation-dissipation theorem. Phys. Rev. B 2019, 99, 235120. [Google Scholar] [CrossRef]
  46. Filatov, M. Spin-restricted ensemble-referenced Kohn–Sham method: Basic principles and application to strongly correlated ground and excited states of molecules. Wires Comp. Mol. Sci. 2015, 5, 146–167. [Google Scholar] [CrossRef]
  47. Pernal, K.; Giesbertz, K.J. Reduced Density Matrix Functional Theory (RDMFT) and Linear Response Time-Dependent RDMFT (TD-RDMFT). Top. Curr. Chem. 2016, 368, 125–183. [Google Scholar]
  48. Sharma, P.; Bernales, V.; Knecht, S.; Truhlar, D.G.; Gagliardi, L. Density matrix renormalization group pair-density functional theory (DMRG-PDFT): Singlet−triplet gaps in polyacenes and polyacetylenes. Chem. Sci. 2019, 10, 1716–1723. [Google Scholar] [CrossRef]
  49. Marian, C.M.; Heil, A.; Kleinschmidt, M. The DFT/MRCI method. WIREs Comput. Mol. Sci. 2019, 9, e1394. [Google Scholar] [CrossRef]
  50. Krylov, A.I. Size-consistent wave functions for bond-breaking: The equation-of-motion spin-flip model. Chem. Phys. Lett. 2001, 338, 375–384. [Google Scholar] [CrossRef]
  51. Canola, S.; Casado, J.; Negri, F. The double exciton state of conjugated chromophores with strong diradical character: Insights from TDDFT calculations. Phys. Chem. Chem. Phys. 2018, 20, 24227–24238. [Google Scholar] [CrossRef]
  52. Su, N.Q.; Li, C.; Yang, W. Describing strong correlation with fractional-spin correction in density functional theory. Proc. Natl. Acad. Sci. USA 2018, 115, 9678–9683. [Google Scholar] [CrossRef] [Green Version]
  53. Christensen, A.S.; Faber, F.A.; von Lilienfeld, O.A. Operators in quantum machine learning: Response properties in chemical space. J. Chem. Phys. 2019, 150, 064105. [Google Scholar] [CrossRef]
  54. Laplaza, R.; Polo, V.; Contreras-García, J. Localizing electron density errors in density functional theory. Phys. Chem. Chem. Phys. 2019, 21, 20927–20938. [Google Scholar] [CrossRef]
  55. Sancho-García, J.C.; Pittner, J.; Čársky, P.; Hubač, I. Multireference coupled-cluster calculations on the energy of activation in the automerization of cyclobutadiene: Assessment of the state-specific multireference Brillouin–Wigner theory. J. Chem. Phys. 2000, 112, 8785–8788. [Google Scholar] [CrossRef]
  56. Bhaskaran-Nair, K.; Demel, O.; Pittner, J. Multireference state-specific Mukherjee’s coupled cluster method with noniterative triexcitations. J. Chem. Phys. 2008, 129, 184105. [Google Scholar] [CrossRef]
  57. Sancho-García, J.C.; Pérez-Jiménez, A.J.; Moscardó, F. A comparison between DFT and other ab initio schemes on the activation energy in the automerization of cyclobutadiene. Chem. Phys. Lett. 2000, 317, 245–251. [Google Scholar] [CrossRef]
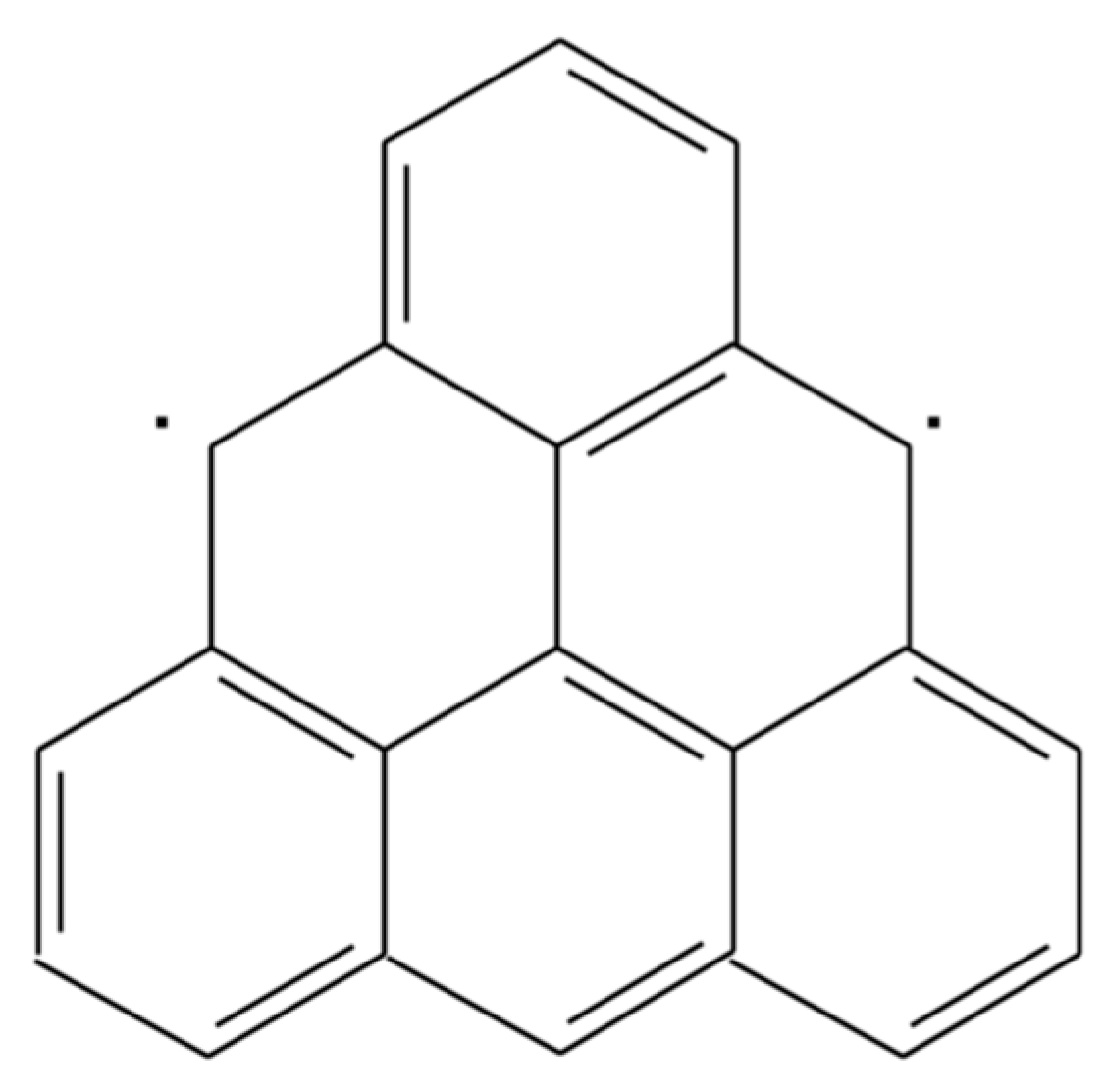
  58. Pavliček, N.; Mistry, A.; Majzik, Z.; Moll, N.; Meyer, G.; Fox, D.J.; Gross, L. Synthesis and characterization of triangulene. Nat. Nanotech. 2017, 12, 308–311. [Google Scholar] [CrossRef]
  59. Ovchinnikov, A.A. Multiplicity of the Ground State of Large Alternant Organic Molecules with Conjugated Bonds. Theor. Chem. Acc. 1978, 47, 297–304. [Google Scholar] [CrossRef]
  60. Das, A.; Müller, T.; Plasser, F.; Lischka, H. Polyradical Character of Triangular Non-Kekule Structures, Zethrenes, p-Quinodimethane-Linked Bisphenalenyl, and the Clar Goblet in Comparison: An Extended Multireference Study. J. Phys. Chem. A 2016, 120, 1625–1636. [Google Scholar] [CrossRef]
  61. Melle-Franco, M. Uthrene, a radically new molecule? Chem. Commun. 2015, 51, 5387–5390. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  62. Soda, T.; Kitagawa, Y.; Onishi, T.; Takano, Y.; Shigeta, Y.; Nagao, H.; Yoshioka, Y.; Yamaguchi, K. Ab initio computations of effective exchange integrals for H-H, H-He-H and Mn2O2 complex: Comparison of broken-symmetry approaches. Chem. Phys. Lett. 2000, 319, 223–230. [Google Scholar] [CrossRef]
Computation 07 00062 g001 550
Figure 1. Automerization reaction of cyclobutadiene.
Figure 1. Automerization reaction of cyclobutadiene.
Computation 07 00062 g001
Computation 07 00062 g002 550
Figure 2. Non-Kekulé triangulene diradical system.
Figure 2. Non-Kekulé triangulene diradical system.
Computation 07 00062 g002

Share and Cite

MDPI and ACS Style

San-Fabián Maroto, E.; Sancho-García, J.-C. Emerging DFT Methods and Their Importance for Challenging Molecular Systems with Orbital Degeneracy. Computation 2019, 7, 62. https://0-doi-org.brum.beds.ac.uk/10.3390/computation7040062

AMA Style

San-Fabián Maroto E, Sancho-García J-C. Emerging DFT Methods and Their Importance for Challenging Molecular Systems with Orbital Degeneracy. Computation. 2019; 7(4):62. https://0-doi-org.brum.beds.ac.uk/10.3390/computation7040062

Chicago/Turabian Style

San-Fabián Maroto, Emilio, and Juan-Carlos Sancho-García. 2019. "Emerging DFT Methods and Their Importance for Challenging Molecular Systems with Orbital Degeneracy" Computation 7, no. 4: 62. https://0-doi-org.brum.beds.ac.uk/10.3390/computation7040062

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop