Accurate Sampling with Noisy Forces from Approximate Computing
Abstract
:1. Introduction
2. Approximate Computing
3. Methodology
4. Computational Details
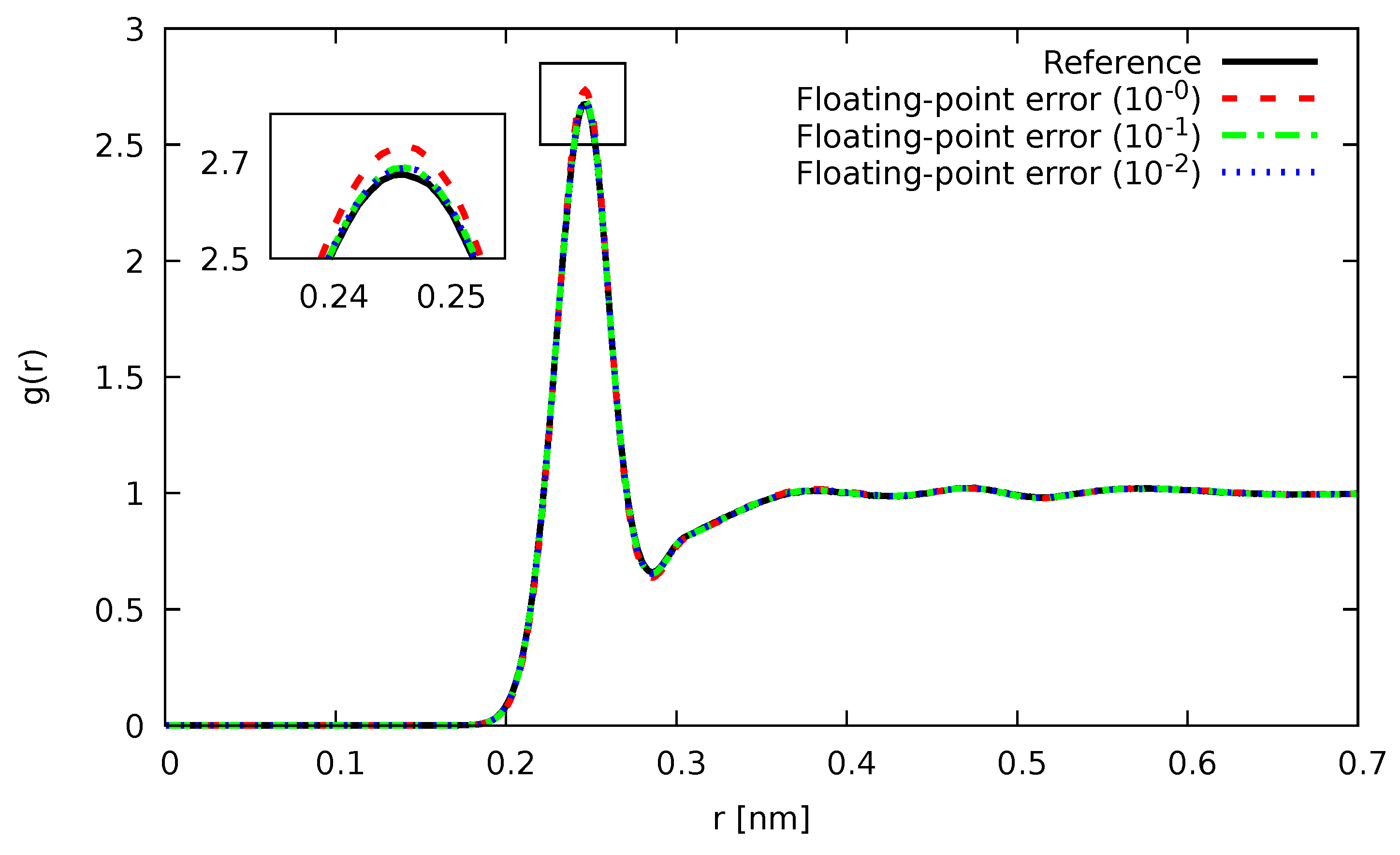
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Alder, B.J.; Wainwright, T.E. Phase Transition for a Hard Sphere System. J. Chem. Phys. 1957, 27, 1208–1209. [Google Scholar] [CrossRef] [Green Version]
- Rahman, A. Correlations in the Motion of Atoms in Liquid Argon. Phys. Rev. 1964, 136, A405–A411. [Google Scholar] [CrossRef]
- Car, R.; Parrinello, M. Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 1985, 55, 2471–2474. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kühne, T.D.; Krack, M.; Mohamed, F.R.; Parrinello, M. Efficient and accurate Car-Parrinello-like approach to Born-Oppenheimer molecular dynamics. Phys. Rev. Lett. 2007, 98, 066401. [Google Scholar] [CrossRef] [Green Version]
- Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.A.; Joannopoulos, J.D. Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045–1097. [Google Scholar] [CrossRef] [Green Version]
- Kühne, T.D. Second generation Car–Parrinello molecular dynamics. WIREs Comput. Mol. Sci. 2014, 4, 391–406. [Google Scholar] [CrossRef] [Green Version]
- Tuckerman, M.E.; Berne, B.J.; Martyna, G.J. Reversible multiple time scale molecular dynamics. J. Chem. Phys. 1992, 97, 1990–2001. [Google Scholar] [CrossRef] [Green Version]
- Snir, M. A note on N-body computations with cutoffs. Theor. Comput. Syst. 2004, 37, 295–318. [Google Scholar] [CrossRef]
- Shan, Y.; Klepeis, J.L.; Eastwood, M.P.; Dror, R.O.; Shaw, D.E. Gaussian split Ewald: A fast Ewald mesh method for molecular simulation. J. Chem. Phys. 2005, 122, 054101. [Google Scholar] [CrossRef] [Green Version]
- Shaw, D.E. A fast, scalable method for the parallel evaluation of distance-limited pairwise particle interactions. J. Comput. Chem. 2005, 26, 1318–1328. [Google Scholar] [CrossRef] [Green Version]
- Gonnet, P. Pairwise Verlet Lists: Combining Cell Lists and Verlet Lists to Improve Memory Locality and Parallelism. J. Comput. Chem. 2012, 33, 76–81. [Google Scholar] [CrossRef] [PubMed]
- Gonnet, P. A quadratically convergent SHAKE in O(n(2)). J. Comput. Phys. 2007, 220, 740–750. [Google Scholar] [CrossRef]
- John, C.; Spura, T.; Habershon, S.; Kühne, T.D. Quantum ring-polymer contraction method: Including nuclear quantum effects at no additional computational cost in comparison to ab initio molecular dynamics. Phys. Rev. E 2016, 93, 043305. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kühne, T.D.; Prodan, E. Disordered Crystals from First Principles I: Quantifying the Configuration Space. Ann. Phys. 2018, 391, 120–149. [Google Scholar] [CrossRef] [Green Version]
- Anderson, J.A.; Lorenz, C.D.; Travesset, A. General purpose molecular dynamics simulations fully implemented on graphics processing units. J. Comput. Phys. 2008, 227, 5342–5359. [Google Scholar] [CrossRef]
- Stone, J.E.; Hardy, D.J.; Ufimtsev, I.S.; Schulten, K. GPU-accelerated molecular modeling coming of age. J. Mol. Graph. Model. 2010, 29, 116–125. [Google Scholar] [CrossRef] [Green Version]
- Eastman, P.; Pande, V.S. OpenMM: A Hardware-Independent Framework for Molecular Simulations. Comput. Sci. Eng. 2010, 12, 34–39. [Google Scholar] [CrossRef] [Green Version]
- Colberg, P.H.; Höfling, F. Highly accelerated simulations of glassy dynamics using GPUs: Caveats on limited floating-point precision. Comput. Phys. Commun. 2011, 182, 1120–1129. [Google Scholar] [CrossRef] [Green Version]
- Brown, W.M.; Kohlmeyer, A.; Plimpton, S.J.; Tharrington, A.N. Implementing molecular dynamics on hybrid high performance computers – Particle–particle particle-mesh. Comput. Phys. Commun. 2012, 183, 449–459. [Google Scholar] [CrossRef]
- Le Grand, S.; Götz, A.W.; Walker, R.C. SPFP: Speed without compromise—A mixed precision model for GPU accelerated molecular dynamics simulations. Comput. Phys. Commun. 2013, 184, 374–380. [Google Scholar] [CrossRef]
- Abraham, A.J.; Murtola, T.; Schulz, R.; Pall, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Herbordt, M.C.; Gu, Y.; VanCourt, T.; Model, J.; Sukhwani, B.; Chiu, M. Computing Models for FPGA-Based Accelerators. Comput. Sci. Eng. 2008, 10, 35–45. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Herbordt, M.C.; Gu, Y.; VanCourt, T.; Model, J.; Sukhwani, B.; Chiu, M. Explicit design of FPGA-based coprocessors for short-range force computations in molecular dynamics simulations. Parallel Comput. 2008, 34, 261–277. [Google Scholar] [CrossRef] [Green Version]
- Shaw, D.E.; Deneroff, M.M.; Dror, R.O.; Kuskin, J.S.; Larson, R.H.; Salmon, J.K.; Young, C.; Batson, B.; Bowers, K.J.; Chao, J.C.; et al. Anton, a Special-purpose Machine for Molecular Dynamics Simulation. In Proceedings of the 34th Annual International Symposium on Computer Architecture, San Diego, CA, USA, 9–13 June 2007; ACM: New York, NY, USA, 2007; pp. 1–12. [Google Scholar] [CrossRef] [Green Version]
- Shaw, D.E.; Grossman, J.P.; Bank, J.A.; Batson, B.; Butts, J.A.; Chao, J.C.; Deneroff, M.M.; Dror, R.O.; Even, A.; Fenton, C.H.; et al. Anton 2: Raising the Bar for Performance and Programmability in a Special-purpose Molecular Dynamics Supercomputer. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, New Orleans, LA, USA, 16–21 November 2014; IEEE Press: Piscataway, NJ, USA, 2014; pp. 41–53. [Google Scholar] [CrossRef]
- Owens, J.D.; Houston, M.; Luebke, D.; Green, S.; Stone, J.E.; Phillips, J.C. GPU Computing. Proc. IEEE 2008, 96, 879–899. [Google Scholar] [CrossRef]
- Preis, T.; Virnau, P.; Paul, W.; Schneider, J.J. GPU accelerated Monte Carlo simulation of the 2D and 3D Ising model. J. Comput. Phys. 2009, 228, 4468–4477. [Google Scholar] [CrossRef]
- Weigel, M. Performance potential for simulating spin models on GPU. J. Comput. Phys. 2012, 231, 3064–3082. [Google Scholar] [CrossRef] [Green Version]
- Brown, F.R.; Christ, N.H. Parallel Supercomputers for Lattice Gauge Theory. Science 1988, 239, 1393–1400. [Google Scholar] [CrossRef]
- Boyle, P.A.; Chen, D.; Christ, N.H.; Clark, M.A.; Cohen, S.D.; Cristian, C.; Dong, Z.; Gara, A.; Joo, B.; Jung, C.; et al. Overview of the QCDSP and QCDOC computers. IBM J. Res. Dev. 2005, 49, 351–365. [Google Scholar] [CrossRef] [Green Version]
- Hut, P.; Makino, J. Astrophysics on the GRAPE Family of Special-Purpose Computers. Science 1999, 283, 501–505. [Google Scholar] [CrossRef] [Green Version]
- Fukushige, T.; Hut, P.; Makino, J. High-performance special-purpose computers in science. Comput. Sci. Eng. 1999, 1, 12–13. [Google Scholar] [CrossRef]
- Belletti, F.; Cotallo, M.; Cruz, A.; Fernandez, L.A.; Gordillo-Guerrero, A.; Guidetti, M.; Maiorano, A.; Mantovani, F.; Marinari, E.; Martin-Mayor, V.; et al. Janus: An FPGA-Based System for High-Performance Scientific Computing. Comput. Sci. Eng. 2009, 11, 48. [Google Scholar] [CrossRef]
- Baity-Jesi, M.; Banos, R.A.; Cruz, A.; Fernandez, L.A.; Gil-Narvion, J.M.; Gordillo-Guerrero, A.; Iniguez, D.; Maiorano, A.; Mantovani, F.; Marinari, E.; et al. Janus II: A new generation application-driven computer for spin-system simulations. Comput. Phys. Commun. 2014, 185, 550–559. [Google Scholar] [CrossRef]
- Meyer, B.; Schumacher, J.; Plessl, C.; Forstner, J. Convey vector personalities—FPGA acceleration with an openmp-like programming effort? In Proceedings of the 22nd International Conference on Field Programmable Logic and Applications (FPL), Oslo, Norway, 29–31 August 2012; pp. 189–196. [Google Scholar] [CrossRef] [Green Version]
- Giefers, H.; Plessl, C.; Förstner, J. Accelerating Finite Difference Time Domain Simulations with Reconfigurable Dataflow Computers. SIGARCH Comput. Archit. News 2014, 41, 65–70. [Google Scholar] [CrossRef]
- Kenter, T.; Förstner, J.; Plessl, C. Flexible FPGA design for FDTD using OpenCL. In Proceedings of the 2017 27th International Conference on Field Programmable Logic and Applications (FPL), Ghent, Belgium, 4–8 September 2017. [Google Scholar] [CrossRef]
- Kenter, T.; Mahale, G.; Alhaddad, S.; Grynko, Y.; Schmitt, C.; Afzal, A.; Hannig, F.; Förstner, J.; Plessl, C. OpenCL-based FPGA Design to Accelerate the Nodal Discontinuous Galerkin Method for Unstructured Meshes. In Proceedings of the 2018 IEEE 26th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Boulder, CO, USA, 29 April–1 May 2018; Volume 1, pp. 189–196. [Google Scholar] [CrossRef]
- Klavík, P.; Malossi, A.C.I.; Bekas, C.; Curioni, A. Changing Computing Paradigms Towards Power Efficiency. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372. [Google Scholar] [CrossRef] [Green Version]
- Plessl, C.; Platzner, M.; Schreier, P.J. Approximate Computing. Inform. Spektrum 2015, 38, 396–399. [Google Scholar] [CrossRef]
- Lass, M.; Kühne, T.D.; Plessl, C. Using Approximate Computing for the Calculation of Inverse Matrix p-th Roots. IEEE Embed. Syst. Lett. 2018, 10, 33–36. [Google Scholar] [CrossRef] [Green Version]
- Angerer, C.M.; Polig, R.; Zegarac, D.; Giefers, H.; Hagleitner, C.; Bekas, C.; Curioni, A. A fast, hybrid, power-efficient high-precision solver for large linear systems based on low precision hardware. Sustain. Comput. Inform. Syst. 2016, 12, 72–82. [Google Scholar] [CrossRef]
- Haidar, A.; Wu, P.; Tomov, S.; Dongarra, J. Investigating half precision arithmetic to accelerate dense linear system solvers. In Proceedings of the 8th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems, Denver, CO, USA, 13 November 2017. [Google Scholar] [CrossRef] [Green Version]
- Haidar, A.; Tomov, S.; Dongarra, J.; Higham, N.J. Harnessing GPU tensor cores for fast FP16 arithmetic to speed up mixed-precision iterative refinement solvers. In Proceedings of the International Conference for High Performance Computing, Networking, Storage, and Analysis, Dallas, TX, USA, 11–16 November 2018. [Google Scholar] [CrossRef] [Green Version]
- Gupta, S.; Agrawal, A.; Gopalakrishnan, K.; Narayanan, P. Deep learning with limited numerical precision. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1737–1746. [Google Scholar]
- NVIDIA Corporation. Tesla P100 Data Sheet; NVIDIA: Santa Clara, CA, USA, 2016. [Google Scholar]
- The Next Platform. Tearing Apart Google’s TPU 3.0 AI Coprocessor. Available online: https://www.nextplatform.com/2018/05/10/tearing-apart-googles-tpu-3-0-ai-coprocessor/ (accessed on 27 April 2020).
- Top 500. Intel Lays Out New Roadmap for AI Portfolio. Available online: https://www.top500.org/news/intel-lays-out-new-roadmap-for-ai-portfolio/ (accessed on 27 April 2020).
- Strzodka, R.; Goddeke, D. Pipelined Mixed Precision Algorithms on FPGAs for Fast and Accurate PDE Solvers from Low Precision Components. In Proceedings of the 14th Annual IEEE Symposium on Field-Programmable Custom Computing Machines, Napa, CA, USA, 24–26 April 2006. [Google Scholar] [CrossRef] [Green Version]
- Kenter, T.; Vaz, G.; Plessl, C. Partitioning and Vectorizing Binary Applications. In Lecture Notes in Computer Science, Proceedings of the International Conference on Reconfigurable Computing: Architectures, Tools and Applications (ARC), Vilamoura, Portugal, 14–16 April 2014; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8405, pp. 144–155. [Google Scholar] [CrossRef]
- Kenter, T.; Schmitz, H.; Plessl, C. Pragma based parallelization—Trading hardware efficiency for ease of use? In Proceedings of the 2012 International Conference on Reconfigurable Computing and FPGAs, Cancun, Mexico, 5–7 December 2012. [CrossRef]
- Microprocessor Standards Committee of the IEEE Computer Society. IEEE Std. 754-2019—IEEE Standard for Floating-Point Arithmetic; IEEE: Toulouse, France, 2019. [Google Scholar]
- Krajewski, F.R.; Parrinello, M. Linear scaling electronic structure calculations and accurate statistical mechanics sampling with noisy forces. Phys. Rev. B 2006, 73, 041105. [Google Scholar] [CrossRef] [Green Version]
- Richters, D.; Kühne, T.D. Self-consistent field theory based molecular dynamics with linear system-size scaling. J. Chem. Phys. 2014, 140, 134109. [Google Scholar] [CrossRef] [Green Version]
- Karhan, K.; Khaliullin, R.Z.; Kühne, T.D. On the role of interfacial hydrogen bonds in “on-water” catalysis. J. Chem. Phys. 2014, 141, 22D528. [Google Scholar] [CrossRef] [Green Version]
- Hutter, J.; Iannuzzi, M.; Schiffmann, F.; VandeVondele, J. CP2K: Atomistic simulations of condensed matter systems. WIREs Comput. Mol. Sci. 2014, 4, 15–25. [Google Scholar] [CrossRef] [Green Version]
- Kühne, T.; Iannuzzi, M.; Del Ben, M.; Rybkin, V.; Seewald, P.; Stein, F.; Laino, T.; Khaliullin, R.; Schütt, O.; Schiffmann, F.; et al. CP2K: An Electronic Structure and Molecular Dynamics Software Package—Quickstep: Efficient and Accurate Electronic Structure Calculations. arXiv 2020, arXiv:physics.chem-ph/2003.03868. [Google Scholar]
- Bazant, M.Z.; Kaxiras, E. Modeling of Covalent Bonding in Solids by Inversion of Cohesive Energy Curves. Phys. Rev. Lett. 1996, 77, 4370–4373. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bazant, M.Z.; Kaxiras, E.; Justo, J.F. Environment-dependent interatomic potential for bulk silicon. Phys. Rev. B 1997, 56, 8542–8552. [Google Scholar] [CrossRef] [Green Version]
- Ricci, A.; Ciccotti, G. Algorithms for Brownian dynamics. Mol. Phys. 2003, 101, 1927–1931. [Google Scholar] [CrossRef]
- Jones, A.; Leimkuhler, B. Adaptive stochastic methods for sampling driven molecular systems. J. Chem. Phys. 2011, 135, 084125. [Google Scholar] [CrossRef] [Green Version]
- Mones, L.; Jones, A.; Goötz, A.W.; Laino, T.; Walker, R.C.; Leimkuhler, B.; Csanyi, G.; Bernstein, N. The Adaptive Buffered Force QM/MM Method in the CP2K and AMBER Software Packages. J. Comput. Chem. 2015, 36, 633–648. [Google Scholar] [CrossRef] [Green Version]
- Leimkuhler, B.; Sachs, M.; Stoltz, G. Hypocoercivity Properties Of Adaptive Langevin Dynamics. arXiv 2019, arXiv:math.PR/1908.09363. [Google Scholar]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511. [Google Scholar] [CrossRef] [Green Version]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [Green Version]
- Scheiber, H.; Shi, Y.; Khaliullin, R.Z. Communication: Compact orbitals enable low cost linear-scaling ab initio molecular dynamics for weakly-interacting systems. J. Chem. Phys. 2018, 148, 231103. [Google Scholar] [CrossRef] [PubMed]
- Röhrig, K.A.F.; Kühne, T.D. Optimal calculation of the pair correlation function for an orthorhombic system. Phys. Rev. E 2013, 87, 045301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kapil, V.; Rossi, M.; Marsalek, O.; Petraglia, R.; Litman, Y.; Spura, T.; Cheng, B.; Cuzzocrea, A.; Meißner, R.H.; Wilkins, D.M.; et al. i-PI 2.0: A universal force engine for advanced molecular simulations. Comput. Phys. Commun. 2019, 236, 214–223. [Google Scholar] [CrossRef] [Green Version]
- Steane, A.M. Efficient fault-tolerant quantum computing. Nature 1999, 399, 124–126. [Google Scholar] [CrossRef]
- Knill, E. Quantum computing with realistically noisy devices. Nature 2005, 434, 39–44. [Google Scholar] [CrossRef] [Green Version]
- Benhelm, J.; Kirchmair, G.; Roos, C.F.; Blatt, R. Towards fault-tolerant quantum computing with trapped ions. Nat. Phys. 2008, 4, 463–466. [Google Scholar] [CrossRef]
- Chow, J.M.; Gambetta, J.M.; Magesan, E.; Abraham, D.W.; Cross, A.W.; Johnson, B.R.; Masluk, N.A.; Ryan, C.A.; Smolin, J.A.; Srinivasan, S.J.; et al. Implementing a strand of a scalable fault-tolerant quantum computing fabric. Nat. Commun. 2014, 5, 4015. [Google Scholar] [CrossRef] [Green Version]
- Efstathiou, G.; Davis, M.; Frenk, C.S.; White, S.D.M. Numerical techniques for large cosmological N-body simulations. Astrophys. J. 1985, 57, 241–260. [Google Scholar] [CrossRef]
- Hernquist, L.; Hut, P.; Makino, J. Discreteness Noise versus Force Errors in N-Body Simulations. Astrophys. J. 1993, 402, L85. [Google Scholar] [CrossRef]
- Lass, M.; Mohr, S.; Wiebeler, H.; Kühne, T.D.; Plessl, C. A Massively Parallel Algorithm for the Approximate Calculation of Inverse P-th Roots of Large Sparse Matrices. In Proceedings of the Platform for Advanced Scientific Computing Conference, Basel, Switzerland, 2–4 July 2018; ACM: New York, NY, USA, 2018; pp. 7:1–7:11. [Google Scholar] [CrossRef]



| Type | Sign | Exponent | Mantissa |
|---|---|---|---|
| IEEE 754 quadruple-precision | 1 | 15 | 112 |
| IEEE 754 double-precision | 1 | 11 | 52 |
| IEEE 754 single-precision | 1 | 8 | 23 |
| IEEE 754 half-precision | 1 | 5 | 10 |
| Bfloat16(truncated IEEE single-precision) | 1 | 8 | 7 |
| 0 | 0.00025 | |
| 1 | 0.0004 | 0.000005 |
| 2 | 0.000009 | 0.000005 |
| 3 | 0.0000009 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rengaraj, V.; Lass, M.; Plessl, C.; Kühne, T.D. Accurate Sampling with Noisy Forces from Approximate Computing. Computation 2020, 8, 39. https://0-doi-org.brum.beds.ac.uk/10.3390/computation8020039
Rengaraj V, Lass M, Plessl C, Kühne TD. Accurate Sampling with Noisy Forces from Approximate Computing. Computation. 2020; 8(2):39. https://0-doi-org.brum.beds.ac.uk/10.3390/computation8020039
Chicago/Turabian StyleRengaraj, Varadarajan, Michael Lass, Christian Plessl, and Thomas D. Kühne. 2020. "Accurate Sampling with Noisy Forces from Approximate Computing" Computation 8, no. 2: 39. https://0-doi-org.brum.beds.ac.uk/10.3390/computation8020039





