Application of the Generalized Laplace Homotopy Perturbation Method to the Time-Fractional Black–Scholes Equations Based on the Katugampola Fractional Derivative in Caputo Type
Abstract
:1. Introduction
- u is the call option depending on the underlying asset prices at time
- are the asset price variables,
- are the volatility function of underlying assets,
- are coefficients so that all risky asset price are at the same level,
- is the volatility of and
- r is the risk-free interest rate,
- T is the expiration date,
- K is strike price of the underlying asset.
2. Preliminaries
- 1.
- 2.
3. Constructive Equations
4. The Generalized Laplace Homotopy Perturbation Method
5. Analytic Solutions for the Time-Fractional Black–Scholes Equation
6. Numerical Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef] [Green Version]
- Atangana, A.; Baleanu, D.; Alsaedi, A. Analysis of time-fractional Hunter-Saxton equation: A model of neumatic liquid crystal. Open Phys. 2016, 14, 145–149. [Google Scholar] [CrossRef]
- Hristov, T. A transient flow of a non-newtonian fluid modelled by a mixed time-space derivative: An improved integral-balance approach. In Mathematical Methods in Engineering; Springer: Cham, Switzerland, 2019; pp. 153–174. [Google Scholar]
- Mainardi, F. Fractional relaxation-oscillation and fractional diffusion-wave phenomena. Chaos Solitons Fractals 1996, 9, 1461–1477. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional differential equations. In Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Rekhviashvili, S.; Pskhu, A.; Agarwal, P.; Jain, S. Application of the fractional oscillator model to describe damped vibrations. Turk. J. Phys. 2019, 3, 236–242. [Google Scholar] [CrossRef]
- Sene, N. Stokes’s first problem for heated flat plate with Atangana-Baleanu fractional derivative. Chaos Solitons Fractals 2018, 117, 68–75. [Google Scholar] [CrossRef]
- Sofuoglu, Y.; Ozalp, N. Fractional order bilingualism model without conversion from dominant unilingual group to bilingual group. Differ. Equ. Dyn. Syst. 2017, 25, 1–9. [Google Scholar] [CrossRef]
- Tarasova, V.V.; Vasily, V.E. Elasticity for economic processes with memory: Fractional differential calculus approach. Fract. Diff. Calc. 2016, 6, 219–232. [Google Scholar] [CrossRef]
- Tariboon, J.; Ntouyas, S.K.; Agarwal, P. New concepts of fractional quantum calculus and applications to impulsive fractional q-difference equations. Adv. Differ. Equ. 2015, 18, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Kilbas, A.; Srivastava, H.M.; Trujillo, J.J. Theory and Application of Fractional Differential Equations. In North Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: Yverdon, Switzerland, 1993. [Google Scholar]
- Katugampola, U.N. New approach to a generalized factional integral. Appl. Math. Comput. 2011, 218, 860–865. [Google Scholar]
- Katugampola, U.N. A new approach to generalized factional derivatives. Bull. Math. Anal. Appl. 2014, 6, 1–15. [Google Scholar]
- Almeida, R.; Malinowska, A.B.; Odzijewicz, T. Fractional differential equations with dependence on the Caputo-Katugampola derivative. J. Comput. Nonlinear Dyn. 2016, 11, 061017. [Google Scholar] [CrossRef] [Green Version]
- Jarad, F.; Abdeljawad, T.; Baleanu, D. On the generalized fractional derivatives and their Caputo modification. J. Nonlinear Sci. Appl. 2017, 10, 2607–2619. [Google Scholar] [CrossRef] [Green Version]
- Mandelbrot, B. The variation of certain speculative prices. J. Bus. 1963, 36, 394–413. [Google Scholar] [CrossRef]
- Peters, E.E. Fractal structure in the capital markets. Financ. Anal. J 1989, 45, 32–37. [Google Scholar] [CrossRef]
- Li, H.Q.; Ma, C.Q. An empirical study of long-term memory of return and volatility in Chinese stock market. J. Financ. Econ. 2005, 31, 29–37. [Google Scholar]
- Huang, T.F.; Li, B.Y.; Xiong, J.X. Test on the chaotic characteristic of Chinese futures market. Syst. Eng. 2012, 30, 43–53. [Google Scholar]
- Kumar, S.; Kumar, D.; Singh, J. Numerical computation of fractional Black–Scholes equation arising in financial market. Egypt. J. Basic Appl. Sci. 2014, 1, 177–183. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N. A different approach to the European option pricing model with new fractional operator. Math. Model. Nat. Phenom. 2018, 13, 12. [Google Scholar] [CrossRef] [Green Version]
- Yavuz, M.; Özdemir, N. A quantitative approach to fractional option pricing problems with decomposition series. Konuralp J. Math. 2014, 6, 102–109. [Google Scholar]
- Ghandehari, M.A.M.; Ranjbar, M. European option pricing of fractional version of the Black–Scholes model: Approach via expansion in series. J. Nonlinear Sci. 2014, 17, 105–110. [Google Scholar]
- Huang, J.; Cen, Z.; Zhao, J. An adaptive moving mesh method for a time-fractional Black–Scholes equation. Adv. Differ. Equ. 2019, 2019, 516. [Google Scholar] [CrossRef] [Green Version]
- Koleva, M.N.; Vulkov, L.G. Numerical solution of time-fractional Black–Scholes equation. J. Comput. Appl. Math. 2017, 17, 1699–1715. [Google Scholar] [CrossRef]
- Song, L.; Wang, W. Solution of the fractional Black-Scholes option pricing model by finite difference method. In Abstract and Applied Analysis; Hindawi: London, UK, 2013. [Google Scholar]
- Ghandehari, M.A.M.; Ranjbar, M. European option pricing of fractional Black-Scholes model with new Lagrange multipliers. Comput. Meth. Differ. Equ. 2014, 2, 1–10. [Google Scholar]
- Kumar, S.; Yildirim, A.; Khan, Y.; Jafari, H.; Sayevand, K.; Wei, L. Analytical solution of fractional Black-Scholes European option pricing equation by using Laplace transform. Fract. Calc. Appl. Anal. 2012, 2, 1–9. [Google Scholar]
- Prathumwan, D.; Trachoo, K. On the solution of two-dimensional fractional Black–Scholes equation for European put option. Adv. Differ. Equ. 2020, 2020, 146. [Google Scholar] [CrossRef]
- Sawangtong, P.; Trachoo, K.; Sawangtong, W.; Wiwattanapataphee, B. The Analytical Solution for the Black-Scholes Equation with Two Assets in the Liouville-Caputo Fractional Derivative Sense. Mathematics 2018, 6, 129. [Google Scholar] [CrossRef] [Green Version]
- Trachoo, K.; Sawangtong, W.; Sawangtong, P. Laplace transform homotopy perturbation method for the two dimensional Black Scholes model with European call option. Math. Comput. Appl. 2017, 22, 23. [Google Scholar] [CrossRef] [Green Version]
- Fall, A.N.; Ndiaye, S.N.; Ndolane, S. Black–Scholes option pricing equations described by the Caputo generalized fractional derivative. Chaos Solitons Fractals 2019, 125, 108–118. [Google Scholar] [CrossRef]
- Ampun, S.; Sawangtong, P. The approximate analytic solution of the time-fractional Black-Scholes equation with a European option based on the Katugampola fractional derivative. Mathematics 2021, 9, 214. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T. Generalized fractional derivatives and Laplace transform. Disc. Cont. Dyn. Syst. S 2019, 13. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, D.S.; de Oliveira, E.C. On a Caputo-type fractional derivative. Adv. Pure Appl. Math. 2019, 10, 81–91. [Google Scholar] [CrossRef]
- Fahd, J.; Abdeljawad, T. A modified Laplace transform for certain generalized fractional operators. Res. Nonlinear Anal. 2018, 2, 88–98. [Google Scholar]
- Fahd, J.; Abdeljawad, T.; Baleanu, D. Caputo-type modification of the Hadamard fractional derivatives. Adv. Differ. Equ. 2012, 142, 1–8. [Google Scholar]
- Aljoudi, S.; Ahmad, B.; Nieto, J.J.; Alsaedi, A. A coupled system of Hadamard type sequential fractional differential equations with coupled strip conditions. Chaos Solitons Fractal 2016, 91, 39–46. [Google Scholar] [CrossRef]
- Etemad, S.; Rezapour, S.; Sakar, F.M. On a fractional Caputo–Hadamard problem with boundary value conditions via different orders of the Hadamard fractional operators. Adv. Differ. Equ. 2020, 272, 1–20. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Saigo, M.; Saxena, R.K. Generalized Mittag-Leffler function and generalized fractional calculus operators. Integral Transforms Spec. Funct. 2004, 14, 31–49. [Google Scholar] [CrossRef]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications; Springer: Berlin, Germany, 2014. [Google Scholar]
- Simon, T. Mittag-Leffler functions and complete monotonicity. Integral Transform. Spec. Funct. 2015, 26, 36–50. [Google Scholar] [CrossRef]
- Contreras, M.; Llanquihuén, A.; Villena, M. On the Solution of the Multi-Assets Black–Scholes Model: Correlation, Eigenvalues and Geometry. J. Math. Financ. 2016, 71, 1772–1783. [Google Scholar] [CrossRef] [Green Version]
- He, J.H. Homotopy perturbation technique. J. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method for bifurcation of nonlinear problems. Int. J. Nonlinear Sci. Numer. Simul. 2005, 6, 207–208. [Google Scholar] [CrossRef]
- Baholian, E.; Azizi, A.; Saeidian, J. Some notes on using the homotopy perturbation method for solving time-dependent differential equations. Math. Comput. Model. 2009, 50, 213–224. [Google Scholar] [CrossRef]
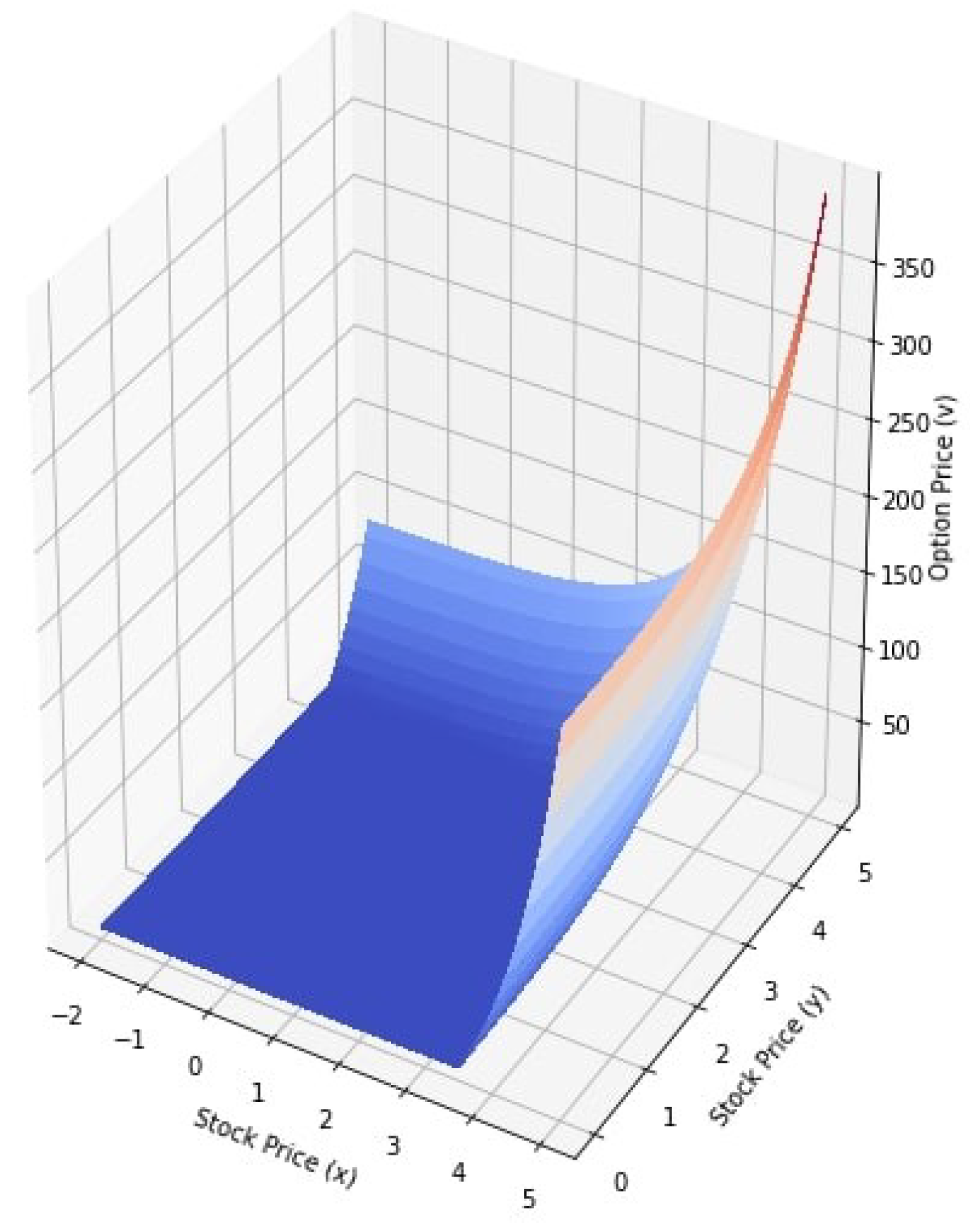
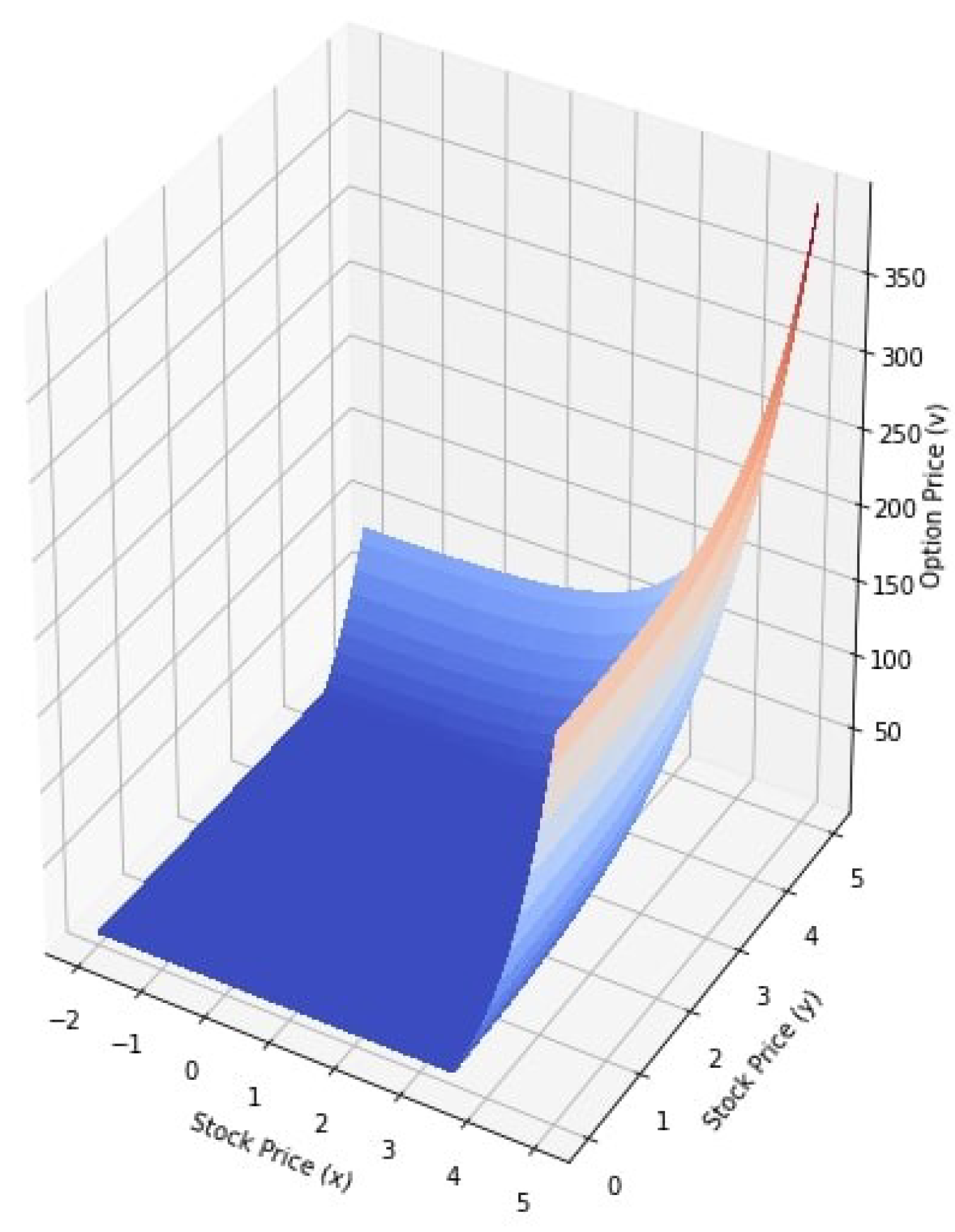

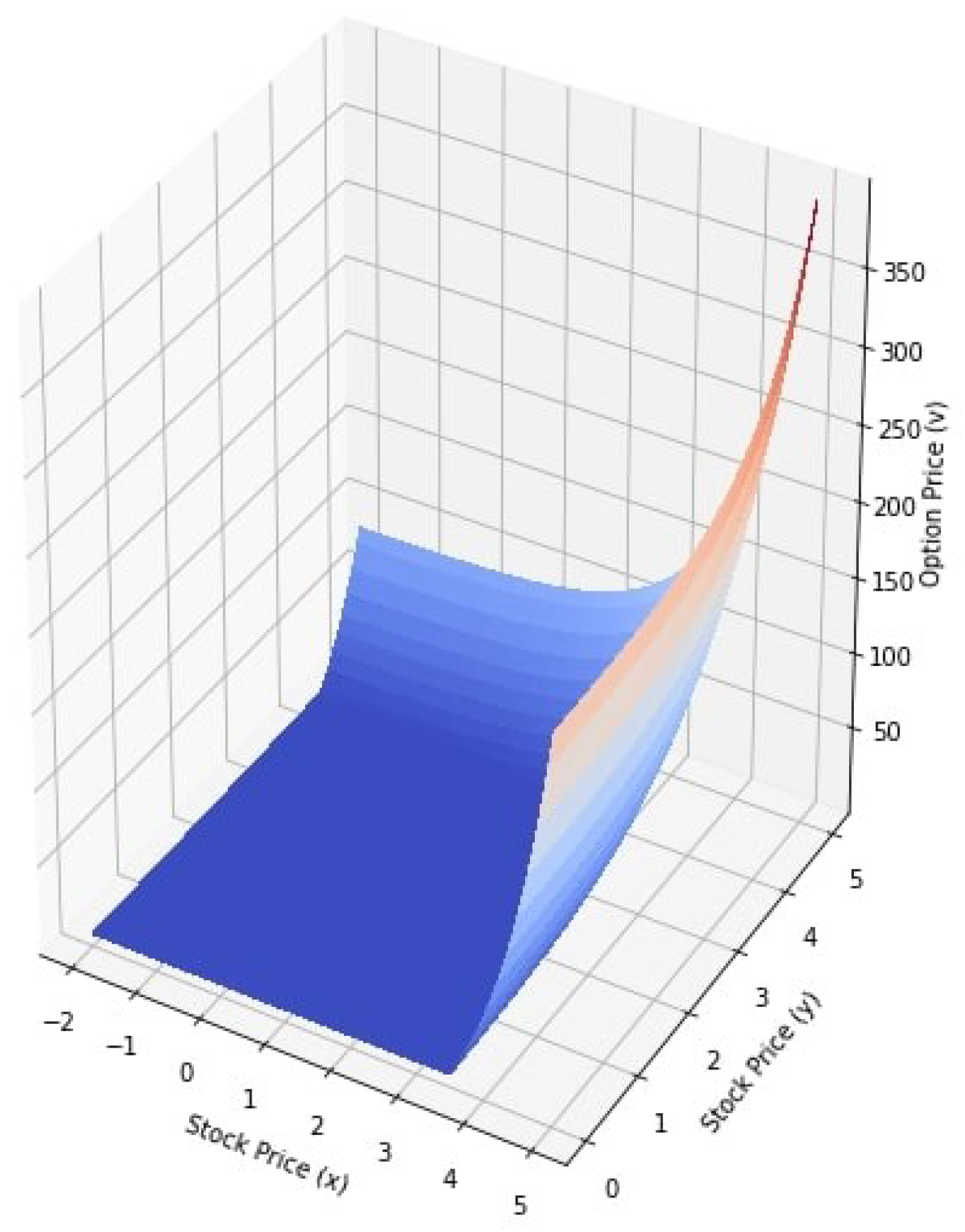
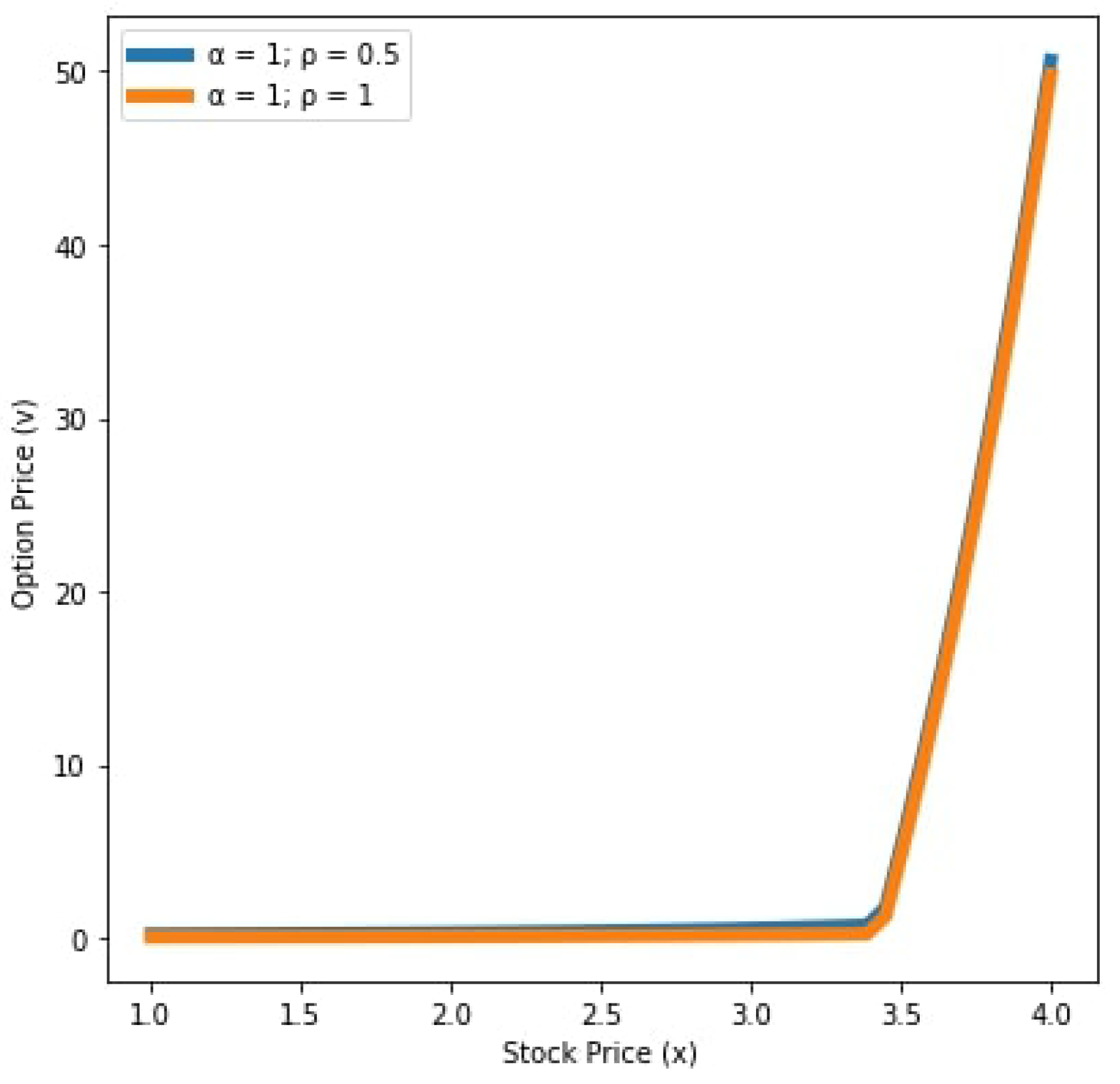
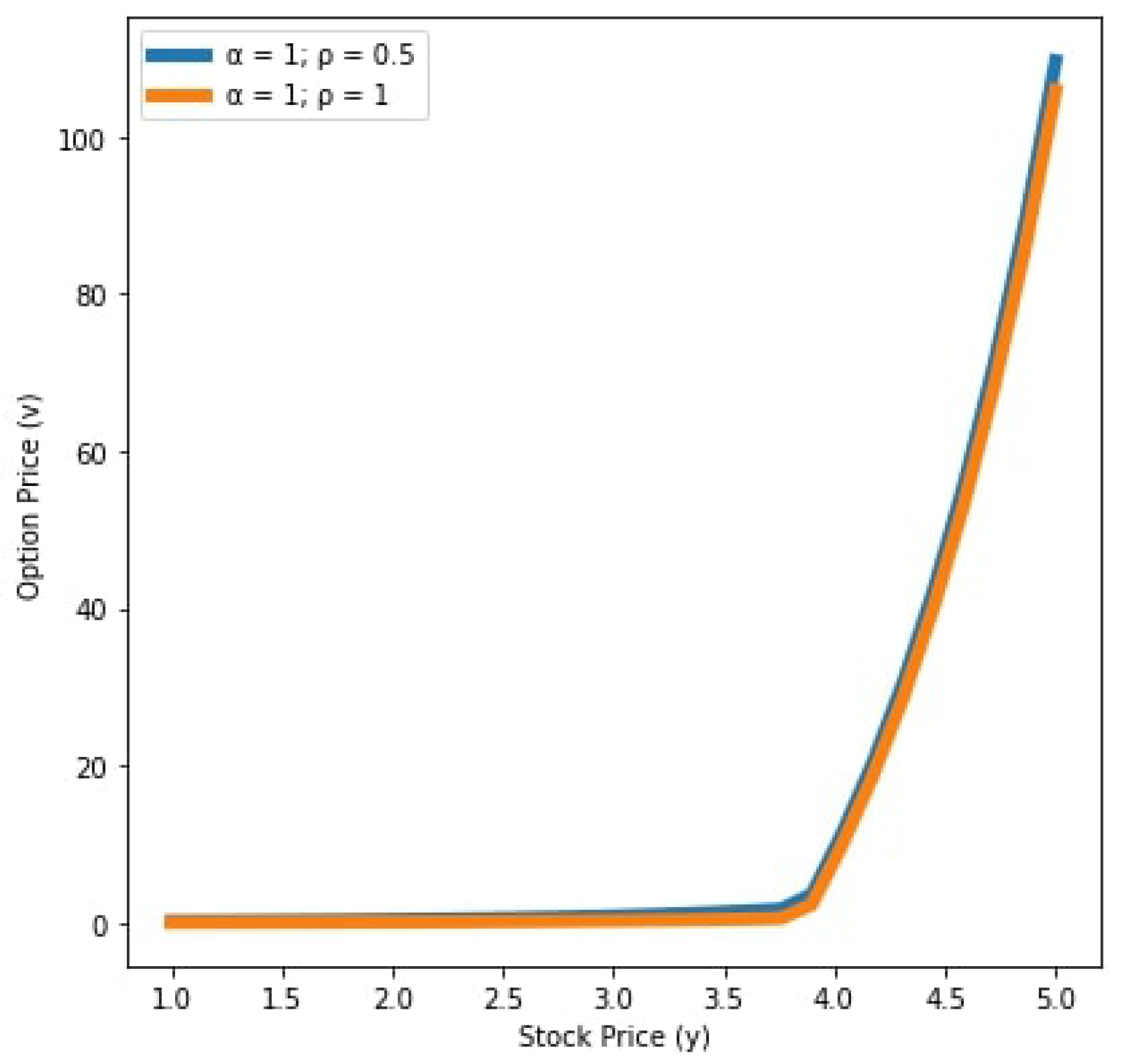
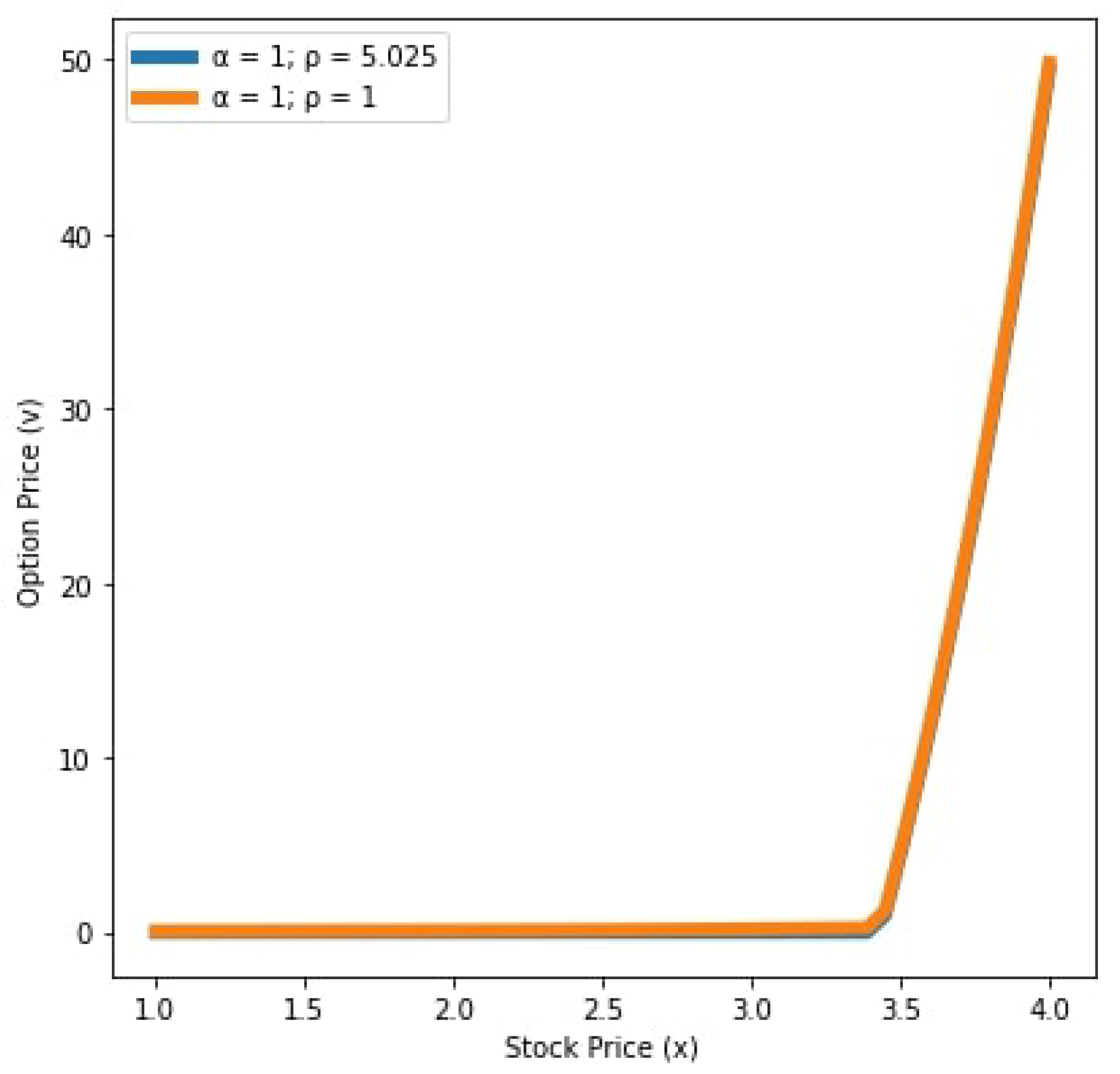

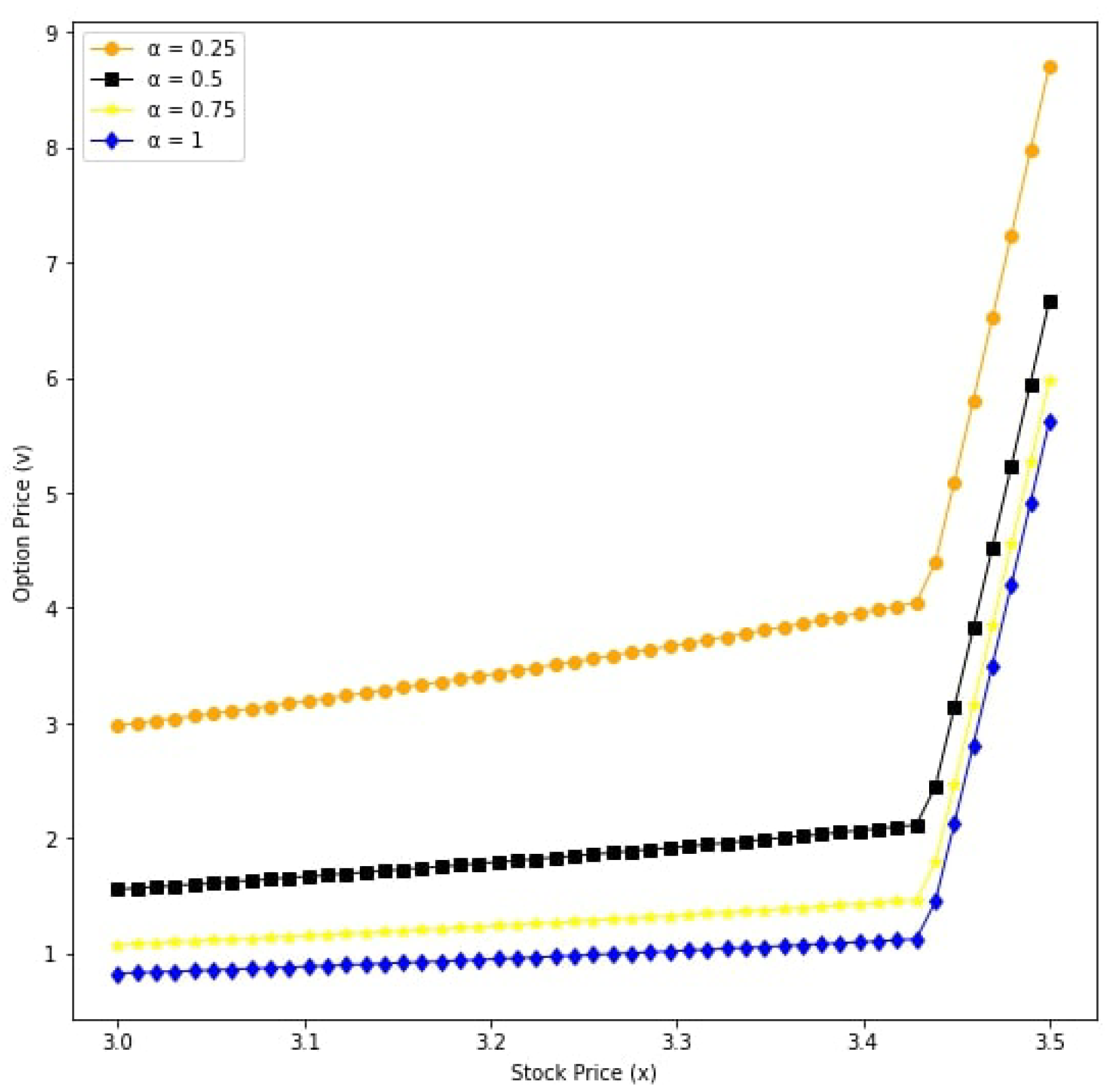
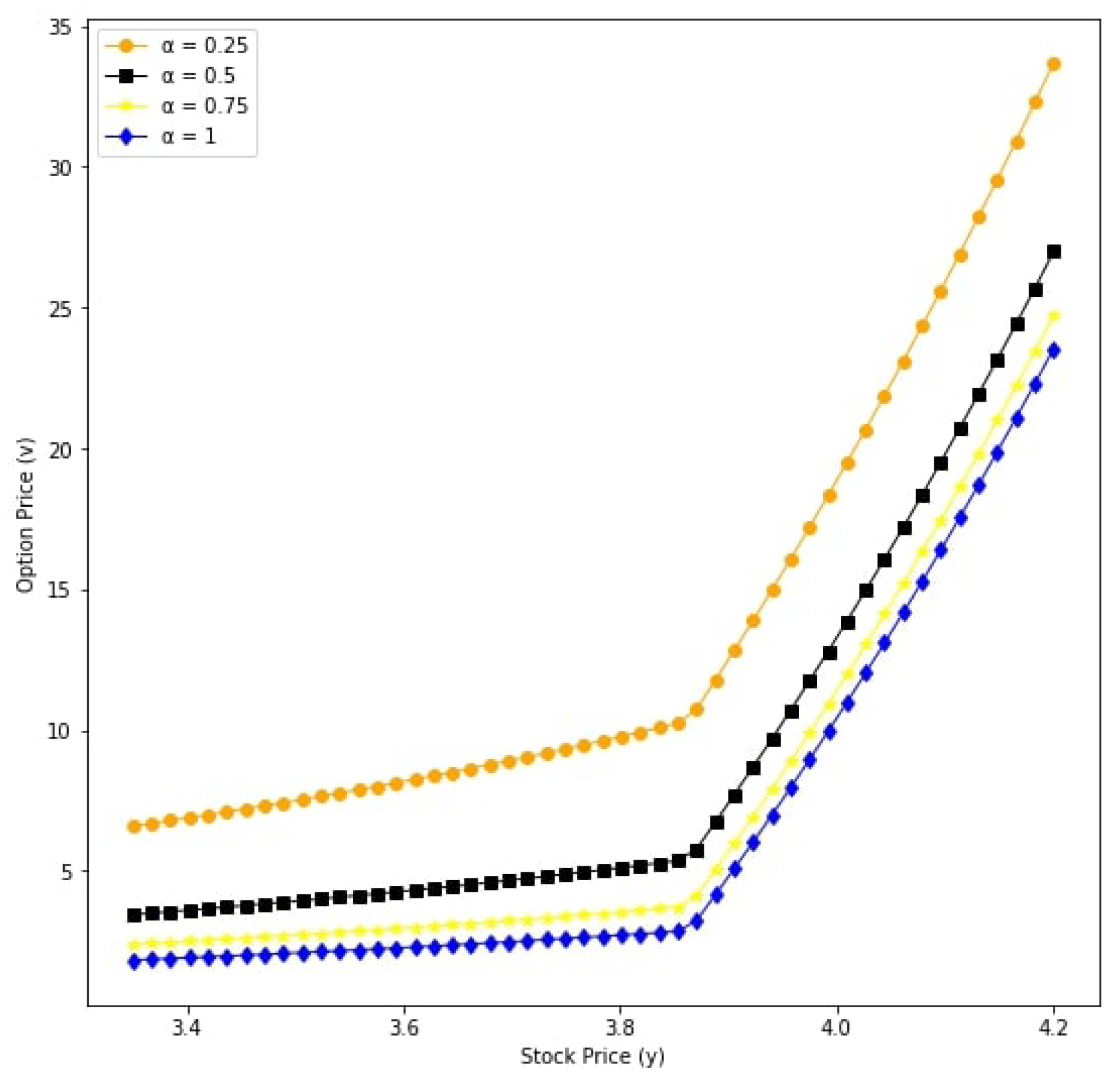
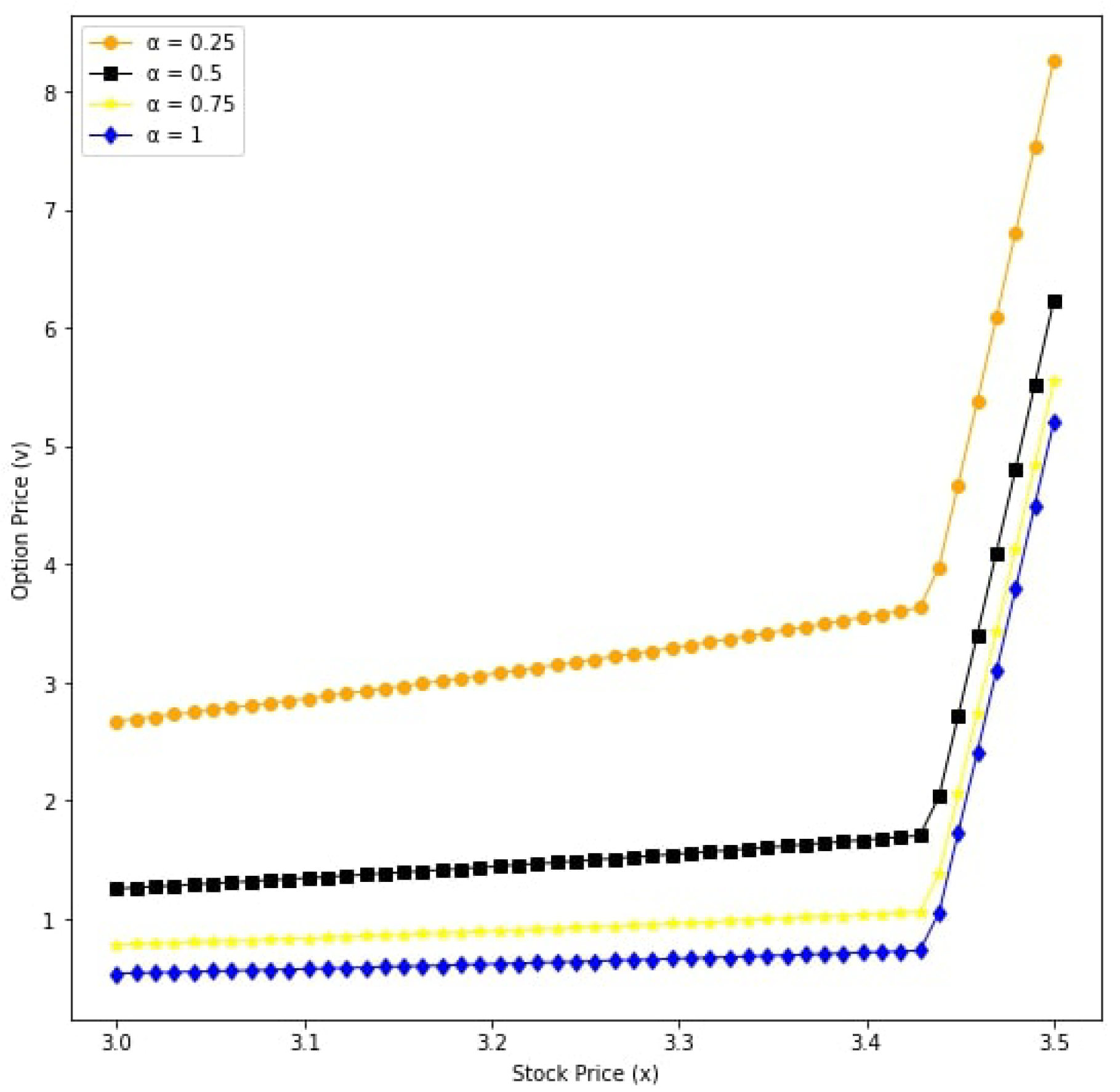
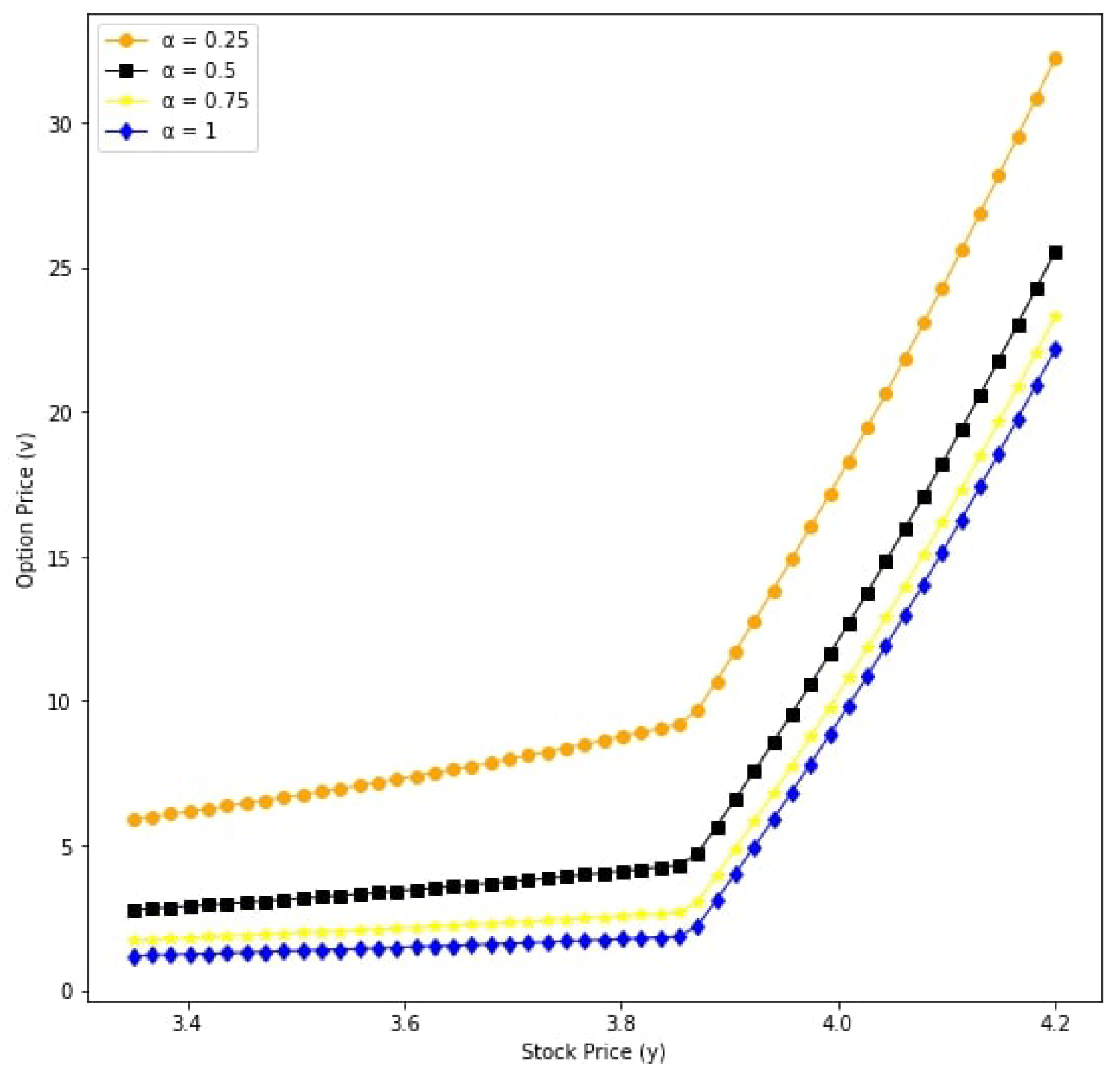
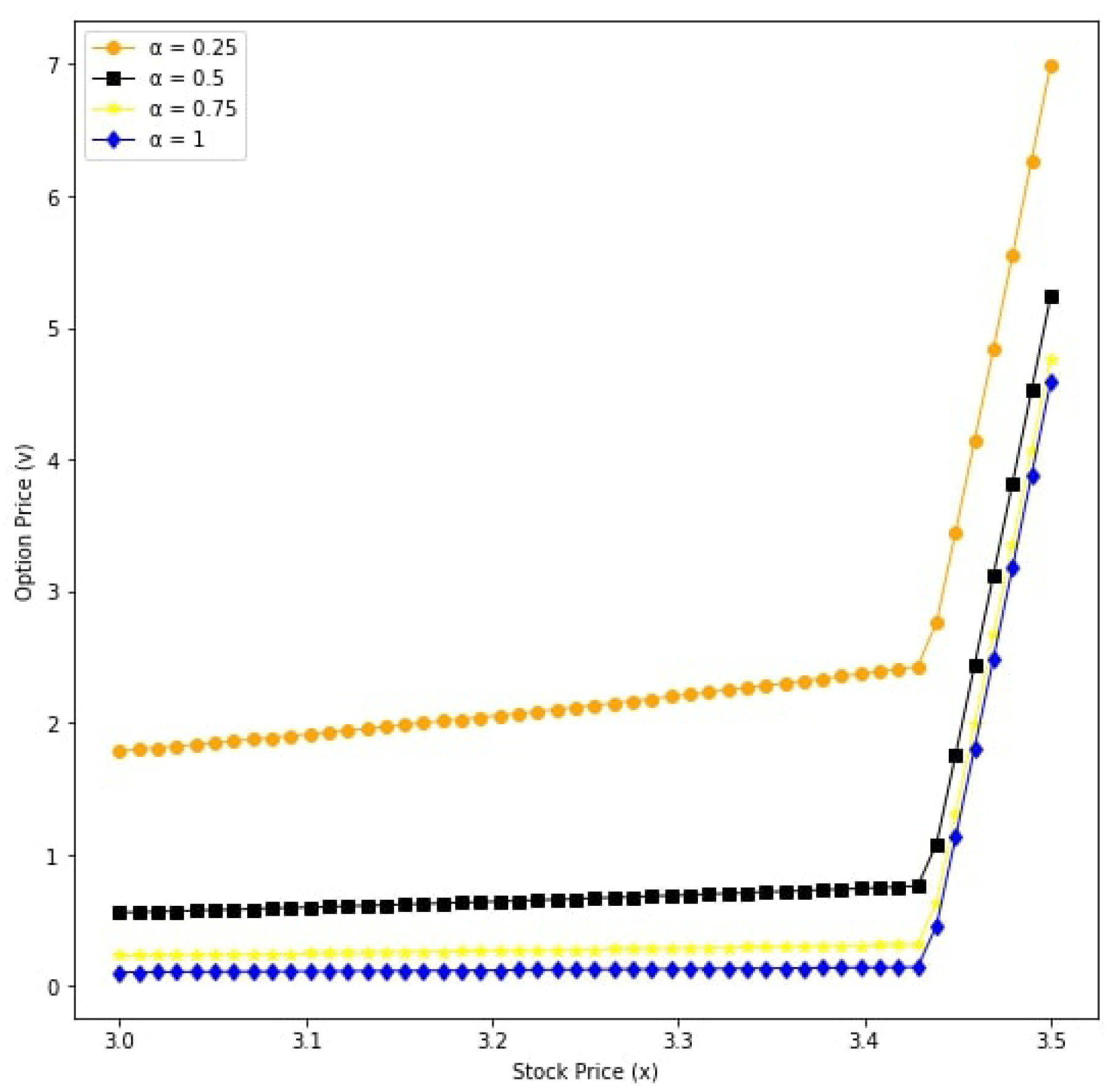
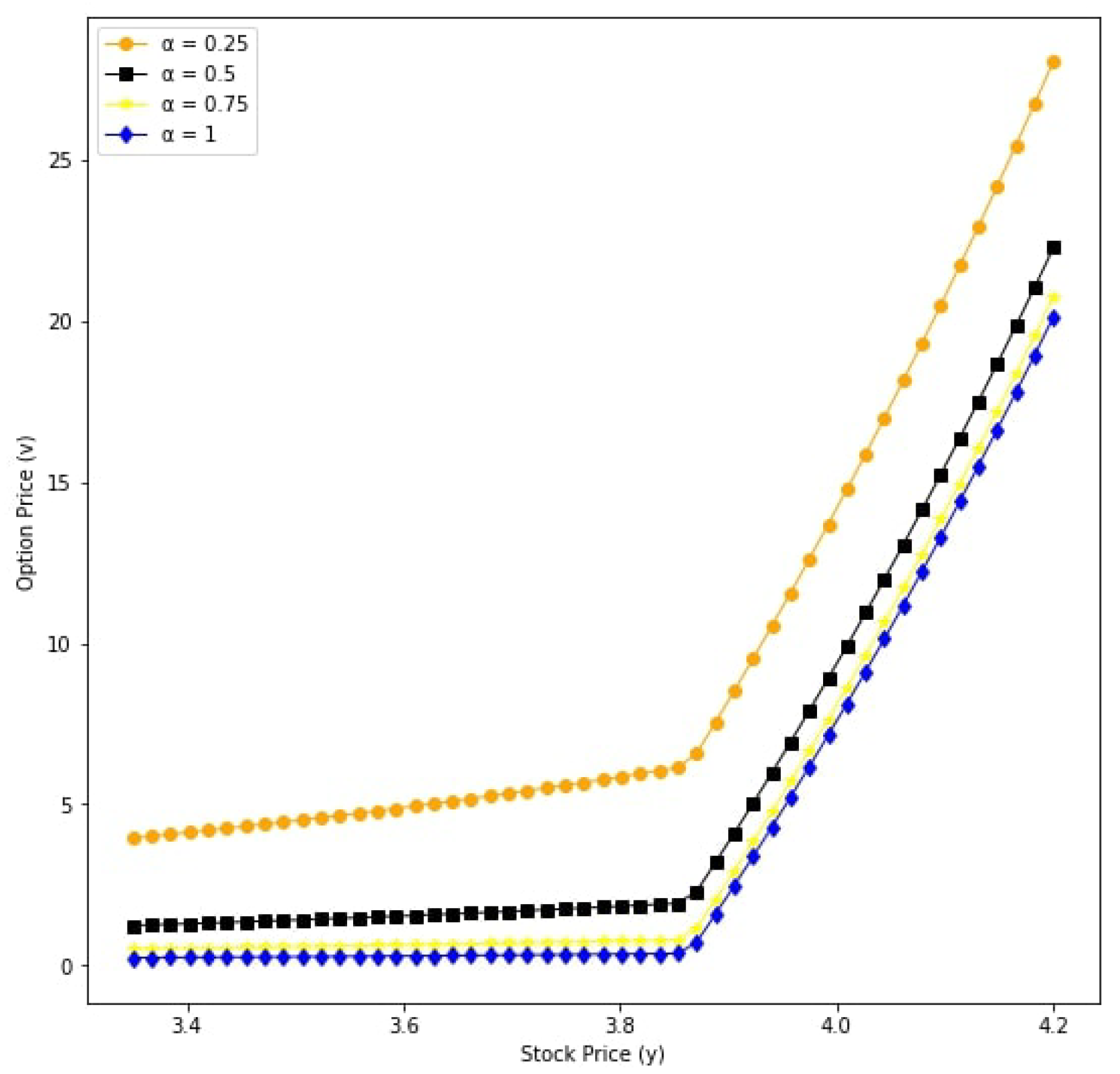
| Parameters | Value |
|---|---|
| strike price (dollars), K | 70 |
| risk-free interest rate (per year), r | 0.05 |
| expiration date (year), T | 1 |
| volatility function of underlying first assets (per year), | 0.1 |
| volatility function of underlying second assets (per year), | 0.2 |
| the volatility of and , | 0.5 |
| 2 | |
| 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
|---|---|---|---|---|---|---|---|
| 0.75 | 1 | 0.75 | 1 | 0.95 | 1 | 1.5 | |
| r | 0.05 | 0.05 | 0.2 | 0.2 | 0.1 | 0.1 | 0.1 |
| 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | |
| T | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | |
| 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | |
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| x | 4.1805 | 4.1805 | 4.1805 | 4.1805 | 4.1805 | 4.1805 | 4.1805 |
| y | 1.6093 | 1.6093 | 1.6093 | 1.6093 | 1.6093 | 1.6093 | 1.6093 |
| v | 72.7786 | 72.4795 | 95.8850 | 95.5376 | 79.8328 | 79.7846 | 79.5009 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thanompolkrang, S.; Sawangtong, W.; Sawangtong, P. Application of the Generalized Laplace Homotopy Perturbation Method to the Time-Fractional Black–Scholes Equations Based on the Katugampola Fractional Derivative in Caputo Type. Computation 2021, 9, 33. https://0-doi-org.brum.beds.ac.uk/10.3390/computation9030033
Thanompolkrang S, Sawangtong W, Sawangtong P. Application of the Generalized Laplace Homotopy Perturbation Method to the Time-Fractional Black–Scholes Equations Based on the Katugampola Fractional Derivative in Caputo Type. Computation. 2021; 9(3):33. https://0-doi-org.brum.beds.ac.uk/10.3390/computation9030033
Chicago/Turabian StyleThanompolkrang, Sirunya, Wannika Sawangtong, and Panumart Sawangtong. 2021. "Application of the Generalized Laplace Homotopy Perturbation Method to the Time-Fractional Black–Scholes Equations Based on the Katugampola Fractional Derivative in Caputo Type" Computation 9, no. 3: 33. https://0-doi-org.brum.beds.ac.uk/10.3390/computation9030033







