A Shoreline Evolution Model with a Groin Structure under Non-Uniform Breaking Wave Crest Impact
Abstract
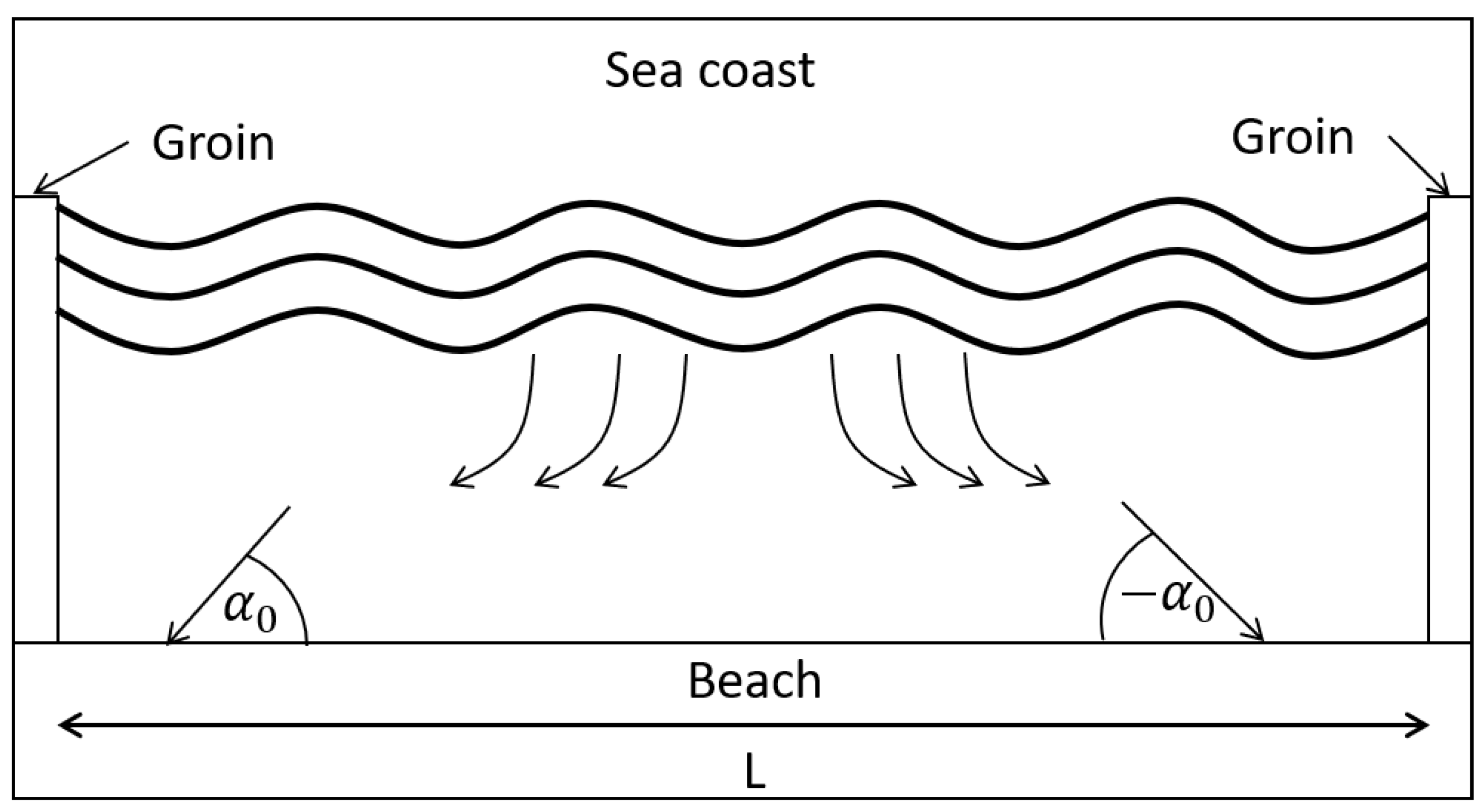
:1. Introduction
2. Governing Equation
2.1. Shoreline Evolution Model
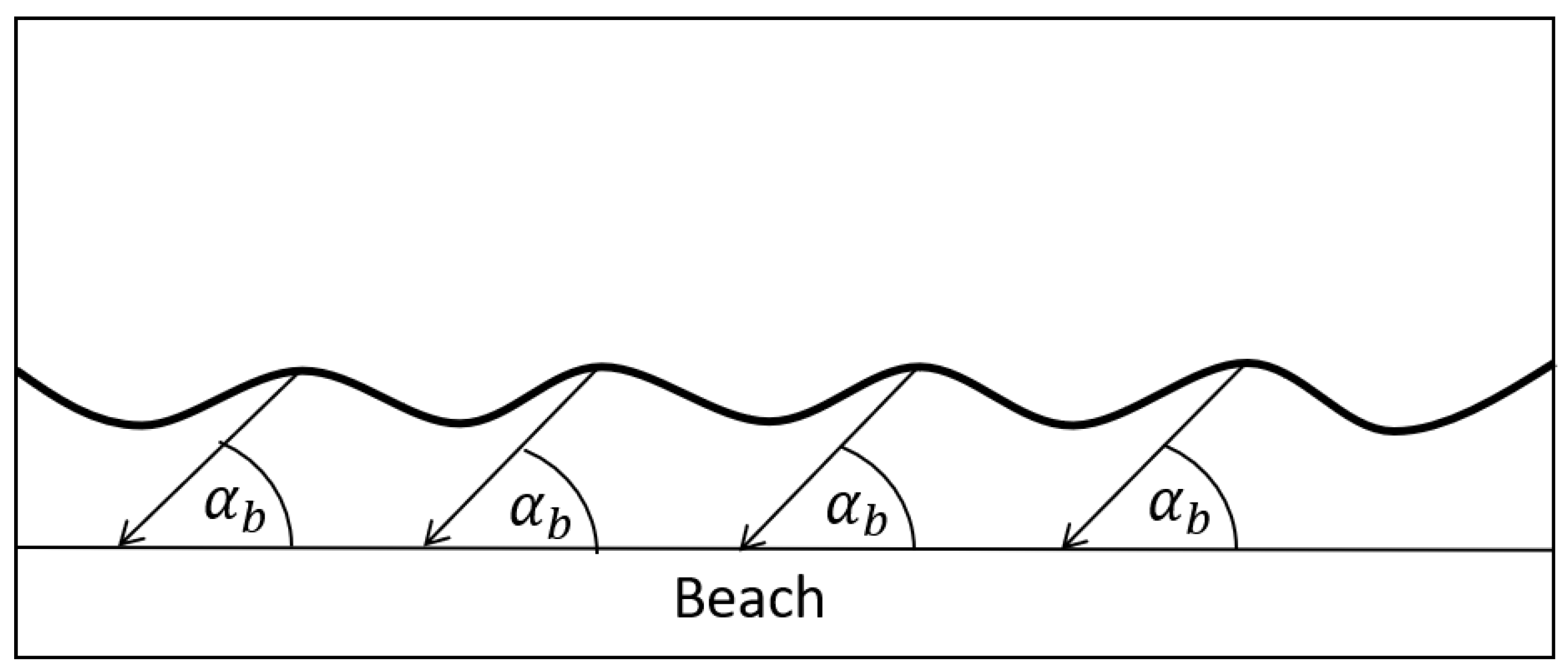
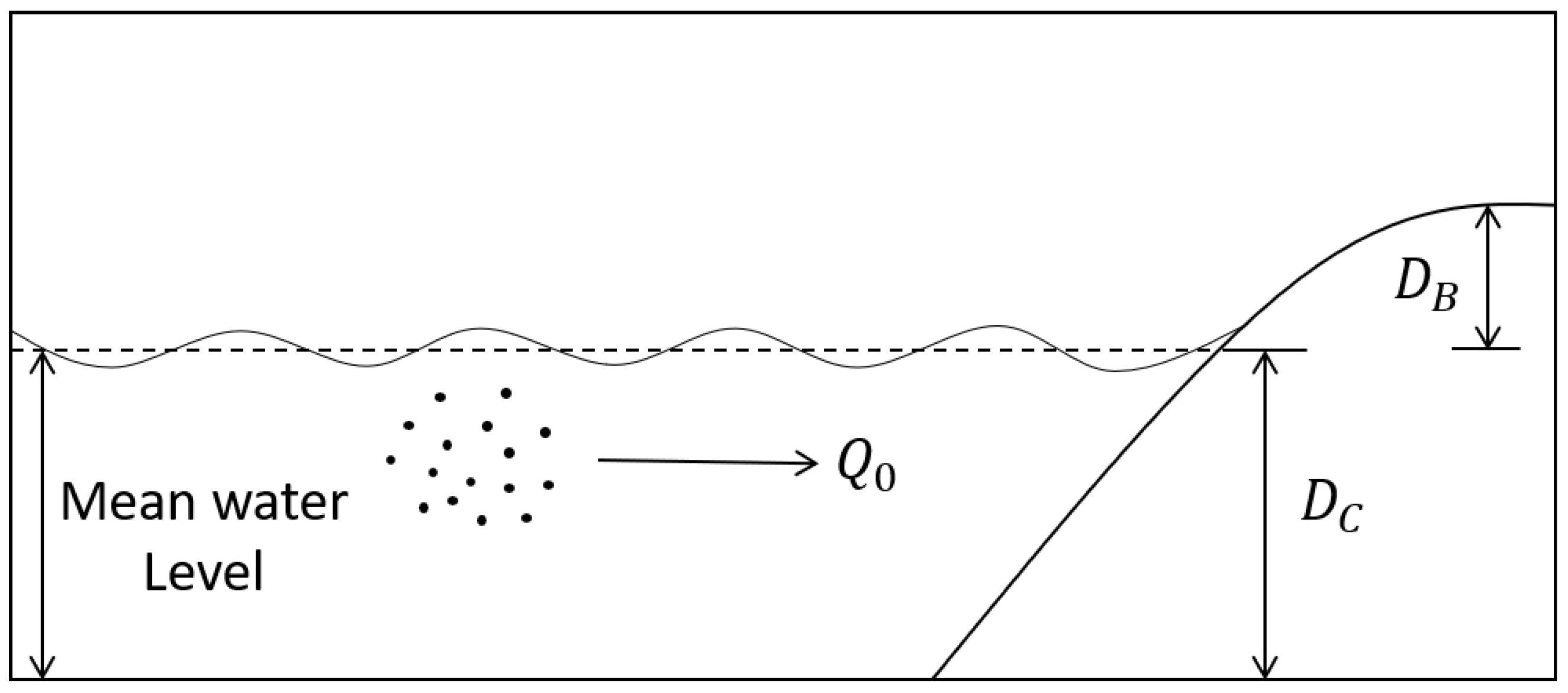
2.2. Physical Parameters
- is the angle between breaking wave crests’ impact angle and x-axis.
- is the long-shore sand transport rate amplitude.
- is the average height of the berm.
- is the average depth of closure.
- L is alongshore.
- T is the time of simulation.
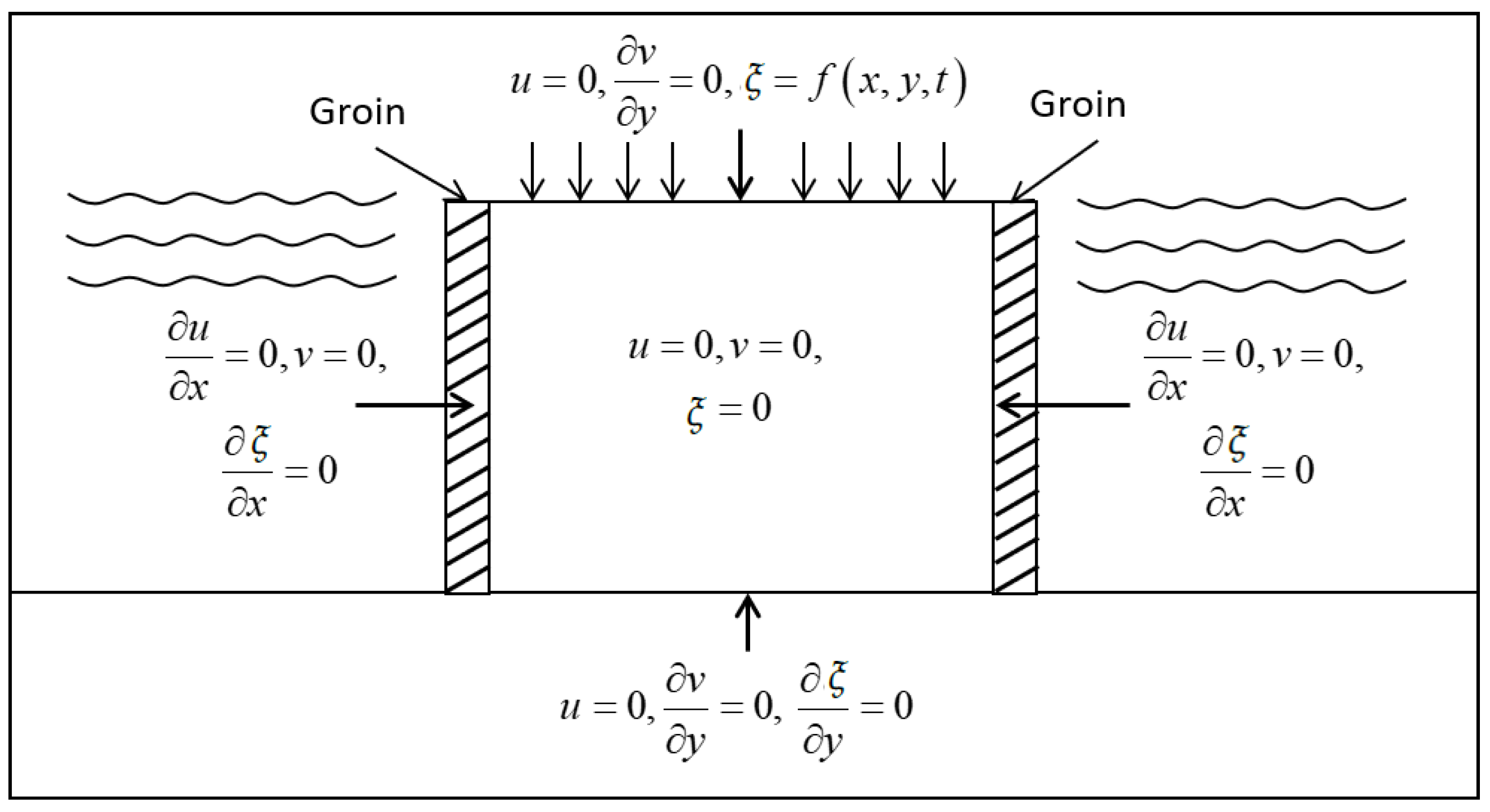
2.3. The Initial and Boundary Conditions
2.4. Wave Crest Impact Model
- is the depth estimated from the average water surface to the seashore bed (m),
- is the elevation of water surface from the average water level at seashore (m),
- is the interpolated bottom topography function of the seashore (m),
- is velocity in the direction of x (m/s),
- is velocity in the direction of y (m/s),
- g is a constant in gravity (9.8 m/s).
2.5. The Initial and Boundary Condition for Wave Crest Impact Model
3. Numerical Techniques
3.1. Grid Spacing
3.2. Traditional Forward Time-Centered Space Technique
3.3. Unconditionally Saulyev Finite Difference Techniques
3.4. Numerical Techniques for the Wave Crest Impact Model
3.5. The Wave Crest Impact
3.6. The Employment of Traditional Forward Time-Centered Space Technique to the Left and the Right Boundary Conditions
4. Physical Parameters’ Setting Techniques
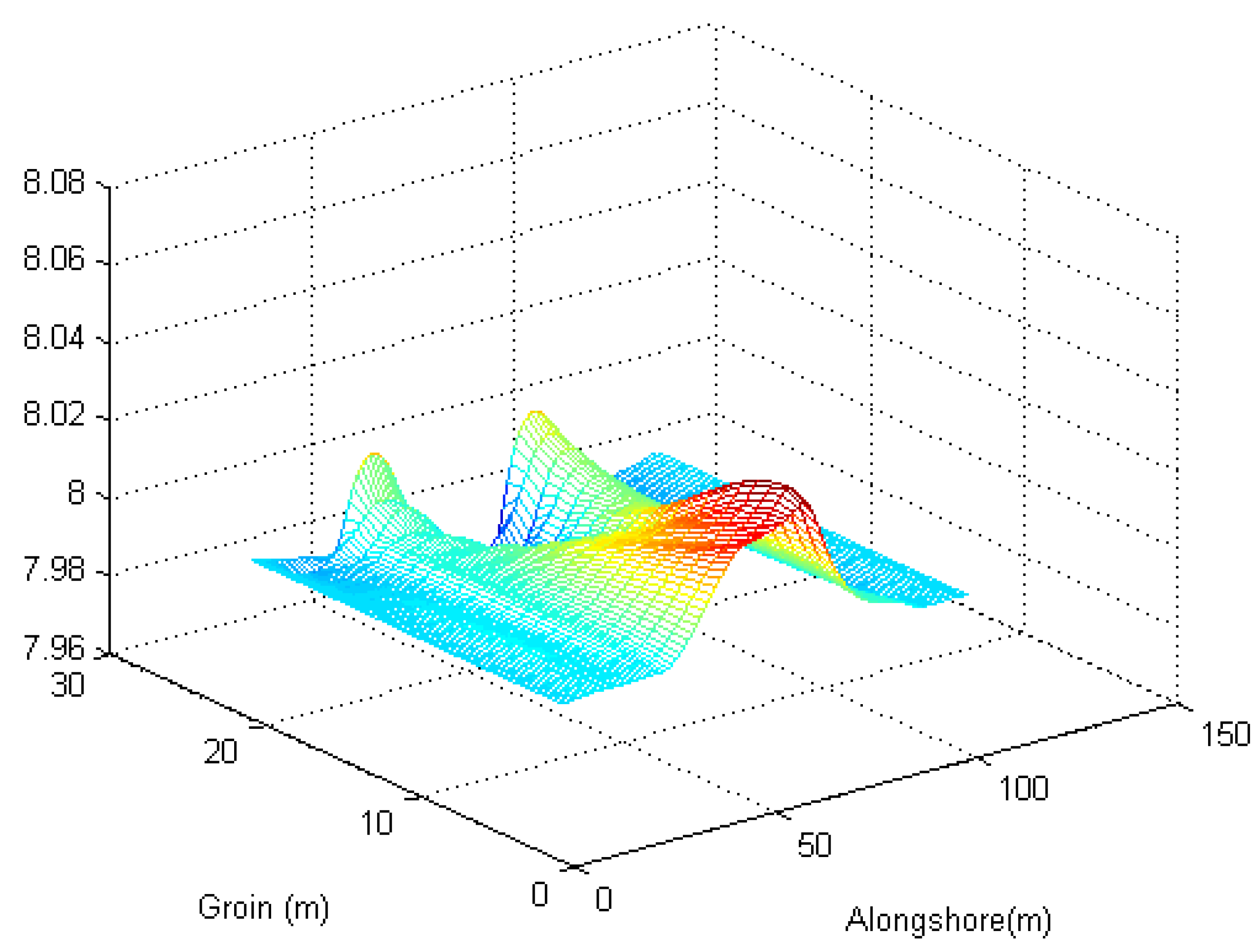
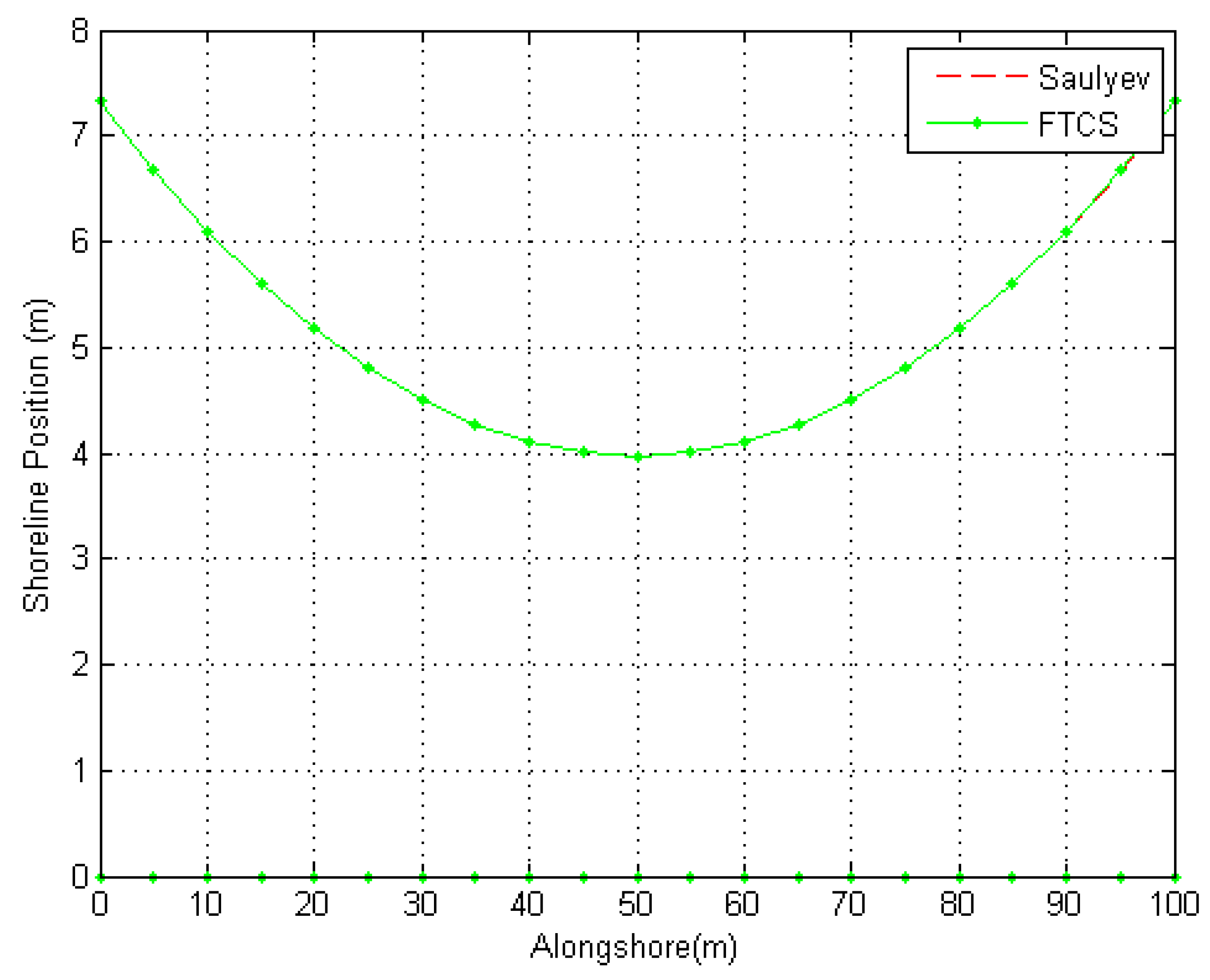
5. Numerical Experiment
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hanson, H.; Kraus, N.C.; Blomgren, S.H. Modern functional design of groin systems. Coast. Eng. 1994, 96, 1327–1342. [Google Scholar]
- Fatimah, E.; Ariff, A.; Aulia, T.B. The influence of single zigzag type porous groin in the change of beach profile. Procedia Eng. 2015, 125, 257–262. [Google Scholar] [CrossRef] [Green Version]
- Bakker, W.T.; Breteler, E.K.; Roos, A. The dynamics of coast with a groin system. Coast. Eng. Proc. 1970, 1, 492–517. [Google Scholar] [CrossRef] [Green Version]
- Bakker, W.T.; Edelman, T. The coastline of river deltas. Coast. Eng. Proc. 1964, 1, 199–218. [Google Scholar] [CrossRef] [Green Version]
- Grijimr, W. Theoretical form of shoreline. Available online: https://ascelibrary.org/doi/abs/10.1061/9780872620056.014 (accessed on 25 March 2021).
- Mahute, B.L.; Soldate, M. Mathematical Modeling of Shoreline Evolution. In US Army Corps of Engineer Waterways Experiment Station; CERC: Rockville, MD, USA, 1977. [Google Scholar]
- Hanson, H.; Larson, M.; Kraus, N.C. Analytical Solution of the One-line Model for Shoreline Changel. In US Army Corps of Engineer Waterways Experiment Station; CERC: Rockville, MD, USA, 1987. [Google Scholar]
- Walton, T.; Chiu, T. A review of analytical technique to solve the sand transport equation and some simplified solution. Coast. Struct. 1979, 809–837. [Google Scholar]
- Pochai, P. Unconditional stable numerical techniques for a water-quality model in a non-uniform flow stream. Adv. Differ. Eq. 2017, 2017, 13. [Google Scholar] [CrossRef] [Green Version]
- Samalerk, P.; Pochai, N. Numerical Simulation of a One-Dimensional Water-Quality Model in a Stream Using a Saulyev Technique with Quadratic Interpolated Initial-Boundary Conditions. Abstr. Appl. Anal. 2018, 2018, 1926519. [Google Scholar] [CrossRef] [Green Version]
- Aminti, P.; Cammelli, C.; Cappietti, L.; Jackson, N.L.; Nordstrom, K.F.; Pranzini, E. Evaluation of Beach Response to Submerged Groin Construction at Marina di Ronchi, Italy, Using Field Data and a Numerical Simulation Model. J. Coast. Res. 2004, 33, 99–120. [Google Scholar]
- Cannata, G.; Tamburrino, M.; Gallerano, F. 3D Numerical Simulation of the Interaction between Waves and a T-Head Groin Structure. J. Mar. Sci. Eng. 2020, 8, 227. [Google Scholar] [CrossRef] [Green Version]
- Setyandito, O.; Purnama, A.C.; Yuwono, N.J.; Wijayanti, Y. Shoreline Change with Groin Coastal Protection Structure at North Java Beach. ComTech Comput. Math. Eng. Appl. 2020, 11, 19–28. [Google Scholar] [CrossRef]
- Ding, Y.; Kim, S.; Frey, A.E. Probabilistic Shoreline Evolution Modeling in Response to Sea Level Changes. World Environ. Water Resour. Congr. 2018. [Google Scholar] [CrossRef]
- Dabees, M.; Kamphuis, J.W. Oneline, A Numerical Model for Shoreline Change. In Proceeding of the 26th Coastal Engineering Conference 1998, Copenhagen, Denmark, 22–26 June 1998; pp. 2668–2681. [Google Scholar]
- Subiyanto, M.M.; Ahmad, M.F.; Husain, M.L. Comparison of numerical method for forward and backward time centered space for long—Term simulation of shoreline evolution. Appl. Math. Sci. 2013, 7, 5165–5173. [Google Scholar] [CrossRef]
- US Army Corp of Engineers. Shore Protection Manual; Coastal Engineering Research Centre: Washington, DC, USA, 1984. [Google Scholar]
- Hoan, L.X. Some result of comparison between numerical and analytical solutions of the one-line model for shoreline change. Vietnam. J. Mech. 2006, 28, 94–102. [Google Scholar] [CrossRef] [Green Version]
- Kraychang, W.; Pochai, N. Numerical Treatment to a Water-Quality Measurement Model in an Opened-Closed Reservoir. Thai J. Math. 2015, 13, 775–788. [Google Scholar]
- Mitchell, A.R. Computational Methods in Partial Differential Equations; John Wiley & Sons Ltd.: London, UK, 1969. [Google Scholar]
- Tenzer, R.; Gladkikh, V. Assessment of density variations of marine sediments with ocean and sediment depths. Sci. World J. 2014, 2014, 823296. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wikipedia. Available online: https://en.wikipedia.org/wiki/Seawater (accessed on 25 March 2021).
- Román-Sierra, J.; Muñoz-Perez, J.J.; Navarro-Pons, M. Beach nourishment effects on sand porosity variability. Coast. Eng. 2014, 83, 221–232. [Google Scholar] [CrossRef] [Green Version]
- Dronkers, J.; van den Berg, J. Available online: http://www.coastalwiki.org/wiki/Coastal_and_marine_sediments?fbclid=IwAR2UkENgXUxyEJIj5tIaau2yPrDOCuRniHu3FqSCrLwVD_KpKMtqXob1iZc (accessed on 25 March 2021).
- GeoInformatics and Space Technology Development Agency (Public Organization) (GISTDA). Available online: http://http://coastalradar.gistda.or.th/wp/?page=announce-small (accessed on 25 March 2021).
- Unyapoti, P.; Pochai, N. A One-Dimensional Mathematical Model of Long-Term Shoreline Evolution with Groin System using an Unconditionally Stable Explicit Finite Difference Method. Int. J. Simul. Syst. Sci. Technol. 2020, 21. [Google Scholar] [CrossRef]
| The sediment density ((kg/m)) | 1700 |
| The sea water’s density ((kg/m)) | 1020 |
| The porosity | 0.406 |
| The non-dimensional coefficient of the particle size function | 0.375 |
| The average height of the berm. ((m)) | 2 |
| The average depth of closure. ((m)) | 8 |
| Month | (m/day) | H (m) |
|---|---|---|
| January 2019 | 8951.04 | 1.5 |
| February 2019 | 6998.4 | 1.5 |
| March 2019 | 5866.56 | 0.5 |
| April 2019 | 6920.64 | 1.5 |
| May 2019 | 5719.68 | 0.5 |
| June 2019 | 5546.88 | 0.5 |
| July 2018 | 8225.28 | 1.5 |
| August 2018 | 9357.12 | 1.5 |
| September 2018 | 13,711.68 | 1.5 |
| October 2018 | 15,085.44 | 2.5 |
| November 2018 | 10,877.76 | 1.5 |
| December 2018 | 11,396.16 | 1.5 |
| Month | (m/day) | D (m/day) |
|---|---|---|
| January 2019 | 1191.99 | 238.3977 |
| February 2019 | 931.96 | 186.3921 |
| March 2019 | 86.80 | 17.3607 |
| April 2019 | 921.61 | 184.3209 |
| May 2019 | 84.63 | 16.9260 |
| June 2019 | 82.07 | 16.4148 |
| July 2018 | 1095.34 | 219.0681 |
| August 2018 | 1246.07 | 249.2130 |
| September 2018 | 1825.95 | 365.1903 |
| October 2018 | 5580.26 | 1116.0520 |
| November 2018 | 1448.57 | 289.7130 |
| December 2018 | 1517.60 | 303.3699 |
| Time | min | ||||||
|---|---|---|---|---|---|---|---|
| day | 0–90 | 90–180 | 180–270 | 270–360 | 360–450 | 450–540 | 540–630 |
| 30 | −0.0186 | −0.0185 | −0.0184 | −0.0182 | −0.0181 | −0.0180 | −0.0179 |
| 60 | 0.0052 | 0.0052 | 0.0051 | 0.0051 | 0.0051 | 0.0051 | 0.0050 |
| 90 | 0.0623 | 0.0621 | 0.0619 | 0.0617 | 0.0615 | 0.0614 | 0.0612 |
| . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . |
| 360 | 0.1306 | 0.1306 | 0.1306 | 0.1306 | 0.1306 | 0.1306 | 0.1306 |
| Time | min | ||||||
| day | 630–720 | 720–810 | 810–900 | 900–990 | 990–1080 | 1080–1170 | 1170–1260 |
| 30 | −0.0178 | −0.0178 | −0.0177 | −0.0176 | −0.0175 | −0.0175 | −0.0174 |
| 60 | 0.0049 | 0.0048 | 0.0047 | 0.0046 | 0.0046 | 0.0046 | 0.0046 |
| 90 | 0.0610 | 0.0608 | 0.0606 | 0.0604 | 0.0602 | 0.0600 | 0.0598 |
| . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . |
| 360 | 0.1307 | 0.1618 | 0.1618 | 0.1618 | 0.1618 | 0.1618 | 0.1619 |
| Time | min | ||||||
| day | 1260–1350 | 1350–1440 | |||||
| 30 | −0.0173 | −0.0172 | |||||
| 60 | 0.0046 | 0.0046 | |||||
| 90 | 0.0597 | 0.0595 | |||||
| . . . | . . . | . . . | |||||
| 360 | 0.1619 | 0.1619 | |||||
| Time (years) | Distance (m) | |||||
|---|---|---|---|---|---|---|
| 0 | 20 | 40 | 60 | 80 | 100 | |
| 1 | 7.3252 | 5.1761 | 4.1060 | 4.1060 | 5.1761 | 7.3252 |
| Time (years) | Distance (m) | |||||
|---|---|---|---|---|---|---|
| 0 | 20 | 40 | 60 | 80 | 100 | |
| 1 | 7.3260 | 5.1764 | 4.1053 | 4.1060 | 5.1756 | 7.3238 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Unyapoti, P.; Pochai, N. A Shoreline Evolution Model with a Groin Structure under Non-Uniform Breaking Wave Crest Impact. Computation 2021, 9, 42. https://0-doi-org.brum.beds.ac.uk/10.3390/computation9040042
Unyapoti P, Pochai N. A Shoreline Evolution Model with a Groin Structure under Non-Uniform Breaking Wave Crest Impact. Computation. 2021; 9(4):42. https://0-doi-org.brum.beds.ac.uk/10.3390/computation9040042
Chicago/Turabian StyleUnyapoti, Pidok, and Nopparat Pochai. 2021. "A Shoreline Evolution Model with a Groin Structure under Non-Uniform Breaking Wave Crest Impact" Computation 9, no. 4: 42. https://0-doi-org.brum.beds.ac.uk/10.3390/computation9040042





