Improved Genetic Algorithm for Phase-Balancing in Three-Phase Distribution Networks: A Master-Slave Optimization Approach
Abstract
:1. Introduction
2. Formulation of the Phase-Balancing Problem
2.1. Objective Function
2.2. Set of Constraints
2.3. Mathematical Model Interpretation
3. Solution Methodology
3.1. Slave Stage: Three-Phase Successive Approximation Power Flow Method
| Algorithm 1: Solution of the three-phase power flow problem for unbalanced distributions networks with Y and loads. |
 |
3.2. Slave Stage: Improved CBGA
3.2.1. Classical Approach
3.2.2. Improved Approach: Vortex Search for Offspring Generation
3.3. General Flow Diagram of the Proposed Master–Slave Improved CBGA
| Algorithm 2: Improved CBGA for solving the phase-balancing problem in three-phase unbalanced distribution networks. |
 |
4. Three-Phase Test Feeders
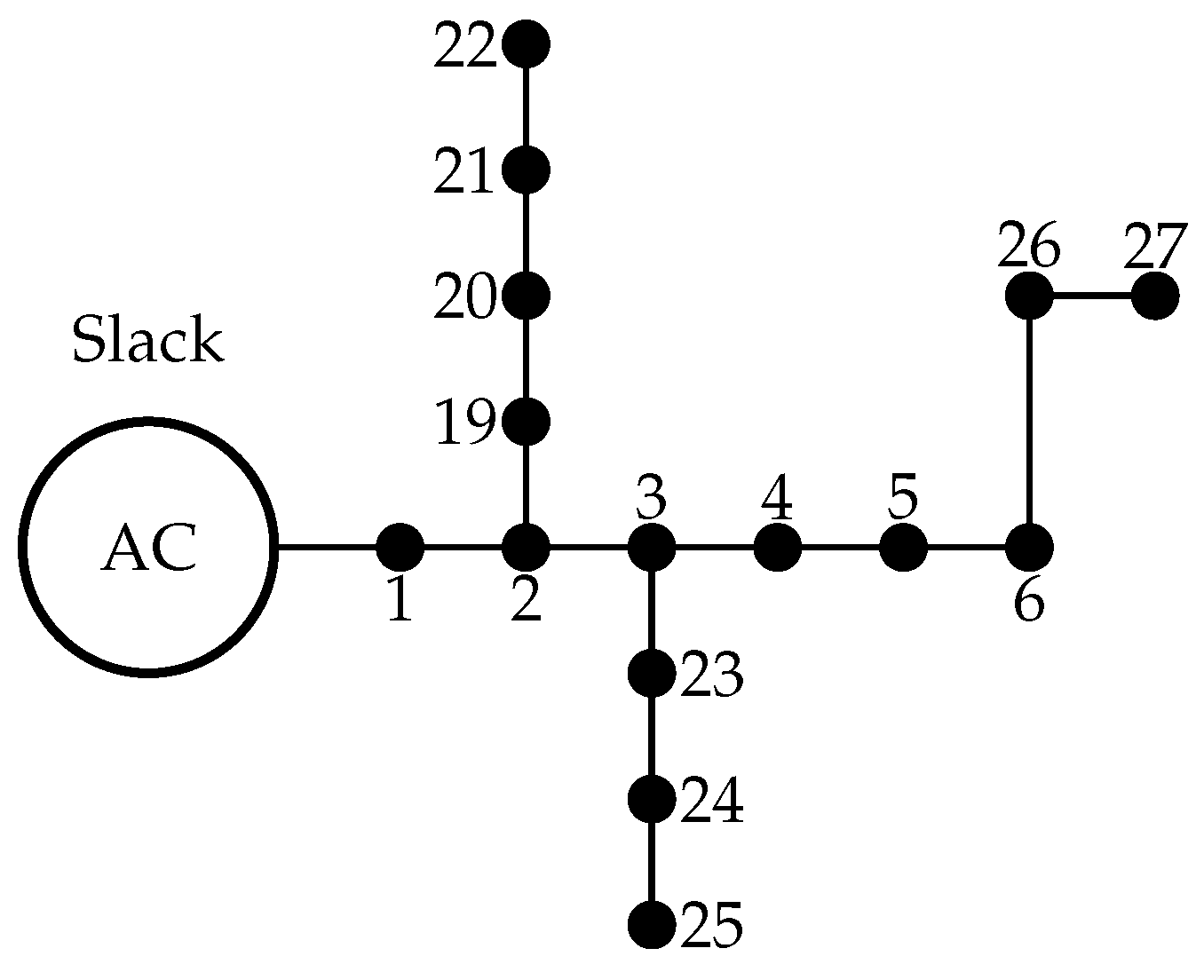
4.1. 15-Bus Test Feeder
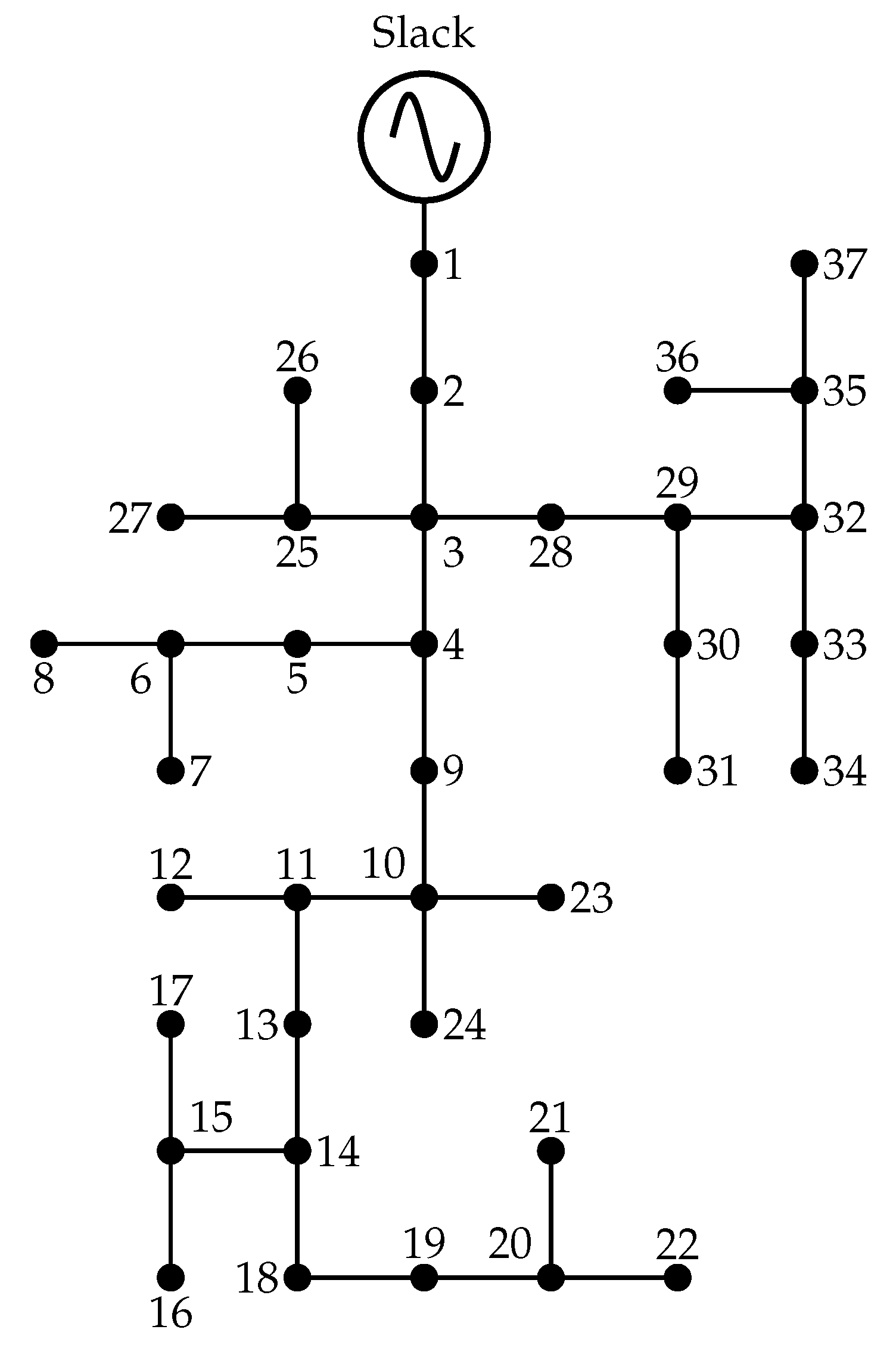
4.2. IEEE 37-Bus Test Feeder
5. Computational Validation
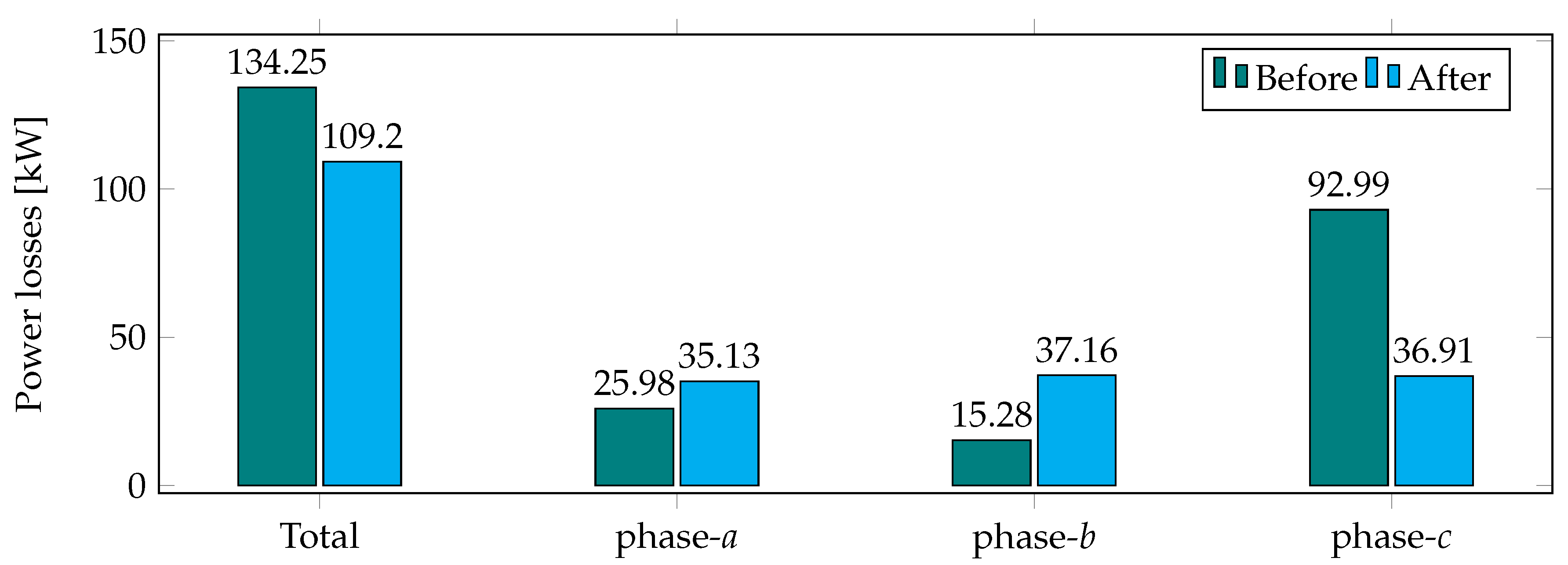
5.1. Analysis of the Peak Load Condition
5.2. Minimization of Annual Energy Loss Costs
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CBGA | Chu & Beasley genetic algorithm |
| VSA | Vortex search algorithm |
| MINLP | Mixed-integer nonlinear programming |
| CREG | Energy and Gas Regulation Commission |
| SCA | Sine-cosine algorithm |
| BHO | Black-hole optimizer |
Nomenclature
| Time period during which the power demands remain constant (h). | |
| Angle of the voltage at node k in phase f at time period t (rad). | |
| Angle of the voltage at node m in phase g at time period t (rad). | |
| Complex three-phase current at demand node d in time period t (A). | |
| Complex demanded three-phase current at k in time period t (A). | |
| Complex demanded current at node k in phase a at time period t (A). | |
| Complex demanded current at node k in phase b at time period t (A). | |
| Complex demanded current at node k in phase c at time period t (A). | |
| Complex three-phase current at source node s in time period t (A). | |
| Apparent power losses of the network (VA) | |
| Complex demanded three-phase power at k in time period t (VA). | |
| Complex demanded power at node k in phase a at time period t (VA). | |
| Complex demanded power at node k between phases a and b at time period | |
| t (VA). | |
| Complex demanded power at node k in phase b at time period t (VA). | |
| Complex demanded power at node k between phases b and c at time period | |
| t (VA). | |
| Complex demanded power at node k in phase c at time period t (VA). | |
| Complex demanded power at node k between phases c and a at time period | |
| t (VA). | |
| Complex three-phase voltage at demand node d in time period t (V). | |
| Complex demanded three-phase voltage at k in time period t (V). | |
| Complex demanded voltage at node k in phase a at time period t (V). | |
| Complex demanded voltage at node k in phase b at time period t (V). | |
| Complex demanded voltage at node k in phase c at time period t (V). | |
| Complex three-phase voltage at source node s in time period t (V). | |
| Three-phase submatrix of the admittance nodal matrix that relates demand | |
| nodes among them (S). | |
| Three-phase submatrix of the admittance nodal matrix that relates demand | |
| and source nodes among them (S). | |
| Three-phase submatrix of the admittance nodal matrix that relates source | |
| and demand nodes among them (S). | |
| Three-phase submatrix of the admittance nodal matrix that relates source | |
| nodes among them (S). | |
| Set containing all the phases of the system. | |
| Set containing all the nodes of the network. | |
| Set containing all the time periods of the operation horizon. | |
| Matrix to calculate the line-to-line voltages from line-to-ground voltages. | |
| Matrix of demand rotation. | |
| Angle of the admittance that relates node k at phase f with node m at phase | |
| g (rad). | |
| Average cost of energy (US$/kWh). | |
| Cost of daily energy losses (US$/day). | |
| Active power generated by source s connected at node k in phase f at time | |
| period t (W). | |
| Active power demanded at node k in phase g at time | |
| period t (W). | |
| Reactive power generated by source s connected at node k in phase f at time | |
| period t (var). | |
| Reactive power demanded at node k in phase g at time | |
| period t (var). | |
| Maximum voltage regulation bound (V). | |
| Minimum voltage regulation bound (V). | |
| Voltage magnitude at node k in phase f at time period t (V). | |
| Voltage magnitude at node m in phase g at time period t (V). | |
| Binary variable that defines the connection of the demand in node k at f in | |
| phase g. | |
| Magnitude of admittance that relates node k at phase f with node m at | |
| phase g (S). |
References
- Temiz, A.; Almalki, A.M.; Kahraman, Ö.; Alshahrani, S.S.; Sönmez, E.B.; Almutairi, S.S.; Nadar, A.; Smiai, M.S.; Alabduljabbar, A.A. Investigation of MV Distribution Networks with High-Penetration Distributed PVs: Study for an Urban Area. Energy Procedia 2017, 141, 517–524. [Google Scholar] [CrossRef]
- Cortés-Caicedo, B.; Avellaneda-Gómez, L.S.; Montoya, O.D.; Alvarado-Barrios, L.; Chamorro, H.R. Application of the Vortex Search Algorithm to the Phase-Balancing Problem in Distribution Systems. Energies 2021, 14, 1282. [Google Scholar] [CrossRef]
- Aboshady, F.M.; Thomas, D.W.P.; Sumner, M. A Wideband Single End Fault Location Scheme for Active Untransposed Distribution Systems. IEEE Trans. Smart Grid 2020, 11, 2115–2124. [Google Scholar] [CrossRef]
- Arias, J.; Calle, M.; Turizo, D.; Guerrero, J.; Candelo-Becerra, J. Historical Load Balance in Distribution Systems Using the Branch and Bound Algorithm. Energies 2019, 12, 1219. [Google Scholar] [CrossRef] [Green Version]
- Montoya, O.D.; Gil-González, W.; Hernández, J.C. Efficient Operative Cost Reduction in Distribution Grids Considering the Optimal Placement and Sizing of D-STATCOMs Using a Discrete-Continuous VSA. Appl. Sci. 2021, 11, 2175. [Google Scholar] [CrossRef]
- Cabrera, J.B.; Veiga, M.F.; Morales, D.X.; Medina, R. Reducing Power Losses in Smart Grids with Cooperative Game Theory. In Advanced Communication and Control Methods for Future Smartgrids; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef] [Green Version]
- Ogunsina, A.A.; Petinrin, M.O.; Petinrin, O.O.; Offornedo, E.N.; Petinrin, J.O.; Asaolu, G.O. Optimal distributed generation location and sizing for loss minimization and voltage profile optimization using ant colony algorithm. SN Appl. Sci. 2021, 3. [Google Scholar] [CrossRef]
- Hooshmand, R.; Soltani, S. Simultaneous optimization of phase balancing and reconfiguration in distribution networks using BF-NM algorithm. Int. J. Electr. Power Energy Syst. 2012, 41, 76–86. [Google Scholar] [CrossRef]
- Al-Sumaiti, A.S.; Kavousi-Fard, A.; Salama, M.; Pourbehzadi, M.; Reddy, S.; Rasheed, M.B. Economic Assessment of Distributed Generation Technologies: A Feasibility Study and Comparison with the Literature. Energies 2020, 13, 2764. [Google Scholar] [CrossRef]
- Rajaram, R.; Kumar, K.S.; Rajasekar, N. Power system reconfiguration in a radial distribution network for reducing losses and to improve voltage profile using modified plant growth simulation algorithm with Distributed Generation (DG). Energy Rep. 2015, 1, 116–122. [Google Scholar] [CrossRef] [Green Version]
- Grigoraș, G.; Neagu, B.C.; Gavrilaș, M.; Triștiu, I.; Bulac, C. Optimal Phase Load Balancing in Low Voltage Distribution Networks Using a Smart Meter Data-Based Algorithm. Mathematics 2020, 8, 549. [Google Scholar] [CrossRef] [Green Version]
- Boroujeni, S.T.; Mardaneh, M.; Hashemi, Z. A Dynamic and Heuristic Phase Balancing Method for LV Feeders. Appl. Comput. Intell. Soft Comput. 2016, 2016, 1–8. [Google Scholar] [CrossRef]
- Granada-Echeverri, M.; Gallego-Rendón, R.A.; López-Lezama, J.M. Optimal Phase Balancing Planning for Loss Reduction in Distribution Systems using a Specialized Genetic Algorithm. Ing. Cienc. 2012, 8, 121–140. [Google Scholar] [CrossRef] [Green Version]
- Montoya, O.D.; Grajales, A.; Hincapié, R.A.; Granada, M. A new approach to solve the distribution system planning problem considering automatic reclosers. Ingeniare. Rev. Chil. Ing. 2017, 25, 415–429. [Google Scholar] [CrossRef] [Green Version]
- Garcés, A.; Castaño, J.C.; Rios, M.A. Phase Balancing in Power Distribution Grids: A Genetic Algorithm with a Group-Based Codification. In Energy Systems; Springer International Publishing: Cham, Switzerland, 2020; pp. 325–342. [Google Scholar] [CrossRef]
- Darmawan, I.; Kuspriyanto, Y.; Priyan, M.I.J. Integration of Genetic and Tabu Search algorithm based load balancing for heterogenous grid computing. In Proceedings of the 2013 International Conference on Computer, Control, Informatics and Its Applications (IC3INA), Jakarta, Indonesia, 19–21 November 2013. [Google Scholar] [CrossRef]
- Li, D.; Qiang, R.; Yoon, S.W. Balanced Adaptive Tabu Search Algorithm to Optimize Dual-gantry Pick-and-place Assembly. Procedia Manuf. 2017, 11, 1892–1899. [Google Scholar] [CrossRef]
- Sim, K.M.; Sun, W.H. Ant colony optimization for routing and load-balancing: Survey and new directions. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2003, 33, 560–572. [Google Scholar] [CrossRef]
- Keskinturk, T.; Yildirim, M.B.; Barut, M. An ant colony optimization algorithm for load balancing in parallel machines with sequence-dependent setup times. Comput. Oper. Res. 2012, 39, 1225–1235. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.Y.; Chen, C.S.; Lin, C.H.; Kang, M.S.; Chuang, H.J.; Huang, C.W. Three-phase balancing of distribution feeders using immune algorithm. IET Gener. Transm. Distrib. 2008, 2, 383. [Google Scholar] [CrossRef]
- Garces, A.; Gil-González, W.; Montoya, O.D.; Chamorro, H.R.; Alvarado-Barrios, L. A Mixed-Integer Quadratic Formulation of the Phase-Balancing Problem in Residential Microgrids. Appl. Sci. 2021, 11, 1972. [Google Scholar] [CrossRef]
- Amon, D.A. A Modified Bat Algorithm for Power Loss Reduction in Electrical Distribution System. Telkomnika Indones. J. Electr. Eng. 2015, 14. [Google Scholar] [CrossRef]
- Toma, N.; Ivanov, O.; Neagu, B.; Gavrila, M. A PSO Algorithm for Phase Load Balancing in Low Voltage Distribution Networks. In Proceedings of the 2018 International Conference and Exposition on Electrical Furthermore, Power Engineering (EPE), Iasi, Romania, 18–19 October 2018. [Google Scholar] [CrossRef]
- Schweickardt, G.; Alvarez, J.M.G.; Casanova, C. Metaheuristics approaches to solve combinatorial optimization problems in distribution power systems. An application to Phase Balancing in low voltage three-phase networks. Int. J. Electr. Power Energy Syst. 2016, 76, 1–10. [Google Scholar] [CrossRef]
- Sathiskumar, M.; Kumar, A.N.; Lakshminarasimman, L.; Thiruvenkadam, S. A self adaptive hybrid differential evolution algorithm for phase balancing of unbalanced distribution system. Int. J. Electr. Power Energy Syst. 2012, 42, 91–97. [Google Scholar] [CrossRef]
- Zhu, J.; Bilbro, G.; Chow, M.Y. Phase balancing using simulated annealing. IEEE Trans. Power Syst. 1999, 14, 1508–1513. [Google Scholar] [CrossRef] [Green Version]
- Montoya, O.D.; Gil-González, W.; Orozco-Henao, C. Vortex search and Chu-Beasley genetic algorithms for optimal location and sizing of distributed generators in distribution networks: A novel hybrid approach. Eng. Sci. Technol. Int. J. 2020, 23, 1351–1363. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W. On the numerical analysis based on successive approximations for power flow problems in AC distribution systems. Electr. Power Syst. Res. 2020, 187, 106454. [Google Scholar] [CrossRef]
- Montoya, O.D.; Giraldo, J.S.; Grisales-Noreña, L.F.; Chamorro, H.R.; Alvarado-Barrios, L. Accurate and Efficient Derivative-Free Three-Phase Power Flow Method for Unbalanced Distribution Networks. Computation 2021, 9, 61. [Google Scholar] [CrossRef]
- Da Cunha, A.S.; Peixoto, F.C.; Prata, D.M. Robust data reconciliation in chemical reactors. Comput. Chem. Eng. 2021, 145, 107170. [Google Scholar] [CrossRef]
- Sereeter, B.; Vuik, K.; Witteveen, C. Newton Power Flow Methods for Unbalanced Three-Phase Distribution Networks. Energies 2017, 10, 1658. [Google Scholar] [CrossRef]
- Shen, T.; Li, Y.; Xiang, J. A Graph-Based Power Flow Method for Balanced Distribution Systems. Energies 2018, 11, 511. [Google Scholar] [CrossRef] [Green Version]
- Oliveira-De-Jesus, P.M.D.; Rojas, A.A.; Gonzalez-Longatt, F.M. Unbalanced Power Flow Analysis in Distribution Systems Using TRX Matrix: Implementation Using DIgSILENT Programming Language. In PowerFactory Applications for Power System Analysis; Springer International Publishing: Cham, Switzerland, 2014; pp. 85–110. [Google Scholar] [CrossRef]
- Doğan, B.; Ölmez, T. Vortex search algorithm for the analog active filter component selection problem. AEU Int. J. Electron. Commun. 2015, 69, 1243–1253. [Google Scholar] [CrossRef]
- Li, P.; Zhao, Y. A quantum-inspired vortex search algorithm with application to function optimization. Nat. Comput. 2018, 18, 647–674. [Google Scholar] [CrossRef]
- Montoya, O.D.; Molina-Cabrera, A.; Chamorro, H.R.; Alvarado-Barrios, L.; Rivas-Trujillo, E. A Hybrid Approach Based on SOCP and the Discrete Version of the SCA for Optimal Placement and Sizing DGs in AC Distribution Networks. Electronics 2020, 10, 26. [Google Scholar] [CrossRef]
- Deeb, H.; Sarangi, A.; Mishra, D.; Sarangi, S.K. Improved Black Hole optimization algorithm for data clustering. J. King Saud Univ. Comput. Inf. Sci. 2020. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Grisales-Noreña, L.; Orozco-Henao, C.; Serra, F. Economic Dispatch of BESS and Renewable Generators in DC Microgrids Using Voltage-Dependent Load Models. Energies 2019, 12, 4494. [Google Scholar] [CrossRef] [Green Version]
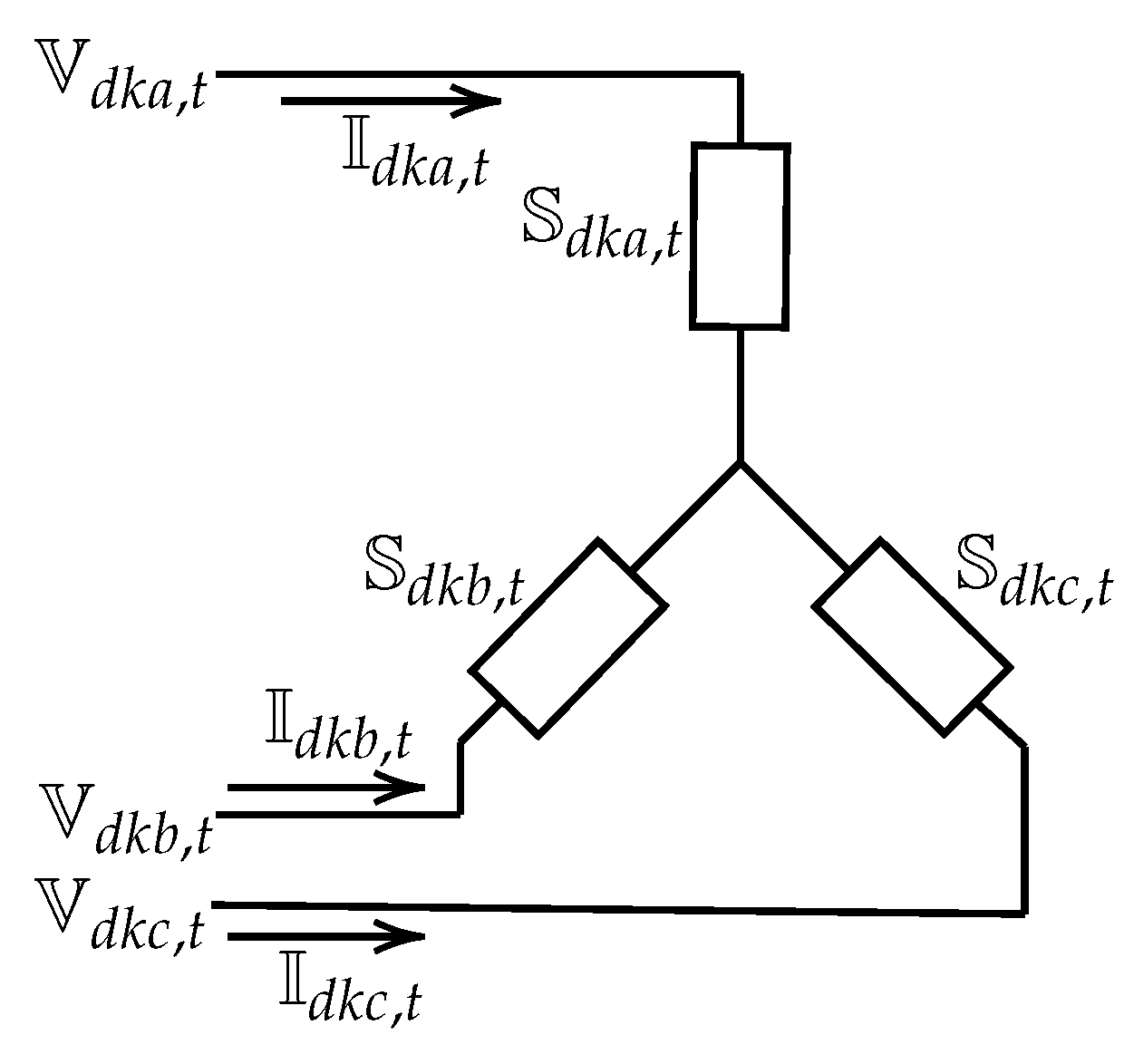
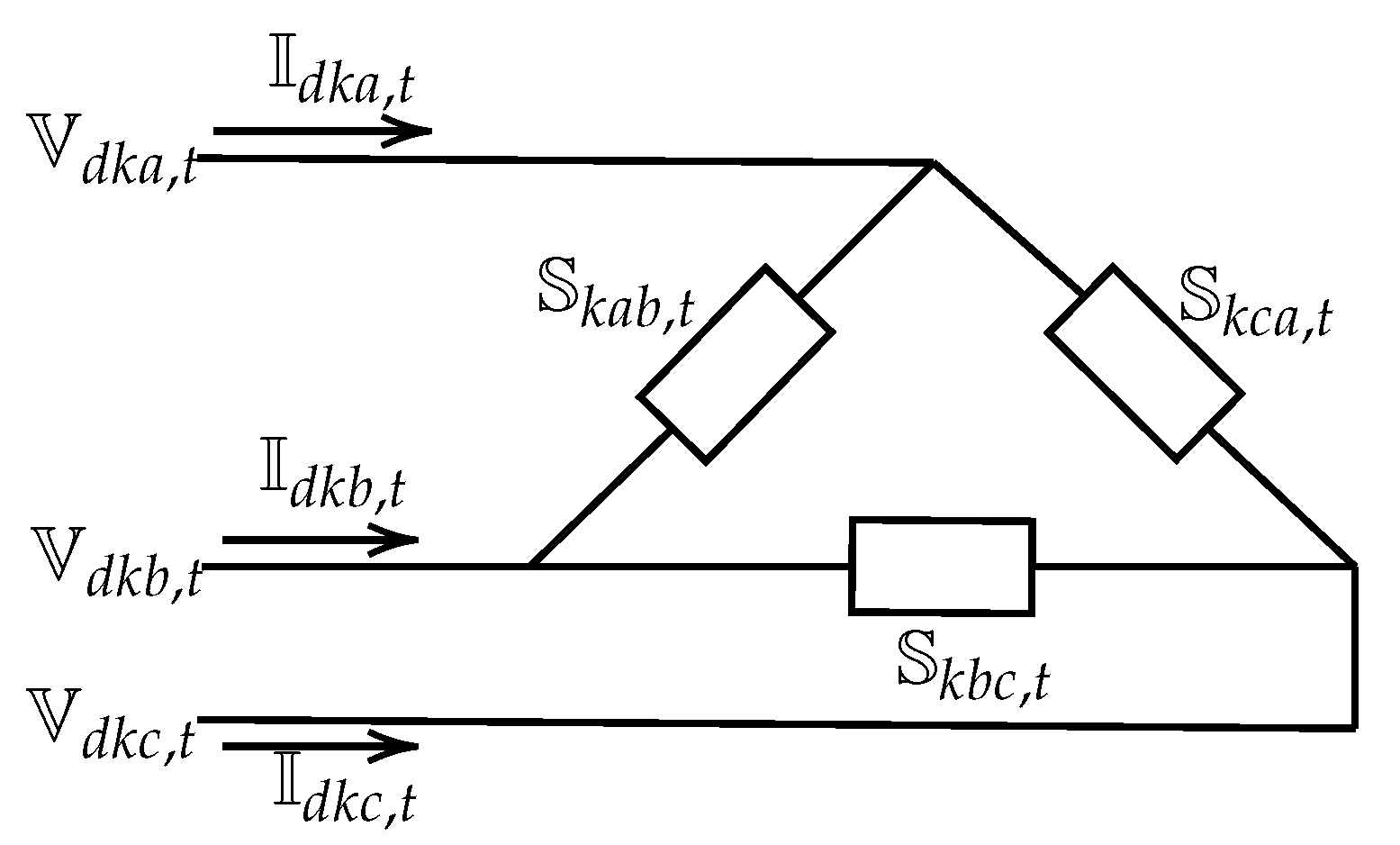


| Connection Type | Phases | Sequence |
|---|---|---|
| 1 | ABC | |
| 2 | CAB | No change |
| 3 | BCA | |
| 4 | ACB | |
| 5 | BAC | Change |
| 6 | CBA |
| Line | Node i | Node j | Cond. | Length (ft) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 1 | 603 | 0 | 0 | 725 | 300 | 1100 | 600 |
| 2 | 2 | 3 | 2 | 776 | 480 | 220 | 720 | 600 | 1040 | 558 |
| 3 | 3 | 4 | 3 | 825 | 2250 | 1610 | 0 | 0 | 0 | 0 |
| 4 | 4 | 5 | 3 | 1182 | 700 | 225 | 0 | 0 | 996 | 765 |
| 5 | 5 | 6 | 4 | 350 | 0 | 0 | 820 | 700 | 1220 | 1050 |
| 6 | 2 | 7 | 5 | 691 | 2500 | 1200 | 0 | 0 | 0 | 0 |
| 7 | 7 | 8 | 6 | 539 | 0 | 0 | 960 | 540 | 0 | 0 |
| 8 | 8 | 9 | 6 | 225 | 0 | 0 | 0 | 0 | 2035 | 1104 |
| 9 | 9 | 10 | 6 | 1050 | 1519 | 1250 | 1259 | 1200 | 0 | 0 |
| 10 | 3 | 11 | 3 | 837 | 0 | 0 | 259 | 126 | 1486 | 1235 |
| 11 | 11 | 12 | 4 | 414 | 0 | 0 | 0 | 0 | 1924 | 1857 |
| 12 | 12 | 13 | 5 | 925 | 1670 | 486 | 0 | 0 | 726 | 509 |
| 13 | 6 | 14 | 4 | 386 | 0 | 0 | 850 | 752 | 1450 | 1100 |
| 14 | 14 | 15 | 2 | 401 | 486 | 235 | 887 | 722 | 0 | 0 |
| Conductor | Impedance Matrix (mi) | ||
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| Line | Node i | Node j | Cond. | Length (ft) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 1 | 1850 | 140 | 70 | 140 | 70 | 350 | 175 |
| 2 | 2 | 3 | 2 | 960 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 3 | 24 | 4 | 400 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 3 | 27 | 3 | 360 | 0 | 0 | 0 | 0 | 85 | 40 |
| 5 | 3 | 4 | 2 | 1320 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 4 | 5 | 4 | 240 | 0 | 0 | 0 | 0 | 42 | 21 |
| 7 | 4 | 9 | 3 | 600 | 0 | 0 | 0 | 0 | 85 | 40 |
| 8 | 5 | 6 | 3 | 280 | 42 | 21 | 0 | 0 | 0 | 0 |
| 9 | 6 | 7 | 4 | 200 | 42 | 21 | 42 | 21 | 42 | 21 |
| 10 | 6 | 8 | 4 | 280 | 42 | 21 | 0 | 0 | 0 | 0 |
| 11 | 9 | 10 | 3 | 200 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 10 | 23 | 3 | 600 | 0 | 0 | 85 | 40 | 0 | 0 |
| 13 | 10 | 11 | 3 | 320 | 0 | 0 | 0 | 0 | 0 | 0 |
| 14 | 11 | 13 | 3 | 320 | 85 | 40 | 0 | 0 | 0 | 0 |
| 15 | 11 | 12 | 4 | 320 | 0 | 0 | 0 | 0 | 42 | 21 |
| 16 | 13 | 14 | 3 | 560 | 0 | 0 | 0 | 0 | 42 | 21 |
| 17 | 14 | 18 | 3 | 640 | 140 | 70 | 0 | 0 | 0 | 0 |
| 18 | 14 | 15 | 4 | 520 | 0 | 0 | 0 | 0 | 0 | 0 |
| 19 | 15 | 16 | 4 | 200 | 0 | 0 | 0 | 0 | 85 | 40 |
| 20 | 15 | 17 | 4 | 1280 | 0 | 0 | 42 | 21 | 0 | 0 |
| 21 | 18 | 19 | 3 | 400 | 126 | 62 | 0 | 0 | 0 | 0 |
| 22 | 19 | 20 | 3 | 400 | 0 | 0 | 0 | 0 | 0 | 0 |
| 23 | 20 | 22 | 3 | 400 | 0 | 0 | 0 | 0 | 42 | 21 |
| 24 | 20 | 21 | 4 | 200 | 0 | 0 | 0 | 0 | 85 | 40 |
| 25 | 24 | 26 | 4 | 320 | 8 | 4 | 85 | 40 | 0 | 0 |
| 26 | 24 | 25 | 4 | 240 | 0 | 0 | 0 | 0 | 85 | 40 |
| 27 | 27 | 28 | 3 | 520 | 0 | 0 | 0 | 0 | 0 | 0 |
| 28 | 28 | 29 | 4 | 80 | 17 | 8 | 21 | 10 | 0 | 0 |
| 29 | 28 | 31 | 3 | 800 | 0 | 0 | 0 | 0 | 85 | 40 |
| 30 | 29 | 30 | 4 | 520 | 85 | 40 | 0 | 0 | 0 | 0 |
| 31 | 31 | 34 | 4 | 920 | 0 | 0 | 0 | 0 | 0 | 0 |
| 32 | 31 | 32 | 3 | 600 | 0 | 0 | 0 | 0 | 0 | 0 |
| 33 | 32 | 33 | 4 | 280 | 0 | 0 | 42 | 21 | 0 | 0 |
| 34 | 34 | 36 | 4 | 760 | 0 | 0 | 42 | 21 | 0 | 0 |
| 35 | 34 | 35 | 4 | 120 | 0 | 0 | 140 | 70 | 21 | 10 |
| Conductor | Impedance Matrix (mi) | ||
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| Method | Solution | Losses (kW) | Reduction (%) | Proc. Time (s) |
|---|---|---|---|---|
| Benchmark case | 134.2472 | 0.00 | - | |
| Classical CBGA | 109.2236 | 18.64 | 6.9435 | |
| BHO | 110.0025 | 18.06 | 8.4850 | |
| SCA | 109.3973 | 18.51 | 34.2865 | |
| VSA | 109.3217 | 18.57 | 39.6831 | |
| Improved CBGA | 109.1980 | 18.66 | 2.0762 |
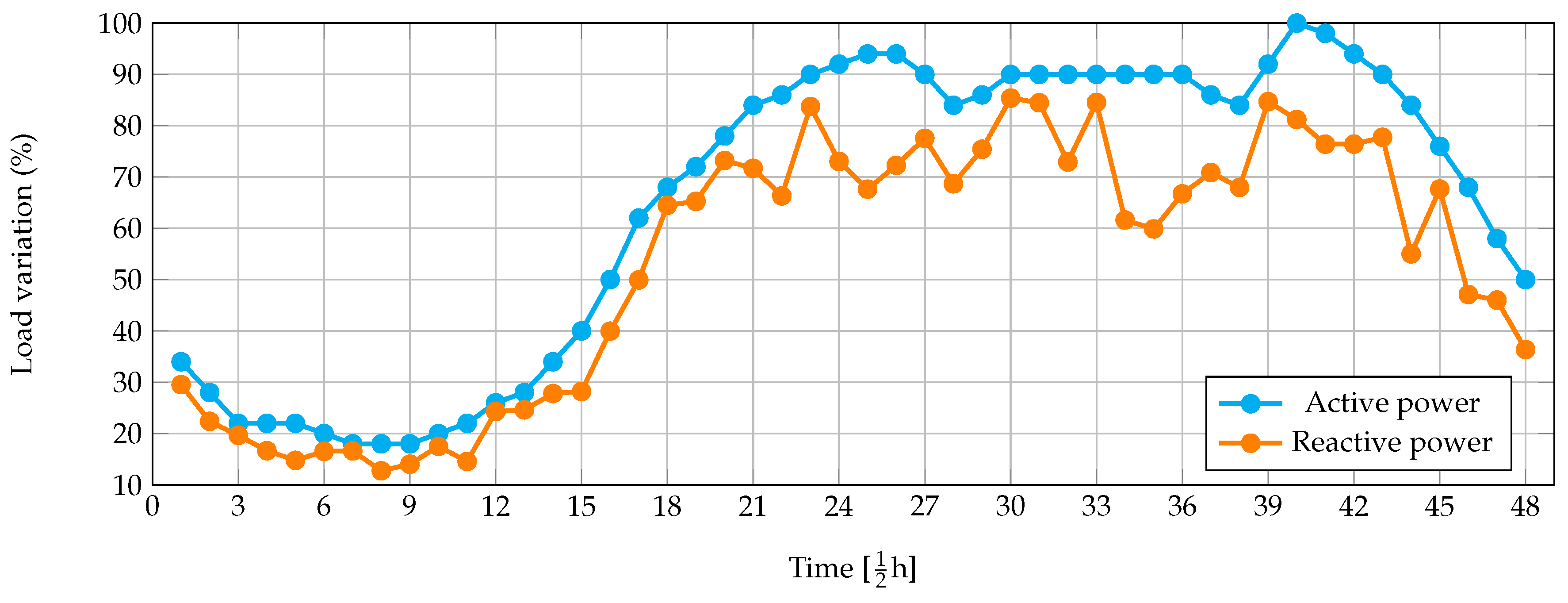
| Period | Act. (pu) | React. (pu) | Period | Act. (pu) | React. (pu) |
|---|---|---|---|---|---|
| 1 | 0.1700 | 0.1477 | 25 | 0.4700 | 0.3382 |
| 2 | 0.1400 | 0.1119 | 26 | 0.4700 | 0.3614 |
| 3 | 0.1100 | 0.0982 | 27 | 0.4500 | 0.3877 |
| 4 | 0.1100 | 0.0833 | 28 | 0.4200 | 0.3434 |
| 5 | 0.1100 | 0.0739 | 29 | 0.4300 | 0.3771 |
| 6 | 0.1000 | 0.0827 | 30 | 0.4500 | 0.4269 |
| 7 | 0.0900 | 0.0831 | 31 | 0.4500 | 0.4224 |
| 8 | 0.0900 | 0.0637 | 32 | 0.4500 | 0.3647 |
| 9 | 0.0900 | 0.0702 | 33 | 0.4500 | 0.4226 |
| 10 | 0.1000 | 0.0875 | 34 | 0.4500 | 0.3081 |
| 11 | 0.1100 | 0.0728 | 35 | 0.4500 | 0.2994 |
| 12 | 0.1300 | 0.1214 | 36 | 0.4500 | 0.3336 |
| 13 | 0.1400 | 0.1231 | 37 | 0.4300 | 0.3543 |
| 14 | 0.1700 | 0.1390 | 38 | 0.4200 | 0.3399 |
| 15 | 0.2000 | 0.1410 | 39 | 0.4600 | 0.4234 |
| 16 | 0.2500 | 0.1998 | 40 | 0.5000 | 0.4061 |
| 17 | 0.3100 | 0.2497 | 41 | 0.4900 | 0.3820 |
| 18 | 0.3400 | 0.3224 | 42 | 0.4700 | 0.3820 |
| 19 | 0.3600 | 0.3263 | 43 | 0.4500 | 0.3887 |
| 20 | 0.3900 | 0.3661 | 44 | 0.4200 | 0.2751 |
| 21 | 0.4200 | 0.3585 | 45 | 0.3800 | 0.3383 |
| 22 | 0.4300 | 0.3316 | 46 | 0.3400 | 0.2355 |
| 23 | 0.4500 | 0.4187 | 47 | 0.2900 | 0.2301 |
| 24 | 0.4600 | 0.3652 | 48 | 0.2500 | 0.1818 |
| Sol. Number | Solution | Losses (US$) |
|---|---|---|
| Benchmark case | 43,226.9376 | |
| Solution 1 | 35,105.2156 | |
| Solution 2 | 35,127.0109 | |
| Solution 3 | 35,133.1683 | |
| Solution 4 | 35,137.2049 | |
| Solution 5 | 35,140.4392 | |
| Solution 6 | 35,154.0686 | |
| Solution 7 | 35,157.9344 | |
| Solution 8 | 35,169.6288 | |
| Solution 9 | 35,179.4097 | |
| Solution 10 | 35,180.3742 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montoya, O.D.; Molina-Cabrera, A.; Grisales-Noreña, L.F.; Hincapié, R.A.; Granada, M. Improved Genetic Algorithm for Phase-Balancing in Three-Phase Distribution Networks: A Master-Slave Optimization Approach. Computation 2021, 9, 67. https://0-doi-org.brum.beds.ac.uk/10.3390/computation9060067
Montoya OD, Molina-Cabrera A, Grisales-Noreña LF, Hincapié RA, Granada M. Improved Genetic Algorithm for Phase-Balancing in Three-Phase Distribution Networks: A Master-Slave Optimization Approach. Computation. 2021; 9(6):67. https://0-doi-org.brum.beds.ac.uk/10.3390/computation9060067
Chicago/Turabian StyleMontoya, Oscar Danilo, Alexander Molina-Cabrera, Luis Fernando Grisales-Noreña, Ricardo Alberto Hincapié, and Mauricio Granada. 2021. "Improved Genetic Algorithm for Phase-Balancing in Three-Phase Distribution Networks: A Master-Slave Optimization Approach" Computation 9, no. 6: 67. https://0-doi-org.brum.beds.ac.uk/10.3390/computation9060067








