Appendix A. Parabolic Problem
We consider the parabolic problem in perforated domain
:
with the following boundary conditions
and initial condition
in
for
.
For approximation by time, we use an implicit approximation with a time step
. We have the following fine grid approximation on
using the IPDG method: find
such that
where
and
is the solution from the previous time step.
The matrix form is following
for
and with
In the multiscale method, we construct a multiscale space similar to the Laplace problem and generate a projection matrix
Finally, we obtain the following coarse grid system for a parabolic problem
where
and calculation of the coarse-scale solution, we reconstruct the fine-scale solution
.
Numerical results. We consider the parabolic problem with . We set the following boundary conditions:
Case 1. Homogeneous boundary conditions on perforations:
and perform simulation for
.
Case 2. Non-homogeneous boundary conditions on perforations:
and perform simulation for
.
We consider three different , 25, and 100. We set zero initial condition and perform a simulation with 40 time steps.
Figure A1.
Parabolic problem with for different time layers with , and 40 (from left to right). Case 1 (homogeneous boundary conditions). Top: Reference solution (). Bottom: Multiscale solution with 12 multiscale basis functions, for , for , for (, , ).
Figure A1.
Parabolic problem with for different time layers with , and 40 (from left to right). Case 1 (homogeneous boundary conditions). Top: Reference solution (). Bottom: Multiscale solution with 12 multiscale basis functions, for , for , for (, , ).
Table A1.
Parabolic problem with , and 100. Case 1 (homogeneous boundary conditions). Relative and error in %. .
Table A1.
Parabolic problem with , and 100. Case 1 (homogeneous boundary conditions). Relative and error in %. .
| M | | | | |
|---|
| | | | | |
|---|
| , |
| 1 | 200 | 86.14 | 99.75 | 101.6 | 134.7 | 83.13 | 157.8 |
| 2 | 300 | 85.57 | 99.22 | 92.55 | 124.4 | 67.41 | 130.3 |
| 4 | 500 | 18.58 | 34.51 | 9.460 | 32.42 | 5.393 | 31.97 |
| 6 | 700 | 8.323 | 28.86 | 5.001 | 27.98 | 3.436 | 27.71 |
| 8 | 900 | 4.445 | 20.53 | 2.774 | 20.93 | 1.959 | 20.08 |
| 12 | 1300 | 2.870 | 14.32 | 1.734 | 13.33 | 1.164 | 13.10 |
| 16 | 1700 | 2.784 | 13.96 | 1.675 | 12.79 | 1.109 | 12.52 |
| 20 | 2100 | 2.693 | 13.28 | 1.635 | 12.06 | 1.076 | 11.84 |
| 24 | 2500 | 2.666 | 13.23 | 1.622 | 11.99 | 1.066 | 11.76 |
| 32 | 3300 | 2.625 | 13.09 | 1.604 | 11.79 | 1.058 | 11.56 |
Figure A2.
Parabolic problem with for different time layers with , and 40 (from left to right). Case 2 (non-homogeneous boundary conditions). Top: Reference solution (). Center: Multiscale solution with 12 multiscale basis functions without perforation basis functions, for , for , and for (, , ). Bottom: Multiscale solution with 12 multiscale basis functions with perforation basis functions, for , for , and for (, ).
Figure A2.
Parabolic problem with for different time layers with , and 40 (from left to right). Case 2 (non-homogeneous boundary conditions). Top: Reference solution (). Center: Multiscale solution with 12 multiscale basis functions without perforation basis functions, for , for , and for (, , ). Bottom: Multiscale solution with 12 multiscale basis functions with perforation basis functions, for , for , and for (, ).
Figure A3.
Parabolic problem with at the final time. Case 1 (left) and Case 2 (right): Relative error with a different number of multiscale basis functions.
Figure A3.
Parabolic problem with at the final time. Case 1 (left) and Case 2 (right): Relative error with a different number of multiscale basis functions.
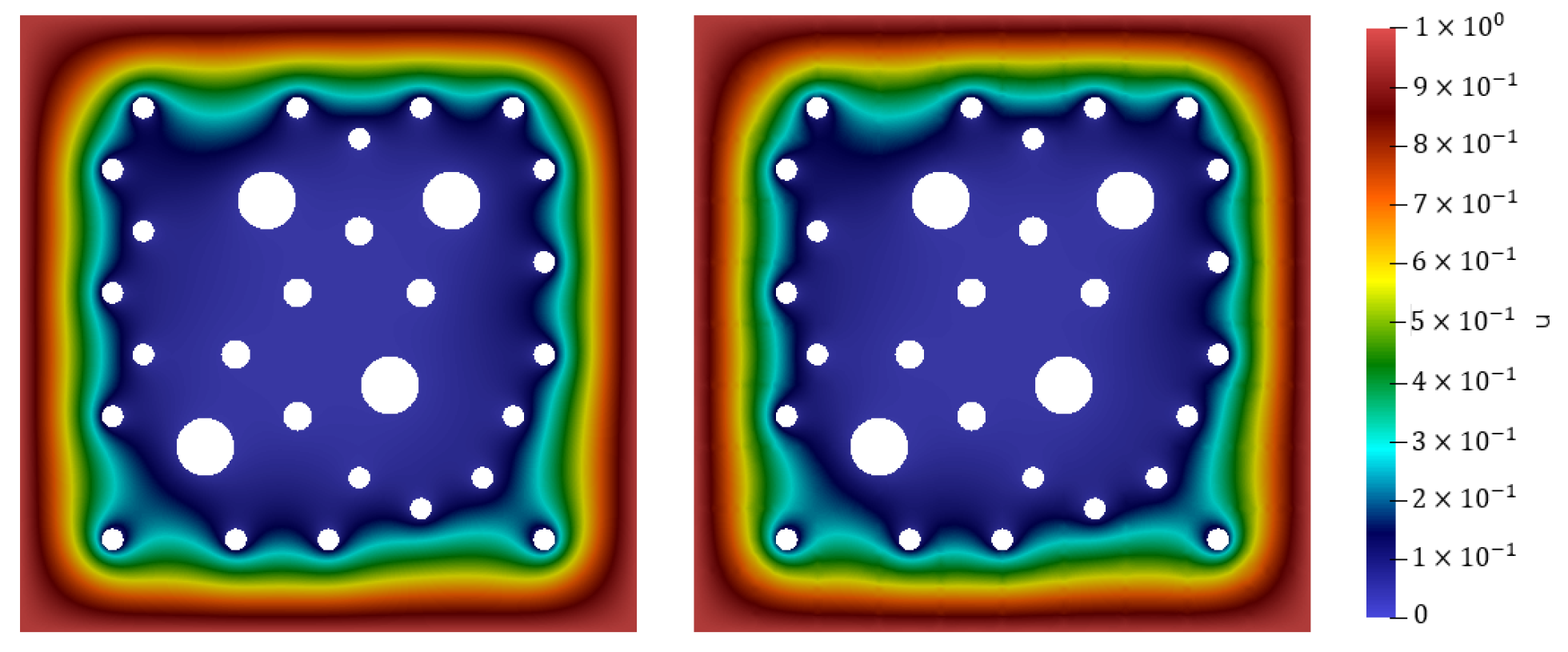
The reference and multiscale solutions at the different times (
with
, and 40) are presented in
Figure A1 for Case 1 and in
Figure A2 for Case 2. The multiscale solution is obtained using 12 multiscale basis functions (
). In the first row, there is a fine-scale solution with
. In the second row, there is a multiscale solution with
for
. In the third row, we give a multiscale solution with
for
in Case 2. We observe a bad multiscale approximation near the perforation boundary for Case 2 with
at final time, if a perforation boundary basis functions is not used to handle non-homogeneous boundary conditions. For
in Case 2, we observe a good multiscale solution with
at final time.
Table A2.
Parabolic problem with , and 100. Case 2 (non-homogeneous boundary conditions). Relative and error in %. = 85,230.
Table A2.
Parabolic problem with , and 100. Case 2 (non-homogeneous boundary conditions). Relative and error in %. = 85,230.
| M | | | | |
|---|
| | | | | |
|---|
| , |
| 1 | 200 | 91.97 | 100.0 | 88.25 | 106.2 | 87.32 | 113.5 |
| 2 | 300 | 84.84 | 98.29 | 79.71 | 107.8 | 80.87 | 119.0 |
| 4 | 500 | 13.88 | 79.31 | 17.52 | 146.2 | 31.49 | 209.5 |
| 6 | 700 | 9.709 | 74.94 | 15.97 | 148.1 | 27.40 | 228.8 |
| 8 | 900 | 8.124 | 72.15 | 14.66 | 147.7 | 22.90 | 240.5 |
| 12 | 1300 | 7.552 | 71.39 | 14.83 | 147.6 | 22.84 | 238.9 |
| 16 | 1700 | 7.330 | 68.91 | 14.40 | 146.1 | 22.90 | 238.7 |
| 20 | 2100 | 7.289 | 68.60 | 14.41 | 145.9 | 22.96 | 238.4 |
| 24 | 2500 | 7.280 | 68.49 | 14.42 | 145.8 | 22.99 | 238.2 |
| 32 | 3300 | 7.264 | 68.39 | 14.42 | 145.8 | 23.01 | 238.1 |
|
| 1 | 251 | 85.93 | 79.07 | 77.39 | 103.4 | 63.56 | 116.3 |
| 2 | 402 | 75.40 | 75.78 | 57.40 | 99.07 | 38.96 | 101.3 |
| 4 | 704 | 7.938 | 38.96 | 5.154 | 35.27 | 6.326 | 36.65 |
| 6 | 1006 | 4.084 | 29.37 | 2.857 | 27.33 | 2.897 | 26.93 |
| 8 | 1308 | 2.339 | 21.96 | 1.566 | 20.95 | 1.394 | 19.50 |
| 12 | 1776 | 1.289 | 14.29 | 0.819 | 13.35 | 0.742 | 12.92 |
| 16 | 2244 | 1.192 | 13.19 | 0.735 | 12.54 | 0.654 | 12.24 |
| 20 | 2644 | 1.129 | 12.19 | 0.701 | 11.78 | 0.619 | 11.59 |
| 24 | 3044 | 1.117 | 11.90 | 0.691 | 11.61 | 0.603 | 11.49 |
| 32 | 3844 | 1.093 | 11.59 | 0.677 | 11.36 | 0.588 | 11.28 |
Table A3.
Parabolic problem. Case 2 (non-homogeneous boundary conditions). Unstructured coarse grids. Relative and error in %. = 85,230.
Table A3.
Parabolic problem. Case 2 (non-homogeneous boundary conditions). Unstructured coarse grids. Relative and error in %. = 85,230.
| M | | Quasi-Structured | Unstructured |
|---|
| | | |
| 1 | 251 | 54.82 | 96.18 | 53.32 | 93.48 |
| 2 | 402 | 30.56 | 79.76 | 41.23 | 94.00 |
| 4 | 704 | 8.184 | 45.51 | 11.60 | 56.13 |
| 6 | 1006 | 4.889 | 34.72 | 6.561 | 41.29 |
| 8 | 1308 | 3.434 | 25.08 | 4.976 | 35.25 |
| 12 | 1776 | 3.944 | 23.14 | 3.725 | 27.85 |
| 16 | 2244 | 1.526 | 17.72 | 2.761 | 23.90 |
| 20 | 2644 | 1.209 | 16.25 | 2.063 | 21.00 |
| 24 | 3044 | 0.999 | 15.26 | 1.775 | 18.64 |
| 32 | 3844 | 0.803 | 14.43 | 1.429 | 16.74 |
The relative errors for parabolic problem (Case 1) between reference solution and multiscale solution for
, and 100 are shown in
Table A1 and in
Figure A3 (left picture). We have a good multiscale solution with nearly 1–2% of
error when we take 12 outer boundary multiscale basis functions.
Table A2 and
Figure A3 (right picture) present relative errors for Case 2. Similar to the previous results for the elliptic equation, we see large errors for
and can obtain a good multiscale solution when we take the sufficient number of multiscale basis functions with outer and perforation boundary multiscale basis functions. For example, if 12 multiscale basis functions (
) are taken, we have 7–22% of
errors for
and reduce errors to
when we add perforation boundary basis functions for
, and 100.
Table A3 shows results for non-homogeneous boundary conditions (Case 2) on quasi-structured and unstructured coarse grids with 100 local domains. We present results for
. Using 32 multiscale basis functions (
), we obtain similar results with less than
of
error for structured, quasi-structured, and unstructured coarse grids with 100 local domains with
(
of
= 85,230).
Appendix B. Thermoelasticity Problem
We consider the thermoelasticity problem in
that is described by a system of equations for temperature and displacement:
We consider Equation (
A2) with the following boundary conditions:
and initial condition
,
in
for
.
For the IPDG method on the fine grid
, we have the following variational formulation: find
such that
where
with
The matrix form is the following:
for
with
For the construction of the multiscale method for the thermoelasticity problem, we construct multiscale spaces for displacement and temperature, separately. Then, we generate projection matrices using multiscale basis functions
Finally, we construct the following coarse grid system for the thermoelasticity problem
where
After calculation of the coarse-scale solution , we reconstruct a fine-scale solution, and .
Numerical results. We consider the thermoelasticity problem with the following boundary conditions:
and on perforations, we set
Case 1. Non-homogeneous boundary condition for elasticity and homogeneous boundary condition for temperature on perforations:
and perform simulation for
.
Case 2. Homogeneous boundary condition for elasticity and non-homogeneous boundary condition for temperature on perforations:
and perform simulation for
.
We set , , , and . We set zero initial conditions for displacement and temperature and perform simulations with 40 time steps.
Figure A4.
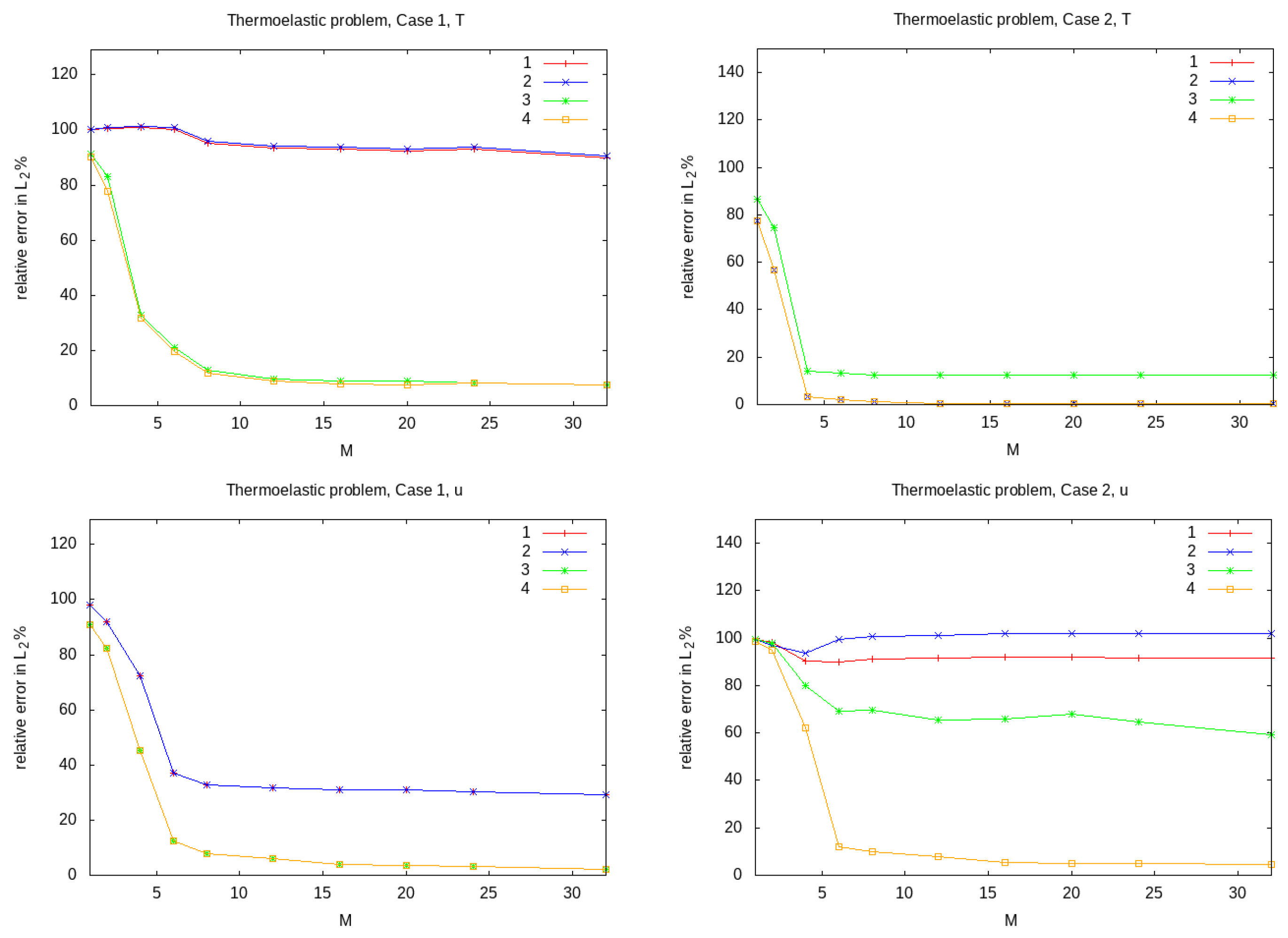
Thermoelasticity problem. Temperature (top) and Displacement (bottom). Case 1 and Case 2: Relative error with a different number of multiscale basis functions. (1) , and , ; (2) , , and ; (3) and , ; (4) and .
Figure A4.
Thermoelasticity problem. Temperature (top) and Displacement (bottom). Case 1 and Case 2: Relative error with a different number of multiscale basis functions. (1) , and , ; (2) , , and ; (3) and , ; (4) and .
Table A4 and
Figure A4 show relative errors for the thermoelasticity problem between a fine-grid and multiscale solution with different multiscale basis functions at the final time. In presented results, we tested different approaches for choosing
and
for the coupled process. Here,
are the number of multiscale basis functions for displacement (
) and temperature (
),
and
are the numbers of degrees of freedom for reference (fine-grid) and multiscale solution, and
and
are the
and
relative errors for
. Here,
with
and
for fine grid solution. For multiscale solution, we have
with
and
.
The results for quasi-structured and unstructured coarse grids with 100 local domains are presented in
Table A5. Numerical results are shown for multiscale space with outer and boundary basis functions (
) for Case 2. We obtain similar results with
and
for displacement and temperature
errors for all grids for
.
Figure A1 and
Figure A2 show the results of the fine-grid and multiscale solvers for the thermoelasticity problem at the final time on structured coarse grid. The temperature distribution is presented on the left figure, the displacement X and Y components are shown in the center and right figures. In presented results, we used 24 multiscale basis functions for displacement and temperature (
,
, and
). Reference solution with
for displacement,
for temperature is shown in the first row. Solution on a coarse grid using outer and perforation boundary multiscale basis functions with
for displacement and
for temperature is shown in the second row.
Table A4.
Thermoelasticity problem. Case 1 and Case 2. . Relative and error in %. .
Table A4.
Thermoelasticity problem. Case 1 and Case 2. . Relative and error in %. .
| M | | | Case 1 | Case 2 |
|---|
| | | | | | | |
| , and , |
| 1 | 300 | 200 | 98.00 | 99.98 | 100.0 | 100.0 | 99.32 | 98.98 | 86.48 | 105.9 |
| 2 | 500 | 300 | 92.01 | 98.38 | 100.6 | 100.4 | 98.04 | 97.07 | 74.55 | 106.3 |
| 4 | 900 | 500 | 72.44 | 93.63 | 100.9 | 98.37 | 90.47 | 73.54 | 14.16 | 142.4 |
| 6 | 1300 | 700 | 36.91 | 87.77 | 100.3 | 93.44 | 90.01 | 55.30 | 13.32 | 143.3 |
| 8 | 1700 | 900 | 32.73 | 85.34 | 95.06 | 87.08 | 91.23 | 50.41 | 12.36 | 143.4 |
| 12 | 2500 | 1300 | 31.88 | 84.32 | 93.31 | 85.43 | 91.41 | 48.40 | 12.25 | 142.2 |
| 16 | 3300 | 1700 | 31.03 | 83.99 | 93.04 | 85.05 | 91.85 | 47.36 | 12.26 | 142.1 |
| 20 | 4100 | 2100 | 30.86 | 83.82 | 92.43 | 84.44 | 91.79 | 47.07 | 12.28 | 142.0 |
| 24 | 4900 | 2500 | 30.37 | 84.07 | 92.89 | 84.64 | 91.69 | 47.56 | 12.30 | 141.9 |
| 32 | 6500 | 3300 | 29.31 | 82.66 | 89.80 | 81.68 | 91.67 | 45.92 | 12.31 | 141.8 |
| , and |
| 1 | 300 | 251 | 98.00 | 99.98 | 99.98 | 100.0 | 99.28 | 97.66 | 77.45 | 123.9 |
| 2 | 500 | 402 | 92.01 | 98.38 | 100.9 | 100.3 | 96.78 | 94.60 | 56.93 | 110.3 |
| 4 | 900 | 704 | 72.44 | 93.63 | 101.1 | 96.89 | 93.48 | 70.98 | 3.306 | 31.18 |
| 6 | 1300 | 1006 | 36.91 | 87.77 | 101.0 | 89.01 | 99.56 | 52.87 | 1.984 | 25.50 |
| 8 | 1700 | 1308 | 32.73 | 85.34 | 95.78 | 82.69 | 100.7 | 48.14 | 1.057 | 19.77 |
| 12 | 2500 | 1776 | 31.88 | 84.32 | 93.97 | 80.77 | 101.3 | 46.12 | 0.441 | 12.77 |
| 16 | 3300 | 2244 | 31.03 | 83.99 | 93.70 | 80.21 | 102.1 | 45.10 | 0.406 | 12.17 |
| 20 | 4100 | 2644 | 30.86 | 83.82 | 93.10 | 79.59 | 102.1 | 44.78 | 0.373 | 11.40 |
| 24 | 4900 | 3044 | 30.37 | 84.07 | 93.56 | 79.69 | 102.0 | 45.30 | 0.374 | 11.34 |
| 32 | 6500 | 3844 | 29.31 | 82.66 | 90.46 | 76.90 | 102.0 | 43.54 | 0.369 | 11.10 |
| and , |
| 1 | 402 | 200 | 90.81 | 68.11 | 91.36 | 96.15 | 99.42 | 95.38 | 86.48 | 105.9 |
| 2 | 704 | 300 | 82.37 | 57.77 | 82.90 | 91.90 | 97.80 | 90.97 | 74.55 | 106.3 |
| 4 | 1308 | 500 | 45.43 | 40.88 | 32.78 | 53.70 | 80.07 | 71.81 | 14.16 | 142.4 |
| 6 | 1912 | 700 | 12.48 | 29.04 | 20.93 | 35.71 | 69.01 | 63.08 | 13.32 | 143.3 |
| 8 | 2516 | 900 | 7.990 | 21.90 | 12.90 | 25.77 | 69.64 | 61.46 | 12.36 | 143.4 |
| 12 | 3452 | 1300 | 6.163 | 17.55 | 9.528 | 20.61 | 65.62 | 56.87 | 12.25 | 142.2 |
| 16 | 4388 | 1700 | 3.989 | 16.40 | 8.771 | 18.66 | 66.02 | 54.52 | 12.26 | 142.1 |
| 20 | 5188 | 2100 | 3.692 | 15.82 | 8.873 | 17.36 | 68.14 | 48.12 | 12.28 | 142.0 |
| 24 | 5988 | 2500 | 3.255 | 15.99 | 8.274 | 16.95 | 64.84 | 46.52 | 12.30 | 141.9 |
| 32 | 7588 | 3300 | 2.283 | 12.90 | 7.604 | 16.74 | 59.34 | 43.95 | 12.31 | 141.8 |
| and |
| 1 | 402 | 251 | 90.81 | 68.11 | 90.19 | 102.7 | 98.54 | 88.17 | 77.45 | 123.9 |
| 2 | 704 | 402 | 82.37 | 57.77 | 77.77 | 99.16 | 95.03 | 80.46 | 56.93 | 110.3 |
| 4 | 1308 | 704 | 45.43 | 40.88 | 31.77 | 54.53 | 62.22 | 56.58 | 3.306 | 31.18 |
| 6 | 1912 | 1006 | 12.48 | 29.04 | 19.71 | 35.62 | 12.12 | 34.48 | 1.984 | 25.50 |
| 8 | 2516 | 1308 | 7.990 | 21.90 | 11.79 | 24.15 | 9.885 | 29.21 | 1.057 | 19.77 |
| 12 | 3452 | 1776 | 6.163 | 17.55 | 8.775 | 19.12 | 7.687 | 25.99 | 0.441 | 12.77 |
| 16 | 4388 | 2244 | 3.989 | 16.40 | 7.970 | 17.15 | 5.304 | 24.32 | 0.406 | 12.17 |
| 20 | 5188 | 2644 | 3.692 | 15.82 | 7.535 | 16.35 | 5.153 | 23.90 | 0.373 | 11.40 |
| 24 | 5988 | 3044 | 3.255 | 15.99 | 8.087 | 16.37 | 5.023 | 24.03 | 0.374 | 11.34 |
| 32 | 7588 | 3844 | 2.283 | 12.90 | 7.530 | 15.66 | 4.698 | 22.09 | 0.369 | 11.10 |
Table A5.
Thermoelasticity problem. Case 2 (homogeneous boundary condition for elasticity and non-homogeneous boundary condition for temperature on perforations). Unstructured coarse grids. . Relative and error in %. .
Table A5.
Thermoelasticity problem. Case 2 (homogeneous boundary condition for elasticity and non-homogeneous boundary condition for temperature on perforations). Unstructured coarse grids. . Relative and error in %. .
| M | | | Quasi-Structured | Unstructured |
|---|
| | | | | | | |
| 1 | 402 | 251 | 98.47 | 91.35 | 76.32 | 103.8 | 98.44 | 93.52 | 72.88 | 95.42 |
| 2 | 704 | 402 | 94.78 | 82.68 | 52.28 | 92.76 | 94.43 | 86.17 | 54.50 | 93.85 |
| 4 | 1308 | 704 | 72.68 | 64.89 | 6.404 | 37.24 | 79.52 | 73.01 | 15.27 | 53.38 |
| 6 | 1912 | 1006 | 51.18 | 54.39 | 3.044 | 32.04 | 62.35 | 63.75 | 7.285 | 37.87 |
| 8 | 2516 | 1308 | 21.07 | 36.85 | 1.496 | 22.45 | 46.90 | 55.00 | 3.408 | 30.38 |
| 12 | 3452 | 1776 | 13.06 | 31.33 | 0.877 | 18.19 | 21.52 | 39.67 | 1.495 | 23.10 |
| 16 | 4388 | 2244 | 8.606 | 27.89 | 0.667 | 16.36 | 12.78 | 32.80 | 0.941 | 20.06 |
| 20 | 5188 | 2644 | 6.745 | 26.25 | 0.543 | 15.19 | 8.371 | 29.68 | 0.667 | 18.02 |
| 24 | 5988 | 3044 | 5.701 | 25.20 | 0.462 | 14.47 | 6.383 | 28.10 | 0.500 | 16.17 |
| 32 | 7588 | 3844 | 4.834 | 24.01 | 0.395 | 13.68 | 4.941 | 26.57 | 0.384 | 14.81 |
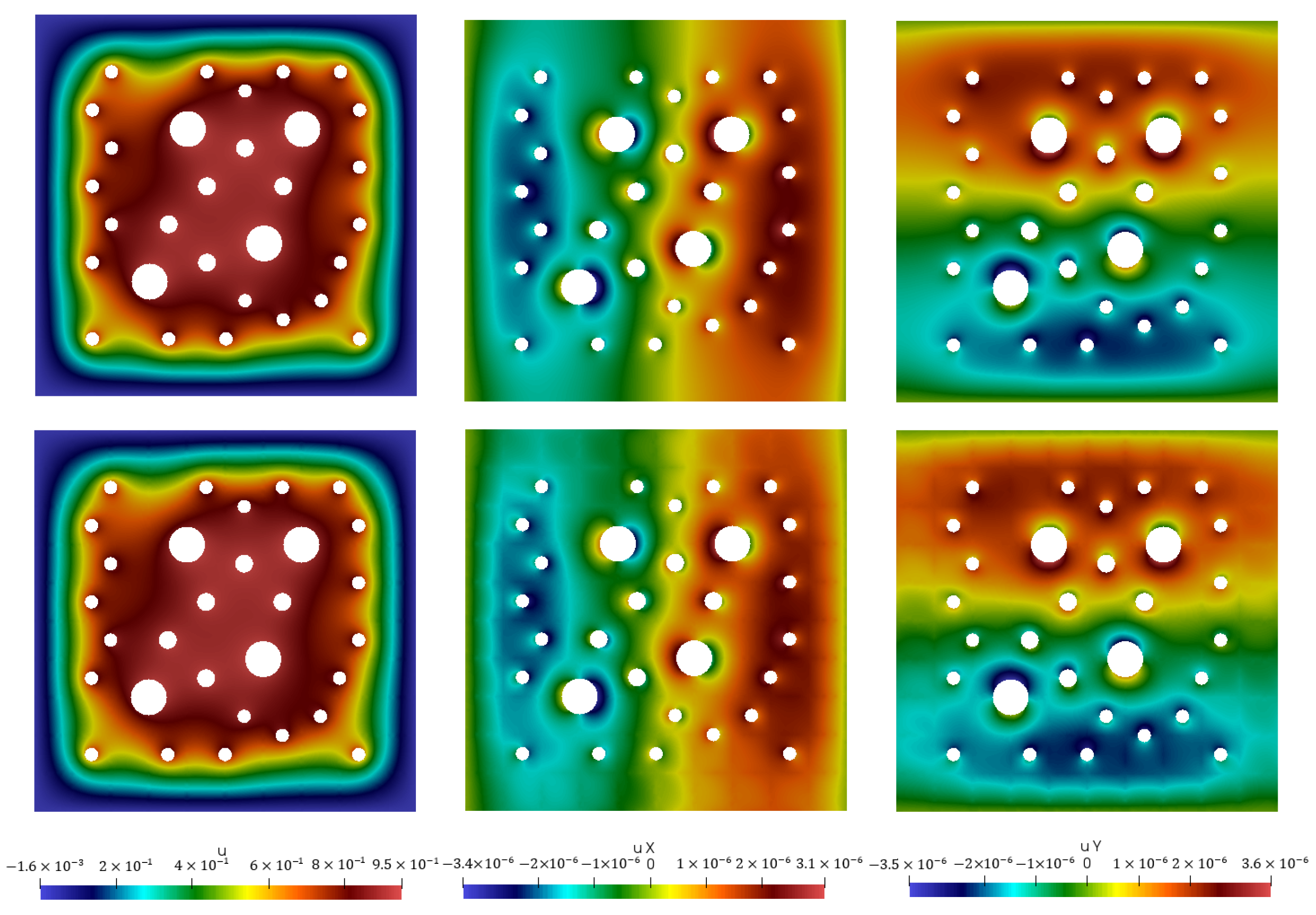
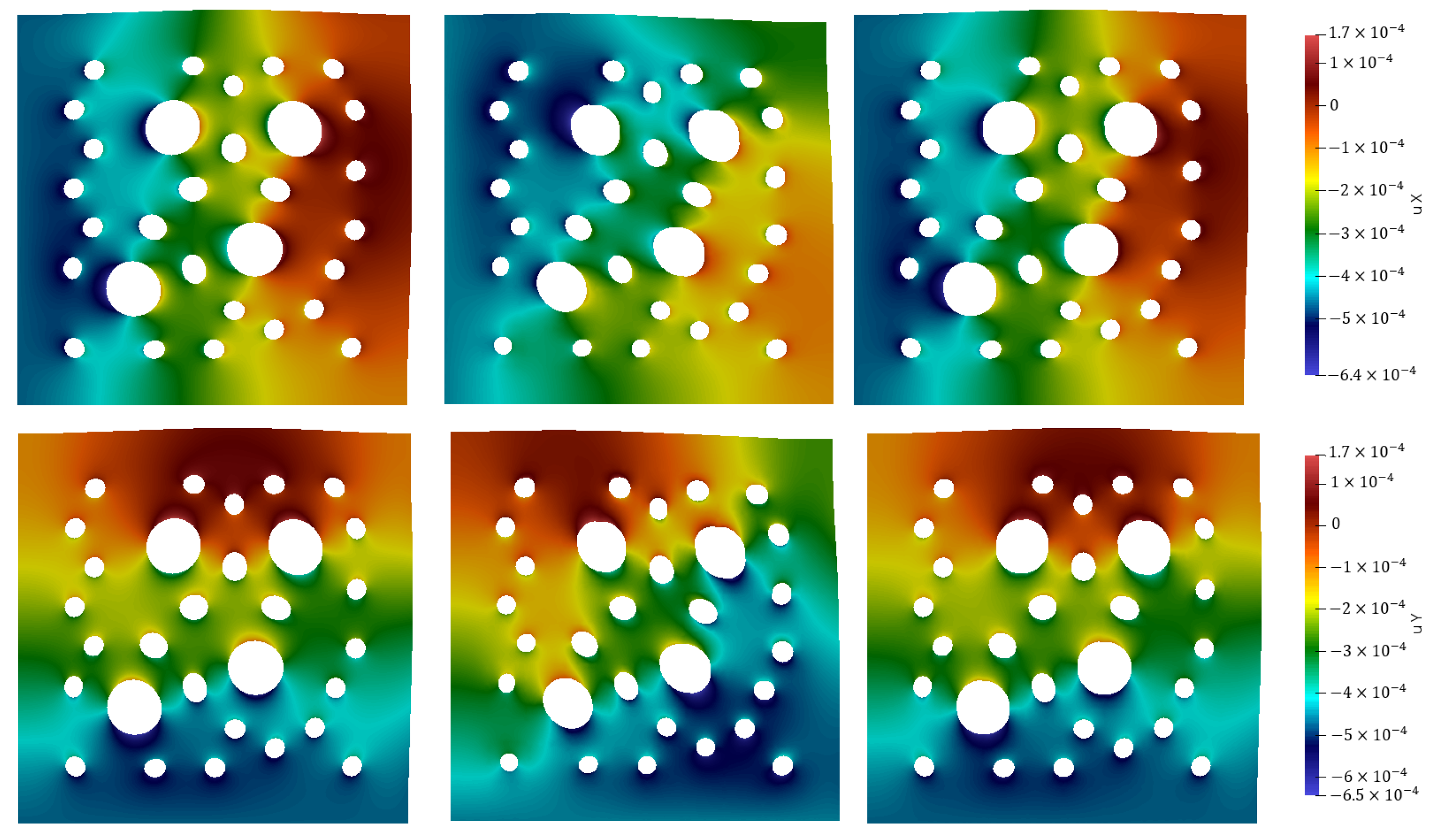
Figure A5.
Thermoelasticity problem. Case 1 (non-homogeneous boundary condition for elasticity and homogeneous boundary condition for temperature on perforations). First column: temperature. Second column: displacement of X-component. Third column: displacement of Y-component. First row: Reference solution (, with 170,460 and = 85,230). Second row: Multiscale solution with 24 multiscale basis functions, and (, with and ).
Figure A5.
Thermoelasticity problem. Case 1 (non-homogeneous boundary condition for elasticity and homogeneous boundary condition for temperature on perforations). First column: temperature. Second column: displacement of X-component. Third column: displacement of Y-component. First row: Reference solution (, with 170,460 and = 85,230). Second row: Multiscale solution with 24 multiscale basis functions, and (, with and ).
Case 1 with non-homogeneous boundary conditions for elasticity and homogeneous boundary conditions for temperature on perforations shows that, for displacement, we should use perforation boundary basis functions in order to approximate the non- homogeneous boundary condition for the elasticity part of the coupled system. For temperature, only outer boundary basis functions can be used because we have homogeneous boundary conditions for temperature. For Case 1 with , , and , we obtain a good results with and of errors for displacement and temperature, respectively. When we use only outer boundary basis functions for displacement (), we obtain a large error for both displacement and temperature. In Case 2 with homogeneous boundary conditions for elasticity and non-homogeneous boundary conditions for temperature on perforations, we can obtain good results with outer and perforation boundary basis functions for both displacement and temperature ( and ). It should be noted that perforation boundary basis functions should be added for displacement due to the coupled process for accurate multiscale approximation even for non-homogeneous boundary conditions for elasticity on perforations.
Figure A6.
Thermoelasticity problem. Case 2 (homogeneous boundary condition for elasticity and non-homogeneous boundary condition for temperature on perforations). First column: temperature. Second column: displacement of X-component. Third column: displacement of Y-component. First row: Reference solution ( with = 170,460 and = 85,230). Second row: Multiscale solution with 24 multiscale basis functions, and (, with and ).
Figure A6.
Thermoelasticity problem. Case 2 (homogeneous boundary condition for elasticity and non-homogeneous boundary condition for temperature on perforations). First column: temperature. Second column: displacement of X-component. Third column: displacement of Y-component. First row: Reference solution ( with = 170,460 and = 85,230). Second row: Multiscale solution with 24 multiscale basis functions, and (, with and ).