Mene Mene Tekel Upharsin: Clerical Speed and Elementary Cognitive Speed are Different by Virtue of Test Mode Only
Abstract
:1. Introduction
1.1. Clerical Speed (Gs)
1.2. Elementary Cognitive Speed (Gt)
1.3. Separability of Speed Factors and Cross-Mode Transfer
1.4. Aims of This Study
2. Materials and Methods
2.1. Sample
2.2. Materials
2.2.1. Paper-and-Pencil Speed Tests
2.2.2. Computer-Based Speed Test
2.2.3. Working Memory Capacity (WMC) Tasks
2.3. Procedure
2.4. Data Analyses
3. Results
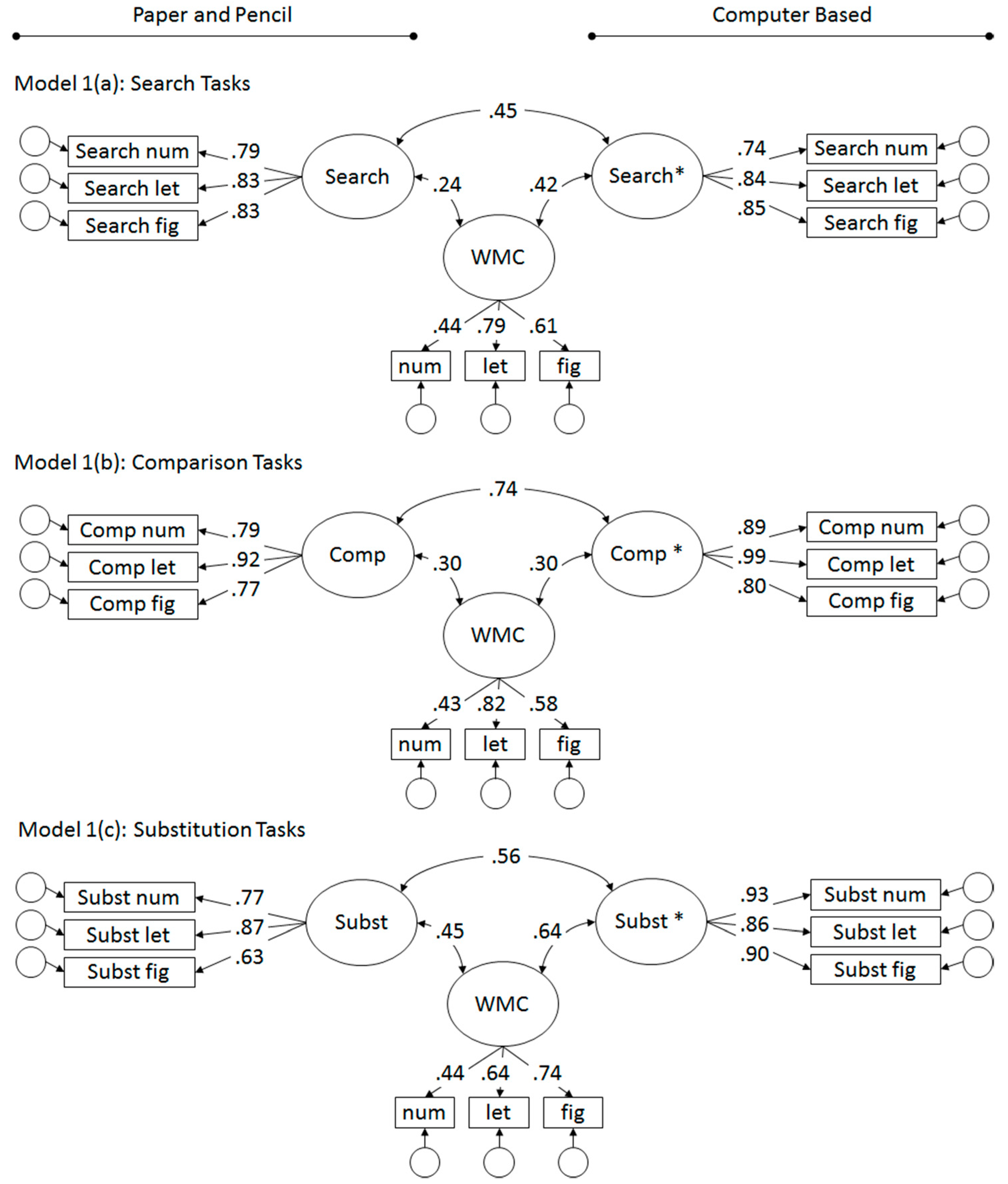
3.1. Preliminary and Separate Analyses for Task Classes
3.2. Joint Analyses across Task Classes
4. Discussion
4.1. Cross Mode Relations
4.2. Relations with WMC
4.3. Task Specificity and the Hierarchical Nature of Mental Speed
4.4. Which Factors are Responsible for the Dissociation of PP and CB Measures?
4.5. How to Assess Mental Speed?
4.6. Limitations of the Present Study
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Difference Test | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Task/Constraint | χ2 (df) | p | χ2 (df) | p | RMSEA [CI] | SRMR | CFI | AIC | BIC |
| Search | |||||||||
| Unconstrained (Model 1(a); see Figure 2) | 35.35 (24) | 0.06 | — | — | 0.06 [0.00; 0.10] | 0.05 | 0.97 | 1695 | 1754 |
| SearchPP − SearchCB = 0 | 55.03 (25) | 0.00 | 19.68 (1) | <0.001 | 0.10 [0.06; 0.13] | 0.14 | 0.93 | 1712 | 1769 |
| SearchPP − SearchCB = 1 | 162.44 (25) | 0.00 | 127.08 (1) | <0.001 | 0.21 [0.18; 0.24] | 0.13 | 0.67 | 1820 | 1876 |
| SearchPP − WMC = SearchCB − WMC | 37.38 (25) | 0.05 | 2.03 (1) | 0.15 | 0.06 [0.00; 0.10] | 0.05 | 0.97 | 1695 | 1751 |
| Comparison | |||||||||
| Unconstrained (Model 1(b); see Figure 2) | 37.60 (24) | 0.04 | — | — | 0.07 [0.02; 0.11] | 0.05 | 0.98 | 1180 | 1239 |
| CompPP − CompCB = 0 | 117.47 (25) | 0.00 | 79.88 (1) | <0.001 | 0.17 [0.14; 0.20] | 0.26 | 0.86 | 1258 | 1314 |
| CompPP − CompCB = 1 | 118.45 (25) | 0.00 | 80.86 (1) | <0.001 | 0.17 [0.14; 0.20] | 0.08 | 0.86 | 1259 | 1315 |
| CompPP − WMC = CompCB − WMC | 37.60 (25) | 0.05 | <0.01 (1) | 0.97 | 0.06 [0.00; 0.10] | 0.05 | 0.98 | 1178 | 1234 |
| Substitution | |||||||||
| Unconstrained (Model 1(c); see Figure 2) | 30.50 (24) | 0.17 | — | — | 0.05 [0.00; 0.09] | 0.04 | 0.99 | 1174 | 1234 |
| SubstPP − SubstCB = 0 | 64.81 (25) | 0.00 | 34.31 (1) | <0.001 | 0.11 [0.08; 0.15] | 0.19 | 0.93 | 1207 | 1263 |
| SubstPP − SubstCB = 1 | 109.18 (25) | 0.00 | 78.68 (1) | <0.001 | 0.16 [0.13; 0.20] | 0.10 | 0.84 | 1251 | 1308 |
| SubstPP − WMC = SubstCB − WMC | 34.10 (25) | 0.11 | 3.60 (1) | 0.06 | 0.05 [0.00; 0.10] | 0.05 | 0.98 | 1176 | 1233 |
Appendix B
| Difference Test | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model/Constraint | χ2 (df) | p | χ2 (df) | p | RMSEA [CI] | SRMR | CFI | AIC | BIC |
| Unconstrained (Model 2; see Figure 3) | 272.90 (168) | 0.00 | — | — | 0.07 [0.06; 0.09] | 0.10 | 0.94 | 1896 | 2074 |
| Relations PP − CB | |||||||||
| SpeedPP − SpeedCB = 0 | 320.48 (169) | 0.00 | 47.59 (1) | <0.001 | 0.08 [0.07; 0.10] | 0.22 | 0.91 | 1941 | 2117 |
| SpeedPP − SpeedCB = 1 | 384.66 (169) | 0.00 | 111.76 (1) | <0.001 | 0.10 [0.09; 0.11] | 0.11 | 0.87 | 2005 | 2181 |
| SearchPP − SearchCB = 0 | 273.66 (169) | 0.00 | 0.76 (1) | 0.38 | 0.07 [0.05; 0.09] | 0.10 | 0.94 | 1894 | 2070 |
| CompPP − CompCB = 0 | 327.89 (169) | 0.00 | 54.99 (1) | <0.001 | 0.09 [0.07; 0.10] | 0.12 | 0.91 | 1949 | 2124 |
| CompPP − CompCB = 1 | 299.67 (169) | 0.00 | 26.77 (1) | <0.001 | 0.08 [0.06; 0.09] | 0.09 | 0.92 | 1920 | 2096 |
| Relations PP − WMC | |||||||||
| SpeedPP − WMC = 0 | 288.21 (169) | 0.00 | 15.31 (1) | <0.001 | 0.08 [0.06; 0.09] | 0.14 | 0.93 | 1909 | 2084 |
| SpeedPP − WMC = 1 | 308.05 (169) | 0.00 | 35.15 (1) | <0.001 | 0.08 [0.07; 0.10] | 0.10 | 0.92 | 1929 | 2104 |
| SearchPP − WMC = 0 | 274.86 (169) | 0.00 | 1.96 (1) | 0.16 | 0.07 [0.06; 0.09] | 0.10 | 0.94 | 1896 | 2071 |
| CompPP − WMC = 0 | 273.00 (169) | 0.00 | 0.10 (1) | 0.75 | 0.07 [0.05; 0.09] | 0.10 | 0.94 | 1894 | 2069 |
| Relations CB − WMC | |||||||||
| SpeedCB − WMC = 0 | 310.27 (169) | 0.00 | 37.37 (1) | <0.001 | 0.08 [0.07; 0.10] | 0.14 | 0.92 | 1931 | 2106 |
| SpeedCB − WMC = 1 | 296.45 (169) | 0.00 | 23.51 (1) | <0.001 | 0.08 [0.06; 0.09] | 0.10 | 0.92 | 1917 | 2093 |
| SearchCB − WMC = 0 | 273.03 (169) | 0.00 | 0.13 (1) | 0.71 | 0.07 [0.05; 0.09] | 0.10 | 0.94 | 1894 | 2069 |
| CompCB − WMC = 0 | 273.03 (169) | 0.00 | 0.14 (1) | 0.71 | 0.07 [0.05; 0.09] | 0.10 | 0.94 | 1894 | 2069 |
| Testing the Symmetry of Relations | |||||||||
| SpeedPP − WMC = SpeedCB − WMC | 277.40 (169) | 0.00 | 4.50 (1) | 0.03 | 0.07 [0.06; 0.09] | 0.10 | 0.94 | 1898 | 2073 |
| SpeedPP − SpeedCB = SpeedPP − WMC | 276.58 (169) | 0.00 | 3.68 (1) | 0.06 | 0.07 [0.06; 0.09] | 0.11 | 0.94 | 1897 | 2073 |
| SpeedPP − SpeedCB = SpeedCB − WMC | 272.92 (169) | 0.00 | 0.02 (1) | 0.88 | 0.07 [0.05; 0.09] | 0.10 | 0.94 | 1894 | 2069 |
References
- Horn, J.L.; Noll, J. A system for understanding cognitive capabilities: A theory and the evidence on which it is based. In Current Topics in Human Intelligence Theories of Intelligence; Detterman, D.K., Ed.; Ablex: Norwood, NJ, USA, 1994; Volume 4, pp. 151–203. [Google Scholar]
- Gregory, R.J. Psychological Testing: History, Principles, and Applications; Allyn & Bacon: Needham, MA, USA, 2004; p. 694. [Google Scholar]
- Kyllonen, P.C. Human cognitive abilities: Their organization, development, and use. In Handbook of Educational Psychology, 3rd ed.; Routledge/Taylor & Francis Group: London, UK, 2016; pp. 121–134. [Google Scholar]
- Horn, J.L.; Noll, J. Human cognitive capabilities: Gf-Gc theory. In Contemporary Intellectual Assessment: Theories, Tests, and Issues; Flanagan, D.P., Genshaft, J.L., Harrison, P.L., Eds.; Guilford Press: New York, NY, USA, 1997; pp. 53–91. [Google Scholar]
- Carroll, J.B. Human Cognitive Abilities: A Survey of Factor-Analytic Studies; Cambridge University Press: New York, NY, USA, 1993. [Google Scholar]
- McGrew, K.S. The Cattell-Horn-Carroll theory of cognitive abilities: Past, present and future. In Contemporary Intellectual Assessment: Theories, Tests, and Issues, 2nd ed.; Flanagan, D.P., Harrison, P.L., Eds.; Guilford Press: New York, NY, USA, 2005; pp. 136–181. [Google Scholar]
- Danthiir, V.; Roberts, R.D.; Schulze, R.; Wilhelm, O. Mental Speed: On Frameworks, Paradigms, and a Platform for the Future. In Handbook of Understanding and Measuring Intelligence; Wilhelm, O., Engle, R.W., Eds.; Sage Publications, Inc.: Thousand Oaks, CA, USA, 2005; pp. 27–46. [Google Scholar]
- Murphy, K.R.; Davidshofer, C.O. Psychological Testing: Principles and Applications; Prentice-Hall: Englewood Cliffs, NJ, USA, 1994; p. 548. [Google Scholar]
- Pryor, R.G.L. Some ethical implications of computer technology. Bull. Aust. Psychol. Soc. 1989, 11, 164–166. [Google Scholar]
- Roberts, R.D.; Stankov, L. Individual differences in speed of mental processing and human cognitive abilities: Toward a taxonomic model. Learn. Individ. Differ. 1999, 11, 1–120. [Google Scholar] [CrossRef]
- Horn, J.L.; Cattell, R.B. Refinement and test of the theory of fluid and crystallized intelligences. J. Educ. Psychol. 1966, 57, 253–270. [Google Scholar] [CrossRef]
- Galton, F. Inquiries into Human Faculty and Its Development; MacMillan Co: New York, NY, USA, 1883. [Google Scholar]
- McKeen Cattell, J. Mental tests and measurements. Mind 1890, 15, 373–381. [Google Scholar] [CrossRef]
- Eysenck, H.J. Speed of information processing, reaction time, and the theory of intelligence. In Speed of Information-Processing and Intelligence; Vernon, P.A., Ed.; Ablex Publishing: Westport, CT, USA, 1987; pp. 21–67. [Google Scholar]
- Jensen, A.R. Reaction time and psychometric g. In A Model for Intelligence; Eysenck, H.J., Ed.; Springer: Berlin, Germany, 1982; pp. 93–132. [Google Scholar]
- Jensen, A.R. Individual differences in the Hick paradigm. In Speed of Information-Processing and Intelligence; Vernon, P.A., Ed.; Ablex Publishing: Westport, CT, USA, 1987; pp. 101–175. [Google Scholar]
- Burns, N.R.; Nettelbeck, T. Inspection time and speed of processing: Sex differences on perceptual speed but not IT. Personal. Individ. Differ. 2005, 39, 439–446. [Google Scholar] [CrossRef]
- Deary, I.J.; Der, G.; Ford, G. Reaction times and intelligence differences: A population-based cohort study. Intelligence 2001, 29, 389–399. [Google Scholar] [CrossRef]
- Deary, I.J.; Ritchie, S.J. Processing speed differences between 70- and 83-year-olds matched on childhood IQ. Intelligence 2016, 55, 28–33. [Google Scholar] [CrossRef] [Green Version]
- Ritchie, S.J.; Tucker-Drob, E.M.; Cox, S.R.; Corley, J.; Dykiert, D.; Redmond, P.; Pattie, A.; Taylor, A.M.; Sibbett, R.; Starr, J.M.; et al. Predictors of ageing-related decline across multiple cognitive functions. Intelligence 2016, 59, 115–126. [Google Scholar] [CrossRef] [Green Version]
- Ritchie, S.J.; Tucker-Drob, E.M.; Deary, I.J. A strong link between speed of visual discrimination and cognitive ageing. Curr. Biol. CB 2014, 24, R681–R683. [Google Scholar] [CrossRef] [Green Version]
- Sheppard, L.D.; Vernon, P.A. Intelligence and speed of information-processing: A review of 50 years of research. Personal. Individ. Differ. 2008, 44, 535–551. [Google Scholar] [CrossRef]
- O’Connor, T.A.; Burns, N.R. Inspection time and general speed of processing. Personal. Individ. Differ. 2003, 35, 713–724. [Google Scholar] [CrossRef] [Green Version]
- Doebler, P.; Scheffler, B. The relationship of choice reaction time variability and intelligence: A meta-analysis. Learn. Individ. Differ. 2016, 52, 157–166. [Google Scholar] [CrossRef]
- Burns, N.R.; Nettelbeck, T.; McPherson, J. Attention and intelligence: A factor analytic study. J. Individ. Differ. 2009, 30, 44–57. [Google Scholar] [CrossRef]
- Kyllonen, P.C.; Sternberg, R.J.; Grigorenko, E.L. g: Knowledge, speed, strategies, or working-memory capacity? A systems perspective. In The General Factor of Intelligence: How General is it? Lawrence Erlbaum Associates Publishers: Mahwah, NJ, USA, 2002; pp. 415–445. [Google Scholar]
- Kovacs, K.; Conway, A.R.A. What Is IQ? Life Beyond “General Intelligence”. Curr. Dir. Psychol. Sci. 2019, 28, 189–194. [Google Scholar] [CrossRef]
- Kovacs, K.; Conway, A.R. Process overlap theory: A unified account of the general factor of intelligence. Psychol. Inq. 2016, 27, 151–177. [Google Scholar] [CrossRef]
- Mead, A.D.; Drasgow, F. Equivalence of computerized and paper-and-pencil cognitive ability tests: A meta-analysis. Psychol. Bull. 1993, 114, 449–458. [Google Scholar] [CrossRef]
- Parks, S.; Bartlett, A.; Wickham, A.; Myors, B. Developing a computerized test of perceptual/clerical speed. Computy. Hum. Behav. 2001, 17, 111–124. [Google Scholar] [CrossRef]
- Kyllonen, P.C.; Zu, J. Use of response time for measuring cognitive ability. J. Int. 2016, 4, 14. [Google Scholar] [CrossRef]
- Schmiedek, F.; Oberauer, K.; Wilhelm, O.; Suess, H.-M.; Wittmann, W.W. Individual differences in components of reaction time distributions and their relations to working memory and intelligence. J. Exp. Psychol. Gen. 2007, 136, 414–429. [Google Scholar] [CrossRef]
- Schmitz, F.; Wilhelm, O. Modeling mental speed: Decomposing response time distributions in elementary cognitive tasks and relations with working memory capacity and fluid intelligence. J. Int. 2016, 4, 13. [Google Scholar] [CrossRef]
- Unsworth, N.; Redick, T.S.; Lakey, C.E.; Young, D.L. Lapses in sustained attention and their relation to executive control and fluid abilities: An individual differences investigation. Intelligence 2010, 38, 111–122. [Google Scholar] [CrossRef]
- Schubert, A.-L.; Frischkorn, G.T.; Hagemann, D.; Voss, A. Trait Characteristics of Diffusion Model Parameters. J. Int. 2016, 4, 7. [Google Scholar] [CrossRef]
- Jensen, A.R. The g Factor: The Science of Mental Ability; Praeger Publishers/Greenwood Publishing Group: Westport, CT, USA, 1998; p. 648. [Google Scholar]
- Neubauer, A.C.; Knorr, E. Three paper-and-pencil tests for speed of information processing: Psychometric properties and correlations with intelligence. Intelligence 1998, 26, 123–151. [Google Scholar] [CrossRef]
- Neubauer, A.C.; Bucik, V. The mental speed-IQ relationship: Unitary or modular? Intelligence 1996, 22, 23–48. [Google Scholar] [CrossRef]
- Danthiir, V.; Wilhelm, O.; Schulze, R.; Roberts, R.D. Factor structure and validity of paper-and-pencil measures of mental speed: Evidence for a higher-order model. In Intelligence; Wilhelm, O., Engle, R.W., Eds.; Elsevier Science: Amsterdam, The Netherlands, 2005; Volume 33, pp. 491–514. [Google Scholar]
- Danthiir, V.; Wilhelm, O.; Roberts, R.D. Further evidence for a multifaceted model of mental speed: Factor structure and validity of computerized measures. Learn. Individ. Differ. 2012, 22, 324–335. [Google Scholar] [CrossRef]
- Ackerman, P.L.; Beier, M.E.; Boyle, M.D. Individual differences in working memory within a nomological network of cognitive and perceptual speed abilities. J. Exp. Psychol. Gene. 2002, 4, 131. [Google Scholar] [CrossRef]
- Schmitz, F.; Rotter, D.; Wilhelm, O. Scoring alternatives for mental speed tests: Measurement issues and validity for working memory capacity and the attentional blink effect. J. Int. 2018, 6, 47. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis; Addison-Wesley: Reading, MA, USA, 1977. [Google Scholar]
- Chuderski, A.; Taraday, M.; Necka, E.; Smolen, T. Storage capacity explains fluid intelligence but executive control does not. Intelligence 2012, 40, 278–295. [Google Scholar] [CrossRef]
- Oberauer, K.; Schulze, R.; Wilhelm, O.; Süß, H.-M. Working memory and intelligence—Their correlation and their relation: Comment on Ackerman, Beier, and Boyle. Psychol. Bull. 2005, 131, 61–65. [Google Scholar] [CrossRef]
- Kyllonen, P.C.; Christal, R.E. Reasoning ability is (little more than) working memory capacity. Intelligence 1990, 14, 389–433. [Google Scholar] [CrossRef]
- Conway, A.R.A.; Cowan, N.; Bunting, M.F.; Therriault, D.J.; Minkoff, S.R. A latent variable analysis of working memory capacity, short-term memory capacity, processing speed, and general fluid intelligence. Intelligence 2002, 30, 163–183. [Google Scholar] [CrossRef]
- Wilhelm, O.; Hildebrandt, A.; Oberauer, K. What is working memory capacity, and how can we measure it? Front. Psychol. 2013, 4, 433. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zech, A.; Bühner, M.; Kröner, S.; Heene, M.; Hilbert, S. The impact of symmetry: Explaining contradictory results concerning working memory, reasoning, and complex problem solving. J. Int. 2017, 5, 22. [Google Scholar] [CrossRef] [PubMed]
- Conway, A.R.A.; Kane, M.J.; Bunting, M.F.; Hambrick, D.Z.; Wilhelm, O.; Engle, R.W. Working memory span tasks: A methodological review and user’s guide. Psychon. Bull. Rev. 2005, 12, 769–786. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Revelle, W. Psych: Procedures for Personality and Psychological Research, 1.5.1.; Northwestern University: Evanston, IL, USA, 2015. [Google Scholar]
- Rosseel, Y. lavaan: An R Package for Structural Equation Modeling. J. Stat. Softw. 2012, 48, 1–36. [Google Scholar] [CrossRef]
- Jorgensen, T.D.; Pornprasertmanit, S.; Schoemann, A.M.; Rosseel, Y. semTools: Useful Tools for Structural Equation Modeling. Available online: https://CRAN.R-project.org/package=semTools (accessed on 1 October 2018).
- Eid, M. A multitrait-multimethod model with minimal assumptions. Psychometrika 2000, 65, 241–261. [Google Scholar] [CrossRef]
- Hu, L.-t.; Bentler, P.M. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Struct. Equ. Modeling 1999, 6, 1–55. [Google Scholar] [CrossRef]
- Kline, R.B. Principles and Practice of Structural Equation Modeling, 4 ed.; Guilford Press: New York, NY, USA, 2016; p. 534. [Google Scholar]
- Weston, R.; Gore, P.A. A brief guide to structural equation modeling. Couns. Psychol. 2006, 34, 719–751. [Google Scholar] [CrossRef]
- Preacher, K.J.; Merkle, E.C. The problem of model selection uncertainty in structural equation modeling. Psychol. Methods 2012, 17, 1–14. [Google Scholar] [CrossRef]
- Van Lent, G. Important considerations in e-assessment. In Toward a Research Agenda on Computer-Based Assessment; Scheuermann, F., Guimarães Pereira, A., Eds.; Office for Official Publications of the European Communities: Luxembourg, Luxembourg, 2008; pp. 97–103. [Google Scholar]
- Burns, N.R.; Nettelback, T. Inspection time in the structure of cognitive abilities: Where does IT fit. Intelligence 2003, 31, 237–255. [Google Scholar] [CrossRef]
- Miller, L.T.; Vernon, P.A. The general factor in short-term memory, intelligence, and reaction time. Intelligence 1992, 16, 5–29. [Google Scholar] [CrossRef]
- Kranzler, J.H.; Jensen, A.R. The nature of psychometric g: Unitary process or a number of independent processes? Intelligence 1991, 15, 397–422. [Google Scholar] [CrossRef]
- Schroeders, U.; Wilhelm, O. Testing reasoning ability with handheld computers, notebooks, and paper and pencil. Eur. J. Psychol. Assess. 2010, 26, 284–292. [Google Scholar] [CrossRef]
- Greaud, V.A.; Green, B.F. Equivalence of conventional and computer presentation of speed tests. Appl. Psychol. Meas. 1986, 10, 23–34. [Google Scholar] [CrossRef]
- Lustig, C.; Hasher, L.; Tonev, S.T. Distraction as a determinant of processing speed. Psychon. Bull. Rev. 2006, 13, 619–625. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Keye, D.; Wilhelm, O.; Oberauer, K.; van Ravenzwaaij, D. Individual differences in conflict-monitoring: Testing means and covariance hypothesis about the Simon and the Eriksen Flanker task. Psychol. Res. Psychol. Forsch. 2009, 73, 762–776. [Google Scholar] [CrossRef]
- Salthouse, T.A. Relations between cognitive abilities and measures of executive functioning. Neuropsychology 2005, 19, 532–545. [Google Scholar] [CrossRef] [PubMed]
- Pahud, O.; Rammsayer, T.H.; Troche, S.J. Elucidating the functional relationship between speed of information processing and speed-, capacity-, and memory-related aspects of psychometric intelligence. Adv. Cognit. Psychol. 2018, 13, 3–13. [Google Scholar] [CrossRef]


| Speed Test | M | SD | Skew | Kurtosis |
|---|---|---|---|---|
| Paper and Pencil | ||||
| Search-Numbers | 275.672 | 44.627 | −0.129 | −0.026 |
| Search-Letters | 288.248 | 46.068 | 0.027 | −0.304 |
| Search-Symbols | 127.960 | 18.006 | 0.508 | 0.050 |
| Comparison-Numbers | 43.968 | 6.670 | 0.171 | −0.335 |
| Comparison-Letters | 39.536 | 6.710 | 0.270 | 0.468 |
| Comparison-Symbols | 30.144 | 5.014 | 0.606 | 0.692 |
| Substitution-Num→Sym | 27.136 | 4.222 | 0.292 | 0.246 |
| Substitution-Let→Num | 29.760 | 4.304 | 0.040 | −0.131 |
| Substitution-Sym→Let | 30.784 | 5.929 | 0.914 | 1.451 |
| Computer Based | ||||
| Search-Numbers | 2.783 | 0.259 | −0.051 | −0.200 |
| Search-Letters | 2.811 | 0.239 | −0.307 | 0.289 |
| Search-Symbols | 2.268 | 0.187 | −0.428 | −0.216 |
| Comparison-Numbers | 1.257 | 0.168 | −0.177 | −0.455 |
| Comparison-Letters | 1.094 | 0.168 | −0.101 | −0.292 |
| Comparison-Symbols | 0.944 | 0.130 | 0.504 | 0.282 |
| Substitution-Num→Sym | 0.808 | 0.131 | 0.597 | 0.503 |
| Substitution-Let→Num | 0.867 | 0.149 | 0.476 | 0.518 |
| Substitution-Sym→Let | 0.917 | 0.121 | 0.281 | 0.486 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmitz, F.; Wilhelm, O. Mene Mene Tekel Upharsin: Clerical Speed and Elementary Cognitive Speed are Different by Virtue of Test Mode Only. J. Intell. 2019, 7, 16. https://0-doi-org.brum.beds.ac.uk/10.3390/jintelligence7030016
Schmitz F, Wilhelm O. Mene Mene Tekel Upharsin: Clerical Speed and Elementary Cognitive Speed are Different by Virtue of Test Mode Only. Journal of Intelligence. 2019; 7(3):16. https://0-doi-org.brum.beds.ac.uk/10.3390/jintelligence7030016
Chicago/Turabian StyleSchmitz, Florian, and Oliver Wilhelm. 2019. "Mene Mene Tekel Upharsin: Clerical Speed and Elementary Cognitive Speed are Different by Virtue of Test Mode Only" Journal of Intelligence 7, no. 3: 16. https://0-doi-org.brum.beds.ac.uk/10.3390/jintelligence7030016





