An Experimental Approach to Investigate the Involvement of Cognitive Load in Divergent Thinking
Abstract
:1. Introduction
1.1. Different Theories of Creative Cognition
1.2. The Be-Creative Effect: Support for the Controlled-Attention Theory?
1.3. The Present Study
2. Methods and Materials
2.1. Preregistration
2.2. Power Analysis
2.3. Participants
2.4. Materials
2.4.1. Divergent Thinking Tasks
2.4.2. Digit-Tracking Task
2.4.3. Ideational Behavior
2.5. Procedure
2.6. Scoring Divergent Thinking Tasks
2.7. Analytical Approach
2.7.1. Testing of Hypotheses
2.7.2. Validation of Divergent Thinking Task Procedure
2.7.3. Exploratory Analyses
- Serial order effect: In addition to the linear mixed-effects model that included only effects of time as predictors, we explored the changes in model fit that occurred when we considered the factors workload and instruction. To track differences between conditions over time, various combinations of additive and interactive terms of both predictors were added as fixed effects into further models. As in the above analysis, intercepts for participants were the random effects.
- Correlations: Finally, we explored correlations between fluency, creative quality, dose (i.e., the number of digits presented during the AUTs in the load condition), accuracy (i.e., the percentage of correct reactions on an event within the digit-tracking task), and RIBS scores. The correlations were calculated separately for each experimental condition.
3. Results
3.1. Testing of Hypotheses
3.2. Validation of Divergent Thinking Task Procedure
3.3. Exploratory Analyses
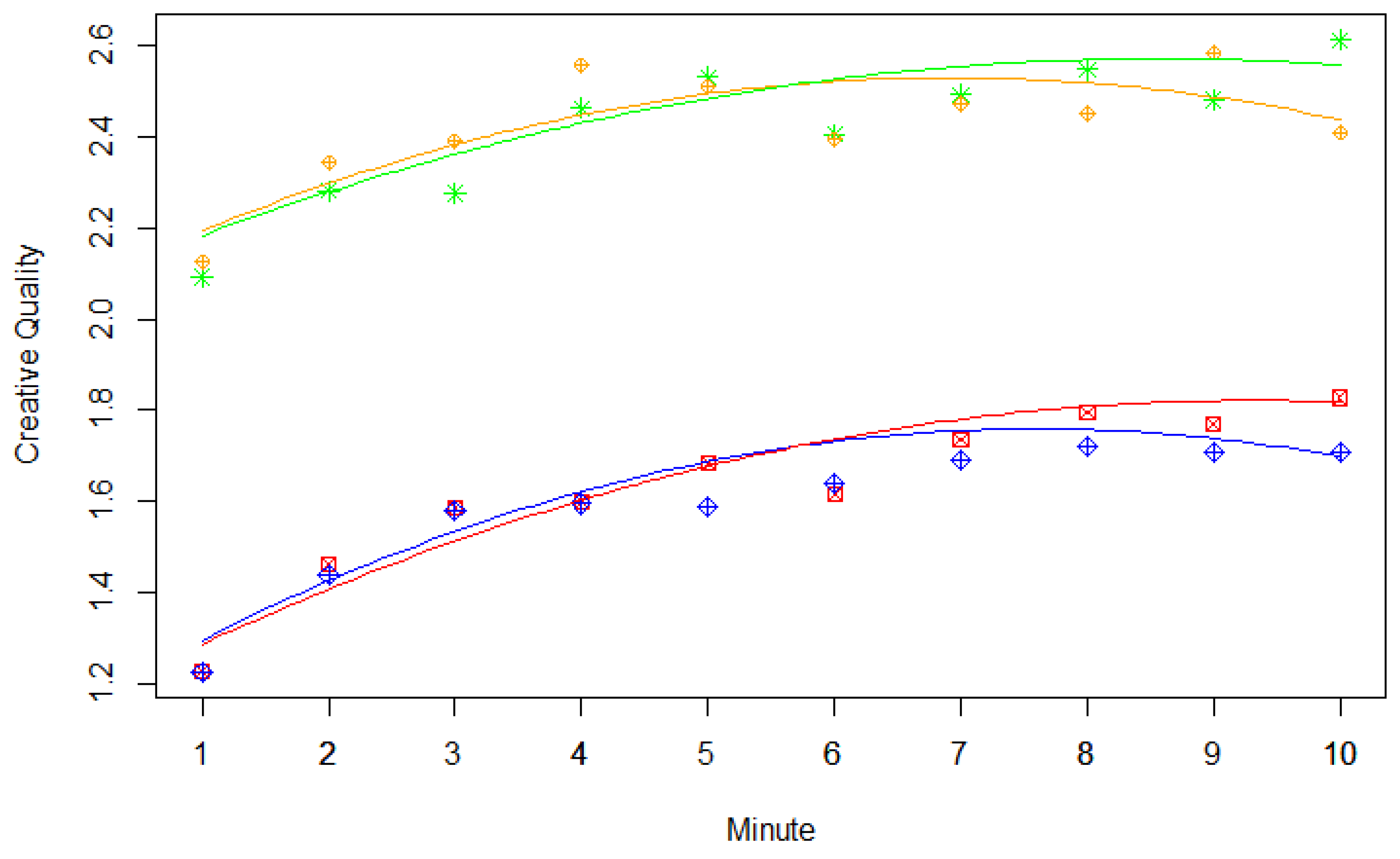
3.3.1. Serial Order Effect—Creative Quality
3.3.2. Serial Order Effect—Flexibility
3.3.3. Correlations
4. Discussion
4.1. Further Interesting Findings
4.2. Strengths and Limitations
4.3. Future Directions
4.4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Category | Object | Frequency |
|---|---|---|
| Tool | Shovel | 0.59 |
| Axe | 0.57 | |
| Pliers | 0.56 | |
| Saw | 0.45 | |
| Furniture | Table | 2.14 |
| Bed | 2.01 | |
| Chair | 1.70 | |
| Cupboard | 1.20 | |
| Vegetable | Tomato | 0.78 |
| Pea | 0.70 | |
| Cucumber | 0.64 | |
| Pepper | 0.45 | |
| Musical instrument | Drum | 1.01 |
| Violin | 0.85 | |
| Trumpet | 0.71 | |
| Flute | 0.65 |
Appendix B
Appendix C
Appendix D
Appendix E
Appendix F
Appendix G
Appendix H
Appendix I
Appendix J
- 3—7—3 → Press Space-key
- 5—9—4 → Don´t do anything
Appendix K
- Name one use for each object that is presented to you.
- Track the digits and press the SPACE-key if you observed 3 digits in a row.
Appendix L
- 1st of each 8 participants: 1 → 2 → 3 → 4
- 2nd of each 8 participants: 3 → 4 → 1 → 2
- 3rd of each 8 participants: 1 → 2 → 4 → 3
- 4th of each 8 participants: 3 → 4 → 2 → 1
- 5th of each 8 participants: 2 → 1 → 3 → 4
- 6th of each 8 participants: 4 → 3 → 1 → 2
- 7th of each 8 participants: 2 → 1 → 4 → 3
- 8th of each 8 participants: 4 → 3 → 2 → 1
References
- Acar, Selcuk, and Mark A. Runco. 2017. Latency predicts category switch in divergent thinking. Psychology of Aesthetics, Creativity, and the Arts 11: 43–51. [Google Scholar] [CrossRef]
- Acar, Selcuk, Mark A. Runco, and Uzeyir Ogurlu. 2019. The moderating influence of idea sequence: A re-analysis of the relationship between category switch and latency. Personality and Individual Differences 142: 214–17. [Google Scholar] [CrossRef]
- Alvarez, Julie A., and Eugene Emory. 2006. Executive function and the frontal lobes: A meta-analytic review. Neuropsychology Review 16: 17–42. [Google Scholar] [CrossRef] [PubMed]
- An, Donggun, Youngmyung Song, and Martha Carr. 2016. A comparison of two models of creativity: Divergent thinking and creative expert performance. Personality and Individual Differences 90: 78–84. [Google Scholar] [CrossRef]
- Bates, Douglas, Martin Mächler, Ben Bolker, and Steve Walker. 2015. Fitting linear mixed-effects models using lme4. Journal of Statistical Software 67: 1–48. [Google Scholar] [CrossRef]
- Beaty, Roger E., and Paul J. Silvia. 2012. Why do ideas get more creative across time? An executive interpretation of the serial order effect in divergent thinking tasks. Psychology of Aesthetics, Creativity, and the Arts 6: 309–19. [Google Scholar] [CrossRef] [Green Version]
- Beaty, Roger E., Paul J. Silvia, Emily C. Nusbaum, Emanuel Jauk, and Mathias Benedek. 2014. The roles of associative and executive processes in creative cognition. Memory & Cognition 42: 1186–97. [Google Scholar] [CrossRef]
- Beaty, Roger E., Yoed N. Kenett, Rick W. Hass, and Danile L. Shacter. 2019. A fan effect for creative thought: Semantic richness facilitates idea quantity but constrains idea quality. PsyArXiv. [Google Scholar] [CrossRef]
- Benedek, Mathias, Fabiola Franz, Moritz Heene, and Aljoscha C. Neubauer. 2012a. Differential effects of cognitive inhibition and intelligence on creativity. Personality and Individual Differences 53: 480–85. [Google Scholar] [CrossRef] [Green Version]
- Benedek, Mathias, Tanja Könen, and Aljoscha C. Neubauer. 2012b. Associative abilities underlying creativity. Psychology of Aesthetics, Creativity, and the Arts 6: 273–81. [Google Scholar] [CrossRef]
- Benedek, Mathias, Emanuel Jauk, Andreas Fink, Karl Koschutnig, Gernot Reishofer, Franz Ebner, and Aljoscha C. Neubauer. 2014a. To create or to recall? Neural mechanisms underlying the generation of creative new ideas. NeuroImage 88: 125–33. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benedek, Mathias, Emanuel Jauk, Markus Sommer, Martin Arendasy, and Aljoscha C. Neubauer. 2014b. Intelligence, creativity, and cognitive control: The common and differential involvement of executive functions in intelligence and creativity. Intelligence 46: 73–83. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bien, Heidrun, Willem J. M. Levelt, and R. Harald Baayen. 2005. Frequency effects in compound production. Proceedings of the National Academy of Sciences of the United States of America 102: 17876–17881. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Briggs, Robert O., and Bruce A. Reinig. 2010. Bounded ideation theory. Journal of Management Information Systems 27: 123–44. [Google Scholar] [CrossRef]
- Brophy, Dennis R. 1998. Understanding, measuring, and enhancing individual creative problem-solving efforts. Creativity Research Journal 11: 123–50. [Google Scholar] [CrossRef]
- Carroll, John B. 1993. Human Cognitive Abilities: A Survey of Factor-Analytic Studies. New York: Cambridge University Press. [Google Scholar]
- Christensen, Paul R., Joy P. Guilford, and Robert C. Wilson. 1957. Relations of creative responses to working time and instructions. Journal of Experimental Psychology 53: 82–88. [Google Scholar] [CrossRef] [PubMed]
- Collins, Allan M., and Elizabeth F. Loftus. 1975. A spreading-activation theory of semantic processing. Psychological Review 82: 407–28. [Google Scholar] [CrossRef]
- Cropley, Arthur. 2006. In praise of convergent thinking. Creativity Research Journal 18: 391–404. [Google Scholar] [CrossRef]
- Diamond, Adele. 2013. Executive functions. Annual Review of Psychology 64: 135–68. [Google Scholar] [CrossRef] [Green Version]
- Engström, Johan, Emma Johansson, and Joakim Östlund. 2005. Effects of visual and cognitive load in real and simulated motorway driving. Transportation Research Part F 8: 97–120. [Google Scholar] [CrossRef]
- Forthmann, Boris, Anne Gerwig, Heinz Holling, Pinar Çelik, Martin Storme, and Todd Lubart. 2016. The be-creative effect in divergent thinking: The interplay of instruction and object frequency. Intelligence 57: 25–32. [Google Scholar] [CrossRef]
- Forthmann, Boris, Heinz Holling, Nima Zandi, Anne Gerwig, Pinar Çelik, Martin Storme, and Todd Lubart. 2017a. Missing creativity: The effect of cognitive workload on rater (dis-)agreement in subjective divergent-thinking scores. Thinking Skills and Creativity 23: 129–39. [Google Scholar] [CrossRef]
- Forthmann, Boris, Heinz Holling, Pinar Çelik, Martin Storme, and Todd Lubart. 2017b. Typing speed as a confounding variable and the measurement of quality in divergent thinking. Creativity Research Journal 29: 257–69. [Google Scholar] [CrossRef]
- Forthmann, Boris, Sandra Regehr, Julia Seidel, Heinz Holling, Pinar Çelik, Martin Storme, and Todd Lubart. 2018. Revisiting the interactive effect of multicultural experience and openness to experience on divergent thinking. International Journal of Intercultural Relations 63: 135–43. [Google Scholar] [CrossRef]
- Forthmann, Boris, Carsten Szardenings, and Heinz Holling. 2020a. Understanding the confounding effect of fluency in divergent thinking scores: Revisiting average scores to quantify artifactual correlation. Psychology of Aesthetics, Creativity, and the Arts 14: 94–112. [Google Scholar] [CrossRef]
- Forthmann, Boris, Sue H. Paek, Denis Dumas, Baptiste Barbot, and Heinz Holling. 2020b. Scrutinizing the basis of originality in divergent thinking tests: On the measurement precision of response propensity estimates. British Journal of Educational Psychology 90: 683–99. [Google Scholar] [CrossRef]
- Friedman, Naomi P., and Akira Miyake. 2004. The reading span test and its predictive power for reading comprehension ability. Journal of Memory & Language 51: 136–58. [Google Scholar] [CrossRef]
- Gabora, Liane. 2010. Revenge of the “Neurds”: Characterizing creative thought in terms of the structure and dynamics of memory. Creativity Research Journal 22: 1–13. [Google Scholar] [CrossRef] [Green Version]
- GenABEL Project Developers. 2013. GenABEL: Genome-Wide Snp Association Analysis. R package Version 1.8-0. Available online: http://CRAN.R-project.org/package=GenABEL (accessed on 29 December 2020).
- Gilhooly, Kenneth J., Evridiki Fioratou, Susan H. Anthony, and Val Wynn. 2007. Divergent thinking: Strategies and executive involvement in generating novel uses for familiar objects. British Journal of Psychology 98: 611–25. [Google Scholar] [CrossRef] [Green Version]
- Guilford, Joy Paul. 1968. Intelligence, Creativity, and Their Educational Implications. San Diego: Robert R. Knapp. [Google Scholar]
- Harrington, David M. 1975. Effects of explicit instructions to “be creative” on the psychological meaning of divergent thinking test scores. Journal of Personality 43: 434–54. [Google Scholar] [CrossRef]
- Hommel, Bernhard. 2015. Between persistence and flexibility: The Yin and Yang of action control. Advances in Motivation Science 2: 33–67. [Google Scholar] [CrossRef]
- Kaufman, James C. 2019. Self-assessments of creativity: Not ideal, but better than you think. Psychology of Aesthetics, Creativity, and the Arts 13: 187–92. [Google Scholar] [CrossRef]
- Kaufman, James C., and Ron A. Beghetto. 2013. In parise of Clark Kent: Creativity metacognition and the importance of teaching kids when (not) to be creative. Roeper Review 35: 155–65. [Google Scholar] [CrossRef]
- Kenett, Yoed N., David Anaki, and Miriam Faust. 2014. Investigating the structure of semantic networks in low and high creative persons. Frontiers in Human Neuroscience 8: 1–16. [Google Scholar] [CrossRef] [Green Version]
- Kim, Kyung Hee. 2005. Can only intelligent people be creative? Journal of Secondary Gifted Education 16: 57–66. [Google Scholar] [CrossRef]
- Lakens, Daniël. 2013. Calculating and reporting effect sizes to facilitate cumulative science: A practical primer for t-tests and ANOVAs. Frontiers in Psychology 4: 1–12. [Google Scholar] [CrossRef] [Green Version]
- Lawrence, Michael A. 2013. ez: Easy Analysis and Visualization of Factorial Experiments. R package Version 4.2-2. Available online: http://CRAN.R-project.org/package=ez (accessed on 29 December 2020).
- Lubart, Todd I. 2001. Models of the creative process: Past, present and future. Creativity Research Journal 13: 295–308. [Google Scholar] [CrossRef]
- Mednick, Sarnoff. 1962. The associative basis of the creative process. Psychological Review 69: 220–32. [Google Scholar] [CrossRef] [Green Version]
- Mumford, Michael, and Tristan McIntosh. 2017. Creative thinking processes: The past and the future. Journal of Creative Behavior 51: 317–22. [Google Scholar] [CrossRef]
- Nijstad, Bernard A., Carsten K. W. De Dreu, Eric F. Rietzschel, and Matthijs Baas. 2010. The dual pathway to creativity model: Creative ideation as a function of flexibility and persistence. European Review of Social Psychology 21: 34–77. [Google Scholar] [CrossRef]
- Nusbaum, Emily C., and Paul J. Silvia. 2011. Are intelligence and creativity really so different? Fluid intelligence, executive processes, and strategy use in divergent thinking. Intelligence 39: 36–45. [Google Scholar] [CrossRef] [Green Version]
- Nusbaum, Emily C., Paul J. Silvia, and Roger E. Beaty. 2014. Ready, set, create: What instructing people to “Be creative” reveals about the meaning and mechanisms of divergent thinking. Psychology of Aesthetics, Creativity, and the Arts 8: 423–32. [Google Scholar] [CrossRef]
- Pan, Xuan, and Huihong Yu. 2016. Different effects of cognitive shifting and intelligence on creativity. Journal of Creative Behavior 52: 212–25. [Google Scholar] [CrossRef]
- Pinheiro, Jose, Douglas Bates, Saikat DebRoy, Deepayan Sarkar, and R Core Team. 2015. nlme: Linear and Nonlinear Mixed Effects Models. R package Version 3.1-120. Available online: http://CRAN.R-project.org/package=nlme (accessed on 29 December 2020).
- R Core Team. 2014. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing, Available online: http://www.R-project.org/ (accessed on 29 December 2020).
- Reiter-Palmon, Roni, Boris Forthmann, and Baptiste Barbot. 2019. Scoring divergent thinking tests: A review and systematic framework. Psychology of Aesthetics, Creativity, and the Arts 13: 144–52. [Google Scholar] [CrossRef]
- Rosen, Virginia M., and Randall W. Engle. 1997. The role of working memory capacity in retrieval. Journal of Experimental Psychology: General 126: 211–27. [Google Scholar] [CrossRef]
- Runco, Mark A., and Selcuk Acar. 2010. Do tests of divergent thinking have an experiential bias? Psychology of Aesthetics, Creativity, and the Arts 4: 144–48. [Google Scholar] [CrossRef]
- Runco, Mark A., and Selcuk Acar. 2012. Divergent thinking as an indicator of creative potential. Creativity Research Journal 24: 66–75. [Google Scholar] [CrossRef]
- Runco, Mark A., and Shawn M. Okuda. 1991. The instructional enhancement of the flexibility and originality scores of divergent thinking tests. Applied Cognitive Psychology 5: 435–41. [Google Scholar] [CrossRef]
- Runco, Mark A., Jonathan A. Plucker, and Woong Lim. 2001. Development and psychometric integrity of a measure of ideational behavior. Creativity Research Journal 13: 393–400. [Google Scholar] [CrossRef]
- Schröder, Astrid, Teresa Gemballa, Steffie Ruppin, and Isabell Wartenburger. 2012. German norms for semantic typicality, age of acquisition, and concept familiarity. Behavior Research Methods 44: 380–94. [Google Scholar] [CrossRef] [Green Version]
- Silvia, Paul J. 2008. Another look at creativity and intelligence: Exploring higher-order models and probable confounds. Personality and Individual differences 44: 1012–21. [Google Scholar] [CrossRef] [Green Version]
- Silvia, Paul J. 2015. Intelligence and creativity are pretty similar after all. Educational Psychology Review 27: 599–606. [Google Scholar] [CrossRef]
- Silvia, Paul J., Beate P. Winterstein, John T. Willse, Christopher M. Barona, Joshua T. Cram, Karl I. Hess, Jenna L. Martinez, and Crystal A. Richard. 2008. Assessing creativity with divergent thinking tasks: Exploring the reliability and validity of new subjective scoring methods. Psychology of Aesthetics, Creativity, and the Arts 2: 68–85. [Google Scholar] [CrossRef]
- Silvia, Paul J., Christopher Martin, and Emily C. Nusbaum. 2009. A snapshot of creativity: Evaluating a quick and simple method for assessing divergent thinking. Thinking Skills and Creativity 4: 79–85. [Google Scholar] [CrossRef] [Green Version]
- Silvia, Paul J., Roger E. Beaty, and Emily C. Nusbaum. 2013. Verbal fluency and creativity: General and specific contributions of broad retrieval ability (Gr) factors to divergent thinking. Intelligence 41: 328–40. [Google Scholar] [CrossRef]
- Steiger, James H. 1980. Tests for comparing elements of a correlation matrix. Psychological Bulletin 87: 245–51. [Google Scholar] [CrossRef]
- Süß, Heinz-Martin, Klaus Oberauer, Werner W. Wittmann, Oliver Wilhelm, and Ralf Schulze. 2002. Working memory capacity explains reasoning ability—And a little bit more. Intelligence 30: 261–88. [Google Scholar] [CrossRef]
- Wallach, Michael A., and Nathan Kogan. 1965. Modes of Thinking in Young Children: A Study of the Creativity-Intelligence Distinction. New York: Holt, Rinehart, & Winston. [Google Scholar]
- Wilken, Andrea, Boris Forthmann, and Heinz Holling. 2020. Instructions moderate the relationship between creative performance in figural divergent thinking and reasoning capacity. Journal of Creative Behavior 54: 582–97. [Google Scholar] [CrossRef]
- Wilson, Robert C., Joy P. Guilford, and Paul R. Christensen. 1953. The measurement of individual differences in originality. Psychological Bulletin 50: 362–70. [Google Scholar] [CrossRef]
- Zabelina, Darya. 2018. Attention and creativity. In The Cambridge Handbook of the Neuroscience of Creativity. Edited by Rex E. Jung and Oshin Vartanian. Cambridge: Cambridge University Press, pp. 161–79. [Google Scholar]
- Zabelina, Darya, Arielle Saporta, and Mark Beeman. 2016a. Flexible or leaky attention in creative people? Distinct patterns of attention for different types of creative thinking. Memory & Cognition 44: 488–98. [Google Scholar] [CrossRef] [Green Version]
- Zabelina, Darya, Lorenza Colzato, Mark Beeman, and Bernhard Hommel. 2016b. Dopamine and the creative mind: Individual differences in creativity are predicted by interactions between dopamine genes DAT and COMT. PLoS ONE 11: e0146768. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Weitao, Zsuzsika Sjoerds, and Bernhard Hommel. 2020. Metacontrol of human creativity: The neurocognitive mechanisms of convergent and divergent thinking. NeuroImage 2010: 116572. [Google Scholar] [CrossRef] [PubMed]
| 1 | The time limit was set to 10 min according to the procedure of Rosen and Engle (1997). |
| 2 | Working memory is considered to be one of the core executive functions (Diamond 2013). As the digit-tracking task used by Rosen and Engle (1997) affected functioning of working memory, it seemed to be an appropriate task for creating workload. |
| 3 | An event is defined by the occurrence of the third odd digit in a row appearing in the sequence. It is synonymous with the term “critical digits” used by Rosen and Engle (1997). |
| 4 | For the practice trials including an AUT, the objects knife and ball as well as stone and cup served as stimuli. These differed from the experimental task stimuli and were not controlled in terms of their lemma frequency. Furthermore, the be-fluent instruction was used for these AUTs. |
| 5 | In practice trials including digit tracking, 12 digits were presented whereby participants had to react on two events. A mistake could be made by either pressing the space bar in the absence of an event or by missing an event. |
| 6 | The ICC was calculated on the basis of the final dataset. Therefore, excluded ideas and ideas from excluded participants were not considered for the calculation. ICC scores, however, did only differ marginally from the unadjusted dataset. |
| 7 | Cohen’s d was calculated using the average standard deviation of both repeated measures (see for example Lakens 2013). |
| 8 | Workload affected fluency, but not in the intended manner (see Table 1). |
| 9 | The impact of workload on creative quality seemed to be greater in the be-fluent instruction condition than in the be-creative instruction condition (see Table 1). This finding contradicted our prediction. |
| 10 | This methodological inadequacy was also visible in the enormously high correlation between dose and fluency in the load conditions. |
| 11 | The SAT (=Scholastic Assessment Test) is a college admission test that is used in the United States of America. |

| Instruction | Workload | Fluency | Quality | Flexibility |
|---|---|---|---|---|
| Be-fluent | No Load | 49.314 (15.253) | 1.949 (0.490) | 0.303 (0.073) |
| Load | 49.608 (15.416) | 1.915 (0.469) | 0.312 (0.081) | |
| Be-creative | No Load | 28.726 (10.962) | 2.931 (0.609) | 0.485 (0.133) |
| Load | 30.314 (10.855) | 2.927 (0.561) | 0.457 (0.105) |
| Covariate | Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | Model 6 | Model 7 | Model 8 | Model 9 |
|---|---|---|---|---|---|---|---|---|---|
| β (SE) | β (SE) | β (SE) | β (SE) | β (SE) | β (SE) | β (SE) | β (SE) | β (SE) | |
| Intercept | 1.448 (0.049) *** | 1.445 (0.050) *** | 1.448 (0.056) *** | 2.000 (0.047) *** | 2.072 (0.057) *** | 1.991 (0.048) *** | 1.997 (0.053) *** | 2.070 (0.061) *** | 2.084 (0.070) *** |
| Time | 0.156 (0.013) *** | 0.156 (0.013) *** | 0.166 (0.018) *** | 0.145 (0.011) *** | 0.125 (0.018) *** | 0.145 (0.011) *** | 0.153 (0.015) *** | 0.133 (0.021) *** | 0.134 (0.025) *** |
| Time2 | −0.010 (0.001) *** | −0.010 (0.001) *** | −0.011 (0.002) *** | −0.009 (0.001) *** | −0.008 (0.002) *** | −0.009 (0.001) *** | −0.010 (0.001) *** | −0.010 (0.002) *** | −0.010 (0.002) *** |
| Load | 0.007 (0.017) | 0.001 (0.055) | 0.015 (0.015) | 0.003 (0.048) | 0.005 (0.048) | −0.023 (0.081) | |||
| Instruction | −0.817 (0.016) *** | −0.926 (0.050) *** | −0.817 (0.015) *** | −0.817 (0.016) *** | −0.925 (0.050) *** | −0.946 (0.071) *** | |||
| Time × load | −0.020 (0.025) | −0.017 (0.022) | −0.017 (0.022) | −0.020 (0.036) | |||||
| Time2 × load | 0.003 (0.002) | 0.003 (0.002) | 0.003 (0.002) | 0.003 (0.003) | |||||
| Time × instruction | 0.029 (0.022) | 0.028 (0.023) | 0.026 (0.032) | ||||||
| Time2 × instruction | −0.001 (0.002) | −0.001 (0.002) | −0.001 (0.003) | ||||||
| Instruction × load | 0.040 (0.100) | ||||||||
| Time × load × instruction | 0.006 (0.045) | ||||||||
| Time2 × load × instruction | −0.001 (0.004) | ||||||||
| AIC | 19,109.92 | 19,111.74 | 19,108.32 | 16,802.46 | 16,794.39 | 16,803.43 | 16,798.43 | 16,790.45 | 16,794.80 |
| BIC | 19,144.89 | 19,153.70 | 19,164.27 | 16,844.42 | 16,850.35 | 16,852.39 | 16,861.38 | 16,867.39 | 16,892.72 |
| (df) | 402.169 (2) ***,a | 0.182 (1) b | 7.417 (2) *,c | 2309.459 (1) ***,d | 12.066 (2) **,e | 1.029 (1) f | 8.998 (2) *,g | 11.981 (2) **,h | 1.649 (3) i |
| Covariate | Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | Model 6 | Model 7 | Model 8 | Model 9 |
|---|---|---|---|---|---|---|---|---|---|
| β (SE) | β (SE) | β (SE) | β (SE) | β (SE) | β (SE) | β (SE) | β (SE) | β (SE) | |
| Intercept | −1.086 (0.050) *** | −1.072 (0.056) *** | −1.060 (0.063) *** | −0.623 (0.060) *** | −0.590 (0.070) *** | −0.611 (0.065) *** | −0.602 (0.072) *** | −0.569 (0.081) *** | −0.603 (0.092) *** |
| Time | −0.700 (0.026) *** | −0.700 (0.026) *** | −0.721 (0.036) *** | −0.742 (0.027) *** | −0.887 (0.045) *** | −0.743 (0.027) *** | −0.764 (0.037) *** | −0.907 (0.052) *** | −0.908 (0.063) *** |
| Time2 | 0.431 (0.030) *** | 0.431 (0.030) *** | 0.417 (0.042) *** | 0.452 (0.031) *** | 0.425 (0.049) *** | 0.452 (0.031) *** | 0.440 (0.043) *** | 0.413 (0.057) *** | 0.411 (0.069) *** |
| Load | −0.030 (0.050) | −0.054 (0.080) | −0.023 (0.050) | −0.043 (0.082) | −0.044 (0.082) | 0.027 (0.121) | |||
| Instruction | −0.804 (0.052) *** | −0.866 (0.082) *** | −0.804 (0.052) *** | −0.804 (0.052) *** | −0.866 (0.082) *** | −0.802 (0.115) *** | |||
| Time × load | 0.041 (0.052) | 0.043 (0.052) | 0.041 (0.052) | 0.044 (0.089) | |||||
| Time2 × load | 0.029 (0.060) | 0.025 (0.061) | 0.025 (0.061) | 0.027 (0.097) | |||||
| Time × instruction | 0.238 (0.056) *** | 0.238 (0.056) *** | 0.246 (0.078) ** | ||||||
| Time2 × instruction | 0.076 (0.063) | 0.076 (0.063) | 0.073 (0.089) | ||||||
| Instruction × load | −0.132 (0.164) | ||||||||
| Time × load × instruction | −0.018 (0.111) | ||||||||
| Time2 × load × instruction | 0.008 (0.126) | ||||||||
| AIC | 9588.79 | 9590.41 | 9593.26 | 9350.04 | 9328.13 | 9351.83 | 9354.74 | 9332.89 | 9337.46 |
| BIC | 9616.76 | 9625.39 | 9642.23 | 9385.01 | 9377.09 | 9393.80 | 9410.70 | 9402.83 | 9428.39 |
| (df) | 843.31 (2) ***,a | 0.37 (1) b | 1.15 (2) c | 240.75 (1) ***,d | 25.92 (2) ***,e | 0.21 (1) f | 1.09 (2) g | 25.85 (2) ***,h | 1.43 (3) i |
| Measure | BF (No Load) | BF (Load) | BC (No Load) | BC (Load) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fluency | Quality | Flexibility | Fluency | Quality | Flexibility | Fluency | Quality | Flexibility | Fluency | Quality | Flexibility | |
| Fluency a | −0.402 | −0.481 | −0.413 | −0.484 | −0.268 | −0.698 | −0.296 | −0.623 | ||||
| Quality a | −0.402 | 0.428 | −0.413 | 0.449 | −0.268 | −0.296 | 0.470 | |||||
| Flexibility a | −0.481 | 0.428 | −0.484 | 0.449 | −0.698 | 0.476 | −0.623 | 0.470 | ||||
| Dose BF | 0.859 | −0.389 | −0.351 | 0.980 | −0.446 | −0.451 | 0.490 | −0.097 | −0.362 | 0.517 | −0.072 | −0.248 |
| Dose BC | 0.439 | 0.024 | −0.294 | 0.520 | −0.101 | −0.325 | 0.666 | −0.353 | −0.581 | 0.975 | −0.369 | −0.651 |
| Accuracy BF | 0.150 | −0.193 | 0.016 | 0.159 | −0.159 | −0.043 | −0.061 | 0.037 | 0.067 | 0.016 | −0.012 | −0.029 |
| Accuracy BC | 0.116 | −0.086 | −0.086 | 0.242 | −0.102 | −0.171 | 0.175 | −0.212 | −0.384 | 0.319 | −0.254 | −0.491 |
| RIBS | 0.047 | 0.036 | 0.159 | −0.026 | 0.080 | 0.439 | −0.072 | −0.110 | 0.137 | 0.077 | −0.125 | −0.107 |
| Measure | M | SD | 2. | 3. | 4. | 5. |
|---|---|---|---|---|---|---|
| 1. Dose BF | 51.588 | 15.946 | 0.515 *** | 0.173 | 0.274 | −0.008 |
| 2. Dose BC | 31.882 | 10.360 | −0.008 | 0.357 * | 0.099 | |
| 3. Accuracy BF | 0.781 | 0.153 | 0.222 | 0.149 | ||
| 4. Accuracy BC | 0.752 | 0.257 | 0.082 | |||
| 5. RIBS a | 3.458 | 0.629 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kleinkorres, R.; Forthmann, B.; Holling, H. An Experimental Approach to Investigate the Involvement of Cognitive Load in Divergent Thinking. J. Intell. 2021, 9, 3. https://0-doi-org.brum.beds.ac.uk/10.3390/jintelligence9010003
Kleinkorres R, Forthmann B, Holling H. An Experimental Approach to Investigate the Involvement of Cognitive Load in Divergent Thinking. Journal of Intelligence. 2021; 9(1):3. https://0-doi-org.brum.beds.ac.uk/10.3390/jintelligence9010003
Chicago/Turabian StyleKleinkorres, Ruben, Boris Forthmann, and Heinz Holling. 2021. "An Experimental Approach to Investigate the Involvement of Cognitive Load in Divergent Thinking" Journal of Intelligence 9, no. 1: 3. https://0-doi-org.brum.beds.ac.uk/10.3390/jintelligence9010003





