Working Memory, Fluid Reasoning, and Complex Problem Solving: Different Results Explained by the Brunswik Symmetry
Abstract
:1. Introduction
1.1. The Brunswik Symmetry Principle
1.2. The Present Study
- 1.
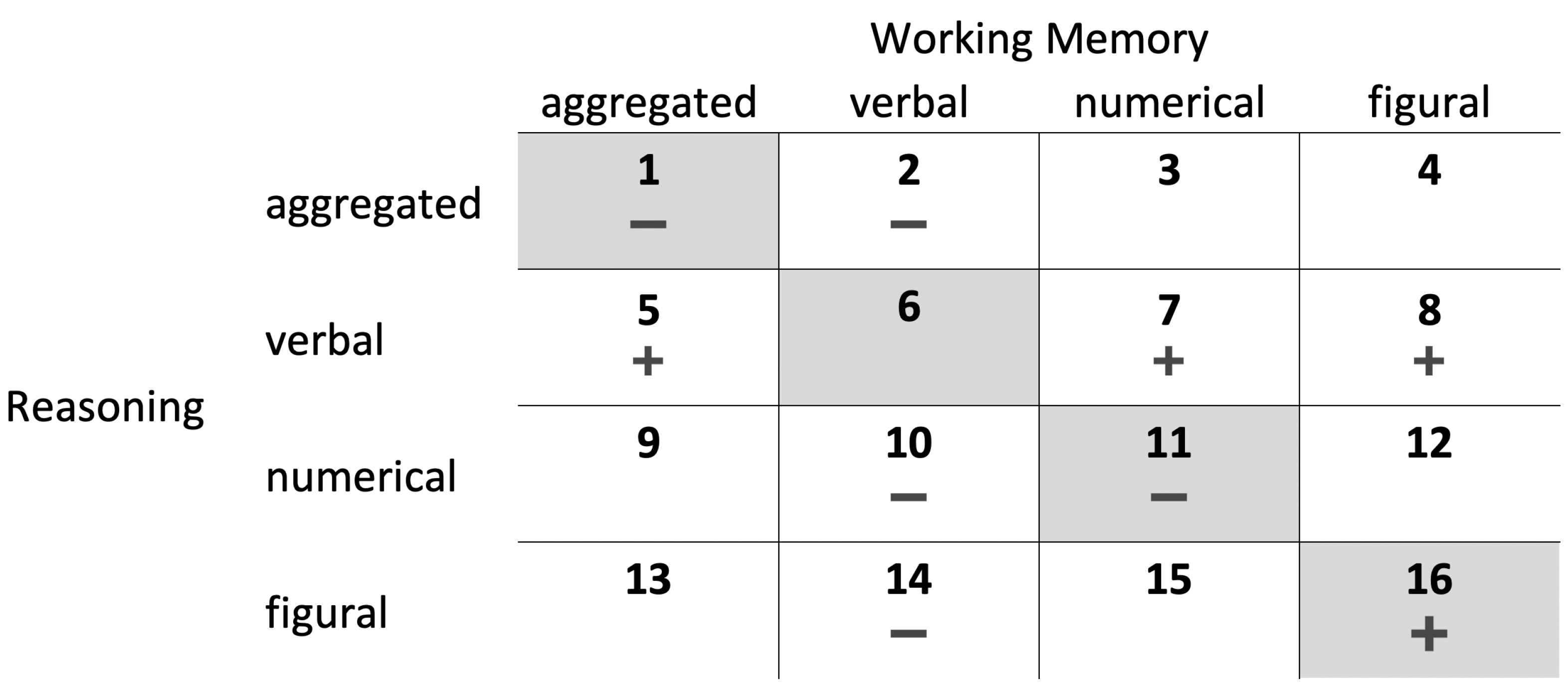
- With regard to the first aim of the study (i.e., replication of previous findings) and, thus, according to Zech et al.’s (2017) results, working memory does not incrementally explain variance in CPS above and beyond fluid reasoning if aggregated (i.e., content-unspecific based on all three content operationalizations; condition 1 in Figure 2) or numerical (condition 11) operationalizations were applied. Furthermore, working memory incrementally explains variance in CPS above and beyond fluid reasoning if figural operationalizations were considered (condition 16). We had no expectations regarding verbal operationalizations (condition 6) as Zech et al.’s (2017) study provided different findings with regard to different CPS aspects, which were not considered in the present study (see below).
- 2.
- With regard to the second aim of the study and in terms of the predictor-predictor symmetry (i.e., considering combinations of different aggregation levels and contents of the operationalizations of the predictors), we expected an asymmetrical (unfair) comparison if a verbal operationalization was combined with any other operationalization as the CPS measure used in the present study had only weak requirements concerning verbal contents. In detail, aggregated (condition 5), numerical (condition 7), and figural (condition 8) working memory should incrementally explain CPS variance above and beyond verbal fluid reasoning. Consequently, verbal working memory should not incrementally explain CPS variance above and beyond aggregated (condition 2), numerical (condition 10), and figural (condition 14) fluid reasoning. We had no specific expectations regarding the other conditions (i.e., 3, 4, 9, 12, 13, and 15). As figural and numerical abilities are rather highly correlated, their interaction within an aggregated operationalization and their relation to an aggregated operationalization is difficult to predict.2
- 3.
- With regard to the CPS measure used in the present study and combinations of the same content (i.e., conditions 1, 6, 11, and 16), a symmetrical (fair) comparison in terms of the predictor-criterion symmetry would be based on figural and numerical operationalizations of working memory and fluid reasoning (as the CPS measure had only weak requirements regarding verbal content). Given equal reliability across all conditions, it means the highest proportion of CPS variance should be explained based on figural working memory and fluid reasoning operationalizations (condition 16), followed by numerical operationalizations of both constructs (condition 11). Verbal operationalizations should explain the least variance in CPS (condition 6). Aggregated operationalizations (condition 1) should explain more CPS variance than verbal operationalizations but it is unclear whether less (due to the irrelevant verbal aspect) or equal/more (due to the combination of figural and numerical aspects) CPS variance than either figural or numerical operationalizations alone. As outlined above, we had no specific expectation in terms of the predictor-criterion symmetry regarding the other conditions combining figural and numerical contents.
2. Materials and Methods
2.1. Participants
2.2. Material
2.2.1. Working Memory
2.2.2. Fluid Reasoning
2.2.3. Complex Problem Solving
2.3. Procedure
2.4. Statistical Analysis
3. Results
3.1. Does Working Memory Incrementally Explain CPS Variance?
3.2. Do Different Combinations Represent Differently Symmetrical Matches?
4. Discussion
4.1. Working Memory, Fluid Reasoning, and CPS
4.2. The Brunswik Symmetry Principle and the Choice of Operationalizations
4.3. Limitations and Future Research
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ackerman, Phillip L., Margaret E. Beier, and Mary O. Boyle. 2005. Working Memory and Intelligence: The Same or Different Constructs? Psychological Bulletin 131: 30–60. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brown, Timothy A. 2015. Confirmatory Factor Analysis for Applied Research, 2nd ed. New York and London: The Guilford Press. [Google Scholar]
- Brunswik, Egon. 1955. Representative design and probabilistic theory in a functional psychology. Psychological Review 62: 193–217. [Google Scholar] [CrossRef] [PubMed]
- Bühner, Markus, Stephan Kröner, and Matthias Ziegler. 2008. Working memory, visual–spatial-intelligence and their relationship to problem-solving. Intelligence 36: 672–80. [Google Scholar] [CrossRef]
- Cohen, Jacob, Patricia Cohen, Stephen G. West, and Leona S. Aiken. 2003. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences, 3rd ed. Mahwah: L. Erlbaum Associates. [Google Scholar]
- Coyle, Thomas R., Anissa C. Snyder, Miranda C. Richmond, and Michelle Little. 2015. SAT non-g residuals predict course specific GPAs: Support for investment theory. Intelligence 51: 57–66. [Google Scholar] [CrossRef]
- Cronbach, Lee J., and Goldine C. Gleser. 1965. Psychological Tests and Personnel Decisions. Oxford: U. Illinois Press. [Google Scholar]
- Cumming, Geoff. 2013. The New Statistics: Why and How. Psychological Science 25: 7–29. [Google Scholar] [CrossRef] [PubMed]
- de Groot, Adrianus Dingeman. 2014. The meaning of “significance” for different types of research [translated and annotated by Eric-Jan Wagenmakers, Denny Borsboom, Josine Verhagen, Rogier Kievit, Marjan Bakker, Angelique Cramer, Dora Matzke, Don Mellenbergh, and Han L. J. Van der Maas]. Acta Psychologica 148: 188–94. [Google Scholar] [CrossRef]
- Dong, Yiran, and Chao-Ying Joanne Peng. 2013. Principled missing data methods for researchers. SpringerPlus 2: 222. [Google Scholar] [CrossRef] [Green Version]
- Dörner, D. Dietrich. 1986. Diagnostik der operativen Intelligenz [Assessment of operative intelligence]. Diagnostica 32: 290–8. [Google Scholar]
- Dörner, Dietrich, and Joachim Funke. 2017. Complex Problem Solving: What It Is and What It Is Not. Frontiers in Psychology 8. [Google Scholar] [CrossRef]
- Dörner, Dietrich, Heinz W. Kreuzig, Franz Reither, and Thea Stäudel. 1983. Lohhausen: Vom Umgang mit Unbestimmtheit und Komplexität [Lohhausen: Dealing with Uncertainty and Complexity]. Bern: Huber. [Google Scholar]
- Dunn, Thomas J., Thom Baguley, and Vivienne Brunsden. 2013. From alpha to omega: A practical solution to the pervasive problem of internal consistency estimation. British Journal of Psychology, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Figueredo, Aurelio José, Paul Robert Gladden, Melissa Marie Sisco, Emily Anne Patch, and Daniel Nelson Jones. 2016. The Unholy Trinity: The Dark Triad, Sexual Coercion, and Brunswik-Symmetry. Evolutionary Psychology. [Google Scholar] [CrossRef] [Green Version]
- Fischer, Andreas, Samuel Greiff, and Joachim Funke. 2012. The process of solving complex problems. The Journal of Problem Solving 4: 19–41. [Google Scholar] [CrossRef] [Green Version]
- Flake, Jessica Kay, and Eiko I. Fried. 2020. Measurement Schmeasurement: Questionable Measurement Practices and How to Avoid Them. Advances in Methods and Practices in Psychological Science 3: 456–65. [Google Scholar] [CrossRef]
- Funke, Joachim, Andreas Fischer, and Daniel V. Holt. 2017. When less is less: Solving multiple simple problems is not complex problem solving—A comment on Greiff et al. (2015). Journal of Intelligence 5: 5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Funke, Joachim, and Peter A. Frensch. 2007. Complex Problem Solving: The European Perspective-10 Years After. In Learning to Solve Complex Scientific Problems. Edited by David H. Jonassen. New York: Lawrence Erlbaum Associates Publishers, pp. 25–47. [Google Scholar]
- Gelman, Andrew, and Eric Loken. 2013. The Garden of Forking Paths: Why Multiple Comparisons Can Be a Problem, Even When There Is No “Fishing Expedition” or “p-Hacking” and the Research Hypothesis Was Posited Ahead of Time. Available online: http://www.stat.columbia.edu/~gelman/research/unpublished/p_hacking.pdf (accessed on 26 November 2020).
- Gignac, Gilles E. 2015. Raven’s is not a pure measure of general intelligence: Implications for g factor theory and the brief measurement of g. Intelligence 52: 71–79. [Google Scholar] [CrossRef]
- Goode, Natassia, and Jens F. Beckmann. 2010. You need to know: There is a causal relationship between structural knowledge and control performance in complex problem solving tasks. Intelligence 38: 345–52. [Google Scholar] [CrossRef]
- Greiff, Samuel, Andreas Fischer, Sascha Wüstenberg, Philipp Sonnleitner, Martin Brunner, and Romain Martin. 2013. A multitrait-multimethod study of assessment instruments for complex problem solving. Intelligence 41: 579–96. [Google Scholar] [CrossRef]
- Greiff, Samuel, Katarina Krkovic, and Jarkko Hautamäki. 2016. The Prediction of Problem-Solving Assessed Via Microworlds: A Study on the Relative Relevance of Fluid Reasoning and Working Memory. European Journal of Psychological Assessment 32: 298–306. [Google Scholar] [CrossRef]
- Greiff, Samuel, Sascha Wüstenberg, and Francesco Avvisati. 2015. Computer-generated log-file analyses as a window into students’ minds? A showcase study based on the PISA 2012 assessment of problem solving. Computers and Education 91: 92–105. [Google Scholar] [CrossRef]
- Jäger, Adolf O., Heinz-Martin Süß, and André Beauducel. 1997. Berliner Intelligenzstruktur-Test. Form 4 [Berlin Intelligence-Structure Test. Version 4]. Göttingen: Hogrefe. [Google Scholar]
- Kretzschmar, André. 2015. Konstruktvalidität des komplexen Problemlösens unter besonderer Berücksichtigung moderner Diagnostischer Ansätze [Construct Validity of Complex Problem Solving with Particular Focus on Modern Assessment Approaches]. Ph.D. Thesis, University of Luxembourg, Luxembourg. [Google Scholar]
- Kretzschmar, André. 2017. Sometimes less is not enough: A commentary on Greiff et al. (2015). Journal of Intelligence 5: 4. [Google Scholar] [CrossRef]
- Kretzschmar, André, and Gilles E. Gignac. 2019. At what sample size do latent variable correlations stabilize? Journal of Research in Personality 80: 17–22. [Google Scholar] [CrossRef] [Green Version]
- Kretzschmar, André, Liena Hacatrjana, and Malgozata Rascevska. 2017. Re-evaluating the psychometric properties of MicroFIN: A multidimensional measurement of complex problem solving or a unidimensional reasoning test? Psychological Test and Assessment Modeling 59: 157–82. [Google Scholar] [CrossRef]
- Kretzschmar, André, Jonas C. Neubert, and Samuel Greiff. 2014. Komplexes Problemlösen, schulfachliche Kompetenzen und ihre Relation zu Schulnoten [Complex problem solving, school competencies and their relation to school grades]. Zeitschrift für Pädagogische Psychologie 28: 205–15. [Google Scholar] [CrossRef]
- Kretzschmar, André, Jonas C. Neubert, Sascha Wüstenberg, and Samuel Greiff. 2016. Construct validity of complex problem solving: A comprehensive view on different facets of intelligence and school grades. Intelligence 54: 55–69. [Google Scholar] [CrossRef]
- Kretzschmar, André, Marion Spengler, Anna-Lena Schubert, Ricarda Steinmayr, and Matthias Ziegler. 2018. The Relation of Personality and Intelligence—What Can the Brunswik Symmetry Principle Tell Us? Journal of Intelligence 6: 30. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kretzschmar, André, and Heinz-Martin Süß. 2015. A study on the training of complex problem solving competence. Journal of Dynamic Decision Making 1: 4. [Google Scholar] [CrossRef]
- Kyriazos, Theodoros A. 2018. Applied Psychometrics: Sample Size and Sample Power Considerations in Factor Analysis (EFA, CFA) and SEM in General. Psychology 9: 2207–30. [Google Scholar] [CrossRef] [Green Version]
- Little, Roderick J. A. 1988. A test of missing completely at random for multivariate data with missing values. Journal of the American Statistical Association 83: 1198–202. [Google Scholar] [CrossRef]
- Lohman, David F., and Joni M. Lakin. 2011. Intelligence and Reasoning. In The Cambridge Handbook of Intelligence. Edited by Robert J. Sternberg and Scott Barry Kaufman. Cambridge and New York: Cambridge University Press, pp. 419–441. [Google Scholar]
- Mainert, Jakob, André Kretzschmar, Jonas C. Neubert, and Samuel Greiff. 2015. Linking complex problem solving and general mental ability to career advancement: Does a transversal skill reveal incremental predictive validity? International Journal of Lifelong Education 34: 393–411. [Google Scholar] [CrossRef]
- McGrew, Kevin S. 2009. CHC theory and the human cognitive abilities project: Standing on the shoulders of the giants of psychometric intelligence research. Intelligence 37: 1–10. [Google Scholar] [CrossRef]
- Müller, Jonas C., André Kretzschmar, and Samuel Greiff. 2013. Exploring exploration: Inquiries into exploration behavior in complex problem solving assessment. Paper presented at 6th International Conference on Educational Data Mining (EDM), Memphis, Tennessee, July 6–9; pp. 336–37. [Google Scholar]
- Oberauer, Klaus, R. Schulze, Oliver Wilhelm, and Heinz-Martin Süß. 2005. Working Memory and Intelligence-Their Correlation and Their Relation: Comment on Ackerman, Beier, and Boyle (2005). Psychological Bulletin 131: 61–65. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oberauer, Klaus, Heinz-Martin Süß, Oliver Wilhelm, and Werner W. Wittmann. 2003. The multiple faces of working memory: Storage, processing, supervision, and coordination. Intelligence 31: 167–193. [Google Scholar] [CrossRef] [Green Version]
- Paunonen, Sampo V., and Michael C. Ashton. 2001. Big Five factors and facets and the prediction of behavior. Journal of Personality and Social Psychology 81: 524–39. [Google Scholar] [CrossRef] [PubMed]
- Rammstedt, Beatrice, Clemens Lechner, and Daniel Danner. 2018. Relationships between Personality and Cognitive Ability: A Facet-Level Analysis. Journal of Intelligence 6: 28. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raven, Jean, John C. Raven, and John Hugh Court. 1998. Manual for Raven’s Progressive Matrices and Vocabulary Scales. San Antonio: Harcourt Assessment. [Google Scholar]
- Redick, Thomas S., Shipstead Zach, Matthew E. Meier, Janelle J. Montroy, Kenny L. Hicks, Nash Unsworth, Michael J. Kane, Zachary D. Hambrick, and Randall W. Engle. 2016. Cognitive predictors of a common multitasking ability: Contributions from working memory, attention control, and fluid intelligence. Journal of Experimental Psychology General 145: 1473–92. [Google Scholar] [CrossRef]
- Rudolph, Julia, Samuel Greiff, Anja Strobel, and Franzis Preckel. 2018. Understanding the link between need for cognition and complex problem solving. Contemporary Educational Psychology 55: 53–62. [Google Scholar] [CrossRef]
- Schermelleh-Engel, Karin, Helfried Moosbrugger, and Hans Müller. 2003. Evaluating the fit of structural equation models: Tests of significance and descriptive goodness-of-fit measures. Methods of Psychological Research 8: 23–74. [Google Scholar]
- Shadish, William R., Thomas D. Cook, and Donald T. Campbell. 2002. Experimental and Quasi-Experimental Designs for Generalized Causal Inference. Boston: Houghton Mifflin. [Google Scholar]
- Spengler, Marion, Oliver Lüdtke, Romain Martin, and Martin Brunner. 2013. Personality is related to educational outcomes in late adolescence: Evidence from two large-scale achievement studies. Journal of Research in Personality 47: 613–25. [Google Scholar] [CrossRef]
- Stadler, Matthias, Miriam Aust, Nicolas Becker, Christoph Niepel, and Samuel Greiff. 2016. Choosing between what you want now and what you want most: Self-control explains academic achievement beyond cognitive ability. Personality and Individual Differences 94: 168–72. [Google Scholar] [CrossRef]
- Stadler, Matthias, Nicolas Becker, Markus Gödker, Detlev Leutner, and Samuel Greiff. 2015. Complex problem solving and intelligence: A meta-analysis. Intelligence 53: 92–101. [Google Scholar] [CrossRef]
- Süß, Heinz-Martin. 1996. Intelligenz, Wissen und Problemlösen: Kognitive Voraussetzungen für erfolgreiches Handeln bei Computersimulierten Problemen [Intelligence, Knowledge and Problem Solving: Cognitive Prerequisites for Successful Behavior in Computer-Simulated Problems]. Göttingen: Hogrefe. [Google Scholar]
- Süß, Heinz-Martin, and André Beauducel. 2005. Faceted Models of Intelligence. In Handbook of Understanding and Measuring Intelligence. Edited by Oliver Wilhelm and Randall W. Engle. Thousand Oaks: Sage Publications, pp. 313–332. [Google Scholar]
- Süß, Heinz-Martin, and André Beauducel. 2015. Modeling the construct validity of the Berlin Intelligence Structure Model. Estudos de Psicologia (Campinas) 32: 13–25. [Google Scholar] [CrossRef] [Green Version]
- Süß, Heinz-Martin, and André Kretzschmar. 2018. Impact of Cognitive Abilities and Prior Knowledge on Complex Problem Solving Performance–Empirical Results and a Plea for Ecologically Valid Microworlds. Frontiers in Psychology 9. [Google Scholar] [CrossRef] [Green Version]
- Thompson, William Hedley, Jessey Wright, Patrick G. Bissett, and Russell A. Poldrack. 2020. Dataset decay and the problem of sequential analyses on open datasets. eLife 9: e53498. [Google Scholar] [CrossRef] [PubMed]
- Wagener, Dietrich. 2001. Psychologische Diagnostik mit komplexen Szenarios-Taxonomie, Entwicklung, Evaluation [Psychological Assessment with Complex Scenarios-Taxonomy, Development, Evaluation]. Lengerich: Pabst Science Publishers. [Google Scholar]
- Wagener, Dietrich, and Werner W. Wittmann. 2002. Personalarbeit mit dem komplexen Szenario FSYS: Validität und Potential von Verhaltensskalen [Human resource management using the complex scenario FSYS: Validity and potential of behavior scales]. Zeitschrift Für Personalpsychologie 1: 80–93. [Google Scholar] [CrossRef]
- Weston, Sara J., Stuart J. Ritchie, Julia M. Rohrer, and Andrew K. Przybylski. 2019. Recommendations for Increasing the Transparency of Analysis of Preexisting Data Sets. Advances in Methods and Practices in Psychological Science. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wilhelm, Oliver. 2005. Measuring reasoning ability. In Handbook of Understanding and Measuring Intelligence. Edited by O. Wilhelm and R. W. Engle. London: Sage, pp. 373–92. [Google Scholar]
- Wilhelm, Oliver, and Ralf Schulze. 2002. The relation of speeded and unspeeded reasoning with mental speed. Intelligence 30: 537–54. [Google Scholar] [CrossRef]
- Wittmann, Werner W. 1988. Multivariate reliability theory: Principles of symmetry and successful validation strategies. In Handbook of Multivariate Experimental Psychology, 2nd ed. Edited by John R. Nesselroade and Raymond B. Cattell. New York: Plenum Press, pp. 505–560. [Google Scholar]
- Wittmann, Werner W., and Keith Hattrup. 2004. The relationship between performance in dynamic systems and intelligence. Systems Research and Behavioral Science 21: 393–409. [Google Scholar] [CrossRef]
- Wittmann, Werner W., and Heinz-Martin Süß. 1999. Investigating the paths between working memory, intelligence, knowledge, and complex problem-solving performances via Brunswik symmetry. In Learning and Individual Differences: Process, Trait and Content Determinants. Edited by P. L. Ackerman, P. C. Kyllonen and R. D. Roberts. Washington, DC: APA, pp. 77–104. [Google Scholar]
- Zech, Alexandra, Markus Bühner, Stephan Kröner, Moritz Heene, and Sven Hilbert. 2017. The Impact of Symmetry: Explaining Contradictory Results Concerning Working Memory, Reasoning, and Complex Problem Solving. Journal of Intelligence 5: 22. [Google Scholar] [CrossRef] [Green Version]
- Ziegler, Matthias, Doreen Bensch, Ulrike Maaß, Vivian Schult, Markus Vogel, and Markus Bühner. 2014. Big Five facets as predictor of job training performance: The role of specific job demands. Learning and Individual Differences 29: 1–7. [Google Scholar] [CrossRef]
| 1. | The link to the Brunswik symmetry principle is not always made explicitly. For example, as the bandwidth-fidelity dilemma (Cronbach and Gleser 1965) is closely related to the Brunswik symmetry principle, studies on this topic can also be interpreted in terms of the Brunswik symmetry principle. |
| 2. | As one reviewer correctly pointed out, one could also expect that figural operationalizations should incrementally explain CPS variance above and beyond numerical operationalizations as we assume that the CPS measure put stronger requirements on figural content compared to numerical content. We address this issue in the Discussion section. |
| 3. | The present study used the performance scale of FSYS which was most comparable to CPS operationalizations of previous studies. FSYS also provides additional behavior-based scales, some of which are experimental in nature and were of insufficient psychometric quality in the present study (see, Kretzschmar and Süß 2015). Thus, these scales were not considered here but are included in the freely available data set. |
| 4. | We have also conducted the analyses with the CPS control performance indicator only (i.e., without the indicator of knowledge acquisition) to examine the robustness of the results. Although the effect sizes (e.g., explained CPS variances) differed, the overall pattern of findings was comparable to that of the aggregated CPS score presented here. |
| 5. | The analyses were also performed on the basis of complete data only (i.e., without missing data, N = ), which resulted in almost identical results to those presented here. |


| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Working memory | |||||||||||
| (1) aggregated | 1.00 | ||||||||||
| (2) verbal | 0.33 [0.19,0.47] | 1.00 | |||||||||
| (3) numerical | 0.43 [0.28,0.57] | 0.38 [0.22,0.52] | 1.00 | ||||||||
| (4) figural | 0.26 [0.11,0.40] | 0.15 [0.00,0.30] | 0.28 [0.12,0.44] | 1.00 | |||||||
| Fluid reasoning | |||||||||||
| (5) aggregated | 0.52 [0.41,0.63] | 0.25 [0.10,0.39] | 0.37 [0.23,0.49] | 0.51 [0.39,0.61] | 1.00 | ||||||
| (6) verbal | 0.25 [0.08,0.40] | 0.28 [0.13,0.42] | 0.05 [−0.12,0.22] | 0.20 [0.04,0.34] | 0.33 [0.17,0.47] | 1.00 | |||||
| (7) numerical | 0.50 [0.37,0.61] | 0.24 [0.10,0.37] | 0.43 [0.30,0.55] | 0.41 [0.27,0.53] | 0.42 [0.27,0.54] | 0.21 [0.04,0.36] | 1.00 | ||||
| (8) figural | 0.42 [0.29,0.53] | 0.04 [−0.11,0.19] | 0.32 [0.19,0.44] | 0.53 [0.41,0.64] | 0.53 [0.41,0.64] | 0.35 [0.19,0.50] | 0.48 [0.35,0.58] | 1.00 | |||
| CPS | |||||||||||
| (9) total | 0.31 [0.13,0.48] | 0.16 [−0.03,0.35] | 0.20 [0.01,0.38] | 0.28 [0.12,0.42] | 0.42 [0.25,0.57] | 0.15 [−0.01,0.31] | 0.38 [0.21,0.54] | 0.42 [0.26,0.56] | 1.00 | ||
| (10) control | 0.32 [0.15,0.47] | 0.13 [−0.05,0.31] | 0.21 [0.02,0.38] | 0.32 [0.16,0.46] | 0.33 [0.16,0.49] | 0.02 [−0.14,0.19] | 0.37 [0.20,0.52] | 0.36 [0.18,0.50] | 0.51 [0.37,0.64] | 1.00 | |
| (11) knowledge | 0.22 [0.02,0.41] | 0.15 [−0.06,0.35] | 0.14 [−0.05,0.33] | 0.16 [−0.00,0.32] | 0.40 [0.20,0.58] | 0.24 [0.06,0.42] | 0.30 [0.10,0.47] | 0.37 [0.20,0.52] | 0.51 [0.37,0.64] | 0.51 [0.37,0.64] | 1.00 |
| M | 0.00 | 0.07 | 0.02 | 0.04 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 57.59 | 5.32 |
| SD | 0.72 | 0.95 | 0.98 | 1.00 | 0.81 | 0.71 | 0.77 | 0.80 | 0.87 | 22.51 | 1.94 |
| ω | 0.57 | 0.88 | 0.82 | 0.73 | 0.74 | 0.54 | 0.66 | 0.72 | 0.69 | 0.80 | 0.41 |
| WM Aggregated | WM Verbal | WM Numerical | WM Figural | |||||
|---|---|---|---|---|---|---|---|---|
| Fluid Reasoning | Model 1 | Model 2 | Model 1 | Model 2 | Model 1 | Model 2 | Model 1 | Model 2 |
| aggregated | Condition 1 | Condition 2 | Condition 3 | Condition 4 | ||||
| a | 0.65 [0.52;0.77] | 0.65 [0.52;0.77] | 0.29 [0.12;0.45] | 0.29 [0.12;0.45] | 0.44 [0.29;0.59] | 0.44 [0.29;0.59] | 0.65 [0.52;0.78] | 0.65 [0.52;0.79] |
| b | 0.53 [0.33;0.71] | 0.49 [0.11;0.83] | 0.53 [0.32;0.72] | 0.52 [0.29;0.72] | 0.53 [0.32;0.72] | 0.52 [0.27;0.77] | 0.52 [0.32;0.71] | 0.53 [0.20;0.93] |
| c | 0.05 [−0.33;0.46] | 0.02 [−0.20;0.25] | 0.01 [−0.26;0.29] | −0.01 [−0.41;0.31] | ||||
| 0.27 [0.10;0.50] | 0.26 [0.11;0.53] | 0.27 [0.10;0.51] | 0.27 [0.10;0.52] | 0.27 [0.10;0.51] | 0.27 [0.10;0.53] | 0.27 [0.10;0.50] | 0.26 [0.10;0.54] | |
| verbal | Condition 5 | Condition 6 | Condition 7 | Condition 8 | ||||
| a | 0.33 [0.12;0.53] | 0.32 [0.11;0.52] | 0.35 [0.17;0.52] | 0.35 [0.16;0.52] | 0.07 [−0.15;0.28] | 0.06 [−0.16;0.27] | 0.28 [0.07;0.47] | 0.27 [0.07;0.46] |
| b | 0.23 [0.01;0.45] | 0.04 [−0.22;0.28] | 0.21 [−0.01;0.43] | 0.14 [−0.09;0.37] | 0.21 [−0.01;0.43] | 0.18 [−0.05;0.40] | 0.22 [0.00;0.44] | 0.10 [−0.14;0.33] |
| c | 0.41 [0.15;0.66] | 0.14 [−0.12;0.39] | 0.24 [0.01;0.48] | 0.33 [0.12;0.55] | ||||
| 0.05 [−0.01;0.20] | 0.17 [0.03;0.42] | 0.04 [−0.01;0.18] | 0.04 [−0.01;0.21] | 0.04 [−0.01;0.18] | 0.08 [0.00;0.29] | 0.04 [−0.01;0.19] | 0.13 [0.03;0.33] | |
| numerical | Condition 9 | Condition 10 | Condition 11 | Condition 12 | ||||
| a | 0.64 [0.49;0.77] | 0.63 [0.48;0.77] | 0.29 [0.11;0.44] | 0.28 [0.11;0.44] | 0.53 [0.37;0.67] | 0.53 [0.37;0.68] | 0.54 [0.38;0.69] | 0.53 [0.37;0.69] |
| b | 0.50 [0.30;0.68] | 0.39 [0.04;0.77] | 0.49 [0.29;0.68] | 0.47 [0.25;0.67] | 0.49 [0.29;0.67] | 0.49 [0.22;0.81] | 0.49 [0.29;0.68] | 0.42 [0.13;0.70] |
| c | 0.14 [−0.30;0.52] | 0.05 [−0.19;0.28] | −0.01 [−0.39;0.31] | 0.12 [−0.17;0.40] | ||||
| 0.24 [0.08;0.46] | 0.23 [0.09;0.48] | 0.23 [0.08;0.46] | 0.23 [0.08;0.46] | 0.23 [0.08;0.44] | 0.23 [0.08;0.49] | 0.24 [0.08;0.45] | 0.23 [0.09;0.46] | |
| figural | Condition 13 | Condition 14 | Condition 15 | Condition 16 | ||||
| a | 0.53 [0.38;0.67] | 0.52 [0.37;0.66] | 0.06 [−0.12;0.24] | 0.05 [−0.13;0.23] | 0.40 [0.24;0.55] | 0.39 [0.24;0.54] | 0.68 [0.54;0.81] | 0.69 [0.54;0.82] |
| b | 0.54 [0.35;0.71] | 0.44 [0.12;0.69] | 0.53 [0.34;0.71] | 0.52 [0.32;0.70] | 0.53 [0.34;0.71] | 0.51 [0.27;0.72] | 0.52 [0.32;0.70] | 0.56 [0.22;0.92] |
| c | 0.16 [−0.15;0.48] | 0.18 [−0.03;0.39] | 0.04 [−0.21;0.31] | −0.05 [−0.44;0.29] | ||||
| 0.29 [0.11;0.51] | 0.28 [0.13;0.52] | 0.28 [0.11;0.50] | 0.31 [0.14;0.54] | 0.28 [0.11;0.50] | 0.27 [0.12;0.51] | 0.27 [0.10;0.48] | 0.27 [0.11;0.52] | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kretzschmar, A.; Nebe, S. Working Memory, Fluid Reasoning, and Complex Problem Solving: Different Results Explained by the Brunswik Symmetry. J. Intell. 2021, 9, 5. https://0-doi-org.brum.beds.ac.uk/10.3390/jintelligence9010005
Kretzschmar A, Nebe S. Working Memory, Fluid Reasoning, and Complex Problem Solving: Different Results Explained by the Brunswik Symmetry. Journal of Intelligence. 2021; 9(1):5. https://0-doi-org.brum.beds.ac.uk/10.3390/jintelligence9010005
Chicago/Turabian StyleKretzschmar, André, and Stephan Nebe. 2021. "Working Memory, Fluid Reasoning, and Complex Problem Solving: Different Results Explained by the Brunswik Symmetry" Journal of Intelligence 9, no. 1: 5. https://0-doi-org.brum.beds.ac.uk/10.3390/jintelligence9010005





