1. Introduction
In a recent issue of the
Journal of Intelligence,
McFarland (
2020) compares traditional latent variable models of intelligence to more recent psychometric network models. In contrast to
Kan et al. (
2019) and
Schmank et al. (
2019), McFarland finds that latent variable models generally outperform network models. McFarland suggests that previous support for network models reported by
Kan et al. (
2019) and
Schmank et al. (
2019) is limited to analyses based on partial, rather than uncorrected, correlation matrices. If correct, this finding calls into question recent claims that psychometric network models provide unique support for theories of intelligence like mutualism and process overlap theory.
We are grateful to McFarland for providing such a detailed comparison of latent variable and network models of intelligence. In many ways, it is representative of his program of research on intelligence, which managed to combine statistical rigor and theoretical impact. Indeed, it has forced us to reconsider both methodological and theoretical aspects of our recent work on psychometric network models of intelligence. It has also provided us with plenty of food for thought and ideas for future research.
At the same time, unfortunately, we get the impression that McFarland misunderstood some methodological details, as well as the overall purpose of
Kan et al. (
2019) and
Schmank et al. (
2019).
Kan et al. (
2020) have already addressed McFarland’s misconceptions of
Kan et al. (
2019) and so we focus here on issues that pertain to
Schmank et al. (
2019). We also report an analysis of Wechsler Adult Intelligence Scale–Fourth Edition (WAIS-IV) data generously provided by McFarland. We conducted the same exact statistical procedures reported in
Schmank et al. (
2019). To preview, the results are consistent with
Schmank et al. (
2019) and
Kan et al. (
2019) and illustrate that network models can account for the psychometric structure of intelligence and should therefore be considered as a viable alternative to latent variable models. For many investigators, network models are an attractive alternative because they are more compatible with recent theories of intelligence like mutualism (
Van Der Maas et al. 2006) and process overlap theory (
Kovacs and Conway 2016). We argue that compatibility between theories and models of intelligence can, and should, guide model selection.
We review here two general concerns with the discussion of our previous research by
McFarland (
2020). First, McFarland states, “[t]he rationale for the use of partial correlations is that one can rule out the relationship between any pair of variables as being due to the other variables in the analysis and thus more readily infer causation” (p. 1). We agree that partial correlations can be used for this purpose; however, this was not the rationale behind the
Schmank et al. (
2019) study. Psychometric network modeling offers an alternative approach to investigations of the underlying structure of individual differences in cognitive abilities (i.e., intelligence), without the assumptions that come with reflective latent variable models (
Conway et al. 2021; see also
Goring et al. 2019). According to the view of intelligence endorsed by
Schmank et al. (
2019), process overlap theory (
Kovacs and Conway 2016), there is no need to assume that (all or some of) the factors in higher-order factor models represent common causes of individual differences in test performance. It is in this sense that process overlap theory fits with the network approach, which also does not assume the presence of reflective latent variables.
Second,
McFarland (
2020) states “[b]oth
Kan et al. (
2019) and
Schmank et al. (
2019) compared model fit indices for network models with those for traditional latent variable models” (p. 1). He then goes on to state “[o]ne problem in attempting to compare network models with traditional latent variable models […] is that the two deal with different aspects of test correlations” (p. 2). The first statement is inconsistent with
Schmank et al. (
2019): “[d]irect model comparisons were not conducted […] we caution readers from making direct comparisons based on the presented model fit indices” (p. 7). To be clear, these two kinds of models can be compared in principle, namely when they are both confirmatory, but this was not the case here. The second statement is also inaccurate. The data for all latent variable and psychometric network modeling analyses were uncorrected correlation matrices.
To be sure, we reviewed our R scripts (
https://osf.io/3wpcm/) but we found no direct comparisons of network models and latent variable models or partial correlations matrices. However, in our original pre-print of the
Schmank et al. (
2019) publication (
https://osf.io/f9d2v/), we did report a direct comparison of the models. We therefore assume that the pre-print was the source of the confusion. To be clear, that pre-print was an unpublished draft and was later revised. The direct comparison between the model fit of latent variable and psychometric network models was not included in
Schmank et al. (
2019).
3. Results
The correlation matrices used in the current project are presented in
Table 1,
Table 2 and
Table 3. Model fit indices are presented in
Table 4,
Table 5 and
Table 6. Two sets of fit indices are reported because we estimated model fit using two R packages: lavaan and openMx. The packages differ with respect to model specification and estimation but the results here are identical. This was established and reported here to check the accuracy of our results and to facilitate reproducibility.
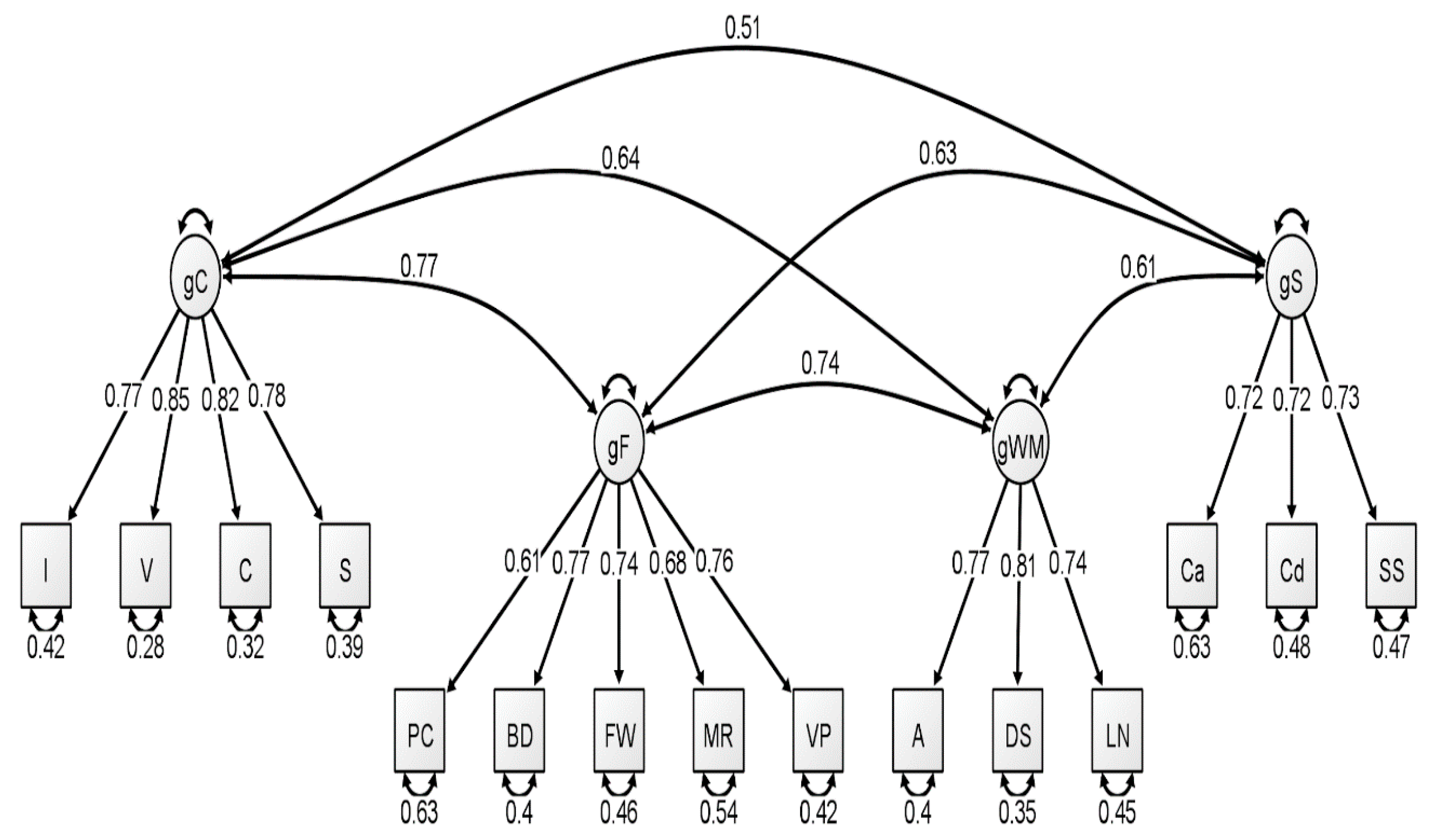
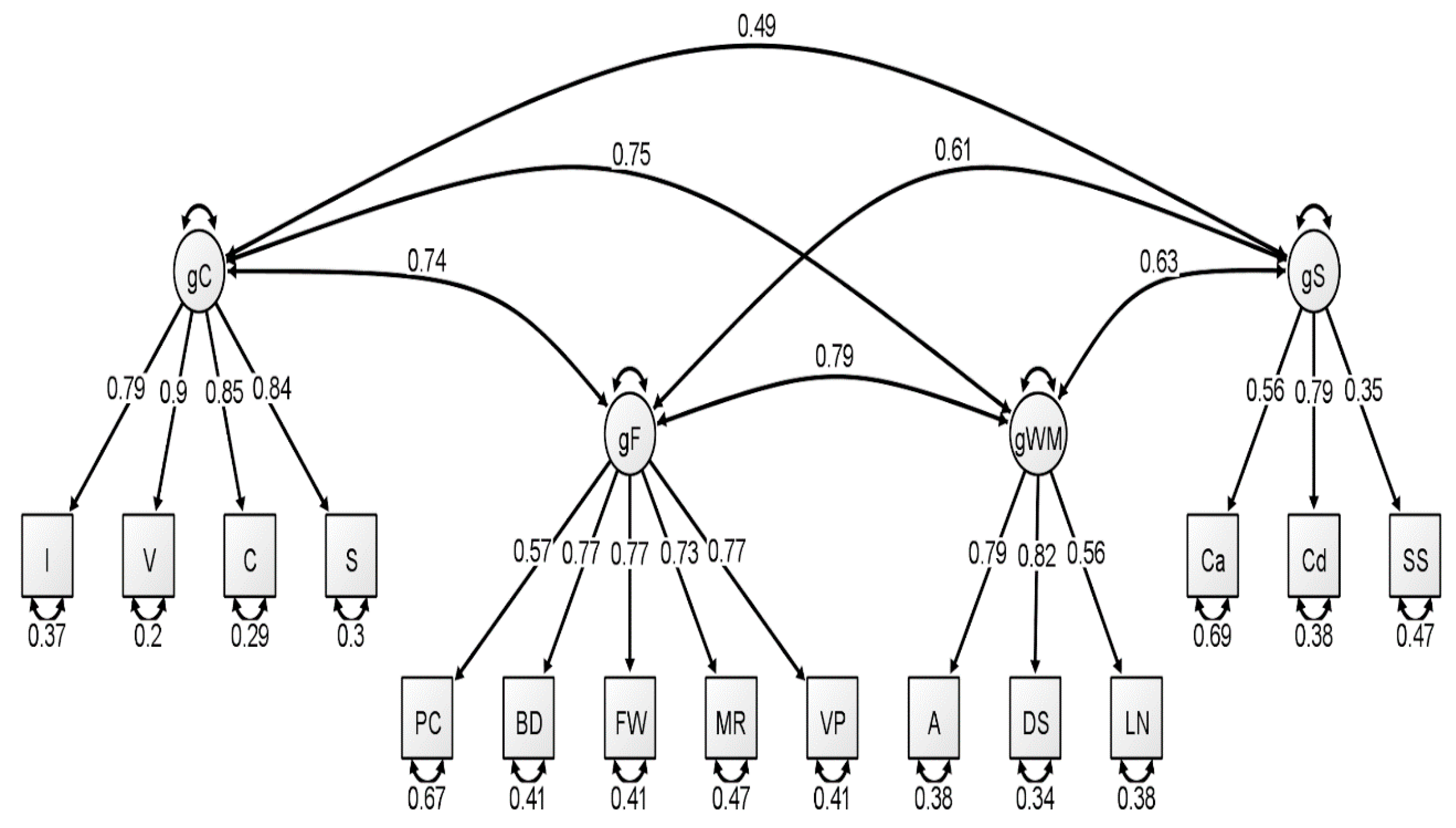
With respect to the latent variable modeling analysis, the correlated four-factor model (Model 1) was preferred over the higher-order model (Model 2), based on model comparisons: Younger Group: Δχ
2(2) = 5.56,
p = 0.06; Middle Group: Δχ
2(2) = 15.36,
p < 0.001; Older Group: Δχ
2(2) = 21.01,
p < 0.001. For a visualization of these three models, see
Figure 1,
Figure 2 and
Figure 3. In our original publication (
Schmank et al. 2019), we presented data representative of the higher-order (g theory) model of intelligence, as this model tends to be the most well-known specification of latent variable models of intelligence. However, our findings after conducting these analyses on the McFarland data are inconsistent with a preference for the higher-order model of intelligence. Thus, when considering latent variable modeling, the three standardized WAIS-IV correlation matrices used by McFarland fit best when specifying a correlated, four-factor latent variable model.
Consistent with the results of
Schmank et al. (
2019), most fit indices indicated that the latent variable models provided an acceptable fit to the WAIS-IV data, with the exception of the chi-square test, which was nonsignificant for all latent variable models. However, the ratio of χ
2 to degrees of freedom was less than 3.00 for three latent variable models: each model attributed to the younger group and for the higher-order model attributed to the older group. The reported RMSEA values for all latent variable models exceeded the conservative value used by the current authors to demonstrate appropriate model fit (all latent variable RMSEA values were 0.07). However, these RMSEA values would be adequate based on more liberal standards (see
Browne and Cudeck 1993;
Schermelleh-Engel et al. 2003). Additionally, comparative fit indices (i.e., CFI and TLI) demonstrated values in the acceptable range for all latent variable analyses. We also considered the quality of each measure by evaluating the standardized factor loadings in each model. The squared value of the standardized factor loading indicates the amount of variance in the measure that can be explained by the overarching latent construct. For the younger group, only two standardized loadings, specific to the fluid reasoning latent variable, failed to surpass the cutoff value of 0.70 that is typically used to indicate a quality measure (see
Schmank et al. 2019). For the middle group, four standardized loadings failed to surpass the 0.70 cutoff value, specific to fluid reasoning, working memory, and processing speed. Finally, the oldest group demonstrated two standardized loadings that failed to reach 0.70, specific to the fluid reasoning and processing speed latent variables.
With respect to the exploratory psychometric network modeling analysis, consistent with
Schmank et al. (
2019), the network models indicated excellent model fit across the majority of reported fit indices. First, only the psychometric network model for the middle group demonstrated a statistically significant χ
2 value (
p < 0.05); however, the value of the ratio between χ
2 and degrees of freedom for each of these models was well below the 3.00 cutoff value determined prior to analyses. Finally, the comparative fit indices (i.e., CFI and TLI) demonstrated near perfect fit, while RMSEA values were well below the cutoff value specified.
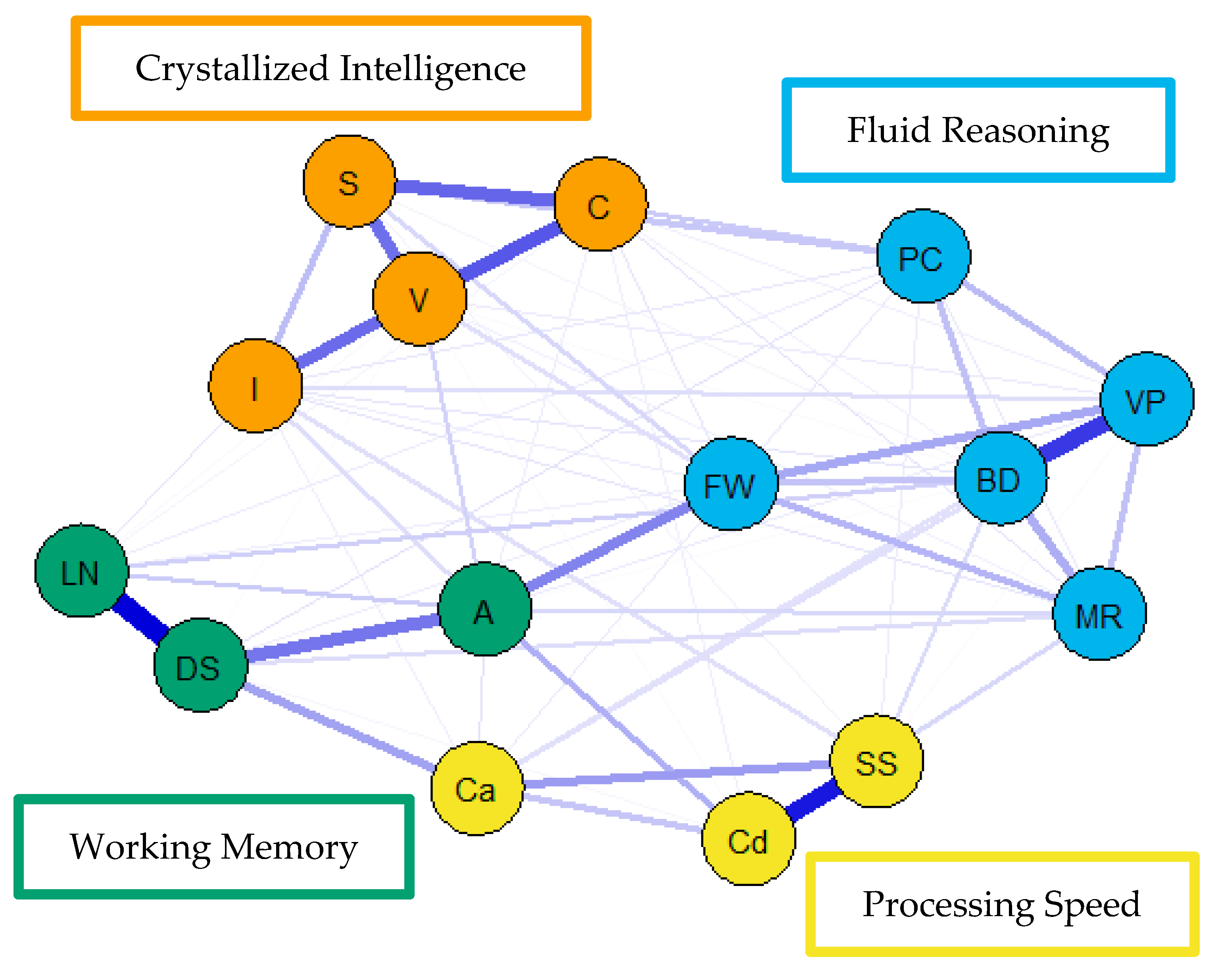
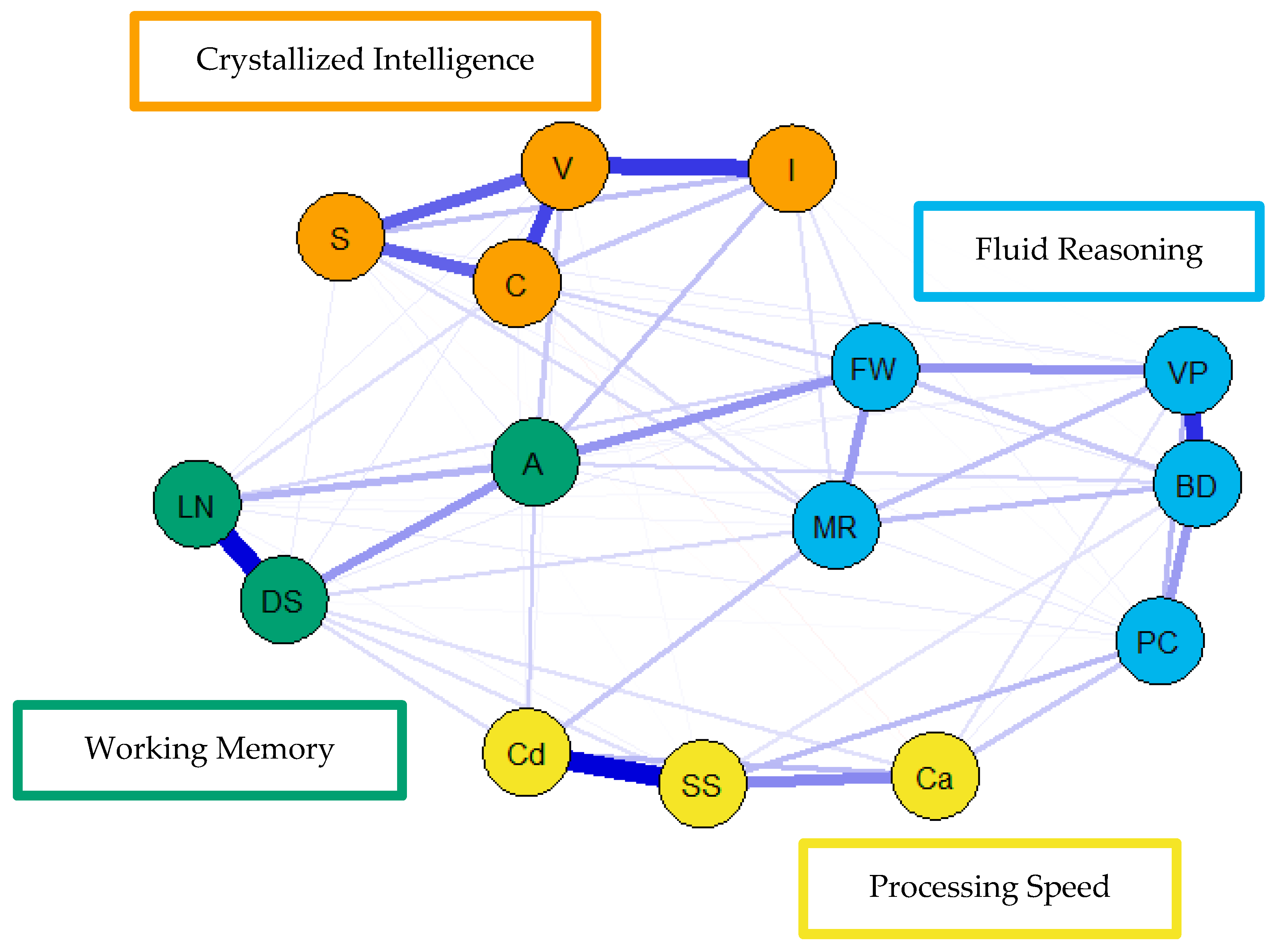
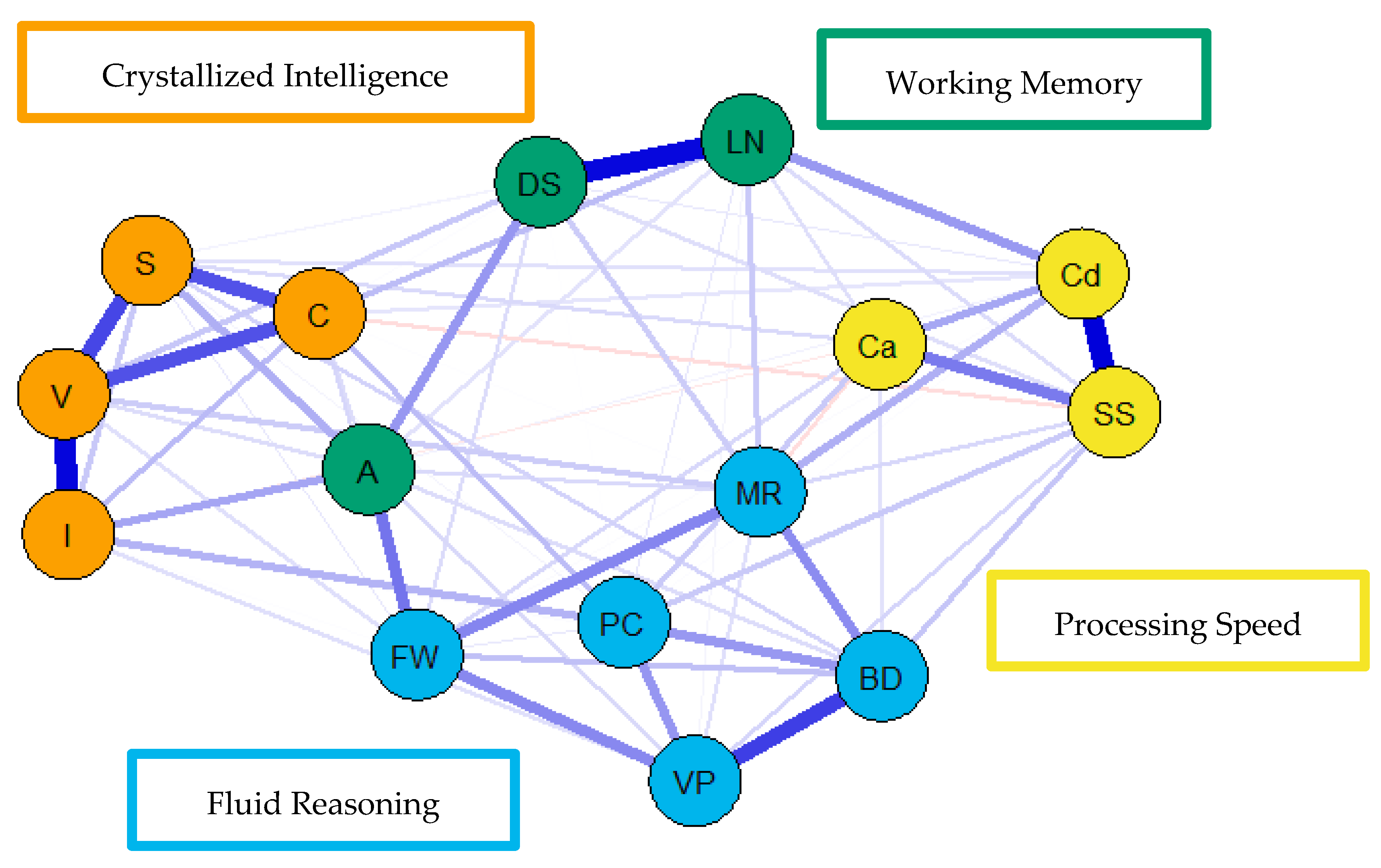
For the visualization of the psychometric network models, see
Figure 4,
Figure 5 and
Figure 6. First, nodes in the models have been colored to reflect the latent structure of the finalized measurement model. Second, the connections between nodes have been colored so that blue and red indicate positive and negative partial correlations, respectively. Third, the width of each connection between nodes represents the magnitude or size of the association or partial correlation estimated between each pair of cognitive task nodes. Additionally, the psychometric network models and their respective exploratory graph analyses revealed four clusters or latent dimensions. For the young (
Figure 4), middle (
Figure 5), and older groups (
Figure 6) these four dimensions reflect crystallized intelligence, fluid reasoning, working memory, and processing speed. Interestingly, the Arithmetic (A) node in the older group network was explained by the crystallized intelligence dimension and not the working memory or fluid reasoning dimensions. Finally, three additional network models were generated that shared an averaged network layout (
Figure 7).
4. Discussion
The current commentary addressed several inaccurate statements made by
McFarland (
2020). The commentary also provided an opportunity to further examine confirmatory latent variable models and exploratory psychometric network models of intelligence. Our general goal was to establish that psychometric network modeling can provide an alternative approach of the psychometric structure of test scores from the WAIS-IV like latent variable modeling. Furthermore, uncorrected correlation matrices of standardized WAIS-IV data provided by
McFarland (
2020) were submitted to the statistical procedures used by
Schmank et al. (
2019).
The results are consistent with the findings presented in
Kan et al. (
2019) and
Schmank et al. (
2019). Based on the criteria provided by
Schreiber et al. (
2006), when confirmatory latent variable modeling and psychometric network modeling techniques were applied to the WAIS-IV correlation matrices provided by
McFarland (
2020), the resulting model fit indices were generally within what best practices and standards deem acceptable. From the perspective of model fit indices, we have corroborated the major findings presented by
Kan et al. (
2019); however, due to the exploratory nature of the psychometric network models and the confirmatory nature of the latent variable models, a direct comparison was not tenable as these types of analyses represent two separate stages of the psychometric research process, exploration, and confirmation.
It is worth restating the main point presented in
Schmank et al. (
2019): that theories of intelligence like mutualism and process overlap theory (
Kovacs and Conway 2016) are incompatible with reflective, higher-order latent variable models. By assuming process overlap theory,
g is viewed as an emergent property or index and not some higher-order reflective factor. Process overlap theory is, however, compatible with psychometric network analysis. Furthermore, the psychometric network models presented in the current project are visual representations of the positive manifold as interconnected networks of the interaction between pairs of cognitive tests, similar to how process overlap theory proposes formative
g using the explanation of the positive manifold via overlapping general and specific processes. Ultimately, this demonstrates that psychometric network models are viable alternatives to latent variable models. In future, projects focused on theory building or theory assessment must first determine the underlying data-generating mechanisms assumed by the theories to establish whether a latent variable or psychometric network approach is most appropriate.
5. Limitations and Future Directions
The aim of this paper was to address specific comments by
McFarland (
2020) regarding the network models reported in
Schmank et al. (
2019). Therefore, many remaining important theoretical issues, as well as further analyses of the current data, are beyond the scope of the current paper. In particular, the conditions of comparability of the model fit of network and latent variable models will probably invoke important exchanges in the future.
A shortcoming of the current study is that it did not address the developmental question introduced by McFarland, that is, we did not repeat the analysis for different age categories. This clearly is a possible line of future research. In particular, such an analysis would make cross-validation possible, just like in the case of McFarland’s analysis.
Additionally, some of the models fitted by McFarland, such as a bifactor model and a penta-factor model, were not investigated in the current paper. Since these were important aspects of McFarland’s paper, further investigation on the matters discussed in this paper should address them. Our purpose with the current paper was to focus on what we perceived as central issues of McFarland’s paper as well as possible misconceptions of our previous results. There are excellent ideas and analyses in
McFarland (
2020) that have not been addressed here and which are worthy of exploration by future research.