1. Introduction
Antibiotic resistance is rising to dangerously high levels in all parts of the world. Over-prescription and misusage cause natural selection that favors strains with new resistance mechanisms, threatening our ability to treat common infectious diseases effectively. Many factors can affect bacterial susceptibility to antibiotics, including the metabolic state and the presence of persistent cells [
1,
2,
3], the microenvironment conditions that affect the antibiotic potency [
4], the physical structure of the population (biofilms) [
5], and the population size, or inoculum, at the site of infection. Indeed, a major power of bacteria is within numbers since it has been well established that as a population, bacteria often survive a concentration of an antimicrobial agent that is lethal to individual cells. In a therapeutic context, this means that the fate of an initial infection depends on the initial load of bacteria—while small infections are easily cleared even with no antibiotics, large infections are hazardous, even when antibiotics are administered at high doses. This phenomenon, known as the “inoculum effect” (IE), is well established in-vitro [
6,
7,
8,
9,
10,
11,
12], as well as in-vivo in animal models and in human patients [
11,
13,
14,
15,
16,
17,
18,
19].
The IE is a bistable effect [
9,
12]—a system is said to be monostable if it always equilibrates to one final state, and bistable when it admits more than one stable state [
20]. In a clinical situation, having bistable behavior is unfavorable since the treatment outcome is difficult to predict even if the dynamics (drug–target interaction) is assumed to be deterministic. Treating with insufficient antibiotics doses can lead to ineffective bacterial clearing and patients mortality [
21], as well as favors the selection of drug-resistant strains [
22,
23]. It is therefore a common practice to administer antibiotics in excessive dosages, which may weaken the immune system. An optimal treatment achieves a complete eradication of the infection with minimal antibiotics dosing, yet, the IE complicates the determination of such an optimal strategy [
12,
23,
24,
25,
26].
There are several known biological mechanisms that were proposed to account for the IE. First, it is known that the
E. coli spontaneous beneficial mutation rate is 10
−5 mutations per genome per generation [
27]. Thus, bacterial populations equal to or larger than 10
5 may contain
genetic heterogeneity to antibiotic resistance [
28,
29].
Phenotypic heterogeneity [
1,
2,
3,
7] is also more prominent in these larger initial populations. This heterogeneity can generate bistability: at low numbers we expect that only one, non-resistant population exists, hence treatment leads to extinction, whereas at high initial numbers heterogeneity may allow a resistant strain to grow, leading to bistability.
Second,
density-dependent mechanisms may also lead to an IE. The bacterial density affects both the cellular state of the cell, and its interactions with the antimicrobial agent. Cellular communication that is sensitive to population density is called quorum sensing. Quorum sensing enables bacteria to synchronize gene expression and alter their properties to become more resistant to different antibiotics. At low cell densities, a large proportion of the signaling factors disperse before they can be used, and so their production provides a small direct or indirect fitness benefit. At high cell densities, a much greater proportion of the signaling factors is available per cell, and consequently bacteria can better cope with the relevant stressor [
30]. Another density-dependent mechanism, which does not involve cellular signaling, is reduction in the antibiotic concentration. For instance,
E. coli secrete the β-lactamase enzyme that cleaves and inactivates β-lactam antibiotics [
31]. A large population produces more β-lactamase then a small population and can therefore degrade the antibiotic faster [
32,
33,
34]. If the population survives and grows, more enzyme is produced and cleaves the antibiotic in a higher rate—a positive feedback mechanism. A similar concept applies when an antibiotic agent binds to its target or to non-specific cell components and its effective concentration is therefore reduced. This might not have much effect when the antibiotic concentration is sufficiently large compared to the population size, but it is expected to lead to a bistable situation at a critical ratio. Even if the antibiotic concentration does not change in time, bistable behavior can arise when growth is proportional to the amount of antibiotic molecules available to each bacterium at the time of exposure [
11,
35]. The above density dependent mechanisms are inherently nonlinear since they do not increase gradually, proportionally to the bacterial load and antimicrobial concentration, but rather have either a threshold or limiting effects.
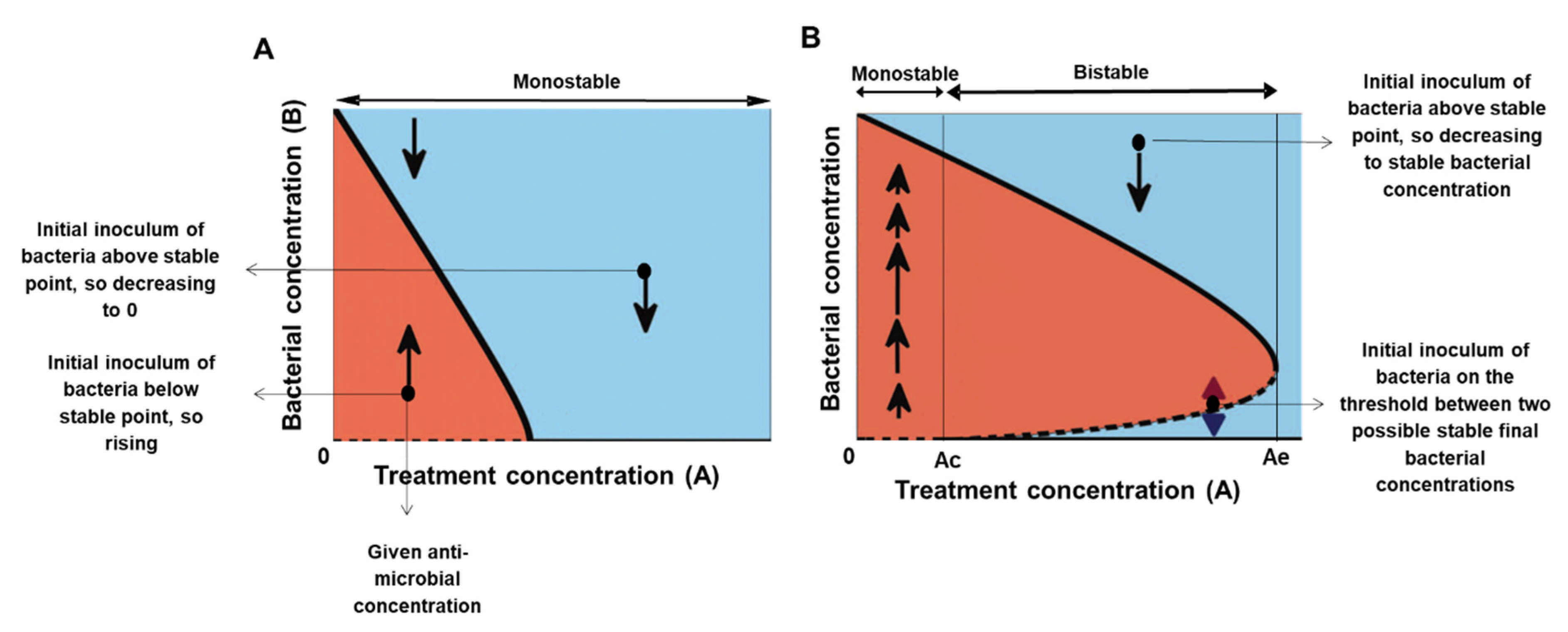
In the bacteria-antimicrobial context, a monostable system corresponds to the case where any initial number of bacteria (
B) reaches the same maximal population size if treated with antibiotic concentration (
A) that does not kill all cells (“sub-lethal treatment”). A lethal treatment leads to eradication of all loads, and therefore, the fate of the system is independent of the initial load (
Figure 1A). In a bistable situation, the fate of the system may depend on its initial load. Here, for a range of the antimicrobial agent concentrations, the bacterial population can assume two possible states (the two solid black lines in
Figure 1B), depending on whether the initial bacterial concentration was above or under the threshold concentration
(dashed black line in
Figure 1B). Three main regimes govern this bistable dependence. First, a minimal antibiotic/peptide concentration
is needed to kill or inhibit a minute number of bacterial cells, so for
, even minute bacterial populations grow, similar to untreated cells. Second, an enormous amount of antimicrobial agent inhibits practically any number of cells, so there exists
such that for
all relevant bacterial densities are growth-inhibited or killed. Third, for
, the greater the concentration of the antimicrobial agent, the larger the bacterial concentration it can inhibit and therefore the threshold concentration
is monotonically increasing with A in this range. It follows that for any given antimicrobial agent concentration in the range
, the fate of the bacterial population depends on whether its initial concentration is above or below
(dotted bottom line,
Figure 1B). We thus have a bistable behaviour for all
(
Figure 1B).
The monostable/bistable behaviors appear in nonlinear models depending on a single dynamic variable—the varying bacterial concentration, inhibited by a fixed control parameter—the antimicrobial agent. The latter determines whether a monostable or bistable behavior ensues (see Malka et al. [
20,
36], where neutrophils play the role of the antimicrobial agent). Notably, other more complex mechanisms may also result in a bistable behavior. By Ockham’s razor principle, since the concentration-dependent bistable mechanism is the simplest adequate model, and such a model involves hardly any assumptions on the specifics of the antimicrobial-bacteria interactions, it provides the main underlying mechanism for in-vitro bacteria-antimicrobial dynamics when the antimicrobial action remains fixed (and possibly for in-vivo dynamics under specific conditions, e.g., neutropenic conditions in the case of neutrophils-bacteria interactions [
20,
36]). The inoculum effect [
11,
34,
35] suggests that a similar underlying mechanism may apply to in-vitro bacteria-antibiotics interactions.
Here, we show that every tested antimicrobial agent showed an inoculum effect for
E.coli cells, regardless of the distinct type and mechanism of action of the antimicrobial agent. In particular, we show, for the first time to the best of our knowledge, that classical antimicrobial peptides that do not have specific targets on the bacterial membrane induce an inoculum effect (this was previously observed for some non-classical antimicrobial peptides [
37]). Moreover, we show that the killing induced by these peptides may be described by an even simpler model than those considered in [
11,
20,
35,
36]; Here, the abrupt kill of the bacteria by the peptides exhibits IE. After this, the surviving bacteria grow with no influence of the peptides.
2. Experimental Materials and Methods
2.1. Commercial Antibiotics
Ampicillin sodium salt, kanamycin sulphate, chloramphenicol, carbenicillin disodium salt, oxacillin sodium salt, and gentamicin solution were purchased from Sigma-Aldrich(Rehovot, Israel). Polymixin B was purchased from Fluka BioChemika (Seelze, Germany). and tetracycline hydrochloride was purchased from Sigma-Aldrich (Rehovot, Israel).
2.2. Peptide Synthesis and Purification
Peptides were synthesized by using a 433A synthesizer (Applied Biosystems Rhenium Modiin, Israel) on rink amide 0.65 mmol/mg MBHA (4-Methylbenzhydrylamine) resin, using Fmoc protected amino acids. The synthesized products were washed thoroughly with DMF (Di-Methyl-Formamide) and DCM (Dichloromethane), then dried and cleaved. Cleavage was performed by addition of 95% trifluoroacetic acid (TFA), 2.5% water, and 2.5% TIS (Titanium(II) Sulphide). The peptides were then purified (>98% homogeneity) by reverse-phase High Performance Liquid Chromatography HPLC (RP-HPLC). Purification was performed using a C18 column and a linear gradient (Melittin—20–80%, K6L9—10–90%, MSI-78 (Pexiganin) 10–90%) of acetonitrile in water (final fluid containing 0.1% TFA (v/v)) for 40 min.
2.3. Medium
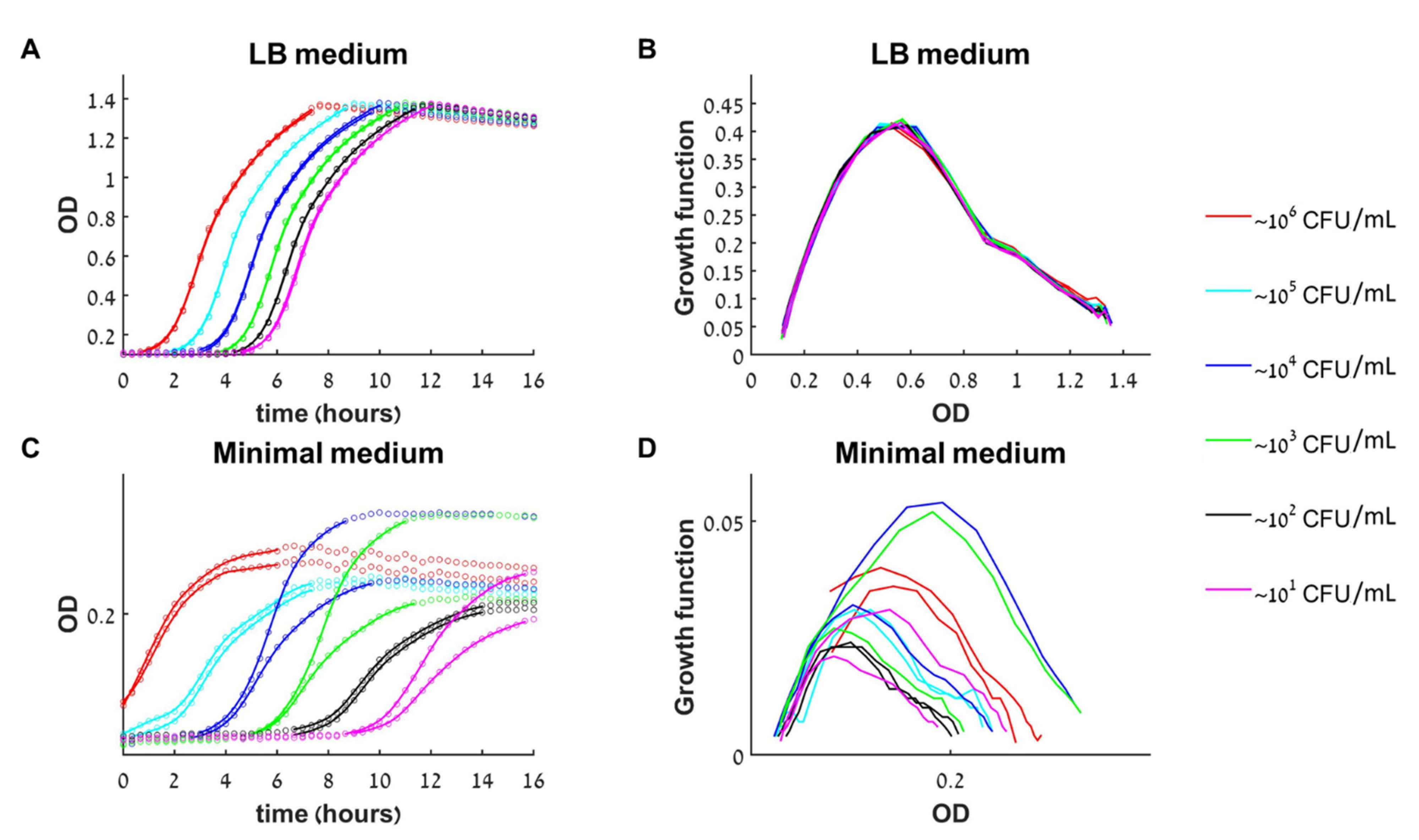
Initially, we tried a BM2 minimal medium [62 mM potassium phosphate buffer, pH 7.0, 7 mM ammonium sulfate, 1 mM magnesium sulfate, 10 μM ferrous sulfate, 0.5% (
w/
v) casamino acids]. We prepared all medium components without glucose, then autoclaved it (sterilize by heating) and then added filtered glucose solution to 0.2% final concentration. Realizing that the minimal medium results in complex behaviour of the control (see discussion of
Figure 2 in results), we used the Luria Broth (LB) medium in all the other experiments as described next.
2.4. Bacterial Strains
E. coli MG1655 with a Lux-kanamycin resistance plasmid (described previously in [
38]) was used for generation of all bacterial growth curves except for the curves generated with kanamycin where non-resistant
E. coli MG1655 was used. Bacteria were grown in minimal medium, Luria Broth (LB) medium or LB+kanamycin (30 µg/mL) medium, shaking in a standard aerated 15 mL tube for bacterial growth at a 37 °C, 200–250 rpm shaking hot room for 4 h (OD
600 = 1–1.5), and then diluted for the experiments.
2.5. Generation of Growth Curves from Various Initial Inoculums
A sterile 96-well plate with a flat bottom was prepared with serial dilutions of the necessary antibiotic/peptide in LB medium (total volume in well 100 µL). In short, an initial high concentration stock of the antibiotic/peptide in DDW was used to make an initial stock in LB to fill 200 µL into wells in row A. Serial dilutions were then made by a multipipette into the other wells already containing 100 µL of LB (the last row was left without antibiotics/peptide as a positive control). Bacteria from a shaking culture as described above were then measured for their OD600 and normalized in 2 mL LB medium to an OD600 of 0.01 (order of 106 colony forming units (CFU)/mL as measured from live counts). Serial dilutions of the bacteria were then made in additional 5 LB tubes (200 µL from previous dilution were transferred into 1800 µL of LB every time after vortexing). One hundred microliters of the highest bacterial dilution were inserted into wells A1-B12, 100 µL of the second highest bacterial dilution into wells C1-D12, etc. The smallest inoculum contains about 5 CFU and, in all experiments’ controls, exhibited growth (was not empty). The prepared plate was placed in an automatic microplate plate-reader for 16 h with medium shaking speed and an OD600 measurement every 20 min.
2.6. Antibacterial Activity
The base minimal inhibitory concentration (bMIC) was determined for each antibiotic/antimicrobial peptide (AMP) based on the above-described growth curves—bacterial populations with an initial inoculum of 106 CFU/mL (2 × 105 CFU per well) that finished with an OD600 lower than a cut-off of 0.35 after a 16-h incubation were considered as extinct or inhibited. The lowest antibiotic/peptide concentration for which both duplicates went extinct is the bMIC. Similarly, density-dependent MICs were generated for lower inoculums using the same cut-off.
2.7. Preparation of Spent Media with Polymixin B (PMB) and Ampicillin (Amp)
Appropriate concentrations of PMB and Amp were prepared in LB medium for subsequent dilutions for an MIC assay described above. E. coli MG1655 were grown in shaking LB until an OD600 of about 0.4–0.6 and diluted into some of the prepared PMB and Amp stocks to an OD600 of 0.1. All types of these media and LB alone were then incubated in shaking in 37 °C for 1 h. Incubated media were centrifuged, and the supernatant was used for a standard MIC assay described above.
2.8. Determination of Antibiotic Potency over Time
E. coli MG1655 were grown in shaking LB overnight (ON) and then centrifuged for 5 min in 3000 rpm and diluted to an OD600 of 1. ampicillin, chloramphenicol, carbenicillin, and tetracycline were added to appropriate concentrations for final MIC determination as indicated in the results to tubes containing either LB or LB and bacteria in an OD600 of 1. Some LB tubes with bacteria in the same density were also incubated with rest without any antibiotics. All tubes were incubated for 24 h in shaking and 37 °C. In addition, another inoculum of E. coli MG1655 was grown in shaking LB ON. After 23 h, the whole process was repeated for the 1 h samples with the new ON culture. When 24 h had passed, all samples were filtered through 0.2 µm syringe filters and appropriate amounts of all corresponding antibiotics were added to the samples that were incubated with bacteria only (without antibiotics). Finally, all samples were diluted by a factor of 2 with fresh LB for the highest antibiotic concentration and by increasing dilutions for a standard MIC assay as described above. In addition, fresh LB with fresh antibiotics was prepared for each antibiotic for a parallel classic MIC assay as a control by the protocol described above. All MIC assays were performed in 96-well plates over 16h of incubation in shaking (250 rpm) and 37 °C. Final results were determined by the sight of turbidity and OD600 measurements.
3. Mathematical Models
Three types of deterministic mathematical models are proposed, all admitting bistable behavior as described in the introduction section; the new bistable immediate kill and then A-independent dynamics model (simplest, chart flow 1), the classical A-dependent dynamics model (simple, chart flow 2), and a classical multiple time-dependent factors A-dependent dynamics model (the most complex model presented here, chart flows 2 and 3). Notably, more complex models taking into account detailed molecular processes, stochastic effects, and/or several phenotypic populations exhibiting bistable behavior may be introduced. One of the main results here is that the two simpler models are adequate for describing the data for some of the antimicrobial agents.
We denote by B(t) (bacterial cells/mL) the concentration of the bacteria at time t (hours) and by A the initial concentration of the antibiotics/peptide (µM). The growth curves under the influence of the antibiotics/peptides reflect the overall population growth, which is decreased/delayed by either killing of substantial portions of the population (peptides or bactericidal antibiotics) or by growth-inhibition (bacteriostatic antibiotics).
3.1. The Bacterial Growth Model
The simplest bacterial limited growth model is of the form:
Such a deterministic one-dimensional mathematical model is expected to be valid for sufficiently large inoculum, for which stochastic fluctuations leading to extinction are non-probable and when the environmental conditions are fixed (e.g., the nutrients supply hardly changes during the experiment). Several analytical forms for
, such as logistic, Gompertz, and others are commonly used [
9,
39]. Here we propose that the growth function,
, can be experimentally found by plotting the change in the bacterial inoculum per time interval
versus
. If, to a good enough approximation, a unique curve is found when this procedure is repeated for several initial inoculum
, then model (1) is adequate for describing the control bacterial dynamics. Otherwise, a more complex model is needed. A threshold condition on the deviations of the experimental
curve from its mean can be set to distinguish between these behaviors.
Flow Chart 1. The bistable kill model (BIK) dynamics. ![Antibiotics 10 00087 i001]()
3.2. The Bistable Immediate Kill Model (BIK)
The model describes a scenario where the bacterial destruction occurs rapidly at some initial kill phase
, after which the surviving bacteria, if such exist, grow as if there are no peptides in the medium, namely, as in the control, see flow chart No 1. The mathematical description of this model includes the control bacterial growth function, F(
B), as above, and a nonlinear kill function,
, so that
is the bacteria concentration after the initial kill phase. Here, the bacterial growth is descried by the equations:
Such a model predicts that if there is bacterial growth, then, if one plots the change in the bacterial inoculum per time interval versus for any initial inoculum and any concentrations of the antimicrobial peptide, a unique bacterial growth function, which is identical to the control growth function, F(B), will emerge. Here, the bistability is due to the nonlinear threshold form of the kill function.
Flow Chart 2. The A-dependent dynamics model (BAD) ![Antibiotics 10 00087 i002]()
3.3. The A-Dependent Dynamics Model (BAD)
The model describes a scenario by which the bacterial destruction or growth inhibition occurs continuously due to the fixed–in-time antibiotics action (See flow chart No 2). The mathematical description of this model is given by a concentration dependent growth function,
, controlling the bacterial growth under a given antibiotics concentration:
Such a model
predicts that if there is bacterial growth, then, if one plots the bacterial growth function (namely
versus
) for different initial inoculum and a fixed antibiotics concentration, a unique growth function
will emerge (yet
different antibiotics concentrations may result in different curves). Depending on the properties of the function
, bistability may emerge (as in
Figure 1B, see [
20,
36]). Then, the MIC increases with the initial inoculum. In [
9], the analytic expressions for the density-dependent MIC of six different forms of
are compared to the experimental density dependent MICs. Here we find the experimentally derived
from which the resulting density dependent MIC s derived.
Flow Chart 3. A bistable multiple factors dynamics model (BMFD) (coupled to flow chart 2). ![Antibiotics 10 00087 i003]()
3.4. The Bistable Multiple Factors A-Dependent Dynamics Models (BMFD)
These models describe scenarios by which the bacterial destruction or growth inhibition depend on additional factors that vary during the experiment, such as antibiotics and β-lactamase concentrations. Mathematically, such models require
at least a two-
dimensional deterministic system, see for example [
11,
35] (it is also plausible that stochastic terms need to be included, see e.g., [
26]). The simplest possible model of this kind is defined by two functions
that describe the bacterial growth and the depletion of the antibiotics’ concentration by natural decay and by the bacterial dynamics—see flow chart No 3:
Such higher-dimensional models are more complex than the BIK and BAD models. Indeed, these can be considered as two limiting cases of the two-dimensional model (4): Very fast depletion of the antibiotics leads to a BIK model, whereas very slow depletion and consumption of the antibiotics means that the antibiotic concentration remains essentially fixed and the BAD model emerges. When the experimental growth function for each antibiotic concentration depends on the bacterial initial load, one concludes that the BIK and BAD models are insufficient to describe the bacterial growth dynamics, so a BMFD model is needed (we do not attempt to fit such models here).
3.5. Experimental Growth Functions
To find the bacterial growth functions experimentally, we process their OD600 counts as follows. First, to avoid noisy oscillations, we cut the signal at the detection level and after the first maxima and smooth the signal by a standard MatLab algorithm, see supplement for details. Then, we plot versus OD(t), thus obtaining the OD growth function. Since the OD is, to a good approximation, linear in the CFU count, for inoculum above the threshold level of 106 CFU/mL, the growth functions, F(B,A), correspond to a linear scaling and shift of the OD growth function graphs.
5. Discussion
In all agents we tested, including all cationic antimicrobial peptides and all conventional antibiotics, independently of their biochemical mechanism of action (
Table 1), we found the inoculum effect. At a certain range of concentrations, which is specific for every drug and experimental setting, the system exhibits a bistable behavior in which large loads survive and small loads are inhibited. We identified three distinct types of bistable dynamics, as summarized in flow chart 4, and developed an experimental framework that enables to determine which type of dynamics is realized for a given antimicrobial agent. In particular, for certain cases (all the cationic antimicrobial peptides and all the commercial bacteriostatic antibiotics we tested), we established experimentally that simple mathematical models (BIK, Equation (2) and BAD, Equation (3), respectively) are adequate for describing the bistable growth dynamics.
Flow Chart 4. The division to three types of bistable dynamics. ![Antibiotics 10 00087 i004]()
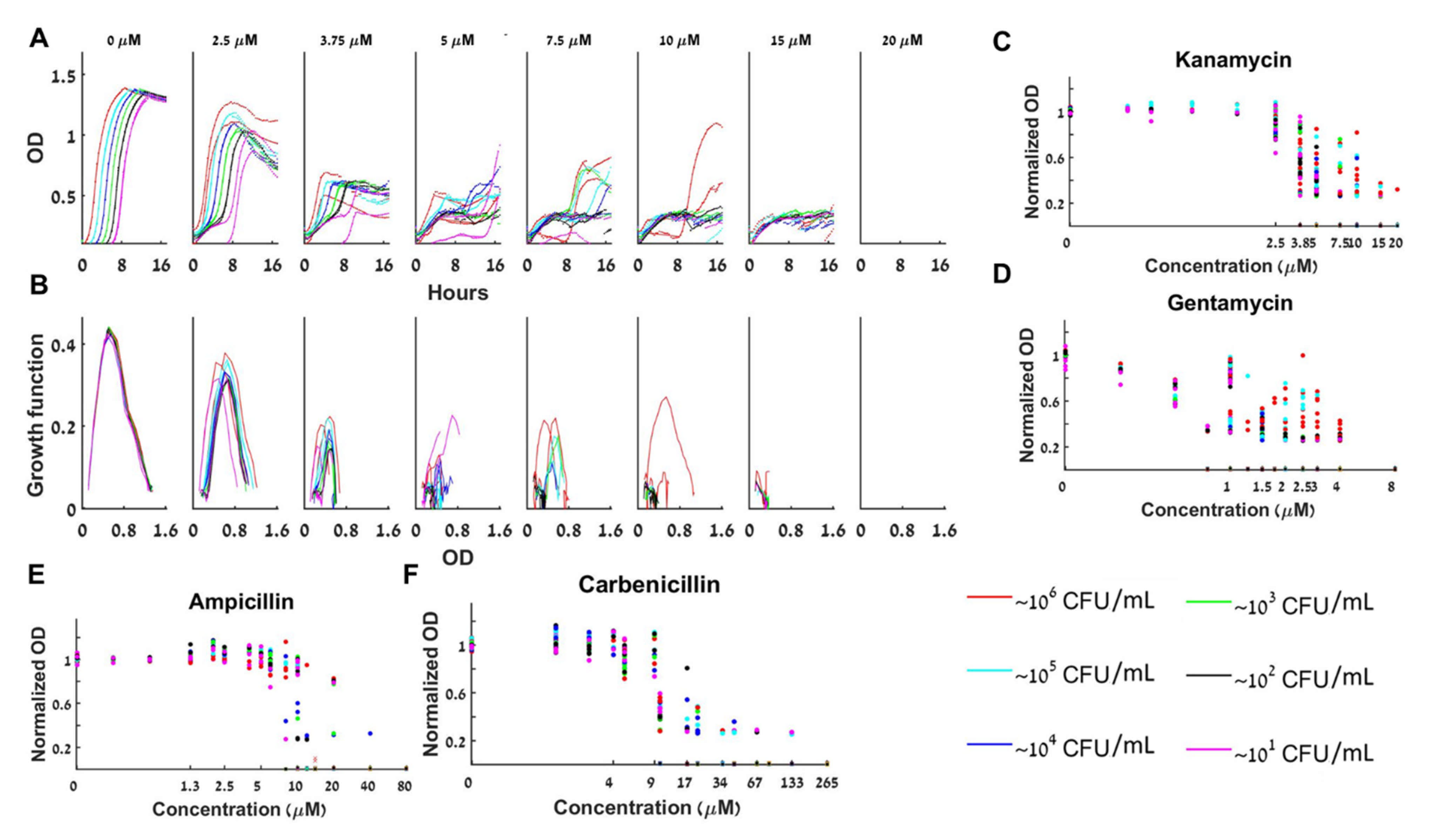
The CAM-induced IE: We found that all the tested peptides (polymixin B, K6L9, MSI, and melittin) lead to a bistable bacterial growth, demonstrating for the first time that antimicrobial peptides induce an inoculum effect (
Figure 3 and
Figure S7 in the supplement).
Because antimicrobial peptides kill bacteria in a mechanical fashion by attaching to the bacterial membrane via electrostatic forces and formation of pores/lesions through which the bacterial content flows out, they cause almost immediate death [
40]. After initial killing by the peptide there are two possible outcomes: Either all bacteria are eradicated, or some live bacteria are left. In the latter case, the live bacteria grow normally as the control, independently of the antimicrobial peptide that was primarily present in the medium (see our control experiments in
Figure S2).
The initial “decision” of whether to go extinct or survive the peptide is highly dependent on the initial bacterial concentration present in the well, and therefore, an inoculum effect occurs. Mechanistically, this model is supported by various biophysical studies done by others and us, showing that CAMPs bind and kill both Gram-negative and positive bacteria within minutes [
41,
42] see
Figure S2. The consequence of this unusual interaction is mathematically described by our BIK model, Equation (2)—there is a density-dependent and concentration-dependent immediate kill function, with the surviving bacteria growing exactly as the control, obeying a deterministic one-dimensional ordinary differential equation with a growth function that is found experimentally (
Figure 3B).
It was recently established that when cell-penetrating peptides are employed in conjunction with AMPs, the MIC is reduced [
43,
44,
45]. We do expect, as we established with all other non-linear antimicrobial mechanisms of action, that IE will be identified also when such combinations are employed. Whether or not the surviving bacteria will grow as the control does (namely exhibiting BIK dynamics), or, perhaps, slower due to the cell-penetrating peptides (BAD or BMFD dynamics), is an open question for future studies.
The complexity of IE induced by antibiotics: We provide an experimental methodology to examine when the growth dynamics is adequately described by a simple one-dimensional model or when higher-dimensional models must be employed.
For the two tested commercial bacteriostatic antibiotics that target the ribosome (tetracycline and chloramphenicol), for a fixed antibiotics concentration, all duplicates, and all different initial loads that grow collapse to one growth function (
Figure 4 and
Figure S4). We conclude that in these cases, when growth occurs, stochastic effects, antibiotics stability, and other limiting factors are insignificant. Thus, the deterministic one-dimensional ordinary differential equation BAD model (Equation (3)) adequately describes the dynamics, with growth functions depending on the initial antibiotics’ concentration [A
0]. We found these functions from the experimental data and observed that they might have multiple maxima for large [A
0] (
Figure 4 and
Figure S4). This can be indicative of a change in the collective behavior of bacteria in stress at higher densities and needs to be further studied. These experimentally derived functions may be utilized in future mathematical models of bacterial growth dynamics such as was done in [
11,
12,
18,
35].
Bacterial growth with beta-lactam antibiotics, which specifically target the cell wall, or with aminoglycosides that inhibit the ribosome, cannot be described by a single time independent ordinary differential equation:
dB/dt is not a function of
B(t). Indeed, we observe that different loads grow differently and even duplicates have different growth curves and different maximal capacity (
Figure 5 and
Figure S5). In some of these cases, the dynamics appears to shift from 1d dynamics in the lower antibiotic concentrations towards at least 2d dynamics for high concentrations (
Figure 5C–F shows that the maximal growth capacity of different loads collapses to one curve for low A but not for large A). Interestingly, the transition seems to occur in concert with the appearance of the bistability.
To describe this behavior, one needs to construct the more complex BMFD mathematical models that include additional variables and time-dependent factors. Equations (2) and (3) provide the simplest type of such models (see [
11,
18] for a variety of such models).
The role of experimental conditions: While growth in rich medium is well described by the traditional limited growth mathematical model (1), minimal medium leads to complex behavior even without the introduction of anti-microbial agents. To eliminate this variability in our experiments, we conducted all experiments with antimicrobials in the rich medium setup and found a bistable range in all of these experiments. Mathematical models show that if one decreases the growth rate at the exponential phase of a one-dimensional BAD model, bistability is suppressed and monostability arises [
20,
36]. An experimental set up that realizes such conditions (e.g., by a chemostat) and its implications on best strategies for treatment protocols are left for future studies.
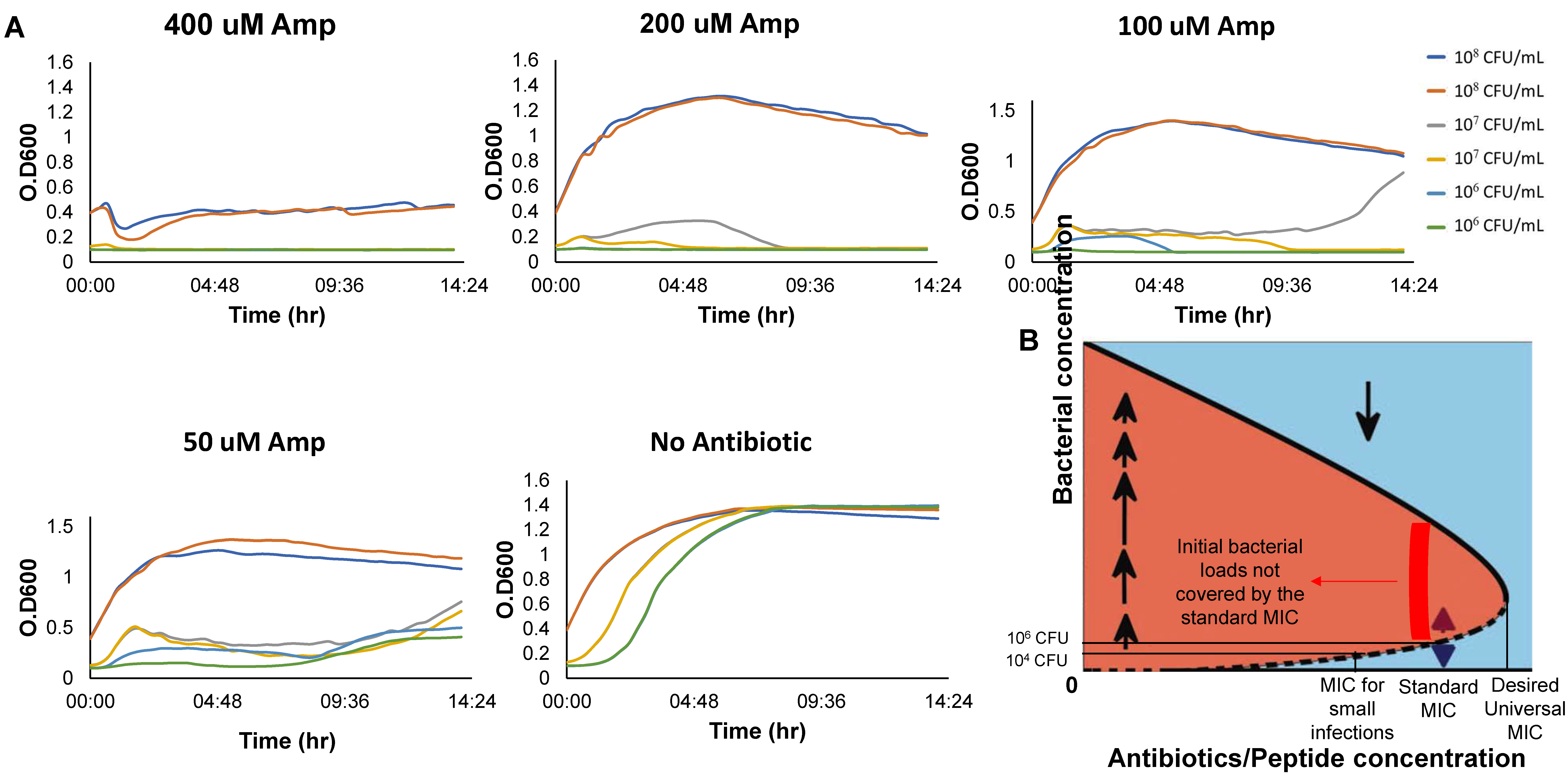
The IE and MIC: We concentrated on establishing the IE for low inoculums, below the standard loads for bMIC. Importantly, an increase in the density dependent MIC with the initial inoculum (as in
Figure 1B) implies bistability whereas a decrease in the density dependent MIC with the inoculum (as in
Figure 1A) is associated with monostability. The mathematical theory shows that bistability typically implies that the standard bMIC is insufficient for fighting inoculums that are larger than the standard inoculum of 10
6 CFU/mL.
Figure 6 demonstrates that this is indeed the case, corroborating similar findings in [
11,
12,
18].
Mechanistic explanation of IE: While IE was identified in previous studies of particular conventional antibiotic agents and bacteria [
10,
11,
12,
13,
14,
18], previous explanations of its appearance included genetic and/or phenotypic population heterogeneity and additional factors that vary during the experiments. These were modelled, for example, by deterministic multi-dimensional equations of classical reaction kinetics [
11,
18] or by two-dimensional PK (Pharmakokinetics)/PD (Pharmakodynamics) dynamics [
12]. Here we show that for some cases (the bacteriostatic antibiotics) the one-dimensional BAD model can explain the resulting growth curves by density-dependent mechanisms alone. By Ockham’s razor principle, we assert that the BAD models are adequate for these cases: The more complex reasoning can be neglected for explaining bacterial growth in rich media under bacteriostatic antibiotics.
On the other hand, we demonstrated that in other cases (bistable bacterial growth with bactericidal and bacteriolytic antibiotics), higher dimensional models are required. These could possibly be described by either density-dependent mechanisms (such as the production of β-lactamase or, for other bacteria, by extracellular PH variations [
12]) or models involving population heterogeneity, see [
11,
12,
18] and references therein. For example, it is well established that
E. coli MG1655 produces β-lactamase, an enzyme that hydrolyses β-lactam antibiotics such as ampicillin and carbenicillin [
11,
38]. If the antibiotic is being inactivated by the bacteria, higher initial loads produce larger concentrations of the enzyme over the course of time, and therefore, the antibiotic concentration will decline faster. Our experimental results with oxacillin demonstrate that even when the β-lactam is not degraded by the bacteria and the drug concentration remains constant over time, IE appears, and the growth dynamic may be still multi-dimensional. Interestingly, these results also exhibit high sensitivity to the experimental settings. This sensitivity could be possibly attributed to the stress induced by the very high antibiotic concentrations (
E. coli are often naturally resistant to oxacillin [
46]), possibly introducing an additional time and antibiotic concentration-dependent factor to the system. Additional experimental work in which these factors are monitored is needed for clarifying the dominant mechanisms involved in the more complex settings. While the identification of mechanisms that control the IE may be pivotal for developing more efficient antimicrobial drugs, we assert that such an identification is inessential and is not always helpful in predicting the bacterial growth dynamics.
Hypothetical therapeutic implications: From a therapeutic point of view, understanding the particular bacterial growth dynamic in the presence of different classes of antimicrobials and starting from various bacterial inoculums is central for the assignment of the correct treatment for various bacterial infections (see [
11,
12,
18]). When early diagnosis and treatment are impossible, the ability to predict bacterial growth dynamics in the presence of a selected treatment becomes indispensable. In such cases, the estimation of bacterial load present in the infection site, and the knowledge of the type of growth dynamic of the infecting bacterium with different antimicrobials, would allow for a personalized treatment in terms of dosage and frequency of treatment [
11,
12,
18,
35,
47].
Models of in-vivo dynamics usually require a BMFD model since the antibiotics clears from the body and the nutrients supply varies. Once an in-vitro BAD model is established, the form of the function
can be identified with the experimentally derived
The study of in-vivo bacterial infections requires additional considerations, such as the presence of the immune system, the clearing of the drugs, as well as environmental conditions that are not only subjected to changes by the bacteria but also by the host (e.g., the host may control limiting factors for the bacterial growth, and such factors invoke higher dimensional dynamics, see
Figure 2C,D). Nevertheless, studies have shown [
17,
48] that quite often, in-vitro results regarding interaction dynamics between bacteria and antimicrobials are indicative of such dynamics in-vivo and may be used as building blocks for the in-vivo models [
36].
Outlook: Our current efforts are concentrated on simulating the results based on the fitting of our experimental data and studying their implications. To achieve a successful clinical treatment, basic growth dynamics rules such as those presented herein should be adapted to include additional parameters such as nutrient limiting factors, drug clearance, the action of the immune system, and the level of drug resistance of the specific bacterial species present at the infection site. Inclusion of these additional factors into the bistability of the basic bacteria-antimicrobial agents’ system can shed light on the relation between in-vitro and in-vivo growth dynamics.