3.1. Interpretation of the Seismic Performance of the Strengthened Specimens
Due to numerous and significant structural deficiencies (for instance, the use of plain steel reinforcement and concrete of low compressive strength, the inadequacy of confinement and the short length of the lap splices which are located in the potential plastic hinge region), the columns found in RC structures of the 1950s–1970s possess poor deformability and low ductility, while also exhibiting a rapidly degrading hysteresis performance, related to catastrophic partial or general collapse. Thus, the efficiency and reliability of the applied retrofit scheme is primarily and inseparably related to the satisfactory transformation of the brittle failure mode to a more ductile one, by securing the full exploitation of the material properties and, hence, the development of the column’s nominal flexural moment capacity.
For this purpose, it was considered of particular interest to evaluate the effectiveness of the two examined strengthening schemes (which include either the CFRP-wrapping of the columns or the use of thin high-strength RC jackets) by comparing the hysteresis behavior of the strengthened columns with the seismic response of two corresponding original column specimens with inadequate lap splices, O
1 and O
2, as well as with that of a control specimen with continuous reinforcement, C
1, which were all tested in a previous work [
3]; see
Figure 5d,
Figure 6 and
Figure 7. The original columns, O
1 and O
2, with lap splices of 200 and 240 mm length, respectively, demonstrated poor seismic performance dominated by premature excessive slipping of the inadequately lap-spliced bars, while they eventually collapsed due to the loss of axial load-carrying capacity. Contrariwise, the control specimen, C
1, performed in a ductile manner when subjected to the same history of reversed inelastic lateral displacements.
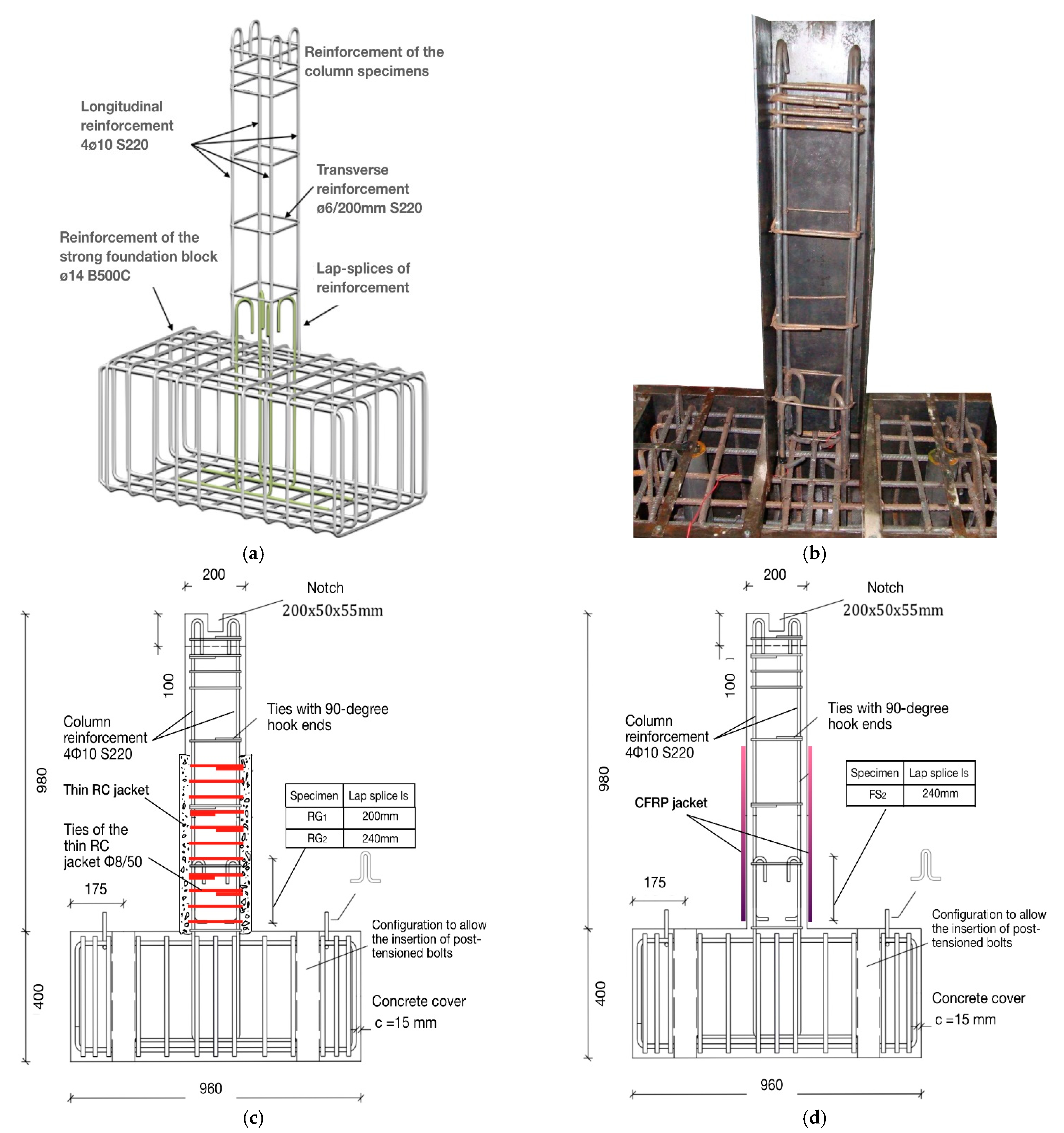
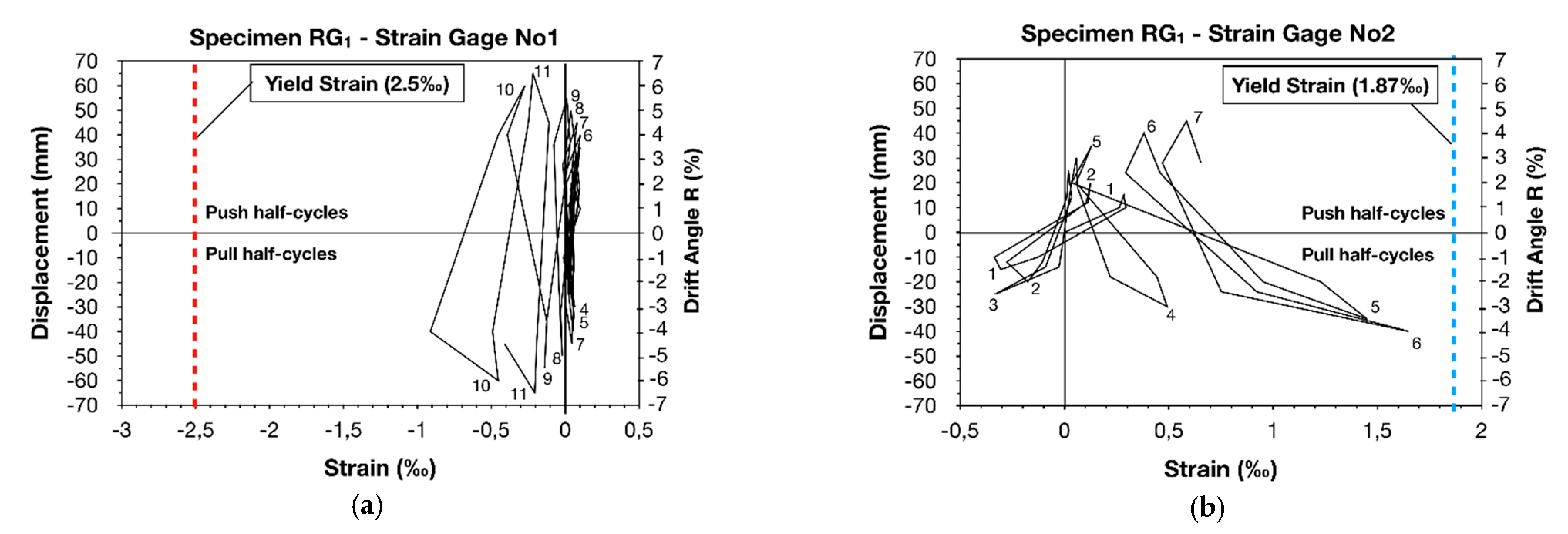
The column specimen RG
1 was pre-earthquake strengthened with a thin RC jacket of high-strength and it was subsequently subjected to eleven cycles of lateral displacement increments. The amount of confinement provided by the ties of the jacket was calculated using Equation (1), while the width of the jacket equaled 15 mm. The seismic behavior of RG
1 is clearly reflected in the hysteresis loops shown in
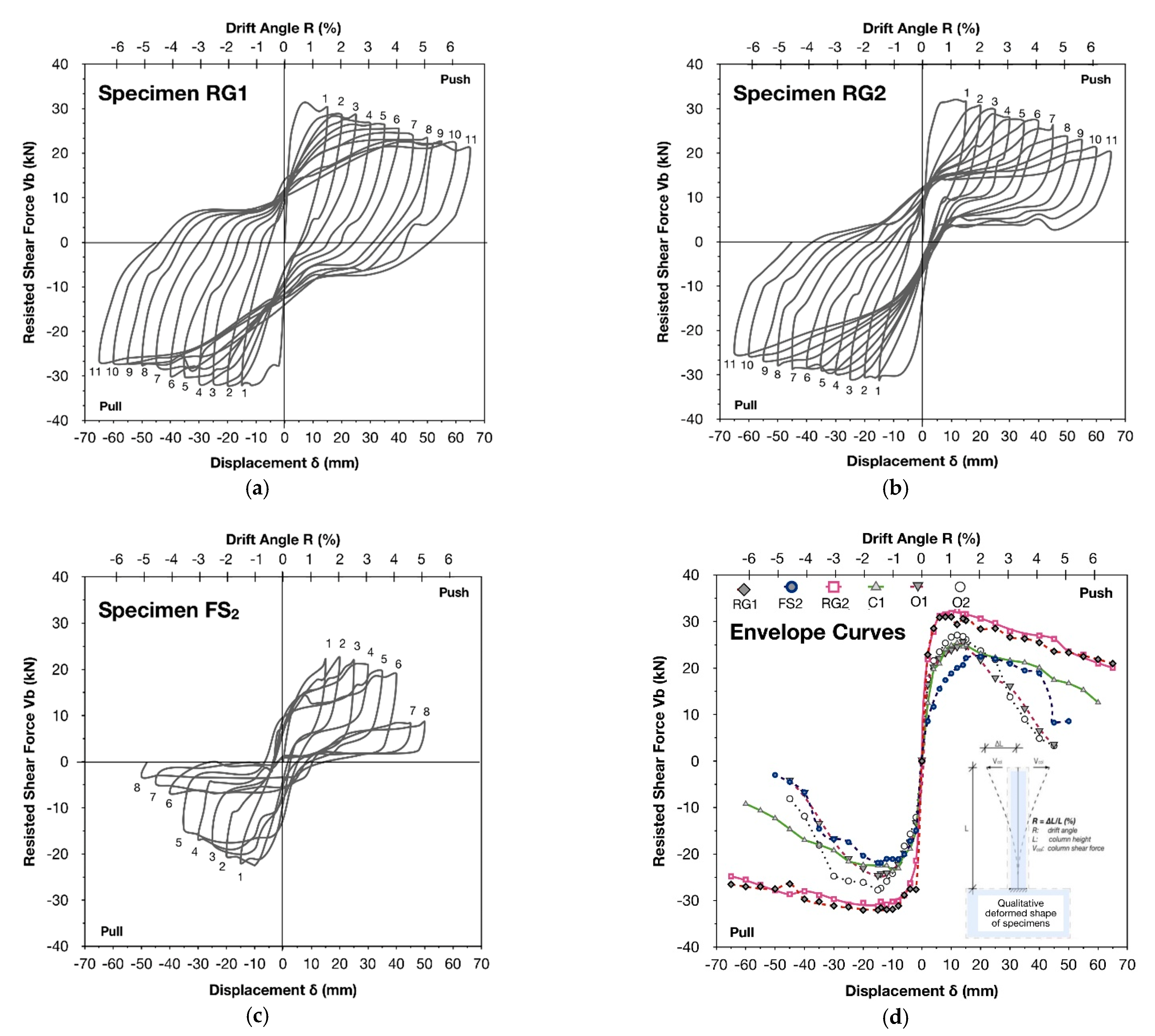
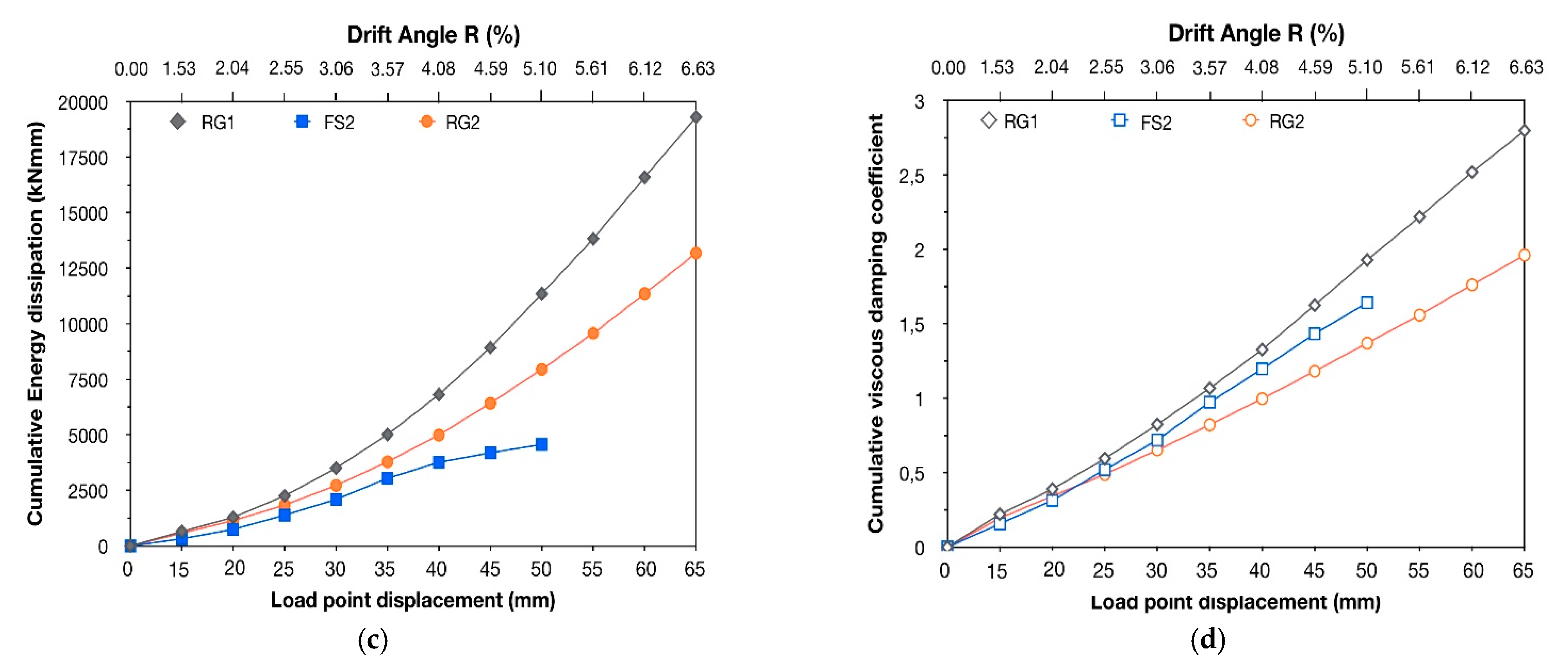
Figure 5a. The lateral bearing strength and peak-to-peak stiffness showed a mild reduction during cycling, while the cumulative hysteresis dissipated energy progressively increased significantly (see
Figure 6).
During the first cycle of the earthquake-type loading, the main flexural crack was formed at the base of the column. This crack gradually dilated with the increase in lateral displacement, resulting in increased post-yield strain of the lap-spliced steel bars. Nevertheless, no other crack was observed on the jacket surface until the end of testing (drift angle equal to R = 6.63%), as can be observed from the failure mode depicted in
Figure 8a. Eventually, the specimen maintained 82.75% and 69.44% of its initial lateral bearing strength in the case of the push-half cycles and the pull half-cycles, respectively. Moreover, the confinement provided by the thin high-strength RC jacket effectively restrained the slipping of the longitudinal column reinforcement. The latter is clearly reflected in the plots of resisted shear force-versus-displacement, illustrated in
Figure 5a, where it can be observed that increasing values of lateral strength are required for further displacing the column free end. For lateral drift angle values, R, higher than 4.59%, the unloading (lower) branch of the push half-cycles and the unloading (upper) branch of the pull half-cycles become almost horizontal, causing slight pinching of the hysteresis loops. This is attributed to the P–
δ effect and the significant influence of the axial load.
During the first two cycles of the earthquake-type loading, the peak-to-peak stiffness of specimen RG
1 deteriorated sharply due to the concrete cracking, showing a reduction of 27.19%. Thereupon, the deterioration rate was slower, while, at the end of testing, the column maintained almost 18% of its initial stiffness (see
Figure 6a).
The strengthened specimen RG
1 also showed a remarkable dissipating hysteresis behavior with constantly increasing values of dissipated seismic energy during the consecutive cycles of loading. In particular, the amount of dissipated seismic energy during the eleventh cycle of loading was increased by almost 318% with respect to the corresponding value during the first cycle (
Figure 6b and
Figure 9c).
Ultimately, the strengthening scheme applied to specimen RG
1 effectively prevented the premature bond-slip failure and excessive bar slipping, while also securing the desirable ductile seismic performance of the column. Furthermore, the thin high-strength RC jacket substantially increased the lateral bearing strength of the enhanced column, RG
1, with respect to the strength of the corresponding original column, O
1, as can be observed in the plots of strength ratio for peak displacement of each cycle-versus-load point displacement, shown in
Figure 7a. For instance, for lateral displacement of 45mm the strength ratio value RG
1/O
1 equals 6.9 and 6.1 for the push half-cycle and the pull half-cycle, respectively. The same is also true in the case of the energy dissipation capacity of specimen RG
1 with respect to that of O
1. In particular, as was obtained in the plots of energy dissipation ratio for peak displacement of each cycle-versus-load point displacement (see
Figure 7b), the energy dissipation ratio value RG
1/O
1 ranged from 1.74 for the first cycle of loading to 4.0 for the seventh cycle, when the original column, O
1, literally collapsed.
It is worth noting that the hysteresis performance of the strengthened column, RG
1, was also improved with respect to that of the control specimen, C
1. In fact, RG
1 showed significantly increased lateral strength values with respect to specimen C
1 (see
Figure 5d), due to the additional ties and the high-strength concrete of the thin RC jacket. An increase of almost 25% in the peak-to-peak stiffness values was also observed throughout testing (see
Figure 6a). This results from the slight increase in the dimensions of the strengthened column’s cross-section, but is mainly caused by the additional confinement provided by the thin high-strength RC jacket. Moreover, during the eleven cycles of the earthquake-type loading the mean value of the energy dissipation ratio, RG
1/C
1, equaled to 1.36. The latter clearly demonstrates the ductile seismic response of the enhanced column RG
1 and, hence, the effectiveness of the applied retrofit scheme.
The enhanced specimen RG
2 was retrofitted similarly to the RG
1. From the plots of resisted shear force-versus-displacement of RG
2 (see
Figure 5b), it can be observed that both the lateral strength and the peak-to-peak stiffness showed a mild reduction during testing, while the energy dissipation capacity of the column gradually increased significantly during the consecutive cycles of the earthquake-type loading. The main flexural crack was formed at the base of the column during the first cycle. Thereafter, this crack dilated progressively with the increase in the reversed lateral displacements of RG
2, causing excessive deformation of the lap-spliced column reinforcement. For a drift angle value equal to R = 4.59% a hairline flexural crack was formed on the jacket surface at the exact location where the lap splices of the reinforcement end, namely at a distance of 240 mm from the foundation block of the specimen. Propagation of this crack occurred in the circumference of the thin high-strength RC jacket, due to the gradual increase in lateral displacement values until the end of testing (see
Figure 8b). However, no significant further dilation of this crack or disintegration of the concrete was observed. Thus, the thin RC jacket satisfactorily confined the column’s critical region to prevent early bond-slip failure and excessive slipping of the bars, while the enhanced column, RG
2, exhibited a ductile dissipating hysteresis behavior.
The slipping of reinforcement was effectively restricted, and it was not before the ninth push half-cycle when bar slipping showed a considerable increase. The latter is perceived in the hysteresis loops of RG
2 by the less steep (almost horizontal) upper branch of the push half-cycles (see
Figure 5b). Notably, this is not true for the pull half-cycles, where the continuously ascending lower branch of the hysteresis loops reveals that increasing values of lateral shear force are required to further displace the column’s free end.
Eventually, after eleven cycles of the earthquake-type loading, the strengthened column specimen, RG
2, maintained 68% (push half-cycles) and 80% (pull half-cycles) of its initial lateral strength (see
Figure 5b). Moreover, the peak-to-peak stiffness values of RG
2 were similar to those of the enhanced column RG
1, as shown in
Figure 6a. The energy dissipation capacity of RG
2 is illustrated in
Figure 6b. As can be observed, the strengthened column showed a remarkable dissipating hysteresis behavior, with constantly increasing values of dissipated seismic energy during testing. The lower vales of the seismic energy dissipated by specimen RG
2 with respect to specimen RG
1 are reflected by the slightly reduced area of the hysteresis loops of RG
2 compared to the loops of RG
1. The latter is primarily caused by the slipping of reinforcement after the seventh push half-cycle of RG
2 and, apparently, by the increased influence of the axial loading (P–
δ effect). This influence is clearly demonstrated by the almost stable values of the resisted shear force, which are required for displacing the column’s free end backwards from the peak displacement of each push half-cycle (see
Figure 5b). Nevertheless, the amount of dissipated seismic energy during the eleventh cycle of loading of specimen RG
2 was increased by almost 220% with respect to the value of the first cycle, while also corresponding to almost 70% of the amount of energy dissipated by specimen RG
1 during the eleventh cycle.
A substantial increase in the lateral-bearing strength of specimen RG
2 with respect to the strength of the corresponding original column, O
2, was also achieved. The latter is clearly demonstrated in the plots of strength ratio for peak displacement of each cycle-versus-load point displacement, illustrated in
Figure 7a. In particular, for drift angle value R = 4.59%, the strength ratio value RG
2/O
2 equals 7.97 and 3.54 for the push half-cycle and the pull half-cycle, respectively. Accordingly, the peak-to-peak stiffness of the enhanced column RG
2 was significantly improved with respect to that of the original specimen, O
2. During the first cycle of the earthquake-type loading, the strengthened column RG
2 showed an 16.5% increase in the peak-to-peak stiffness value with respect to specimen O
2. Thereafter, RG
2 demonstrated a slower stiffness degradation rate during the consecutive cycles of loading. For lateral displacement value of 40 mm the original column, O
2, collapsed due to the loss of axial load carrying capacity, while specimen RG
2 retained 32.9% of its initial stiffness. Furthermore, after eleven cycles of inelastic lateral displacement amplitudes (drift angle value, R, equal to 6.63%), specimen RG
2 maintained 16.65 % of its initial stiffness value shown during the first cycle. In
Figure 7b the energy dissipation capacity ratio for peak displacement of each cycle-versus-load point displacement is presented. As can be observed, a significant improvement in the dissipating hysteresis performance of RG
2 with respect to O
2 was indisputably achieved, due to the external confinement provided by the thin high-strength RC jacket. Indeed, the energy dissipation ratio RG
2/O
2 ranged from 1.29 to 2.40 during testing.
Therefore, the strengthened column, RG
2, exhibited a ductile overall seismic response, which was almost similar to the behavior of the control specimen, C
1, with the continuous longitudinal reinforcing bars (see
Figure 5d and
Figure 6b). In particular, RG
2 showed significantly higher values of lateral bearing strength than the specimen C
1, while also achieving an increase of almost 25% in the peak-to-peak stiffness values. As with specimen RG
1, this resulted from the slight increase in the dimensions of the strengthened column’s cross-section, but is mainly caused by the additional confinement provided by the thin high-strength RC jacket. Furthermore, the mean value of the energy dissipation ratio, RG
2/C
1, during testing, equaled 0.98. Consequently, the strengthening interventions implemented on specimen RG
2 effectively secured the satisfactory ductile seismic performance of the enhanced column and, thus, were proved to constitute a reliable and efficient strengthening scheme for improving the seismic behavior of columns found in existing pre-1960s–1970s RC structures.
Specimen FS
2 was strengthened pre-earthquake by wrapping two layers of CFRP textile around the critical column region. The number of the required layers was determined using Equation (1). The column eventually exhibited brittle failure due to excessive slipping of the lap-spliced bars. In particular, during the first cycle of the earthquake-type loading, the main flexural crack was formed at the column base. The damage gradually evolved with the increase in lateral displacement values during the subsequent cycles, while progressive slipping of the lap-spliced reinforcement also occurred. As a result, the cracking at the column base sequentially dilated, and disconnection of the column from the strong foundation block of the specimen eventuated for drift angle values, R, was greater than 4.08 % (see
Figure 8c). At the end of testing of FS
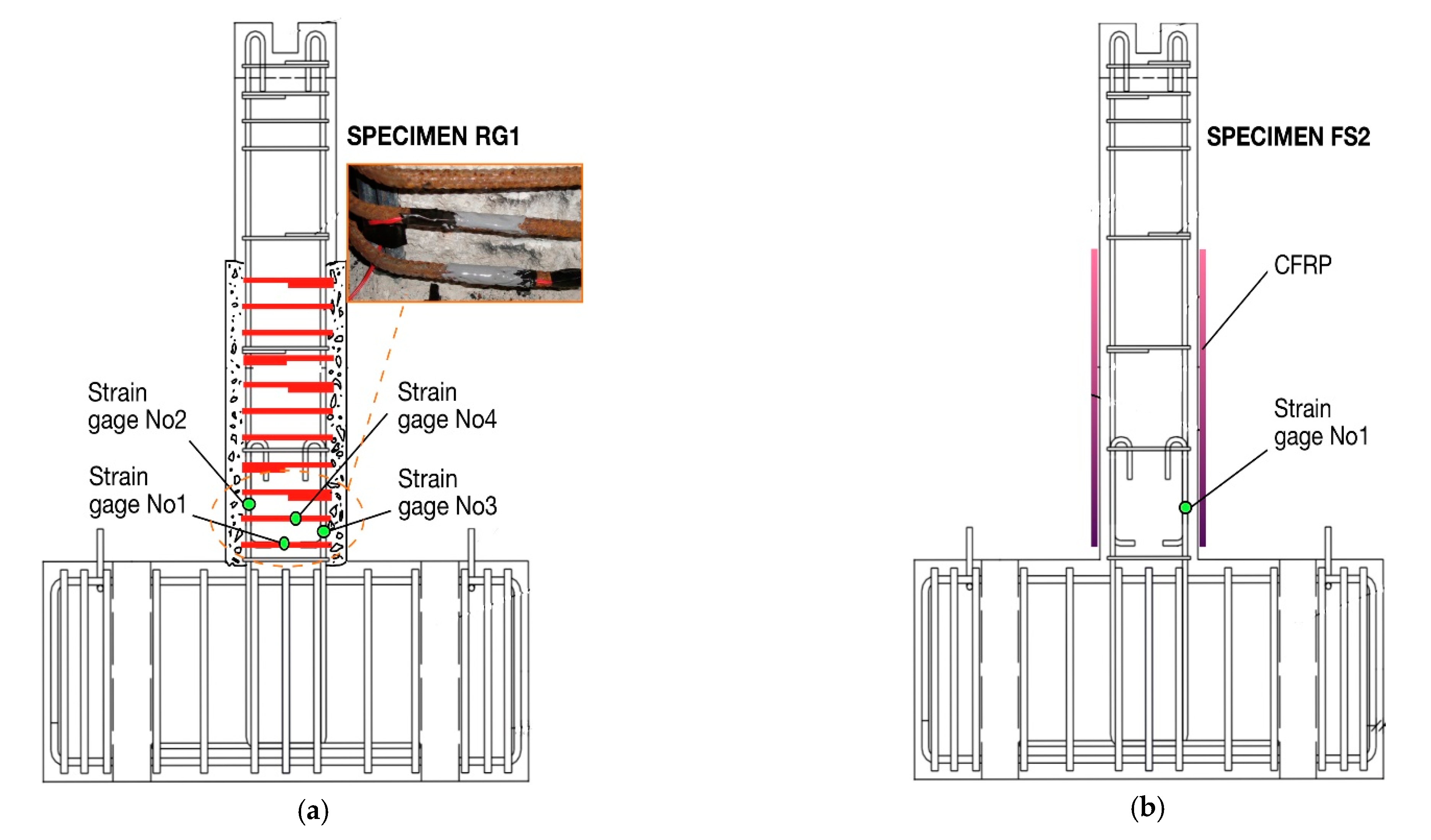
2 (after eight cycles of reversed inelastic lateral displacements), the pullout of the column’s longitudinal reinforcing bars was apparent. The excessive slipping of the bars was also ascertained from the data acquired from strain gages, which were attached to the bars, showing almost stable steel strain values during the consecutive loading cycles (see Figure 11e) [
23]. In
Figure 8c, the failure mode of specimen FS
2 is depicted, characterized by excessive residual deformation and rotation of the column. From the plots of energy dissipation capacity-versus-load point displacement (see
Figure 6b), it can be observed that the strengthened column, FS
2, performed similarly to specimens C
1 and RG
2 during the first five cycles of the reversed inelastic lateral displacements (drift angle, R, equal to 3.57%), while subsequently showing a degrading hysteresis behavior similar to that of the corresponding original column specimen, O
2. The latter is also clearly demonstrated on the hysteresis loops of FS
2 (see
Figure 5c). For instance, rapid deterioration of lateral bearing strength and peak-to-peak stiffness, intensive pinching of the hysteresis loops around the axes, horizontal branches showing excessive bar slipping and poor energy dissipation capacity dominated the hysteresis behavior of the column after the sixth push half-cycle and the fifth pull half-cycle of the seismic loading. The peak-to-peak stiffness of specimen FS
2 deteriorated more sharply during the first three cycles, while it subsequently deteriorated with a slower rate. For a lateral drift angle, R, equal to 5.10%, the peak-to-peak stiffness of FS
2 equaled only 1% of its initial value during the first cycle of loading (see
Figure 6a). The hysteretic energy dissipation capacity of specimen FS
2 was similar to the capacities of C
1 and RG
2 for up to a drift angle value, R, equal to 3.57%, while afterwards it was rapidly reduced due to the excessive slipping of reinforcement (see
Figure 6b). Nevertheless, the confinement provided by wrapping the two layers of the CFRP textile around the column of specimen FS
2 improved the failure mode of the specimen with respect to that of the corresponding original specimen, O
2 [
3]. In particular, the evolution of damage was delayed, since excessive disintegration of the core concrete and loss of the concrete cover were effectively restricted. The strengthened column FS
2 initially showed a dissipating hysteresis behavior until the fifth cycle of the seismic loading. Thereupon, excessive slipping of the lap-spliced reinforcement dominated the cyclic response of the specimen, causing a degrading overall hysteresis response.
According to the capacity design approach, RC structures should be able to withstand increased values of inelastic cyclic deformations during strong seismic excitations, to allow for the dissipation of a significant amount of kinetic energy through damping. Therefore, the structures should possess adequate displacement ductility to develop acceptable damage in the plastic hinges, while preserving the structural integrity and preventing partial or general collapse. Thus, the equivalent viscous damping is highly related to the deformability, while consisting of both the elastic and the hysteretic damping. The latter is crucial for the seismic response of RC structures and depends on the post-yielding characteristics of the structural members. Furthermore, the desirable ductile seismic performance requires an adequate energy dissipation capacity of the members, which, in turn, results in higher equivalent viscous damping ratios. Contrarily, the RC structural members with low energy dissipation capacity exhibit poor hysteresis behavior, while being susceptible to collapse due to the cumulative dissipated energy under small deformations.
In order to evaluate the capacity of RC structural members for dissipating seismic energy, Equation (2) was used [
38]. According to this equation, the equivalent viscous damping coefficient, ζ
eq, is expressed as the ratio of the dissipated energy within a given cycle of the earthquake-type loading (represented by the area S
ABCDEFA) to the elastic strain energy associated with the maximum force and displacement of the given hysteresis loop (represented by the areas
SOCC′ and
SOFF′) (see
Figure 9a). The energy dissipation capacity and the equivalent viscous damping coefficient, ζ
eq, per cycle of loading are depicted in
Figure 6b and
Figure 9b, while in
Figure 9c,d, the cumulative dissipated energy and the cumulative equivalent viscous damping coefficient of specimens FS
2, RG
1 and RG
2 for different drift ratio values are illustrated.
The enhanced columns RG
1 and RG
2 showed similar lateral resistance throughout testing and, therefore, similar elastic strain energy values (see
Figure 5a,b and
Figure 9a). As a result, the cumulative equivalent viscous damping coefficient values of specimen RG
1 were higher than the corresponding ones of column RG
2, because the latter showed a lower energy dissipation capacity with respect to RG
1 (see
Figure 6b and
Figure 9b–d). Additionally, it is worth noting that specimen FS
2, which was strengthened by CFRP-wrapping, dissipated an almost similar amount of seismic energy with specimen RG
2 during the first five loading cycles (up to a drift angle ratio equal to 3.57%) (see
Figure 6b). However, the shear resistance of FS
2 was a portion of that of RG
2 (see
Figure 5b,c). As a result, the elastic strain energy values of FS
2 were significantly lower with respect to the ones of RG
2. Consequently, the values of cumulative equivalent viscous damping coefficient of specimen FS
2 appear to be slightly increased when compared to the corresponding ones of RG
2 (see
Figure 9b,d).
3.3. Theoretical Conciderations
Kalogeropoulos and Tsonos [
3,
7] recently proposed a modified version of the analytical model proposed by Tsonos [
41,
42,
43], to predict the seismic performance of RC columns of both existing pre-1960–1970s and modern RC structures. The latter can be achieved by controlling the adequacy of length of the lap-spliced reinforcement. Furthermore, the formulation is used to precisely determine the necessary confinement which should be provided by the strengthening material during the retrofitting of existing RC structures, in order to prevent early failure of the lap splices. Thus, the implementation of the proposed methodology ensures the satisfactory design of the retrofit schemes, which allows for the yielding of the inadequately lap-spliced bars and the development of the column’s nominal flexural moment capacity.
In
Figure 13 and
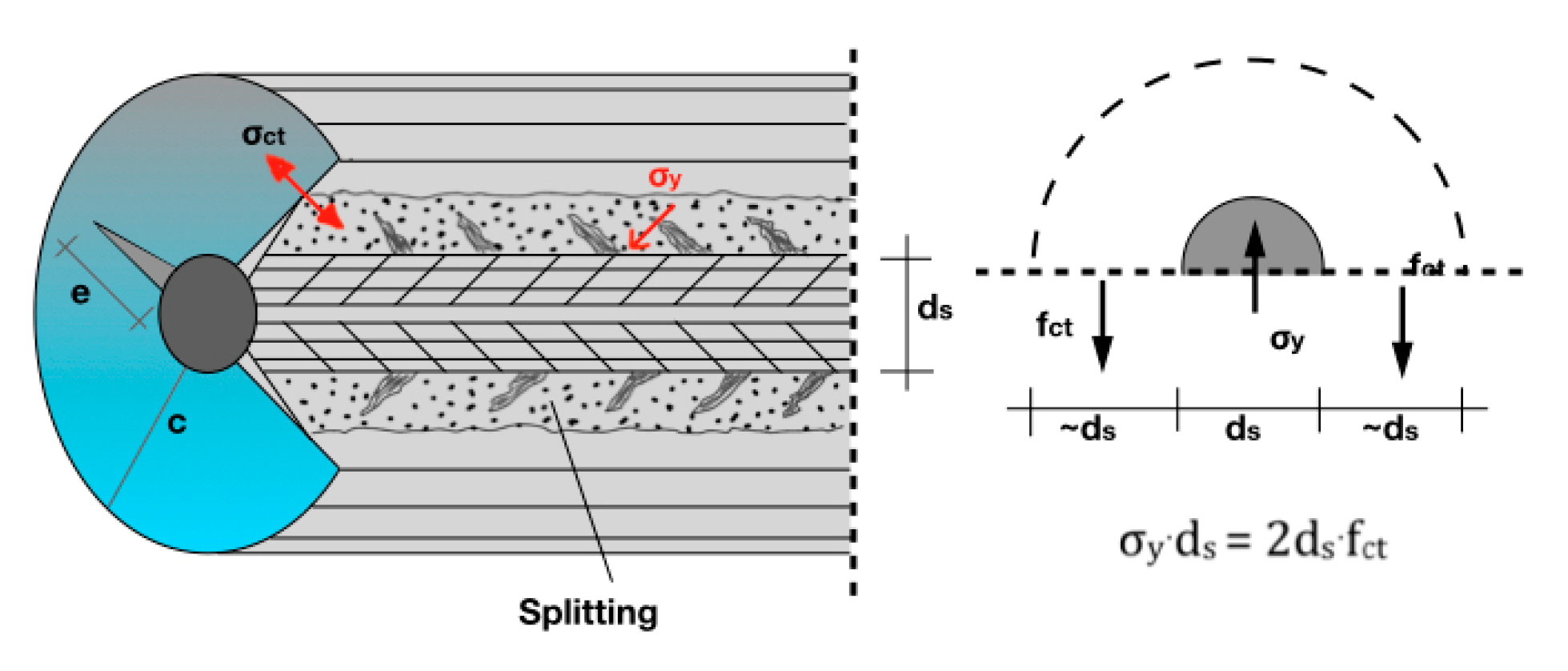
Figure 14, the details of the lap-spliced column reinforcing bars are depicted. As can be observed, the shear forces, acting on a 45 degree angle [
44], are resisted by the concrete compression struts that act between diagonally opposite corners of each rectangular section “abcd”. The diagonal compression strut mechanism depends on the concrete strength and, therefore, failure of the concrete causes a limitation of the strength of the lap splice, due to the gradual crushing along the cross-diagonal cracks, and especially along the potential failure plane, KLMN (see
Figure 14b). Meanwhile, slipping of the bars occurs.
According to the proposed methodology, which was presented in detail in previous works [
3,
7], the ultimate strength of the lap splice is given by Equation (3), where the values of
x and
ψ are given by Equations (4) and (5), respectively and the aspect ratio value
α = h/b is always equal to 1.0. The increased value of the concrete compressive strength,
, due to the confinement provided by the jacket, is calculated using Equations (6) and (7) [
45].
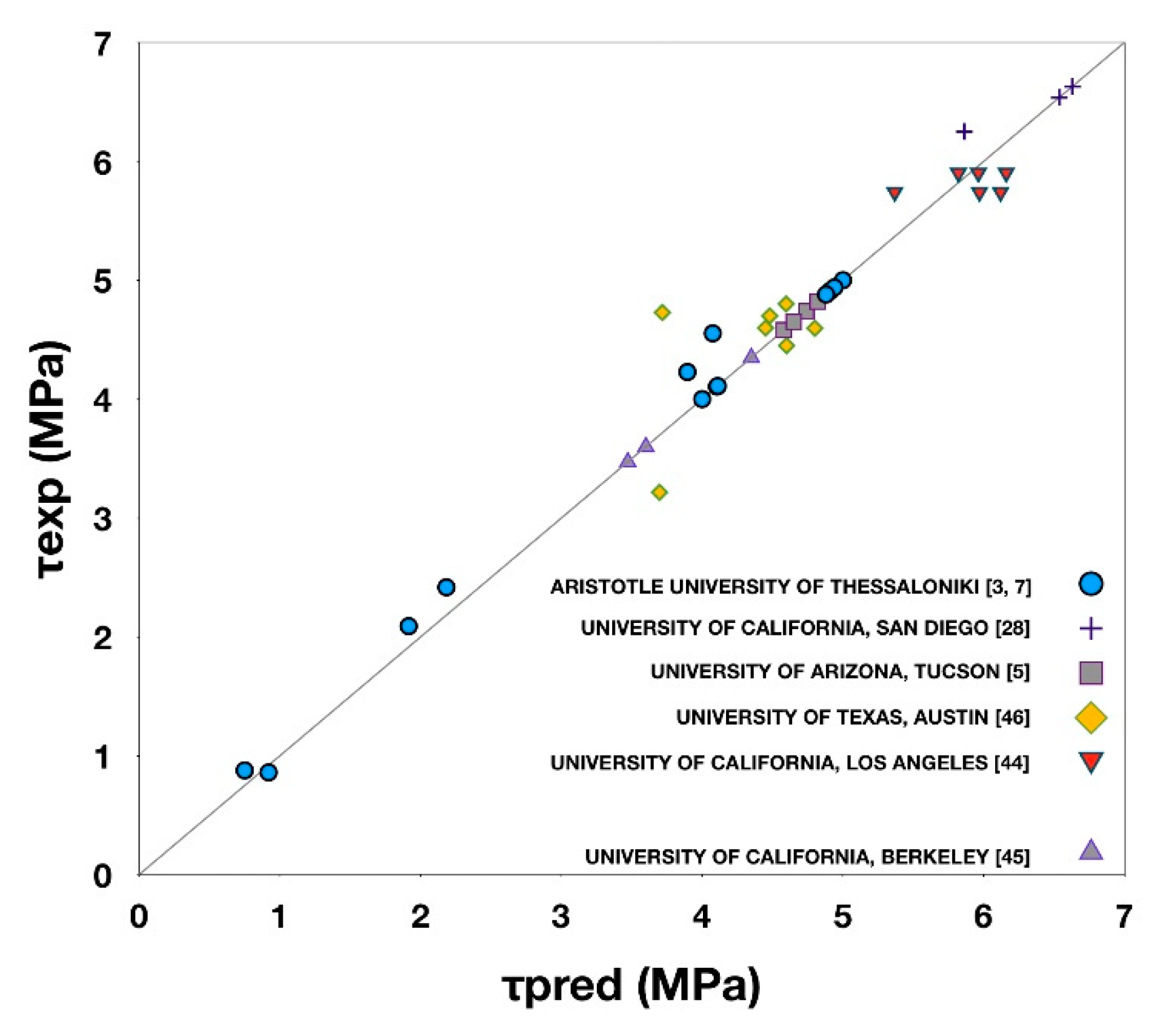
The validity of the proposed analytical model was checked using experimental data from 13 column specimens tested in the Laboratory of Reinforced Concrete Structures and Masonry Buildings of the Aristotle University of Thessaloniki [
3,
7], as well as data from 23 similar experiments found in the literature [
5,
30,
46,
47,
48] (see
Figure 15). In
Table 4, the shear capacities and the predicted actual values of the lap splice shear stress are shown. In particular, the value of actual shear stress in the potential failure plane between the lap-spliced bars when yielding of the bars occurs is
. Thus,
is calculated when the tension force acting in the bar,
, equals the bond force developed between the bar and the concrete along the lap splice,
, where
is the area of the potential failure plane. The coeficient
is calculated from Equations (3)–(7), and the ultimate shear stress is subsequently given by the expression
. The value of
is calculated from the expression
, where
is the stress value calculated according to the Hook’s law (
) using the maximum measured steel strain value,
. The latter is measured experimentally by strain gages attached to the steel bar (
). If the measured maximum strain,
, exceeds the yielding strain,
, then
is used to calculate the developed stress (
since the Hook’ law is not applied in the post-yielding range. According to the analytical formulation when the calculated shear stress is lower than the ultimate strength,
, then the predicted actual value of the lap splice shear stress will be near
, because the lap splice permits the yielding of reinforcement
. Contrarily, when
lap, splice failure occurs prior to the yielding of reinforcement and
. In the case of specimens RG
1 and RG
2, it was demonstrated that the implementation of the analytical model ensured the satisfactory design of the thin RC jackets, which provided adequate confinement to the lap splice region and allowed for the yielding of the inadequately lap-spliced bars.