Rediscovering Majority Logic in the Post-CMOS Era: A Perspective from In-Memory Computing
Abstract
:1. Introduction
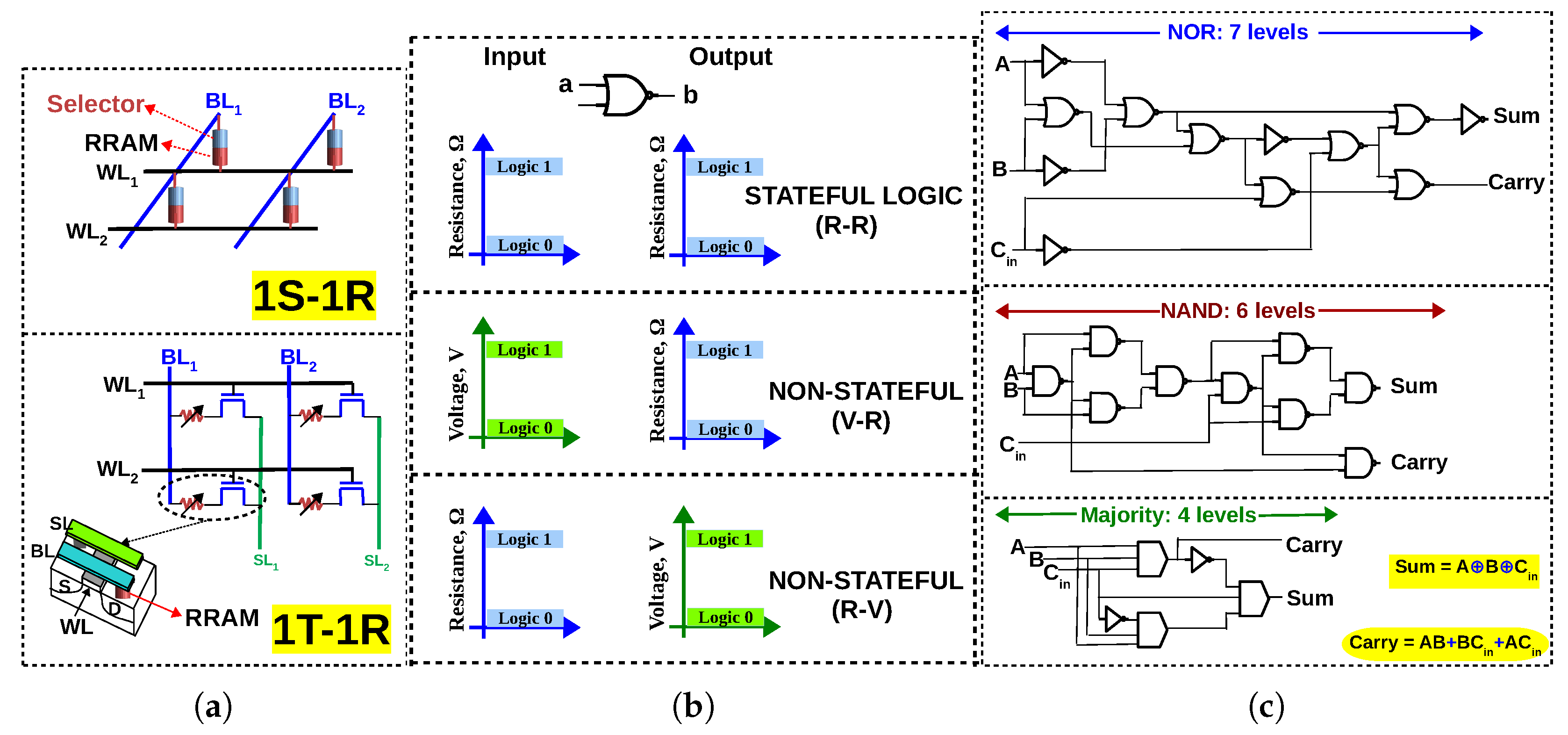
2. Memristive Logic
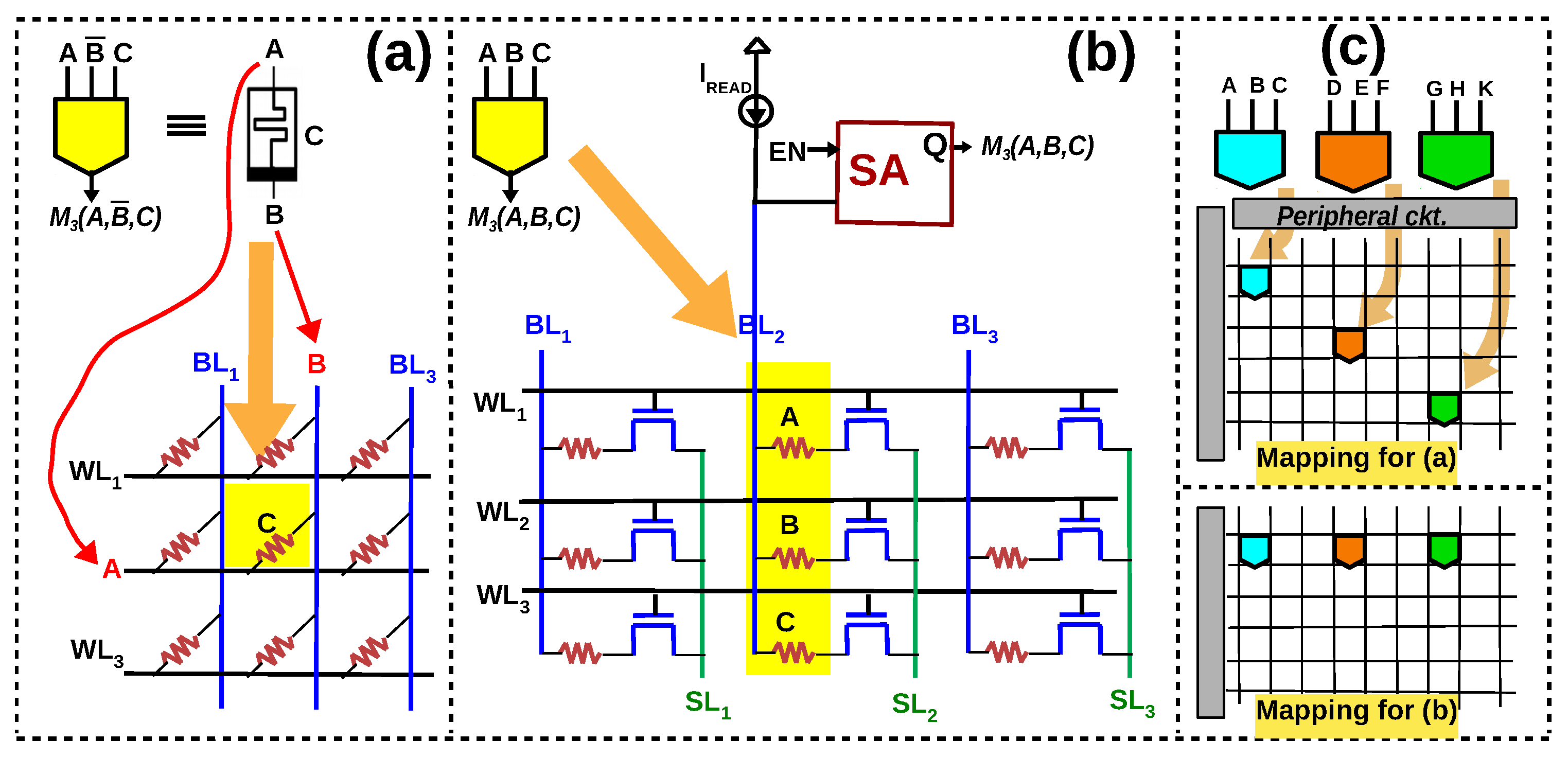
3. In-Memory Majority Logic
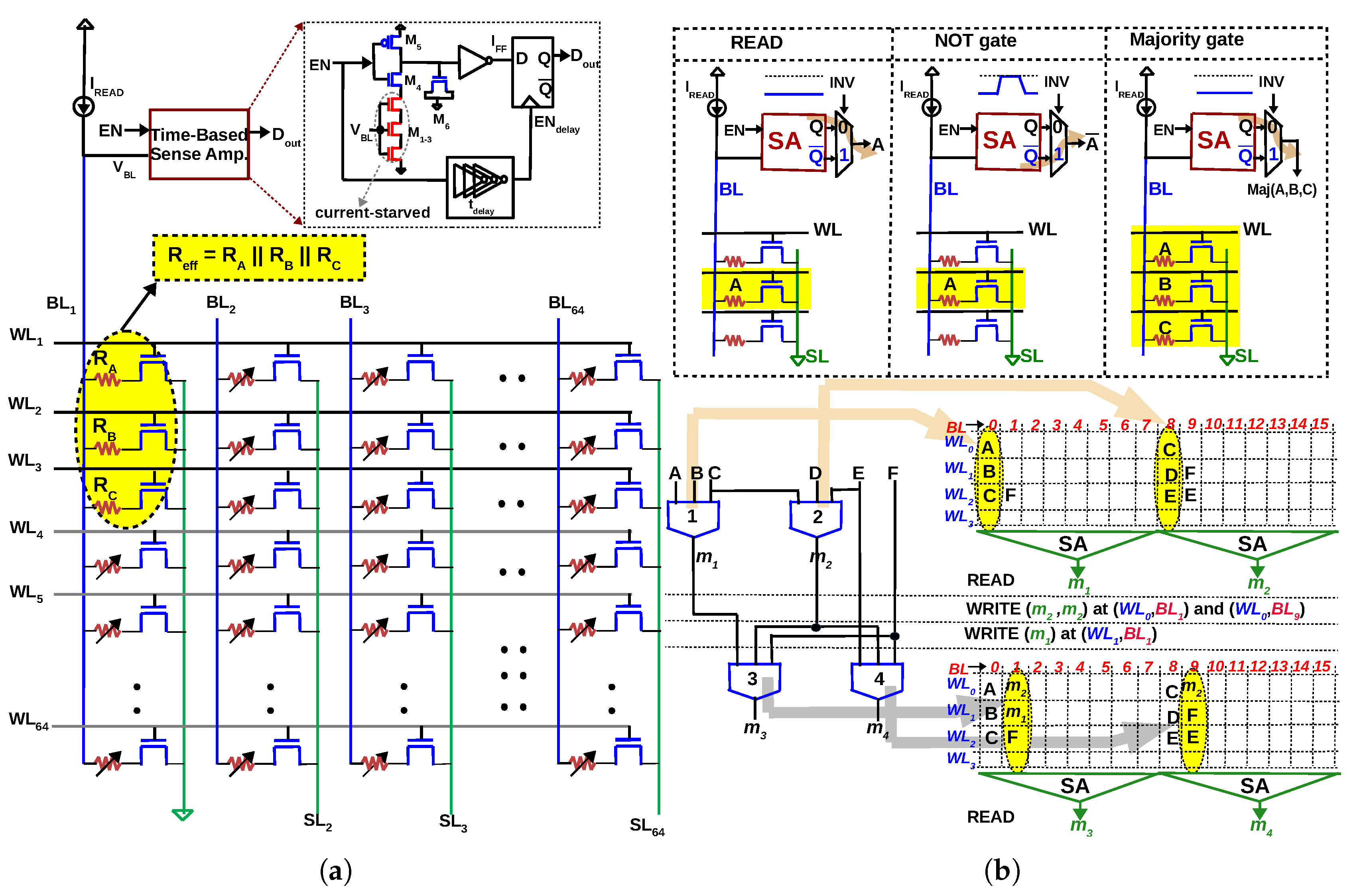
3.1. V–R Majority Logic
3.2. R–V Majority Logic
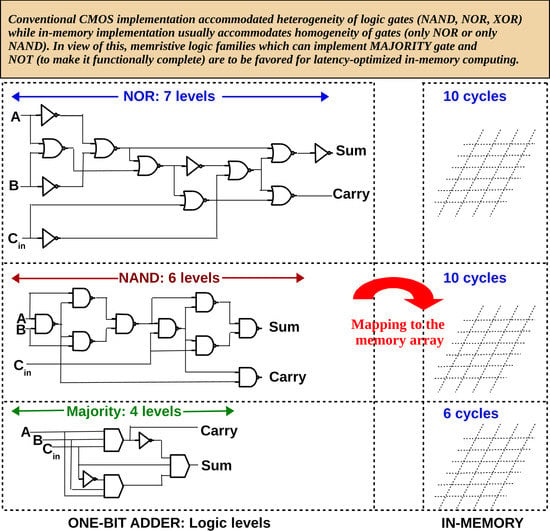
4. In-Memory One-Bit Full Adders Using Different Logic Primitives
5. In-Memory Eight-Bit Adders Using Different Logic Primitives
6. Conclusions
Funding
Conflicts of Interest
References
- Theis, T.N.; Wong, H.P. The End of Moore’s Law: A New Beginning for Information Technology. Comput. Sci. Eng. 2017, 19, 41–50. [Google Scholar] [CrossRef]
- Bohr, M.T.; Young, I.A. CMOS Scaling Trends and Beyond. IEEE Micro 2017, 37, 20–29. [Google Scholar] [CrossRef]
- Shalf, J.M.; Leland, R. Computing beyond Moore’s Law. Computer 2015, 48, 14–23. [Google Scholar] [CrossRef]
- Nikonov, D.E.; Young, I.A. Benchmarking of Beyond-CMOS Exploratory Devices for Logic Integrated Circuits. IEEE J. Explor. Solid State Comput. Devices Circuits 2015, 1, 3–11. [Google Scholar] [CrossRef]
- Testa, E.; Soeken, M.; Amar, L.G.; De Micheli, G. Logic Synthesis for Established and Emerging Computing. Proc. IEEE 2019, 107, 165–184. [Google Scholar] [CrossRef]
- Young, I.A.; Nikonov, D.E. Principles and trends in quantum nano-electronics and nano-magnetics for beyond-CMOS computing. In Proceedings of the 2017 47th European Solid-State Device Research Conference (ESSDERC), Leuven, Belgium, 11–14 September 2017; pp. 1–5. [Google Scholar]
- Ciubotaru, F.; Talmelli, G.; Devolder, T.; Zografos, O.; Heyns, M.; Adelmann, C.; Radu, I.P. First experimental demonstration of a scalable linear majority gate based on spin waves. In Proceedings of the 2018 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 1–5 December 2018; pp. 36.1.1–36.1.4. [Google Scholar] [CrossRef]
- Imre, A.; Csaba, G.; Ji, L.; Orlov, A.; Bernstein, G.H.; Porod, W. Majority Logic Gate for Magnetic Quantum-Dot Cellular Automata. Science 2006, 311, 205–208. [Google Scholar] [CrossRef] [PubMed]
- Breitkreutz, S.; Kiermaier, J.; Eichwald, I.; Ju, X.; Csaba, G.; Schmitt-Landsiedel, D.; Becherer, M. Majority Gate for Nanomagnetic Logic With Perpendicular Magnetic Anisotropy. IEEE Trans. Magn. 2012, 48, 4336–4339. [Google Scholar] [CrossRef]
- Oya, T.; Asai, T.; Fukui, T.; Amemiya, Y. A Majority-Logic Nanodevice Using a Balanced Pair of Single-Electron Boxes. J. Nanosci. Nanotechnol. 2002, 2, 333–342. [Google Scholar] [CrossRef]
- Amarú, L.; Gaillardon, P.; De Micheli, G. Majority-based synthesis for nanotechnologies. In Proceedings of the 2016 21st Asia and South Pacific Design Automation Conference (ASP-DAC), Macau, China, 25–28 January 2016; pp. 499–502. [Google Scholar] [CrossRef] [Green Version]
- Amarú, L.; Gaillardon, P.E.; Micheli, G.D. Majority-Inverter Graph: A New Paradigm for Logic Optimization. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2016, 35, 806–819. [Google Scholar] [CrossRef] [Green Version]
- Jaberipur, G.; Parhami, B.; Abedi, D. Adapting Computer Arithmetic Structures to Sustainable Supercomputing in Low-Power, Majority-Logic Nanotechnologies. IEEE Trans. Sustain. Comput. 2018, 3, 262–273. [Google Scholar] [CrossRef]
- Pudi, V.; Sridharan, K.; Lombardi, F. Majority Logic Formulations for Parallel Adder Designs at Reduced Delay and Circuit Complexity. IEEE Trans. Comput. 2017, 66, 1824–1830. [Google Scholar] [CrossRef]
- Amarú, L.; Gaillardon, P.; Mitra, S.; De Micheli, G. New Logic Synthesis as Nanotechnology Enabler. Proc. IEEE 2015, 103, 2168–2195. [Google Scholar] [CrossRef]
- Parhami, B.; Abedi, D.; Jaberipur, G. Majority-Logic, its applications, and atomic-scale embodiments. Comput. Electr. Eng. 2020, 83, 106562. [Google Scholar] [CrossRef]
- Reuben, J.; Ben-Hur, R.; Wald, N.; Talati, N.; Ali, A.; Gaillardon, P.E.; Kvatinsky, S. Memristive Logic: A Framework for Evaluation and Comparison. In Proceedings of the Power And Timing Modeling, Optimization and Simulation (PATMOS), Thessaloniki, Greece, 25–27 September 2017; pp. 1–8. [Google Scholar]
- Reuben, J.; Talati, N.; Wald, N.; Ben-Hur, R.; Ali, A.H.; Gaillardon, P.E.; Kvatinsky, S. A Taxonomy and Evaluation Framework for Memristive Logic. In Handbook of Memristor Networks; Chua, L., Sirakoulis, G.C., Adamatzky, A., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 1065–1099. [Google Scholar] [CrossRef]
- Simmons, J.G.; Verderber, R.R. New conduction and reversible memory phenomena in thin insulating films. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1967, 301, 77–102. [Google Scholar] [CrossRef]
- Borghetti, J.; Snider, G.S.; Kuekes, P.J.; Yang, J.J.; Stewart, D.R.; Williams, R.S. ‘Memristive’ switches enable ‘stateful’ logic operations via material implication. Nature 2010, 464, 873–876. [Google Scholar] [CrossRef]
- Zhou, F.; Guckert, L.; Chang, Y.F.; Swartzlander, E.E.; Lee, J. Bidirectional voltage biased implication operations using SiOx based unipolar memristors. Appl. Phys. Lett. 2015, 107, 183501. [Google Scholar] [CrossRef]
- Talati, N.; Ben-Hur, R.; Wald, N.; Haj-Ali, A.; Reuben, J.; Kvatinsky, S. mMPU—A Real Processing-in-Memory Architecture to Combat the von Neumann Bottleneck. In Applications of Emerging Memory Technology: Beyond Storage; Suri, M., Ed.; Springer: Singapore, 2020; pp. 191–213. [Google Scholar] [CrossRef]
- Rahimi Azghadi, M.; Chen, Y.C.; Eshraghian, J.K.; Chen, J.; Lin, C.Y.; Amirsoleimani, A.; Mehonic, A.; Kenyon, A.J.; Fowler, B.; Lee, J.C.; et al. Complementary Metal-Oxide Semiconductor and Memristive Hardware for Neuromorphic Computing. Adv. Intell. Syst. 2020, 2, 1900189. [Google Scholar] [CrossRef] [Green Version]
- Chang, K.C.; Chang, T.C.; Tsai, T.M.; Zhang, R.; Hung, Y.C.; Syu, Y.E.; Chang, Y.F.; Chen, M.C.; Chu, T.J.; Chen, H.L.; et al. Physical and chemical mechanisms in oxide-based resistance random access memory. Nanoscale Res. Lett. 2015, 10. [Google Scholar] [CrossRef] [Green Version]
- Reuben, J.; Fey, D.; Wenger, C. A Modeling Methodology for Resistive RAM Based on Stanford-PKU Model With Extended Multilevel Capability. IEEE Trans. Nanotechnol. 2019, 18, 647–656. [Google Scholar] [CrossRef] [Green Version]
- Golonzka, O.; Arslan, U.; Bai, P.; Bohr, M.; Baykan, O.; Chang, Y.; Chaudhari, A.; Chen, A.; Clarke, J.; Connor, C.; et al. Non-Volatile RRAM Embedded into 22FFL FinFET Technology. In Proceedings of the 2019 Symposium on VLSI Technology, Kyoto, Japan, 9–14 June 2019; pp. T230–T231. [Google Scholar] [CrossRef]
- Hsieh, C.C.; Chang, Y.F.; Chen, Y.C.; Shahrjerdi, D.; Banerjee, S.K. Highly Non-linear and Reliable Amorphous Silicon Based Back-to-Back Schottky Diode as Selector Device for Large Scale RRAM Arrays. ECS J. Solid State Sci. Technol. 2017, 6, N143–N147. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.Y.; Chen, P.H.; Chang, T.C.; Chang, K.C.; Zhang, S.D.; Tsai, T.M.; Pan, C.H.; Chen, M.C.; Su, Y.T.; Tseng, Y.T.; et al. Attaining resistive switching characteristics and selector properties by varying forming polarities in a single HfO2-based RRAM device with a vanadium electrode. Nanoscale 2017, 9, 8586–8590. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Lin, C.Y.; Kim, M.H.; Kim, T.H.; Kim, H.; Chen, Y.C.; Chang, Y.F.; Park, B.G. Dual Functions of V/SiOx/AlOy/p++Si Device as Selector and Memory. Nanoscale Res. Lett. 2018, 13. [Google Scholar] [CrossRef]
- Chen, C.; Lin, C.; Chen, P.; Chang, T.; Shih, C.; Tseng, Y.; Zheng, H.; Chen, Y.; Chang, Y.; Lin, C.; et al. The Demonstration of Increased Selectivity During Experimental Measurement in Filament-Type Vanadium Oxide-Based Selector. IEEE Trans. Electr. Devices 2018, 65, 4622–4627. [Google Scholar] [CrossRef]
- Ben-Hur, R.; Ronen, R.; Haj-Ali, A.; Bhattacharjee, D.; Eliahu, A.; Peled, N.; Kvatinsky, S. SIMPLER MAGIC: Synthesis and Mapping of In-Memory Logic Executed in a Single Row to Improve Throughput. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2019. [Google Scholar] [CrossRef]
- Adam, G.C.; Hoskins, B.D.; Prezioso, M.; Strukov, D.B. Optimized stateful material implication logic for three- dimensional data manipulation. Nano Res. 2016, 9, 3914–3923. [Google Scholar] [CrossRef]
- Kumar, A.P.; Aditya, B.; Sony, G.; Prasanna, C.; Satish, A. Estimation of power and delay in CMOS circuits using LCT. Indones. J. Electr. Eng. Comput. Sci. 2019, 14, 990–998. [Google Scholar]
- Rumi, Z.; Walus, K.; Wei, W.; Jullien, G.A. A method of majority logic reduction for quantum cellular automata. IEEE Trans. Nanotechnol. 2004, 3, 443–450. [Google Scholar] [CrossRef]
- Kvatinsky, S.; Satat, G.; Wald, N.; Friedman, E.G.; Kolodny, A.; Weiser, U.C. Memristor-Based Material Implication (IMPLY) Logic: Design Principles and Methodologies. IEEE Trans. Very Larg. Scale Integr. (VLSI) Syst. 2014, 22, 2054–2066. [Google Scholar] [CrossRef]
- Lehtonen, E.; Poikonen, J.H.; Laiho, M. Memristive Stateful Logic. In Handbook of Memristor Networks; Chua, L., Sirakoulis, G.C., Adamatzky, A., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 1101–1121. [Google Scholar] [CrossRef]
- Shen, W.; Huang, P.; Fan, M.; Han, R.; Zhou, Z.; Gao, B.; Wu, H.; Qian, H.; Liu, L.; Liu, X.; et al. Stateful Logic Operations in One-Transistor-One- Resistor Resistive Random Access Memory Array. IEEE Electr. Device Lett. 2019, 40, 1538–1541. [Google Scholar] [CrossRef]
- Ielmini, D.; Wong, H.S.P. In-memory computing with resistive switching devices. Nat. Electr. 2018, 1, 333–343. [Google Scholar] [CrossRef]
- Gupta, S.; Imani, M.; Rosing, T. FELIX: Fast and Energy-efficient Logic in Memory. In Proceedings of the International Conference on Computer-Aided Design (ICCAD ’18), San Diego, CA, USA, 5–8 November 2018; pp. 55:1–55:7. [Google Scholar] [CrossRef]
- Reuben, J.; Fey, D. A Time-based Sensing Scheme for Multi-level Cell (MLC) Resistive RAM. In Proceedings of the 2019 IEEE Nordic Circuits and Systems Conference (NORCAS): NORCHIP and International Symposium of System-on-Chip (SoC), Helsinki, Finland, 29–30 October 2019; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Reuben, J.; Biglari, M.; Fey, D. Incorporating Variability of Resistive RAM in Circuit Simulations Using the Stanford–PKU Model. IEEE Trans. Nanotechnol. 2020, 19, 508–518. [Google Scholar] [CrossRef]
- Gaillardon, P.; Amaru, L.; Siemon, A.; Linn, E.; Waser, R.; Chattopadhyay, A.; De Micheli, G. The Programmable Logic-in-Memory (PLiM) computer. In Proceedings of the 2016 Design, Automation Test in Europe Conference Exhibition (DATE), Dresden, Germany, 14–18 March 2016; pp. 427–432. [Google Scholar]
- Shirinzadeh, S.; Soeken, M.; Gaillardon, P.; Drechsler, R. Logic Synthesis for RRAM-Based In-Memory Computing. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2018, 37, 1422–1435. [Google Scholar] [CrossRef]
- Bhattacharjee, D.; Easwaran, A.; Chattopadhyay, A. Area-constrained technology mapping for in-memory computing using ReRAM devices. In Proceedings of the 2017 22nd Asia and South Pacific Design Automation Conference (ASP-DAC), Chiba, Japan, 16–19 January 2017; pp. 69–74. [Google Scholar] [CrossRef]
- Reuben, J. Binary Addition in Resistance Switching Memory Array by Sensing Majority. Micromachines 2020, 11, 496. [Google Scholar] [CrossRef]
- Reuben, J.; Pechmann, S. A Parallel-friendly Majority Gate to Accelerate In-memory Computation. In Proceedings of the 2020 IEEE 31st International Conference on Application-Specific Systems, Architectures and Processors (ASAP), Manchester, UK, 6–8 July 2020; pp. 93–100. [Google Scholar]
- Fey, D.; Reuben, J. Direct state transfer in MLC based memristive ReRAM devices for ternary computing. In Proceedings of the 2020 European Conference on Circuit Theory and Design (ECCTD), Sofia, Bulgaria, 7–10 September 2020; pp. 1–5. [Google Scholar]
- Hur, R.B.; Wald, N.; Talati, N.; Kvatinsky, S. SIMPLE MAGIC: Synthesis and In-memory Mapping of Logic Execution for Memristor-aided Logic. In Proceedings of the 36th International Conference on Computer-Aided Design (ICCAD ’17), Irvine, CA, USA, 13–16 November 2017; pp. 225–232. [Google Scholar]
- Huang, P.; Kang, J.; Zhao, Y.; Chen, S.; Han, R.; Zhou, Z.; Chen, Z.; Ma, W.; Li, M.; Liu, L.; et al. Reconfigurable Nonvolatile Logic Operations in Resistance Switching Crossbar Array for Large-Scale Circuits. Adv. Mater. 2016, 28, 9758–9764. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.; Zhou, F.; Fowler, B.W.; Chen, Y.; Hsieh, C.; Guckert, L.; Swartzlander, E.E.; Lee, J.C. Memcomputing (Memristor + Computing) in Intrinsic SiOx-Based Resistive Switching Memory: Arithmetic Operations for Logic Applications. IEEE Trans. Electr. Devices 2017, 64, 2977–2983. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, M.Y.; Li, Y.; Zhou, Y.X.; Wang, Z.R.; Hu, S.Y.; Long, S.B.; Liu, M.; Miao, X.S. Reprogrammable logic in memristive crossbar for in-memory computing. J. Phys. D Appl. Phys. 2017, 50, 505102. [Google Scholar] [CrossRef]
- Teimoory, M.; Amirsoleimani, A.; Shamsi, J.; Ahmadi, A.; Alirezaee, S.; Ahmadi, M. Optimized implementation of memristor-based full adder by material implication logic. In Proceedings of the 2014 21st IEEE International Conference on Electronics, Circuits and Systems (ICECS), Marseille, France, 7–10 December 2014; pp. 562–565. [Google Scholar]
- Rohani, S.G.; Taherinejad, N.; Radakovits, D. A Semiparallel Full-Adder in IMPLY Logic. IEEE Trans. Very Larg. Scale Integr. (VLSI) Syst. 2019, 28, 297–301. [Google Scholar] [CrossRef]
- Kim, K.M.; Williams, R.S. A Family of Stateful Memristor Gates for Complete Cascading Logic. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 4348–4355. [Google Scholar] [CrossRef]
- Siemon, A.; Drabinski, R.; Schultis, M.J.; Hu, X.; Linn, E.; Heittmann, A.; Waser, R.; Querlioz, D.; Menzel, S.; Friedman, J.S. Stateful Three-Input Logic with Memristive Switches. Sci. Rep. 2019, 9, 14618. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Yuan, R.; Zhu, Z.; Liu, K.; Jing, Z.; Cai, Y.; Wang, Y.; Yang, Y.; Huang, R. Memristor-Based Efficient In-Memory Logic for Cryptologic and Arithmetic Applications. Adv. Mater. Technol. 2019, 4, 1900212. [Google Scholar] [CrossRef]
- Siemon, A.; Menzel, S.; Bhattacharjee, D.; Waser, R.; Chattopadhyay, A.; Linn, E. Sklansky tree adder realization in 1S1R resistive switching memory architecture. Eur. Phys. J. Spec. Top. 2019, 228, 2269–2285. [Google Scholar] [CrossRef]
- Revanna, N.; Swartzlander, E.E. Memristor based adder circuit design. In Proceedings of the 2016 50th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 6–9 November 2016; pp. 162–166. [Google Scholar]
- Wang, Z.; Li, Y.; Su, Y.; Zhou, Y.; Cheng, L.; Chang, T.; Xue, K.; Sze, S.M.; Miao, X. Efficient Implementation of Boolean and Full-Adder Functions with 1T1R RRAMs for Beyond Von Neumann In-Memory Computing. IEEE Trans. Electr. Devices 2018, 65, 4659–4666. [Google Scholar] [CrossRef]
- Cheng, L.; Li, Y.; Yin, K.S.; Hu, S.Y.; Su, Y.T.; Jin, M.M.; Wang, Z.R.; Chang, T.C.; Miao, X.S. Functional Demonstration of a Memristive Arithmetic Logic Unit (MemALU) for In-Memory Computing. Adv. Funct. Mater. 2019, 29, 1905660. [Google Scholar] [CrossRef]
- Kim, Y.S.; Son, M.W.; Song, H.; Park, J.; An, J.; Jeon, J.B.; Kim, G.Y.; Son, S.; Kim, K.M. Stateful In-Memory Logic System and Its Practical Implementation in a TaOx-Based Bipolar-Type Memristive Crossbar Array. Adv. Intell. Syst. 2020, 2, 1900156. [Google Scholar] [CrossRef] [Green Version]
- Xiao, T.P.; Bennett, C.H.; Hu, X.; Feinberg, B.; Jacobs-Gedrim, R.; Agarwal, S.; Brunhaver, J.S.; Friedman, J.S.; Incorvia, J.A.C.; Marinella, M.J. Energy and Performance Benchmarking of a Domain Wall-Magnetic Tunnel Junction Multibit Adder. IEEE J. Explor. Solid State Comput. Devices Circuits 2019, 5, 188–196. [Google Scholar] [CrossRef]




| A | B | C | ||||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| A | B | C | |||
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 3.3 k | |
| 0 | 0 | 1 | 0 | 4.8 k | |
| 0 | 1 | 0 | 0 | 4.8 k | |
| 0 | 1 | 1 | 1 | 8.7 k | |
| 1 | 0 | 0 | 0 | 4.8 k | |
| 1 | 0 | 1 | 1 | 8.7 k | |
| 1 | 1 | 0 | 1 | 8.7 k | |
| 1 | 1 | 1 | 1 | 44.4 k |
| Primitive | Structure | Latency | Ref |
|---|---|---|---|
| IMPLY | 1D–1R | 43 steps | [50] |
| IMPLY | 1R | 35 steps | [32] |
| IMPLY | 1R | 27 steps | [51] |
| IMPLY | 1R | 23 steps | [52] |
| IMPLY(semi-parallel) | 1T–1R | 17 steps | [53] |
| IMPLY | 1T–1R | 13 steps | [54] |
| ORNOR | 1T–1R | 17 steps | [55] |
| NOR | 1S–1R | 10 steps | [48] |
| NAND | 1S–1R | 10 steps | [49] |
| XOR+NAND (unipolar memristors) | 1S–1R | 8 steps | [56] |
| MAJORITY+NOT | 1T–1R | 6 steps | [45] |
| Primitive | Array | Adder Type | Latency | Comment/Ref |
|---|---|---|---|---|
| IMPLY | 1S-1R | Ripple carry | 58 | Each step is IMPLY operation [35] |
| IMPLY+OR | 1S-1R | Ripple Carry | 54 | Each step is IMPLY/OR/NOR operation [60] |
| IMPLY | – | Parallel-prefix | 25 | Each step is IMPLY operation [58] |
| NOR/NOT | 1T-1R | Look-Ahead | 48 | Each step has one or more NOR/NOT operations [61] |
| NOR | 1S-1R | algorithm | 38 | Each step has one or more NOR operations [18] |
| OR/AND | 1S-1R | Parallel-prefix | 37 | Each step has one or more OR/AND operation [57] |
| ORNOR | 1S-1R | Parallel-clocking | 31 | Each step has one or more ORNOR/IMPLY operation [55] |
| MAJORITY+NOT | 1T-1R | Parallel-prefix | 19 | Each step is Majority/NOT or WRITE [46] |
| XOR | 1T-1R | Ripple carry | 16 * | Each step is XOR [59] |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reuben, J. Rediscovering Majority Logic in the Post-CMOS Era: A Perspective from In-Memory Computing. J. Low Power Electron. Appl. 2020, 10, 28. https://0-doi-org.brum.beds.ac.uk/10.3390/jlpea10030028
Reuben J. Rediscovering Majority Logic in the Post-CMOS Era: A Perspective from In-Memory Computing. Journal of Low Power Electronics and Applications. 2020; 10(3):28. https://0-doi-org.brum.beds.ac.uk/10.3390/jlpea10030028
Chicago/Turabian StyleReuben, John. 2020. "Rediscovering Majority Logic in the Post-CMOS Era: A Perspective from In-Memory Computing" Journal of Low Power Electronics and Applications 10, no. 3: 28. https://0-doi-org.brum.beds.ac.uk/10.3390/jlpea10030028