A Method for Optimizing and Spatially Distributing Heating Systems by Coupling an Urban Energy Simulation Platform and an Energy System Model
Abstract
:1. Introduction
State of the Art
2. Materials and Methods
2.1. The Two Case Studies
2.2. The Modelling Framework
2.2.1. The Simstadt Model
2.2.2. The KomMod Model
2.2.3. The Heating Grid Disaggregation Algorithm
- The street segment with the global highest heating density (taken in this paper).
- A street segment adjacent to a potential site for a future heating station.
- The street segment with the highest heating density among all segments adjacent to an existing grid.
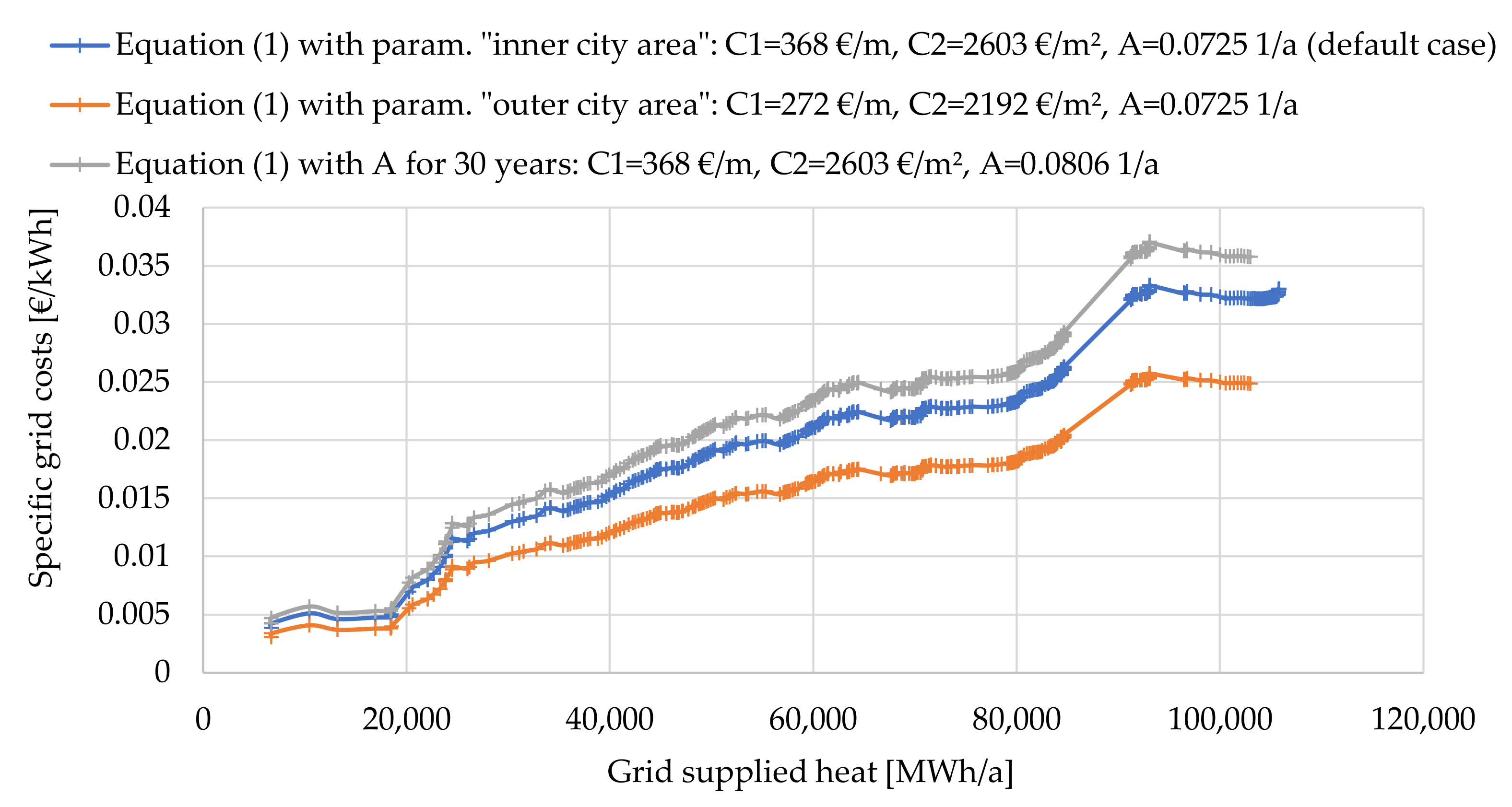
2.2.4. Computing the Optimal Grid
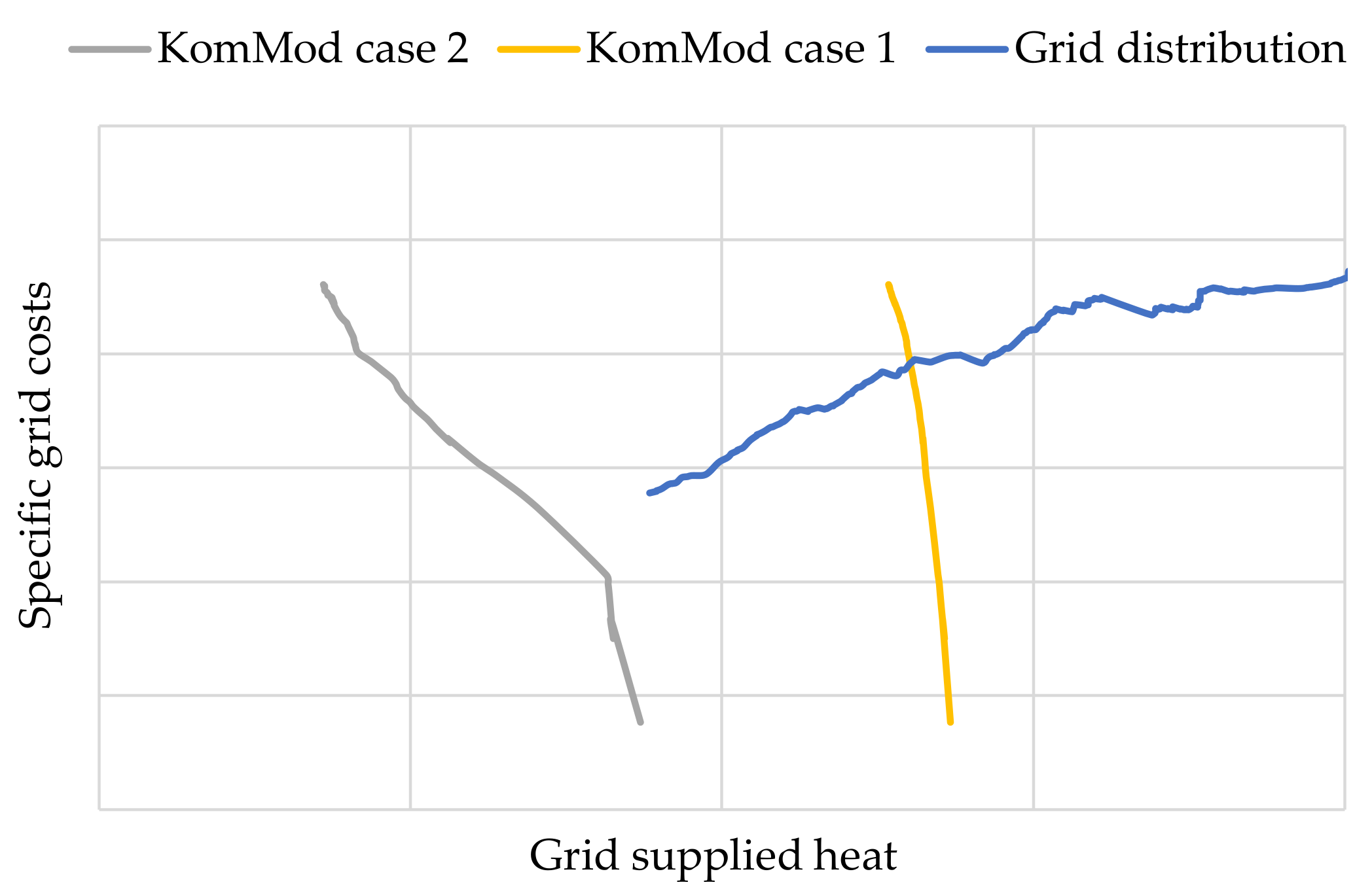
- The two curves have an intersection. In that case, the intersection point yields the optimal amount of grid-supplied heat, as at this point, the specific grid costs from KomMod and the cost determined via the grid distribution algorithm are approximately the same (KomMod case 1 in Figure 3).
- The two curves do not intersect, with the KomMod curve generally yielding smaller values for the grid-supplied heat. In this case, KomMod suggests using district heating only at costs that are lower than the costs associated with heating grid installations in the studied area. Therefore, district heating is economically not feasible. (KomMod case 2 in Figure 3).
3. Results
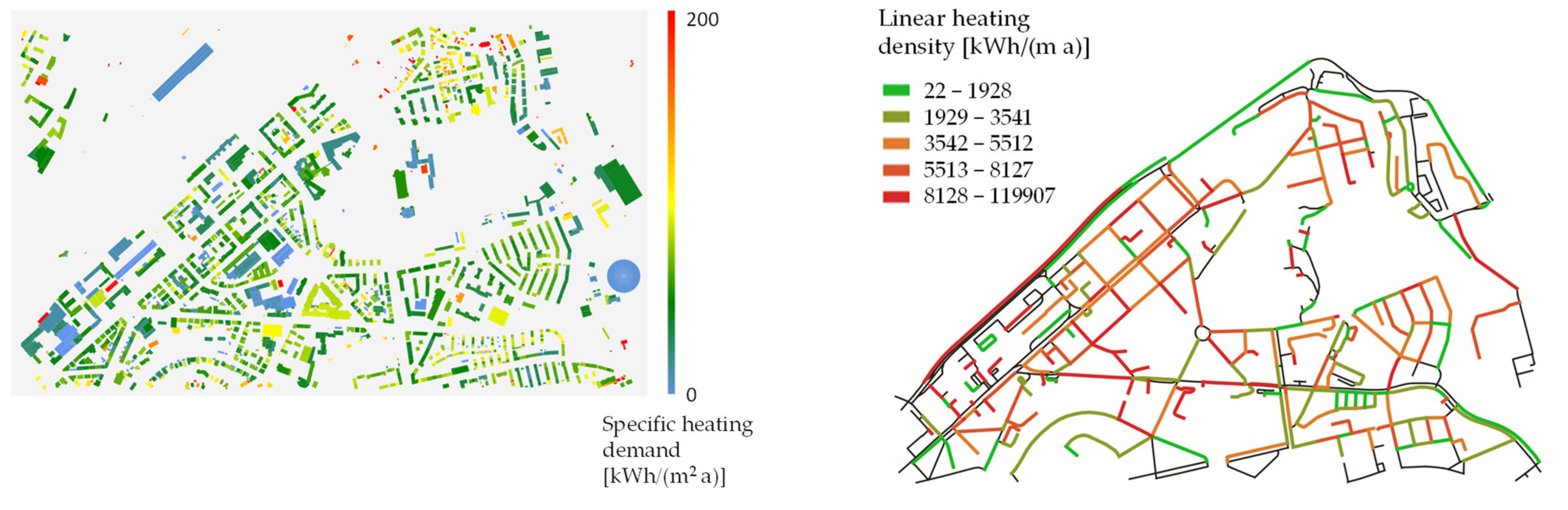
3.1. Linear Heating Density and Grid Costs
3.2. Optimal Grid Layout
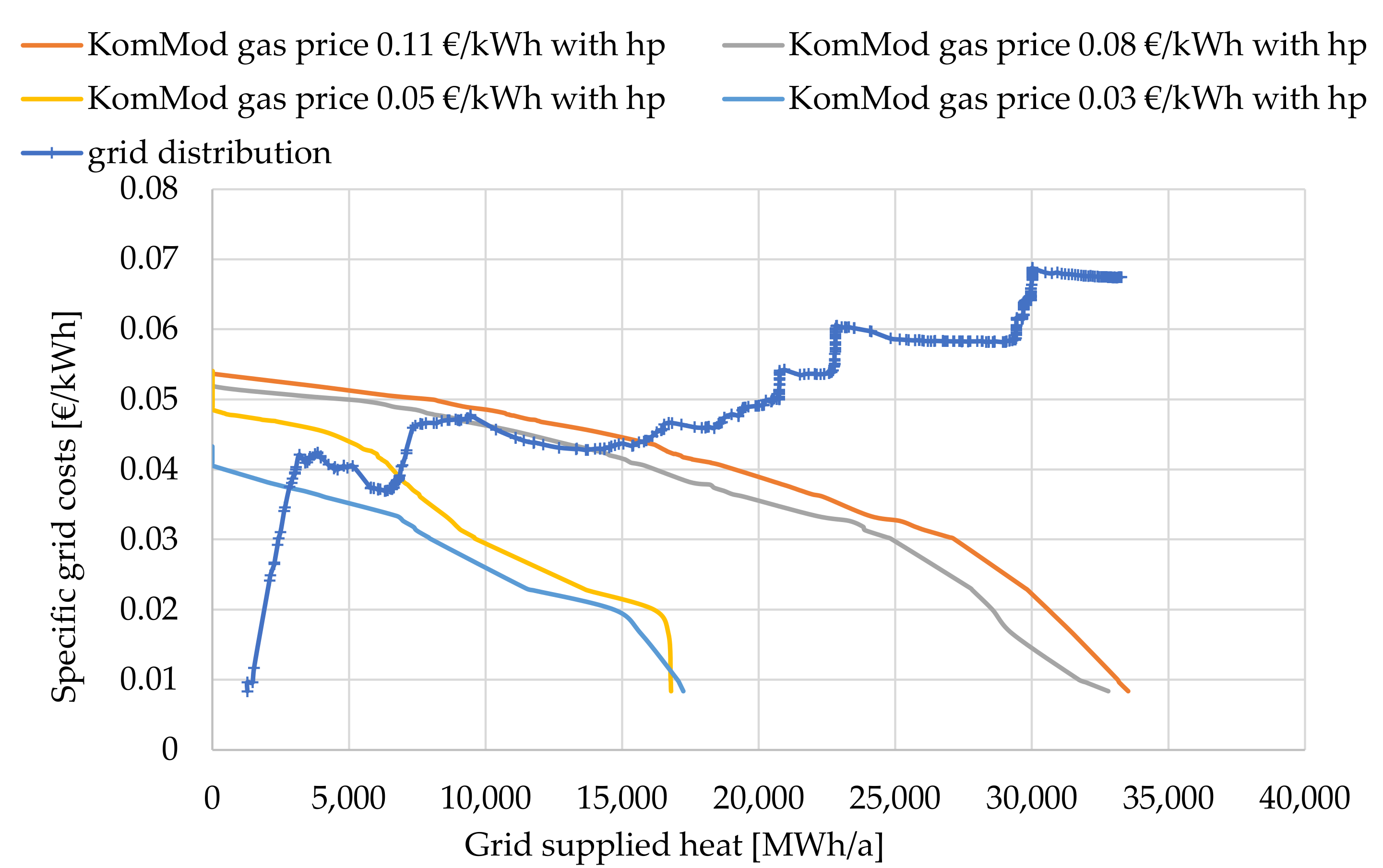
3.2.1. Case Study Stuttgart-Stöckach: Fuel Cost Variation
3.2.2. Case Study Rainau: Fuel Cost Variation
3.2.3. Case Study Stöckach: Grid Connection
3.3. Summary of the Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bundesministerium für Wirtschaft und Energie. Zahlen und Fakten: Energiedaten. 2020. Available online: http://www.bmwi.de/DE/Themen/Energie/energiedaten.html (accessed on 28 March 2021).
- Strogies, M.; Gniffke, P. Berichterstattung unter der Klimarahmenkonvention der Vereinten Nationen und dem Kyoto-Protokoll 2021, Nationaler Inventarbericht zum Deutschen, Treibhausgasinventar 1990–2019, Umweltbundesamt—UNFCCC-Submission; Climate Change; Umweltbundesamt: Dessau, Germany, 2021. [Google Scholar]
- Lund, H.; Werner, S.; Wiltshire, R.; Svendsen, S.; Thorsen, J.E.; Hvelplund, F.; Mathiesen, B.V. 4th Generation District Heating (4GDH): Integrating smart thermal grids into future sustainable energy systems. Energy 2014, 68, 1–11. [Google Scholar] [CrossRef]
- Nussbaumer, T.; Thalmann, S. Influence of system design on heat distribution costs in district heating. Energy 2016, 101, 496–505. [Google Scholar] [CrossRef]
- Dochev, I.; Peters, I.; Seller, H.; Schuchardt, G.K. Analysing district heating potential with linear heat density. A case study from Hamburg. Energy Proc. 2018, 149, 410–419. [Google Scholar] [CrossRef]
- Nouvel, R.; Zirak, M.; Coors, V.; Eicker, U. The influence of data quality on urban heating demand modeling using 3D city models. Comput. Environ. Urban Syst. 2017, 64, 68–80. [Google Scholar] [CrossRef]
- Dall’O’, G.; Galante, A.; Torri, M. A methodology for the energy performance classification of residential building stock on an urban scale. Energy Build. 2012, 48, 211–219. [Google Scholar] [CrossRef]
- Reinhart, C.; Dogan, T.; Jakubiec, J.A.; Rakha, T.; Sang, A. Umi-an urban simulation environment for building energy use, daylighting and walkability. In Proceedings of the 13th Conference of International Building Performance Simulation Association, Chambery, France, 26–28 August 2013. [Google Scholar]
- Weiler, V.; Stave, J.; Eicker, U. Renewable Energy Generation Scenarios Using 3D Urban Modeling Tools—Methodology for Heat Pump and Co-Generation Systems with Case Study Application. Energies 2019, 12, 403. [Google Scholar] [CrossRef] [Green Version]
- Eggers, J.-B. Das Kommunale Energiesystemmodell KomMod: Konzeption, Implementierung und Anwendung an den Praxisbeispielen Frankfurt am Main und Freiburg-Haslach; Dissertation; Technische Universität Berlin: Berlin, Germany, 2018. [Google Scholar]
- Jalil-Vega, F.; Hawkes, A.D. The effect of spatial resolution on outcomes from energy systems modelling of heat decarbonisation. Energy 2018, 155, 339–350. [Google Scholar] [CrossRef]
- Lopion, P.; Markewitz, P.; Robinius, M.; Stolten, D. A review of current challenges and trends in energy systems modeling. Renew. Sustain. Energy Rev. 2018, 96, 156–166. [Google Scholar] [CrossRef]
- Prina, M.G.; Casalicchio, V.; Kaldemeyer, C.; Manzolini, G.; Moser, D.; Wanitschke, A.; Sparber, W. Multi-objective investment optimization for energy system models in high temporal and spatial resolution. Appl. Energy 2020, 264, 114728. [Google Scholar] [CrossRef]
- Yang, J.; Xiang, Y.; Wei, X.; Yao, H.; Liu, J.; Gou, J. Planning-objective based representative day selection for optimal investment decision of distribution networks. Energy Rep. 2020, 6, 543–548. [Google Scholar] [CrossRef]
- Richter, J. Dimension—A Dispatch and Investment Model for European Electricity Markets. EWI Working Paper 11/03. 2011. Available online: https://www.econstor.eu/handle/10419/74393 (accessed on 20 March 2021).
- Keirstead, J.; Calderon, C. Capturing spatial effects, technology interactions, and uncertainty in urban energy and carbon models: Retrofitting newcastle as a case-study. Energy Policy 2012, 46, 253–267. [Google Scholar] [CrossRef] [Green Version]
- Omu, A.; Choudhary, R.; Boies, A. Distributed energy resource system optimisation using mixed integer linear programming. Energy Policy 2013, 61, 249–266. [Google Scholar] [CrossRef]
- Fazlollahi, S.; Girardin, L.; Maréchal, F. Clustering urban areas for optimizing the design and the operation of district heating energy systems. In Proceedings of the 24th European Symposium on Computer Aided Process Engineering—ESCAPE 24, Budapest, Hungary, 15–18 June 2014. [Google Scholar]
- Fischer, D.; Härtl, A.; Wille-Haussmann, B. Model for electric load profiles with high time resolution for German households. Energy Build. 2015, 92, 170–179. [Google Scholar] [CrossRef]
- Kelly, S. Do homes that are more energy efficient consume less energy? A structural equation model of the English residential sector. Energy 2011, 36, 5610–5620. [Google Scholar] [CrossRef]
- Torabi Moghadam, S.; Delmastro, C.; Corgnati, S.P.; Lombardi, P. Urban energy planning procedure for sustainable development in the built environment: A review of available spatial approaches. J. Clean. Prod. 2017, 165, 811–827. [Google Scholar] [CrossRef]
- Martinaitis, V.; Zavadskas, E.K.; Motuzienė, V.; Vilutienė, T. Importance of occupancy information when simulating energy demand of energy efficient house: A case study. Energy Build. 2015, 101, 64–75. [Google Scholar] [CrossRef]
- Wang, D.; Orehounig, K.; Carmeliet, J. Dynamic building energy demand modelling at urban scale for the case of Switzerland. In CLIMA 2016-Proceedings of the 12th REHVA World Congress, Aalborg, Denmark, 22–25 May 2016; Department of Civil Engineering, Aalborg University: Aalborg, Denmark, 2016. [Google Scholar]
- Hofierka, J.; Suri, M. The solar radiation model for Open source GIS: Implementation and applications. In Proceedings of the Open Source GIS-GRASS Users Conference, Trento, Italy, 11–13 September 2002; pp. 51–70. [Google Scholar]
- Redweik, P.; Catita, C.; Brito, M. Solar energy potential on roofs and facades in an urban landscape. Sol. Energy 2013, 97, 332–341. [Google Scholar] [CrossRef]
- Lukač, N.; Žlaus, D.; Seme, S.; Žalik, B.; Štumberger, G. Rating of roofs’ surfaces regarding their solar potential and suitability for PV systems, based on LiDAR data. Appl. Energy 2013, 102, 803–812. [Google Scholar] [CrossRef]
- Gagliano, A.; Patania, F.; Nocera, F.; Capizzi, A.; Galesi, A. GIS-Based Decision Support for Solar Photovoltaic Planning in Urban Environment. In Sustainability in Energy and Buildings; Springer: Berlin/Heidelberg, Germany, 2013; pp. 865–874. [Google Scholar]
- Dorer, V.; Allegrini, J.; Orehounig, K.; Moonen, P.; Upadhyay, G.; Kämpf, J.; Carmeliet, J. Modelling the urban microclimate and its impact on the energy demand of buildings and building clusters. Proc. BS 2013, 2013, 3483–3489. [Google Scholar]
- Kaden, R.; Kolbe, T.H. City-wide total energy demand estimation of buildings using semantic 3D city models and statistical data. In ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences. WG II/2, Proceedings of the ISPRS 8th 3D GeoInfo Conference & WG II/2 Workshop (Volume II-2/W1), Istanbul, Turkey, 27–29 November 2013; Copernicus GmbH: Göttingen, Germany, 2013; pp. 163–171. ISBN 2194-9042. [Google Scholar]
- Hong, T.; Chen, Y.; Lee, S.H.; Piette, M.A. CityBES: A web-based platform to support city-scale building energy efficiency. Urban Comput. 2016, 14, 2016. [Google Scholar]
- Mróz, T.M. Planning of community heating systems modernization and development. Appl. Therm. Eng. 2008, 28, 1844–1852. [Google Scholar] [CrossRef]
- Jalil-Vega, F.; Hawkes, A.D. Spatially resolved model for studying decarbonisation pathways for heat supply and infrastructure trade-offs. Appl. Energy 2018, 210, 1051–1072. [Google Scholar] [CrossRef]
- Marquant, J.; Omu, A.; Orehounig, K.; Evins, R.; Carmeliet, J. Application of spatial temporal clustering to facilitate energy system modelling. In Proceedings of the BS2015: 14th Conference of International Building Performance Simulation Association, Hyderabad, India, 7–9 December 2015. [Google Scholar]
- Unternährer, J.; Moret, S.; Joost, S.; Maréchal, F. Spatial clustering for district heating integration in urban energy systems: Application to geothermal energy. Appl. Energy 2017, 190, 749–763. [Google Scholar] [CrossRef] [Green Version]
- Morvaj, B.; Evins, R.; Carmeliet, J. Optimising urban energy systems: Simultaneous system sizing, operation and district heating network layout. Energy 2016, 116, 619–636. [Google Scholar] [CrossRef]
- Nouvel, R.; Brassel, K.-H.; Bruse, M.; Duminil, E.; Coors, V.; Eicker, U. SimStadt, a new workflow-driven urban energy simulation platform for CityGML city models. In Proceedings of CISBAT 2015 International Conference “Future Buildings and Districts—Sustainability from Nano to Urban Scale”, Lausanne, Switzerland, 9–11 September 2015; EPFL Solar Energy and Building Physics Laboratory: Lausanne, Switzerland, 2015. [Google Scholar]
- Köhler, S. Stochastic Generation of Household Electricity Load Profiles in 15-minute Resolution on Building Level for Whole City Quarters. In Proceedings of Energy Challenges for the Next Decade, Ljubljana, Slovenia, 25–28 August 2019; School of Economics and Business, University of Ljubljana: Ljubljana, Slovenia, 2019. [Google Scholar]
- Bao, K.; Padsala, R.; Thrän, D.; Schröter, B. Urban Water Demand Simulation in Residential and Non-Residential Buildings Based on a CityGML Data Model. ISPRS Int. J. Geo-Inf. 2020, 9, 642. [Google Scholar] [CrossRef]
- Bao, K.; Padsala, R.; Coors, V.; Thrän, D.; Schröter, B. A Method for Assessing Regional Bioenergy Potentials Based on GIS Data and a Dynamic Yield Simulation Model. Energies 2020, 13, 6488. [Google Scholar] [CrossRef]
- Zirak, M.; Weiler, V.; Hein, M.; Eicker, U. Urban models enrichment for energy applications: Challenges in energy simulation using different data sources for building age information. Energy 2020, 190, 116292. [Google Scholar] [CrossRef]
- Landeshauptstadt Stuttgart. Stadtmessungsamt. Available online: https://www.stuttgart.de/vv/verwaltungseinheit/stadtmessungsamt.php (accessed on 11 March 2021).
- Landesamt für Geoinformation und Landentwicklung, Baden-Württemberg. 3D-Gebäudemodelle. Available online: https://www.lgl-bw.de/unsere-themen/Produkte/Geodaten/3D-Gebaeudemodelle/ (accessed on 2 March 2021).
- Fischer, D.; Wolf, T.; Scherer, J.; Wille-Haussmann, B. A stochastic bottom-up model for space heating and domestic hot water load profiles for German households. Energy Build. 2016, 124, 120–128. [Google Scholar] [CrossRef]
- Meteotest. Meteonorm. Available online: https://meteonorm.com/en/ (accessed on 12 August 2020).
- VDI-Gesellschaft Technische Gebäudeausrüstung. VDI 4710-2: Meteorological Data for Technical Building Sevices Purposes-Degree Days; Verein Deutscher Ingenieure e.V.: Düsseldorf, Germany, 2007. [Google Scholar]
- Bruse, M.; Nouvel, R.; Wate, P.; Kraut, V.; Coors, V. An Energy-Related CityGML ADE and Its Application for Heating Demand Calculation. Int. J. 3D Inf. Modeling 2015, 4, 59–77. [Google Scholar] [CrossRef]
- Rossknecht, M.; Airaksinen, E. Concept and Evaluation of Heating Demand Prediction Based on 3D City Models and the CityGML Energy ADE—Case Study Helsinki. ISPRS Int. J. Geo-Inf. 2020, 9, 602. [Google Scholar] [CrossRef]
- Romero Rodríguez, L.; Duminil, E.; Sánchez Ramos, J.; Eicker, U. Assessment of the photovoltaic potential at urban level based on 3D city models: A case study and new methodological approach. Sol. Energy 2017, 146, 264–275. [Google Scholar] [CrossRef]
- Fourer, R.; Gay, D.M.; Kernighan, B.W. AMPL: A Mathematical Programing Language. In Algorithms and Model Formulations in Mathematical Programming; Wallace, S.W., Ed.; Springer: Berlin/Heidelberg, Germany, 1989; pp. 150–151. ISBN 978-3-642-83726-5. [Google Scholar]
- Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual. 2021. Available online: https://www.gurobi.com/wp-content/plugins/hd_documentations/documentation/9.0/refman.pdf (accessed on 11 May 2021).
- Persson, U.; Werner, S. Heat distribution and the future competitiveness of district heating. Appl. Energy 2011, 88, 568–576. [Google Scholar] [CrossRef]
- Sterchele, P.; Brandes, J.; Heilig, J.; Wrede, D.; Kost, C.; Schlegl, T.; Bett, A.; Henning, H.-M. Wege zu Einem Klimaneutralem Energiesystem: Die Deutsche Energiewende im Kontext Gesellschaftlicher Verhaltensweisen; Fraunhofer Institute for Solar Energy Systems: Freiburg, Germany, 2020. [Google Scholar]
- Duic, N.; Stefanic, N.; Lulic, Z.; Krajacic, G.; Puksec, T.; Novosel, T. EU28 Fuel Prices for 2015, 2030 and 2050: Deliverable 6.1: Future Fuel Price Review; Faculty of Mechanical Engineering and Naval Architecture, University of Zagreb: Zagreb, Croatia, 2017. [Google Scholar]
- Björkqvist, O.; Idefeldt, J.; Larsson, A. Risk assessment of new pricing strategies in the district heating market. Energy Policy 2010, 38, 2171–2178. [Google Scholar] [CrossRef]





| Urban: Stuttgart-Stöckach | Rural: Rainau | |
|---|---|---|
| Buildings included in the model [−] | 1858 | 1838 |
| Area of the case study [m2] | 2,064,000 | 29,840,000 |
| Heating demand calculated with Simstadt for medium refurbishment scenario [GWh/a] | 106 | 40 |
| Areal heating demand density [kWh/(m2 a)] | 51.4 | 1.3 |
| Number of street segments (part of street between two intersections) [−] | 439 | 498 |
| Stöckach | Rainau | ||
|---|---|---|---|
| Possible technologies | Electricity converters | Photovoltaic | |
| Gas-fired CHP | |||
| Import | |||
| Wind power plants | |||
| Decentral thermal converters | Gas and oil boilers | Gas, wood and oil boilers | |
| Air-sourced heat pumps | Air and ground-sourced heat pumps | ||
| Solar heaters | |||
| Central thermal converters | Gas-fired CHP | ||
| Ground-sourced heat pumps | |||
| Cost data | Import electricity price [EUR/kWh] | 0.15 | |
| Technology installation and maintenance costs | According to [52] | ||
| Natural gas price [EUR/kWh] | Varied between 0.03 and 0.11 | ||
| Price for oil and wood | 0.02 EUR/kWh higher than natural gas price (based on historic price differences between gas, oil and wood) | ||
| Fuel Price in EUR/kWh | S-Stöckach CHP | S-Stöckach CHP + Heat Pump | Rainau CHP | Rainau CHP + Heat Pump |
|---|---|---|---|---|
| 0.03 | 51.1% | 95.0% | 4.5% | 8.4% |
| 0.05 | 49.4% | 86.2% | 20.3% | |
| 0.08 | 26.5% | 91.2% | 41.8% | |
| 0.11 | 6.9% | 87.6% | 47.3% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steingrube, A.; Bao, K.; Wieland, S.; Lalama, A.; Kabiro, P.M.; Coors, V.; Schröter, B. A Method for Optimizing and Spatially Distributing Heating Systems by Coupling an Urban Energy Simulation Platform and an Energy System Model. Resources 2021, 10, 52. https://0-doi-org.brum.beds.ac.uk/10.3390/resources10050052
Steingrube A, Bao K, Wieland S, Lalama A, Kabiro PM, Coors V, Schröter B. A Method for Optimizing and Spatially Distributing Heating Systems by Coupling an Urban Energy Simulation Platform and an Energy System Model. Resources. 2021; 10(5):52. https://0-doi-org.brum.beds.ac.uk/10.3390/resources10050052
Chicago/Turabian StyleSteingrube, Annette, Keyu Bao, Stefan Wieland, Andrés Lalama, Pithon M. Kabiro, Volker Coors, and Bastian Schröter. 2021. "A Method for Optimizing and Spatially Distributing Heating Systems by Coupling an Urban Energy Simulation Platform and an Energy System Model" Resources 10, no. 5: 52. https://0-doi-org.brum.beds.ac.uk/10.3390/resources10050052







