1. Introduction
In the original configuration of the Collective Atomic Recoil Lasing (CARL, [
1,
2]) an ensemble of
N initially randomly distributed atoms set in the arm of a ring cavity scatters photons in the reverse direction of an incident laser injected along the cavity axis [
3,
4]. The process arises due to a collective instability, where each atom is affected by the optical field scattered by the other atoms. After the production of ultra-cold atomic samples, a similar phenomenon was first demonstrated using a cigar-shaped Bose–Einstein Condensate (BEC) [
5] and later using a cold, thermal gas [
6], named Superradiant Rayleigh Scattering. In [
5], superradiant scattered light was observed to propagate along the major axis of the atomic cloud, simultaneous with the formation of a matter-wave momentum grating in the cloud. Some features of this phenomenon have been described by single-mode/mean-field models similar to that of the (CARL) [
7,
8,
9,
10,
11,
12]. These mean-field models are appropriate in certain specific cases, where there is a well-defined propagation axis and consequently, to a good approximation, a single spatial mode, e.g., in a single-mode cavity or in a highly elongated sample where its major axis defines an ‘end-fire mode’ [
7] which dominates the emission direction. In general, however, for arbitrary shapes of atomic ensembles, many spatial modes are involved simultaneously in the collective scattering process.
In a recent paper, we presented a model able to describe collective scattering of light by an atomic cloud into multiple vacuum modes, when this is irradiated by an optical field [
13]. For the sake of simplicity, in the model a scalar field was assumed, neglecting polarization effects and near-field terms in the scattered light. The model’s equations, which follows the particles’ trajectories with the sole dependency of their positions, were implemented in a molecular dynamics (MD) code. The response of a two-dimensional cold atomic gas was proven to be sensitive to the cloud’s shape and to its major axis’ orientation with respect to the propagation axis of the incident field. Any change in these features triggers distinct pattern formation in the cloud, due to the atomic redistribution caused by different scattering events. The atomic rearrangements vary from unidimensional gratings to organizations in two dimensions, occurring when the cloud’s major axis is aligned or not with the propagation axis of the pump field, respectively. The scattering was proven to befall across the major axis of the cloud with no need for an optical resonator. Patterns similar to those observed in [
5] with a BEC in the momentum space have been shown in [
13], but in the real space and with thermal atoms. In addition, the capabilities of the code were demonstrated by showing the formation of a density grating when the study of collective light-scattering was extended to a three-dimension atomic cloud.
Specifically, three main shapes and orientations were investigated in [
13] with different outcomes. On the one hand, when the cloud is elongated perpendicularly to the incident field, the atomic scattering occurs mainly across the perpendicular axis (the longest path), which combined with the pump translates in a 2D density pattern formation. On the other hand, the grating formations observed in both 2D and 3D profiles, elongated along the pump propagation axis, exhibit analogies with the ones observed in either the collective atomic recoil lasing (CARL) [
1], which enhances the backscattered light, or in the free-electron laser (FEL) [
14]. In addition, a third case with a spherical cloud was investigated. With this configuration, any density grating was expected due to the lack of any longest scattering path. However, the peculiarity of this case is that an electrostrictive force, generated by collective scattering, slightly deforms the initially spherical shape. Then, the cloud is stretched along the pump’s propagation direction and compressed along the perpendicular direction, by outlining two preferred scattering paths along its edges. The resulting two-dimensional density grating differs from the one observed in a perpendicular elongated cloud, since the light is scattered at an angle larger than
with respect to the pump’s incident axis.
In the present paper, we extend the former scalar model of [
13] to a full vectorial model of light. The polarization effects are shown to be relevant in the scattering process: since the radiation electric field is transverse, propagation along the pump’s polarization direction is not allowed. The study is substantially extended by considering 3D collective scattering with different distributions and orientations of the atomic cloud. Moreover, we investigate the three-dimensional intensity spatial profiles, for a better understanding of the grating formation for each configuration. The vectorial model, likewise its scalar version, has been derived from a multimode theory, where the vacuum radiation modes are adiabatically eliminated. The resulting
N coupled equations, where each atom of the cloud is subdued to the radiation force produced by the other
atoms, are now also accounting for the polarization effects of the incident and scattered fields. These new equations, although more complex due to the presence of addition short-range terms, are also eligible to be implemented in MD codes. The algorithm used in the current letter has been adapted to work with the rather new open-source programming language developed by the MIT, Julia. The former algorithm employed in the scalar study, Verlet velocity, has been substituted with its close relative leapfrog algorithm, or in this case the variant “Verlet leapfrog”, included in one of Julia’s packages [
15]. The vectorial model is introduced in
Section 2, together with a brief description of the employed MD algorithm, the chosen inter-particle interaction, and the rescaling of the motion equations. These results, for the 2D and 3D geometries, are discussed in
Section 3.1 and
Section 3.2, respectively. Further details of the analytical derivation of the model can be found in the
Appendix A.
3. Results
There are several variables that can be adjusted to obtain different results when keeping the system parameters fixed, such as the pump frequency or the detuning, among others. For instance, we can talk about the space dimensions of the gas (2D or 3D); the cloud’s orientation with respect to the incident laser beam, which can accommodate different directions for the polarization vector; the shape of the cloud, being elliptical, which includes many degrees of elongation, or circular; and the density distribution of the atoms in the cloud (e.g., Gaussian or uniform). To give some hierarchy to such a variety, the central concept that will allow the characterization of such a complex system will be the space dimensions of the systems: 2D and 3D. The same numerical random seed has been introduced when defining the initial positions for the atoms inside both the flat and the volumetric clouds. The incident field’s polarization is linear, perpendicular to its propagation axis (z axis) and parallel to x or y axis. Restricting the number of system configurations available even further, only the off-axis scattering (elongated 2D/3D clouds with their major axis perpendicular to the incident field propagation direction) is here investigated. The analysis of this configuration allows visualization of the effects derived from having the polarization field parallel or perpendicular to the major axis of the cloud.
3.1. Polarized Light-Scattering from a 2D Atomic Cloud
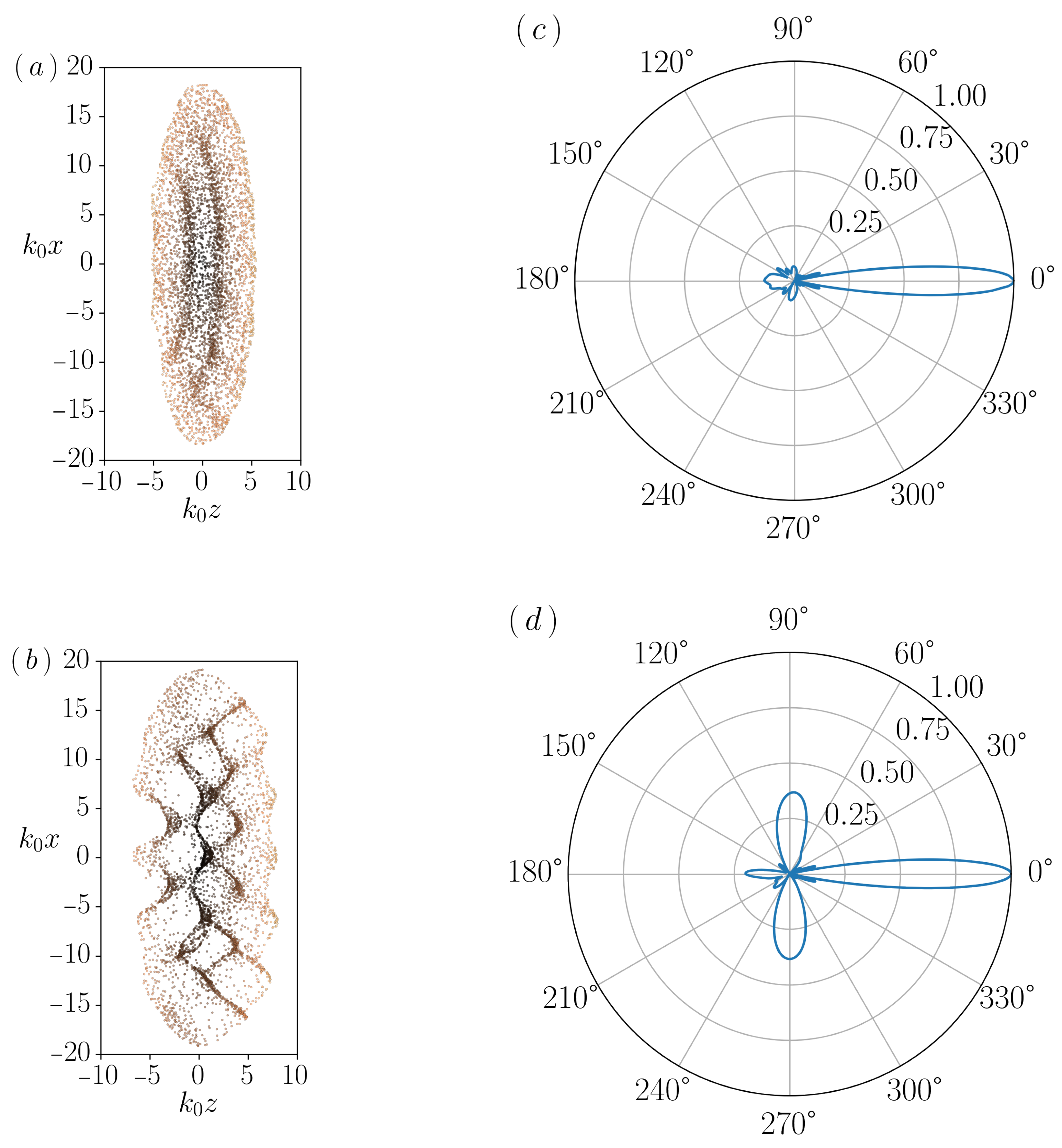
3.1.1. Pump Polarization Parallel to the Major Axis of an Elliptical Cloud: Backscattering and 1D Grating Formation
When the cloud stretches along the
x axis, the atoms experiences a total momentum change of
[
13], i.e., depending whether the photon is emitted downward (positive sign) or upward (negative sign). When the fact that light cannot be scattered along the direction of its polarization is added to this calculated scattering event, the only possible scattering direction for the current case is the
z axis. This suppresses the
component of the total recoil momentum. This suppression has obvious implications both in the grating generated in the cloud and the bunching profile, due to the combined action of the external and scattered fields.
The results shown in
Figure 2 exhibit remarkable changes in the grating pattern generated in the cold vapor, in comparison with the scalar case, caused by the scattering restriction imposed by the polarization vector. The polarization blocks the scattering across the transverse direction (
x axis), leaving the light with the only choice but to scatter along the propagation axis of the pump field (
z axis). The initial distribution, shown in panel (a), is modified into a pure 1D grating pattern depicted in plot (b) of this figure. The grating is a consequence of the two only possible atomic momentum changes: some atoms remain in place, with a net kick close to zero, while others endure a double momentum kick, with a momentum variation of
.
The bunching profiles shown in the polar plot of
Figure 2d is consistent with the grating patterns appearing in panel (b). The intensity pattern manifests more similarities with the one generated in the scalar case with an elliptical cloud parallel to the propagation axis, than with the analogous case that presents the same cloud orientation: only the lobes representing the forward and backwards scattering direction are visible. The backscattering lobe is somewhat distorted and not as clear as in the scalar model, although it preserves some symmetry. The main cause for a deformation of this kind may come from the dipole-dipole force which starts to push the atoms towards the right of the plot. The force pushes with greater strength the atoms located close to the origin at
, where the optical thickness is larger, displacing them towards positive value of
z faster than the ones located at the tips of the cloud (with larger
value). Summarizing, the radiation force transforms the expected straight strips of bunches of atoms, into arcs. These are equidistantly separated with a periodic space between them of
.
3.1.2. Pump Polarization Perpendicular to the Major Axis of An Elliptical Cloud: Off-Axis Scattering
We repeat the previous simulation, but now with the pump field polarization directed along the y axis. The new system does not experience any propagation restriction, because the polarization is perpendicular to the plane containing the atomic cloud. Therefore, a bi-dimensional grating similar to that obtained with the scalar model is expected to be observed for this system.
The grating portrayed in
Figure 3b is not very different than the one obtained for the scalar system (see [
13]). As predicted, pump polarization along the
y axis does not affect the dynamics in the
plane. The slight differences observed between the vectorial and scalar models arise from the short-range interaction terms. In fact, the force equation has now some additional short-range terms (
with
), and the terms that are typified in both models (
with
), are not identical. Moreover, the cut-off parameter has been augmented to
, instead of the
from the scalar study. The adjustment of this parameter does not affect the validity of the results, but its alteration certainly introduces a slight modification in the way particles interact with each other.
Analyzing the bunching factor in plot (d) of the same figure, it is possible to confirm that the system eventually responds as in the scalar case, providing a similar 2D pattern: two large lobes appear along the positive and negative directions of the longest scattering path (
x axis). An earlier time snapshot is presented in
Figure 3a,c, showing the effects of a non-negligible thickness that allows the generation of a transient 1D grating. After the preliminary formation of a longitudinal grating, the scattering direction is defined along the main axis of the ellipsoidal cloud (i.e., the
x axis), hence reshaping the 1D grating into a 2D grating.
In both the simulations presented so far, we observe some atoms slowly drifting outward from the center of the ellipse. For instance, observing
Figure 3, it can be identified how the cloud in (b) has expanded its area in comparison with that in (a). This is due to the ’collisions’ between the atoms: when two atoms become to close each other, the short-range terms in the force give them a kick, which is numerically controlled by the cut-off parameter, set to
. To control numerically the stability of the simulation, we have assumed a cut-off parameter
larger than the one adopted for the scalar case in ref. [
13] (
). If this value were to be applied to the present simulations with the vectorial model, the cloud would suffer a stronger and faster repulsion, making the 2D grating impossible to appear.
3.2. Scattering from 3D Cloud of a Linearly Polarized Field
3.2.1. Pump Field Perpendicular to Ellipsoid’s Major Axis with In-Plane Polarization
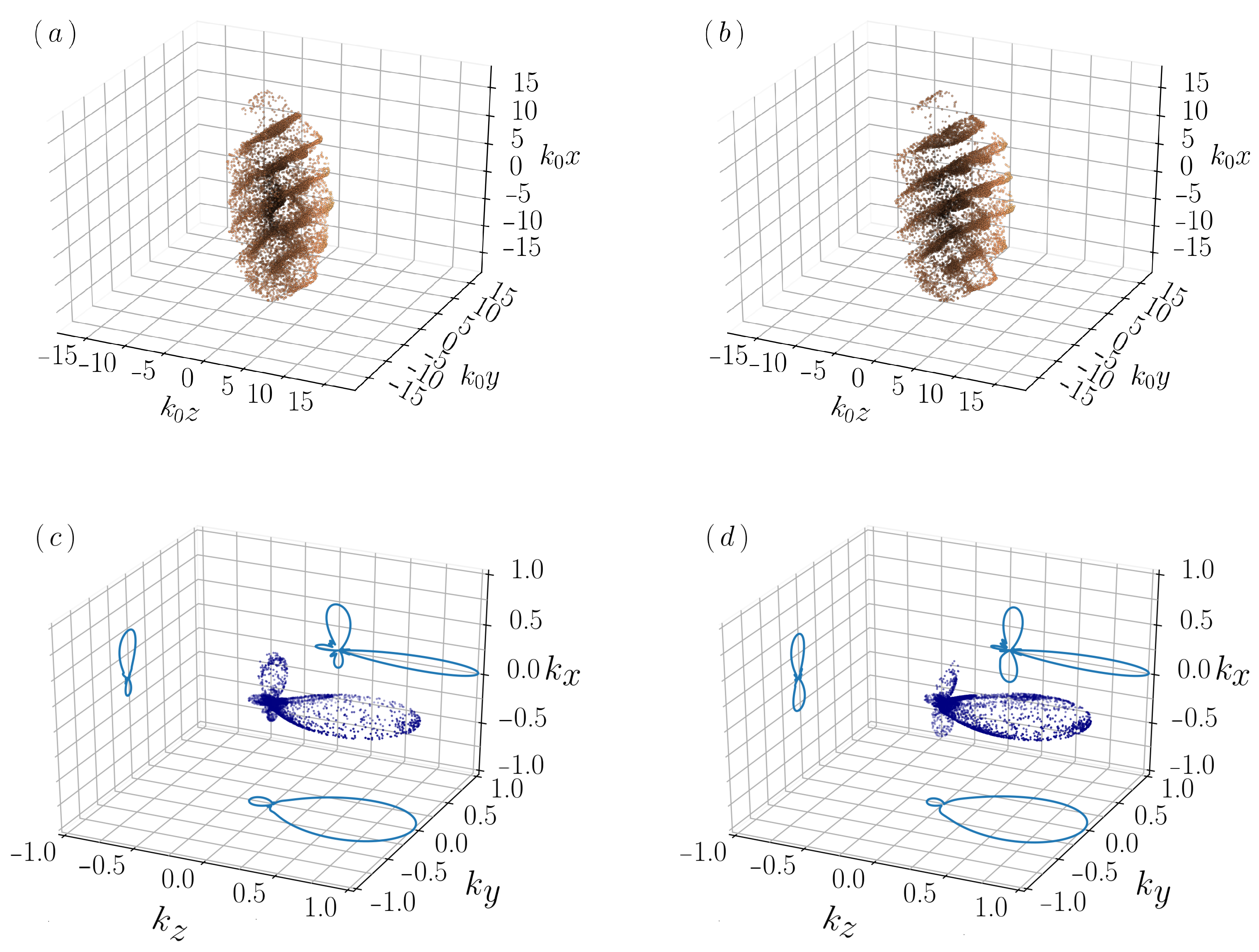
The first three-dimensional case, like in the 2D system, is investigated with the pump linearly polarized along the
x axis, which forbids the scattering along that axis. Since in 3D space there are still two more propagation directions that are allowed, it is expected that the light forms a series of atomic rods (composed of several hundreds of atoms each) along the axis of the polarization vector. Again, the result is due to the combination of the photons transferred from the pump to the scattered modes along the
y and
z axes. Such scenario can be discerned in
Figure 4b, where these atomic rods are not completely straight, displaying an arched shape, as in the 2D system, due to the effect of an electrostrictive force [
13]. Since the optical thickness is larger on the central (
) plane (located at
), the central area endures a greater force from the pump field than the tips of the cloud, which gives to the atomic rods their characteristic arched shape. The complete suppression of the bunching along the polarization axis, can be observed in
Figure 4c, where the lobes along the polarization directions (
x axis) are completely missing.
3.2.2. Pump Field Perpendicular to Ellipsoid’s Major Axis with Out-of-Plane Polarization
The external optical field is here considered with the polarization vector rotated
with respect to the previous case, i.e., along the
y axis. As the scattering is forbidden along the pump polarization
y axis, tilted planes of particles are now visible in two chosen time instants: faintly drawn in
Figure 5a and well defined in panel (b) of the same figure. The snapshot in (a) shows a grating composed of these tilted planes in formation. The planes with a positive slope are more visible because the atomic recoil is first directed downwards (towards negatives value of the
x axis), which is confirmed by the upwards lobe of the bunching factor in panel (c). The titled planes with a negatives slope are also represented in a second snapshot (b) at a later time. Here they are dimly traced due to the latter appearance of the downwards scattering, which is represented by the downward lobe of the bunching factor in panel (d).
In addition, we do not observe any lobe in the bunching factor along the
y axis either, as expected, since it is the pump polarization direction. The asymmetry observed in the lobes of bunching factor along the
x-axis—see
Figure 5c—is due the random initial conditions of the numerical simulations. This asymmetry is less evident at later time instant—
Figure 5d—when the collective scattering process becomes dominant.
3.2.3. Pump Field Parallel to Ellipsoid’s Major Axis
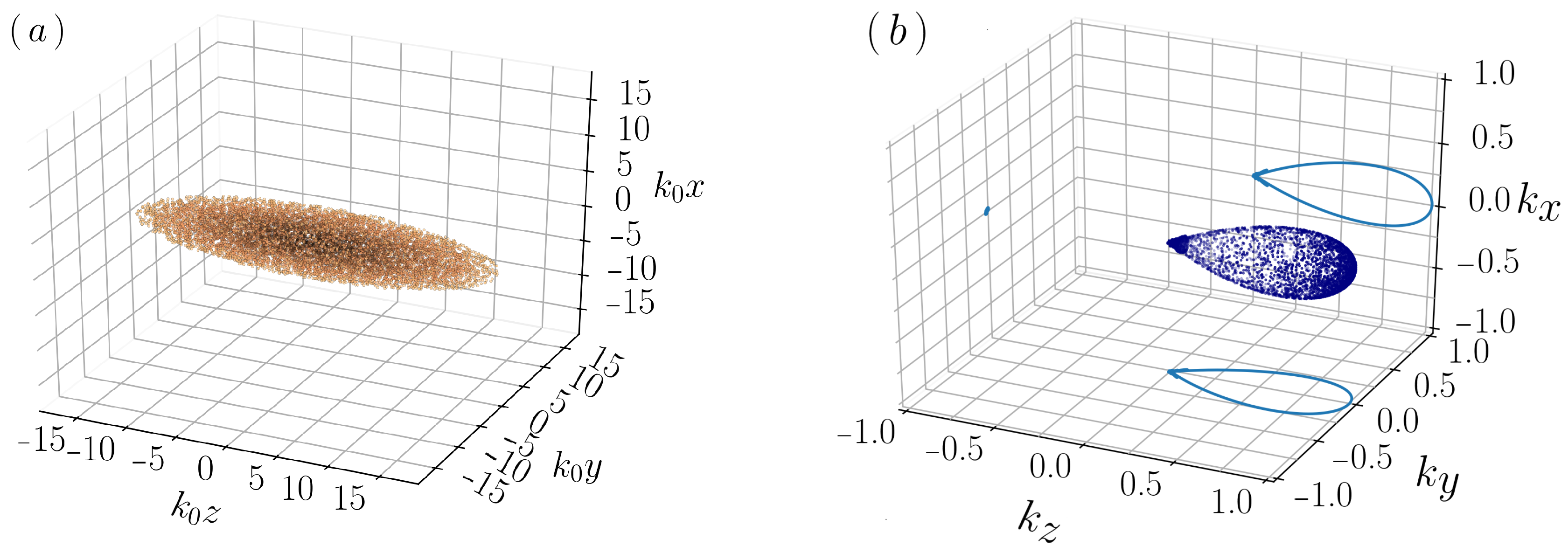
We display the pattern emerging in a characteristic “cigar-shaped” cloud of cold atoms, which elongates along the propagation axis of the pump. The cloud evolved in the presence of a linearly polarized pump field, whose initial distribution and bunching intensity profile are shown in
Figure 6, is shown in
Figure 7. The plots in this figure are at the same time for a cloud with same shape and initial conditions, with snapshots (a) and (c) for a pump polarized along
x and snapshots (b) and (c) for a pump polarized along
y.
A similar behavior than the one observed in ref. [
13] with the scalar model in the 2D and 3D cases, is here seen in the bunching profile of the vectorial model. For both pump polarization cases, the bunching snapshots in
Figure 7c,d show a large lobe emerging backward along the
z axis (pump field axis), together with the forward lobe already present at the time
in
Figure 6b and due to the diffraction of the pump field [
13]. The backward lobe is the well-known signature of the collective recoil lasing effect.
There are some interesting features that can be highlighted from the snapshots (a) and (b) of
Figure 7. First, both panels show the cloud atomic density redistribution into a longitudinal 1D grating. Secondly, the polarization effects are visible in both the cases: the left panel shows horizontal grating due to the suppressed scattering in the vertical direction, whereas the right panel shows a vertical grating, consequence of the forbidden scattering along the horizontal direction. Lastly, both clouds undergo a squeezing effect on the radial traverse direction with respect to the
z axis, stronger at the right-end of both ensembles. This electrostriction effect is a phenomenon typically observed in dielectrics, which can change their shape whenever they are subject to a strong electric field.
In the collective recoil lasing this electrostrictive effect was already observed by the scalar model in [
13], with a 2D and a 3D atomic distribution. The current analysis confirms the presence of this effect with a more realistic model taking into account the light polarization. This force is not yet well understood and further investigation is needed for a satisfactory explanation. For instance, it appears that the effect rides along the cloud like a wave: it starts at the right tip of the cloud, as displayed in
Figure 7a,c, and it travels backwards along the
z axis. After this sort of backwards-propagating wave has passed a section, this section is not susceptible to the polarization vector of the field anymore, but it is still reactive to the gradient of the radiation force. There are some studies which have experimentally observed similar results, as the one presented in [
21].
3.2.4. Scattering from a Spherical Atomic Distribution
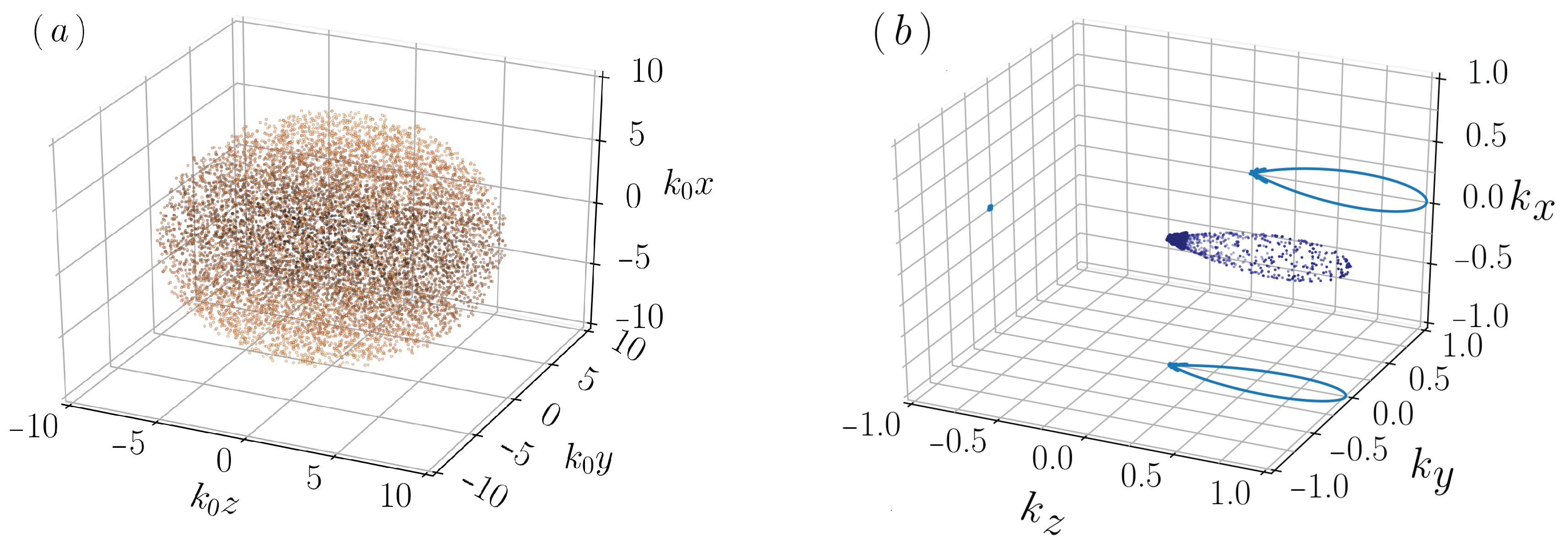
As with previous cases, a density grating also emerged when a spherical cluster of atoms is probed (see
Figure 8), although no tilted planes are defined for such case. This comes because of the symmetry of the spherical initial cloud, so that no initial preferred scattering directions are present, and the atoms start to scatter randomly, except that in the direction of the polarization vector. We observed that two dynamics occurring at the same time in this case: the first one moves the inner atoms towards the shell and the outer atoms inwards; the second one distributes the particles into bunches, avoiding the polarization vector axis. On the one hand, the first action seems to be due to the electrostrictive force (outer atoms moving inwards) and the scattering effect (inner atoms moving outwards, thanks to a higher optical thickness along the
z axis). The combination of these two processes deforms the edges of the cloud into an ’egg-like’ shape. In addition, this effect forces the atoms to be forward-displaced faster the closer they are to the outer shell, due to the definition of a preferred scattering path.
On the other hand, the second dynamics arises because of the photon-scattering, which starts to occur across this newly defined longest path along the external shell of the cloud. The scattering helps sketching arched rods of atoms on the outer surface vertically—
Figure 9a—or horizontally—
Figure 9b—oriented, depending on the polarization vector of the pump field. If the pump were to be set as a scalar field as in ref. [
13], a collection of concentric circles could be spotted. However, in reality, such circles would represent the edges of shallow circular cones, which have their center located on the
z axis, with a value smaller than the values of their edges.
Observing the bunching formations, in
Figure 9c,d, it is possible to see that the projections onto the (
) plane present an elongated shape along
y and
x, respectively, as direct consequence of having a linearly polarized pump field. When the scalar model is used, these projections appear as a clover with four leaves, and they represent a segmentation of the spherical cloud into smaller spherical bunches of atoms following a 3D pattern.
4. Conclusions
The main scope of this work is to show the density grating formation caused by collective atomic recoil lasing, triggered in a cold atomic cloud when a polarized external optical field is applied. The results attained are similar to the ones observed with a previous scalar model [
13], with the exception that when the scattering direction coincides with the polarization vector of the pump field, the scattered field is suppressed. Minor differences are seen between the patterns achieved for the scalar and the vectorial models, due to the presence of different short-range terms in either model. If the cold atomic vapor is shaped into a spherical distribution, the simulations succeed in clearly showing the electrostrictive nature of the force generated by the collective scattering process: the cloud suffers an elongation along the pump propagation axis, hence establishing the longest scattering path along the edge or the outer shell of a 2D or 3D systems, respectively. However, the experimental observation of CARL when the cold atomic vapor is shaped into a spherical distribution remains a difficult task, compared to the more favorable ellipsoidal case. Nevertheless, the role of the electrostrictive force creating some preferred direction where collective scattering set up, it is intriguing and should deserve a deeper investigation.
The present model of equations has also some numerical advantages. In fact, since the model only depends on the particles’ positions, it allows its implementation into molecular dynamics (MD) algorithm, typically employed in other scientific fields. The new open-access programming language Julia has revealed to be of great instrument to implement such MD codes, making it swift when using the built-in Julia algorithms, while allowing the accurate following of the trajectory of each particle and respecting the energy conservation of the system.