“Amplified Spontaneous Emission” in Micro- and Nanolasers
Abstract
:1. Introduction
2. Laser Threshold at the Micro- and Nanoscale
3. Summary of Existing Evidence for Photon Bursts
3.1. Experimental Observations
- E.1
- E.2
- Direct observation of photon bursts in a narrow, but well accessible interval of pump values before the onset of (noisy) cw laser oscillation in a microlaser (cf. Figure 3 in [72]);
- E.3
- Narrow, structureless decay of the second-order time-delayed autocorrelation with typical width both in microlasers and metallo-dielectric nanolasers (cf. Figure 5 in [72], Figure 3 in [75] and Figure 3 in [76]). Similar observation in lasing devices built upon photonic crystal nanostructures (cf. Figure 4 in [77]);
- E.4
- Report of a peak superimposed on the second-order time-delayed autocorrelation, , for same-(pump)-pulse, attributed to ASE in a metallo-dielectric nanolaser (cf. Figure 3 in [75]). This additional peak disappears as lasing is established;
- E.5
- Low-frequency broadband rf spectrum with cutoff compatible with the width of (cf. Figure 8 in [78]) (micro-VCSEL). The lack of spectral structure (except a gradual decay towards the cutoff) is compatible with irregularly occurring bursts;
- E.6
3.2. Interpretation
4. Relationship between Bursts and —Experimental Considerations
5. Theoretical Models
5.1. Differential Models
- D.1
- The addition of spontaneous emission, for instance as a constant contribution (cf. Equation (7)), breaks the transcritical bifurcation [97,98,99] which characterizes the standard REs written for macroscopic lasers [50,96]. This is a consequence of the finite cavity volume (expressed by the fraction of spontaneous emission coupled into the lasing mode, ) and is related to the disappearance of the thermodynamic limit, recovered when (cf. [67] for details). Its immediate, and partly counterintuitive, consequence is a progressive stabilization of the laser operation as increases (cf. Section 6): nanodevices are more stable than their macroscopic counterparts. For an interesting physical application of imperfect bifurcations, cf. [100].
- D.2
- Differential models have so far considered only the coherent part of the electromagnetic field, without introducing an independent random field for the description of spontaneous emission. The latter is added onto the coherent part (as a coherent contribution from the spontaneous relaxation processes, e.g., in REs) but does not exist as a variable in itself. This is an important conceptual point which prevents a correct description of the below-threshold region. Some stochastic models (Section 5.2) introduce the incoherent field as an independent variable, albeit without the concept of random phase, since they are based on a photon number concept.
- D.3
- As noted in [101] through a numerical integration of discretized REs, the integer nature of photons and emitters makes itself felt at the nanoscale (and even at the mesoscale [102]). This introduces an intrinsic noise, entirely missed by the differential models, and leads to a background granularity which cannot be replaced by other means. In this sense, discrete models (cf. Section 5.2 and Section 5.3) hold superior predictive power for small devices.
- D.4
- The introduction of Langevin terms in differential models to simulate fluctuations has two shortcomings: it may lead to negative photon numbers (thus numerical instabilities) when the latter is very small (thus close to threshold, especially in nanolasers) and to an incorrect approximation of the noise distribution. The former problem could be solved by abandoning the photon number representation, but the latter reposes on the approximation of Poissonian processes (true physical statistics of light-matter interaction) with Gaussian ones; such replacement holds only for large arguments, a condition violated at small photon numbers [103].
5.2. Stochastic Simulators
5.3. Stochastic Predictions
- N.1
- N.2
- N.3
- Prediction of photon bursts in the laser output for semiconductor nanolaser in dynamical regimes between Classes A and B (cf. Figure 7 in [116]);
- N.4
- Prediction of superthermal statistics (free-running, Quantum Well laser, Figure 7 in [119]);
- N.5
- Prediction of superthermal statistics using a Gillespie algorithm in a model with pump blocking, suited to Quantum Dot modelling (cf. Figure 5 in [104]).
6. Phase Space Information
6.1. Eigenvalue Analysis
6.2. Eigenvector Analysis
6.3. Topological Conclusions
7. Symmetry Break between Spontaneous and Stimulated Processes
8. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Einstein, A. Zur Quantentheorie der Strahlung. Phys. Z. 1917, 18, 121–128. [Google Scholar]
- Barnes, N.P.; Walsh, B.M. Amplified Spontaneous Emission—Application to Nd:YAG Lasers. IEEE J. Quantum Electron. 1999, 35, 101–109. [Google Scholar] [CrossRef]
- Brenner, P.; Bar-On, O.; Jakoby, M.; Allegro, I.; Richards, B.S.; Paetzold, U.W.; Howard, I.A.; Scheuer, J.; Lemmer, U. Continuous wave amplified spontaneous emission in phase-stable lead halide perovskites. Nat. Commun. 2019, 10, 988. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Pan, W.; Zeng, X.; Dong, J.; Cui, S.; Feng, Y. Relative intensity noise comparison of fiber laser and amplified spontaneous emission sources. Opt. Fiber Technol. 2020, 54, 102119. [Google Scholar] [CrossRef]
- Boggio, J.M.C.; Tenenbaum, S.; Fragnito, H.L. Amplification of broadband noise pumped by two lasers in optical fibers. J. Opt. Soc. Am. 2001, B18, 1428–1435. [Google Scholar] [CrossRef] [Green Version]
- Muniz-Cánovas, P.; Barmenkov, Y.O.; Kir’yanov, A.V.; Cruz, J.L.; Andrés, M.V. ASE narrow-band noise pulsing in erbiumdoped fiber amplifier and its effect on selfphase modulation. Opt. Express 2019, 27, 8520–8528. [Google Scholar] [CrossRef] [Green Version]
- Peters, G.I.; Allen, L. Amplified spontaneous emission I. The threshold condition. J. Phys. A 1971, 4, 238–243. [Google Scholar] [CrossRef]
- Allen, L.; Peters, G.I. Amplified Spontaneous Emission and OH Molecules in the Interstellar Medium. Nat. Phys. Sci. 1972, 235, 143–144. [Google Scholar] [CrossRef]
- Casperson, L.W. Threshold characteristics of mirrorless lasers. J. Appl. Phys. 1977, 48, 256–262. [Google Scholar] [CrossRef]
- Ali, A.W.; Kolb, A.C.; Anderson, A.D. Theory of the Pulsed Molecular Nitrogen Laser. Appl. Opt. 1967, 6, 2115–2119. [Google Scholar] [CrossRef]
- Kartashov, D.; Ališauskas, S.; Pugžlys, A.; Shneider, M.N.; Baltuška, A. Theory of a filament initiated nitrogen laser. J. Opt. B 2015, 48, 094016. [Google Scholar] [CrossRef]
- Javan, A.; Bennett, W.R., Jr.; Herriott, D.R. Population Invresion and Continous Optical Maser Oscillation in a Gas Discharge Containing a He-He Mixture. Phys. Rev. Lett. 1961, 6, 106–110. [Google Scholar] [CrossRef] [Green Version]
- Hetherington, A.; Burrel, G.J.; Moss, T.S. Properties of the He-Ne Ring Lasers at 3.39 microns. Infrared Phys. 1969, 9, 109–124. [Google Scholar] [CrossRef]
- Haag, G.; Munz, M.; Marowsky, G. Amplified Spontaneous Emission (ASE) in Laser Oscillators and Amplifiers. IEEE J. Quantum Electron. 1983, QE-19, 1149–1160. [Google Scholar] [CrossRef]
- Svelto, O.; Taccheo, S.; Svelto, C. Analysis of amplified spontaneous emission: Some corrections to the Linford formula. Opt. Commun. 1998, 149, 277–282. [Google Scholar] [CrossRef]
- Henry, C.H. Theory of Spontaneous Emission Noise in Open Resonators and its Application to Lasers and Optical Amplifiers. J. Lightwave Technol. 1986, LT-4, 288–297. [Google Scholar] [CrossRef]
- Letokhov, V.S. Astrophysical Lasers. Quantum Electron. 2002, 32, 1065–1079. [Google Scholar] [CrossRef]
- Bonifacio, R.; Casagrande, F.; Casati, G. Cooperative and Chaotic Transition of a Free Electron Laser Hamiltonian Model. Opt. Commoun. 1982, 40, 219–223. [Google Scholar] [CrossRef]
- Bonifacio, R.; Casagrande, F. Instabilities and Quantum Initiation in the Free Electron Laser. Opt. Commun. 1984, 50, 251–255. [Google Scholar] [CrossRef]
- Bonifacio, R.; Casagrande, F. Instability Threshold, Quantum Initiation and Photon Statistics in High-Gain Free Electron Lasers. Nucl. Instr. Methods Phys. Res. 1985, A237, 168–179. [Google Scholar] [CrossRef]
- Benediktovitch, A.; Mercadier, L.; Peyrusse, O.; Przystawik, A.; Laarmann, T.; Langbehn, B.; Bomme, C.; Erk, B.; Correa, J.; Mossé, C.; et al. Amplified spontaneous emission in the extreme ultraviolet by expanding xenon clusters. Phys. Rev. A 2020, 101, 063412. [Google Scholar] [CrossRef]
- Bonnefond, S.; Cazareth, J.; Abélanet, S.; Reynaud, A.; Vassalli, M.; Brau, F.; Lippi, G.L. Multiple scattering-assisted fluorescence amplification: Towards biological applications. arXiv 2019, arXiv:1908.10199. [Google Scholar]
- Cao, H.; Xu, J.Y.; Chang, S.-H.; Ho, S.T. Transition from amplified spontaneous emission to laser action in strongly scattering media. Phys. Rev. E 2000, 61, 1985–1989. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anni, M.; Lattante, S.; Cingolani, R.; Gigli, G.; Barbarella, G.; Favaretto, L. Emission properties of organic random lasers. Phys. Stat. Sol. C 2004, 1, 450–453. [Google Scholar] [CrossRef]
- Beenakker, C.W.J. Thermal Radiation and Amplified Spontaneous Emission from a Random Medium. Phys. Rev. Lett. 1998, 81, 1829–1832. [Google Scholar] [CrossRef] [Green Version]
- Xue, M.; Gao, C.; Niu, L.; Zhu, S.; Sun, C. Influence of amplified spontaneous emission on laser linewidth in a fiber amplifier. Appl. Opt. 2020, 59, 2610–2614. [Google Scholar] [CrossRef] [PubMed]
- Cubeddu, R.; Silvestri, S.D.; Svelto, O. Subnanosecond Amplified Spontaneous Emission Pulses by a Nitrogen Pumped Dye Laser. Opt. Commun. 1980, 34, 460–462. [Google Scholar] [CrossRef]
- Ivanov, V.V.; Maksimchuk, A.; Mourou, G. Amplified spontaneous emission in a Ti:sapphire regenerative amplifier. Appl. Opt. 2013, 42, 7231–7234. [Google Scholar] [CrossRef]
- Keppler, S.; Sävert, A.; Körner, J.; Hornung, M.; Liebetrau, H.; Hein, J.; Kaluza, M.C. The generation of amplified spontaneous emission in high-power CPA laser systems. Laser Photonics Rev. 2016, 10, 264–277. [Google Scholar] [CrossRef] [Green Version]
- Speiser, J. Scaling of thin-disk lasers—Influence of amplified spontaneous emission. J. Opt. Soc. Am. 2009, B 26, 26–35. [Google Scholar] [CrossRef]
- Malko, A.V.; Mikhailovsky, A.A.; Petruska, M.A.; Hollingsworth, J.A.; Htoon, H.; Bawendi, M.G.; Klimov, V.I. From amplified spontaneous emission to microring lasing using nanocrystal quantum dot solids. Appl. Phys. Lett. 2002, 81, 1303–1305. [Google Scholar] [CrossRef]
- Zimmler, M.A.; Bao, J.; Capasso, F.; Müller, S.; Ronning, C. Laser action in nanowires: Observation of the transition from amplified spontaneous emission to laser oscillation. Appl. Phys. Lett. 2008, 93, 051101. [Google Scholar] [CrossRef]
- Guzelturk, B.; Kelestemur, Y.; Olutas, M.; Delikanli, S.; Demir, H.V. Amplified Spontaneous Emission and Lasing in Colloidal Nanoplatelets. AC Nano 2014, 8, 6599–6605. [Google Scholar] [CrossRef] [PubMed]
- She, C.; Fedin, I.; Dolzhnikov, D.S.; Demortière, A.; Schaller, R.D.; Pelton, M.; Talapin, D.V. Low-Threshold Stimulated Emission Using Colloidal Quantum Wells. Nano Lett. 2014, 14, 2772–2777. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pisignano, D.; Anni, M.; Gigli, G.; Cingolani, R.; Zavelani-Rossi, M.; Lanzani, G.; Barbarella, G.; Favaretto, L. Amplified spontaneous emission and efficient tunable laser emission from a substituted thiophene-based oligomer. Appl. Phys. Lett. 2002, 81, 3534–3536. [Google Scholar] [CrossRef]
- Liu, X.; Py, C.; Tao, Y.; Li, Y.; Ding, J.; Day, M. Low-threshold amplified spontaneous emission and laser emission in a polyfluorene derivative. Appl. Phys. Lett. 2004, 84, 2727–2729. [Google Scholar] [CrossRef]
- Calzado, E.M.; Boj, P.G.; Díaz-García, M.A. Amplified Spontaneous Emission Properties of Semiconducting Organic Materials. Int. J. Mol. Sci. 2010, 11, 2546–2565. [Google Scholar] [CrossRef] [Green Version]
- Blazek, M.; Hartmann, S.; Molitor, A.; Elsaesser, W. Unifying intensity noise and second-order coherence properties of amplified spontaneous emission sources. Opt. Lett. 2011, 36, 3455–3457. [Google Scholar] [CrossRef]
- Klaers, J.; Schmitt, J.; Vewinger, F.; Weitz, M. Bose–Einstein condensation of photons in an optical microcavity. Nature 2010, 468, 545–548. [Google Scholar] [CrossRef] [Green Version]
- Schmitt, J.; Damm, T.; Dung, D.; Vewinger, F.; Klaers, J.; Weitz, M. Observation of Grand-Canonical Number Statistics in a Photon Bose-Einstein Condensate. Phys. Rev. Lett. 2014, 112, 030401. [Google Scholar] [CrossRef] [Green Version]
- Walker, B.T.; Rodrigues, J.D.; Dhar, H.S.; Oulton, R.F.; Mintert, F.; Nyman, R.A. Non-stationary statistics and formation jitter in transient photon condensation. Nat. Commun. 2020, 11, 1390. [Google Scholar] [CrossRef] [PubMed]
- Hakala, T.K.; Moilanen, A.J.; Väkeväinen, A.I.; Guo, R.; Martikainen, J.-P.; Daskalakis, K.S.; Rekola, H.T.; Julku, A.; Törmä, P. Bose–Einstein condensation in a plasmonic lattice. Nat. Phys. 2018, 14, 739–744. [Google Scholar] [CrossRef] [Green Version]
- Barland, S.; Azam, P.; Lippi, G.L.; Nyman, R.A.; Kaiser, R. Photon Thermalization and a Condensation Phase Transition in an Electrically Pumped Semiconductor Microresonator. Available online: http://www.kaiserlux.de/coldatoms/Articles/VCSELPhotonthermalization.pdf (accessed on 19 January 2021).
- Greffet, J.-J.; Bouchon, P.; Brucoli, G.; Marquier, F. Light Emission by Nonequilibrium Bodies: Local Kirchhoff Law. Phys. Rev. X 2018, 8, 021008. [Google Scholar] [CrossRef] [Green Version]
- Wojszvzyk, L.; Monin, H.; Greffet, J.-J. Light Emission by a Thermalized Ensemble of Emitters Coupled to a Resonant Structure. Adv. Opt. Mater. 2019, 7, 1801697. [Google Scholar] [CrossRef]
- Tsakmakidis, K.L.; Boyd, R.W.; Yablonovitch, E.; Zhang, X. Large spontaneous-emission enhancements in metallic nanostructures: Towards LEDs faster than lasers. Opt. Express 2016, 24, 17916–17927. [Google Scholar] [CrossRef] [Green Version]
- van Exter, M.P.; van Doorn, A.K.J.; Woerdman, J.P. Effect of Spatial Filtering on the Spontaneous Emission Spectrum of a Sub-Threshold VCSEL. J. Sel. Top. Quantum Electron. 1995, 1, 601–605. [Google Scholar] [CrossRef]
- Kesler, M.P.; Harder, C. Spontaneous Emission and Gain in GaAlAs Quantum Well Lasers. IEEE J. Quantum Electron. 1991, QE-27, 1812–1816. [Google Scholar] [CrossRef]
- Gross, M.; Haroche, S. Superradiance: An essay on the theory of collective spontaneous emission. Phys. Rep. 1982, 93, 301–396. [Google Scholar] [CrossRef]
- Siegman, A.E. Lasers; University Science Books: Mill Valley, CA, USA, 1986. [Google Scholar]
- Doronin, I.V.; Andrianov, E.S.; Zyablovsky, A.A.; Pukhov, A.A.; Lozovik, Y.E.; Vinogradov, A.P.; Lisyansky, A.A. Second-order coherence properties of amplified spontaneous emission. Opt. Express 2019, 27, 10991–11005. [Google Scholar] [CrossRef]
- Zyablovsky, A.A.; Doronin, I.V.; Andrianov, E.S.; Pukhov, A.A.; Lozovik, Y.E.; Vinogradov, A.P.; Lisyansky, A.A. Formation of positive feedback and coherent emission in a cavity-free system. Opt. Express 2019, 27, 35376–35384. [Google Scholar] [CrossRef]
- Woerdman, J.P.; van Exter, M.P.; van Druten, N.J. Quantum Noise of Small lasers. Adv. At. Mol. Opt. Phys. 2001, 47, 205–248. [Google Scholar]
- Soda, H.; Iga, K.I.; Kitahara, C.; Suematsu, Y. GaInAsP/InP Surface Emitting Injection Lasers. Jpn. J. Appl. Phys. 1979, 18, 2329–2330. [Google Scholar] [CrossRef]
- Choquette, K.D.; Hou, H.Q.; Lear, K.L.; Chui, H.C.; Geib, K.M.; Mar, A.; Hammons, B.E. Self-pulsing oxide-confined vertical-cavity lasers with ultralow operating current. Electron. Lett. 1996, 32, 459–460. [Google Scholar] [CrossRef] [Green Version]
- Yokoyama, H.; Brorson, S.D. Rate equation analysis of microcavity lasers. J. Appl. Phys. 1989, 66, 4801–4805. [Google Scholar] [CrossRef]
- Martini, F.D.; Jacobovitz, G.R. Anomalous Spontaneous-Stimulated-Decay Phase Transition and Zero-Threshold Laser Action in a Microscopic Cavity. Phys. Rev. Lett. 1988, 60, 1711–1714. [Google Scholar] [CrossRef]
- Martini, F.D.; Cairo, F.; Mataloni, P.; Verzegnassi, F. Thresholdless Microlaser. Phys. Rev. A 1992, 46, 4220–4233. [Google Scholar] [CrossRef]
- Degiorgio, V.; Scully, M.O. Analogy between the laser threshold region and a second-order phase transition. Phys. Rev. A 1970, 2, 1170–1177. [Google Scholar] [CrossRef]
- Graham, R.; Haken, H. Laser light—First example of a second-order phase transition far from thermal equilibrium. Z. Physik 1970, 237, 31–46. [Google Scholar] [CrossRef]
- Grossmann, S.; Richter, P.H. Laser Threshold and Nonlinear Landau Fluctuation Theory of Phase Transitions. Z. Physik 1971, 242, 458–475. [Google Scholar] [CrossRef]
- Dohm, V. Nonequilibrium phase transition in laser-active media. Solid State Commun. 1972, 11, 1273–1276. [Google Scholar] [CrossRef]
- Björk, G.; Yamamoto, Y. Analysis of semiconductor microcavity lasers using rate equations. IEEE J. Quantum Electron. 1991, QE-27, 2386–2396. [Google Scholar]
- Ning, C.Z. What is Laser Threshold? J. Sel. Top. Quantum Electron. 2013, 19, 1500304. [Google Scholar] [CrossRef]
- Editorial: Scrutinizing Lasers. Nat. Photonics 2017, 11, 139. Available online: https://0-www-nature-com.brum.beds.ac.uk/articles/nphoton.2017.28 (accessed on 19 January 2021). [CrossRef] [Green Version]
- Samuel, I.D.W.; Namdas, E.B.; Turnbull, G.A. How to recognize lasing. Nat. Photon. 2009, 3, 546–549. [Google Scholar] [CrossRef]
- Rice, P.R.; Carmichael, H.J. Photon statistics of a cavity-QED laser: A comment on the laser phase-transition analogy. Phys. Rev. A 1994, 50, 4318–4329. [Google Scholar] [CrossRef]
- Carroll, M.; D’Alessandro, G.; Lippi, G.L.; Oppo, G.-L.; Papoff, F. Thermal, quantum anti-bunching and lasing thresholds from single emitters to macroscopic devices. arXiv 2020, arXiv:2011.10805. [Google Scholar]
- van Druten, N.J.; Lien, Y.; Serrat, C.; Oemrawsingh, S.S.R.; van Exter, M.P.; Woerdman, J.P. Laser with thresholdless intensity fluctuations. Phys. Rev. A 2000, 62, 053808. [Google Scholar] [CrossRef]
- Schlottmann, E.; von Helversen, M.; Leymann, H.A.; Lettau, T.; Krüger, F.; Schmidt, M.; Schneider, C.; Kamp, M.; Höfling, S.; Beyer, J.; et al. Exploring the Photon-Number Distribution of Bimodal Microlasers with a Transition Edge Sensor. Phys. Rev. Appl. 2018, 9, 064030. [Google Scholar] [CrossRef] [Green Version]
- Lebreton, A.; Abram, I.; Braive, R.; Sagnes, I.; Robert-Philip, I.; Beveratos, A. Unequivocal Differentiation of Coherent and Chaotic Light through Interferometric Photon Correlation Measurements. Phys. Rev. Lett. 2013, 110, 163603. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Puccioni, G.P.; Lippi, G.L. Dynamical Buildup of Lasing in Mesoscale Devices. Sci. Rep. 2015, 5, 15858. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Wang, G.; Puccioni, G.P.; Lippi, G.L. Exploration of VCSEL ultra-low biasing scheme for pulse generation. J. Opt. Soc. Am. 2019, B36, 799–804. [Google Scholar] [CrossRef]
- Lebreton, A.; Abram, I.; Braive, R.; Sagnes, I.; Robert-Philip, I.; Beveratos, A. Theory of interferometric photon-correlation measurements: Differentiating coherent from chaotic light. Phys. Rev. A 2013, 88, 013801. [Google Scholar] [CrossRef] [Green Version]
- Pan, S.H.; Gu, Q.; Amili, A.E.; Vallini, F.; Fainman, Y. Dynamic hysteresis in a coherent high-β nanolaser. Optica 2016, 3, 1260–1265. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Aktas, D.; Alibart, O.; Picholle, É.; Puccioni, G.P.; Tanzilli, S.; Lippi, G.L. Superthermal-light emission and nontrivial photon statistics in small lasers. Phys. Rev. A 2020, 101, 063835. [Google Scholar] [CrossRef]
- Ota, Y.; Kakuda, M.; Watanabe, K.; Iwamoto, S.; Arakawa, Y. Thresholdless quantum dot nanolaser. Opt. Express 2017, 25, 19981–19994. [Google Scholar] [CrossRef]
- Wang, T.; Vergnet, H.; Puccioni, G.P.; Lippi, G.L. Dynamics at threshold in mesoscale lasers. Phys. Rev. A 2017, 96, 013803. [Google Scholar] [CrossRef] [Green Version]
- Kreinberg, S.; Laiho, K.; Lohof, F.; Hayenga, W.E.; Holewa, P.; Gies, C.; Khajavikhan, M.; Reitzenstein, S. Thresholdless transition to coherent emission at telecom wavelengths from coaxial nanolasers. Laser Photonics Rev. 2020, 14, 2000065. [Google Scholar] [CrossRef]
- Ulrich, S.M.; Gies, C.; Ates, S.; Wiersig, J.; Reitzenstein, S.; Hofmann, C.; Löffler, A.; Forchel, A.; Jahnke, F.; Michler, P. Photon Statistics of Semiconductor Microcavity Lasers. Phys. Rev. Lett. 2007, 98, 043906. [Google Scholar] [CrossRef]
- Arecchi, F.T.; Berné, A.; Sona, A.; Burlamacchi, P. Photocount Distributions and Field Statistics. IEEE J. Quantum Electron. 1966, QE-2, 341–350. [Google Scholar] [CrossRef]
- Arecchi, F.T.; Degiorgio, V. Statistical Properties of Laser Radiation During a Transient Buildup. Phys. Rev. A 1971, 3, 1108–1124. [Google Scholar] [CrossRef]
- Puccioni, G.P.; Lippi, G.L. Stochastic Simulator for modeling the transition to lasing. Opt. Express 2015, 23, 2369–2374. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Puccioni, G.P.; Lippi, G.L. Photon bursts at lasing onset and modeling issues in micro-VCSELs. J. Mod. Optics 2020, 67, 55–68. [Google Scholar] [CrossRef]
- Loudon, R. The Quantum Theory of Light, 2nd ed.; Oxford University Press: Oxford, UK, 1983. [Google Scholar]
- Wang, T.; Puccioni, G.P.; Lippi, G.L. Onset of Lasing in Small Devices: The Identification of the First Threshold through Autocorrelation Resonance. Ann. Physik 2018, 530, 1800086. [Google Scholar] [CrossRef]
- Jagsch, S.T.; Triviño, N.V.; Lohof, F.; Callsen, G.; Kalinowski, S.; Rousseau, I.M.; Barzel, R.; Carlin, J.F.; Jahnke, F.; Butté, R.; et al. A quantum optical study of thresholdless lasing features in high-β nitride nanobeam cavities. Nat. Comm. 2018, 9, 564. [Google Scholar] [CrossRef] [Green Version]
- Arecchi, F.T.; Bonifacio, R. Theory of optical maser amplifiers. IEEE J. Quantum Electron. 1965, 1, 169–178. [Google Scholar] [CrossRef]
- McNeil, B. Due credit for Maxwell–Bloch equations. Nat. Photon. 2015, 9, 207. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics, 2nd ed.; Wiley: New York, NY, USA, 1975. [Google Scholar]
- Allen, L.; Eberly, J.H. Optical Resonance and Two-Level Atoms; Dover: New York, NY, USA, 1987. [Google Scholar]
- Narducci, L.M.; Abraham, N.B. Laser Physics and Laser Instabilities; World Scientific: Singapore, 1988. [Google Scholar]
- Gies, C.; Wiersig, J.; Lorke, M.; Jahnke, F. Semiconductor model for quantum-dot-based microcavity lasers. Phys. Rev. A 2007, 75, 013803. [Google Scholar] [CrossRef]
- Chow, W.W.; Jahnke, F.; Gies, C. Emission properties of nanolasers during the transition to lasing. Light Sci. Appl. 2014, 3, e201. [Google Scholar] [CrossRef] [Green Version]
- Lettau, T.; Leymann, H.A.M.; Melcher, B.; Wiersig, J. Superthermal photon bunching in terms of simple probability distributions. Phys. Rev. A 2018, 97, 053835. [Google Scholar] [CrossRef] [Green Version]
- Coldren, L.A.; Corzine, S.W. Diode Lasers and Photonic Integrated Circuits; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Solari, H.G.; Natiello, M.A.; Mindlin, G.B. Nonlinear Dynamics A Two-Way Trip from Physics to Math; Institute of Physics: Bristol, UK, 1996. [Google Scholar]
- Chapter 2: Bifurcations. Available online: https://courses.physics.ucsd.edu/2011/Spring/physics221a/LECTURES/CH02_BIFURCATIONS.pdf (accessed on 27 October 2020).
- Liu, P.; Shi, J.; Wang, Y. Imperfect transcritical and pitchfork bifurcations. J. Funct. An. 2007, 251, 573–600. [Google Scholar] [CrossRef] [Green Version]
- Mandel, P.; Erneux, T. Laser Lorenz equations with a time-dependent parameter. Phys. Rev. Lett. 1984, 53, 1818–1820. [Google Scholar] [CrossRef]
- Lebreton, A.; Abram, I.; Takemura, N.; Kuwata-Gonokami, M.; Robert-Philip, I.; Beveratos, A. Stochastically sustained population oscillations in high-β nanolasers. New J. Phys. 2013, 15, 033039. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Puccioni, G.P.; Lippi, G.L. How mesoscale lasers can answer fundamental questions related to nanolasers. In Nanophotonics VI; International Society for Optics and Photonics: Bellingham, WA, USA, 2016; p. 98840B. [Google Scholar]
- Lippi, G.L.; Mørk, J.; Puccioni, G.P. Analytical vs. Numerical Langevin Description of Noise in Small Laser. arXiv 2019, arXiv:1902.08859. [Google Scholar]
- André, E.C.; Mørk, J.; Wubs, M. Efficient stochastic simulation of rate equations and photon statistics of nanolasers. Opt. Express 2020, 28, 32632–32646. [Google Scholar] [CrossRef] [PubMed]
- Meiser, D.; Ye, J.; Carlson, D.R.; Holland, M.J. Prospects for a millihertz-linewidth laser. Phys. Rev. Lett. 2009, 102, 163601. [Google Scholar] [CrossRef] [Green Version]
- Meiser, D.; Holland, M.J. Steady-state superradiance with alkaline-earth-metal atoms. Phys. Rev. A 2010, 81, 033847. [Google Scholar] [CrossRef] [Green Version]
- Bohnet, J.G.; Chen, Z.; Weiner, J.M.; Meiser, D.; Holland, M.J.; Thompson, J.K. A steady-state superradiant laser with less than one intracavity photon. Nature 2012, 484, 78–81. [Google Scholar] [CrossRef]
- André, E.C.; Protsenko, I.E.; Uskov, A.V.; Mork, J.; Wubs, M. On collective Rabi splitting in nanolasers and nano-LEDs. Opt. Lett. 2019, 44, 1415–1418. [Google Scholar] [CrossRef] [Green Version]
- Leymann, H.A.M.; Foerster, A.; Jahnke, F.; Wiersig, J.; Gies, C. Sub-and superradiance in nanolasers. Phys. Rev. Appl. 2015, 4, 044018. [Google Scholar] [CrossRef]
- Jahnke, F.; Gies, C.; Aßmann, M.; Bayer, M.; Leymann, H.A.M.; Foerster, A.; Wiersig, J.; Schneider, C.; Kamp, M.; Höfling, S. Giant photon bunching, superradiant pulse emission and excitation trapping in quantum-dot nanolasers. Nat. Commun. 2016, 7, 11540. [Google Scholar] [CrossRef] [Green Version]
- Kreinberg, S.; Chow, W.W.; Wolters, J.; Schneider, C.; Gies, C.; Jahnke, F.; Höfling, S.; Kamp, M.; Reitzenstein, S. Emission from quantum-dot high-β microcavities: Transition from spontaneous emission to lasing and the effects of superradiant emitter coupling. Light Sci. Appl. 2017, 6, e17030. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mork, J.; Lippi, G.L. Rate equation description of quantum noise in nanolasers with few emitters. Appl. Phys. Lett. 2018, 112, 141103. [Google Scholar] [CrossRef]
- Wang, T.W.X.; Deng, Z.; Sun, J.; Puccioni, G.P.; Wang, G.; Lippi, G.L. Dynamics of a micro-VCSEL operated in the threshold region under low-level optical feedback. J. Sel. Top. Quantum Electron. 2019, 25, 1700308. [Google Scholar] [CrossRef]
- Roy-Choudhury, K.; Haas, S.; Levi, A.F.J. Quantum fluctuations in small lasers. Phys. Rev. Lett. 2009, 102, 053902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roy-Choudhury, K.; Levi, A.F.J. Quantum fluctuations in very small laser diodes. Phys. Rev. A 2010, 81, 013827. [Google Scholar] [CrossRef] [Green Version]
- Vallet, A.; Chusseau, L.; Philippe, F.; Jean-Marie, A. Low-dimensional Systems and Nanostructures Markov model of quantum fluctuations at the transition to lasing of semiconductor nanolasers. Physica E 2019, 105, 97–104. [Google Scholar] [CrossRef] [Green Version]
- Tredicce, J.R.; Arecchi, F.T.; Lippi, G.L.; Puccioni, G.P. Instabilities in lasers with an injected signal. J. Opt. Soc. Am. 1985, B2, 173–183. [Google Scholar] [CrossRef] [Green Version]
- Fennell, P.G.; Melnik, S.; Gleeson, J.P. Limitations of discrete-time approaches to continuous-time contagion dynamics. Phys. Rev. E 2016, 94, 052125. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Deng, Z.L.; Sun, J.C.; Wang, X.H.; Puccioni, G.P.; Wang, G.F.; Lippi, G.L. Photon statistics and dynamics of nanolasers subject to intensity feedback. Phys. Rev. A 2020, 101, 023803. [Google Scholar] [CrossRef] [Green Version]
- Cohen-Tannoudji, C.; Diu, B.; Laloe, F. Quantum Mechanics; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Wang, T.; Zou, J.L.; Zhao, W.S.; Puccioni, G.P.; Lin, X.; Chen, H.S.; Wang, F.G.; Lippi, G.L. Methodological investigation into the noise influence on nanolasers’ large signal modulation. arXiv 2020, arXiv:2010.15576. [Google Scholar]
- Lippi, G.L.; Barland, S.; Monsieur, F. Invariant Integral and the Transition to Steady States in Separable Dynamical Systems. Phys. Rev. Lett. 2000, 85, 62–65. [Google Scholar] [CrossRef] [PubMed]
- Lippi, G.L.; Mork, J.; Puccioni, G.P. Numerical solutions to the Laser Rate Equations with noise: Technical issues, implementation and pitfalls. In Nanophotonics VII; International Society for Optics and Photonics: Bellingham, WA, USA, 2018; p. 106722B. [Google Scholar]
- Kaganskiy, A.; Kreinberg, S.; Porte, X.; Reitzenstein, S. Micropillar lasers with site-controlled quantum dots as active medium. Optica 2019, 6, 404–409. [Google Scholar] [CrossRef]

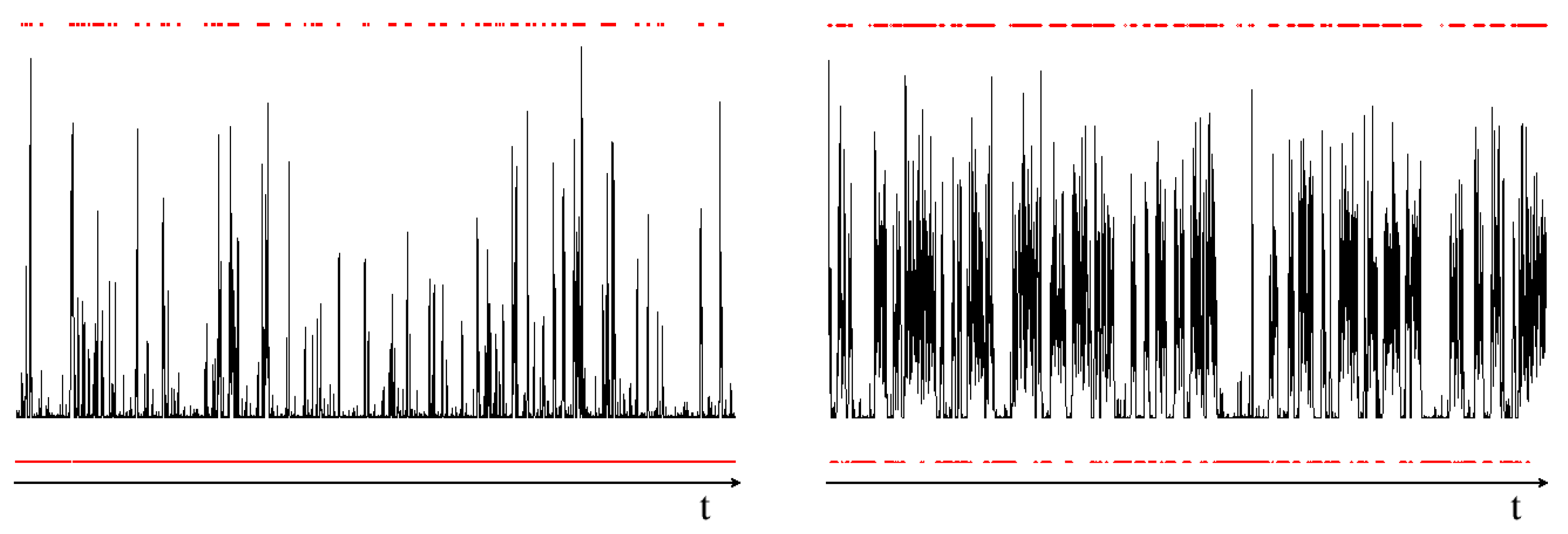
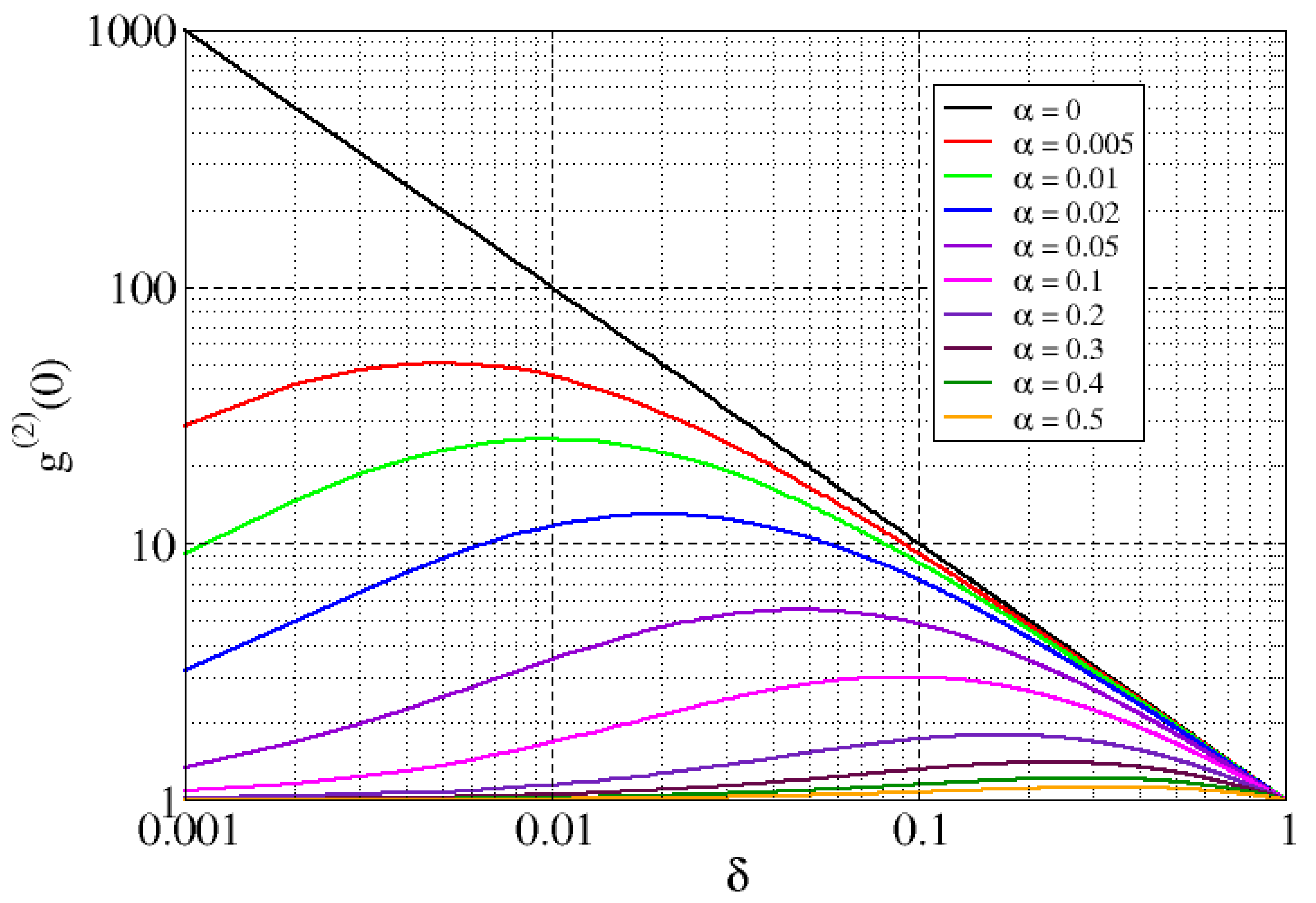
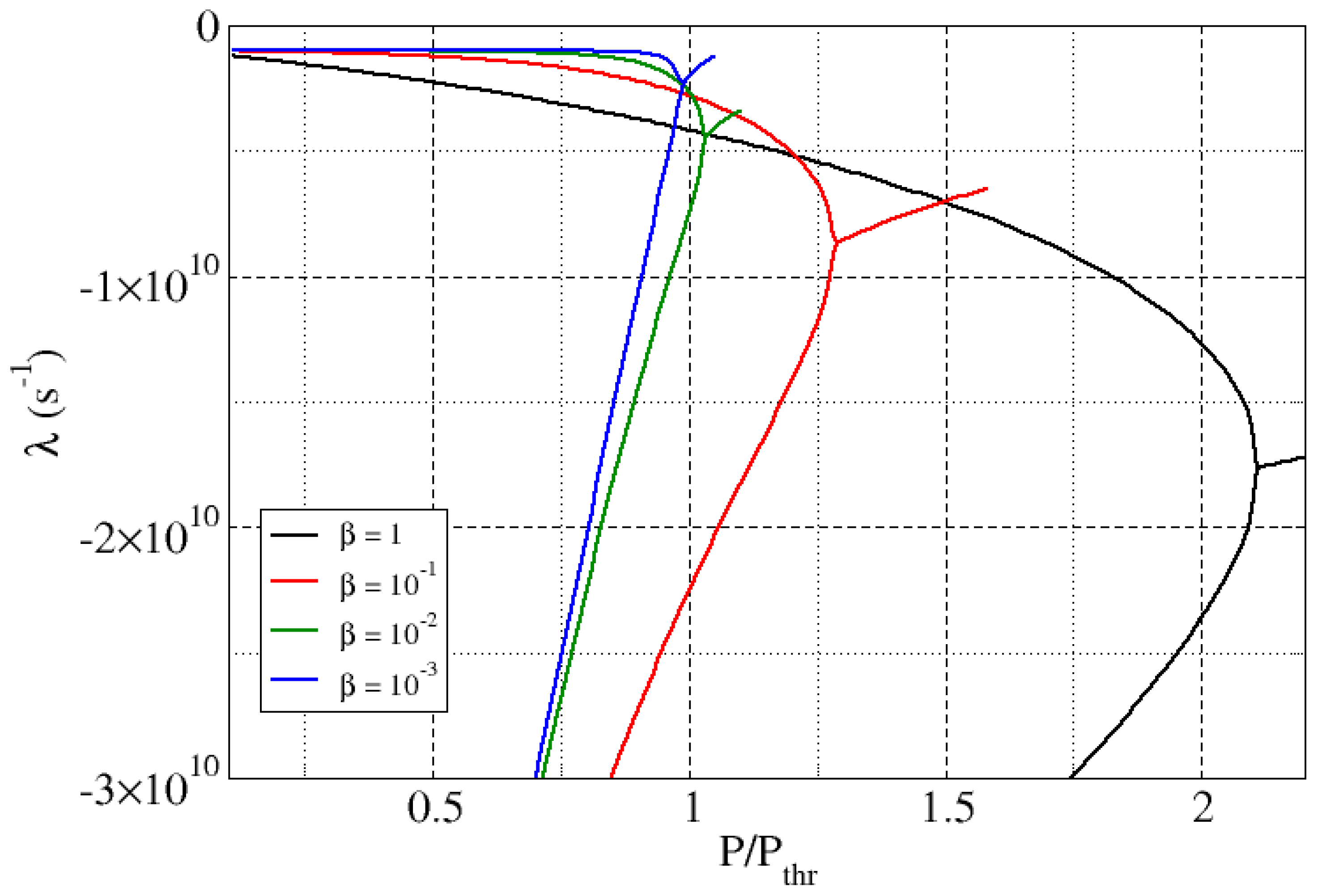

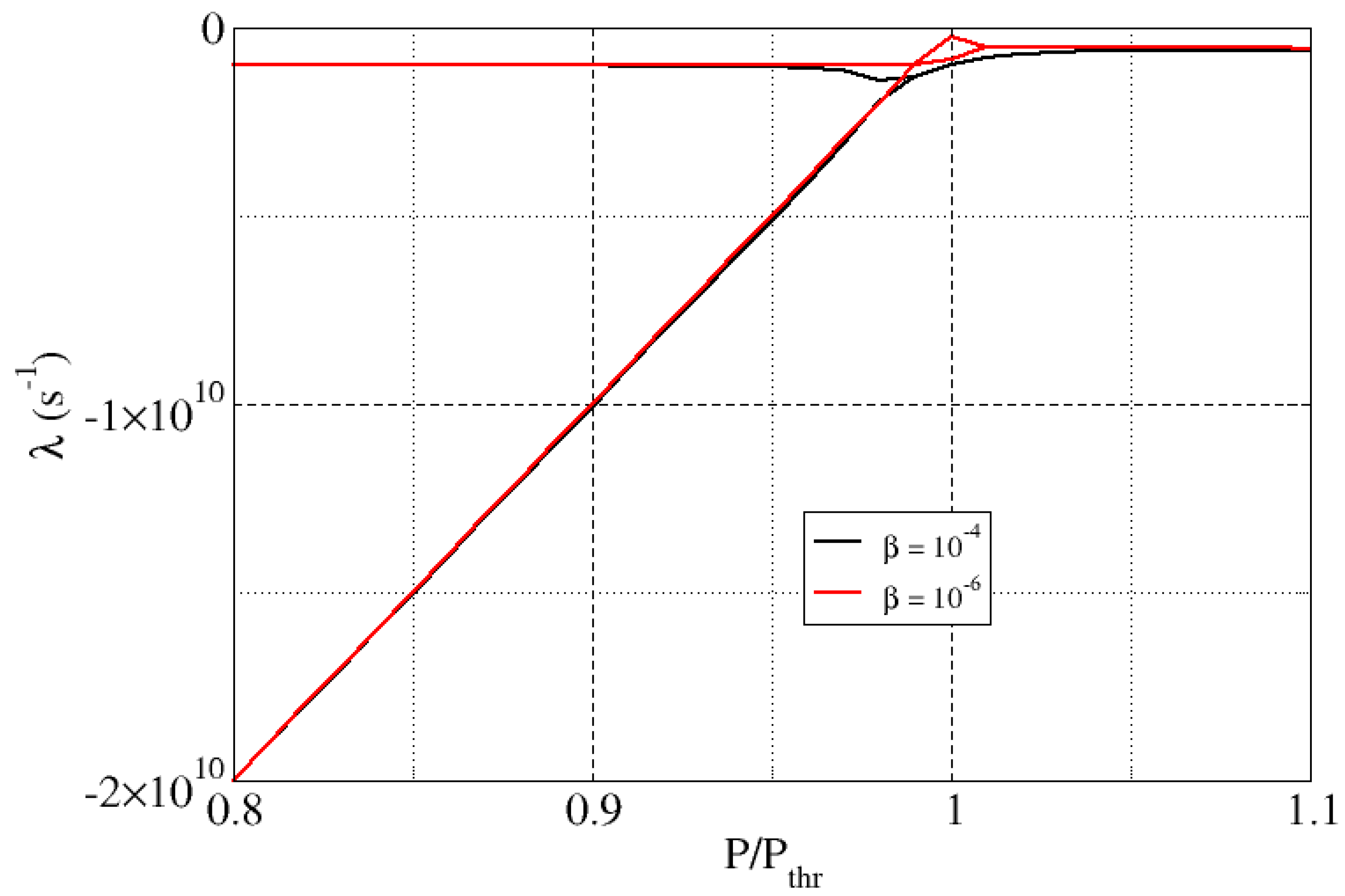
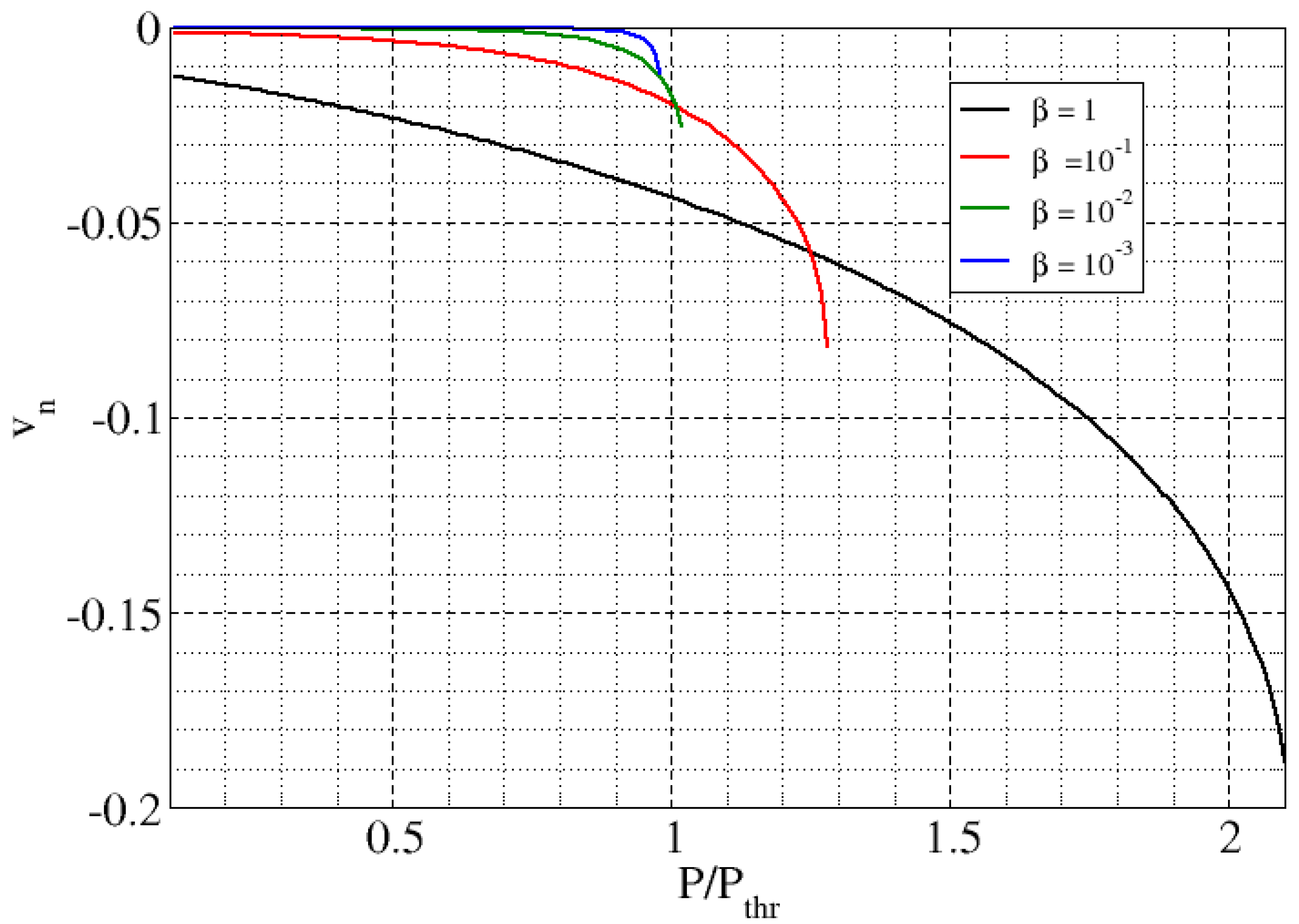
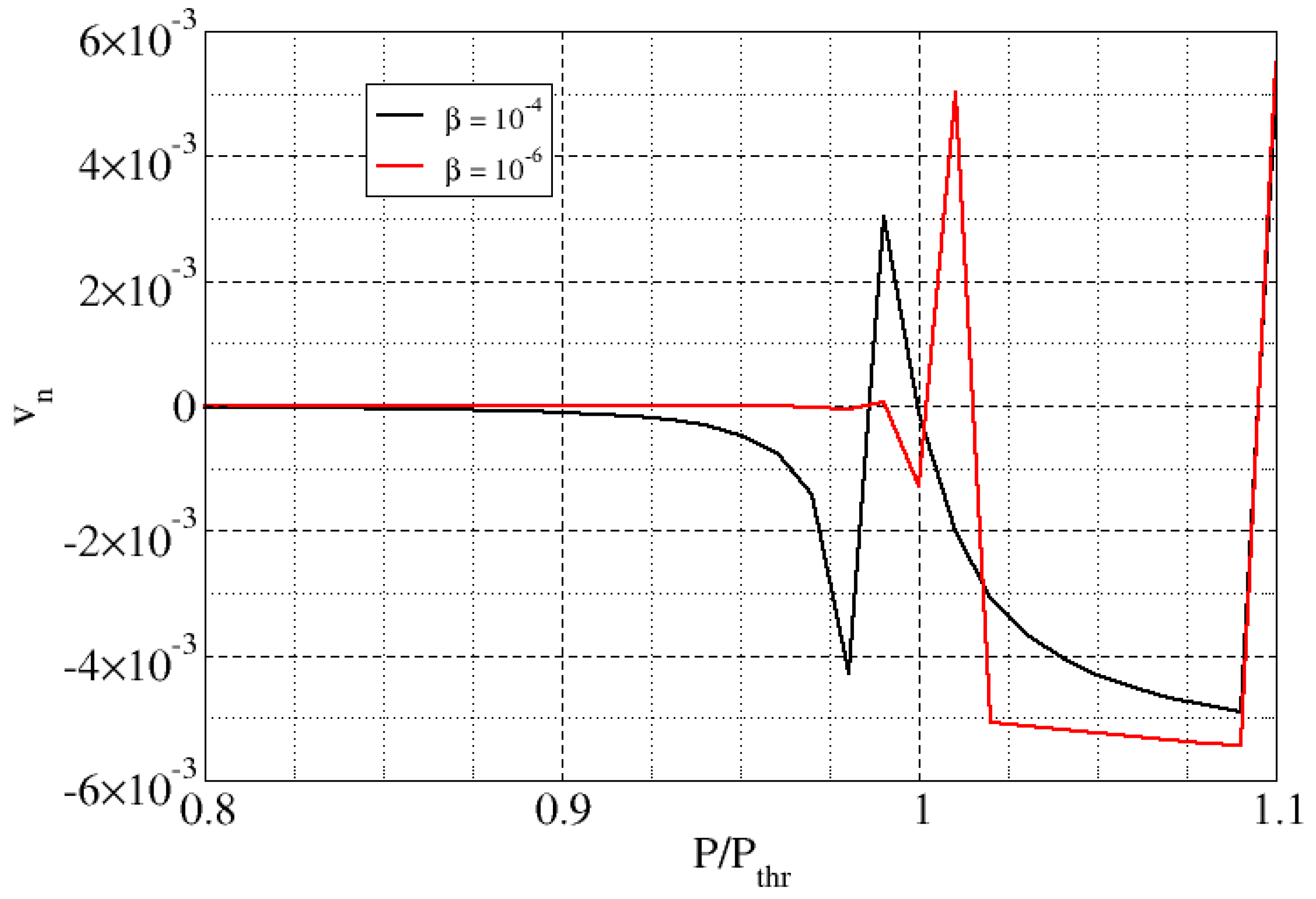
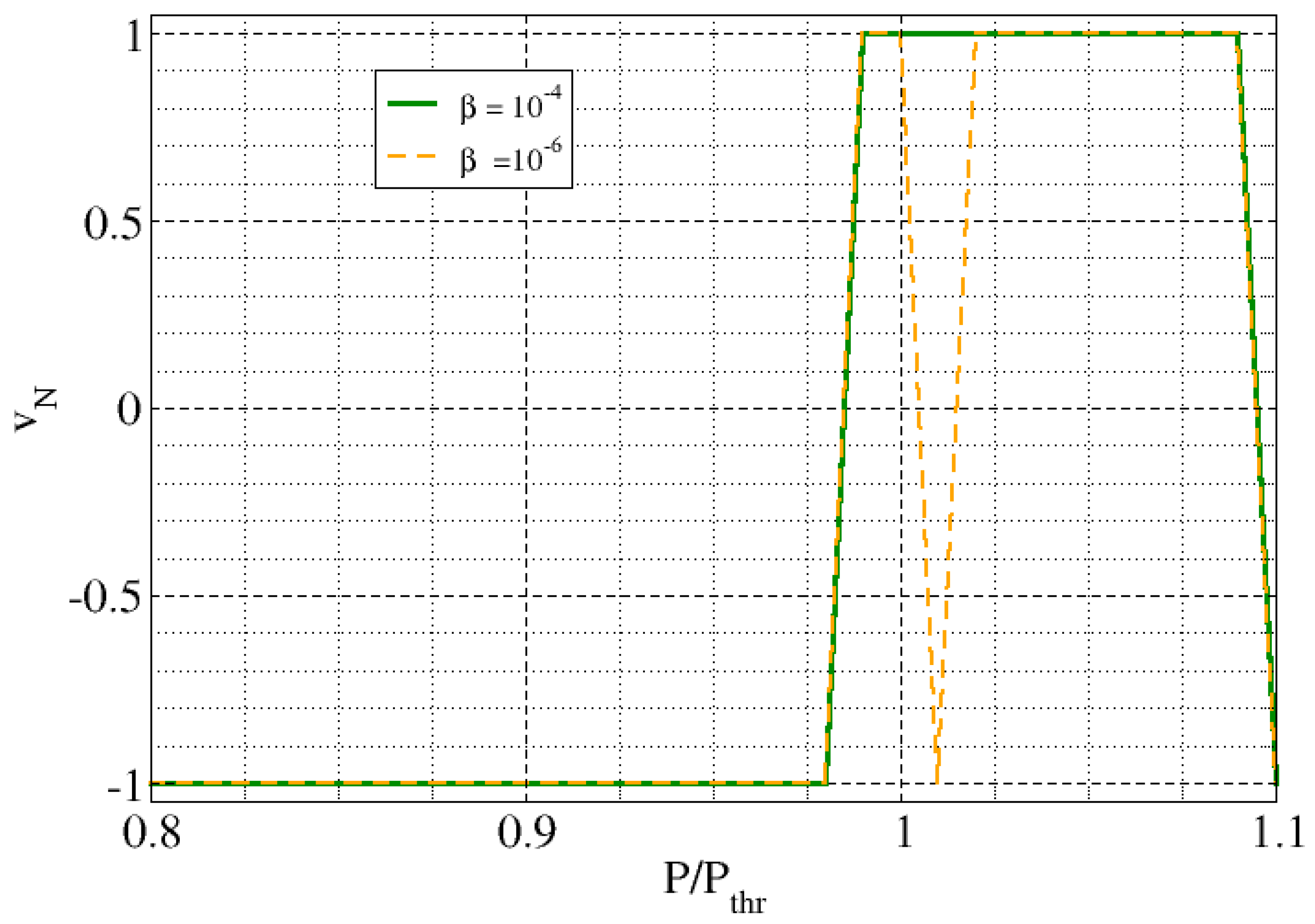

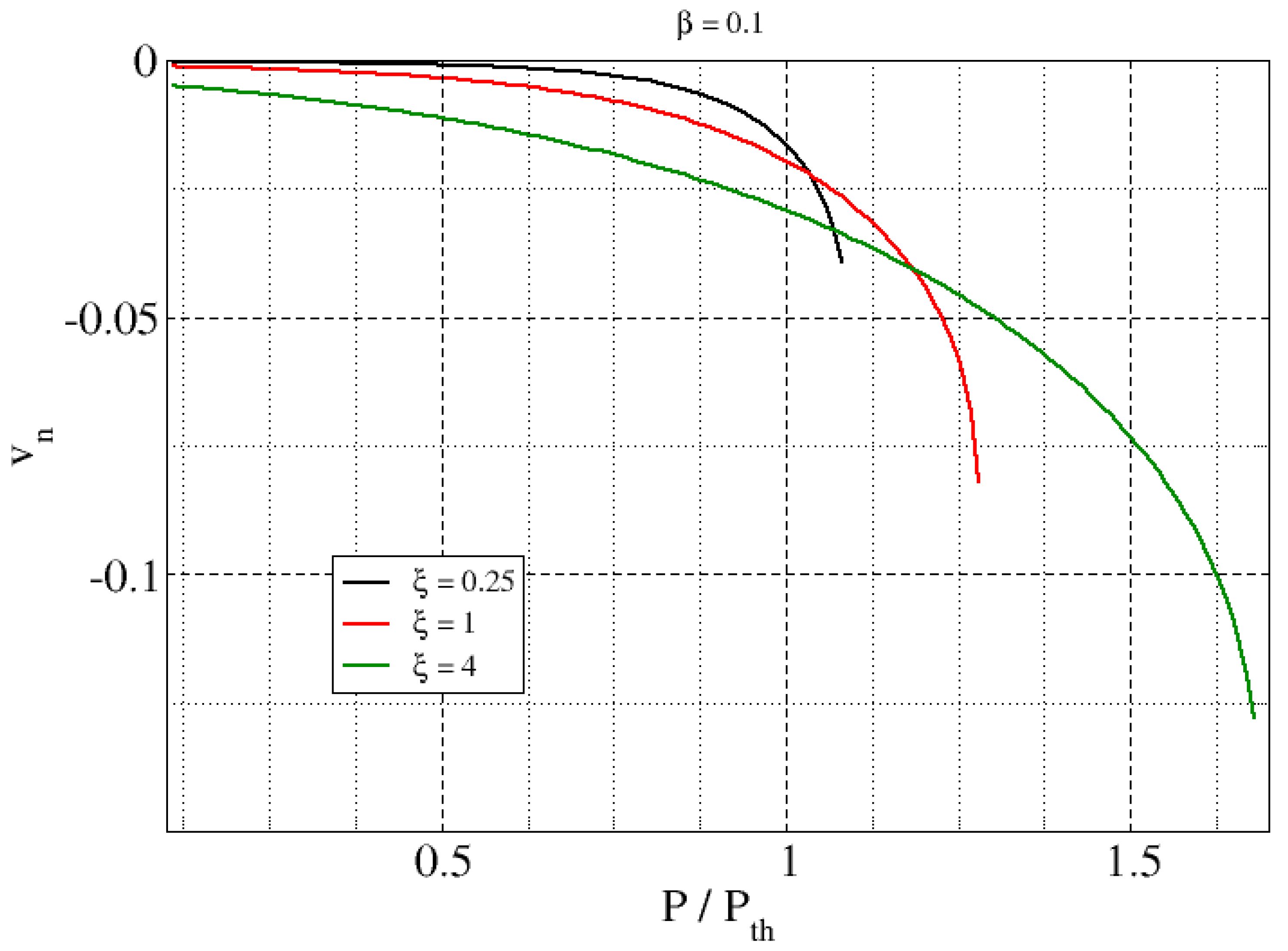
| Feature | Consequence | Comment |
|---|---|---|
| >2 | Allows for a univocal identification of the presence of photon bursts (superthermal bunching) in the temporal laser emission | |
| Does not exclude the presence of photon bursts, but does not allow the certain identification, since other kinds of signals, such as strongly oscillating photon numbers, may give the same value of (cf. e.g., Figure 4c in [76]). | ||
| Frequent bursts | Filling of the measurement window | Frequent bursts increase the fraction of the temporal window in which the photon bursts are measured, reducing the value of . This is not a parasitic effect and signals convergence towards cw laser emission |
| Detection bandwidth | Smaller and broader pulses | Controls the measured value of the autocorrelation signal reducing its value relative to the real one; reduces the range of pump values for the observation of photon bursts |
| Detection background | Lower contrast | Reduces the estimated value of ; reduces the range of pump values for the observation of photon bursts |
| Signal contrast | Ratio between photon bursts and background | Directly affects the estimate of . Improvements in height detection or reduction in background lead towards a more realistic evaluation of |
| Far below threshold | Very infrequent bursts | Likelihood of detecting an actual burst very low compared to the accumulation of background shot noise; results in often-observed drop in at very low pump |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lippi, G.L. “Amplified Spontaneous Emission” in Micro- and Nanolasers. Atoms 2021, 9, 6. https://0-doi-org.brum.beds.ac.uk/10.3390/atoms9010006
Lippi GL. “Amplified Spontaneous Emission” in Micro- and Nanolasers. Atoms. 2021; 9(1):6. https://0-doi-org.brum.beds.ac.uk/10.3390/atoms9010006
Chicago/Turabian StyleLippi, Gian Luca. 2021. "“Amplified Spontaneous Emission” in Micro- and Nanolasers" Atoms 9, no. 1: 6. https://0-doi-org.brum.beds.ac.uk/10.3390/atoms9010006





