Fundamental Parameters Related to Selenium Kα and Kβ Emission X-ray Spectra
Abstract
:1. Introduction
2. Theory
2.1. Atomic Fundamental Parameters
2.2. Relativistic Calculations
2.3. Line Shapes
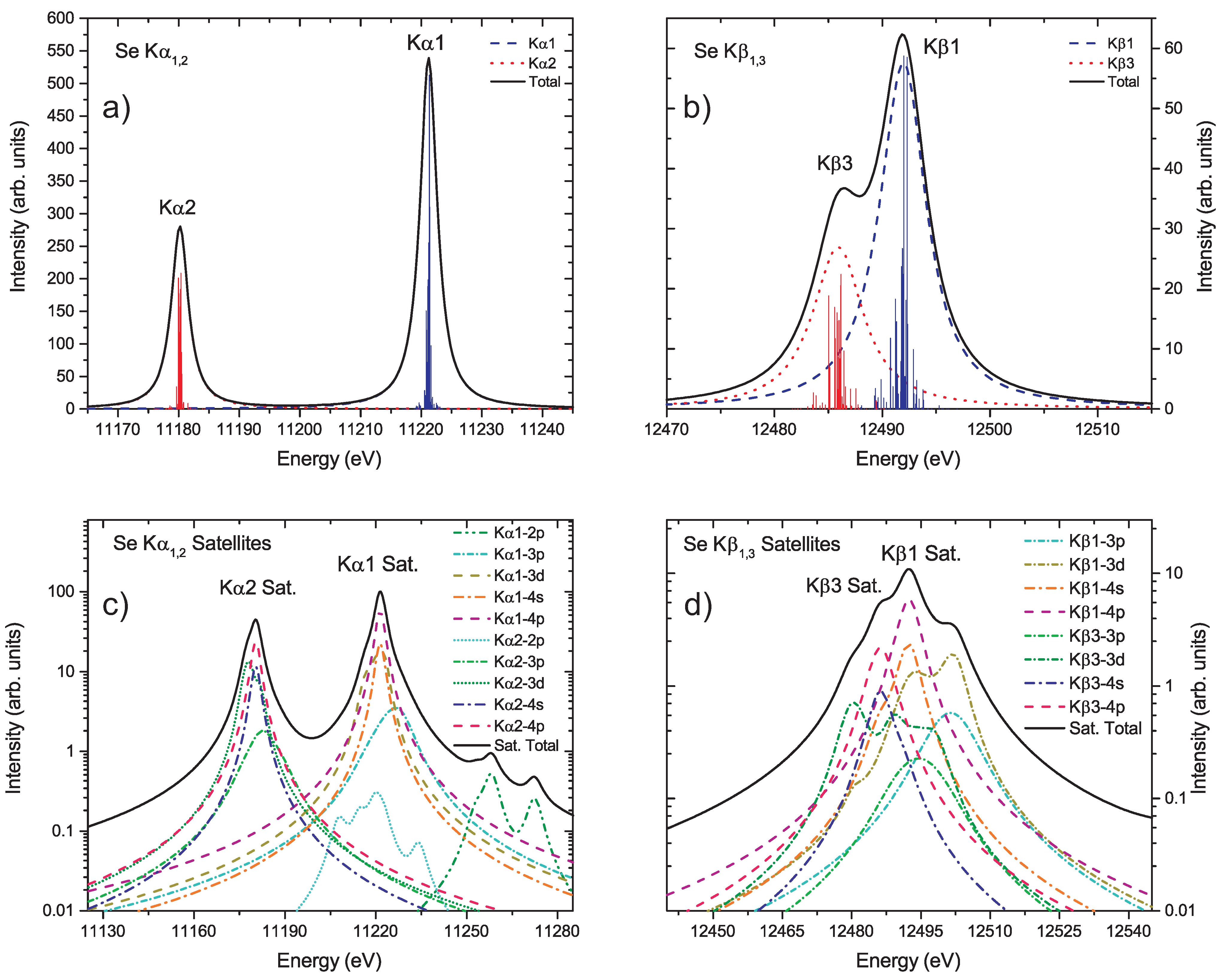
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MCDF | Multiconfiguration Dirac-Fock code |
| QED | Quantum Electrodynamics |
| DCS | Double-Crystal Spectrometer |
References
- Schmidt, S.; Willig, M.; Haack, J.; Horn, R.; Adamczak, A.; Ahmed, M.A.; Amaro, F.D.; Amaro, P.; Biraben, F.; Carvalho, P.; et al. The next generation of laser spectroscopy experiments using light muonic atoms. J. Phys. Conf. Ser. 2018, 1138, 012010. [Google Scholar] [CrossRef]
- Kasthurirangan, S.; Saha, J.K.; Agnihotri, A.N.; Banerjee, A.; Kumar, A.; Misra, D.; Santos, J.P.; Costa, A.M.; Indelicato, P.; Mukherjee, T.K.; et al. High-resolution x-ray spectra from highly charged Si, S and Cl ions showing evidence of fluorescence active resonant states. J. Phys. Conf. Ser. 2014, 488, 132027. [Google Scholar] [CrossRef] [Green Version]
- Santos, J.P.; Costa, A.M.; Marques, J.P.; Martins, M.C.; Indelicato, P.; Parente, F. X-ray-spectroscopy analysis of electron-cyclotron-resonance ion-source plasmas. Phys. Rev. A 2010, 82, 062516. [Google Scholar] [CrossRef]
- Shah, C.; López-Urrutia, J.R.C.; Gu, M.F.; Pfeifer, T.; Marques, J.; Grilo, F.; Santos, J.P.; Amaro, P. Revisiting the Fe xvii Line Emission Problem: Laboratory Measurements of the 3s–2p and 3d–2p Line-formation Channels. Astrophys. J. 2019, 881, 100. [Google Scholar] [CrossRef]
- Kahoul, A.; Aylikci, V.; Aylikci, N.K.; Cengiz, E.; Apaydın, G. Updated database and new empirical values for K-shell fluorescence yields. Radiat. Phys. Chem. 2012, 81, 713–727. [Google Scholar] [CrossRef]
- Kostroun, V.O.; Chen, M.H.; Crasemann, B. Atomic Radiation Transition Probabilities to the 1s State and Theoretical K-Shell Fluorescence Yields. Phys. Rev. A 1971, 3, 533–545. [Google Scholar] [CrossRef]
- Walters, D.L.; Bhalla, C.P. Nonrelativistic Auger Rates, X-Ray Rates, and Fluorescence Yields for the K Shell. Phys. Rev. A 1971, 3, 1919–1927. [Google Scholar] [CrossRef]
- Chantler, C.T.; Lowe, J.A.; Grant, I.P. High-accuracy reconstruction of titanium x-ray emission spectra, including relative intensities, asymmetry and satellites, and ab initio determination of shake magnitudes for transition metals. J. Phys. At. Mol. Opt. Phys. 2013, 46, 015002. [Google Scholar] [CrossRef] [Green Version]
- Chantler, C.T.; Kinnane, M.N.; Su, C.H.; Kimpton, J.A. Characterization of Kα spectral profiles for vanadium, component redetermination for scandium, titanium, chromium, and manganese, and development of satellite structure for Z=21 to Z=25. Phys. Rev. A 2006, 73, 012508. [Google Scholar] [CrossRef] [Green Version]
- Chantler, C.T.; Hayward, A.C.L.; Grant, I.P. Theoretical Determination of Characteristic X-Ray Lines and the Copper Kα Spectrum. Phys. Rev. Lett. 2009, 103, 123002. [Google Scholar] [CrossRef]
- Guerra, M.; Sampaio, J.M.; Madeira, T.I.; Parente, F.; Indelicato, P.; Marques, J.P.; Santos, J.P.; Hoszowska, J.; Dousse, J.C.; Loperetti, L.; et al. Theoretical and experimental determination of L-shell decay rates, line widths, and fluorescence yields in Ge. Phys. Rev. A 2015, 92, 022507. [Google Scholar] [CrossRef] [Green Version]
- Ito, Y.; Tochio, T.; Yamashita, M.; Fukushima, S.; Vlaicu, A.M.; Syrocki, Ł.; Słabkowska, K.; Weder, E.; Polasik, M.; Sawicka, K.; et al. Structure of high-resolution Kβ1,3 x-ray emission spectra for the elements from Ca to Ge. Phys. Rev. A 2018, 97, 052505. [Google Scholar] [CrossRef] [Green Version]
- Ito, Y.; Tochio, T.; Yamashita, M.; Fukushima, S.; Vlaicu, A.M.; Marques, J.P.; Sampaio, J.M.; Guerra, M.; Santos, J.P.; Syrocki, Ł.; et al. Structure of Kα1,2- and Kβ1,3-emission x-ray spectra for Se, Y, and Zr. Phys. Rev. A 2020, 102, 052820. [Google Scholar] [CrossRef]
- Słabkowska, K.; Rzadkiewicz, J.; Syrocki, Ł.; Szymańska, E.; Shumack, A.; Polasik, M.; Pereira, N.R.; JET contributors. On the interpretation of high-resolution x-ray spectra from JET with an ITER-like wall. J. Phys. At. Mol. Opt. Phys. 2015, 48, 144028. [Google Scholar] [CrossRef]
- Zeeshan, F.; Hoszowska, J.; Dousse, J.C.; Sokaras, D.; Weng, T.C.; Alonso-Mori, R.; Kavčič, M.; Guerra, M.; Sampaio, J.M.; Parente, F.; et al. Diagram, valence-to-core, and hypersatellite Kβ X-ray transitions in metallic chromium. X-ray Spectrom. 2019, 48, 351–359. [Google Scholar] [CrossRef] [Green Version]
- Deslattes, R.D.; Kessler, E.; Indelicato, P.; de Billy, L.; Lindroth, E.; Anton, J. X-ray transition energies: New approach to a comprehensive evaluation. Rev. Mod. Phys. 2003, 75, 36–99. [Google Scholar] [CrossRef]
- Hudson, L.T.; Cline, J.P.; Henins, A.; Mendenhall, M.H.; Szabo, C.I. Contemporary x-ray wavelength metrology and traceability. Radiat. Phys. Chem. 2019, 167, 108392. [Google Scholar] [CrossRef]
- Marcus, H.M.; Albert, H.; Lawrence, T.H.; Csilla, I.S.; Donald, W.; James, P.C. High-precision measurement of the x-ray Cu Kα spectrum. J. Phys. At. Mol. Opt. Phys. 2017, 50, 115004. [Google Scholar]
- Mendenhall, M.H.; Hudson, L.T.; Szabo, C.I.; Henins, A.; Cline, J.P. The molybdenum K-shell x-ray emission spectrum. J. Phys. At. Mol. Opt. Phys. 2019, 52, 215004. [Google Scholar] [CrossRef]
- Joseph, F.; Bradley, A.; Douglas, B.; William, D.; Johnathon, G.; Gene, H.; Lawrence, H.; Young, J.; Kelsey, M.; Galen, O.N.; et al. A reassessment of absolute energies of the X-ray L lines of lanthanide metals. Metrologia 2017, 54, 494. [Google Scholar]
- Prior, M.H. Radiative decay rates of metastable Ar III and Cu II ions. Phys. Rev. A 1984, 30, 3051–3056. [Google Scholar] [CrossRef] [Green Version]
- Parpia, F.A.; Johnson, W.R. Radiative decay rates of metastable one-electron atoms. Phys. Rev. A 1982, 26, 1142–1145. [Google Scholar] [CrossRef]
- Desclaux, J. A multiconfiguration relativistic DIRAC-FOCK program. Comput. Phys. Commun. 1975, 9, 31–45. [Google Scholar] [CrossRef]
- Indelicato, P.; Desclaux, J.P. Multiconfiguration Dirac-Fock calculations of transition energies with QED corrections in three-electron ions. Phys. Rev. A 1990, 42, 5139–5149. [Google Scholar] [CrossRef] [PubMed]
- Grant, I.P.; Quiney, H.M. Foundations of the Relativistic Theory of Atomic and Molecular Structure. Adv. At. Mol. Phys. 1988, 23, 37–86. [Google Scholar]
- Indelicato, P. Projection operators in multiconfiguration Dirac-Fock calculations: Application to the ground state of heliumlike ions. Phys. Rev. A 1995, 51, 1132–1145. [Google Scholar] [CrossRef]
- Parpia, F.A.; Fischer, C.F.; Grant, I.P. GRASP92: A package for large-scale relativistic atomic structure calculations. Comput. Phys. Commun. 1996, 94, 249. [Google Scholar] [CrossRef]
- Mohr, P.J.; Plunien, G.; Soff, G. QED corrections in heavy atoms. Phys. Rep. 1998, 293, 227–369. [Google Scholar] [CrossRef]
- Audi, G.; Wapstra, A.H.; Thibault, C. The Ame2003 atomic mass evaluation: (II). Tables, graphs and references. Nucl. Phys. A 2003, 729, 337. [Google Scholar] [CrossRef]
- Angeli, I.; Marinova, K.P. Table of experimental nuclear ground state charge radii: An update. At. Data Nucl. Data Tables 2013, 99, 69. [Google Scholar] [CrossRef]
- Löwdin, P.O. Quantum Theory of Many-particle systems. I. Physical interpretations by means of density matrices, natural spin-orbitals, and convergence problems in the method of configurational interaction. Phys. Rev. 1955, 97, 1474. [Google Scholar] [CrossRef]
- Kozioł, K. MCDF-RCI predictions for structure and width of X-ray line of Al and Si. J. Quant. Spectrosc. Radiat. Transf. 2014, 149, 138–145. [Google Scholar] [CrossRef] [Green Version]
- Ito, Y.; Tochio, T.; Ohashi, H.; Yamashita, M.; Fukushima, S.; Polasik, M.; Słabkowska, K.; Syrocki, Ł.; Szymanska, E.; Rzadkiewicz, J.; et al. Kα1,2 x-ray linewidths, asymmetry indices, and [KM] shake probabilities in elements Ca to Ge and comparison with theory for Ca, Ti, and Ge. Phys. Rev. A 2016, 94, 042506. [Google Scholar] [CrossRef]
- Armstrong, B.H. Spectrum line profiles: The Voigt function. J. Quant. Spectrosc. Radiat. Transf. 1967, 7, 61–88. [Google Scholar] [CrossRef]
- Zaghloul, M.R.; Ali, A.N. Algorithm 916: Computing the Faddeyeva and Voigt Functions. ACM Trans. Math. Softw. 2012, 38, 15. [Google Scholar] [CrossRef]
- Katriel, J. A comment on the reducibility of the Voigt functions. J. Phys. Math. Gen. 1982, 15, 709–710. [Google Scholar] [CrossRef]
- Yang, S. A unification of the Voigt functions. Int. J. Math. Educ. Sci. Technol. 1994, 25, 845–851. [Google Scholar] [CrossRef]
- Luque, J.M.; Calzada, M.D.; Saez, M. A new procedure for obtaining the Voigt function dependent upon the complex error function. J. Quant. Spectrosc. Radiat. Transf. 2005, 94, 151–161. [Google Scholar] [CrossRef]
- Schoonjans, T.; Brunetti, A.; Golosio, B.; Sanchez Del Rio, M.; Solé, V.A.; Ferrero, C.; Vincze, L. The xraylib library for X-ray-matter interactions. Recent developments. Spectrochim. Acta Part B At. Spectrosc. 2011, 66, 776–784. [Google Scholar] [CrossRef]
- Krause, M.O. Atomic radiative and radiationless yields for K and L shells. J. Phys. Chem. Ref. Data 1979, 8, 307–327. [Google Scholar] [CrossRef] [Green Version]
- Bambynek, W.; Crasemann, B.; Fink, R.W.; Freund, H.U.; Mark, H.; Swift, C.D.; Price, R.E.; Rao, P.V. X-Ray Fluorescence Yields, Auger, and Coster-Kronig Transition Probabilities. Rev. Mod. Phys. 1972, 44, 716–813. [Google Scholar] [CrossRef]
- Hubbell, J.H.; Trehan, P.N.; Singh, N.; Chand, B.; Mehta, D.; Garg, M.L.; Garg, R.R.; Singh, S.; Puri, S. A Review, Bibliography, and Tabulation of K, L, and Higher Atomic Shell X-Ray Fluorescence Yields. J. Phys. Chem. Ref. Data 1994, 23, 339–364. [Google Scholar] [CrossRef]
- Krause, M.O.; Oliver, J.H. Natural widths of atomic K and L levels, Kα X-ray lines and several KLL Auger lines. J. Phys. Chem. Ref. Data 1979, 8, 329–338. [Google Scholar] [CrossRef] [Green Version]
- Guerra, M.; Sampaio, J.M.; Parente, F.; Indelicato, P.; Hönicke, P.; Müller, M.; Beckhoff, B.; Marques, J.P.; Santos, J.P. Theoretical and experimental determination of K- and L-shell x-ray relaxation parameters in Ni. Phys. Rev. A 2018, 97, 042501. [Google Scholar] [CrossRef] [Green Version]
- Daoudi, S.; Kahoul, A.; Aylikci, N.K.; Sampaio, J.M.; Marques, J.P.; Aylikci, V.; Sahnoune, Y.; Kasri, Y.; Deghfel, B. Review of experimental photon-induced Kβ/Kα intensity ratios. At. Data Nucl. Data Tables 2020, 132, 101308. [Google Scholar] [CrossRef]
| This Work | XrayLib [39] | Krause [40] | Kostroun et al. [6] | Walters & Bahalla [7] | Bambynek [41] | Hubbell et al. [42] |
|---|---|---|---|---|---|---|
| A-B | Siegbahn | This Work | This Work | Relative | Ito et al. | Krause & Oliver |
| Method 1 | Method 2 | difference | [13] | [43] | ||
| K-L | K | 3.319 | 3.405(2) | 2.5% | 3.468(20) | 3.33(20) |
| K-L | K | 3.294 | 3.371(3) | 2.3% | 3.414(39) | 3.46(21) |
| K-M | K | 4.925 | 5.109(7) | 3.6% | 4.085(87) | |
| K-M | K | 5.411 | 5.815(15) | 7.0% | 5.50(10) | |
| Subshell Widths | ||||||
| Subshell | Radiative | Radiationless | ||||
| K | 1.344 | 9.034 | ||||
| L1 | 1.209 | 5.652 | ||||
| L2 | 1.826 | 1.029 | ||||
| L3 | 1.748 | 1.054 | ||||
| M1 | 1.038 | 2.749 | ||||
| M2 | 2.654 | 3.162 | ||||
| M3 | 2.339 | 2.676 | ||||
| M4 | 2.201 | 4.419 | ||||
| M5 | 2.305 | 4.900 | ||||
| This Work | This Work (from Spectrum) | Daoudi et al. |
|---|---|---|
| Method 1 | Method 2 | [45] |
| 0.154 | 0.163(8) | 0.1631(5) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerra, M.; Sampaio, J.M.; Vília, G.R.; Godinho, C.A.; Pinheiro, D.; Amaro, P.; Marques, J.P.; Machado, J.; Indelicato, P.; Parente, F.; et al. Fundamental Parameters Related to Selenium Kα and Kβ Emission X-ray Spectra. Atoms 2021, 9, 8. https://0-doi-org.brum.beds.ac.uk/10.3390/atoms9010008
Guerra M, Sampaio JM, Vília GR, Godinho CA, Pinheiro D, Amaro P, Marques JP, Machado J, Indelicato P, Parente F, et al. Fundamental Parameters Related to Selenium Kα and Kβ Emission X-ray Spectra. Atoms. 2021; 9(1):8. https://0-doi-org.brum.beds.ac.uk/10.3390/atoms9010008
Chicago/Turabian StyleGuerra, Mauro, Jorge M. Sampaio, Gonçalo R. Vília, César A. Godinho, Daniel Pinheiro, Pedro Amaro, José P. Marques, Jorge Machado, Paul Indelicato, Fernando Parente, and et al. 2021. "Fundamental Parameters Related to Selenium Kα and Kβ Emission X-ray Spectra" Atoms 9, no. 1: 8. https://0-doi-org.brum.beds.ac.uk/10.3390/atoms9010008






