Interactions of Ions and Ultracold Neutral Atom Ensembles in Composite Optical Dipole Traps: Developments and Perspectives
Abstract
:1. Introduction
2. Materials and Methods
Ultracold Ion–Atom Interactions in Optical Dipole Traps
3. Results
Impact of Fluctuating Dipole Trap Alignment
- All results reported in [41] were obtained by averaging over several experimental realizations.
- Individual realizations showed substantial fluctuations of ODT overlap. That is, the atoms were aligned with the center of the Paul trap in about every third realization which was observed using absorption imaging in reference measurements carried out without Ba ions. Since the imaging of the atomic cloud was not part of the experimental sequence, it was not possible to post-selectively restrict the analysis to the cases where overlap was detected. Consequently, the measurements reported in [41] represent averaging over situations where the ions are overlapped with the atoms and those where the ion–atom overlap was strongly reduced or negligible.
- An increase of the ion–atom interaction time in the biODT did not lead to a significant enhancement of optical trapping probabilities. Seemingly, this would imply that the cooling is not improved beyond the level shown in Figure 3.
- Repeating the experiment with different experimental parameters such as average trap overlap and initial ion temperature resulting from long-term drifts robustly yielded the same change of the apparent temperature determined after the ion–atom interaction phase in the biODT within the reported uncertainties.
- Longer ramp-up durations of the VIS/NIR ODTs, that is, build-up of the bichromatic potential, lead to formation of Rb and Rb parasitic ions. For example, with a doubled ramp-up duration (2 ms) we observe the occurrence of such events with a probability of about 0.1 to 0.2. The production rate strongly depends on the intensities of the dipole trap beams, predominantly that of the VIS ODT.
4. Discussion and Perspectives
4.1. Influence of Parasitic Ions on Sympathetic Cooling
4.2. Adapted Configurations for Experiments in the Ultracold Regime of Interactions
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Smith, W.W.; Makarov, O.P.; Lin, J. Cold ion-neutral collisions in a hybrid trap. J. Mod. Opt. 2005, 52, 2253–2260. [Google Scholar] [CrossRef]
- Grier, A.T.; Cetina, M.; Oručević, F.; Vuletić, V. Observation of Cold Collisions between Trapped Ions and Trapped Atoms. Phys. Rev. Lett. 2009, 102, 223201. [Google Scholar] [CrossRef]
- Schmid, S.; Härter, A.; Denschlag, J.H. Dynamics of a Cold Trapped Ion in a Bose–Einstein Condensate. Phys. Rev. Lett. 2010, 105, 133202. [Google Scholar] [CrossRef]
- Zipkes, C.; Palzer, S.; Sias, C.; Köhl, M. A trapped single ion inside a Bose–Einstein condensate. Nature 2010, 464, 388–391. [Google Scholar] [CrossRef] [Green Version]
- Ravi, K.; Lee, S.; Sharma, A.; Werth, G.; Rangwala, S. Cooling and stabilization by collisions in a mixed ion–atom system. Nat. Commun. 2012, 3, 1126. [Google Scholar] [CrossRef] [Green Version]
- Hall, F.H.J.; Willitsch, S. Millikelvin Reactive Collisions between Sympathetically Cooled Molecular Ions and Laser-Cooled Atoms in an Ion-Atom Hybrid Trap. Phys. Rev. Lett. 2012, 109, 233202. [Google Scholar] [CrossRef] [Green Version]
- Rellergert, W.G.; Sullivan, S.T.; Kotochigova, S.; Petrov, A.; Chen, K.; Schowalter, S.J.; Hudson, E.R. Measurement of a Large Chemical Reaction Rate between Ultracold Closed-Shell 40Ca Atoms and Open-Shell 174Yb Ions Held in a Hybrid Atom-Ion Trap. Phys. Rev. Lett. 2011, 107, 243201. [Google Scholar] [CrossRef] [Green Version]
- Härter, A.; Denschlag, J.H. Cold atom–ion experiments in hybrid traps. Contemp. Phys. 2014, 55, 33–45. [Google Scholar] [CrossRef] [Green Version]
- Haze, S.; Sasakawa, M.; Saito, R.; Nakai, R.; Mukaiyama, T. Cooling Dynamics of a Single Trapped Ion via Elastic Collisions with Small-Mass Atoms. Phys. Rev. Lett. 2018, 120, 043401. [Google Scholar] [CrossRef] [Green Version]
- Meir, Z.; Sikorsky, T.; Ben-shlomi, R.; Akerman, N.; Dallal, Y.; Ozeri, R. Dynamics of a Ground-State Cooled Ion Colliding with Ultracold Atoms. Phys. Rev. Lett. 2016, 117, 243401. [Google Scholar] [CrossRef] [Green Version]
- Tomza, M.; Jachymski, K.; Gerritsma, R.; Negretti, A.; Calarco, T.; Idziaszek, Z.; Julienne, P.S. Cold hybrid ion–atom systems. Rev. Mod. Phys. 2019, 91, 035001. [Google Scholar] [CrossRef] [Green Version]
- Deiglmayr, J.; Göritz, A.; Best, T.; Weidemüller, M.; Wester, R. Reactive collisions of trapped anions with ultracold atoms. Phys. Rev. A 2012, 86, 043438. [Google Scholar] [CrossRef] [Green Version]
- Dutta, S.; Sawant, R.; Rangwala, S.A. Collisional Cooling of Light Ions by Cotrapped Heavy Atoms. Phys. Rev. Lett. 2017, 118, 113401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sivarajah, I.; Goodman, D.S.; Wells, J.E.; Narducci, F.A.; Smith, W.W. Evidence of sympathetic cooling of Na+ ions by a Na magneto-optical trap in a hybrid trap. Phys. Rev. A 2012, 86, 063419. [Google Scholar] [CrossRef] [Green Version]
- Feldker, T.; Fürst, H.; Hirzler, H.; Ewald, N.V.; Mazzanti, M.; Wiater, D.; Tomza, M.; Gerritsma, R. Buffer gas cooling of a trapped ion to the quantum regime. Nat. Phys. 2020, 16, 413–416. [Google Scholar] [CrossRef]
- Rellergert, W.G.; Sullivan, S.T.; Schowalter, S.J.; Kotochigova, S.; Chen, K.; Hudson, E.R. Evidence for sympathetic vibrational cooling of translationally cold molecules. Nature 2013, 495, 490–494. [Google Scholar] [CrossRef] [PubMed]
- Goodman, D.S.; Sivarajah, I.; Wells, J.E.; Narducci, F.A.; Smith, W.W. Ion–neutral-atom sympathetic cooling in a hybrid linear rf Paul and magneto-optical trap. Phys. Rev. A 2012, 86, 033408. [Google Scholar] [CrossRef] [Green Version]
- Weckesser, P.; Thielemann, F.; Wiater, D.; Wojciechowska, A.; Karpa, L.; Jachymski, K.; Tomza, M.; Walker, T.; Schaetz, T. Observation of Feshbach resonances between a single ion and ultracold atoms. arXiv 2021, arXiv:2105.09382. [Google Scholar]
- Wolf, J.; Deiß, M.; Krükow, A.; Tiemann, E.; Ruzic, B.P.; Wang, Y.; D’Incao, J.P.; Julienne, P.S.; Denschlag, J.H. State-to-state chemistry for three-body recombination in an ultracold rubidium gas. Science 2017, 358, 921–924. [Google Scholar] [CrossRef] [Green Version]
- Rouse, I.; Willitsch, S. Superstatistical Energy Distributions of an Ion in an Ultracold Buffer Gas. Phys. Rev. Lett. 2017, 118, 143401. [Google Scholar] [CrossRef] [Green Version]
- Chen, K.; Sullivan, S.T.; Hudson, E.R. Neutral gas sympathetic cooling of an ion in a Paul trap. Phys. Rev. Lett. 2014, 112, 143009. [Google Scholar] [CrossRef] [Green Version]
- Dieterle, T.; Berngruber, M.; Hölzl, C.; Löw, R.; Jachymski, K.; Pfau, T.; Meinert, F. Transport of a Single Cold Ion Immersed in a Bose–Einstein Condensate. Phys. Rev. Lett. 2021, 126, 033401. [Google Scholar] [CrossRef]
- Smith, W.; Goodman, D.; Sivarajah, I.; Wells, J.; Banerjee, S.; Cote, R.; Michels, H.; Mongtomery, J.A., Jr.; Narducci, F. Experiments with an ion-neutral hybrid trap: Cold charge-exchange collisions. Appl. Phys. B 2014, 114, 75–80. [Google Scholar] [CrossRef]
- Cetina, M.; Grier, A.T.; Vuletić, V. Micromotion-Induced Limit to Atom-Ion Sympathetic Cooling in Paul Traps. Phys. Rev. Lett. 2012, 109, 253201. [Google Scholar] [CrossRef]
- Kleinbach, K.S.; Engel, F.; Dieterle, T.; Löw, R.; Pfau, T.; Meinert, F. Ionic Impurity in a Bose–Einstein Condensate at Submicrokelvin Temperatures. Phys. Rev. Lett. 2018, 120, 193401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schmid, T.; Veit, C.; Zuber, N.; Löw, R.; Pfau, T.; Tarana, M.; Tomza, M. Rydberg Molecules for Ion-Atom Scattering in the Ultracold Regime. Phys. Rev. Lett. 2018, 120, 153401. [Google Scholar] [CrossRef] [Green Version]
- Schneider, C.; Enderlein, M.; Huber, T.; Schaetz, T. Optical trapping of an ion. Nat. Photonics 2010, 4, 772–775. [Google Scholar] [CrossRef] [Green Version]
- Lambrecht, A.; Schmidt, J.; Weckesser, P.; Debatin, M.; Karpa, L.; Schaetz, T. Long lifetimes and effective isolation of ions in optical and electrostatic traps. Nat. Photonics 2017, 11, 704–707. [Google Scholar] [CrossRef]
- Schmidt, J.; Lambrecht, A.; Weckesser, P.; Debatin, M.; Karpa, L.; Schaetz, T. Optical Trapping of Ion Coulomb Crystals. Phys. Rev. X 2018, 8, 021028. [Google Scholar] [CrossRef] [Green Version]
- Schaetz, T. Trapping ions and atoms optically. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 102001. [Google Scholar] [CrossRef]
- Karpa, L. Trapping Single Ions and Coulomb Crystals with Light Fields; Springer Briefs in Physics; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef] [Green Version]
- Schneider, C.; Enderlein, M.; Huber, T.; Dürr, S.; Schaetz, T. Influence of static electric fields on an optical ion trap. Phys. Rev. A 2012, 85, 013422. [Google Scholar] [CrossRef] [Green Version]
- Cormick, C.; Schaetz, T.; Morigi, G. Trapping ions with lasers. New J. Phys. 2011, 13, 043019. [Google Scholar] [CrossRef]
- Härter, A.; Krükow, A.; Brunner, A.; Schnitzler, W.; Schmid, S.; Denschlag, J.H. Single Ion as a Three-Body Reaction Center in an Ultracold Atomic Gas. Phys. Rev. Lett. 2012, 109, 123201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Härter, A.; Krükow, A.; Brunner, A.; Hecker Denschlag, J. Long-term drifts of stray electric fields in a Paul trap. Appl. Phys. B 2013, 114, 275–281. [Google Scholar] [CrossRef] [Green Version]
- Krükow, A.; Mohammadi, A.; Härter, A.; Denschlag, J.H.; Pérez-Ríos, J.; Greene, C.H. Energy Scaling of Cold Atom-Atom-Ion Three-Body Recombination. Phys. Rev. Lett. 2016, 116, 193201. [Google Scholar] [CrossRef] [Green Version]
- Krükow, A.; Mohammadi, A.; Härter, A.; Hecker Denschlag, J. Reactive two-body and three-body collisions of Ba+ in an ultracold Rb gas. Phys. Rev. A 2016, 94, 10–13. [Google Scholar] [CrossRef] [Green Version]
- Grimm, R.; Weidemüller, M.; Ovchinnikov, Y.B. Optical dipole traps for neutral atoms. Adv. At. Mol. Opt. Phys. 2000, 42, 95–170. [Google Scholar]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 885–964. [Google Scholar] [CrossRef] [Green Version]
- Weckesser, P.; Thielemann, F.; Hoenig, D.; Lambrecht, A.; Karpa, L.; Schaetz, T. Trapping, shaping, and isolating of an ion Coulomb crystal via state-selective optical potentials. Phys. Rev. A 2021, 103, 013112. [Google Scholar] [CrossRef]
- Schmidt, J.; Weckesser, P.; Thielemann, F.; Schaetz, T.; Karpa, L. Optical Traps for Sympathetic Cooling of Ions with Ultracold Neutral Atoms. Phys. Rev. Lett. 2020, 124, 053402. [Google Scholar] [CrossRef] [Green Version]
- Huber, T.; Lambrecht, A.; Schmidt, J.; Karpa, L.; Schaetz, T. A far-off-resonance optical trap for a Ba+ ion. Nat. Commun. 2014, 5, 5587. [Google Scholar] [CrossRef] [Green Version]
- Tuchendler, C.; Lance, A.M.; Browaeys, A.; Sortais, Y.R.P.; Grangier, P. Energy distribution and cooling of a single atom in an optical tweezer. Phys. Rev. A 2008, 78, 033425. [Google Scholar] [CrossRef] [Green Version]
- Härter, A.; Krükow, A.; Deiß, M.; Drews, B.; Tiemann, E.; Denschlag, J.H. Population distribution of product states following three-body recombination in an ultracold atomic gas. Nat. Phys. 2013, 9, 512–517. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Mechanics; Pergamon Press: Oxford, UK, 1969. [Google Scholar]
- Vedel, F.; Vedel, M.; Evans March, R. New Schemes for resonant ejection in r.f. quadrupolar ion traps. Int. J. Mass Spectrom. Ion Processes 1990, 99, 125–138. [Google Scholar] [CrossRef]
- Yu, N.; Dehmelt, H.; Nagourney, W. Noise-free parametric energy multiplication for frequency measurements of an anharmonic mono-ion oscillator. J. Appl. Phys. 1993, 73, 8650–8652. [Google Scholar] [CrossRef]
- Razvi, M.A.; Chu, X.Z.; Alheit, R.; Werth, G.; Blümel, R. Fractional frequency collective parametric resonances of an ion cloud in a Paul trap. Phys. Rev. A 1998, 58, R34–R37. [Google Scholar] [CrossRef]
- Schmidt, J.; Hönig, D.; Weckesser, P.; Thielemann, F.; Schaetz, T.; Karpa, L. Mass-selective removal of ions from Paul traps using parametric excitation. Appl. Phys. B 2020, 126, 176. [Google Scholar] [CrossRef] [PubMed]
- Monroe, C.; Meekhof, D.M.; King, B.E.; Jefferts, S.R.; Itano, W.M.; Wineland, D.J.; Gould, P. Resolved-sideband Raman cooling of a bound atom to the 3D zero-point energy. Phys. Rev. Lett. 1995, 75, 4011–4014. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vuletić, V.; Chin, C.; Kerman, A.; Chu, S. Degenerate Raman Sideband Cooling of Trapped Cesium Atoms at Very High Atomic Densities. Phys. Rev. Lett. 1998, 81, 5768–5771. [Google Scholar] [CrossRef] [Green Version]
- Morigi, G.; Eschner, J.; Keitel, C.H. Ground State Laser Cooling Using Electromagnetically Induced Transparency. Phys. Rev. Lett. 2000, 85, 4458–4461. [Google Scholar] [CrossRef] [Green Version]
- Karpa, L.; Bylinskii, A.; Gangloff, D.; Cetina, M.; Vuletić, V. Suppression of Ion Transport due to Long-Lived Subwavelength Localization by an Optical Lattice. Phys. Rev. Lett. 2013, 111, 163002. [Google Scholar] [CrossRef] [Green Version]
- Passagem, H.F.; Colín-rodríguez, R.; Tallant, J.; Cesar, P.; Bouloufa-maafa, N.; Dulieu, O.; Marcassa, L.G. Continuous Loading of Ultracold Ground-State 85Rb2 Molecules in a Dipole Trap Using a Single Light Beam. Phys. Rev. Lett. 2019, 122, 123401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Christianen, A.; Zwierlein, M.W.; Groenenboom, G.C.; Karman, T. Photoinduced Two-Body Loss of Ultracold Molecules. Phys. Rev. Lett. 2019, 123, 123402. [Google Scholar] [CrossRef] [Green Version]
- Gregory, P.D.; Blackmore, J.A.; Bromley, S.L.; Cornish, S.L. Loss of Ultracold 87Rb 133Cs Molecules via Optical Excitation of Long-Lived Two-Body Collision Complexes. Phys. Rev. Lett. 2020, 124, 163402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bause, R.; Schindewolf, A.; Tao, R.; Duda, M.; Chen, X.Y.; Quéméner, G.; Karman, T.; Christianen, A.; Bloch, I.; Luo, X.Y. Collisions of ultracold molecules in bright and dark optical dipole traps. arXiv 2021, arXiv:2103.00889. [Google Scholar]
- Gersema, P.; Voges, K.K.; zum Alten Borgloh, M.M.; Koch, L.; Hartmann, T.; Zenesini, A.; Ospelkaus, S.; Lin, J.; He, J.; Wang, D. Probing photoinduced two-body loss of ultracold non-reactive bosonic 23Na87Rb and 23Na39K molecules. arXiv 2021, arXiv:2103.00510. [Google Scholar]
- Morsch, O.; Oberthaler, M. Dynamics of Bose–Einstein condensates in optical lattices. Rev. Mod. Phys. 2006, 78, 179–215. [Google Scholar] [CrossRef]
- Endres, M.; Bernien, H.; Keesling, A.; Levine, H.; Anschuetz, E.R.; Krajenbrink, A.; Senko, C.; Vuletic, V.; Greiner, M.; Lukin, M.D. Atom-by-atom assembly of defect-free one-dimensional cold atom arrays. Science 2016, 354, 1024–1027. [Google Scholar] [CrossRef] [Green Version]
- Barredo, D.; de Léséleuc, S.; Lienhard, V.; Lahaye, T.; Browaeys, A. An atom-by-atom assembler of defect-free arbitrary two-dimensional atomic arrays. Science 2016, 354, 1021–1023. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barredo, D.; Lienhard, V.; de Léséleuc, S.; Lahaye, T.; Browaeys, A. Synthetic three-dimensional atomic structures assembled atom by atom. Nature 2018, 561, 79–82. [Google Scholar] [CrossRef] [Green Version]
- Krych, M.; Skomorowski, W.; Pawłowski, F.; Moszynski, R.; Idziaszek, Z. Sympathetic cooling of the Ba+ ion by collisions with ultracold Rb atoms: Theoretical prospects. Phys. Rev. A 2011, 83, 032723. [Google Scholar] [CrossRef] [Green Version]
- Leibfried, D. Ions captured in the spotlight. Nat. Photonics 2017, 11, 688–690. [Google Scholar] [CrossRef]
- Hamann, S.; Haycock, D.; Klose, G.; Pax, P.; Deutsch, I.; Jessen, P. Resolved-Sideband Raman Cooling to the Ground State of an Optical Lattice. Phys. Rev. Lett. 1998, 80, 4149–4152. [Google Scholar] [CrossRef] [Green Version]



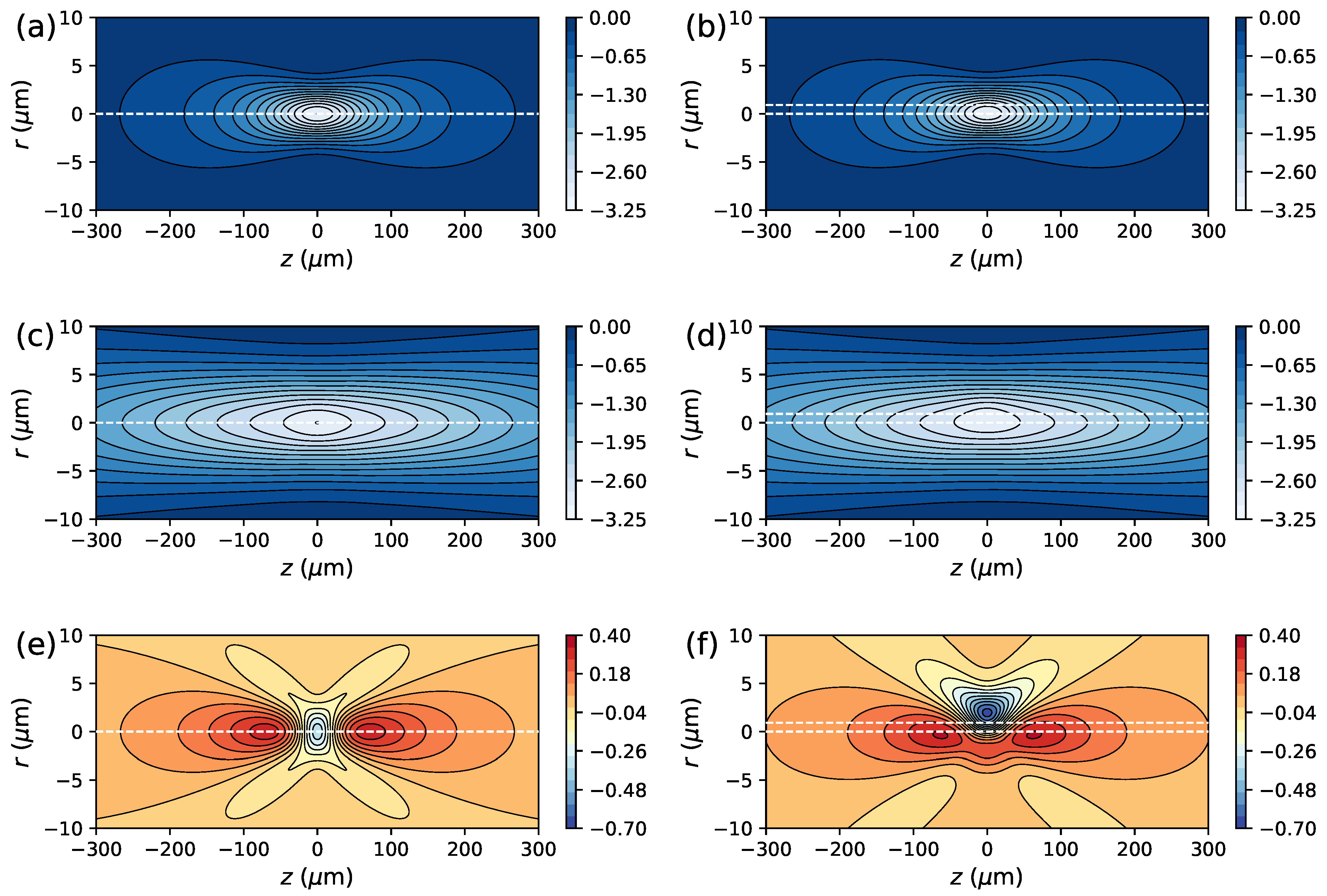



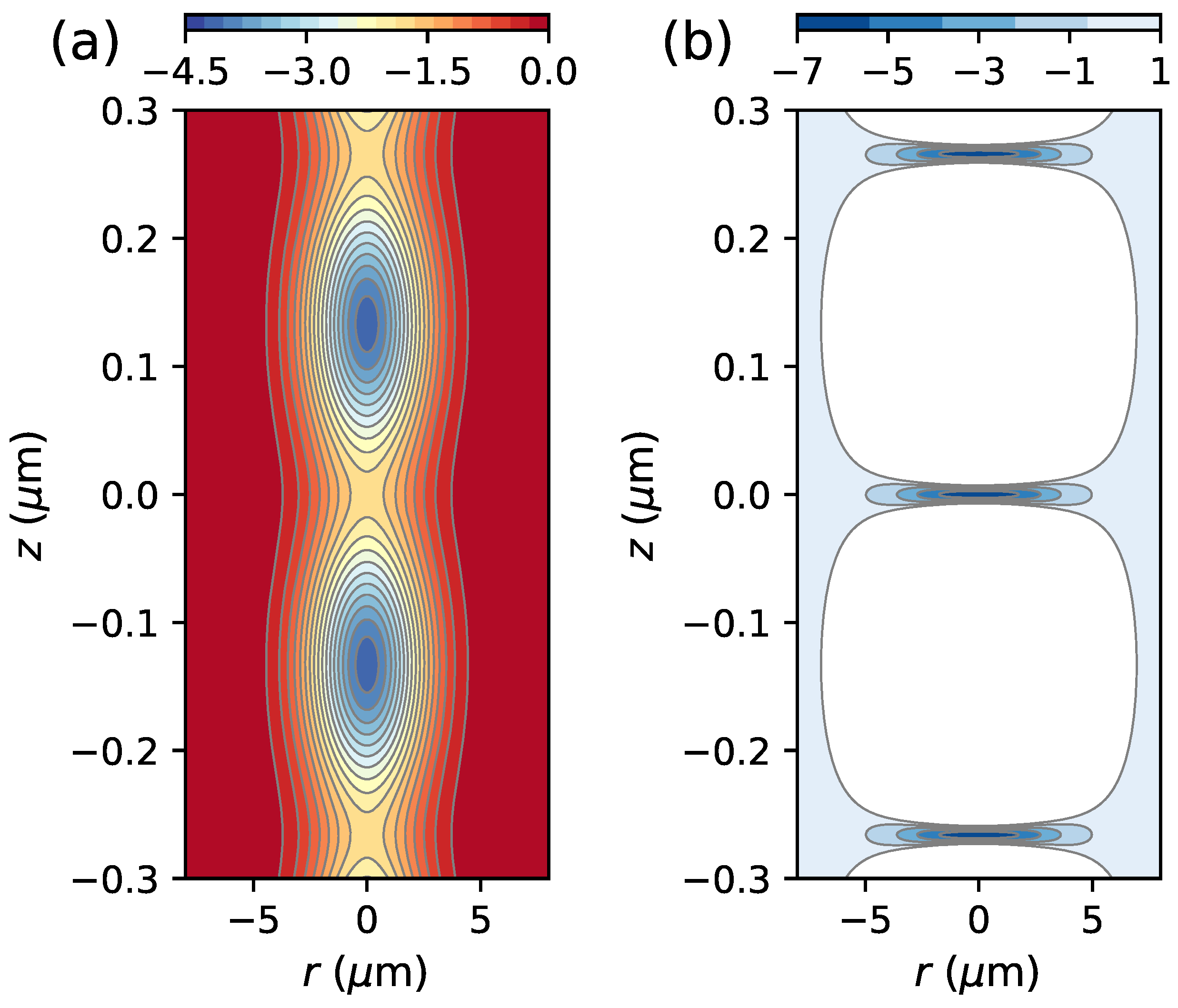
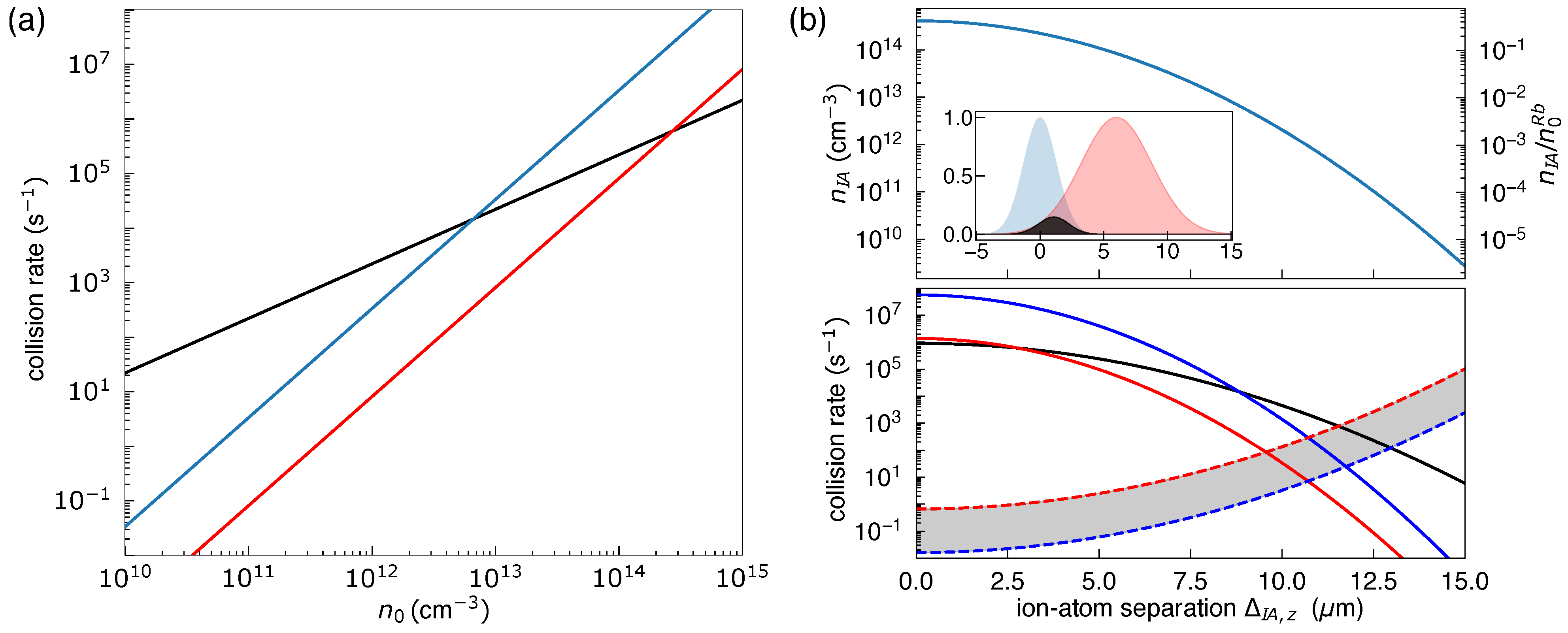
| Ba | Rb | |
|---|---|---|
| 469/106 | ||
| 3.7 | ||
| 860 | 1257 | |
| 1.3 | 35 | |
| Ba | Rb | |
|---|---|---|
| 176/469 | ||
| 3.7 | ||
| 2.7 | 44.5 | |
| 1.67 | 1.65 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karpa, L. Interactions of Ions and Ultracold Neutral Atom Ensembles in Composite Optical Dipole Traps: Developments and Perspectives. Atoms 2021, 9, 39. https://0-doi-org.brum.beds.ac.uk/10.3390/atoms9030039
Karpa L. Interactions of Ions and Ultracold Neutral Atom Ensembles in Composite Optical Dipole Traps: Developments and Perspectives. Atoms. 2021; 9(3):39. https://0-doi-org.brum.beds.ac.uk/10.3390/atoms9030039
Chicago/Turabian StyleKarpa, Leon. 2021. "Interactions of Ions and Ultracold Neutral Atom Ensembles in Composite Optical Dipole Traps: Developments and Perspectives" Atoms 9, no. 3: 39. https://0-doi-org.brum.beds.ac.uk/10.3390/atoms9030039






