A Refined Lines/Regions and Lines/Lines Topological Relations Model Based on Whole-Whole Objects Intersection Components
Abstract
:1. Introduction
2. Definition of the Intersection Component and Introduction of the Node Degree
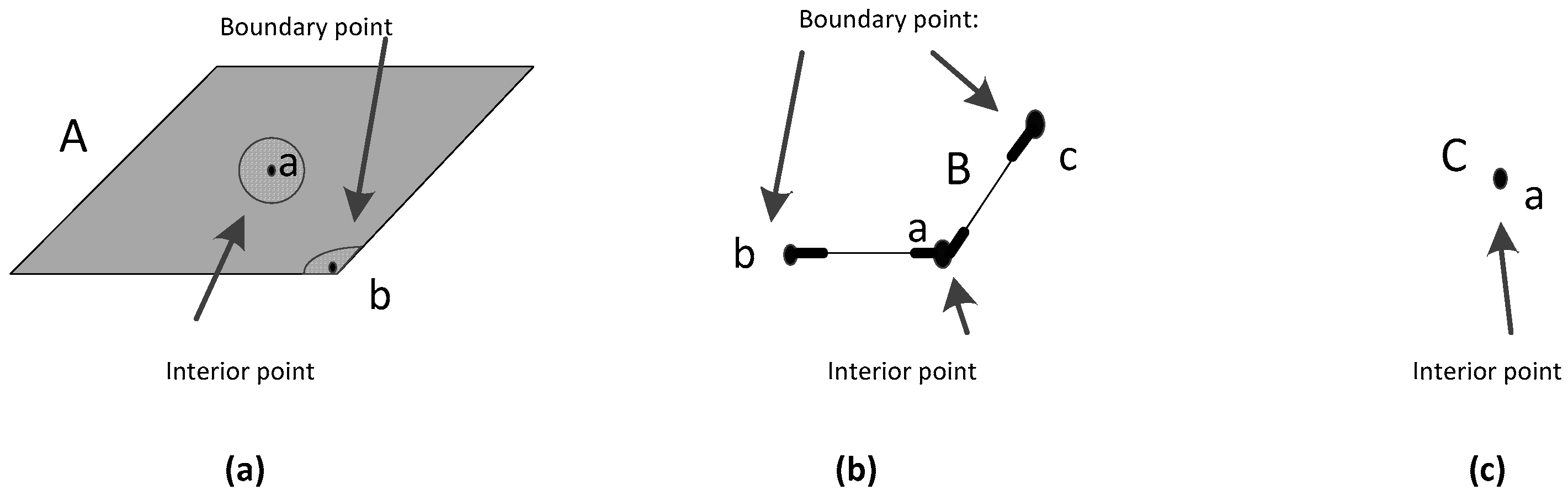
2.1. The Definition of a Simple Spatial Object
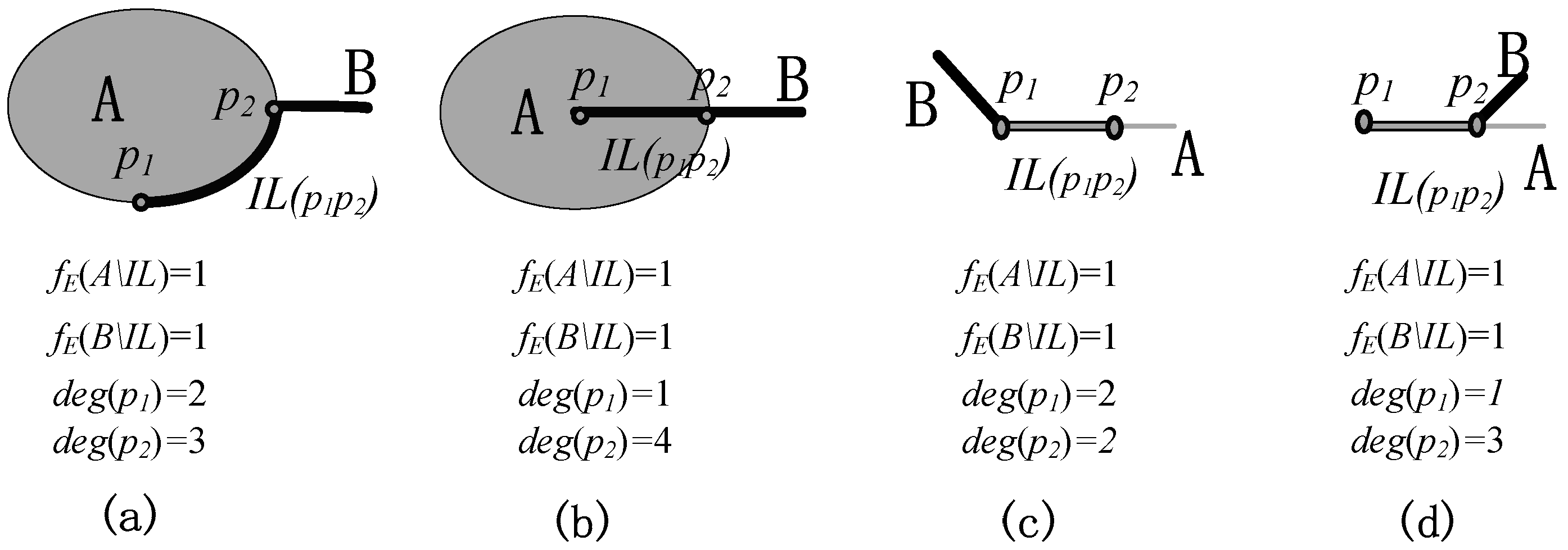
2.2. The Definition of Intersection Components
2.3. Introduction of the Node Degree
3. Classification of Intersection-Lines and Intersection-Points Based on Node Degrees
3.1. Classification of the Intersection-Line between the Line and Region
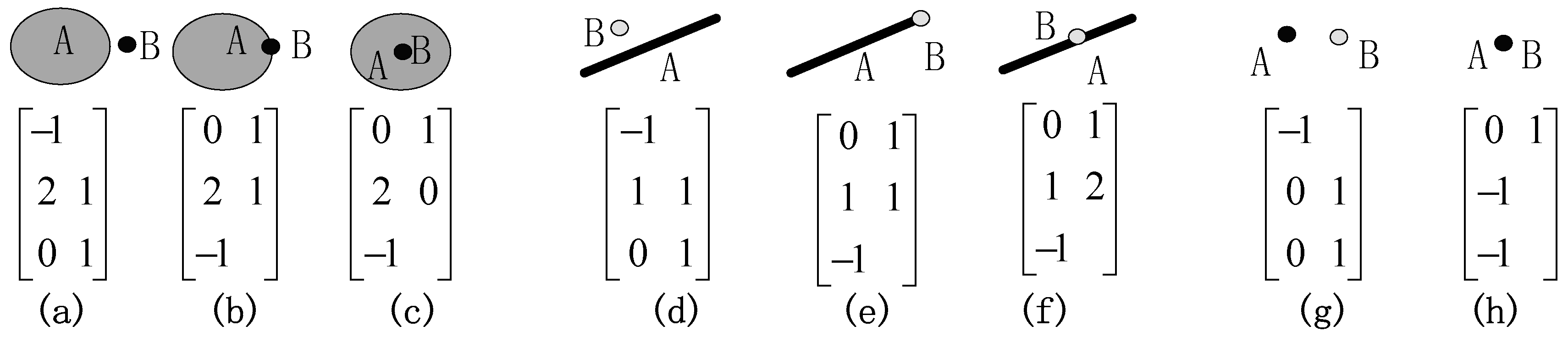
- Case of degree-pairs (1,1), (1,2), (1,3) and (1,4). If the node degrees of the intersection-line endpoints are both one, the endpoints must be located inside the region and their adjacent point kinds must be Null; otherwise, at least one intersection-line endpoint will be connected with more than one edge. Therefore, there is only one type of degree-pair (1,1), as shown in Figure 9a. If one endpoint is inside the region and the other intersection-line endpoint is not inside, the other endpoint has at least three or more edges connected with it, so there is no degree-pair (1,2). If the node degree of the other endpoint is three, its adjacent point kind must be On (Figure 9b) or Null (Figure 9c), otherwise this endpoint will have 1 adjacent edge or four adjacent edges. Therefore, there are only two types of degree-pair (1,3). If the node degree of the other endpoint is four, its adjacent point kind must be Out (Figure 9d) or In (Figure 9f); otherwise, there will be less than 4 edges meeting at the endpoint.
- Case of degree-pairs (2,2), (2,3), and (2,4). If the node degrees of the intersection-line endpoints are both two, they must be on the boundary of the region and their adjacent point kinds must be Null; otherwise, the number of edges meeting at the endpoint will not be equal to two. Therefore, there is only one type of degree-pair (2,2), as shown in Figure 9h. If one endpoint is on the boundary of the region and the node degree of the other endpoint is three, its adjacent point kind must be Out (Figure 9f) or In (Figure 9g); otherwise, its endpoint will meet at two edges. Therefore, there are only two types of degree-pair (2,3) and no type of degree-pair (2,4).
- Case of degree-pairs (3,3) and (3,4). If the node degrees of the intersection-line endpoints are both three, their adjacent point kinds can be Out, In, On, or Null. Therefore, there are six () possible types of degree-pair (3,3), and they are shown in Figure 9i–n, respectively. If the node degree of one endpoint is three and the other is four, the adjacent point kind of the endpoints with node degree 3 must be Null or On, and the adjacent point kind of the endpoints with node degree 4 must be Out or In. Therefore, there are four (* ) types of degree-pair (3,4), as shown in Figure 9o–r.
- Case of degree-pairs (4,4). If the node degrees of the intersection-line endpoints are both 4, their adjacent point kinds must be Out or In; otherwise, there will be less than 4 edges meeting at the endpoints. Therefore, there are three asymmetric types of degree-pair (4,4), as shown in Figure 9s–u.
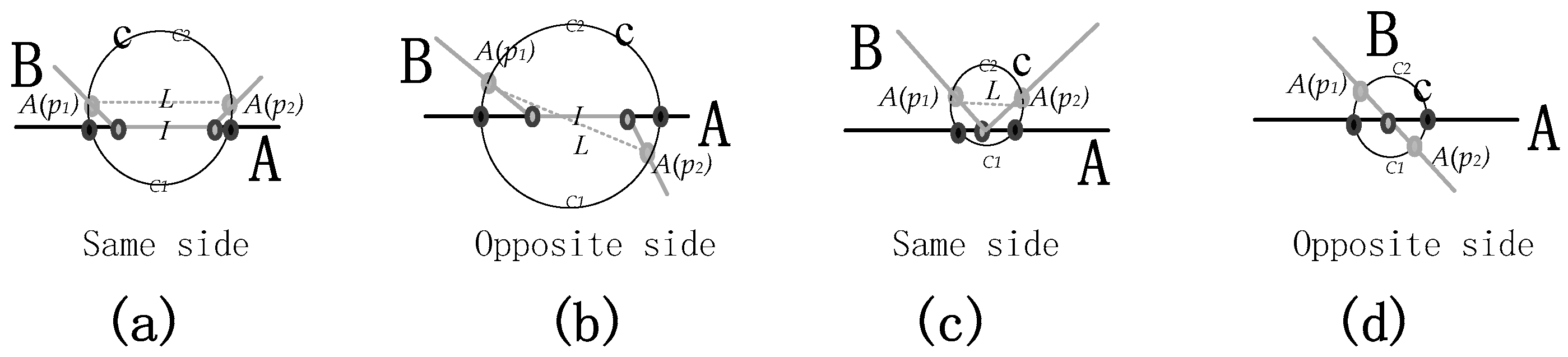
3.2. Classification of the Intersection-Line between Line and Line
- Case of degree-pairs (1,1), (1,2), and (1,3). If the node degrees of the intersection-line endpoints are both one, they must be the boundary points of the lines and their adjacent point kinds must be Null (Figure 10a). If one endpoint is on the boundary of a line and the node degree of the other endpoint is two, its adjacent point kind must be Null (Figure 10b). If the node degree of the other endpoint is three, its adjacent point kind must be Out (Figure 10e); otherwise, there will be less than three edges meeting at the endpoint. Therefore, there is only one type of degree-pairs (1,1), (1,2), and (1,3), respectively.
- Case of degree-pairs (2,2) and (2,3). If the node degrees of the intersection-line endpoints are both two, the adjacent point kind of one endpoint must be Null, and the other one’s adjacent point kind can be Null or Out. Therefore, there are two types of degree-pair (2,2), as shown in Figure 10c,d. If the node degree of one endpoint is three, its adjacent point kind must be Out (Figure 10f); otherwise, there will be less than three edges meeting at the endpoint. Therefore, there is only one type of degree-pair (2,3).
- Case of degree-pairs (3,3). If the node degree of the intersection-line endpoints is both three, their adjacent point kinds both must be Out, and their comprehensive kinds could be SS or OS. Therefore, there are two asymmetric types of degree-pair (3,3), as shown in Figure 10g,h.
3.3. Classification of the Intersection-Point
4. Hierarchical Representation of the Topological Relations of Line/Region and Line/Line
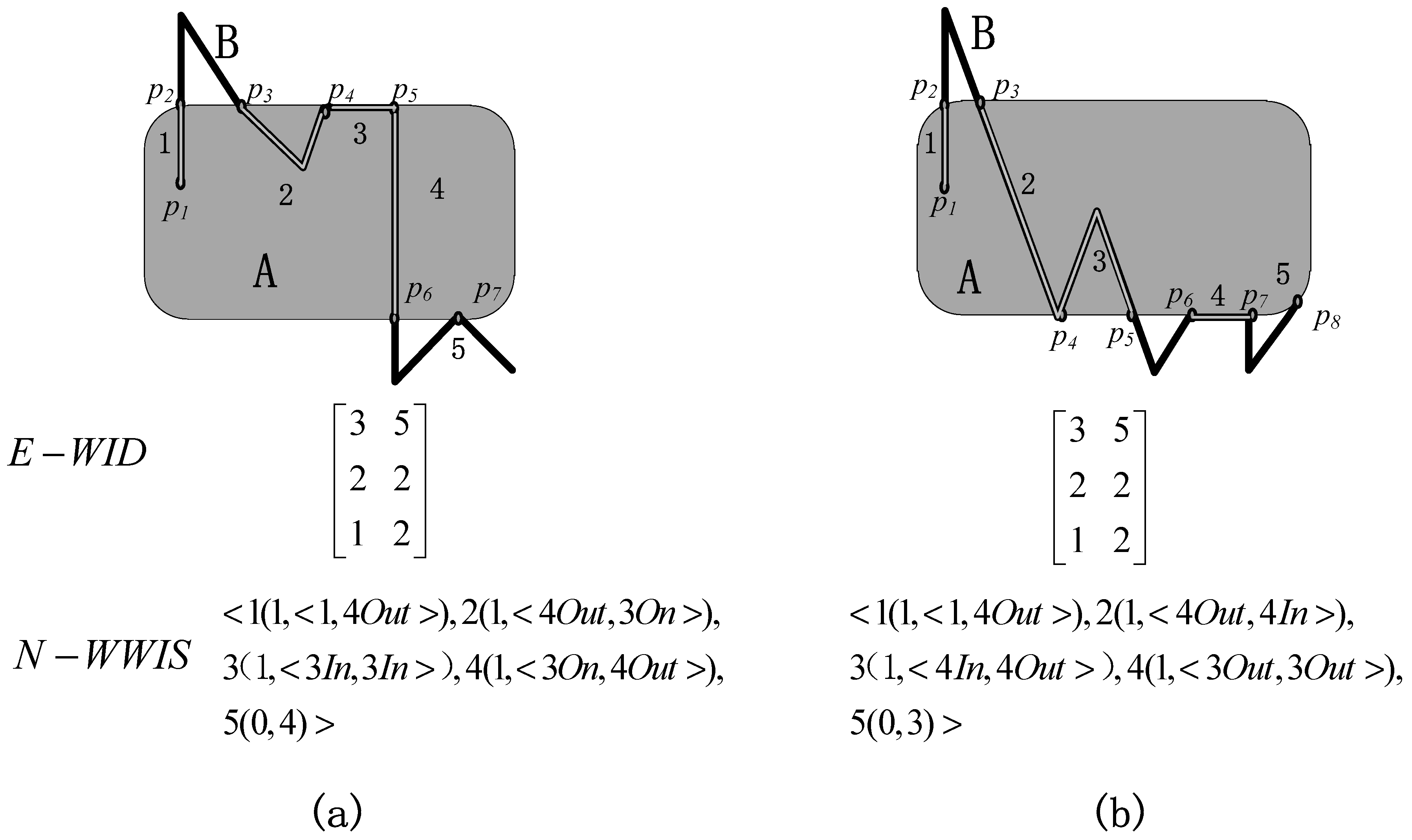
4.1. Using the E-WID Model to Represent Coarse Relations
4.2. Using the N-WWIS Model to Represent Refined Relations
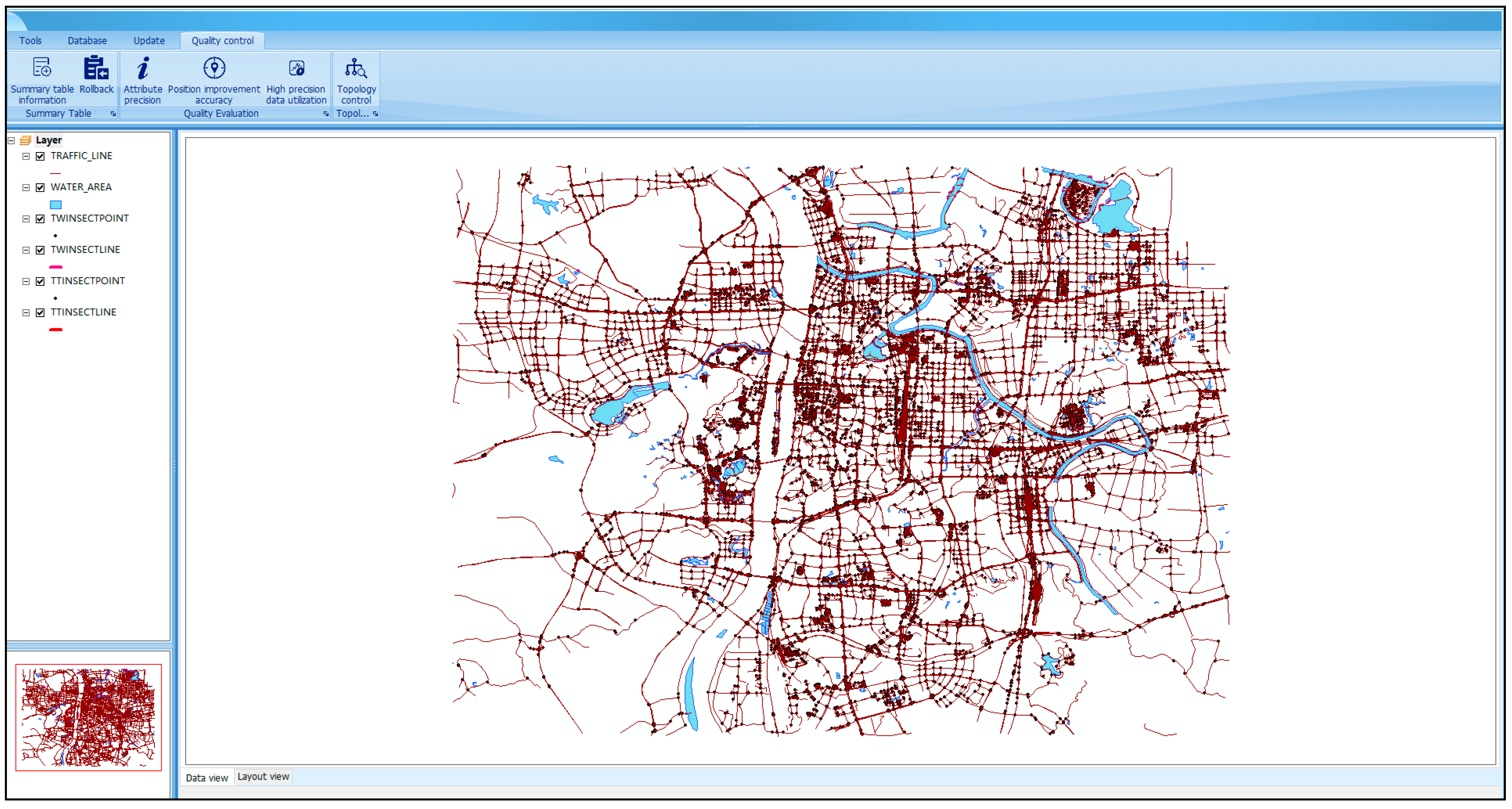
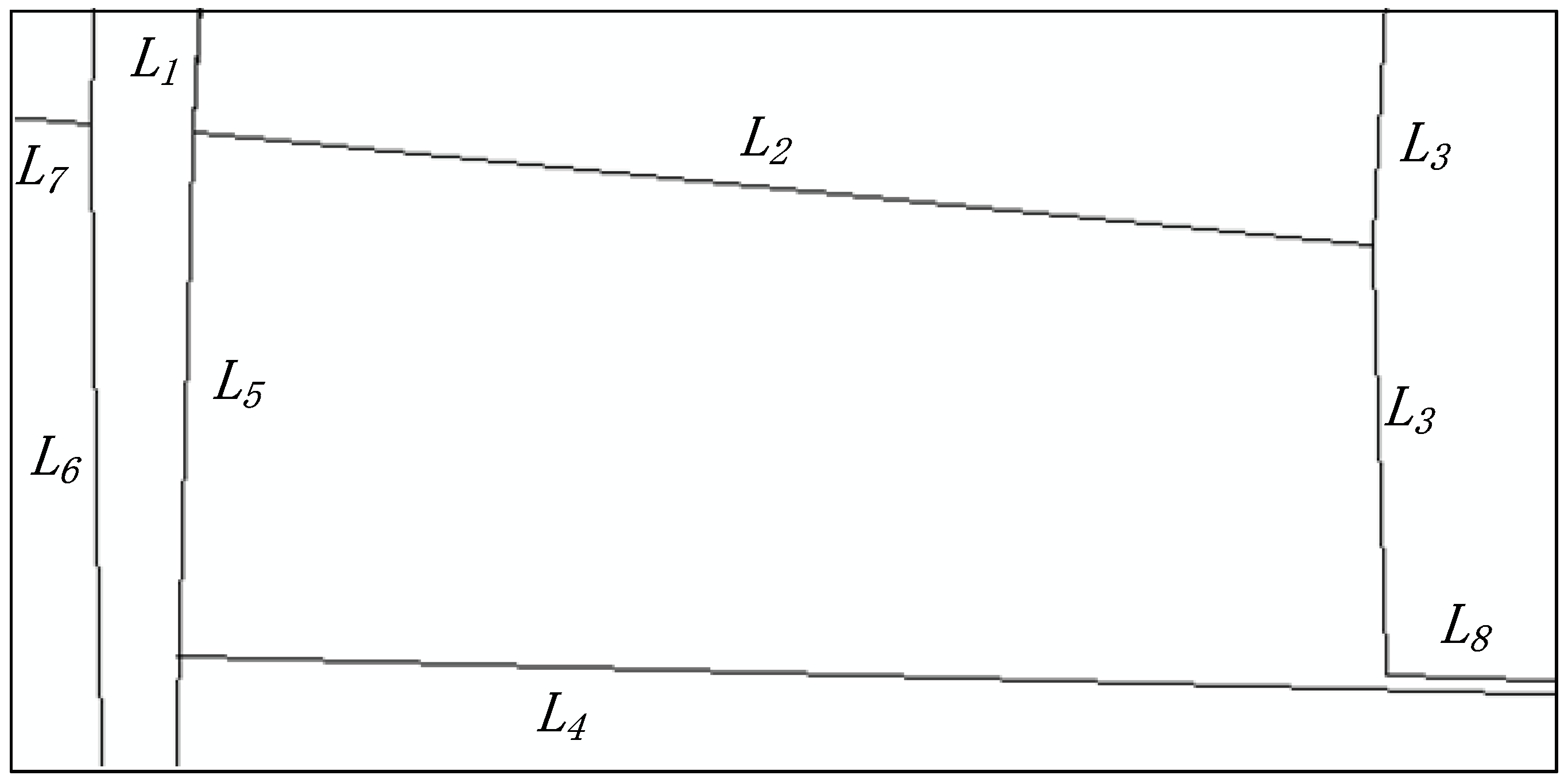
5. Experimental Application
- Download OSM data (XML format), and convert them to the Chinese national fundamental geographic information data model using the transformation method and the object-oriented spatiotemporal data model.
- Set the tolerance (i.e., 1 m) based on experience for the computation of refined lines/regions topological relations.
- Select one line Li (1 ≤ i ≤ n) from the line data set and use the Minimal Bounding Rectangle of Li as the regions to filter out the data. This can reduce the number of regions that have no intersection with the line Li.
- Calculate the refined N-WWIS topological relations between the line Li and the filtered regions automatically, and store the non-disjoint regions and the refined descriptions of their relations to form the intersection components (include intersection-line and intersection-point) types set {A, B,…, W}.
- Return to Steps 3 and 4, start the calculation of refined relations between another line and the filtered regions and store relevant data until all objects in the line data set have been calculated.
- For each intersection component in the types set, match it to the rules set for automatically (or semi-automatically) dealing with each potential topological conflict.
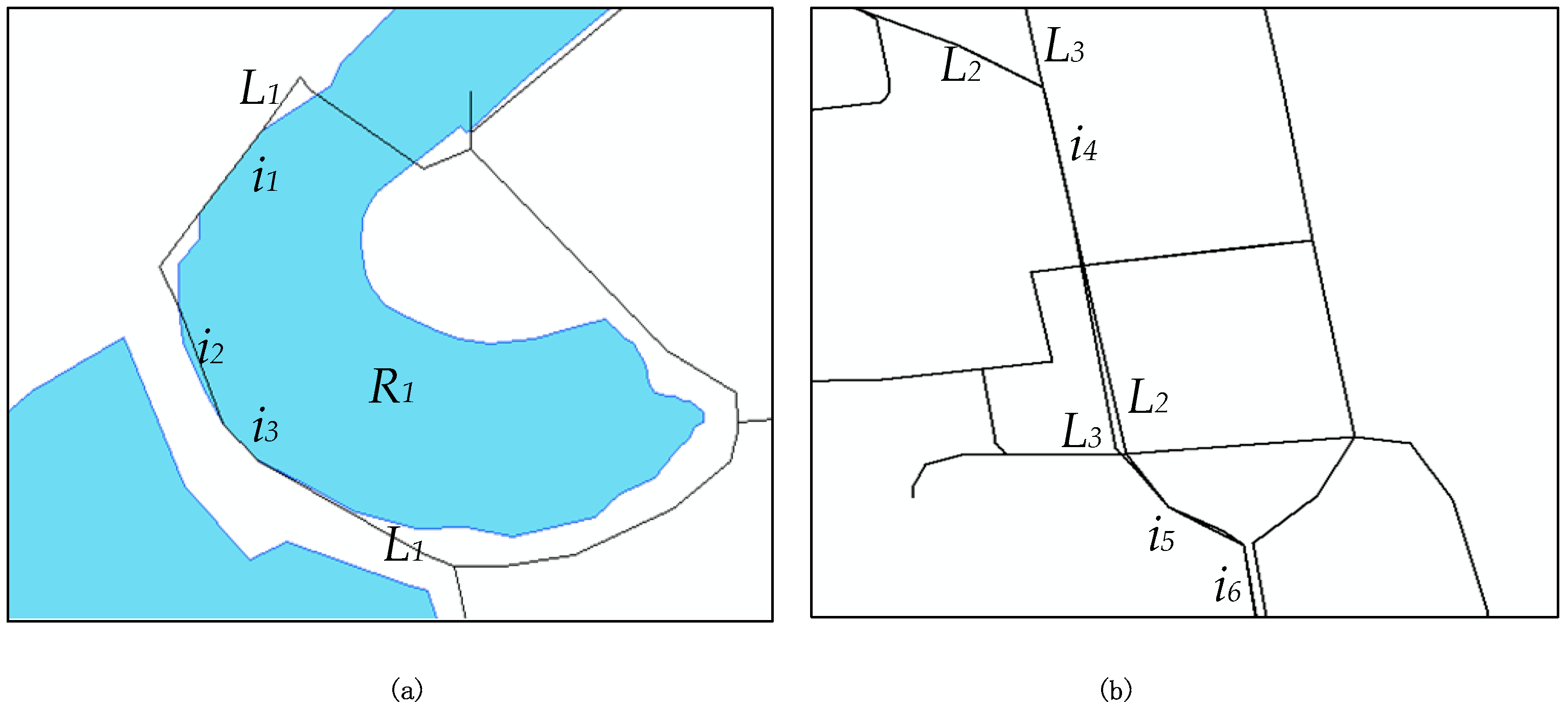
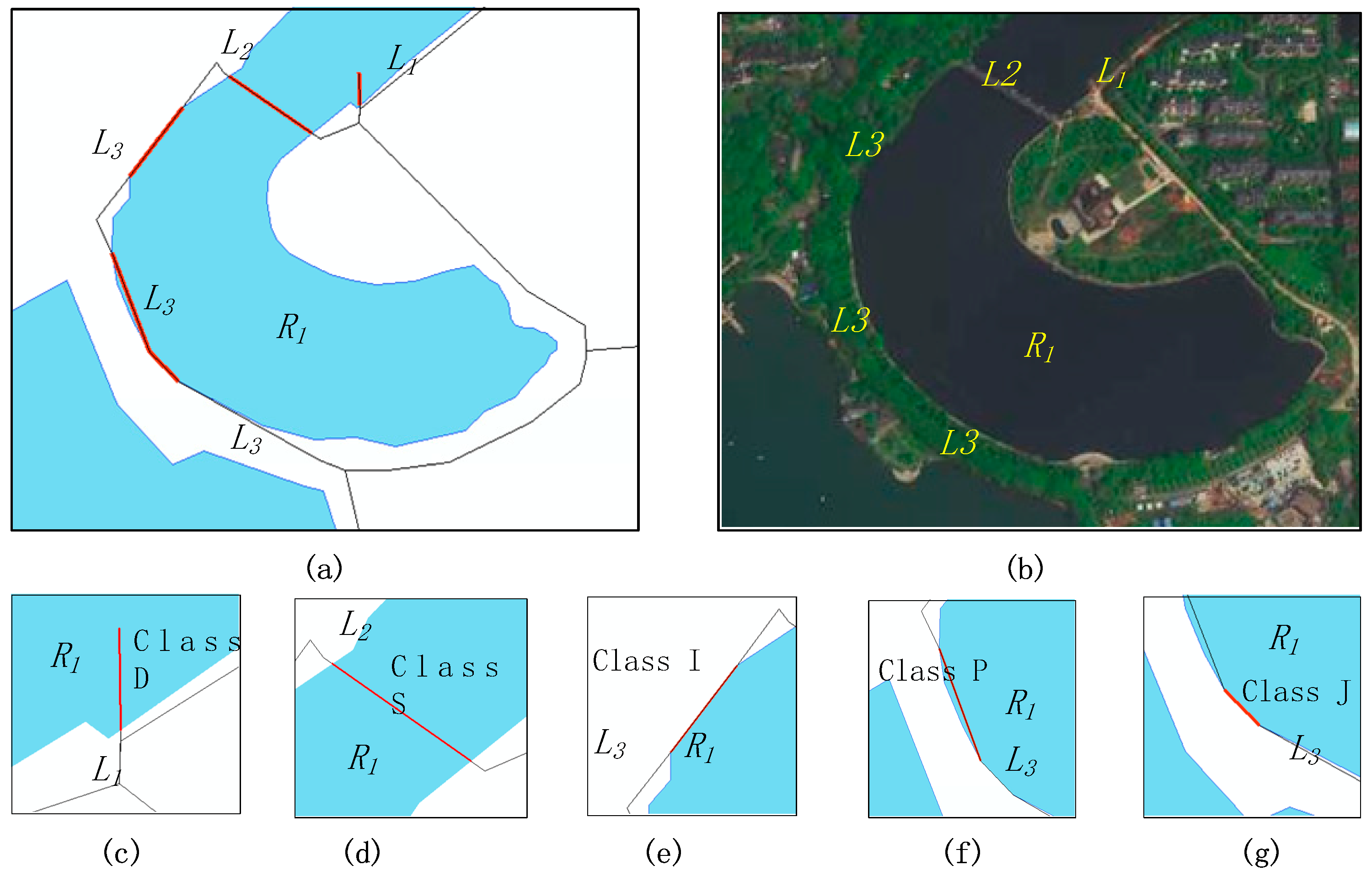
5.1. Examples of Intersection Components between Lines and Regions
5.2. Examples of Intersection Components between Lines
6. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Egenhofer, M.; Franzosa, R. Point-set Topological Spatial Relations. Int. J. Geogr. Inf. Sci. 1991, 5, 161–174. [Google Scholar] [CrossRef] [Green Version]
- Egenhofer, M.; Herring, J. Categorizing Binary Topological Relationships between Regions, Lines, Points in Geographic Databases. In A Framework for the Definitions of Topological Relationships and An Algebraic Approach to Spatial Reasoning within This Framework; NCGIA Technical Reports; National Center for Geographic Information and Analysis: Santa Barbara, CA, USA, 1991; pp. 91–97. [Google Scholar]
- Egenhofer, M.; Sharma, J.; Mark, D. A Critical Comparison of the 4-Intersection and 9-Intersection Models for Spatial Relations: Formal Analysis. In Autocarto 11; McMaster, R., Armstrong, M., Eds.; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 1993. [Google Scholar]
- Clementini, E.; Felice, P.D. A Comparison of Methods for Representing Topological relationships. Inf. Sci. 1995, 3, 149–178. [Google Scholar] [CrossRef]
- Chen, J.; Li, C.M.; Li, Z.L.; Christopher, G. A Voronoi-based 9-intersection model for spatial relations. Int. J. Geogr. Inf. Sci. 2001, 15, 201–220. [Google Scholar] [CrossRef]
- Shen, J.; Zhou, T.; Chen, M. A 27-Intersection Model for Representing Detailed Topological Relations between Spatial Objects in Two-Dimensional Space. ISPRS Int. Geo-Inf. 2017, 6, 37. [Google Scholar] [CrossRef] [Green Version]
- Egenhofer, M.; Mark, D.M. Modeling Conceptual Neighborhoods of Topological Line-Region Relations. Int. J. Geogr. Inf. Sci. 1995, 9, 555–565. [Google Scholar] [CrossRef]
- Kurara, Y.; Egenhofer, M. The 9+ intersection for topological relationships between a directed line segment and a region. In Workshop on Behavior and Monitoring Interpretation; Gottfried, B., Ed.; CEUR-WS.org: Munich, Germany, 2007; pp. 62–76. [Google Scholar]
- Formica, A.; Mazzei, M.; Pourabbas, E.; Rafanelli, M. Enriching the semantics of the directed polyline–polygon topological relationships: The DLP-intersection matrix. J. Geogr. Syst. 2017, 192, 13–19. [Google Scholar] [CrossRef]
- Shen, J.; Huang, Y.; Chen, M. Topological relations between a directed line and a directed region. Trans. GIS 2020, 24, 526–548. [Google Scholar] [CrossRef]
- Deng, M.; Cheng, T.; Chen, X.; Li, Z. Multi-level Topological Relations between Spatial Regions Based Upon Topological Invariants. Geoinformatica 2007, 11, 239–267. [Google Scholar] [CrossRef]
- Randell, D.; Cui, Z.; Cohn, A. A spatial logical based on regions and connection. In Proceedings of the 3rd International Conference on Knowledge Representation and Reasoning, Cambridge, MA, USA, 25–29 October 1992; Kaufmann, M., San, M., Eds.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1992; pp. 165–176. [Google Scholar]
- Cui, Z.; Cohn, A.; Randell, D. Qualitative and Topological Relationships in Spatial Databases. In Proceedings of the Third International Symposium on Advances in Spatial Databases, Singapore, 23–25 June 1993; Abel, D., Ooi, B.C., Eds.; Springer: Singapore, 1993; pp. 293–315. [Google Scholar]
- Li, Z.L.; Zhao, R.; Chen, J. A Voronoi-based spatial algebra for spatial relations. Prog. Nat. Sci. 2002, 12, 50–58. [Google Scholar]
- Zhou, X.G.; Chen, J.; Zhan, F.B.; Li, Z.; Madden, M.; Zhao, R.L.; Liu, W.Z. A Euler-number-based Topological Computation Model for Land Parcel Database Updating. Int. J. Geogr. Inf. Sci. 2013, 27, 1983–2005. [Google Scholar] [CrossRef]
- Deng, M. A Hierarchical Representation of Line-Region Topological Relations. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2008, XXXVII, 25–30. [Google Scholar]
- Clementini, E.; Di, F.P. Topological invariants for lines. IEEE Trans. Knowl. Data. Eng. 1998, 10, 38–54. [Google Scholar] [CrossRef]
- Wu, C. Detailed model of topological and metric relationships between a line and region. Arab. J. Geosci. 2019, 12, 130. [Google Scholar] [CrossRef]
- Li, Z.L.; Deng, M. A hierarchical approach to the line-line topological relations. In Progress in Spatial Data Handling; Springer: Heidelberg, Germany, 2006; pp. 365–382. [Google Scholar]
- Egenhofer, M.; Franzosa, R. On the Equivalence of Topological Relations. Int. J. Geogr. Inf. Sci. 1995, 9, 133–152. [Google Scholar] [CrossRef]
- Li, Z.L.; Li, Y.L.; Chen, Y.Q. Basic Topological Models for Spatial Entities in 3-dimensional Space. GeoInformatica 2000, 4, 419–433. [Google Scholar] [CrossRef]
- Liu, K.; Shi, W. Extended model of topological relationships between spatial objects in geographic information systems. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 264–275. [Google Scholar] [CrossRef]
- ISO. 19107. In Geographic Information–Spatial Schema; Technical Report; ISO: Geneva, Switzerland, 2003.
- Lee, J.M. Introduction to Topological Manifolds; Springer: New York, NY, USA, 2011. [Google Scholar]
- Tu, L.W. An Introduction to Manifolds, 2nd ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Muscat, J.; Buhagiar, D. Connective Spaces. Mem. Fac. Sci. Eng. Shimane Univ. 2006, 39, 1–13. [Google Scholar]
- Clementini, E.; Felice, P.D. A model for representing topological relationships between complex geometric features in spatial databases. Inf. Sci. 1996, 90, 121–136. [Google Scholar] [CrossRef]
- Schneider, M.; Behr, T. Topological relationships between complex spatial objects. ACM Trans. Database Sys. 2006, 31, 39–81. [Google Scholar] [CrossRef]
- Armstrong, M.A. Basic Topology; McGraw-Hill Book Company: London, UK, 1979. [Google Scholar]
- Euler, L. Solutio problematis ad geometriam situs pertinentis. Comment. Acad. Sci. Petropolitanae 1741, 8, 128–140. [Google Scholar]
- Frank, H. Graph Theory; Addison-Wesley: Reading, MA, USA, 1969. [Google Scholar]
- Bondy, J.A.; Murty, U.S.R. Graph Theory; Springer: Berlin, Germany, 2008; Volume 311, pp. 359–372. [Google Scholar]
- Zhao, Y.J.; Zhou, X.G.; Li, G.Q.; Xing, H.F. A Spatio-Temporal VGI Model Considering Trust-Related Information. ISPRS Int. Geo-Inf. 2016, 5, 10. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.G.; Zeng, L.; Jiang, Y.; Zhou, K.; Zhao, Y. Dynamic Integrating OSM data to Borderland Database. ISPRS Int. Geo-Inf. 2015, 4, 1707–1728. [Google Scholar] [CrossRef] [Green Version]
- Girindran, R.; Boyd, D.; Rosser, J.; Vijayan, D.; Long, G.; Robinson, D. On the Reliable Generation of 3D City Models from Open Data. Urban Sci. 2020, 4, 47. [Google Scholar] [CrossRef]
- Giovanella, A.; Bradley, P.E.; Wursthorn, S. Evaluation of Topological Consistency in CityGML. ISPRS Int. J. Geo-Inf. 2019, 8, 278. [Google Scholar] [CrossRef] [Green Version]






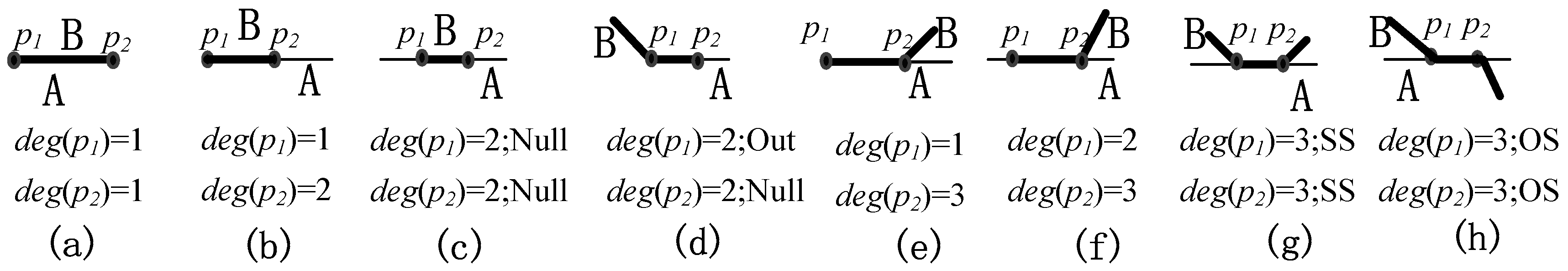






| Class | Type | Number | Class | Type | Number |
|---|---|---|---|---|---|
| A | <1, 1> (Figure 9a) | 5 | M | <3Null, 3On> (Figure 9m) | 1 |
| B | <1, 3Null> (Figure 9b) | 3 | N | <3On, 3On> (Figure 9n) | 1 |
| C | <1, 3On> (Figure 9c) | 15 | O | <3Null, 3Out> (Figure 9o) | 7 |
| D | <1, 4Out> (Figure 9d) | 17 | P | <3On, 3Out> (Figure 9p) | 2 |
| E | <1, 4In> (Figure 9e) | 9 | Q | <3Null, 4In> (Figure 9q) | 1 |
| F | <2, 3Out> (Figure 9f) | 2 | R | <3On, 4In> (Figure 9r) | 1 |
| G | <2, 3In> (Figure 9g) | 8 | S | <4Out, 4Out> (Figure 9s) | 121 |
| H | <2, 2> (Figure 9h) | 1 | T | <4In, 4Out> (Figure 9t) | 7 |
| I | <3Out, 3Out> (Figure 9i) | 3 | U | <4In, 4In> (Figure 9u) | 1 |
| J | <3In, 3Out> (Figure 9j) | 1 | V | <3> (Figure 12a) | 7 |
| K | <3In, 3In> (Figure 9k) | 1 | W | <4> (Figure 12b) | 4 |
| L | <3Null, 3Null> (Figure 9l) | 3 |
| Class | Corresponding Type | Number |
|---|---|---|
| a | <1, 1> (Figure 10a) | 2 |
| b | <1, 2> (Figure 10b) | 1 |
| c | <2Null, 2Null> (Figure 10c) | 4 |
| d | <2Out, 2Null> (Figure 10d) | 1 |
| e | <1, 3> (Figure 10e) | 1 |
| f | <2, 3> (Figure 10f) | 6 |
| g | <3SS, 3SS> (Figure 10g) | 4 |
| h | <3OS, 3OS> (Figure 10h) | 3 |
| i | <2> (Figure 12c) | 3793 |
| j | <3> (Figure 12d) | 4162 |
| k | <4SS> (Figure 12e) | 25 |
| l | <4OS> (Figure 12f) | 1714 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; He, H.; Hou, D.; Li, R.; Zheng, H. A Refined Lines/Regions and Lines/Lines Topological Relations Model Based on Whole-Whole Objects Intersection Components. ISPRS Int. J. Geo-Inf. 2021, 10, 15. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi10010015
Zhou X, He H, Hou D, Li R, Zheng H. A Refined Lines/Regions and Lines/Lines Topological Relations Model Based on Whole-Whole Objects Intersection Components. ISPRS International Journal of Geo-Information. 2021; 10(1):15. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi10010015
Chicago/Turabian StyleZhou, Xiaoguang, Hongyuan He, Dongyang Hou, Rui Li, and Heng Zheng. 2021. "A Refined Lines/Regions and Lines/Lines Topological Relations Model Based on Whole-Whole Objects Intersection Components" ISPRS International Journal of Geo-Information 10, no. 1: 15. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi10010015




