Pairwise Coarse Registration of Indoor Point Clouds Using 2D Line Features
Abstract
:1. Introduction
2. Materials and Methods
2.1. Indoor Point Cloud Datasets
2.2. Registration Method
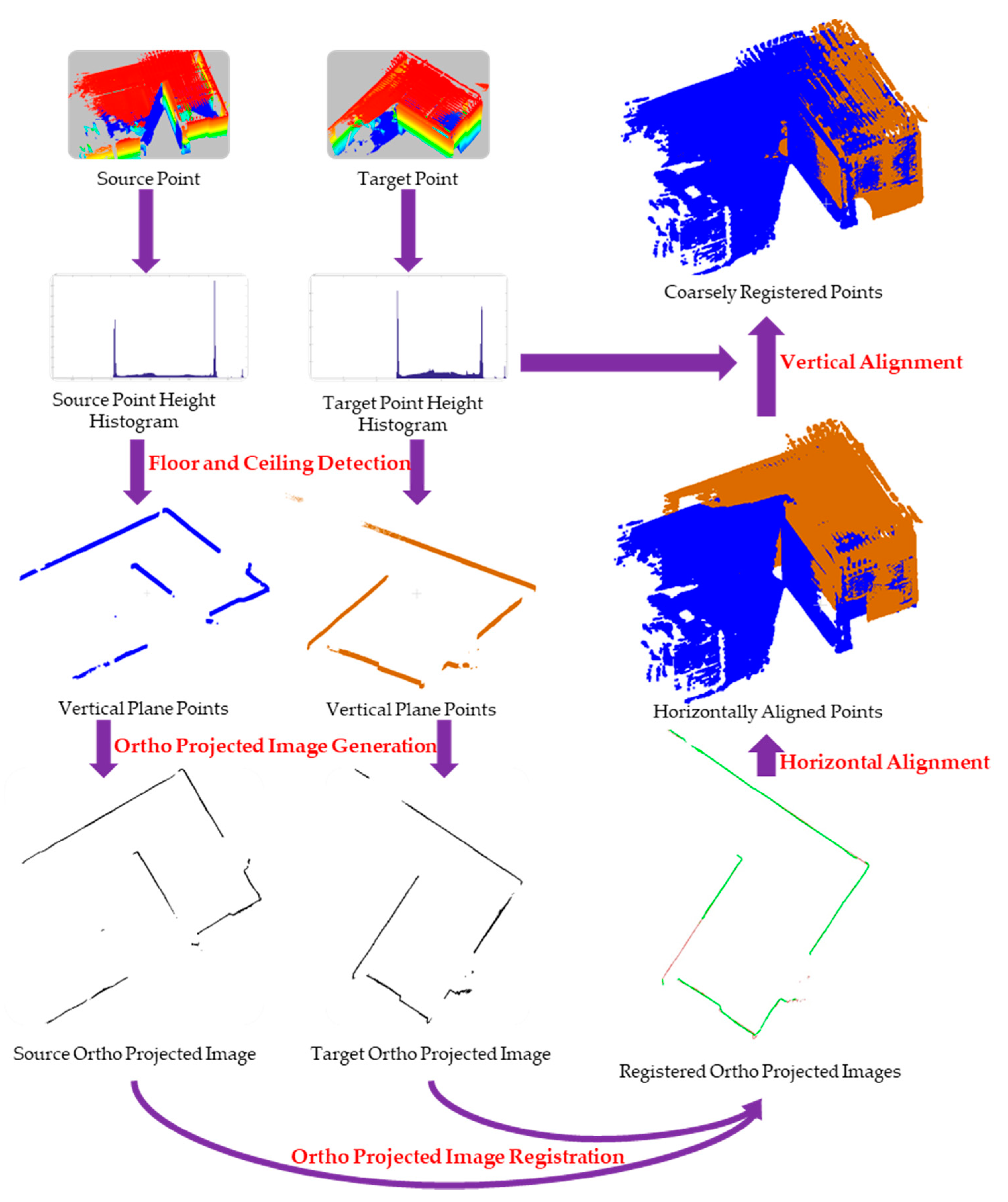
2.2.1. Registration Framework
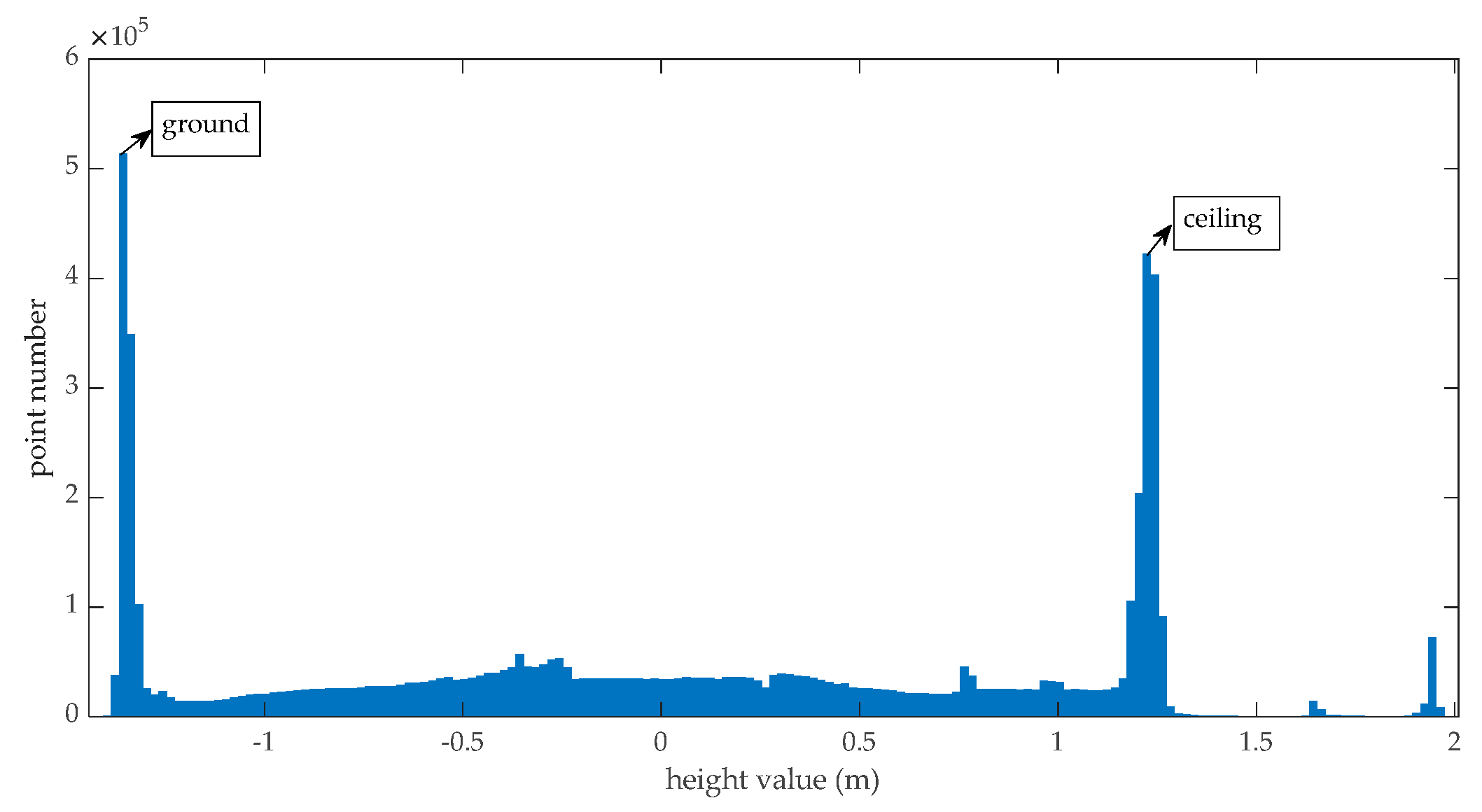
2.2.2. Ortho-Projected Image Generation
2.2.3. Ortho-Projected Images Registration
2.2.4. Point Cloud Registration
3. Results
3.1. Evaluation Metric Descriptions
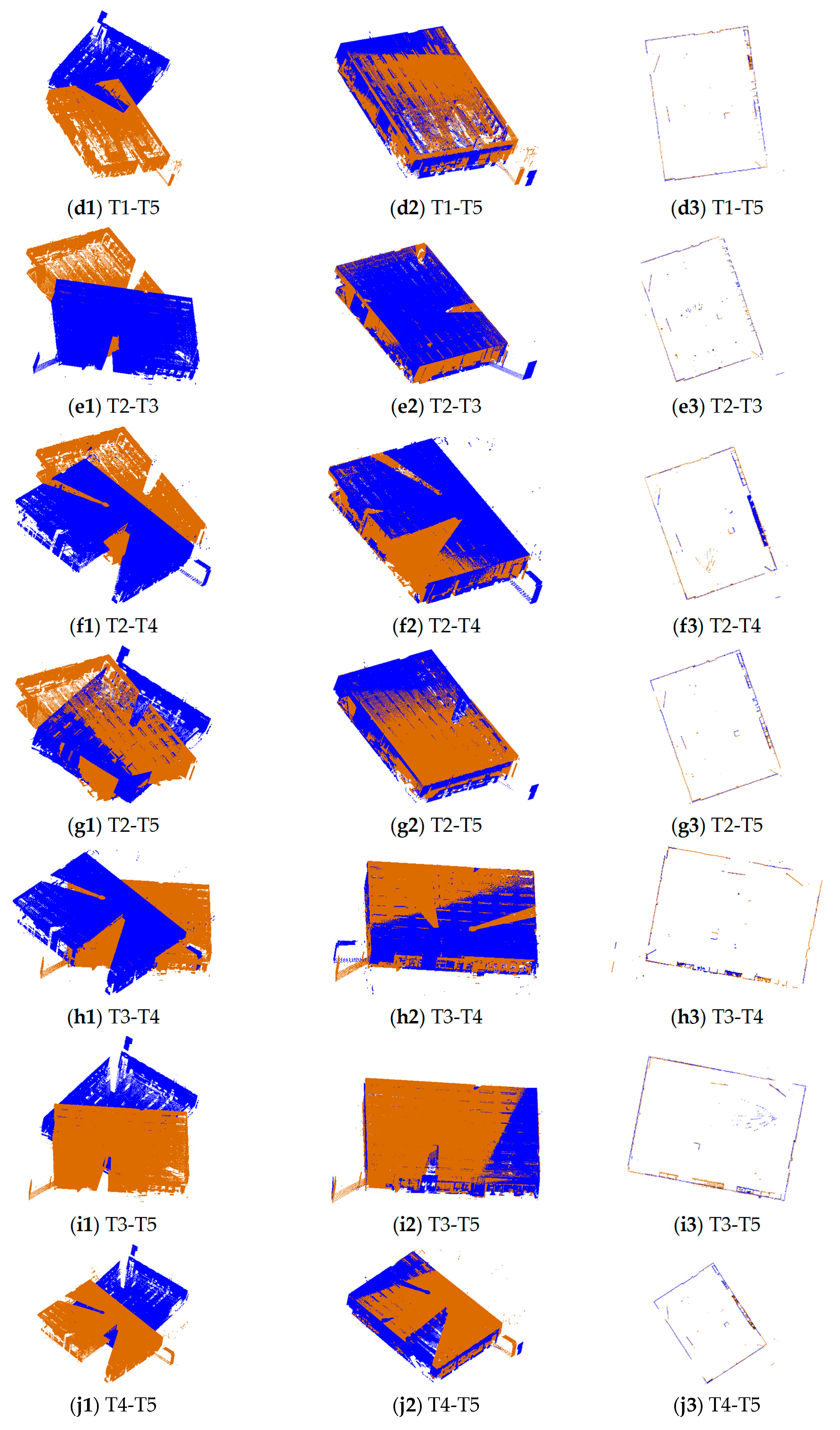
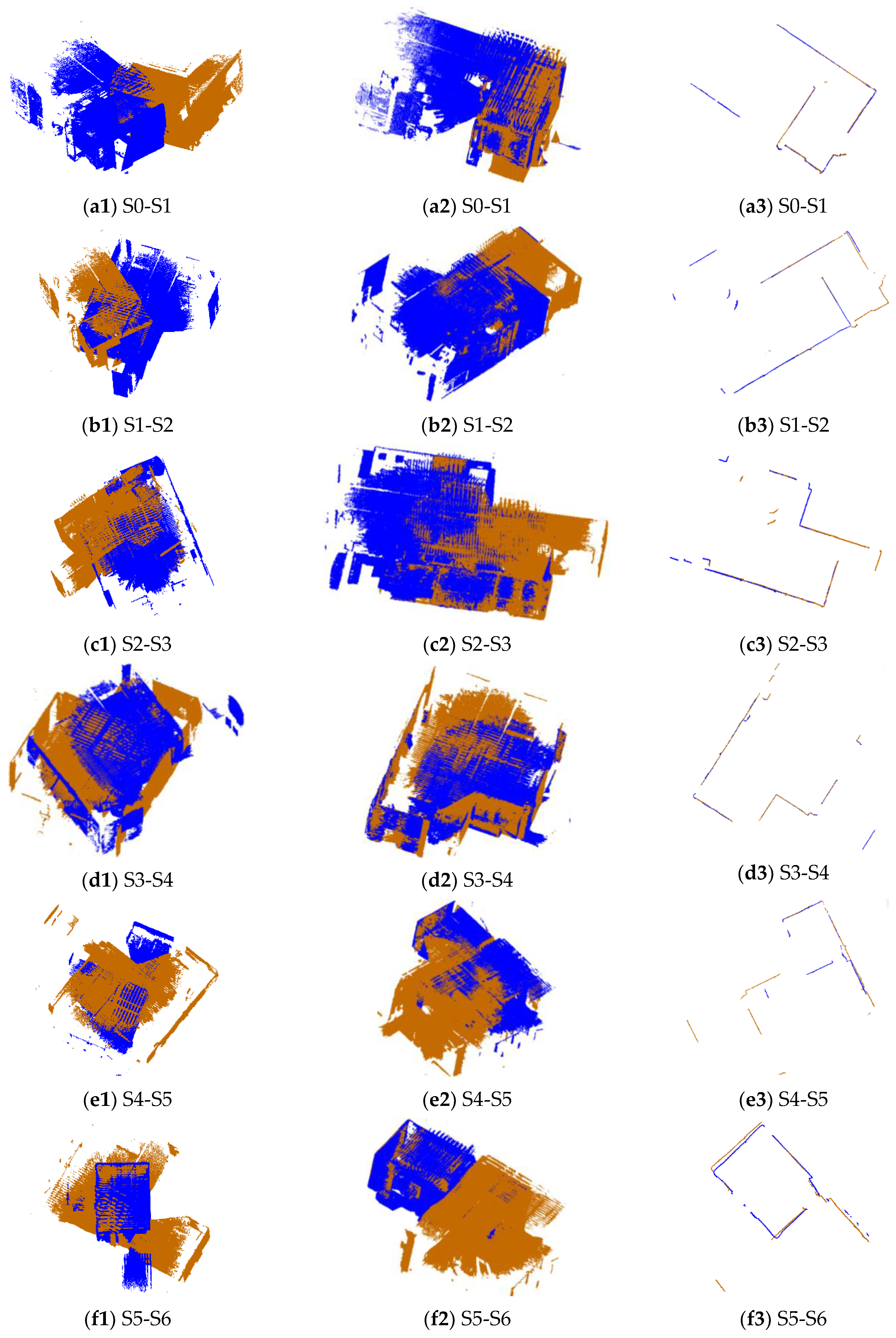
3.2. Qualitative Evaluations
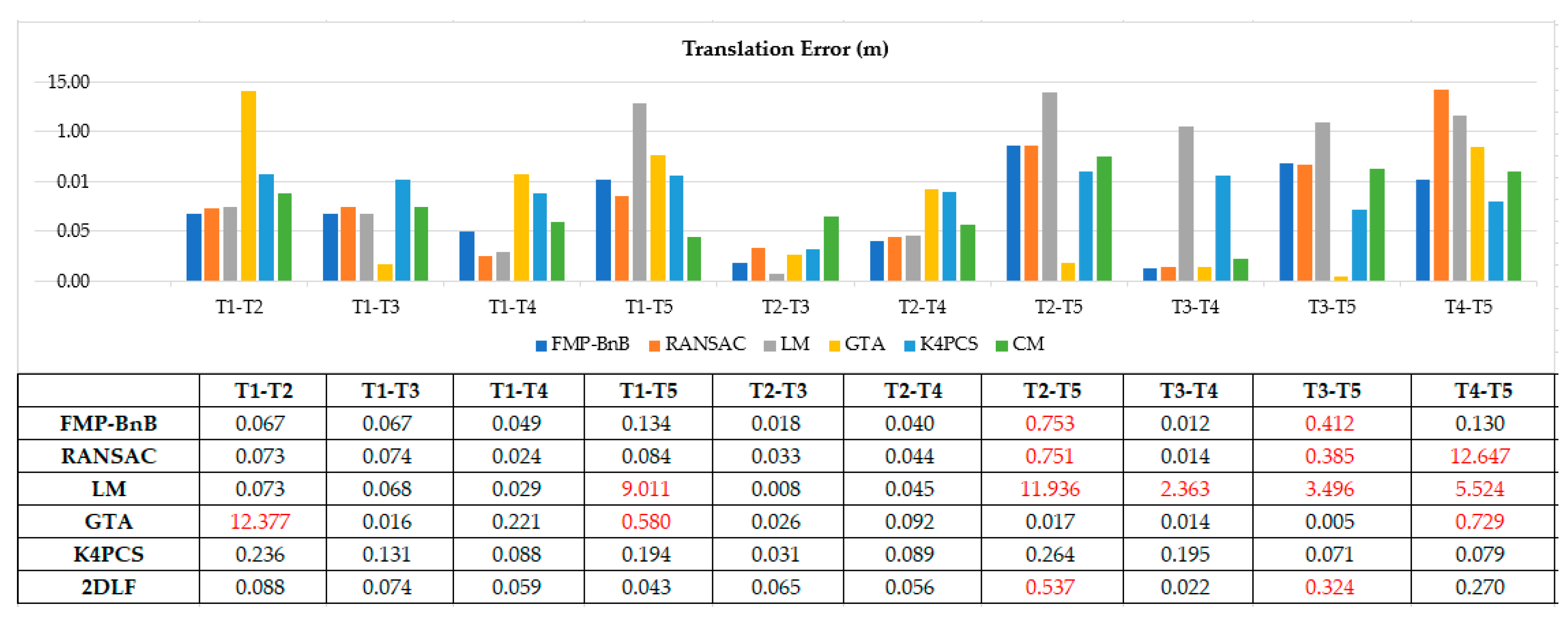
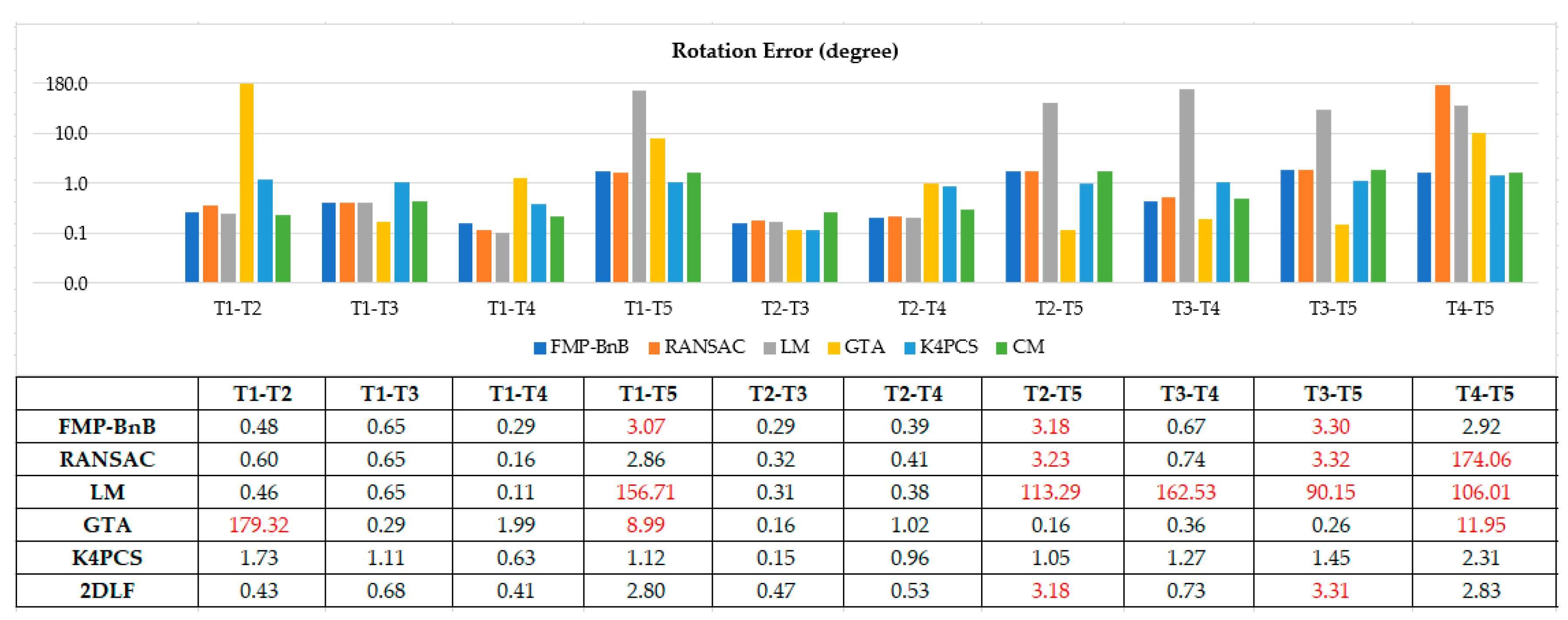
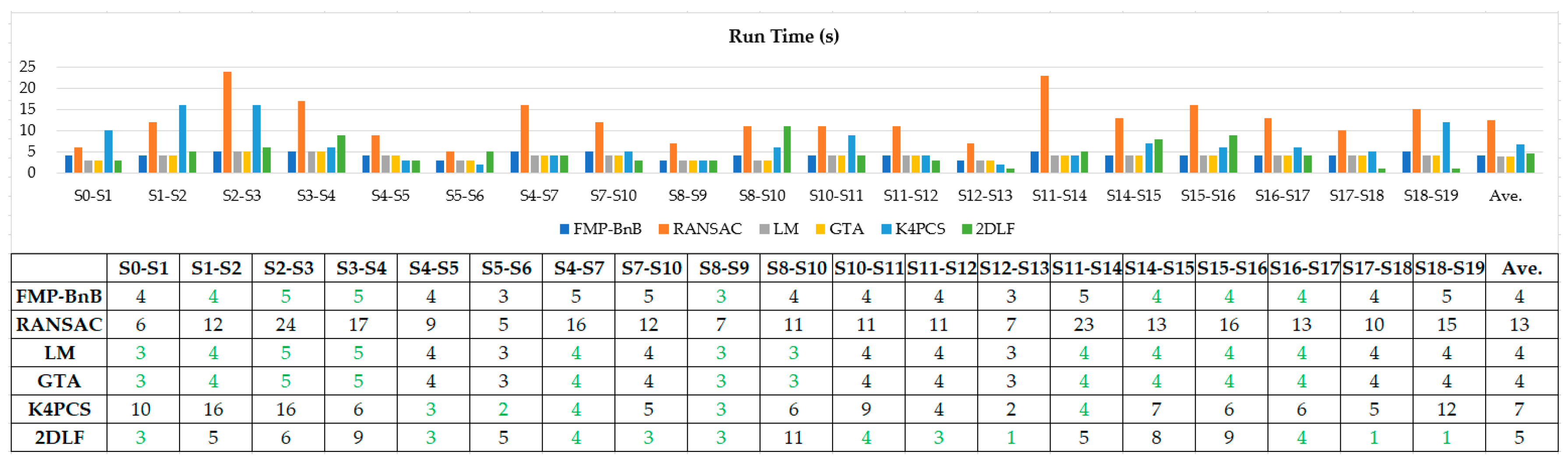
3.3. Quantitative Evaluations
4. Discussion
4.1. Accuracy and Time Efficiency
4.2. Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Iman Zolanvari, S.M.; Laefer, D.F. Slicing Method for curved façade and window extraction from point clouds. ISPRS J. Photogramm. 2016, 119, 334–346. [Google Scholar] [CrossRef]
- Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F.; et al. Terrestrial laser scanning in forest inventories. ISPRS J. Photogramm. 2016. [Google Scholar] [CrossRef]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei canyon (N-Z). ISPRS J. Photogramm. 2013, 82, 10–26. [Google Scholar] [CrossRef] [Green Version]
- Mahmood, B.; Han, S. 3D Registration of Indoor Point Clouds for Augmented Reality; American Society of Civil Engineer: Reston, VA, USA, 2019; pp. 1–8. [Google Scholar]
- Mahmood, B.; Han, S.; Lee, D. BIM-Based Registration and Localization of 3D Point Clouds of Indoor Scenes Using Geometric Features for Augmented Reality. Remote Sens. 2020, 12, 2302. [Google Scholar] [CrossRef]
- Bueno, M.; González-Jorge, H.; Martínez-Sánchez, J.; Lorenzo, H. Automatic point cloud coarse registration using geometric keypoint descriptors for indoor scenes. Automat. Constr. 2017, 81, 134–148. [Google Scholar] [CrossRef]
- Li, F.; Zlatanova, S.; Koopman, M.; Bai, X.; Diakité, A. Universal path planning for an indoor drone. Automat. Constr. 2018, 95, 275–283. [Google Scholar] [CrossRef]
- Ochmann, S.; Vock, R.; Wessel, R.; Klein, R. Automatic reconstruction of parametric building models from indoor point clouds. Comput. Graph. 2016, 54, 94–103. [Google Scholar] [CrossRef] [Green Version]
- Shi, W.; Ahmed, W.; Li, N.; Fan, W.; Xiang, H.; Wang, M. Semantic Geometric Modelling of Unstructured Indoor Point Cloud. ISPRS Int. J. Geo-Inf. 2019, 8, 9. [Google Scholar] [CrossRef] [Green Version]
- Navvis. Unleash the Power of Digital Buildings. Available online: https://www.navvis.com/ (accessed on 17 September 2020).
- Introducing the Intel RealSense LiDAR Camera L515. Available online: https://www.intel.com/content/www/us/en/architecture-and-technology/realsense-overview.html (accessed on 17 September 2020).
- Kinect for Windows. Available online: https://developer.microsoft.com/en-us/windows/kinect/ (accessed on 17 September 2020).
- Besl, P.J.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Rusinkiewicz, S.; Levoy, M. Efficient variants of the ICP algorithm. In Proceedings of the Third International Conference on 3-D Digital Imaging and Modeling, Quebec City, QC, Canada, 28 May–1 June 2001; pp. 145–152. [Google Scholar]
- Han, J.; Yin, P.; He, Y.; Gu, F. Enhanced ICP for the Registration of Large-Scale 3D Environment Models: An Experimental Study. Sensors 2016, 16, 228. [Google Scholar] [CrossRef]
- Biber, P.; Stra Ss Er, W. The normal distributions transform: A new approach to laser scan matching. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No. 03CH37453), Las Vegas, NV, USA, 27–31 October 2003; pp. 2743–2748. [Google Scholar]
- Takeuchi, E.; Tsubouchi, T. A 3-D scan matching using improved 3-D normal distributions transform for mobile robotic mapping. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 3068–3073. [Google Scholar]
- Magnusson, M. The Three-Dimensional Normal-Distributions Transform: An Efficient Representation for Registration, Surface Analysis, and Loop Detection. Ph.D. Thesis, Örebro Universitet, Örebro, Sweden, 2009. [Google Scholar]
- Johnson, A.E.; Hebert, M. Using spin images for efficient object recognition in cluttered 3D scenes. IEEE Trans. Pattern Anal. 1999, 21, 433–449. [Google Scholar] [CrossRef] [Green Version]
- Makadia, A.; Patterson, A.; Daniilidis, K. Fully Automatic Registration of 3D Point Clouds. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; pp. 1297–1304. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Marton, Z.C.; Beetz, M. Aligning point cloud views using persistent feature histograms. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3384–3391. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast point feature histograms (FPFH) for 3D registration. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar]
- Dong, Z.; Yang, B.; Liu, Y.; Liang, F.; Li, B.; Zang, Y. A novel binary shape context for 3D local surface description. ISPRS J. Photogramm. 2017, 130, 431–452. [Google Scholar] [CrossRef]
- Yang, B.; Zang, Y. Automated registration of dense terrestrial laser-scanning point clouds using curves. ISPRS J. Photogramm. 2014, 95, 109–121. [Google Scholar] [CrossRef]
- Dold, C.; Brenner, C. Registration of terrestrial laser scanning data using planar patches and image data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2006, 36, 78–83. [Google Scholar]
- Kelbe, D.; van Aardt, J.; Romanczyk, P.; van Leeuwen, M.; Cawse-Nicholson, K. Marker-Free Registration of Forest Terrestrial Laser Scanner Data Pairs With Embedded Confidence Metrics. IEEE Trans. Geosci. Remote 2016, 54, 4314–4330. [Google Scholar] [CrossRef]
- Zeng, A.; Song, S.; Nießner, M.; Fisher, M.; Xiao, J.; Funkhouser, T. 3dmatch: Learning local geometric descriptors from rgb-d reconstructions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Hulunono, HI, USA, 21–26 July 2017; pp. 1802–1811. [Google Scholar]
- Zhang, Z.; Sun, L.; Zhong, R.; Chen, D.; Xu, Z.; Wang, C.; Qin, C.; Sun, H.; Li, R. 3-D Deep Feature Construction for Mobile Laser Scanning Point Cloud Registration. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1904–1908. [Google Scholar] [CrossRef]
- Pujol-Miro, A.; Casas, J.R.; Ruiz-Hidalgo, J. Correspondence matching in unorganized 3D point clouds using Convolutional Neural Networks. Image Vision Comput. 2019, 83, 51–60. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. arXiv 2017, arXiv:1612.00593v2. [Google Scholar]
- Deng, H.; Birdal, T.; Ilic, S. PPFNet: Global Context Aware Local Features for Robust 3D Point Matching. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 195–205. [Google Scholar]
- Aoki, Y.; Goforth, H.; Srivatsan, R.A.; Lucey, S. PointNetLK: Robust & Efficient Point Cloud Registration using PointNet. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 7163–7172. [Google Scholar]
- Mellado, N.; Aiger, D.; Mitra, N.J. SUPER 4PCS Fast Global Pointcloud Registration via Smart Indexing. Comput. Graph. Forum 2014, 33, 205–215. [Google Scholar] [CrossRef] [Green Version]
- Theiler, P.W.; Wegner, J.D.; Schindler, K. Keypoint-based 4-Points Congruent Sets—Automated marker-less registration of laser scans. ISPRS J. Photogramm. 2014, 96, 149–163. [Google Scholar] [CrossRef]
- Ge, X. Automatic markerless registration of point clouds with semantic-keypoint-based 4-points congruent sets. ISPRS J. Photogramm. 2017, 130, 344–357. [Google Scholar] [CrossRef] [Green Version]
- Järemo Lawin, F.; Danelljan, M.; Shahbaz Khan, F.; Forssén, P.; Felsberg, M. Density adaptive point set registration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 3829–3837. [Google Scholar]
- Tsin, Y.; Kanade, T. A Correlation-Based Approach to Robust Point Set Registration; Springer: Berlin/Heidelberg, Germany, 2004; pp. 558–569. [Google Scholar]
- Jian, B.; Vemuri, B.C. Robust point set registration using gaussian mixture models. IEEE Trans. Pattern Anal. 2010, 33, 1633–1645. [Google Scholar] [CrossRef] [PubMed]
- Myronenko, A.; Song, X. Point set registration: Coherent point drift. IEEE Trans. Pattern Anal. 2010, 32, 2262–2275. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsai, C.; Huang, C.; Chi-Yi, T.; Chih-Hung, H. Indoor Scene Point Cloud Registration Algorithm Based on RGB-D Camera Calibration. Sensors 2017, 17, 1874. [Google Scholar] [CrossRef] [Green Version]
- Sanchez, J.; Denis, F.; Checchin, P.; Dupont, F.; Trassoudaine, L. Global Registration of 3D LiDAR Point Clouds Based on Scene Features: Application to Structured Environments. Remote Sens. 2017, 9, 1014. [Google Scholar] [CrossRef] [Green Version]
- Pavan, N.L.; Dos Santos, D.R.; Khoshelham, K. Global Registration of Terrestrial Laser Scanner Point Clouds Using Plane-to-Plane Correspondences. Remote Sens. 2020, 12, 1127. [Google Scholar] [CrossRef] [Green Version]
- Cai, Z.; Chin, T.; Bustos, A.P.; Schindler, K. Practical optimal registration of terrestrial LiDAR scan pairs. ISPRS J. Photogramm. 2019, 147, 118–131. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Zhang, X.; Xu, Y.; Chen, X. Efficient Coarse Registration of Pairwise TLS Point Clouds Using Ortho Projected Feature Images. ISPRS Int. J. Geo-Inf. 2020, 9, 255. [Google Scholar] [CrossRef]
- Ge, X.; Hu, H. Object-based incremental registration of terrestrial point clouds in an urban environment. ISPRS J. Photogramm. 2020, 161, 218–232. [Google Scholar] [CrossRef]
- Zhang, T.Y.; Suen, C.Y. A fast parallel algorithm for thinning digital patterns. Commun. ACM 1984, 27, 236–239. [Google Scholar] [CrossRef]
- Matasyx, J.; Kittlery, C.G.J. Progressive probabilistic Hough transform. In Proceedings of the British Machine Vision Conference, Southampton, UK, 14–17 September 1998; pp. 26.1–26.10. [Google Scholar]
- Dong, Z.; Liang, F.; Yang, B.; Xu, Y.; Zang, Y.; Li, J.; Wang, Y.; Dai, W.; Fan, H.; Hyyppä, J.; et al. Registration of large-scale terrestrial laser scanner point clouds: A review and benchmark. ISPRS J. Photogramm. 2020, 163, 327–342. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Zhou, Q.; Park, J.; Koltun, V. Fast Global Registration; Springer: Berlin/Heidelberg, Germany, 2016; pp. 766–782. [Google Scholar]
- Albarelli, A.; Rodolà, E.; Torsello, A. A game-theoretic approach to fine surface registration without initial motion estimation. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 430–437. [Google Scholar]
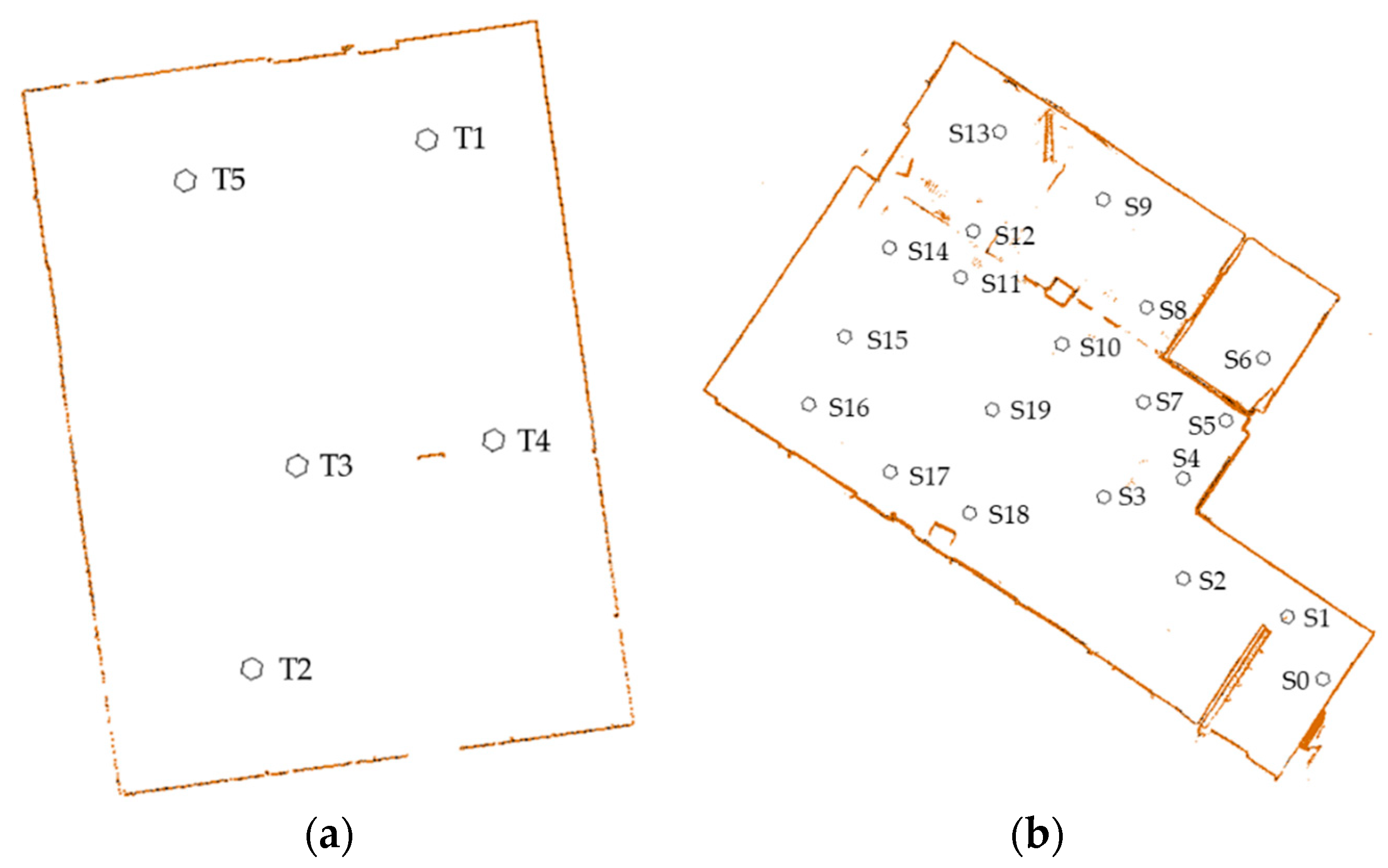










| Dataset | Description | Abbr. | #Scans | #Points | Used Pairs | Dimensions (m) | |
|---|---|---|---|---|---|---|---|
| 1 | Simple Big Office Room | SR | 5 | T1 | 10720371 | T1-T2 T1-T3 | 16 × 11 × 3 |
| T2 | 10707764 | T1-T4 T1-T5 | |||||
| T3 | 10729371 | T2-T3 T2-T4 | |||||
| T4 | 10694987 | T2-T5 T3-T4 | |||||
| T5 | 10753198 | T3-T5 T4-T5 | |||||
| 2 | Complex Office Space with Multiple Rooms | CB | 20 | S0 | 6071466 | S0-S1 S1-S2 S2-S3 S3-S4 S4-S5 S5-S6 S4-S7 S7-S10 S8-S9 S8-S10 S10-S11 S11-S12 S12-S13 S11-S14 S14-S15 S15-S16 S16-S17 S17-S18 S18-S19 | 18 × 11 × 2.7 |
| S1 | 6054560 | ||||||
| S2 | 5877122 | ||||||
| S3 | 5593724 | ||||||
| S4 | 5847040 | ||||||
| S5 | 5964762 | ||||||
| S6 | 6028178 | ||||||
| S7 | 5475755 | ||||||
| S8 | 5103696 | ||||||
| S9 | 5302832 | ||||||
| S10 | 5038474 | ||||||
| S11 | 4990545 | ||||||
| S12 | 4812543 | ||||||
| S13 | 5631427 | ||||||
| S14 | 5182758 | ||||||
| S15 | 5542010 | ||||||
| S16 | 5746671 | ||||||
| S17 | 5851471 | ||||||
| S18 | 5665512 | ||||||
| S19 | 5482208 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Zhang, X.; Tan, J.; Liu, H. Pairwise Coarse Registration of Indoor Point Clouds Using 2D Line Features. ISPRS Int. J. Geo-Inf. 2021, 10, 26. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi10010026
Li Z, Zhang X, Tan J, Liu H. Pairwise Coarse Registration of Indoor Point Clouds Using 2D Line Features. ISPRS International Journal of Geo-Information. 2021; 10(1):26. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi10010026
Chicago/Turabian StyleLi, Zhen, Xiaoming Zhang, Junxiang Tan, and Hua Liu. 2021. "Pairwise Coarse Registration of Indoor Point Clouds Using 2D Line Features" ISPRS International Journal of Geo-Information 10, no. 1: 26. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi10010026





