Study on Fractal Characteristics of Migration-Population Flow—Evidence from Egypt
Abstract
:1. Introduction
1.1. Background
1.2. Literature Review
1.3. Aim and Question
2. Study Area
2.1. Egypt Is A Typical Desert Country
2.2. Research on Population Dynamics and Migration in Egypt Attracts Attention
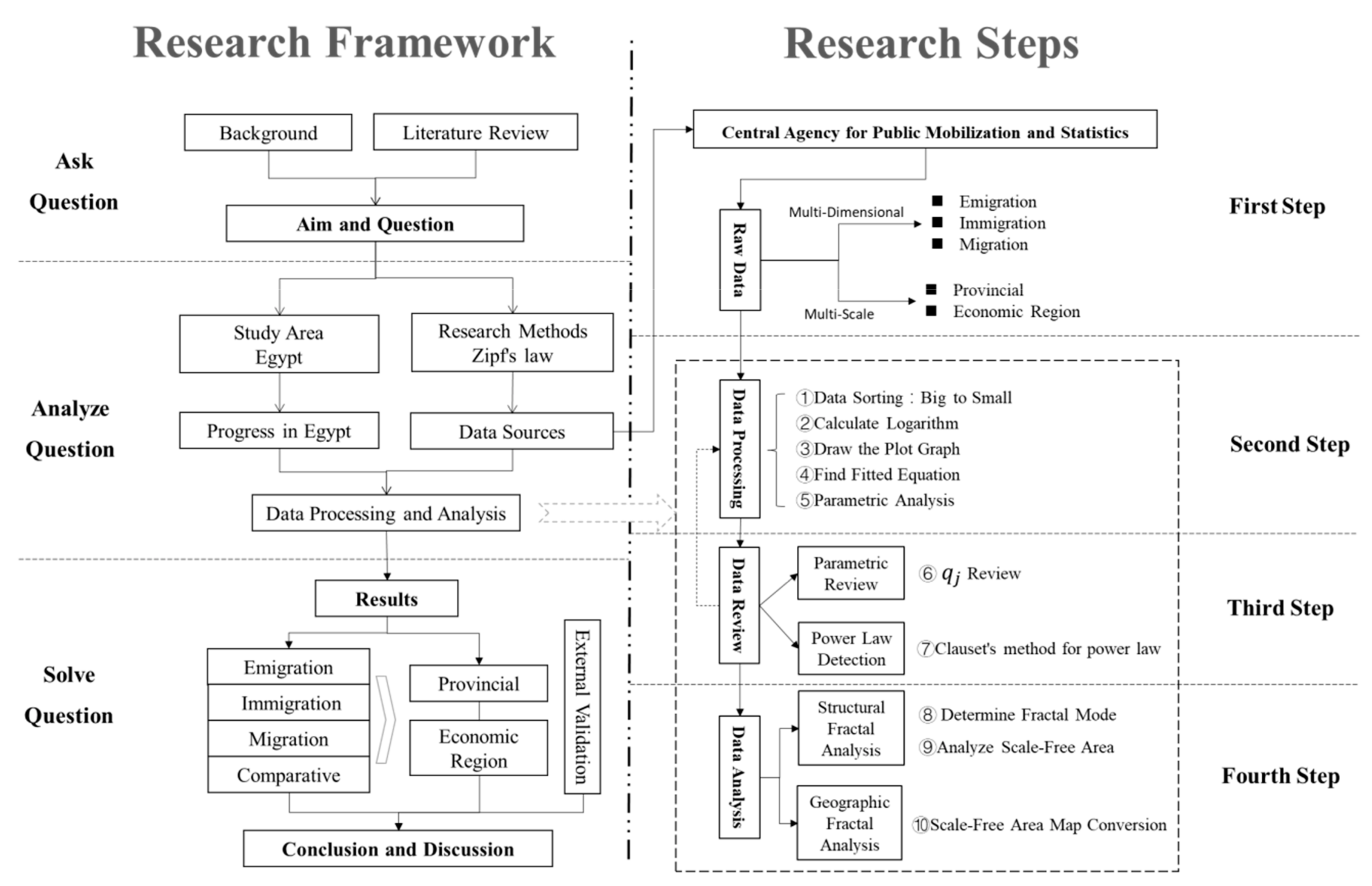
3. Research Methods and Data Sources
3.1. Research Methods
3.2. Research Steps
3.3. Data Sources and Processing
4. Results
4.1. Emigration: Previous Residence
4.1.1. Provincial Spatial Scale
4.1.2. Economic Region Spatial Scale
4.2. Immigration: Current Residence
4.2.1. Provincial Spatial Scale
4.2.2. Economic Region Spatial Scale
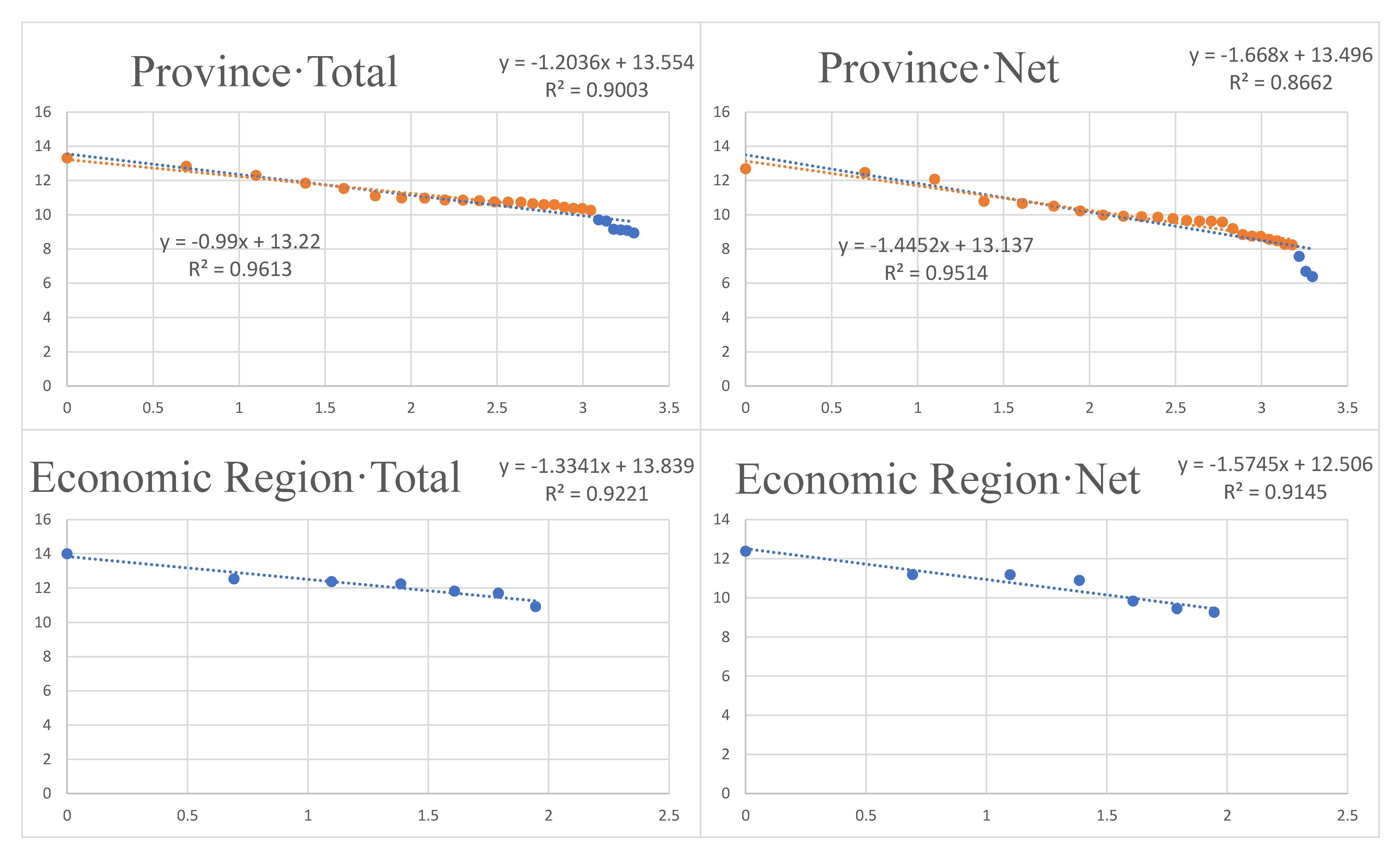
4.3. Migration: Total and Net Quantity
4.3.1. Provincial Spatial Scale
4.3.2. Economic Region Spatial Scale
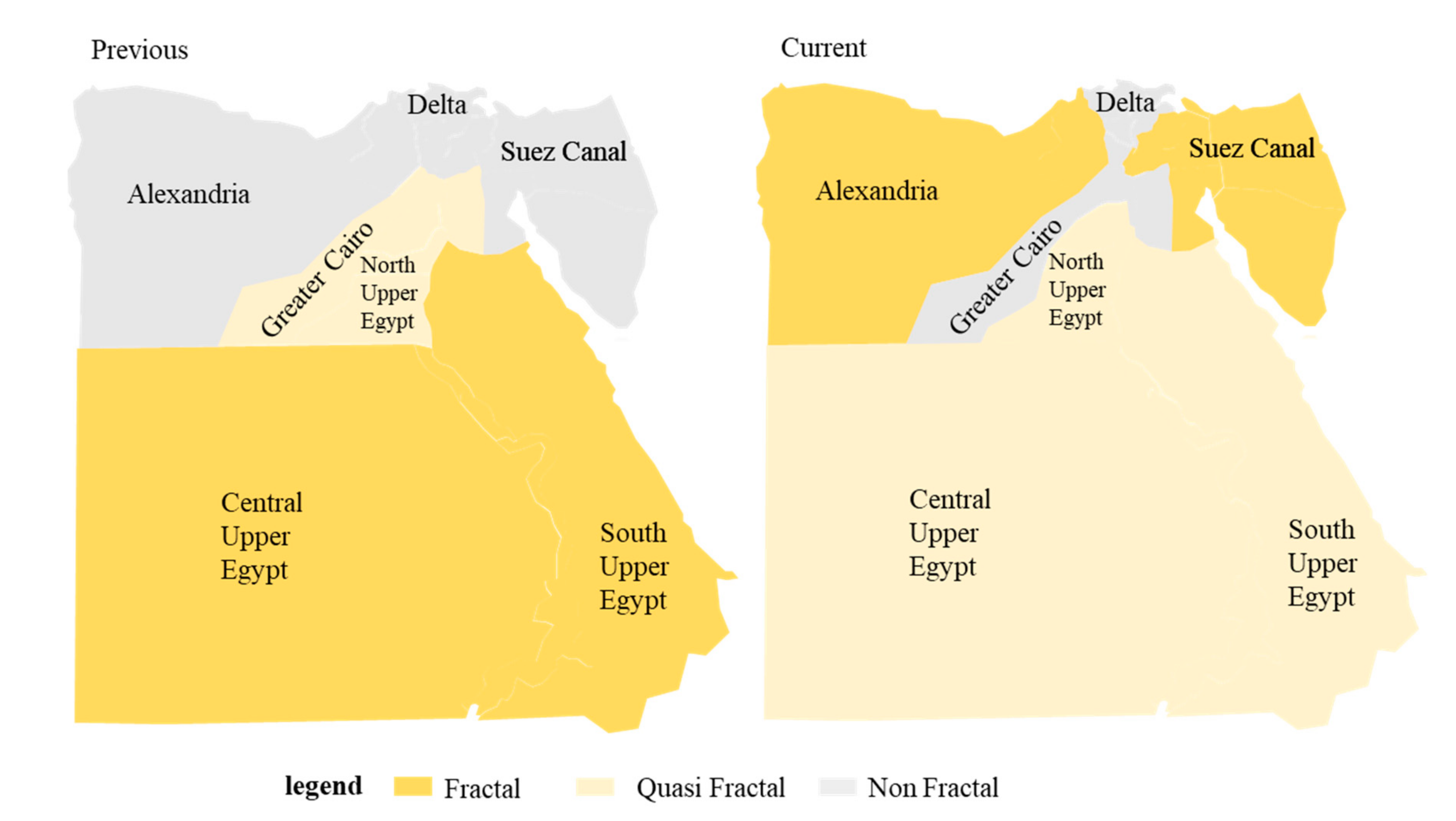
4.4. Comparative Analysis between Previous and Current Residence
4.4.1. Provincial Spatial Scale
4.4.2. Economic Region Spatial Scale
5. Discussion
5.1. Geographical Data of Migration Population Has Fractal Characteristics
5.2. Distance Is the Key Factor in Determining Geographic Fractal
5.3. Use of a Power-Law to Fit a Distribution May Not Always Be Suitable
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Provinces | All | Non-Scale Range | |
|---|---|---|---|
| First | Second | ||
| Egypt | y = −1.3158x + 12.927, R2 = 0.9788 | ||
| Cairo | y = −1.4411x + 11.484, R2 = 0.652 | y = −0.4369x + 10.055, R2 = 0.989 | y = −5.0755x + 22.046, R2 = 0.9294 |
| Alexandria | y = −1.8607x + 11.041, R2 = 0.7249 | y = −0.9783x + 9.7353, R2 = 0.9905 | y = −8.286x + 30.072, R2 = 0.9124 |
| Port Said | y = −1.7256x + 8.6634, R2 = 0.8817 | y = −1.5669x + 8.6315, R2 = 0.9807 | |
| Suez | y = −1.4932x + 8.5701, R2 = 0.8395 | y = −1.572x + 9.0448, R2 = 0.9827 | |
| Damietta | y = −1.7249x + 8.5281, R2 = 0.9365 | y = −1.5464x + 8.2547, R2 = 0.9675 | |
| Dakahlia | y = −1.7376x + 9.8787, R2 = 0.8437 | y = −1.3859x + 9.4823, R2 = 0.964 | y = −5.2482x + 20.333, R2 = 0.9702 |
| Sharkia | y = −1.454x + 10.154, R2 = 0.7777 | y = −0.8025x + 9.2042, R2 = 0.966 | y = −4.605x + 19.418, R2 = 0.9247 |
| Kalyubia | y = −2.1107x + 12.04, R2 = 0.7522 | y = −1.8536x + 12.214, R2 = 0.9699 | |
| Kafr El Sheikh | y = −1.8636x + 9.3505, R2 = 0.848 | y = −4.0777x + 15.658, R2 = 0.9863 | |
| Gharbia | y = −1.7797x + 9.6651, R2 = 0.8303 | y = −0.8031x + 8.3753, R2 = 0.9358 | y = −3.2112x + 13.805, R2 = 0.9758 |
| Menoufia | y = −1.8017x + 9.7431, R2 = 0.8604 | y = −1.3458x + 9.0631, R2 = 0.9752 | |
| Behera | y = −1.8569x + 10.147, R2 = 0.6703 | y = −1.1892x + 9.1297, R2 = 0.9554 | |
| Ismailia | y = −1.9403x + 10.21, R2 = 0.8382 | y = −0.9512x + 8.9085, R2 = 0.9385 | y = −6.9579x + 25.186, R2 = 0.9201 |
| Giza | y = −1.9275x + 12.481, R2 = 0.7886 | y = −0.9773x + 10.839, R2 = 0.944 | y = −8.6463x + 32.607, R2 = 0.9188 |
| Beni−Suef | y = −1.5429x + 8.3172, R2 = 0.9267 | y = −1.4023x + 8.103, R2 = 0.9769 | |
| Fayoum | y = −1.9578x + 9.1911, R2 = 0.9249 | y = −2.3328x + 10.199, R2 = 0.9509 | |
| Menia | y = −1.4379x + 8.6447, R2 = 0.9582 | ||
| Asyout | y = −1.6464x + 8.9695, R2 = 0.9271 | y = −1.4669x + 8.695, R2 = 0.956 | |
| Suhag | y = −1.7235x + 9.2828, R2 = 0.8933 | y = −1.4769x + 8.8963, R2 = 0.9631 | |
| Qena | y = −1.642x + 8.4421, R2 = 0.8628 | y = −1.3694x + 8.0254, R2 = 0.928 | |
| Aswan | y = −1.7799x + 8.7121, R2 = 0.9027 | y = −1.7044x + 8.799, R2 = 0.9646 | |
| Luxor | y = −1.5664x + 7.7752, R2 = 0.9190 | y = −1.4451x + 7.714, R2 = 0.9506 | |
| Red Sea | y = −1.5001x + 9.7428, R2 = 0.6982 | y = −0.9256x + 8.8688, R2 = 0.9550 | |
| ElWadi ElGidid | y = −1.6801x + 8.608, R2 = 0.8876 | y = −2.0763x + 9.6857, R2 = 0.9618 | |
| Matrouh | y = −1.7127x + 8.6756, R2 = 0.7094 | y = −1.1891x + 8.0503, R2 = 0.9638 | |
| North Sinai | y = −2.5988x + 9.5084, R2 = 0.8193 | y = −1.7251x + 8.5873, R2 = 0.9360 | |
| South Sinai | y = −0.9525x + 7.3836, R2 = 0.8874 | y = −0.8211x + 7.1852, R2 = 0.9522 | |
| Provinces | All | Non-Scale Range | |
|---|---|---|---|
| First | Second | ||
| Cairo | y = −1.9202x + 12.461, R2 = 0.7516 | y = −0.6461x + 9.9449, R2 = 0.9536 | y = −2.8252x + 15.46, R2 = 0.9757 |
| Alexandria | y = −1.8882x + 11.159, R2 = 0.7189 | y = −1.4121x + 10.414, R2 = 0.9608 | |
| Port Said | y = −1.5571x + 10.196, R2 = 0.8816 | y = −1.1493x + 9.6023, R2 = 0.9716 | |
| Suez | y = −1.6334x + 10.524, R2 = 0.9271 | y = −1.7271x + 10.854, R2 = 0.9619 | |
| Damietta | y = −1.6063x + 10.386, R2 = 0.9043 | y = −1.5196x + 10.414, R2 = 0.9791 | |
| Dakahlia | y = −1.7153x + 10.057, R2 = 0.7894 | y = −0.898x + 9.0357, R2 = 0.9466 | y = −4.5185x + 18.076, R2 = 0.9642 |
| Sharkia | y = −1.9601x + 10.95, R2 = 0.9258 | y = −2.5387x + 12.553, R2 = 0.9882 | |
| Kalyubia | y = −1.8803x + 9.5979, R2 = 0.9676 | y = −1.7901x + 9.4569, R2 = 0.9849 | |
| Kafr El Sheikh | y = −1.953x + 10.376, R2 = 0.8005 | y = −0.9697x + 8.9918, R2 = 0.9502 | y = −5.1457x + 19.61, R2 = 0.9617 |
| Gharbia | y = −1.774x + 9.8234, R2 = 0.8340 | y = −0.5367x + 8.3227, R2 = 0.9555 | |
| Menoufia | y = −1.9655x + 10.179, R2 = 0.9234 | y = −2.259x + 10.955, R2 = 0.9595 | |
| Behera | y = −2.035x + 10.352, R2 = 0.9291 | y = −1.9553x + 10.224, R2 = 0.9502 | |
| Ismailia | y = −1.6233x + 8.7208, R2 = 0.8958 | y = −1.6086x + 8.8792, R2 = 0.9515 | |
| Giza | y = −1.4941x + 9.2068, R2 = 0.8093 | y = −0.5442x + 7.3717, R2 = 0.9443 | |
| Beni−Suef | y = −2.085x + 9.9794, R2 = 0.9399 | y = −2.0149x + 9.8688, R2 = 0.9542 | |
| Fayoum | y = −2.0727x + 9.8407, R2 = 0.9592 | y = −1.9293x + 9.6233, R2 = 0.9816 | |
| Menia | y = −1.8802x + 10.285, R2 = 0.8947 | y = −1.7559x + 10.085, R2 = 0.9635 | |
| Asyout | y = −1.5455x + 9.8179, R2 = 0.9661 | ||
| Suhag | y = −1.3674x + 9.7215, R2 = 0.9346 | y = −1.5257x + 10.206, R2 = 0.9659 | |
| Qena | y = −1.887x + 9.864, R2 = 0.9063 | y = −1.541x + 9.3468, R2 = 0.9759 | |
| Aswan | y = −1.6587x + 8.6376, R2 = 0.9103 | y = −2.259x + 10.215, R2 = 0.9753 | |
| Luxor | y = −1.8149x + 8.2318, R2 = 0.9441 | y = −2.0784x + 8.8999, R2 = 0.977 | |
| Red Sea | y = −1.1185x + 6.6284, R2 = 0.8726 | y = −0.5883x + 5.7921, R2 = 0.9671 | y = −2.5416x + 10.528, R2 = 0.9762 |
| ElWadi ElGidid | y = −1.401x + 6.1218, R2 = 0.9368 | y = −1.6185x + 6.6048, R2 = 0.9578 | |
| Matrouh | y = −1.2897x + 6.8193, R2 = 0.8428 | y = −1.1217x + 6.7657, R2 = 0.9661 | |
| North Sinai | y = −2.1179x + 8.8854, R2 = 0.8597 | y = −1.4497x + 7.9977, R2 = 0.9596 | y = −4.295x + 14.995, R2 = 0.9837 |
| South Sinai | y = −1.3274x + 6.4733, R2 = 0.7432 | y = −0.4051x + 5.3883, R2 = 0.9643 | y = −3.2354x + 11.632, R2 = 0.9662 |
| Economic Region | Previous | Current |
|---|---|---|
| Greater Cairo | y = −1.3274x + 12.708, R2 = 0.9285 | y = −1.7162x + 12.177, R2 = 0.8372 |
| Alexandria | y = −1.0906x + 10.573, R2 = 0.844 | y = −1.9511x + 11.312, R2 = 0.9575 |
| Suez Canal | y = −1.3778x + 10.866, R2 = 0.8551 | y = −1.8215x + 11.644, R2 = 0.9696 |
| Delta | y = −1.5822x + 10.759, R2 = 0.7604 | y = −1.5847x + 11.393, R2 = 0.8386 |
| North Upper Egypt | y = −1.1548x + 9.4668, R2 = 0.9087 | y = −1.8213x + 10.649, R2 = 0.929 |
| Central Upper Egypt | y = −0.9468x + 8.9529, R2 = 0.9574 | y = −1.2711x + 9.5109, R2 = 0.9004 |
| South Upper Egypt | y = −1.1114x + 10.175, R2 = 0.9753 | y = −1.5728x + 10.649, R2 = 0.9271 |
| Provinces | Exponential Fitting Equation | Gabaix’s Double Logarithmic Equation | Fractal Types |
|---|---|---|---|
| Alexandria | y = 0.1291e5.017x, R2 = 0.9482 | y = −1.3248x + 10.179, R2 = 0.9528 y = −5.0344x + 20.716, R2 = 0.974 | Bifractals power law |
| Port Said | y = 0.2717e4.308x, R2 = 0.9839 | y = −1.3313x + 9.556, R2 = 0.8465 | Exponential distribution |
| Damietta | y = 0.282e4.2252x, R2 = 0.9672 | y = −1.3725x + 9.7234, R2 = 0.8671 | Exponential distribution |
| Gharbia | y = 0.5706e3.4957x, R2 = 0.9472 | y = −1.4583x + 9.0016, R2 = 0.7848 | Exponential distribution |
| Giza | y = 0.0231e6.8991x, R2 = 0.9951 | y = −1.0916x + 8.3725, R2 = 0.953 | Monofractal power law |
| Qena | y = 0.0972e5.2512x, R2 = 0.9619 | y = −2.1131x + 10.376, R2 = 0.902 | Exponential distribution |
| Matrouh | y = 0.5797e3.3953x, R2 = 0.9936 | y = −1.4121x + 7.0392, R2 = 0.8736 | Exponential distribution |
| Provinces | Exponential Fitting Equation | Gabaix’s Double Logarithmic Equation | Fractal Types |
|---|---|---|---|
| Port Said | y = 0.2676e4.0399x, R2 = 0.9598 | y = −1.4625x + 8.2661, R2 = 0.9698 | Monofractal power law |
| Suez | y = 0.5488e3.625x, R2 = 0.9779 | y = −1.465x + 8.7067, R2 = 0.9786 | Monofractal power law |
| Kalyubia | y = 0.0032e8.7817x, R2 = 0.9764 | y = −1.9653x + 11.574, R2 = 0.6602 | Exponential distribution |
| Kafr El Sheikh | y = 0.4126e3.7293x, R2 = 0.9479 | y = −2.0188x + 9.657, R2 = 0.8757 | Exponential distribution |
| Menoufia | y = 0.1857e4.6402x, R2 = 0.9767 | y = −1.8379x + 9.756 R2 = 0.8431 | Exponential distribution |
| Behera | y = 0.2614e4.364x, R2 = 0.9883 | y = −1.6558x + 9.7598, R2 = 0.6905 | Exponential distribution |
| Aswan | y = 0.2592e4.1266x, R2 = 0.9442 | y = −1.9994x + 9.2411, R2 = 0.9516 | Monofractal power law |
| Luxor | y = 0.2083e4.4891x, R2 = 0.9530 | y = −1.3183x + 7.3393, R2 = 0.9577 | Monofractal power law |
| Red Sea | y = 0.3394e4.2229x, R2 = 0.9904 | y = −1.2866x + 9.1306, R2 = 0.6705 | Exponential distribution |
| Matrouh | y = 0.4026e3.8311x, R2 = 0.9881 | y = −1.2586x + 7.7037, R2 = 0.799 | Exponential distribution |


References
- De Haas, H. Migration and Development: A Theoretical Perspective. Int. Migr. Rev. 2010, 44, 227–264. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stillwell, J.; Daras, K.; Bell, M.; Lomax, N. The Image Studio: A Tool for Internal Migration Analysis and Modelling. Appl. Spat. Anal. Policy 2014, 1, 5–23. [Google Scholar] [CrossRef]
- Ravenstein, E.G. The Laws of Migration. J. Stat. Soc. 1885, 48, 167–235. [Google Scholar] [CrossRef]
- Heberle, R. The Causes of Rural-Urban Migration a Survey of German Theories. The Am. J. Sociol. 1938, 43, 932–950. [Google Scholar] [CrossRef]
- Zipf, G.K. The P1P2 /D Hypothesis: On Intercity Movement of Persons. Am. Sociol. Rev. 1946, 11, 677–686. [Google Scholar] [CrossRef]
- Wilson, A.G. Entropy in Urban and Regional Modelling; London Pion: London, UK, 1970. [Google Scholar]
- Plane, D.A.; Henrie, C.J.; Perry, M.J. Migration up and down the Urban Hierarchy and across the Life Course. Acad. Sci. USA 2005, 102, 15313–15318. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Davis, K.F.; D’Odorico, P.; Laio, F.; Ridolfi, L. Global Spatio-Temporal Patterns in Human Migration: A Complex Network Perspective. PLoS ONE 2013, 8, e53723. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.Y. Evolution and Characteristics of Spatial Economic Structure in Ningxia Province. J. Arid Land Resour. Environ. 2010, 24, 10–14. [Google Scholar]
- Liu, S.H.; Hu, Z.; Deng, Y.; Wang, Y.J. The Regional Types of China’s Floating Population: Identification Methods and Spatial Patterns. J. Geogr. Sci. 2011, 21, 35–48. [Google Scholar] [CrossRef] [Green Version]
- Qiao, L.Y.; Li, Y.R.; Liu, Y.S.; Yang, R. The Spatio-Temporal Change of China’s Net Floating Population at County Scale from 2000 to 2010. Asia Pac. Viewp. 2016, 57, 365–378. [Google Scholar] [CrossRef]
- Liang, Z.; Ma, Z.D. China’s Floating Population: New Evidence from the 2000 Census. Popul. Dev. Rev. 2004, 30, 467–478. [Google Scholar] [CrossRef]
- Liang, Z.; Li, Z.; Ma, Z.D. Changing Patterns of the Floating Population in China, 2000-2010. Popul. Dev. Rev. 2014, 4, 695–716. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, J.W.; Yu, Z.; Wei, Y.D.; Yang, L.Q. Changing Distribution of Migrant Population and Its Influencing Factors in Urban ChinA: Economic Transition, Public Policy, and Amenities. Habitat Int. 2019, 94, 102063. [Google Scholar] [CrossRef]
- Wang, L.C.; Xue, C.X. Spatio-Temporal Characteristics and Influencing Factors of Urban Floating Population in China From 2011 to 2015. Chin. J. Popul. Resour. Environ. 2019, 4, 359–373. [Google Scholar] [CrossRef]
- Levytska, O.; Mulska, O.; Ivaniuk, U.; Kunytska-lliash, M.; Vasyltsic, T.; Lupak, R. Modelling the Conditions Affecting Population Migration Activity in the Eastern European Region: The Case of Ukraine. Tem. J. Technol. Educ. Manag. Inform. 2020, 2, 507–514. [Google Scholar] [CrossRef]
- Shumway, J.M.; Otterstrom, S.M. Spatial Patterns of Migration and Income Change in the Mountain West:The Dominance of Service-Based, Amenity-Rich Counties. Prof. Geogr. 2010, 53, 492–502. [Google Scholar] [CrossRef]
- Sobolevsky, S.; Szell, M.; Campari, R.; Couronne, T.; Smoreda, Z.; Ratti, C. Delineating Geographical Regions with Networks of Human Interactions in an Extensive Set of Countries. PLoS ONE 2013, 8, e81707. [Google Scholar] [CrossRef] [Green Version]
- Hawelka, B.; Sitko, I.; Beinat, E.; Sobolevsky, S.; Kazakopoulos, P.; Ratti, C. Geo-Located Twitter as Proxy for Global Mobility Patterns. Cartogr. Geogr. Inf. Sci. 2014, 41, 260–271. [Google Scholar] [CrossRef] [Green Version]
- Porat, I.; Benguigui, L. Global Migration Topology Analysis and Modeling of Bilateral Flow Network 2006–2010. EPL 2016, 115, 18002. [Google Scholar] [CrossRef]
- Salvati, L.; Serra, P.; Bencardino, M.; Carlucci, M. Re-Urbanizing the European City: A Multivariate Analysis of Population Dynamics during Expansion and Re-Cession Times. Eur. J. Popul. 2018, 4, 1–28. [Google Scholar]
- Shi, Q.J.; Liu, T. Glimpsing China’s Future Urbanization from the Geography of a Floating Population. Environ. Plan. 2019, 51, 817–819. [Google Scholar] [CrossRef] [Green Version]
- Fan, C.C. Interprovincial Migration, Population Redistribution, and Regional Development in China: 1990 and 2000 Census Comparisons. The Prof. Geogr. 2005, 57, 295–311. [Google Scholar] [CrossRef]
- Liu, C.; Otsubo, K.; Wang, Q.X.; Ichinose, T.; Ishimura, S. Spatial and Temporal Changes of Floating Population in China Between 1990 and 2000. Chin. Geogr. Sci. 2007, 2, 3–13. [Google Scholar] [CrossRef]
- Cully, M. More Than Additions to Population: The Economic and Fiscal Impact of Immigration. Aust. Econ. Rev. 2012, 45, 344–349. [Google Scholar] [CrossRef]
- Luo, J.J.; Zhang, X.L.; Wu, Y.Z.; Shen, L.Y.; Xing, X.S. Urban Land Expansion and the Floating Population in China: For Production or for Living? Cities 2018, 74, 219–228. [Google Scholar] [CrossRef]
- Gao, D.J.; Peng, J.L.; Zi, L. Study on the Relationship between the Population Migration and Region Economy Based on the Framework of VAR Model:A Case Study of Chongqing. Northwest Popul. J. 2020, 110, 50–53. [Google Scholar]
- Hoffman, M.T.; Skowno, A.; Bell, W.; Mashele, S. Long-Term Changes in Land Use, Land Cover and Vegetation in the Karoo Drylands of South Africa: Implications for Degradation Monitoring. Afr. J. Range Forage Sci. 2018, 35, 209–221. [Google Scholar] [CrossRef]
- Liu, Z.F.; He, C.Y.; Yang, Y.J.; Fang, Z.H. Planning Sustainable Urban Landscape under the Stress of Climate Change in the Drylands of Northern ChinA: A Scenario Analysis Based on LUSD-Urban Model. J. Clean. Prod. 2020, 244. [Google Scholar] [CrossRef]
- Liu, Z.F.; Yang, Y.J.; He, C.Y.; Tu, M.Z. Climate Change Will Constrain the Rapid Urban Expansion in Drylands: A Scenario Analysis with the Zoned Land Use Scenario Dynamics-Urban Model. Sci. Total Environ. 2019, 651, 2772–2786. [Google Scholar] [CrossRef]
- He, C.Y.; Li, J.W.; Zhang, X.L.; Liu, Z.F.; Zhang, D. Will Rapid Urban Expansion in, the Drylands of Northern China Continue: A Scenario Analysis Based on the Land Use Scenario Dynamics-Urban Model and the Shared Socioeconomic Pathways. J. Clean. Prod. 2017, 165, 57–69. [Google Scholar] [CrossRef]
- Jenerette, G.D.; Miller, G.; Buyantuev, A.; Pataki, D.E.; Gillespie, T.; Pincetl, S. Urban Vegetation and Income Segregation in Drylands: A Synthesis of Seven Metropolitan Regions in the South-Western United States. Environ. Res. Lett. 2013, 8. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.F.; Verburg, P.H.; Wu, J.G.; He, C.Y. Understanding Land System Change Through Scenario-Based Simulations: A Case Study from the Drylands in Northern China. Environ. Manag. 2017, 59, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Mcpeak, J.G.; Little, P.D. Land Use and Tenure Insecurity in the Drylands of Southern Ethiopia. J. Dev. Stud. 2019, 55, 1307–1324. [Google Scholar] [CrossRef]
- Gong, B.H.; Liu, Z.F. Assessing Impacts of Land Use Policies on Environmental Sustainability of Oasis Landscapes with Scenario Analysis: The Case of Northern China. Landsc. Ecol. 2020. [Google Scholar] [CrossRef]
- Rubio, M.C.; Sales, R.; Abraham, E.; Rubio, M.F.; Diaz, F.; Rubio, C. Land Use Planning in Drylands: Participatory Processes in Diagnosing the Physical-Biological Subsystem. Appl. Spat. Anal. Policy 2020. [Google Scholar] [CrossRef]
- El Amrousi, M.; Paleologos, E.K.; Caratelli, P. Are Garden Cities in the Desert Sustainable? The Oasis City of Al Ain in the Emirate of Abu Dhabi. Int. Rev. Spat. Plan. Sustain. Dev. A Plan. Strateg. Des. Concepts 2018, 6, 79–94. [Google Scholar]
- Burian, A.; Karaya, R.; Wernersson, J.E.V.; Egberth, M.; Likirwa, B.; Nyberg, G. A Community-Based Evaluation of Population Growth and Agro-Pastoralist Resilience in Sub-saharan Drylands. Environ. Sci. Policy 2018, 92, 323–330. [Google Scholar] [CrossRef]
- Heider, G.; Jobbagy, E.G.; Tripaldi, A. Use of Semi-Arid Space by Prehispanic Population: The Role of Dune Landscapes as Eco-Refuges in Central Argentina. Boletín Soc. Geol. Mex. 2019, 71, 229–248. [Google Scholar] [CrossRef]
- Rufino, I.A.A.; Da Silva, S.T. Change Analysis of Population Dynamics and Climate Variability in the Brazilian Semi-arid Region: A Methodological Approach. Bol. Ciênc. Geod. 2017, 23, 166–181. [Google Scholar] [CrossRef]
- Qi, S.Z.; Zheng, Z.P. Environmental Hazards from Population Pressure in the Jinta Oasis, Arid Northwestern China. Nat. Hazards 2013, 65, 985–989. [Google Scholar] [CrossRef]
- Qi, W.; Liu, S.H. Research on the Rank-Size Distribution Rule of China’s Urban Floating Population. Geogr. Res. 2015, 34, 1981–1993. [Google Scholar]
- Wang, X.M.; Hao, R.; Zhao, N.; Huo, J. Statistical Characteristics of Dynamics for Population Migration Driven by the Economic Interests. Physica, A. Stat. Mech. Appl. 2016, 451, 123–134. [Google Scholar]
- Chen, Y.G. A Wave-Spectrum Analysis of Urban Population Density: Entropy, Fractal, and Spatial Localization. Discret. Dyn. Nat. Soc. 2008, 4, 47–58. [Google Scholar] [CrossRef] [Green Version]
- Newman, T.J.; Antonovics, J.; Wilbur, H.M. Population Dynamics with a Refuge: Fractal Basins and the Suppression of Chaos. Theor. Popul. Biol. 2002, 62, 121–128. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, J.; Kramer, T.A. Adjustable Discretized Population Balance Equations: Numerical Simulation and Parameter Estimation for Fractal Aggregation and Break-Up. Colloids Surf. A Physicochem. Eng. Asp. 2007, 292, 173–188. [Google Scholar] [CrossRef]
- Sutton, K.; Fahmi, W. Cairo’s Urban Growth and Strategic Master Plans in the Light of Egypt’s 1996 Population Census Results. Cities 2001, 18, 135–149. [Google Scholar] [CrossRef]
- Stewart, D.J.; Yin, Z.Y.; Bullard, S.M.; Maclachlan, J.T. Assessing the Spatial Structure of Urban and Population Growth in the Greater Cairo Area, Egypt: A GIS and Imagery Analysis Approach. Urban Stud. 2004, 41, 95–116. [Google Scholar] [CrossRef]
- Ibrahiem, D.M. Road Energy Consumption, Economic Growth, Population and Urbanization in Egypt: Cointegration and Causality Analysis. Environ. Dev. Sustain. 2018, 20, 1053–1066. [Google Scholar] [CrossRef]
- Ghanem, S.K. The Relationship between Population and the Environment and Its Impact on Sustainable Development in Egypt Using a Multi-Equation Model. Environ. Dev. Sustain. 2018, 20, 305–342. [Google Scholar] [CrossRef]
- McCormick, B.; Wahba, J. Return International Migration and Geographical Inequality: The Case of Egypt. J. Afr. Econ. 2003, 12, 500–532. [Google Scholar] [CrossRef] [Green Version]
- Afifi, T. The Environmental Root Causes Triggering Economic Migration: The Case of Egypt. In Environment, Forced Migration and Social Vulnerability; Springer: Berlin/Heidelberg, 2010. [Google Scholar]
- Pettit, H.; Ruijtenberg, W. Migration as Hope and Depression: Existential Im/Mobilities in and beyond Egypt. Mobilities 2019, 14, 730–744. [Google Scholar] [CrossRef] [Green Version]
- Arouri, M.; Cuong, N.V. Wealth Inequality and Inter-Governorate Migration: Evidence from Egypt. Prog. Dev. Stud. 2020, 20, 119–139. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, S.; Zhao, S. Study on the Spatial Pattern of Migration Population in Egypt and Its Flow Field Characteristics from the Perspective of “Source-Flow-Sink”. Sustainability 2021, 13, 350. [Google Scholar] [CrossRef]
- Gao, P.C.; Liu, Z.; Liu, G.; Zhao, H.R.; Xie, X.X. Unified Metrics for Characterizing the Fractal Nature of Geographic Features. Ann. Am. Assoc. Geogr. 2017, 1, 1315–1331. [Google Scholar] [CrossRef]
- Jiang, B.; Yin, J.J. Ht-Index for Quantifying the Fractal or Scaling Structure of Geographic Features. Ann. Assoc. Am. Geogr. 2014, 104, 530–541. [Google Scholar] [CrossRef]
- Mukhopadhyay, B.; Mukherjee, P.K.; Bhattacharya, D.; Sengupta, S. Delineation of Arsenic-Contaminated Zones in Bengal Delta, IndiA: A Geographic Information System and Fractal Approach. Environ. Geol. 2006, 49, 1009–1020. [Google Scholar] [CrossRef]
- Barmaki, M.D.; Rezaei, M.; Madadi, S. Use of Fractal Dimensions Analysis in Geographic Information System and Remote Sensing Techniques to Iden-Tify Groundwater Prospective Zones in the Anar-Dashtegol Anticline, Iran. Carbonates Evaporites 2019, 35, 4. [Google Scholar] [CrossRef]
- Jarraya, M.; Guermazi, A.; Niu, J.B.; Duryea, J.; Lynch, J.A.; Roemer, F.W. Multi-Dimensional Reliability Assessment of Fractal Signature Analysis in an Outpatient Sports Medicine Population. Ann. Anat.—Anat. Anz. 2015, 202, 57–60. [Google Scholar] [CrossRef]
- Ayres, R. Tourism as a Passport to Development in Small States: Reflections on Cyprus. Int. J. Soc. Econ. 2000, 27, 114–133. [Google Scholar] [CrossRef]
- Alperovich, G. The Size Distribution of Cities: On the Empirical Validity of the Rank-Size Rule. J. Urban. Econ. 1984, 16, 232–239. [Google Scholar] [CrossRef]
- Brakman, S.; Garretsen, H.; Van Marrewijk, C.; Van Den Berg, M. The Return of Zipf: Towards a Further Understanding of the Rank-Size Distribution. J. Reg. Sci. 1999, 39, 183–213. [Google Scholar] [CrossRef]
- Guerin-Pace, F. Rank-Size Distribution and the Process of Urban Growth. Urban Stud. 1995, 32, 551–562. [Google Scholar] [CrossRef]
- Chen, Y.G.; Wang, J.J. Recursive Subdivision of Urban Space and Zipf’s law. Phys. A Statal Mech. Appl. 2014, 395, 392–404. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.G. The Mathematical Relationship between Zipf’s Law and the Hierarchical Scaling Law. Phys. A Statal Mech. Appl. 2012, 391, 3285–3299. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.G. Zipf’s Law, Hierarchical Structure, and Cards-Shuffling Model for Urban Development. Discret. Dyn. Nat. Soc. 2012. [Google Scholar] [CrossRef]
- Benguigui, L.; Daoud, M. Is the Suburban Railway System a Fractal? Geogr. Anal. 2010, 23, 362–368. [Google Scholar] [CrossRef]
- White, R.; Engelen, G. Urban Systems Dynamics and Cellular Automata: Fractal Structures between Order and Chaos. Chaos Solitons Fractals 1994, 4, 563–583. [Google Scholar] [CrossRef]
- Benguigui, L.; Blumenfeld-Lieberthal, E. The End of a Paradigm: Is Zipf’s Law Universal? J. Geogr. Syst. 2011, 13, 87–100. [Google Scholar] [CrossRef]
- Jiang, B.; Yin, J.J.; Liu, Q.L. Zipf’s Law for All the Natural Cities around the World. Int. J. Geogr. Inf. Sci. 2015, 29, 498–522. [Google Scholar] [CrossRef]
- Ioannides, Y.M.; Overman, H.G. Zipf’s Law for Cities: An Empirical Examination. Reg. Sci. Urban. Econ. 2003, 33, 127–137. [Google Scholar] [CrossRef] [Green Version]
- Jiang, B.; Jia, T. Zipf’s Law for All the Natural Cities in the United States: A Geospatial Perspective. Int. J. Geogr. Inf. Sci. 2011, 25, 1269–1281. [Google Scholar] [CrossRef]
- González-Val, R. Deviations from Zipf’s Law for American Cities: An Empirical Examination. Urban Stud. 2011, 48, 1017–1035. [Google Scholar] [CrossRef] [Green Version]
- Fang, L.; Li, P.; Song, S.F. China’s Development Policies and City Size Distribution: An Analysis Based on Zipf’s Law. Urban Stud. 2017, 54, 2818–2834. [Google Scholar] [CrossRef]
- Ye, X.Y.; Xie, Y.C. Re-Examination of Zipf’s Law and Urban Dynamic in China: A Regional Approach. Ann. Reg. Sci. 2012, 49, 135–156. [Google Scholar] [CrossRef]
- Peng, G.H. Zipf’s Law for Chinese Cities: Rolling Sample Regressions. Phys. A Stat. Mech. Appl. 2010, 389, 3804–3813. [Google Scholar] [CrossRef]
- Lalanne, A. Zipf’s Law and Canadian Urban Growth. Urban Stud. 2014, 51, 1725–1740. [Google Scholar] [CrossRef]
- Giesen, K.; Sudekum, J. Zipf’s Law for Cities in the Regions and the Country. J. Econ. Geogr. 2011, 11, 667–686. [Google Scholar] [CrossRef] [Green Version]
- Knudsen, T. Zipf’s Law for Cities and Beyond: The Case of Denmark. Am. J. Econ. Sociol. 2001, 60, 123–146. [Google Scholar] [CrossRef]
- Josic, H.; Basic, M. Reconsidering Zipf’s Law for Regional Development: The Case of Settlements and Cities in Croatia. Misc. Geogr. 2018, 22, 22–30. [Google Scholar] [CrossRef] [Green Version]
- Bergs, R. The Detection of Natural Cities in The Netherlands snocturnal Satellite Imagery and Zipf’s Law. Rev. Reg. Res.-Jahrb. Fur Reg. 2018, 38, 111–140. [Google Scholar] [CrossRef]
- Cielik, A.; Teresiński, J. Does Zipf’s Law Hold for Polish Cities? Misc. Geogr. 2016, 20, 5–10. [Google Scholar] [CrossRef] [Green Version]
- Kwok, T.S. Zipf’s Law and Urban Growth in Malaysia. Urban Stud. 2007, 44, 1–14. [Google Scholar]
- Basu, B.; Bandyapadhyay, S. Zipf’s Law and Distribution of Population in Indian Cities. Indian J. Phys. 2009, 83, 1575–1582. [Google Scholar] [CrossRef]
- Morudu, H.D. Developing Annual Population and Gross Domestic Product Estimates for Local Municipality Development Mod-Els in South Africa: Applications of Zipf’s Rule from 2001 to 2013. S. Afr. Geogr. J. 2016, 98, 367–385. [Google Scholar] [CrossRef]
- Kundak, S.; Dkmeci, V. A Rank-Size Rule Analysis of The City System at The Country and Province Level in Turkey. ICONARP Int. J. Archit. Plan. 2018, 6, 77–98. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.G. Scale Symmetric Spatial Complexity of Fractal Urban System; Science Press: Beijing, China, 2008. [Google Scholar]
- Zhou, C.P.; Ge, D.M. Disparity of Tourism Scale and a Research on its System for Rank- Scale Distribution—Take Zhejiang Province for Example. Econ. Geogr. 2010, 30, 345–350. [Google Scholar]
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-Law Distributions in Empirical Data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef] [Green Version]
- Hanel, R.; Corominas-Murtra, B.; Liu, B.; Thurner, S. Fitting Power-Laws in Empirical Data with Estimators That Work for All Exponents. PLoS ONE 2017, 12, e0170920. [Google Scholar] [CrossRef] [Green Version]
- Gabaix, X.; Ibragimov, R. Rank-1/2: A Simple Way to Improve the OLS Estimation of Tail Exponents. J. Bus. Econ. Stat. 2011, 29, 24–39. [Google Scholar] [CrossRef] [Green Version]
- Xiao, D.Q. Cognitive Geography: People-Oriented Geographic Information Science; Science Press: Beijing, China, 2013. [Google Scholar]
- Tobler, W. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Malevergne, Y.; Pisarenko, V.; Sornette, D. Empirical Distributions of Log-Returns: Between the Stretched Exponential and the Power Law? Quant. Financ. 2005, 5, 379–401. [Google Scholar] [CrossRef]







| Country | Area (million km2) | Population (million) | GDP per Capita ($) | |
|---|---|---|---|---|
| 1 | Egypt | 1.00 | 98.58 | 2508 |
| 2 | Afghanistan | 0.65 | 29.70 | 679 |
| 3 | Algeria | 2.38 | 42.20 | 4279 |
| 4 | Iraq | 0.44 | 38.12 | 5415 |
| 5 | Australia | 7.69 | 2.51 | 51,581 |
| 6 | Bahrain | 0.0007 | 1.50 | 22,333 |
| 7 | Israel (Palestine) | - | - | - |
| 8 | Jordan | 0.089 | 10.31 | 4108 |
| 9 | Kazakhstan | 2.73 | 18.39 | 9271 |
| 10 | Chile | 0.76 | 18.75 | 16,100 |
| 11 | Kyrgzstan | 0.20 | 6.40 | 1267 |
| 12 | Eritrea | 0.12 | 5.97 | 1060 |
| 13 | Libya | 1.76 | 6.68 | 7235 |
| 14 | Mongolia | 1.57 | 32.00 | 3975 |
| 15 | Namibia | 0.82 | 2.41 | 6031 |
| 16 | Niger | 1.27 | 21.47 | 430 |
| 17 | Oman | 0.31 | 4.69 | 15,565 |
| 18 | Peru | 1.29 | 31.24 | 7002 |
| 19 | Saudi Arabia | 2.25 | 33.41 | 23,712 |
| 20 | Sudan | 1.88 | 40.78 | 808 |
| 21 | Syria | 0.19 | 16.91 | - |
| 22 | Turkmenistan | 0.49 | 5.62 | 7669 |
| 23 | UAE | 0.084 | 9.40 | 68,000 |
| 24 | Uzbekistan | 0.45 | 33.38 | 1500 |
| 25 | Yemen | 0.56 | 28.5 | 944 |
| 26 | Qatar | 0.221 | 2.64 | 69,026 |
| 27 | Iran | 164.5 | 81.69 | 5220 |
| Spatial Pattern | Distribution | Power | ||
|---|---|---|---|---|
| 1 | <0.6 | Over Dispersion | Normal | Centralization |
| 2 | 0.6–0.9 | Balanced Distribution | ||
| 3 | 0.9–1.5 | Optimal Distribution | Normal-Pareto | Balance |
| 4 | 1.5–2.5 | Primacy Distribution | Pareto | Decentralization |
| 5 | >2.5 | Over Concentration |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Wang, X.; Ma, Z. Study on Fractal Characteristics of Migration-Population Flow—Evidence from Egypt. ISPRS Int. J. Geo-Inf. 2021, 10, 45. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi10020045
Zhao S, Wang X, Ma Z. Study on Fractal Characteristics of Migration-Population Flow—Evidence from Egypt. ISPRS International Journal of Geo-Information. 2021; 10(2):45. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi10020045
Chicago/Turabian StyleZhao, Sidong, Xingping Wang, and Zhishan Ma. 2021. "Study on Fractal Characteristics of Migration-Population Flow—Evidence from Egypt" ISPRS International Journal of Geo-Information 10, no. 2: 45. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi10020045







