Empirical Insights from a Study on Outlier Preserving Value Generalization in Animated Choropleth Maps
Abstract
:1. Introduction
1.1. Solutions Proposed to Reduce Cognitive Load
1.2. Research Gap
1.3. Document Organization
2. Methods
2.1. Animated Map Stimuli
2.2. Response Items
2.2.1. Outlier Response Items
2.2.2. Trend Response Items
2.3. Study Design and Implementation
- 3-second countdown and automatic start of the animation.
- Immediate replacement of the animation with response items for local outliers to choose from (Figure 2).
- Rating of the difficulty of the task.
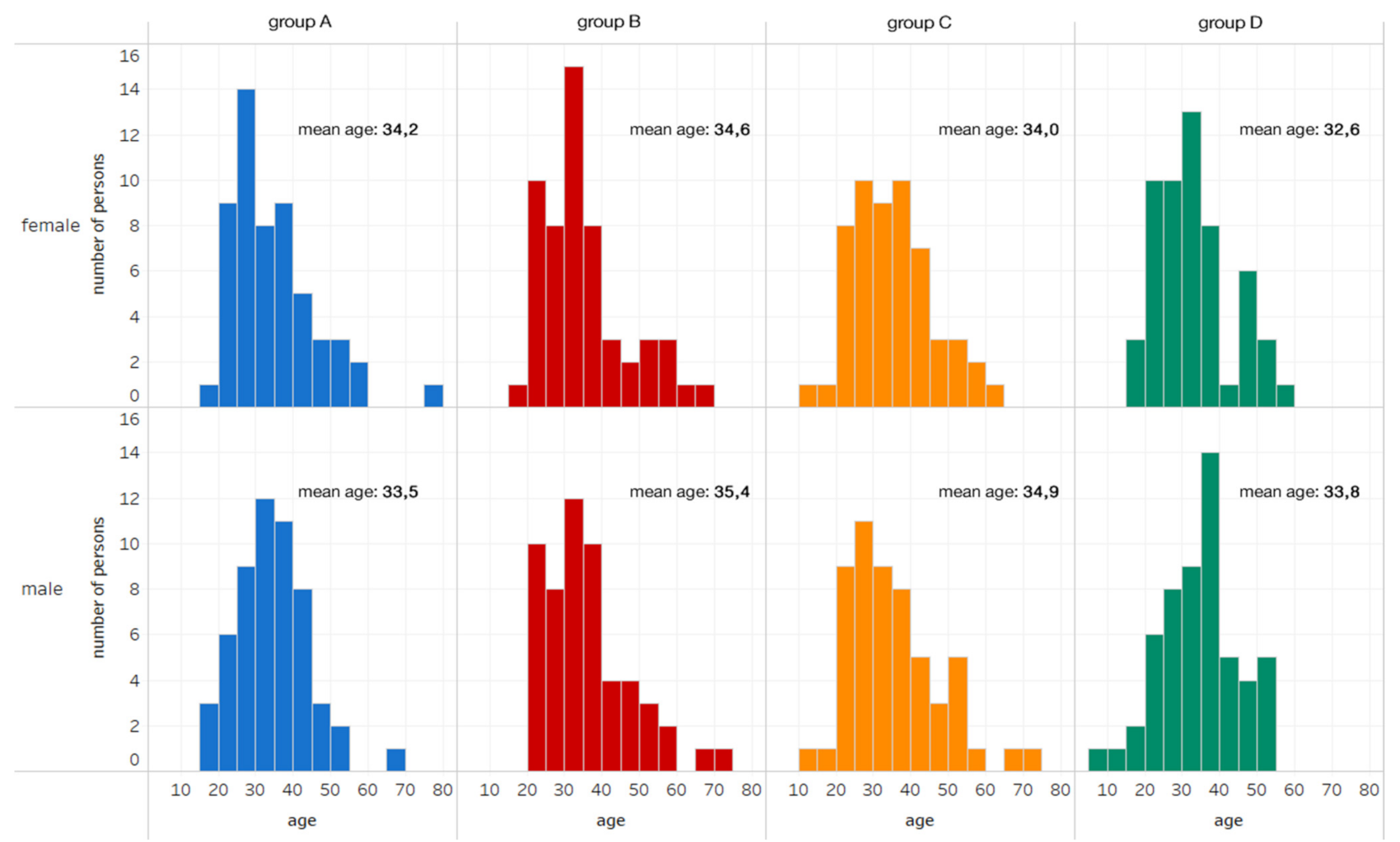
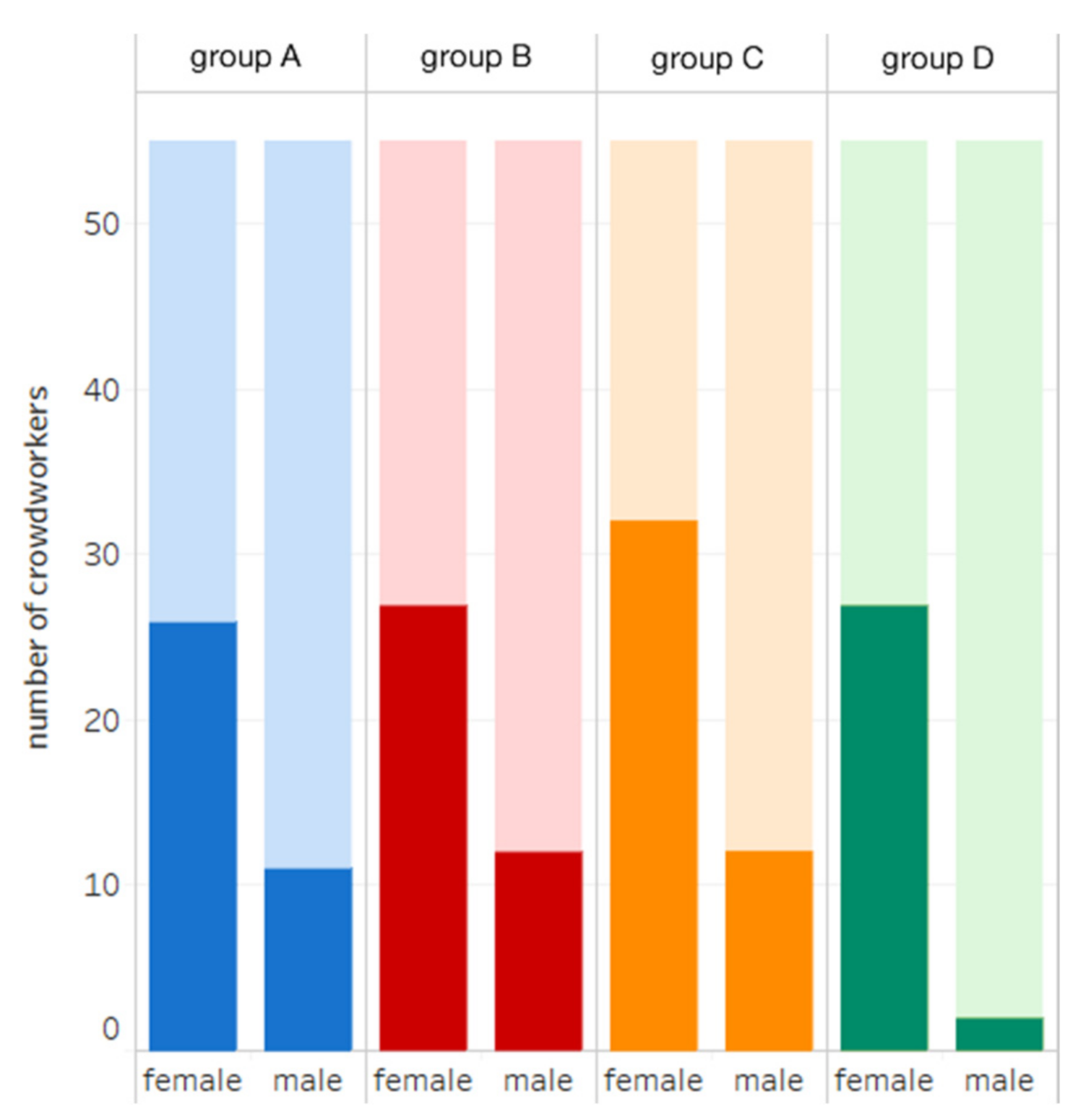
2.4. Participants and Data
3. Results
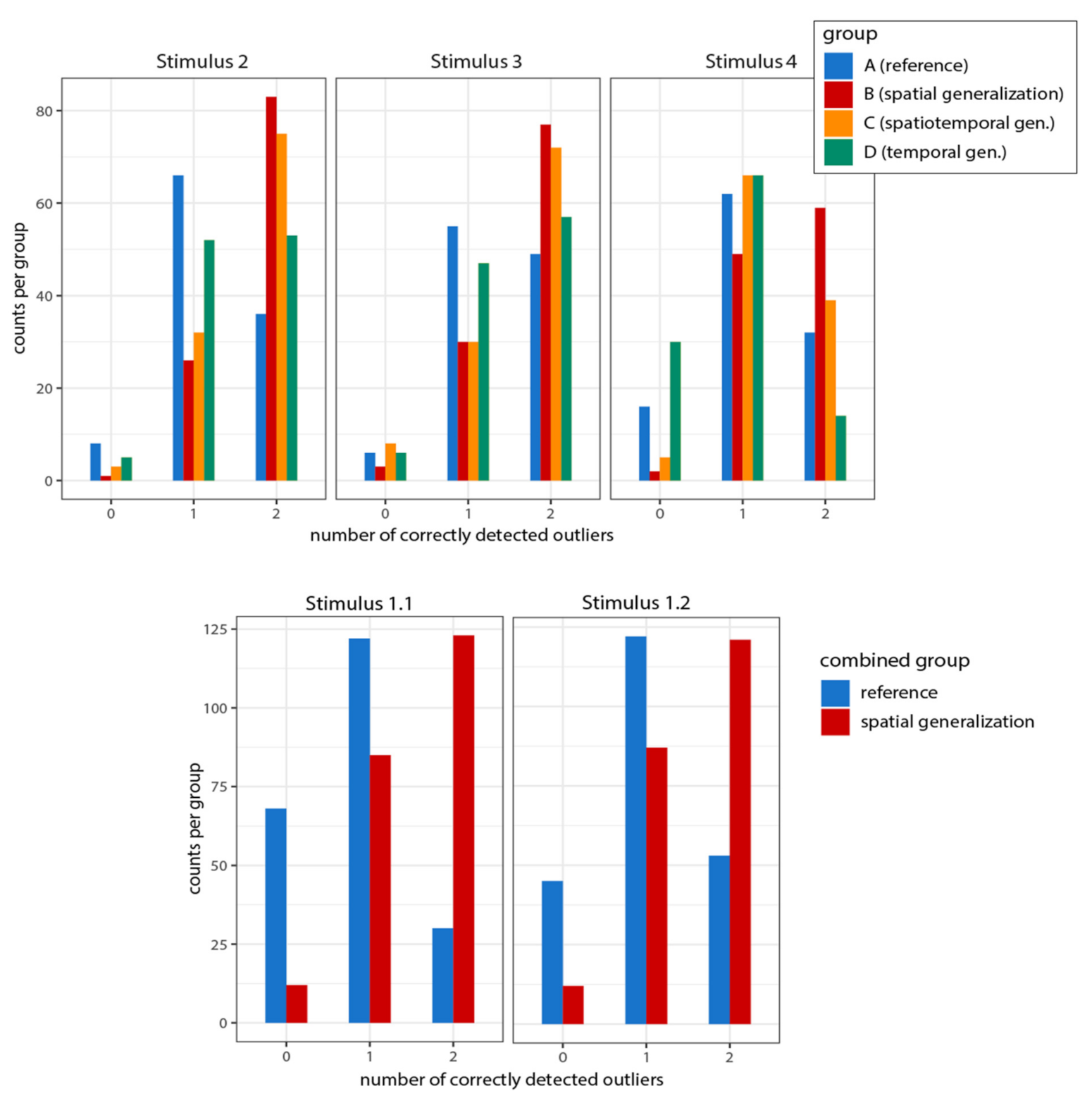
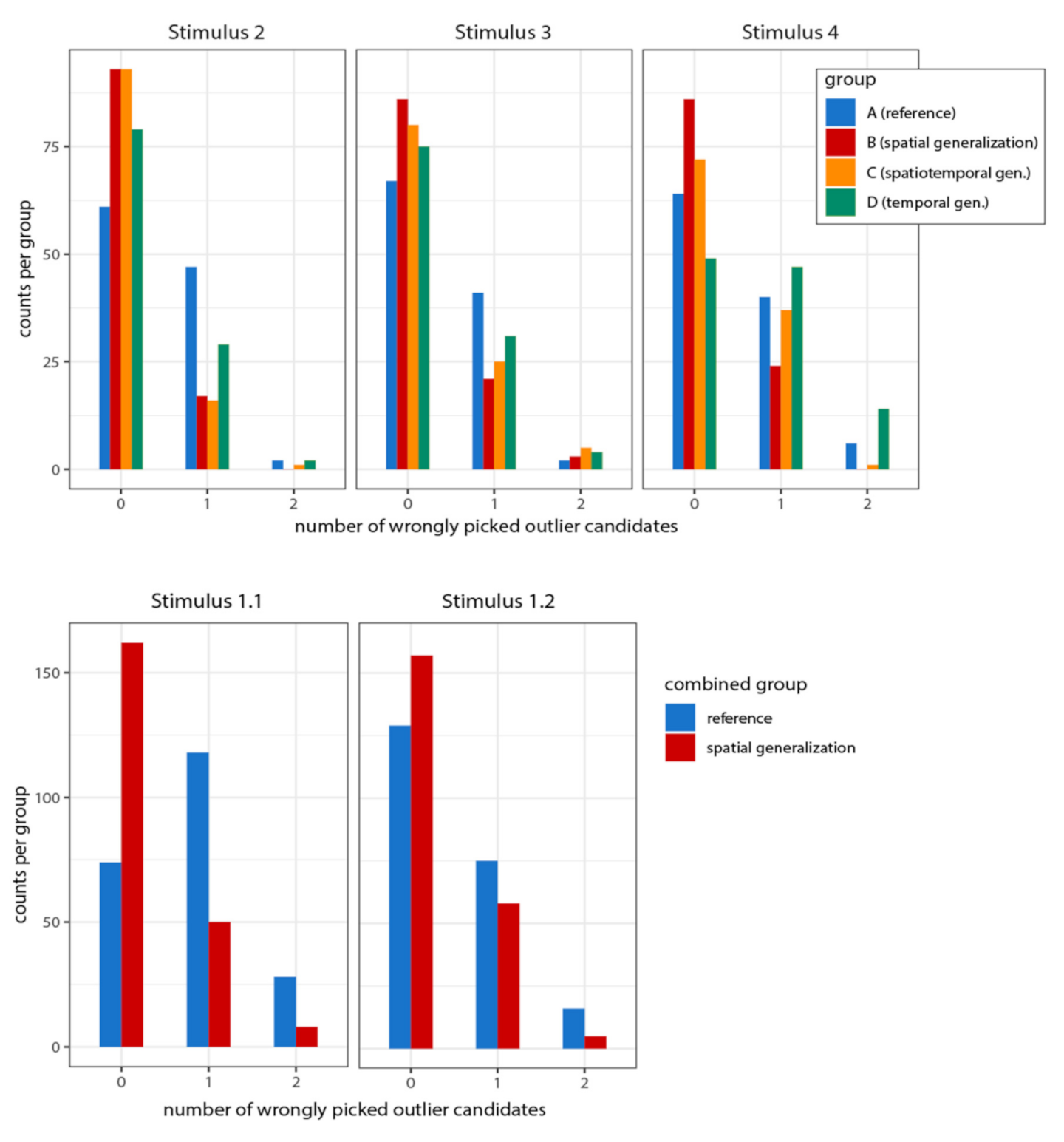
3.1. Local Outlier Detection
3.1.1. Correctly Detected Local Outliers
3.1.2. False Positive Outliers
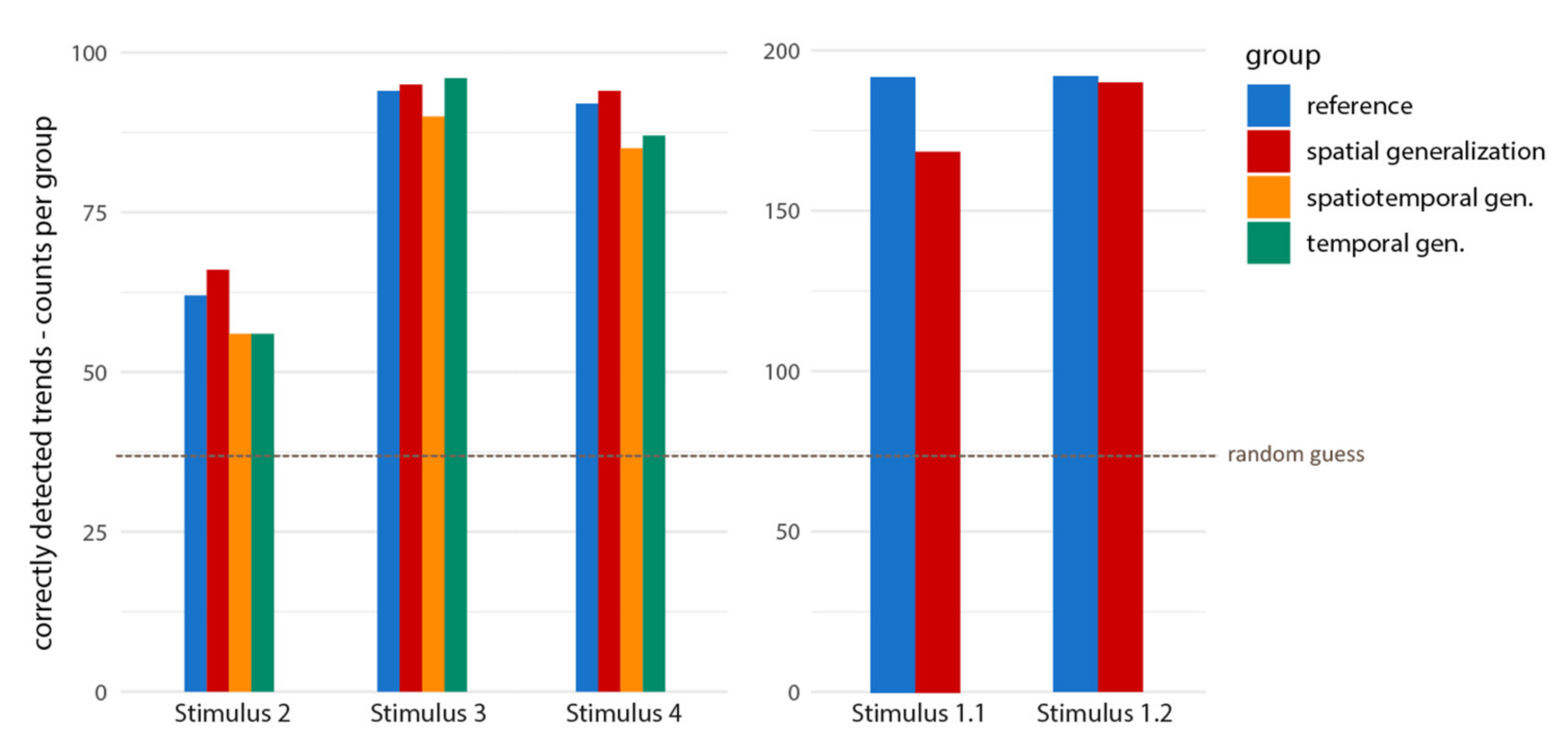
3.2. Global Trend
3.3. Person-Related Covariates
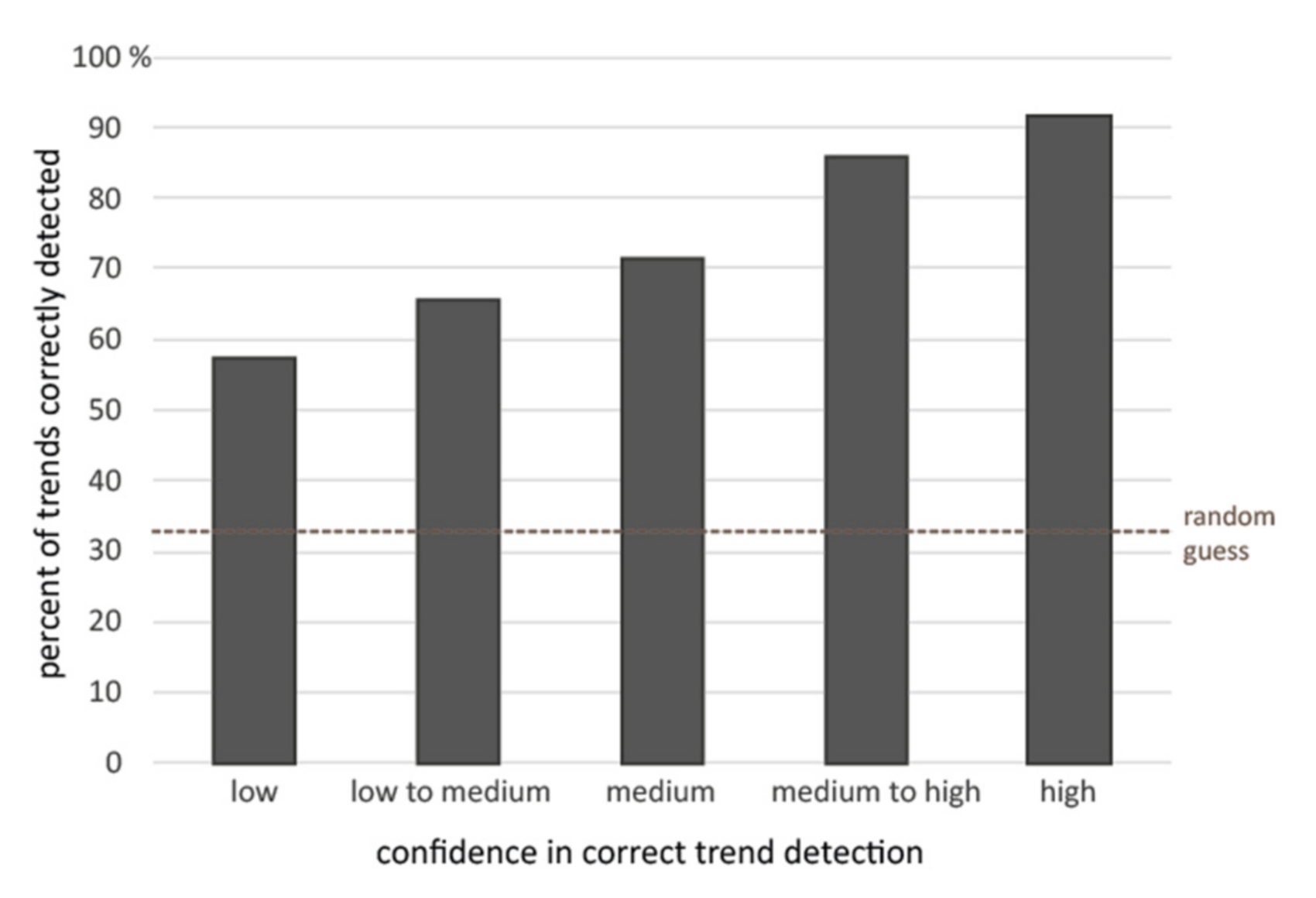
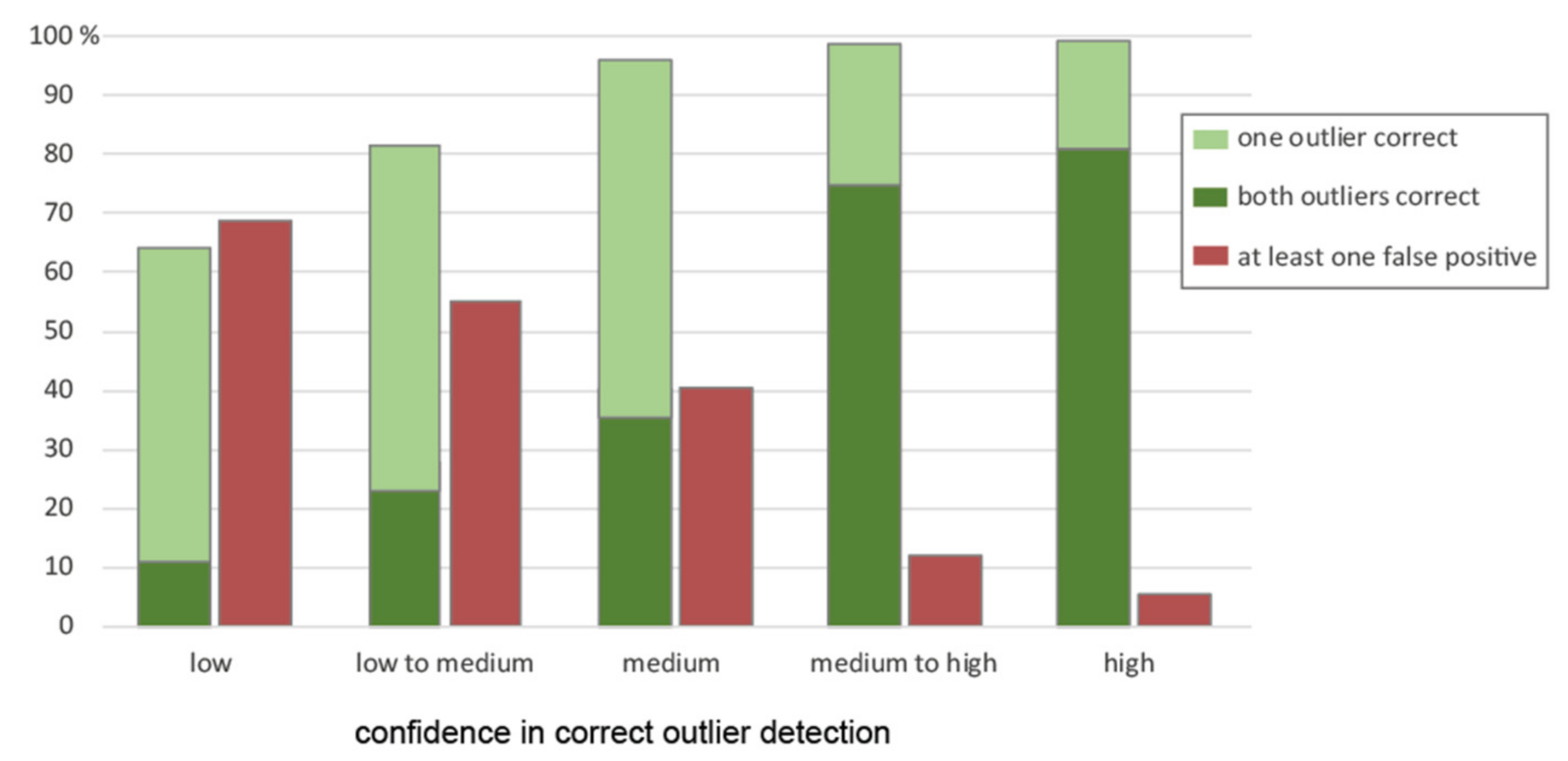
3.4. Self-Confidence
3.5. Strategies for Perception and Memorization
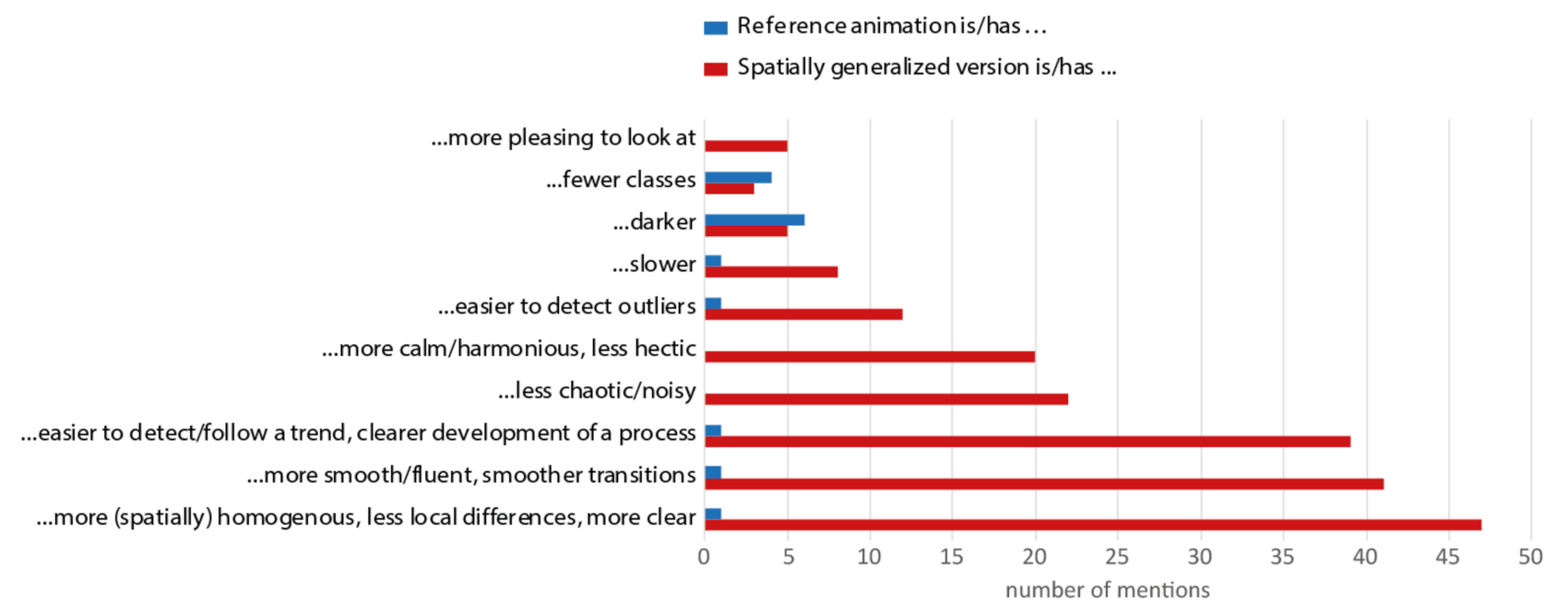
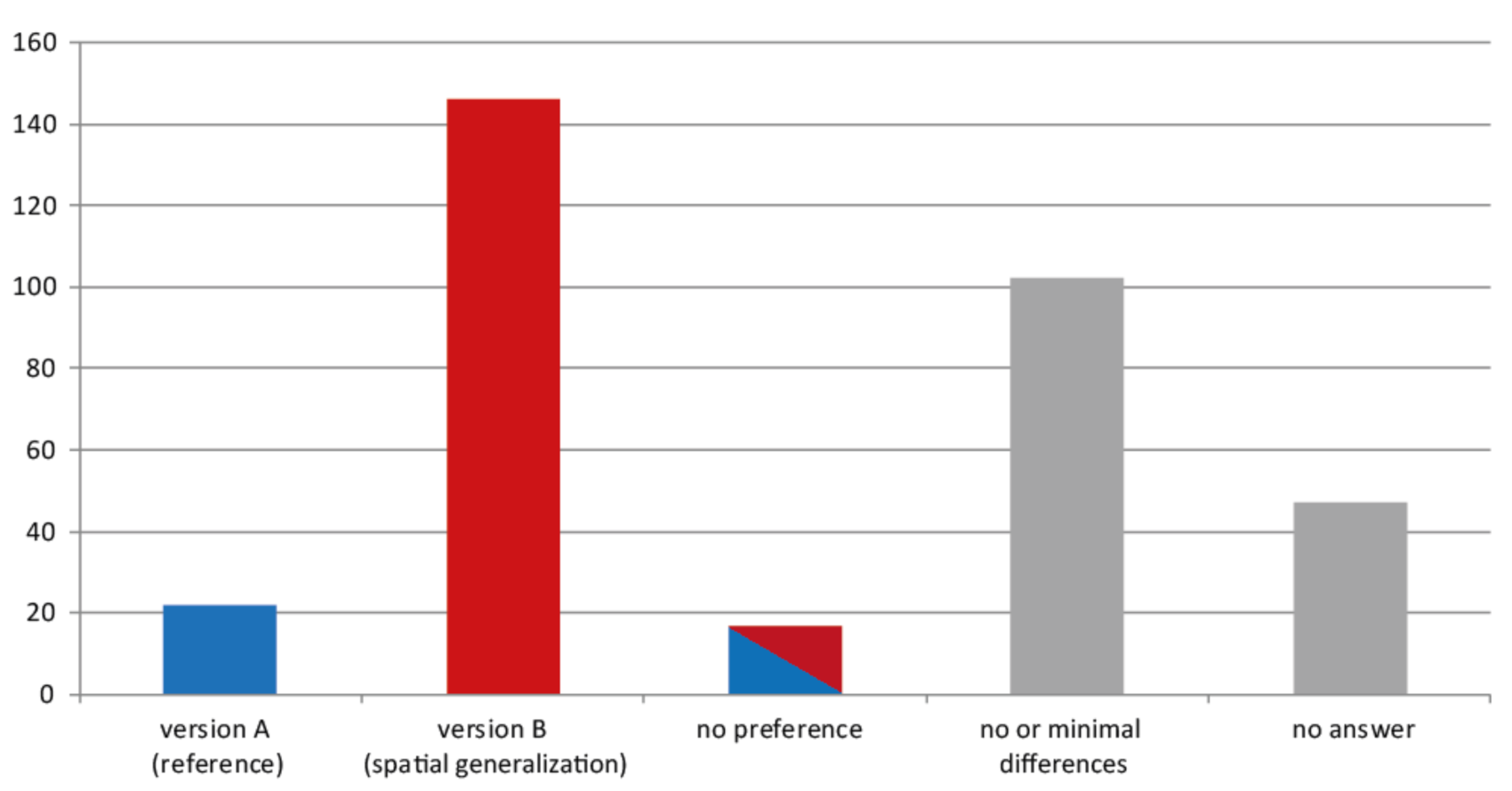
3.6. Described Perception and Preference
4. Discussion
4.1. Local Outlier Detection
4.2. Global Trend Detection
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harrower, M. The Cognitive Limits of Animated Maps. Cartographica 2007, 42, 349–357. [Google Scholar] [CrossRef]
- Goldsberry, K.; Battersby, S. Issues of Change Detection in Animated Choropleth Maps. Cartogr. Int. J. Geogr. Inf. Geovis. 2009, 44, 201–215. [Google Scholar] [CrossRef] [Green Version]
- DuBois, M.; Battersby, S.E. A Raster-Based Neighborhood Model for Evaluating Complexity in Dynamic Maps. In Proceedings of the AutoCarto 2012, Columbus, OH, USA, 16–18 September 2012. [Google Scholar]
- Rosenholtz, R. Capabilities and limitations of peripheral vision. Annu. Rev. Vis. Sci. 2016, 2, 437–457. [Google Scholar] [CrossRef] [Green Version]
- Sweller, J. Cognitive load during problem solving: Effects on learning. Cogn. Sci. 1988, 12, 257–285. [Google Scholar] [CrossRef]
- Sweller, J.; van Merriënboer, J.J.; Paas, F. Cognitive architecture and instructional design: 20 years later. Educ. Psychol. Rev. 2019, 31, 1–32. [Google Scholar] [CrossRef] [Green Version]
- Luck, S.J.; Vogel, E.K. The capacity of visual working memory for features and conjunctions. Nature 1997, 390, 279–281. [Google Scholar] [CrossRef]
- Metaferia, M.T. Visual Enhancement of Animated Time Series to Reduce Change Blindness. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2011. [Google Scholar]
- Harrower, M.; Fabrikant, S.I. The role of map animation for geographic visualization. In Geographic Visualization. Concepts, Tools and Applications; Dodge, M., Derby, M.M., Turner, M., Eds.; John Wiley & Sons: Chichester, UK, 2008; pp. 49–65. [Google Scholar]
- Harrower, M. Tips for designing effective animated maps. Cartogr. Perspect. 2003, 63–65. [Google Scholar] [CrossRef]
- Kraak, M.-J.; Edsall, R.; MacEachren, A.M. Cartographic animation and legends for temporal maps: Exploration and or interaction. In Proceedings of the 18th International Cartographic Conference, Stockholm, Sweden, 23–27 June 1997; pp. 253–261. [Google Scholar]
- Midtbø, T. Advanced legends for interactive dynamic maps. In Proceedings of the 23th International Cartographic Conference “Cartography for everyone and for you”, Moscow, Russia, 4–10 August 2007; pp. 4–10. [Google Scholar]
- Muehlenhaus, I. Web Cartography: Map Design for Interactive and Mobile Devices; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Opach, T.; Gołębiowska, I.; Fabrikant, S.I. How Do People View Multi-Component Animated Maps? Cartogr. J. 2014, 51, 330–342. [Google Scholar] [CrossRef]
- Fish, C.; Goldsberry, K.P.; Battersby, S. Change blindness in animated choropleth maps: An empirical study. Cartogr. Geogr. Inf. Sci. 2011, 38, 350–362. [Google Scholar] [CrossRef]
- Battersby, S.E.; Goldsberry, K.P. Considerations in Design of Transition Behaviors for Dynamic Thematic Maps. Cartogr. Perspect. 2010, 16–32. [Google Scholar] [CrossRef]
- Cybulski, P.; Medyńska-Gulij, B. Cartographic redundancy in reducing change blindness in detecting extreme values in spatio-temporal maps. ISPRS Int. J. Geo-Inf. 2018, 7, 8. [Google Scholar] [CrossRef] [Green Version]
- Multimäki, S.; Ahonen-Rainio, P. Temporally Transformed Map Animation for Visual Data Analysis. In Proceedings of the GEO Processing 2015: The 7th International Conference on Advanced Geographic Information Systems, Applications, and Services, Lisbon Portugal, 22–27 February 2015; pp. 25–31. [Google Scholar]
- Monmonier, M. Minimum-change categories for dynamic temporal choropleth maps. J. Pa. Acad. Sci. 1994, 68, 42–47. [Google Scholar]
- Monmonier, M. Temporal generalization for dynamic maps. Cartogr. Geogr. Inf. Syst. 1996, 23, 96–98. [Google Scholar] [CrossRef]
- Harrower, M. Visualizing change: Using cartographic animation to explore remotely-sensed data. Cartogr. Perspect. 2001, 30–42. [Google Scholar] [CrossRef]
- Harrower, M. Unclassed animated choropleth maps. Cartogr. J. 2007, 44, 313–320. [Google Scholar] [CrossRef]
- McCabe, C.A. Effects of Data Complexity and Map Abstraction on the Perception of Patterns in Infectious Disease Animations. Master’s Thesis, The Pennsylvania State University, University Park, PA, USA, 2009. [Google Scholar]
- Ogao, P.J.; Kraak, M.J. Defining visualization operations for temporal cartographic animation design. Int. J. Appl. Earth Obs. Geoinf. 2002, 4, 23–31. [Google Scholar] [CrossRef]
- Slocum, T.A.; Slutter, R.S., Jr.; Kessler, F.C.; Yoder, S.C. A Qualitative Evaluation of MapTime, A Program For Exploring Spatiotemporal Point Data. Cartographica 2004, 39, 43–68. [Google Scholar] [CrossRef] [Green Version]
- Traun, C.; Mayrhofer, C. Complexity reduction in choropleth map animations by autocorrelation weighted generalization of time-series data. Cartogr. Geogr. Inf. Sci. 2018, 45, 221–237. [Google Scholar] [CrossRef]
- Moran, P.A.P. Note on Continuous Stochastic Phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
- Crump, M.J.C.; McDonnell, J.V.; Gureckis, T.M. Evaluating Amazon’s Mechanical Turk as a Tool for Experimental Behavioral Research. PLoS ONE 2013, 8, e57410. [Google Scholar] [CrossRef] [Green Version]
- Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Ellis, A.R.; Burchett, W.W.; Harrar, S.W.; Bathke, A.C. Nonparametric inference for multivariate data: The R package npmv. J. Stat. Softw. 2017, 76, 1–18. [Google Scholar]
- Levin, D.T.; Momen, N.; Drivdahl, S.B.; Simons, D.J. Change Blindness Blindness: The Metacognitive Error of Overestimating Change-detection Ability. Vis. Cogn. 2000, 7, 397–412. [Google Scholar] [CrossRef]
- Simons, D.J. Attentional capture and inattentional blindness. Trends Cogn. Sci. 2000, 4, 147–155. [Google Scholar] [CrossRef]
- Wolfe, J.M.; Horowitz, T.S. Five factors that guide attention in visual search. Nat. Hum. Behav. 2017, 1, 0058. [Google Scholar] [CrossRef]
- Koch, C.; Ullman, S. Shifts in selective visual attention: Towards the underlying neural circuitry. Hum. Neurobiol. 1985, 4, 219–227. [Google Scholar] [PubMed]
- Veale, R.; Hafed, Z.M.; Yoshida, M. How is visual salience computed in the brain? Insights from behaviour, neurobiology and modelling. Philos. Trans. R. Soc. B Biol. Sci. 2017, 372, 20160113. [Google Scholar] [CrossRef]
- Bruce, N.D.; Tsotsos, J.K. Saliency, attention, and visual search: An information theoretic approach. J. Vis. 2009, 9, 5. [Google Scholar] [CrossRef]
- Itti, L.; Koch, C.; Niebur, E. A model of saliency-based visual attention for rapid scene analysis. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 1254–1259. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Tong, M.H.; Marks, T.K.; Shan, H.; Cottrell, G.W. SUN: A Bayesian framework for saliency using natural statistics. J. Vis. 2008, 8, 32. [Google Scholar] [CrossRef] [Green Version]
- Davies, C.; Fabrikant, S.I.; Hegarty, M. Toward Empirically Verified Cartographic Displays. In The Cambridge Handbook of Applied Perception Research; Szalma, J.L., Scerbo, M.W., Hancock, P.A., Parasuraman, R., Hoffman, R.R., Eds.; Cambridge University Press: Cambridge, UK, 2015; pp. 711–730. [Google Scholar]
- Fabrikant, S.I.; Goldsberry, K. Thematic relevance and perceptual salience of dynamic geovisualization displays. In Proceedings of the 22th ICA/ACI International Cartographic Conference, A Coruña, Spain, 9–16 July 2005. [Google Scholar]
- Koehler, K.; Guo, F.; Zhang, S.; Eckstein, M.P. What do saliency models predict? J. Vis. 2014, 14, 14. [Google Scholar] [CrossRef]
- Yantis, S. How visual salience wins the battle for awareness. Nat. Neurosci. 2005, 8, 975–977. [Google Scholar] [CrossRef]
- Slocum, T.A.; McMaster, R.B.; Kessler, F.C.; Howard, H.H. Thematic Cartography and Geovisualization, 3rd ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Brown, R.O.; MacLeod, D.I. Color appearance depends on the variance of surround colors. Curr. Biol. 1997, 7, 844–849. [Google Scholar] [CrossRef] [Green Version]
- Liesefeld, H.R.; Moran, R.; Usher, M.; Müller, H.J.; Zehetleitner, M. Search efficiency as a function of target saliency: The transition from inefficient to efficient search and beyond. J. Exp. Psychol. Human Percept. Perform. 2016, 42, 821. [Google Scholar] [CrossRef] [Green Version]
- Wagemans, J.; Elder, J.H.; Kubovy, M.; Palmer, S.E.; Peterson, M.A.; Singh, M.; von der Heydt, R. A century of Gestalt psychology in visual perception: I. Perceptual grouping and figure–ground organization. Psychol. Bull. 2012, 138, 1172–1217. [Google Scholar] [CrossRef] [Green Version]
- Snowden, R.; Thompson, P.; Troscianko, T. Basic Vision: An Introduction to Visual Perception; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Wandell, B.A.; Dumoulin, S.O.; Brewer, A.A. Visual field maps in human cortex. Neuron 2007, 56, 366–383. [Google Scholar] [CrossRef] [Green Version]
- Griffin, A.L.; MacEachren, A.M.; Hardisty, F.; Steiner, E.; Li, B. A comparison of animated maps with static small-multiple maps for visually identifying space-time clusters. Ann. Assoc. Am. Geogr. 2006, 96, 740–753. [Google Scholar] [CrossRef] [Green Version]
- Shulman, G.L.; Sullivan, M.A.; Gish, K.; Sakoda, W.J. The Role of Spatial-Frequency Channels in the Perception of Local and Global Structure. Perception 1986, 15, 259–273. [Google Scholar] [CrossRef]
- Sowden, P.T.; Schyns, P.G. Channel surfing in the visual brain. Trends Cogn. Sci. 2006, 10, 538–545. [Google Scholar] [CrossRef] [Green Version]
- Nothdurft, H.-C. Attention shifts to salient targets. Vis. Res. 2002, 42, 1287–1306. [Google Scholar] [CrossRef] [Green Version]
- Billino, J.; Bremmer, F.; Gegenfurtner, K.R. Differential aging of motion processing mechanisms: Evidence against general perceptual decline. Vis. Res. 2008, 48, 1254–1261. [Google Scholar] [CrossRef] [Green Version]
- Snowden, R.J.; Kavanagh, E. Motion Perception in the Ageing Visual System: Minimum Motion, Motion Coherence, and Speed Discrimination Thresholds. Perception 2006, 35, 9–24. [Google Scholar] [CrossRef]
- Bak, C.; Kocak, A.; Erdem, E.; Erdem, A. Spatio-Temporal Saliency Networks for Dynamic Saliency Prediction. IEEE Trans. Multimedia 2018, 20, 1688–1698. [Google Scholar] [CrossRef] [Green Version]






| Group A | Group B | Group C | Group D | ∑ | |
|---|---|---|---|---|---|
| None or little experience with maps | 17 | 12 | 17 | 11 | 57 |
| Active map use, no background in cartography | 35 | 38 | 34 | 44 | 151 |
| Basic knowledge in cartography | 37 | 34 | 30 | 23 | 124 |
| Advanced cart. knowledge, active mapping | 17 | 23 | 23 | 26 | 89 |
| Expert knowledge in cartography | 4 | 3 | 6 | 6 | 19 |
| ∑ | 110 | 110 | 110 | 110 | 440 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Traun, C.; Schreyer, M.L.; Wallentin, G. Empirical Insights from a Study on Outlier Preserving Value Generalization in Animated Choropleth Maps. ISPRS Int. J. Geo-Inf. 2021, 10, 208. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi10040208
Traun C, Schreyer ML, Wallentin G. Empirical Insights from a Study on Outlier Preserving Value Generalization in Animated Choropleth Maps. ISPRS International Journal of Geo-Information. 2021; 10(4):208. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi10040208
Chicago/Turabian StyleTraun, Christoph, Manuela Larissa Schreyer, and Gudrun Wallentin. 2021. "Empirical Insights from a Study on Outlier Preserving Value Generalization in Animated Choropleth Maps" ISPRS International Journal of Geo-Information 10, no. 4: 208. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi10040208






