The Soil Nutrient Digital Mapping for Precision Agriculture Cases in the Trans-Ural Steppe Zone of Russia Using Topographic Attributes
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Dong, W.; Wu, T.; Luo, J.; Sun, Y.; Xia, L. Land Parcel-Based Digital Soil Mapping of Soil Nutrient Properties in an Alluvial-Diluvia Plain Agricultural Area in China. Geoderma 2019, 340, 234–248. [Google Scholar] [CrossRef]
- Ma, Y.; Minasny, B.; Wu, C. Mapping Key Soil Properties to Support Agricultural Production in Eastern China. Geoderma Reg. 2017, 10, 144–153. [Google Scholar] [CrossRef]
- Savin, I.Y.; Ovechkin, S.V. On the Updating of Medium-Scale Soil Maps. Eurasian Soil Sci. 2014, 47, 987–994. [Google Scholar] [CrossRef]
- McBratney, A.B.; Mendonça Santos, M.L.; Minasny, B. On Digital Soil Mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Arrouays, D.; Grundy, M.; Hartemink, A.E.; Hempel, J.; Heuvelink, G.B.M.; Hong, S.Y.; Lagacherie, P.; Lelyk, G.; Mcbratney, A.B.; Mckenzie, N.J.; et al. GlobalSoilMap: Toward a Fine-Resolution Global Grid of Soil Properties. Adv. Agron. 2014, 125, 93–134. [Google Scholar] [CrossRef]
- Dokuchaev, V.V. Our Steppes—At One Time and Now; Yevdokimoff Press: St. Petersburg, Russia, 1892. (In Russian) [Google Scholar]
- Jenny, H. Factors of Soil Formation, A System of Quantitative Pedology; McGraw-Hill: New York, NY, USA, 1941. [Google Scholar]
- Jenny, H. Derivation of State Factor Equations of Soils and Ecosystems. Soil Sci. Soc. Am. J. 1961, 25, 385–388. [Google Scholar] [CrossRef]
- Mehnatkesh, A.; Ayoubi, S.; Jalalian, A.; Sahrawat, K.L. Relationships between Soil Depth and Terrain Attributes in a Semi Arid Hilly Region in Western Iran. J. Mt. Sci. 2013, 10, 163–172. [Google Scholar] [CrossRef]
- McKenzie, N.J.; Gessler, P.E.; Ryan, P.J.; O’Connell, D.A. The role of terrain analysis in soil mapping. In Terrain Analysis: Principles and Applications; Wilson, J.P., Gallant, J.C., Eds.; John Wiley and Sons: New York, NY, USA, 2000; pp. 245–265. [Google Scholar]
- Moore, I.D.; Gessler, P.E.; Nielsen, G.A.; Peterson, G.A. Soil Attribute Prediction Using Terrain Analysis. Soil Sci. Soc. Am. J. 1993, 57, 443–452. [Google Scholar] [CrossRef]
- Odeha, I.O.A.; McBratney, A.B.; Chittleborough, D.J. Spatial Prediction of Soil Properties from Landform Attributes Derived from a Digital Elevation Model. Geoderma 1994, 63, 197–214. [Google Scholar] [CrossRef]
- Florinsky, I.V.; Eilers, R.G.; Manning, G.R.; Fuller, L.G. Prediction of Soil Properties by Digital Terrain Modelling. Environ. Model. Softw. 2002, 17, 295–311. [Google Scholar] [CrossRef]
- Mulder, V.L.; de Bruin, S.; Schaepman, M.E.; Mayr, T.R. The Use of Remote Sensing in Soil and Terrain Mapping—A Review. Geoderma 2011, 162, 1–19. [Google Scholar] [CrossRef]
- Gopp, N.V.; Nechaeva, T.V.; Savenkov, O.A.; Smirnova, N.V.; Smirnov, V.V. The Methods of Geomorphometry and Digital Soil Mapping for Assessing Spatial Variability in the Properties of Agrogray Soils on a Slope. Eurasian Soil Sci. 2017, 50, 20–29. [Google Scholar] [CrossRef]
- Takoutsing, B.; Weber, J.C.; Martín, J.A.R.; Shepherd, K.; Aynekulu, E.; Sila, A. An Assessment of the Variation of Soil Properties with Landscape Attributes in the Highlands of Cameroon. Land Degrad. Dev. 2018, 29, 2496–2505. [Google Scholar] [CrossRef]
- Sena, N.C.; Veloso, G.V.; Fernandes-Filho, E.I.; Francelino, M.R.; Schaefer, C.E.G.R. Analysis of Terrain Attributes in Different Spatial Resolutions for Digital Soil Mapping Application in Southeastern Brazil. Geoderma Reg. 2020, 21, e00268. [Google Scholar] [CrossRef]
- Komissarov, M.; Ogura, S. Siltation and Radiocesium Pollution of Small Lakes in Different Catchment Types Far from the Fukushima Daiichi Nuclear Power Plant Accident Site. Int. Soil Water Conserv. Res. 2020, 8, 56–65. [Google Scholar] [CrossRef]
- Bartelletti, C.; Giannecchini, R.; Avanzi, G.D.; Galanti, Y.; Mazzali, A. The Influence of Geological–Morphological and Land Use Settings on Shallow Landslides in the Pogliaschina T. Basin (Northern Apennines, Italy). J. Maps 2017, 13, 142–152. [Google Scholar] [CrossRef] [Green Version]
- Chai, Y.; Jiang, S.; Guo, W.; Qin, M.; Pan, J.; Bahadur, A.; Shi, G.; Luo, J.; Jin, Z.; Liu, Y.; et al. The Effect of Slope Aspect on the Phylogenetic Structure of Arbuscular Mycorrhizal Fungal Communities in an Alpine Ecosystem. Soil Biol. Biochem. 2018, 126, 103–113. [Google Scholar] [CrossRef]
- Gabbasova, I.M.; Suleymanov, R.R.; Khabirov, I.K.; Komissarov, M.A.; Garipov, T.T.; Sidorova, L.V.; Nazyrova, F.I. Multiple Assessment of the Soil Cover in the Area of Natural Monuments Tra-Tau and Yurak-Tau Monadnocks under Conditions of Technogenic Loads. Eurasian Soil Sci. 2014, 47, 35–46. [Google Scholar] [CrossRef]
- Suleymanov, R.; Yaparov, I.; Saifullin, I.; Vildanov, I.; Shirokikh, P.; Suleymanov, A.; Komissarov, M.; Liebelt, P.; Nigmatullin, A.; Khamidullin, R. The Current State of Abandoned Lands in the Northern Forest-Steppe Zone at the Republic of Bashkortostan (Southern Ural, Russia). Span. J. Soil Sci. 2020, 10, 29–44. [Google Scholar] [CrossRef]
- Suleymanov, A.R. Geomorphometric and geoinformation approach to meliorative evaluation of the territory. In Climate Change Impacts on Hydrological Processes and Sediment Dynamics: Measurement, Modelling and Management; Chalov, S., Golosov, V., Li, R., Tsyplenkov, A., Eds.; Springer Proceedings in Earth and Environmental Sciences; Springer International Publishing: Cham, Switzerland, 2019; pp. 72–75. [Google Scholar] [CrossRef]
- Forkuor, G.; Hounkpatin, O.K.L.; Welp, G.; Thiel, M. High Resolution Mapping of Soil Properties Using Remote Sensing Variables in South-Western Burkina Faso: A Comparison of Machine Learning and Multiple Linear Regression Models. PLoS ONE 2017, 12, e0170478. [Google Scholar] [CrossRef]
- Zhou, T.; Geng, Y.; Chen, J.; Sun, C.; Haase, D.; Lausch, A. Mapping of Soil Total Nitrogen Content in the Middle Reaches of the Heihe River Basin in China Using Multi-Source Remote Sensing-Derived Variables. Remote Sens. 2019, 11, 2934. [Google Scholar] [CrossRef] [Green Version]
- Kingsley, J.; Lawani, S.; Esther, A.; Ndiye, K.; Sunday, O.; Penížek, V. Predictive Mapping of Soil Properties for Precision Agriculture Using Geographic Information System (GIS) Based Geostatistics Models. Mod. Appl. Sci. 2019, 13, 60. [Google Scholar] [CrossRef] [Green Version]
- John, K.; Abraham Isong, I.; Michael Kebonye, N.; Okon Ayito, E.; Chapman Agyeman, P.; Marcus Afu, S. Using Machine Learning Algorithms to Estimate Soil Organic Carbon Variability with Environmental Variables and Soil Nutrient Indicators in an Alluvial Soil. Land 2020, 9, 487. [Google Scholar] [CrossRef]
- Tranmer, M.; Murphy, J.; Elliot, M.; Pampaka, M. Multiple Linear Regression, 2nd ed.; Cathie Marsh Institute Working Paper; Cathie Marsh Institute: Manchester, UK, 2020. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Shmilovici, A. Support vector machines. In Data Mining and Knowledge Discovery Handbook; Maimon, O., Rokach, L., Eds.; Springer: Boston, MA, USA, 2009; pp. 231–247. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E. Data Mining: Practical Machine Learning Tools and Techniques, 2nd ed.; Elsevier: San Francisco, CA, USA, 2005; p. 525. [Google Scholar]
- Heung, B.; Ho, H.C.; Zhang, J.; Knudby, A.; Bulmer, C.E.; Schmidt, M.G. An Overview and Comparison of Machine-Learning Techniques for Classification Purposes in Digital Soil Mapping. Geoderma 2016, 265, 62–77. [Google Scholar] [CrossRef]
- Guan, X.; Wang, S.; Gao, Z.; Lv, Y. Dynamic Prediction of Soil Salinization in an Irrigation District Based on the Support Vector Machine. Math. Comput. Model. 2013, 58, 719–724. [Google Scholar] [CrossRef]
- Parveen, N.; Zaidi, S.; Danish, M. Support Vector Regression Model for Predicting the Sorption Capacity of Lead (II). Perspect. Sci. 2016, 8, 629–631. [Google Scholar] [CrossRef] [Green Version]
- Mahmoudzadeh, H.; Matinfar, H.R.; Taghizadeh-Mehrjardi, R.; Kerry, R. Spatial Prediction of Soil Organic Carbon Using Machine Learning Techniques in Western Iran. Geoderma Reg. 2020, 21, e00260. [Google Scholar] [CrossRef]
- IUSS Working Group WRB. World reference base for soil resources. In International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; World Soil Resources Reports No. 106; FAO: Rome, Italy, 2014. [Google Scholar]
- Jones, J.B., Jr. (Ed.) Soil Analysis Handbook of Reference Methods, 1st ed.; CRC Press: Boca Raton, FL, USA, 1999; p. 264. [Google Scholar]
- Pansu, M.; Gautheyrou, J. Handbook of Soil Analysis: Mineralogical, Organic and Inorganic Methods; Springer: Berlin, Germany, 2006; p. 993. [Google Scholar]
- Carter, M.R.; Gregorich, E.G. (Eds.) Soil Sampling and Methods of Analysis, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2008; p. 1264. [Google Scholar]
- Mallows, C.L. Some Comments on Cp. Technometrics 2000, 42, 87–94. [Google Scholar] [CrossRef]
- Mattera, D.; Haykin, S. Support vector machines for dynamic reconstruction of a chaotic system. In Advances in Kernel Methods: Support Vector Learning; MIT Press: Cambridge, MA, USA, 1999; pp. 211–241. [Google Scholar]
- Cherkassky, V.; Ma, Y. Practical selection of SVM parameters and noise estimation for SVM regression. Neural Netw. 2004, 17, 113–126. [Google Scholar] [CrossRef] [Green Version]
- Hengl, T.; Heuvelink, G.B.M.; Kempen, B.; Leenaars, J.G.B.; Walsh, M.G.; Shepherd, K.D.; Sila, A.; MacMillan, R.A.; de Jesus, J.M.; Tamene, L.; et al. Mapping Soil Properties of Africa at 250 m Resolution: Random Forests Significantly Improve Current Predictions. PLoS ONE 2015, 10, e0125814. [Google Scholar] [CrossRef] [PubMed]
- Heuvelink, G.B.M.; Angelini, M.E.; Poggio, L.; Bai, Z.; Batjes, N.H.; van den Bosch, R.; Bossio, D.; Estella, S.; Lehmann, J.; Olmedo, G.F.; et al. Machine Learning in Space and Time for Modelling Soil Organic Carbon Change. Eur. J. Soil Sci. 2020, 1–17. [Google Scholar] [CrossRef]
- Zeraatpisheh, M.; Ayoubi, S.; Jafari, A.; Tajik, S.; Finke, P. Digital Mapping of Soil Properties Using Multiple Machine Learning in a Semi-Arid Region, Central Iran. Geoderma 2019, 338, 445–452. [Google Scholar] [CrossRef]
- Jaber, S.M.; Lant, C.L.; Al-Qinna, M.I. Estimating Spatial Variations in Soil Organic Carbon Using Satellite Hyperspectral Data and Map Algebra. Int. J. Remote Sens. 2011, 32, 5077–5103. [Google Scholar] [CrossRef]
- Vaudour, E.; Gomez, C.; Fouad, Y.; Lagacherie, P. Sentinel-2 Image Capacities to Predict Common Topsoil Properties of Temperate and Mediterranean Agroecosystems. Remote Sens. Environ. 2019, 223, 21–33. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015; Available online: http://www.Rproject.org (accessed on 15 November 2020).
- RStudio. Integrated Development Environment for R; RStudio: Boston, MA, USA, 2015; Available online: http://www.r-studio.com (accessed on 15 November 2020).
- Gabbasova, I.M.; Garipov, T.T.; Komissarov, M.A.; Suleimanov, R.R.; Suyundukov, Y.T.; Khasanova, R.F.; Sidorova, L.V.; Komissarov, A.V.; Suleimanov, A.R.; Nazyrova, F.I. The Impact of Fires on the Properties of Steppe Soils in the Trans-Ural Region. Eurasian Soil Sci. 2019, 52, 1598–1607. [Google Scholar] [CrossRef]
- Silatsa, F.B.T.; Yemefack, M.; Tabi, F.O.; Heuvelink, G.B.M.; Leenaars, J.G.B. Assessing Countrywide Soil Organic Carbon Stock Using Hybrid Machine Learning Modelling and Legacy Soil Data in Cameroon. Geoderma 2020, 367, 114260. [Google Scholar] [CrossRef]
- Sun, X.-L.; Wang, Y.; Wang, H.-L.; Zhang, C.; Wang, Z.-L. Digital Soil Mapping Based on Empirical Mode Decomposition Components of Environmental Covariates. Eur. J. Soil Sci. 2019, 70, 1109–1127. [Google Scholar] [CrossRef]
- Mosleh, Z.; Salehi, M.H.; Jafari, A.; Borujeni, I.E.; Mehnatkesh, A. The Effectiveness of Digital Soil Mapping to Predict Soil Properties over Low-Relief Areas. Environ. Monit. Assess. 2016, 188, 195. [Google Scholar] [CrossRef]
- Gallant, J.C.; Dowling, T.I. A Multiresolution Index of Valley Bottom Flatness for Mapping Depositional Areas. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Sahabiev, I.A.; Ryazanov, S.S.; Kolcova, T.G.; Grigoryan, B.R. Selection of a Geostatistical Method to Interpolate Soil Properties of the State Crop Testing Fields Using Attributes of a Digital Terrain Model. Eurasian Soil Sci. 2018, 51, 255–267. [Google Scholar] [CrossRef]
- Wang, S.; Zhuang, Q.; Wang, Q.; Jin, X.; Han, C. Mapping Stocks of Soil Organic Carbon and Soil Total Nitrogen in Liaoning Province of China. Geoderma 2017, 305, 250–263. [Google Scholar] [CrossRef]
- Adhikari, K.; Hartemink, A.E.; Minasny, B.; Kheir, R.B.; Greve, M.B.; Greve, M.H. Digital Mapping of Soil Organic Carbon Contents and Stocks in Denmark. PLoS ONE 2014, 9, e105519. [Google Scholar] [CrossRef] [PubMed]
- Assami, T.; Hamdi-Aїssa, B. Digital Mapping of Soil Classes in Algeria—A Comparison of Methods. Geoderma Reg. 2019, 16, e00215. [Google Scholar] [CrossRef]
- Mondejar, J.P.; Tongco, A.F. Estimating Topsoil Texture Fractions by Digital Soil Mapping—A Response to the Long Outdated Soil Map in the Philippines. Sustain. Environ. Res. 2019, 29, 31. [Google Scholar] [CrossRef] [Green Version]
- Khaziev, F.K. Soils of Bashkortostan. In Ecologic-Genetic and Agroproductive Characterization; Gilem: Ufa, Russia, 1995; Volume 1, p. 385. (In Russian) [Google Scholar]
- Gabbasova, I.M.; Suleimanov, R.R.; Khabirov, I.K.; Komissarov, M.A.; Fruehauf, M.; Liebelt, P.; Garipov, T.T.; Sidorova, L.V.; Khaziev, F.K. Temporal changes of eroded soils depending on their agricultural use in the southern Cis-Ural region. Eurasian Soil Sci. 2016, 49, 1204–1210. [Google Scholar] [CrossRef]
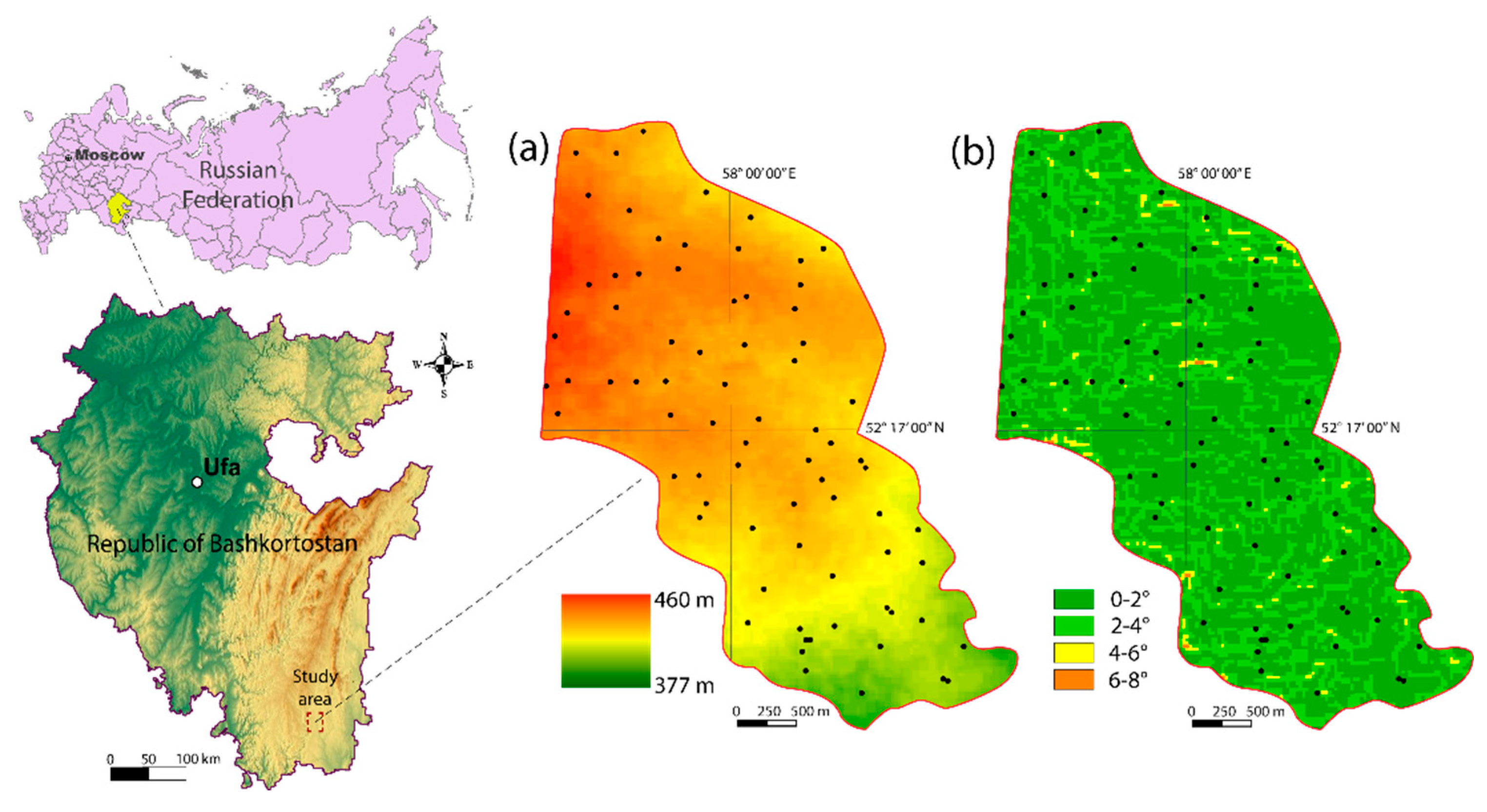
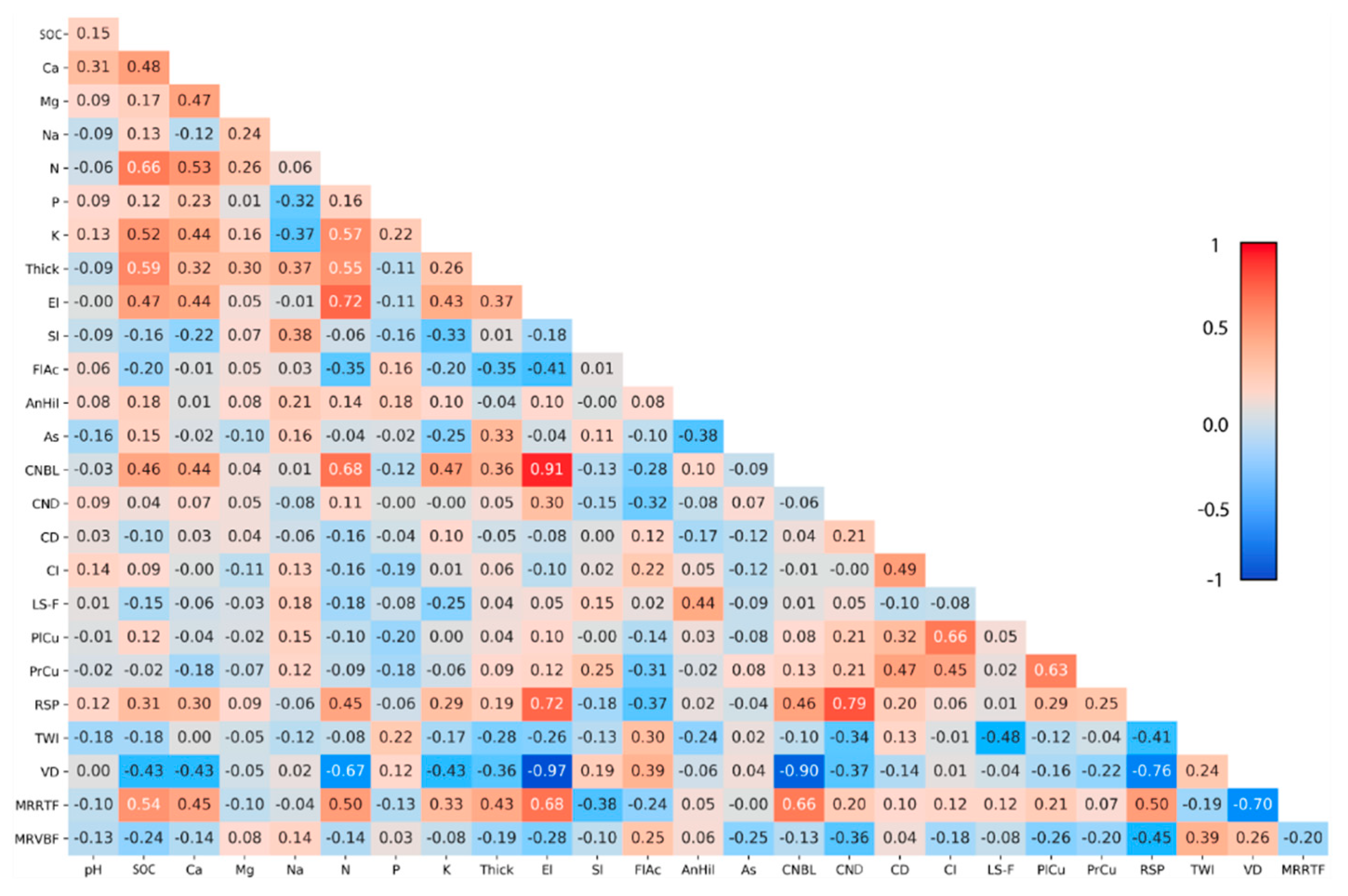

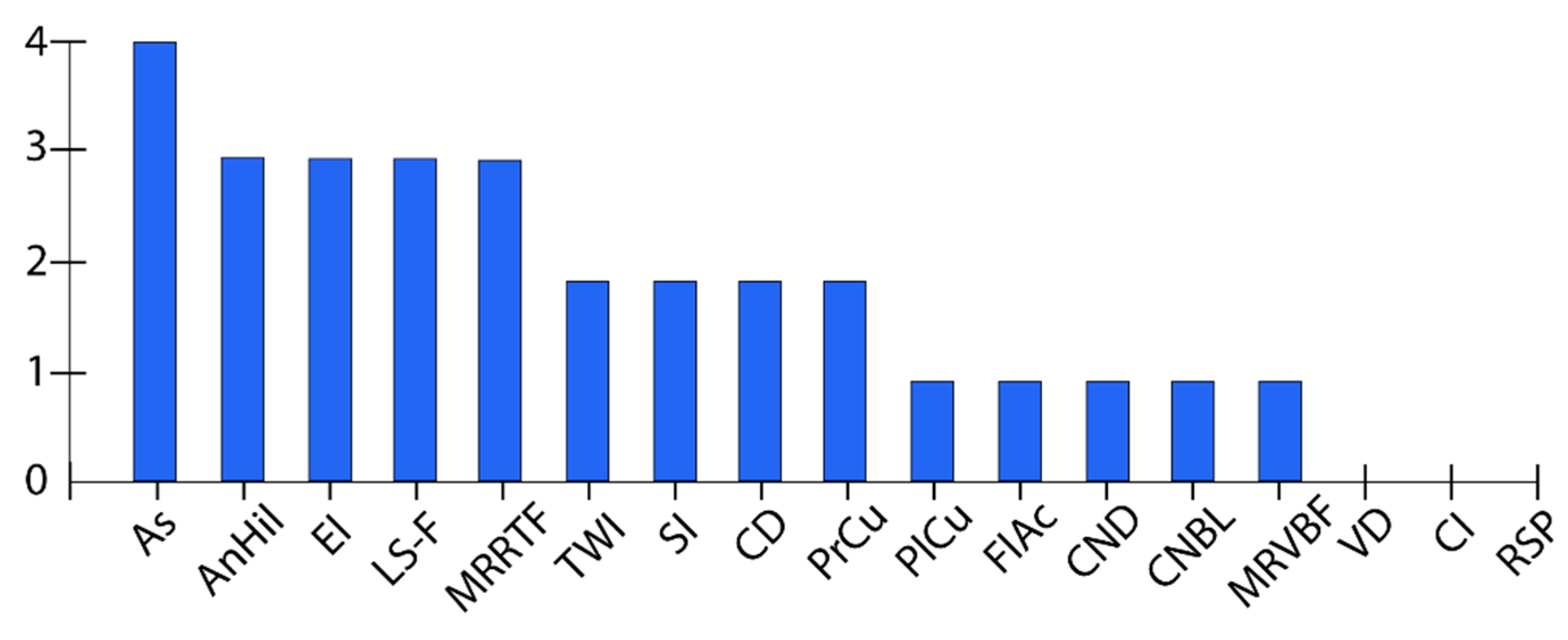

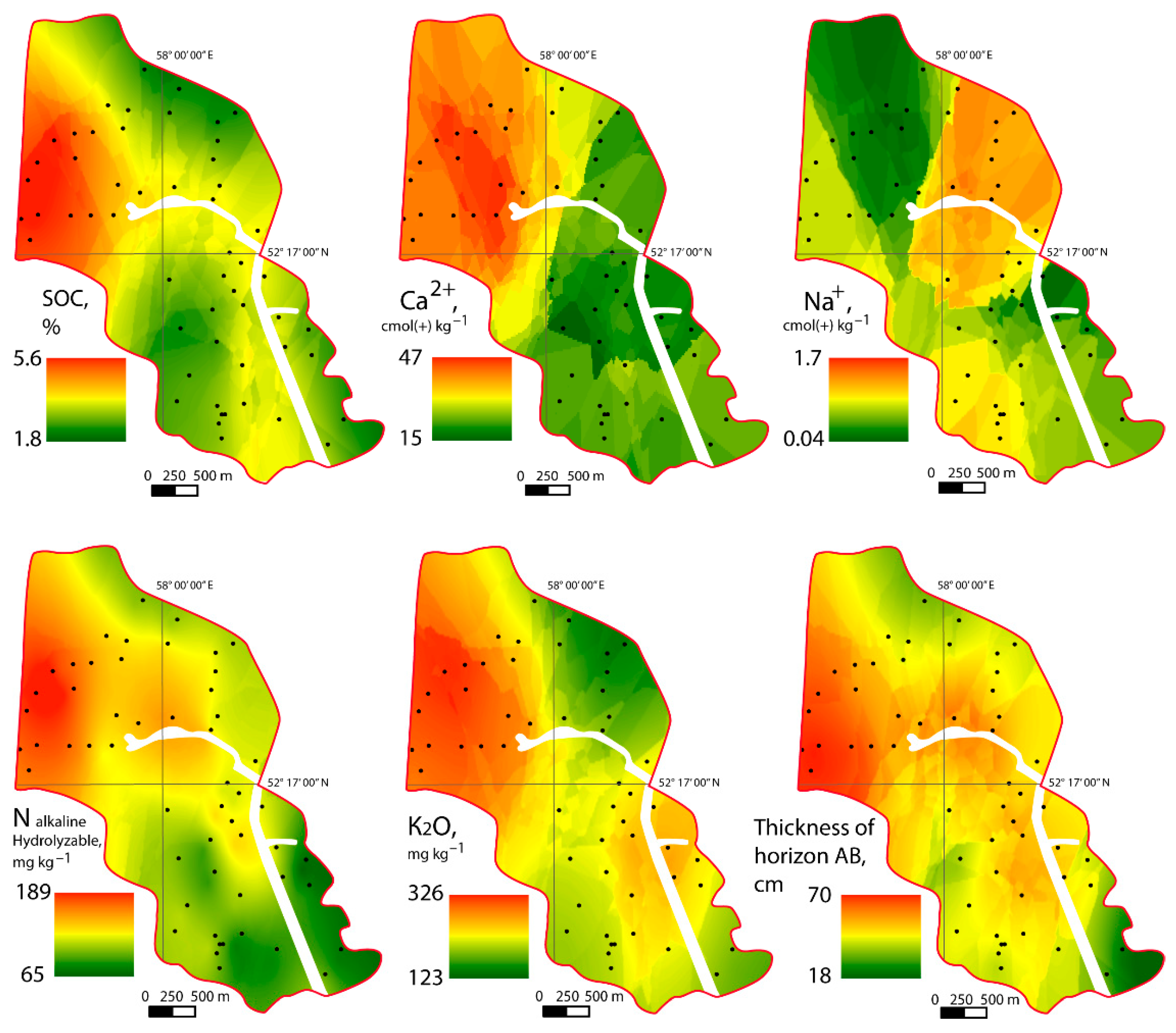
| № | Topographic Attributes | Acronym |
|---|---|---|
| 1 | Elevation | El |
| 2 | Aspect | As |
| 3 | Slope | Sl |
| 4 | Profile curvature | PrCu |
| 5 | Plan curvature | PlCu |
| 6 | Flow accumulation | FlAc |
| 7 | Analytical hillshading | AnHil |
| 8 | Channel network base level | CNBL |
| 9 | Channel network distance | CND |
| 10 | Convergence index | CI |
| 11 | LS-Factor | LS-F |
| 12 | Topographic wetness index | TWI |
| 13 | Valley depth | VD |
| 14 | Closed depressions | CD |
| 15 | Relative slope position | RSP |
| 16 | Multiresolution ridge top flatness | MRRTF |
| 17 | Multiresolution valley bottom flatness | MRVBF |
| Parameter | SOC, % | The Thickness of AB Horizon, (cm) | pH (H2O) | N Alkaline Hydrolyzable, mg kg−1 | Exchangeable Cations | Available | |||
|---|---|---|---|---|---|---|---|---|---|
| Ca2+ | Mg2+ | Na+ | P2O5 | K2O | |||||
| cmol(+) kg−1 | mg kg−1 | ||||||||
| n = 76 | |||||||||
| Mean | 3.7 | 44.1 | 6.8 | 132.6 | 31.8 | 9.7 | 0.3 | 1.8 | 220.2 |
| Min | 1.8 | 18 | 6.4 | 65 | 15 | 5 | 0.04 | 0.4 | 123 |
| Max | 5.6 | 70 | 8.0 | 189 | 47 | 15 | 1.7 | 4.6 | 326 |
| SD | 0.9 | 9.3 | 0.3 | 26.6 | 6.2 | 2.2 | 0.3 | 0.8 | 52.7 |
| CV (%) | 24.3 | 20.9 | 4.4 | 20.1 | 19.5 | 22.7 | 113.3 | 44.4 | 23.9 |
| Soil Parametr | Number of Variables | Variables for Modeling | MLR | SVM | SVM Parameters | |||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | C | Gamma | |||
| SOC | 5 | AnHil, As, LS-F, TWI, MRRTF | 0.52 | 0.60 | 0.66 | 0.53 | 1 | 0.2 |
| Na | 5 | Sl, AnHil, As, PlCu, MRVBF | 0.35 | 0.21 | 0.49 | 0.20 | 1 | 0.2 |
| Ca | 4 | El, CD, PrCu, MRRTF | 0.31 | 5.84 | 0.43 | 5.33 | 1 | 0.2 |
| N | 5 | El, Sl, AnHil, LS-F, PrCu | 0.66 | 15.31 | 0.74 | 14.23 | 1 | 0.2 |
| P | 2 | AnHil, TWI | 0.11 | 1.64 | 0.16 | 0.73 | 0.1 | 0.2 |
| Mg | 2 | VD, MRRTF | 0.04 | 10.05 | 0.20 | 2.09 | 1 | 0.5 |
| K | 8 | El, CNBL, Sl, As, CND, CD, LS-F, TWI | 0.57 | 35.51 | 0.62 | 32.34 | 1 | 0.2 |
| pH | 1 | TWI | 0.03 | 6.61 | 0.02 | 0.30 | 0.1 | 0.2 |
| Thickness of AB | 3 | FlAc, As, MRRTF | 0.35 | 47.03 | 0.52 | 6.81 | 1 | 0.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suleymanov, A.; Abakumov, E.; Suleymanov, R.; Gabbasova, I.; Komissarov, M. The Soil Nutrient Digital Mapping for Precision Agriculture Cases in the Trans-Ural Steppe Zone of Russia Using Topographic Attributes. ISPRS Int. J. Geo-Inf. 2021, 10, 243. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi10040243
Suleymanov A, Abakumov E, Suleymanov R, Gabbasova I, Komissarov M. The Soil Nutrient Digital Mapping for Precision Agriculture Cases in the Trans-Ural Steppe Zone of Russia Using Topographic Attributes. ISPRS International Journal of Geo-Information. 2021; 10(4):243. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi10040243
Chicago/Turabian StyleSuleymanov, Azamat, Evgeny Abakumov, Ruslan Suleymanov, Ilyusya Gabbasova, and Mikhail Komissarov. 2021. "The Soil Nutrient Digital Mapping for Precision Agriculture Cases in the Trans-Ural Steppe Zone of Russia Using Topographic Attributes" ISPRS International Journal of Geo-Information 10, no. 4: 243. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi10040243







