Toward Improving Image Retrieval via Global Saliency Weighted Feature
Abstract
:1. Introduction
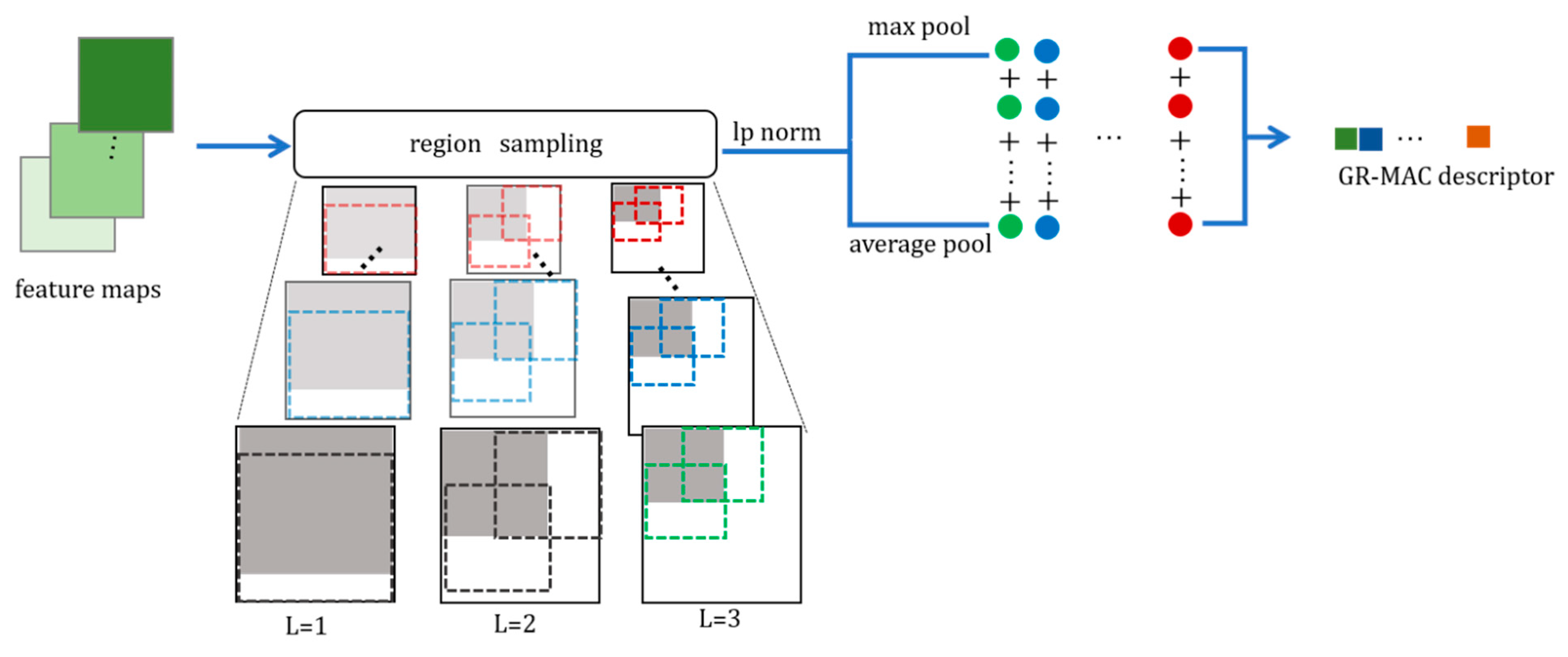
- We introduce a novel feature pooling method, named generalized R-MAC, which can capture the information contained in all the feature points in each region of R-MAC [25] instead of only considering the maximum value of the feature points in each region.
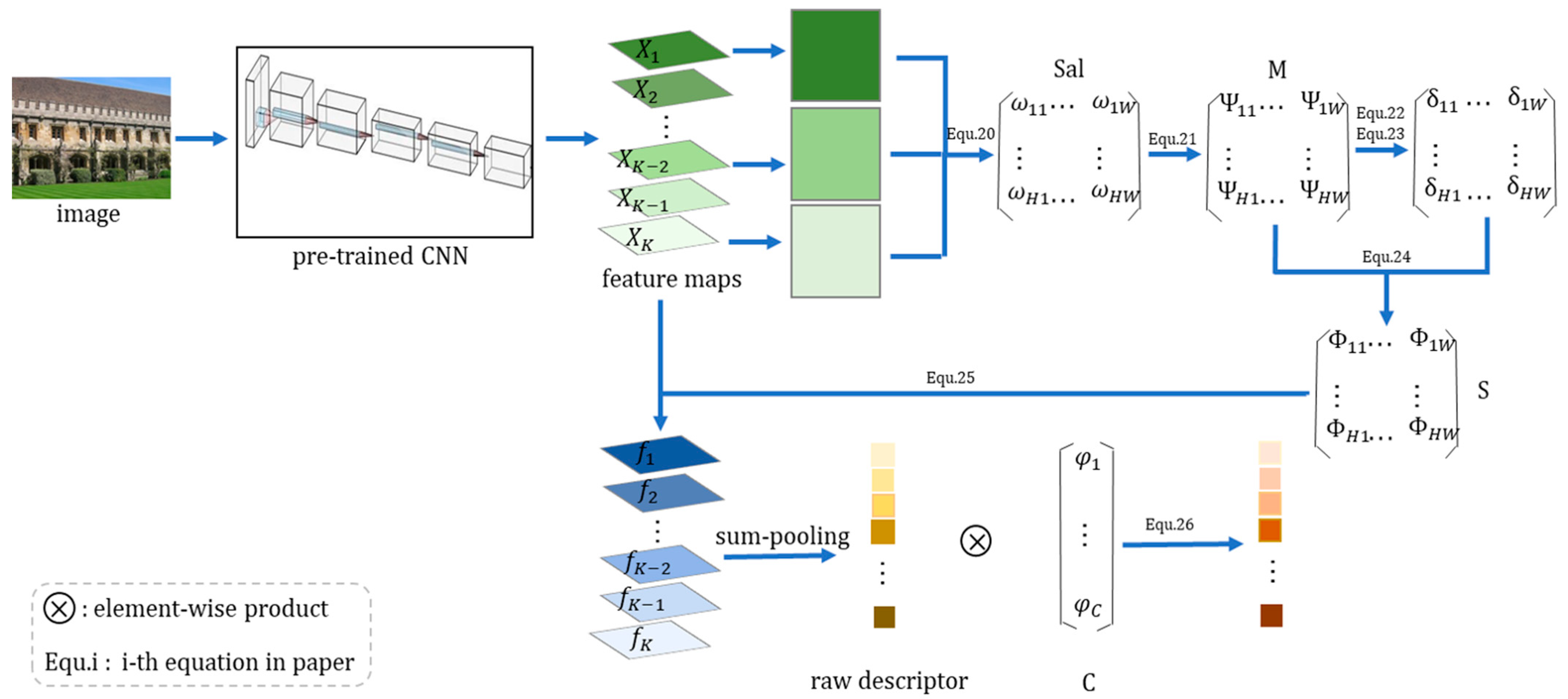
- We present an approach for the aggregation of convolutional features, including nonparametric saliency weighting and pooling steps. It focuses more attention on the convolutional features of the salient region without losing the information of the entire building (target region).
- We conducted comprehensive experiments on several popular data sets, and the outcomes demonstrate that our method provides state-of-the-art results without any fine-tuning.
2. Related Work
2.1. Aggregation Methods
2.2. Normalization and Whitening
2.3. Similarity Measurement Method
2.4. Query Expansion
3. Proposed Method
3.1. Algorithm Background
3.2. Generalized R-MAC
3.3. Saliency Joint Weighting Method
4. Experiments and Evaluation
4.1. Data Set
- Oxford5k data set [33]: This data set is provided by Flickr and contains 11 landmarks in the Oxford data set and a total of 5063 images.
- Paris6k data set [35]: Paris6k is also provided by Flickr. There are 11 categories of Paris buildings, which includes 6412 images and 5 query regions altogether for each class.
- Holidays data set [36]: The Holidays data set consists of 500 groups of similar images; each group has a query image for a total of 1491 images.
- Revisited Oxford and Paris [37]: The Revised-Oxford (Roxford) and Revisited-Paris (Rparis) data sets consist of 4993 and 6322 images, respectively; each data set has 70 queries images. They re-examine the oxford5k and paris6k data sets by deleting comments and adding images. There are three difficulty levels of evaluation protocol: easy, medium, and hard.
4.2. Test Environment and Details
4.3. Testing the Two Modules Separately
4.4. Feature Aggregation Method Comparison
4.5. Discussion
4.6. Parameter Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alzu’bi, A.; Amira, A.; Ramzan, N. Content-Based Image Retrieval with Compact Deep Convolutional Features. Neurocomputing 2017, 249, 95–105. [Google Scholar] [CrossRef] [Green Version]
- Smeulders, A.W.M.; Worring, M.; Santini, S.; Gupta, A.; Jain, R. Content-based image retrieval at the end of the early. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 22, 1349–1380. [Google Scholar] [CrossRef]
- Yue-Hei Ng, J.; Yang, F.; Davis, L.S. Exploiting local features from deep networks for image retrieval. In Proceedings of 2015 Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, New York, NY, USA, 7–12 June 2015; pp. 53–61. [Google Scholar]
- Zheng, L.; Yang, Y.; Tian, Q. SIFT Meets CNN: A Decade Survey of Instance Retrieval. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 1224–1244. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chum, O.; Philbin, J.; Sivic, J.; Isard, M.; Zisserman, A. Total recall: Automatic query expansion with a generative feature model for object retrieval. In Proceedings of the 2007 IEEE 11th International Conference on Computer Vision, Rio de Janeiro, Brazil, 14–21 October 2007; pp. 1–8. [Google Scholar]
- Chum, O.; Mikulik, A.; Perdoch, M.; Matas, J. Total recall II: Query expansion revisited. In Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 889–896. [Google Scholar]
- Filip, R.; Giorgos, T.; Ondrej, C. Fine-tuning CNN Image Retrieval with No Human Annotation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 41, 1655–1668. [Google Scholar]
- Jégou, H.; Chum, O. Negative evidences and co-occurrences in image retrieval: The benefit of PCA and whitening. In Proceedings of the 2012 European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 774–787. [Google Scholar]
- Oliva, A.; Torralba, A. Modeling the Shape of the Scene: A Holistic Representation of the Spatial Envelope. Int. J. Comput. Vision 2001, 42, 145–175. [Google Scholar] [CrossRef]
- Oliva, A.; Torralba, A. Scene-centered description from spatial envelope properties. In Proceedings of the 2002 International Workshop on Biologically Motivated Computer Vision, Tübingen, Germany, 22–24 November 2002; pp. 263–272. [Google Scholar]
- Jain, A.K.; Vailaya, A. Image retrieval using color and shape. Pattern Recognit. 1996, 29, 1233–1244. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vision 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Tolias, G.; Furon, T.; Jégou, H. Orientation covariant aggregation of local descriptors with embeddings. In Proceedings of the 2014 European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 382–397. [Google Scholar]
- Bay, H.; Tuytelaars, T.; Van Gool, L. Surf: Speeded up robust features. In Proceedings of the 2006 European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 404–417. [Google Scholar]
- Sivic, J.; Zisserman, A. Video Google: A text retrieval approach to object matching in videos. In Proceedings of the 2003 Computer Vision, IEEE International Conference on, Nice, France, 13–16 October 2003; p. 1470. [Google Scholar]
- Jégou, H.; Perronnin, F.; Douze, M.; Sánchez, J.; Pérez, P.; Schmid, C. Aggregating local image descriptors into compact codes. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 34, 1704–1716. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perronnin, F.; Dance, C. Fisher kernels on visual vocabularies for image categorization. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Perronnin, F.; Sánchez, J.; Mensink, T. Improving the fisher kernel for large-scale image classification. In Proceedings of the 2010 European Conference on Computer Vision, Heraklion, Crete, Greece, 5–11 September 2010; pp. 143–156. [Google Scholar]
- Jégou, H.; Zisserman, A. Triangulation embedding and democratic aggregation for image search. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 23–28 June 2014; pp. 3310–3317. [Google Scholar]
- Cimpoi, M.; Maji, S.; Vedaldi, A. Deep filter banks for texture recognition and segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3828–3836. [Google Scholar]
- Ghodrati, A.; Diba, A.; Pedersoli, M.; Tuytelaars, T.; Van Gool, L. DeepProposals: Hunting Objects and Actions by Cascading Deep Convolutional Layers. Int. J. Comput. Vision 2017, 124, 115–131. [Google Scholar] [CrossRef] [Green Version]
- Babenko, A.; Slesarev, A.; Chigorin, A.; Lempitsky, V. Neural codes for image retrieval. Proceedings of 2014 European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 584–599. [Google Scholar]
- Babenko, A.; Lempitsky, V. Aggregating local deep features for image retrieval. In Proceedings of the 2015 IEEE International Conference on Computer Vision, NW Washington, DC, USA, 7–13 December 2015; pp. 1269–1277. [Google Scholar]
- Razavian, A.S.; Sullivan, J.; Carlsson, S.; Maki, A. Visual instance retrieval with deep convolutional networks. Trans. Media Technol. Appl. 2016, 4, 251–258. [Google Scholar] [CrossRef] [Green Version]
- Tolias, G.; Sicre, R.; Jégou, H. Particular object retrieval with integral max-pooling of CNN activations. arXiv 2015, arXiv:1511.05879. [Google Scholar]
- Kalantidis, Y.; Mellina, C.; Osindero, S. Cross-dimensional weighting for aggregated deep convolutional features. In Proceedings of the 2016 European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 685–701. [Google Scholar]
- Hao, J.; Wang, W.; Dong, J.; Tan, T. MFC: A multi-scale fully convolutional approach for visual instance retrieval. In Proceedings of the 2017 IEEE International Conference on Multimedia & Expo Workshops (ICMEW), San Diego, CA, USA, 23–27 July 2018; pp. 513–518. [Google Scholar]
- Sharif Razavian, A.; Azizpour, H.; Sullivan, J.; Carlsson, S. CNN features off-the-shelf: An astounding baseline for recognition. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition Workshops, Columbus, OH, USA, 24–27 June 2014; pp. 806–813. [Google Scholar]
- Xu, J.; Wang, C.; Qi, C.; Shi, C.; Xiao, B. Unsupervised Semantic-Based Aggregation of Deep Convolutional Features. IEEE Trans. Image Process. 2019, 28, 601–611. [Google Scholar] [CrossRef] [PubMed]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Gordo, A.; Larlus, D. Beyond instance-level image retrieval: Leveraging captions to learn a global visual representation for semantic retrieval. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 21–26 July 2017; pp. 6589–6598. [Google Scholar]
- Mikolajczyk, K.; Matas, J. Improving descriptors for fast tree matching by optimal linear projection. In Proceedings of the 2007 IEEE 11th International Conference on Computer Vision, Rio de Janeiro, Brazil, 14–21 October 2007; pp. 1–8. [Google Scholar]
- Philbin, J.; Chum, O.; Isard, M.; Sivic, J.; Zisserman, A. Object retrieval with large vocabularies and fast spatial matching. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Zhai, Y.; Shah, M. Visual attention detection in video sequences using spatiotemporal cues. In Proceedings of the 14th ACM International Conference on Multimedia, Santa Barbara, CA, USA, 23–27 October 2006; pp. 815–824. [Google Scholar]
- Philbin, J.; Chum, O.; Isard, M.; Sivic, J.; Zisserman, A. Lost in quantization: Improving particular object retrieval in large scale image databases. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Jegou, H.; Douze, M.; Schmid, C. Hamming embedding and weak geometric consistency for large scale image search. In Proceedings of the 2008 European Conference on Computer Vision, Marseille, France, 12–18 October 2008; pp. 304–317. [Google Scholar]
- Radenović, F.; Iscen, A.; Tolias, G.; Avrithis, Y.; Chum, O. Revisiting oxford and paris: Large-scale image retrieval benchmarking. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5706–5715. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Liu, P.; Gou, G.; Guo, H.; Zhang, D.; Zhou, Q. Fusing Feature Distribution Entropy with R-MAC Features in Image Retrieval. Entropy 2019, 21, 1037. [Google Scholar] [CrossRef] [Green Version]
- Mohedano, E.; McGuinness, K.; O’Connor, N.E.; Salvador, A.; Marques, F.; Giró-i-Nieto, X. Bags of local convolutional features for scalable instance search. In Proceedings of the 2016 ACM on International Conference on Multimedia Retrieval, Vancouver, BC, Canada, 6–9 June 2016; pp. 327–331. [Google Scholar]
- Maaten, L.V.D. Accelerating t-SNE using tree-based algorithms. J. Mach. Learn. Res. 2014, 15, 3221–3245. [Google Scholar]






| Method | Oxford5k | Paris6k | Holidays |
|---|---|---|---|
| R-MAC [25] | 66.85 | 82.24 | 88.88 |
| GR-MAC | 70.35 | 83.62 | 89.58 |
| Method | Easy | Medium | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ROxford | RParis | ROxford | RParis | |||||||||
| mAP | P@1 | P@5 | mAP | P@1 | P@5 | mAP | P@1 | P@5 | mAP | P@1 | P@5 | |
| R-MAC GR-MAC | 58.74 63.33 | 83.82 85.29 | 73.97 78.24 | 78.50 80.15 | 95.71 95.71 | 93.43 93.71 | 39.40 42.26 | 84.29 84.29 | 67.14 70.19 | 61.56 63.86 | 95.71 95. 71 | 96.26 96.29 |
| Method | Oxford5k | Paris6k | Holidays |
|---|---|---|---|
| Crow [26] | 68.09 | 77.88 | 89.50 |
| SJW | 69.62 | 79.41 | 89.74 |
| Method | Easy | Medium | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ROxford | RParis | ROxford | RParis | |||||||||
| mAP | P@1 | P@5 | mAP | P@1 | P@5 | mAP | P@1 | P@5 | mAP | P@1 | P@5 | |
| Crow SJW | 61.23 63.09 | 85.29 88.24 | 75.00 75.00 | 77.46 78.68 | 97.14 97.14 | 92.57 93.71 | 46.10 47.36 | 87.14 87.14 | 72.38 72.57 | 59.99 60.90 | 97.14 97.14 | 95.14 96.00 |
| Method | Dim | Oxford5k | Paris6k | Holidays |
|---|---|---|---|---|
| Original retrieval results | ||||
| GR-MAC | 512 | 70.35 | 83.62 | 89.58 |
| SJW | 512 | 69.62 | 79.41 | 89.74 |
| GSW | 512 | 72.90 | 83.60 | 90.56 |
| After query expansion (QE) | ||||
| GR-MAC+QE | 512 | 79.20 | 89.86 | 90.36 |
| SJW+QE | 512 | 74.79 | 86.17 | 89.53 |
| GSW+QE | 512 | 79.87 | 89.55 | 91.51 |
| Method | Dim | Oxford5k | Paris6k | Holidays |
|---|---|---|---|---|
| Original retrieval results | ||||
| SPoC [23] | 256 | 53.10 | - | 80.20 |
| MFC [27] | 256 | 68.40 | 83.40 | - |
| MAC [28] | 512 | 55.01 | 74.73 | 75.23 |
| SPoC [23] | 512 | 56.40 | 72.30 | 79.00 |
| MFC [27] | 512 | 70.60 | 83.30 | - |
| R-MAC [25] | 512 | 66.71 | 83.02 | 84.04 |
| GeM [7] | 512 | 67.90 | 74.80 | 83.20 |
| Crow [26] | 512 | 70.80 | 79.70 | 85.10 |
| FDE [39] | 512 | 69.64 | 83.56 | 85.90 |
| SBA [29] | 512 | 72.00 | 82.30 | - |
| GSW (ours) | 512 | 72.90 | 83.60 | 90.56 |
| After query expansion (QE) | ||||
| Crow+QE [26] | 512 | 74.90 | 84.80 | 88.46 |
| MAC+QE [24] | 512 | 74.21 | 82.84 | - |
| R-MAC+QE [25] | 512 | 77.33 | 86.45 | 90.94 |
| FDE+QE [39] | 512 | 78.48 | 86.53 | - |
| BoW-CNN+QE [40] | 512 | 78.80 | 84.80 | - |
| SBA+QE [29] | 512 | 74.80 | 86.00 | - |
| GSW(ours)+QE | 512 | 79.87 | 89.55 | 91.51 |
| Method | Easy | Medium | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ROxford | RParis | ROxford | RParis | |||||||||
| mAP | P@1 | P@5 | mAP | P@1 | P@5 | mAP | P@1 | P@5 | mAP | P@1 | P@5 | |
| MAC [24] | 44.34 | 72.06 | 60.59 | 63.39 | 92.86 | 90.29 | 32.20 | 71.43 | 56.29 | 49.09 | 94.29 | 93.14 |
| SPoC [23] | 44.31 | 67.65 | 56.54 | 68.06 | 92.86 | 91.71 | 30.33 | 65.71 | 49.71 | 50.92 | 92.86 | 94.57 |
| R-MAC [25] | 58.74 | 83.82 | 73.97 | 78.50 | 95.71 | 93.43 | 39.40 | 84.29 | 67.14 | 61.56 | 95.71 | 96.26 |
| GeM [7] | 58.83 | 85.29 | 75.74 | 76.85 | 94.29 | 92.29 | 42.68 | 87.14 | 72.29 | 60.80 | 97.14 | 95.14 |
| Crow [26] | 61.23 | 85.29 | 75.00 | 77.46 | 97.14 | 92.57 | 46.10 | 87.14 | 72.38 | 59.99 | 97.14 | 96.00 |
| GR-MAC (ours) | 63.33 | 85.29 | 78.24 | 80.15 | 95.71 | 93.71 | 42.26 | 84.29 | 70.19 | 63.86 | 95.71 | 96.29 |
| SJW (ours) | 63.09 | 88.24 | 75.00 | 78.68 | 97.14 | 93.71 | 47.36 | 87.14 | 72.57 | 60.90 | 97.14 | 96.00 |
| GSW (ours) | 66.70 | 88.24 | 80.00 | 81.43 | 95.71 | 94.10 | 48.13 | 88.57 | 75.05 | 64.68 | 95.71 | 96.57 |
| After query expansion (QE) | ||||||||||||
| MAC+QE | 53.03 | 73.53 | 64.41 | 78.98 | 92.86 | 90.57 | 38.62 | 72.86 | 60.29 | 64.50 | 92.86 | 93.14 |
| R-MAC+QE | 75.04 | 88.24 | 84.04 | 88.20 | 95.71 | 95.14 | 53.59 | 85.71 | 75.90 | 73.13 | 97.14 | 96.29 |
| GeM+QE | 68.12 | 89.71 | 81.47 | 85.87 | 94.29 | 93.14 | 51.29 | 88.57 | 76.00 | 71.13 | 95.71 | 95.71 |
| Crow+QE | 65.98 | 85.29 | 78.53 | 83.61 | 95.71 | 94.86 | 48.88 | 84.29 | 74.14 | 66.25 | 97.14 | 97.14 |
| GSW+QE | 76.17 | 91.18 | 85.29 | 88.34 | 95.71 | 96.00 | 55.22 | 88.57 | 79.71 | 72.48 | 97.14 | 97.43 |
| L | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| R-MAC [25] | 56.34 | 63.09 | 66.85 | 67.79 |
| GR-MAC | 65.13 | 70.03 | 70.35 | 70.07 |
| 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | 100% | |
|---|---|---|---|---|---|---|---|---|---|---|
| mAP | 69.23 | 69.58 | 69.62 | 69.57 | 69.44 | 69.33 | 69.29 | 69.23 | 69.23 | 69.21 |
| 1 | 10 | 100 | 500 | |
|---|---|---|---|---|
| mAP | 69.41 | 69.51 | 69.62 | 68.60 |
| α | β | mAP |
|---|---|---|
| 0.1 | 0.9 | 70.75 |
| 0.2 | 0.8 | 71.62 |
| 0.3 | 0.7 | 72.37 |
| 0.4 | 0.6 | 72.60 |
| 0.5 | 0.5 | 72.85 |
| 0.6 | 0.4 | 72.90 |
| 0.7 | 0.3 | 72.62 |
| 0.8 | 0.2 | 70.61 |
| 0.9 | 0.1 | 68.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Wu, J.; Zhang, D.; Liu, P. Toward Improving Image Retrieval via Global Saliency Weighted Feature. ISPRS Int. J. Geo-Inf. 2021, 10, 249. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi10040249
Zhao H, Wu J, Zhang D, Liu P. Toward Improving Image Retrieval via Global Saliency Weighted Feature. ISPRS International Journal of Geo-Information. 2021; 10(4):249. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi10040249
Chicago/Turabian StyleZhao, Hongwei, Jiaxin Wu, Danyang Zhang, and Pingping Liu. 2021. "Toward Improving Image Retrieval via Global Saliency Weighted Feature" ISPRS International Journal of Geo-Information 10, no. 4: 249. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi10040249






