1. Introduction
Modern navigation satellite systems can transmit three or more frequency signals. GPS and QZSS introduced the L5 signal, in addition to the current L1 and L2 signals. Chinese Beidou satellites can transmit L2, L7 and L6 signals, and Galileo was designed to provide signals centred at L1, E6, E5B and E5A. The third frequency is close to the second frequency, which creates favourable conditions for directly fixing extra wide-lane (EWL) ambiguity and further achieving wide-lane (WL) and narrow-lane (NL) ambiguity resolutions (AR). Thus, using triple-frequency signals to improve the efficiency and reliability of AR in long baselines has become an active research topic.
Triple-frequency combinations can be divided into EWL, WL and NL combinations according to their wavelength, varying from longest to shortest. The EWL combination has the longest wavelength, and its magnitude is many times larger than that of the combination noise and the ionospheric residual. Employing the least squares (LS) algorithm, the EWL ambiguity can be determined by using the single epoch observable [
1]. Combining the resolved EWL ambiguity with the original phase observations and pseudorange observations to resolve WL ambiguity, the success rate of such WL resolutions can reach 99% in epoch-wise data processing [
2,
3]. Compared to the EWL and WL resolutions, the narrow-lane IAR is more easily affected by the ionospheric residual and the combination noise because its wavelength is small [
2]. As such, extensive research has been conducted in this area, and some modified methods have been developed.
One typical resolution is to select geometry-free and ionosphere-free (GIF) models characterized by smaller ionospheric effects and a lack of geometry coupling. A new combination selection strategy based on ionospheric terms with smaller total noise levels was proposed for the GPS, Galileo and BDS systems [
4]. Similarly, combination sets of Galileo’s three frequencies were also proposed with smaller ratios between the combination ionospheric delay and wavelength, as well as their corresponding combination noise varying from 0.1 to 0.2 cycles [
5,
6]. However, for the many proposed “virtual” ionosphere-free (IF) combinations, most proposals reduce the ionospheric effect but do not actually remove it. Thus, these NL ambiguity resolutions are still affected by the ionospheric effect when the ionosphere is active or when these algorithms are applied to long baselines. In some of the special combination methods, the estimated coefficients fully satisfy the GIF conditions. However, these combinations lead to a stable NL ambiguity root mean square (RMS) value of approximately 3.5 cycles [
2]. Nearly 200 observations of float NL estimates must be smoothed for the NL resolution to achieve a small estimation error of 0.25 cycles, and the number of necessary smoothed NL estimates will be decreased if the noise level is decreased.
To overcome the aforementioned deficiencies in GIF models, many researchers have extended the concepts and algorithms of TCAR to allow for their use with the geometry-based model [
4,
7,
8,
9,
10,
11,
12]. These studies involve the use of large numbers of unknown parameters in the estimation process, and the convergence of these unknowns is time consuming. To address the issue of ionospheric delays, some ionosphere-free techniques have been used; however, these approaches sacrifice the integer nature of the ambiguity and make it difficult to find integer ambiguity candidates [
13]. Recent experiments have verified that DD ionospheric delays can be treated as unknown parameters accompanied with coordinates and ambiguities. In turn, the advantage becomes more significant, especially when this type of resolution is applied to long baselines [
14]. To further shorten the time required for successful IAR, some scholars propose using external ionospheric constraints to strength ionospheric estimates. One way to accurately estimate the DD ionospheric delay is to interpolate the ionospheric delay from the permanent GNSS network. The magnitude of precision of the ionospheric estimation can be defined to the nearest centimetre. Such a wide GNSS network is not available in most places, especially in rural and marine areas [
15]. The global ionospheric TEC map (GIM) can also provide an estimation of ionospheric delay, and its precision is 2–8 TECu, which hardly satisfies the requirement of being treated as an ionospheric constraint [
16]. In addition, the DD ionospheric delay can also be estimated by combining the raw observables and the resolved ambiguities. The precision of ionospheric estimates can achieve magnitudes defined to the nearest centimetre only after estimates from tens of epochs are smoothed [
17]. Compared with the operation of extracting ionospheric estimates from external information, this method is more convenient to use; however, the smoothing duration is too long to satisfy real-time positioning.
In real-time positioning applications, the ionospheric delay that is treated as an ionospheric constraint should be estimated with the filtering process; for the ionosphere-weighted TCAR, a crucial question is how to shorten the time to obtain more accurate ionospheric estimates. In view of this requirement, we modified the previously mentioned method. The main improvements in our algorithm are as follows: (1) A new ionospheric model is proposed to estimate DD ionospheric delays to obtain more accurate ionospheric estimates over a shorter time period; (2) We use the epoch-differenced ionospheric information to smooth ionospheric model estimates by employing the Hatch algorithm. To optimize the smoothed ionosphere estimations, the optimal smoothing length is defined, and a resolution for diagnosing wrongly determined WL ambiguities is also proposed; (3) The resolved ionospheric information from the second step is treated as a pseudorange to enhance the strength of the current observation model; thus, the geometry-based model is extended to an ionosphere-weighted model. To assess the performance of the new proposed TCAR algorithm, experiments are carried out, and the conclusions are given. Compared with other navigation systems, the GPS system has the highest observation quality and the most precise orbit/clock estimations, in addition to some Block IIF satellites in orbit that can transmit triple-frequency signals. Based on these results, we use the GPS system as an example to illustrate our method along with other systems.
The study is organized as follows: In
Section 2, we revisit briefly the fundamental mathematical model and several assumptions and conventions concerning the TCAR method, especially regarding combinations. In
Section 3, we review and analyse the current TCAR method. In
Section 4, we explicitly describe the new ionospheric model and how to extend the geometry-based model to the ionosphere-weighted model by incorporating more realistic ionospheric delays as constraints. In
Section 5, we conduct relevant experiments to evaluate the performance of our new TCAR method. Finally, in
Section 6, we offer some concluding remarks about the method.
2. On the Fundamental Combinations Concerning TCAR
In this section, we briefly revisit some fundamental information regarding combinations. The new ambiguity resolution focuses on DD combinations; thus for simplicity, the DD operator B is omitted in the following sections unless specified otherwise.
Without loss of generality, suppose f
1, f
2, f
3 are the frequencies of the three carriers, and they satisfy f
1 > f
2 > f
3; N
(1,0,0), N
(0,1,0) and N
(0,0,1) are DD ambiguities on the three frequencies; the subscribe represents different frequency for the corresponding DD phase observables. The DD non-dispersive delay mainly consists of geometric distances and tropospheric delay. I
1 denotes the DD ionospheric delay with respect to the first frequency. The parameters at the end of the equations represent the pseudorange and phase measurement noise, respectively. In the following sections, the standard deviations of pseudorange and phased observables are assumed to be 0.2 m and 0.003 m, respectively [
2]. Assuming that the combination coefficients i, j and k are arbitrary integers, the linear combined DD pseudorange observation can be modelled as follows:
where the combined ambiguity, combination wavelength, ionosphere and noise amplitude factors, for the EWL, WL and NL combinations are summarized in
Table 1.
4. New Ionosphere-Weighted Model
Compared with the current TCAR methods, the new TCAR method has been modified in two aspects: first, the EWL and WL ambiguities, as well as the pseudorange and phase observables, are combined to formulate a new ionospheric model to estimate the DD ionospheric delays (refer to
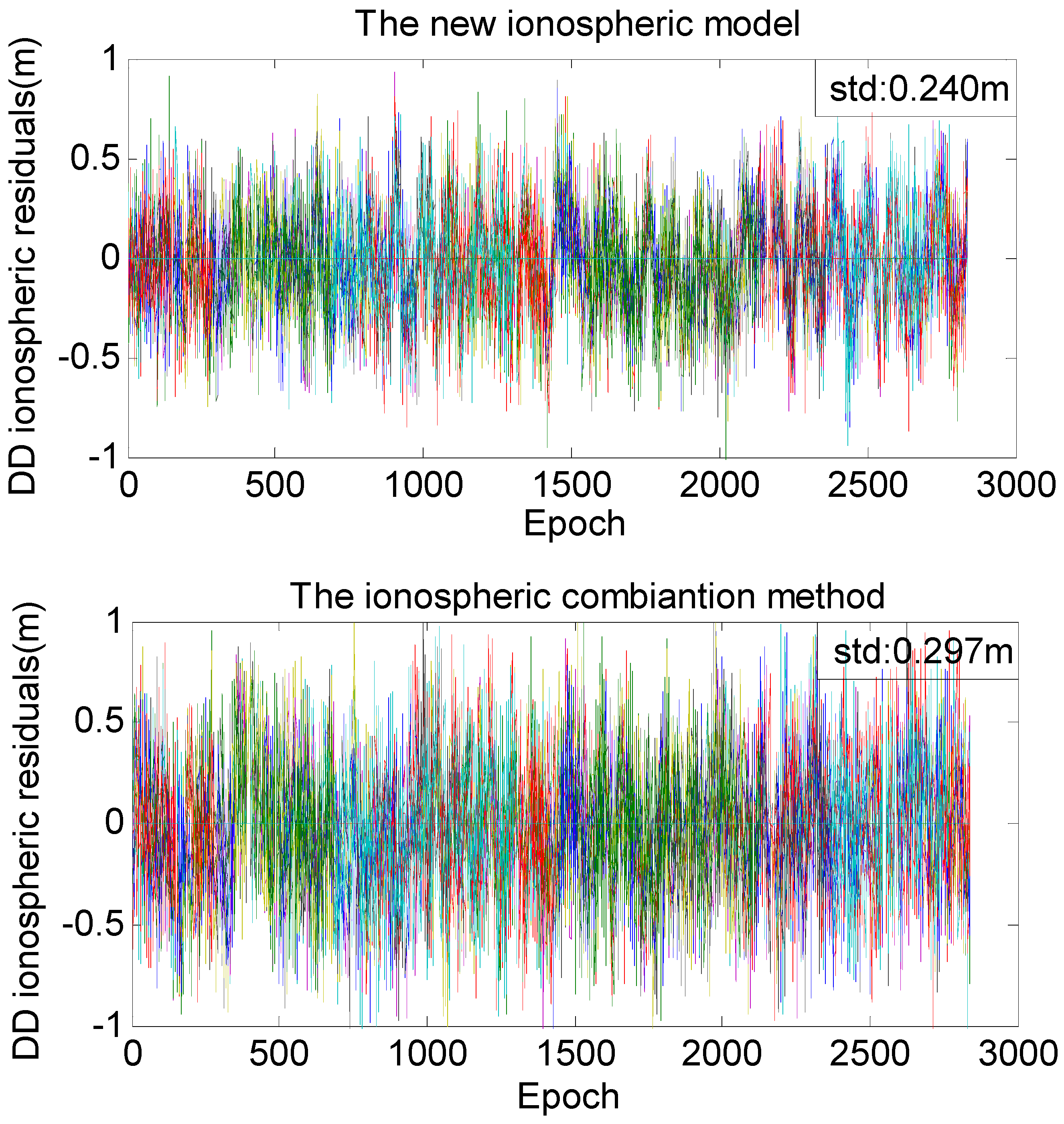
Section 4.1). Compared with the ionospheric combination method, which performs ionospheric estimates at a precision level of 0.3 m [
22], the new ionospheric model has more degrees of freedom. Additionally, model estimates have been instantaneously smoothed by the epoch-differenced ionospheric information with high precision (refer to
Section 4.2). Thus, the precision of real-time ionospheric estimates is expected to be better than 0.1 m. Second, ionospheric estimations with high precision are added into the geometry-based model, extending the geometry-related model into an ionosphere-weighted model (refer to
Section 4.3). Ionospheric constraints can help to enhance the strength of the observation model and thereby reduce convergence time of unknowns, especially the ionospheric unknown. These modifications help to shorten the time to TFFS compared to the current observation model without any constraints.
It is known that EWL ambiguity can be reliably determined in a single epoch. Even for long baselines with hundreds of kilometres, the success rate of the current EWL AR can reach 99%. The EWL resolution in the new method also refers to Equations (2) and (3). We then used Equation (4) to resolve the WL ambiguities.
4.1. New Model of Estimating DD Ionospheric Delay
Before the DD ionospheric model is formulated, the following independent variables exist: three pseudorange observations, three phase observations, two EWL ambiguities and two WL ambiguities. To increase the degrees of freedom in the model and avoid singularities, only eight variables can be selected, and the corresponding general model can be used to calculate the ionospheric delay, expressed as follows:
To optimize the model, Equation (7) should obey the following constraints:
Geometry-free condition:
Retain the remaining DD ionosphere delay:
Eliminate N(1,0,0):
Eliminate N(0,1,0):
Eliminate N(0,0,1):
Minimize the noise condition:
The pseudorange and phase observables are correlated with each other by shared errors. However, the correlations are eliminated and do not contribute to the minimum noise condition due to geometry-free constraints; a detailed deduction process is outlined by Vollath and Sauer [
23]. Based on this, the ratio of pseudorange and phase noise is important in minimizing the noise condition, and it directly affects estimation of the unknowns.
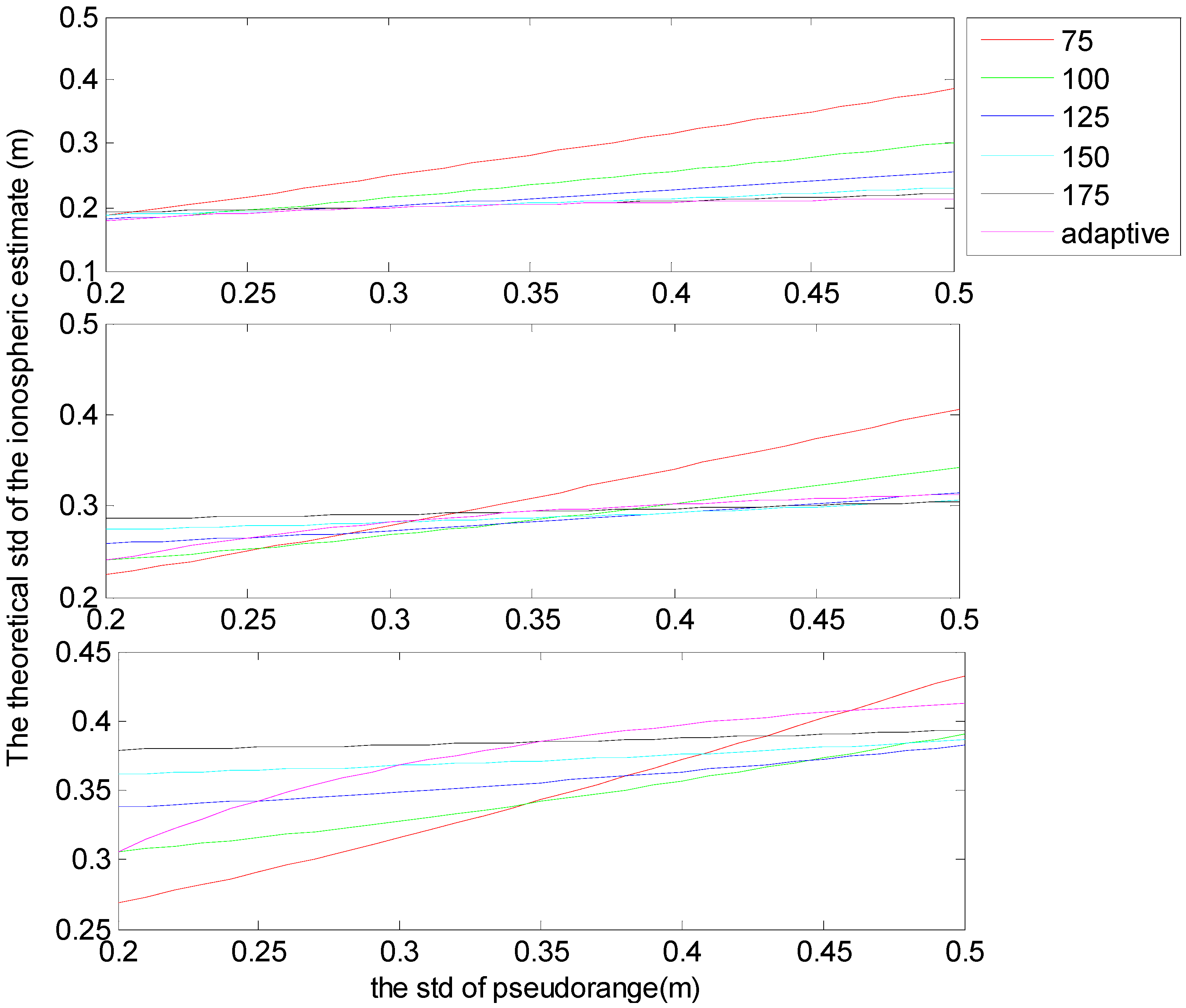
Figure 1 illustrates correlations between theoretical standard deviations of optimal DD ionospheric estimations and phase noise, as well as correlations between standard deviations of ionospheric estimations and pseudorange noise. Although the ratio of pseudorange and phase noise may occasionally vary, estimates using 125 as the ratio are the closest to that from the adaptive estimates, and the deviations are smaller than when the ratio is 75, 100, 125 and 150. Based on the above deductions and to enable straightforward computation, we set the ratio to 125; estimations of the unknowns from Equation (7) are summarized in
Table 2.
As we all know, the standard deviation (std) of phase observables mainly range from 0.2 mm to 0.3 mm. When the phase noise is around 0.3 mm, the corresponding std of pseudorange observable often limits from 0.3 m to 0.4 m. For the above-mentioned conditions,
Figure 2 presents the corresponding differences between ionospheric estimates and adaptive estimates. It can be seen from
Figure 2, the estimates from the ratio of 125 is almost the closest to that from the adaptive estimates. Although there are two exceptions: in the top panel, when pseudorange noise ranges from 0.3 m to 0.35 m, the difference between ionospheric estimated from the ratio of 125 is larger than that from the ratio of 150; and, in the bottom panel, when pseudorange noise range from 0.3 m to 0.35 m, the difference between ionospheric estimated from the ratio of 125 is larger than that from the ratio of 100. However, for these two exceptional conditions, the maximum difference is only 0.7 mm, which happens at the top panel when the pseudorange is 0.35 m. Thus, the deviation is not obvious, and the ionospheric estimates from ratio of 125 is still can be believed has the optimum performance.
4.2. Smoothed Ionospheric Delay Estimates
We can obtain epoch-differenced ionospheric information with high precision by using the following equations:
where the symbol
k represents the current epoch. After ionosphere has been determined, we use Equation (10) to obtain more precise DD ionospheric estimates.
In Equation (10), weighting factor equals to inversion of the smoothing length.
Considering higher-order ionosphere effects and combination noise, the standard deviation of ionosphere will generally range from 0.01 to 0.02 m [
24,
25]. In
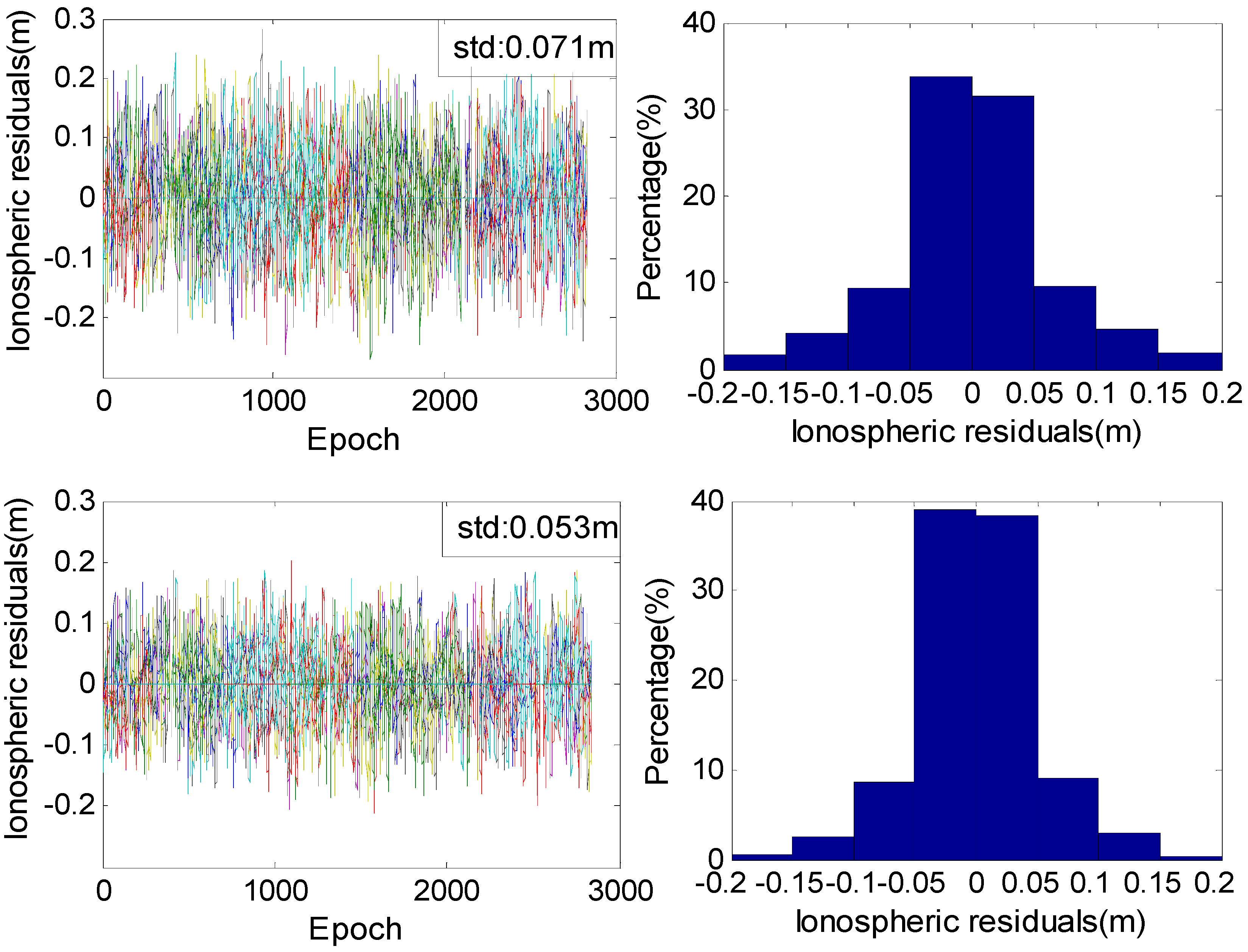
Figure 3, given the same smoothing length, the precision of ionospheric delay estimates from the new method is always better than that from the current ionospheric combination method. When the standard deviation of ionospheric is 0.02 m, the precision of ionospheric from the new method initially improves as the smoothing length increases, reaching an optimal smoothing length at 16 epochs, and then the standard deviation increases as the length increases. If ionospheric has a standard deviation of 0.01 m, the new method obtains ionospheric with nearly the same standard deviation when the smoothing length is equal to or more than 16 epochs. With the new method, when Equation (10) is used to estimate ionospheric, the smoothing window should updates instantaneously, and the maximum smoothing length could be set to 16 epochs.
In Equation (10), if the two WL ambiguities are not correctly determined, the ionospheric estimates from Equation (7) will be seriously deteriorated, which thus affects the current estimate and the 15 subsequent epochs’ ionospheric estimates from Equation (10). Although this phenomenon is rare, we use the following test to avoid it:
where adaptive value is an empirical value set to 1.0.
Table 2 suggests that wrongly determined WL ambiguities will cause a systematic bias in ionosphere of at least 2. In addition,
Figure 3 shows that the standard deviation of adaptive value is slightly smaller than 0.4 and that the double values of the standard deviation of adaptive value is only 0.8. Based on the two deductions, setting adaptive value to 1.0 can distinguish whether the WL ambiguities are wrong fixed or not. If the test fails, one could use the results derived from Equation (12) as the optimal ionospheric estimate for the current epoch.
4.3. NL Ambiguity Resolution
To transform DD ionospheric estimates from Step 2 into ionospheric constraints, derived ionospheric estimates are employed as pseudoranges and assimilated into the current observation model. After this step, Equation (5) can be extended as follows:
where the parameters at the left of the equation represents the difference between the ionospheric delay estimate and the actual delay In the filtering process, the covariance between ionospheric delay estimate and other observables (or combinations) can be computed by the error propagation law. In addition, the variance of its own is conservatively set as follows:
where three adaptive value are set to 5, 10 and 16, respectively. The values in Equation (14) are determined according to
Figure 3, and they will be further evaluated in later experiments to confirm proper value settings. We used the LAMBDA algorithm to search and fix ambiguities, and the epoch is identified as fixed when the ratio is larger than 3. Ratio is estimated by using Equation (15):
where Equation (15) is used for the squared norm of ambiguity residuals of the best, and second-best integer solution, respectively, as measured by the squared norm of the ambiguity residual vector. C is the discriminative value, a fixed value is used in many software package, e.g., 3, which is also the same in our experiments.
These ionospheric estimates may enhance the strength of the current model and thereby shorten the convergence time of the unknowns. This assumption will also be verified in subsequent tests using actual observational data.
6. Summary
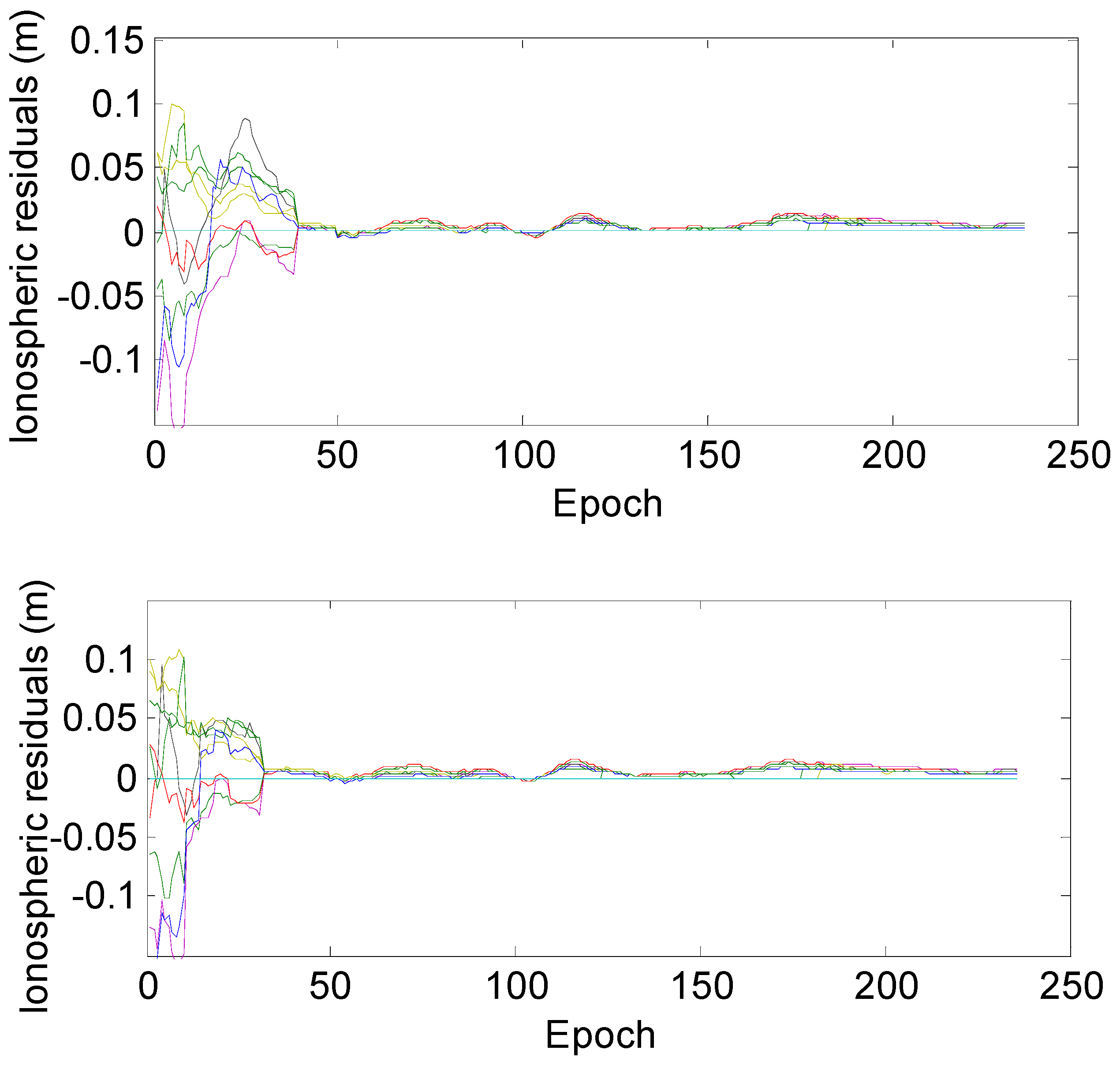
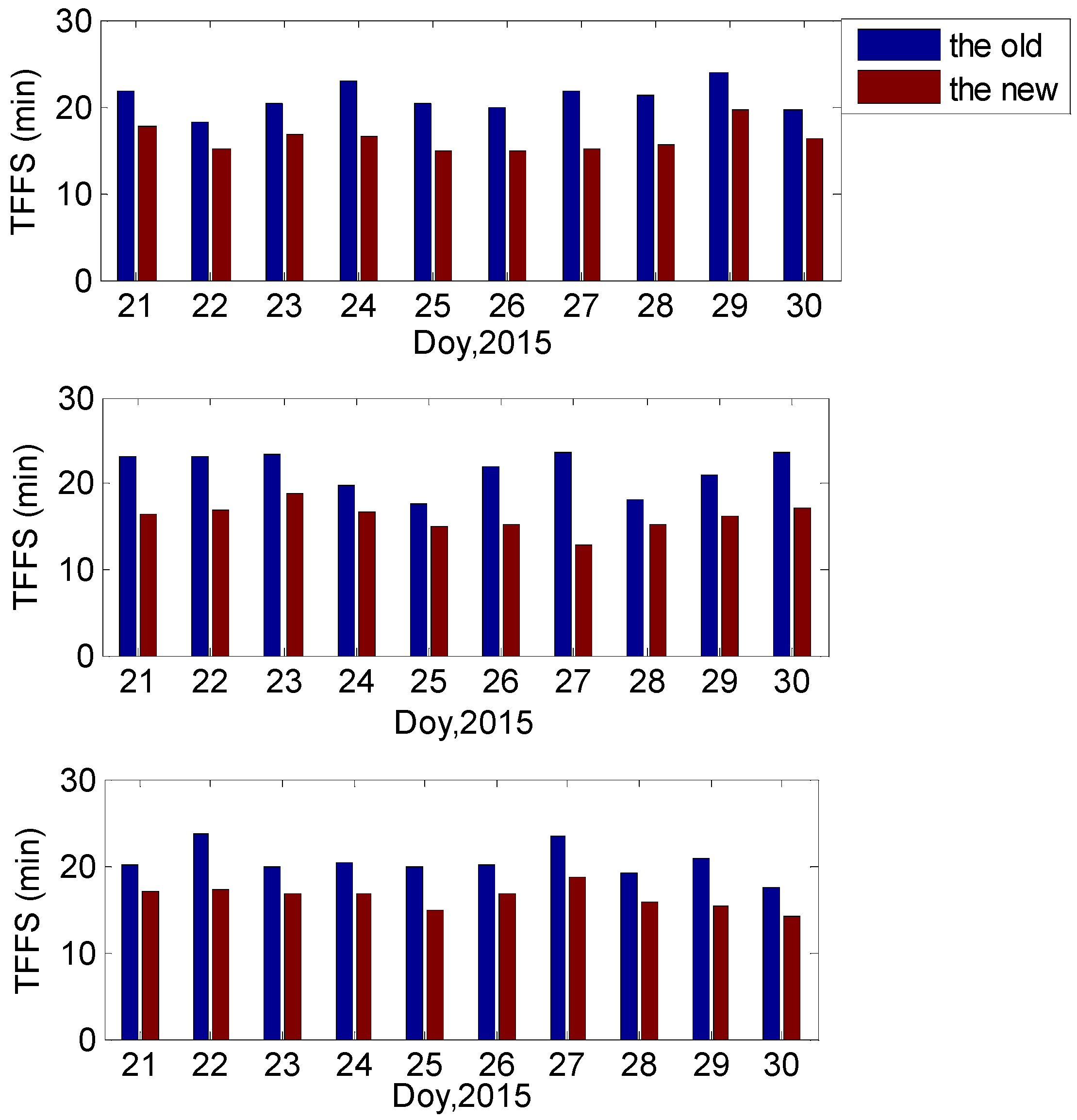
Being affected by DD ionospheric residuals, the current TCARs need to accumulate long periods of data for successful IAR. Current IAR algorithms generally take 20 to 25 min, which is a little long for fast positioning. To shorten the IAR time, we propose a new TCAR algorithm by adding realistic ionospheric information constraints. We modified the current TCAR methods in three aspects. First, a new ionospheric model is developed to estimate the DD ionospheric delay. Compared to previous combination methods, the original pseudorange and phase observations are introduced to increase the degrees of freedom and minimize noise constraints. In doing so, the ionospheric delay estimates are globally optimized. Both theoretical derivations and the experimental results indicate that the precision of the ionospheric delay estimated from our new model is 20% higher than that from the current ionospheric combination method. Second, the epoch-differenced ionospheric information is used to smooth the ionospheric delay by employing the Hatch algorithm. Using theoretical derivations and sensitivity tests, we found that the most suitable smoothing length is 16 epochs and that the smoothed ionospheric delay could reach a magnitude of precision defined to the nearest centimetre. For cases in which wrongly determined WL ambiguities deteriorate the precision of smoothed ionospheric delay estimations, we also proposed a set of error diagnosis and resolutions. Third, the smoothed ionospheric delays obtained from Step 2 are treated as pseudorange observable values and are added to the original model to strengthen the original observation equation, thus extending the current geometry-based model into an ionosphere-weighted model. The results show that this model can improve the convergence efficiency of the unknowns, especially the ionospheric unknown. The model creates favourable conditions for fast and successful IAR. After the above three modifications, the new formulated TCAR algorithm reduces the IAR convergence time by 20% compared to the current TCAR method. If we use the new ionospheric model to estimate ionospheric delay before the filtering process, the convergence time is expected to be shorter.
In summary, we investigated, theoretically and practically, the feasibility of employing a new ionospheric model as constraints to speed up the IAR. The direct benefit is that the new model reduces IAR time by 20% compared to the current TCAR method. Additionally, it provides precise information to further investigate long-baseline relative positioning, especially for the Beidou system, which features triple-frequency data on all satellites. The ionospheric delay used in the constraints is provided in real time by our method, acting as an optional way of assisting real-time relative positioning. We also provide a new strategy for estimating DD ionospheric delay with a precision to the nearest centimetre, which is expected to be helpful for directly studying the ionosphere.